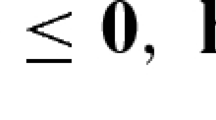Exact Solution of Two Location Problems via Branch-and-Bound

Abstract

In 1960, Land and Doig published a paper that most scholars recognize as the first description of a now well-known technique for solving difficult optimization problems by solving a sequence of easier, restricted subproblems (Land and Doig 1960). Little et al. (1963) named this technique “Branch-and-Bound” (B&B), and used it to solve the traveling salesman problem. Although the method is described and used in several papers in the 1960s (see for example, Lawler and Wood ), the description below, provided by Hillier and Lieberman (1980), succinctly captures the idea.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In 1960, Land and Doig published a paper that most scholars recognize as the first description of a now well-known technique for solving difficult optimization problems by solving a sequence of easier, restricted subproblems (Land and Doig 1960). Little et al. (1963) named this technique “Branch-and-Bound” (B&B), and used it to solve the traveling salesman problem. Although the method is described and used in several papers in the 1960s (see for example, Lawler and Wood 1966), the description below, provided by Hillier and Lieberman (1980), succinctly captures the idea.

The basic idea of the branch-and-bound technique is the following: suppose (to be specific) that the objective function is to be minimized. Assume that an upper bound on the optimal value of the objective function is available. (This is usually the value of the objective function for the best feasible solution identified thus far.) The first step is to partition the set of all feasible solutions into several subsets, and for each one, a lower bound is obtained for the value of the objective function of the solutions within that subset. Those subsets whose lower bounds exceed the current upper bound on the objective value are then excluded from further consideration. (A subset that is excluded for this or other legitimate reasons is said to be fathomed.) One of the remaining subsets, say, the one with the smallest lower bound, is then partitioned further into several subsets. Their lower bounds are obtained in turn and used as before to exclude some of these subsets from further consideration. From all the remaining subsets, another one is selected for further partitioning and so on. This process is repeated again and again until a feasible solution is found such that the corresponding value of the objective function is no greater than the lower bound for any subset. Such a feasible solution must be optimal since none of the subsets can contain a better solution.

The method of partitioning the set of feasible solutions into subsets (branching) is relatively straightforward for integer variables, particularly when these can take on only one of two values, zero or one. Thus, a partition is created when one of these variables is set to zero in one subset, and set to one in the other subset. An easy way to envision the partitioning process is through what is called the branch-and-bound tree. The top node of the tree represents the original problem. Two branches can be created from this node by selecting one of the variables, and setting it equal to zero in one branch and to one in the other branch. Each of the resulting nodes can be further partitioned via the selection of another variable and a repetition of the above process.

To create bounds at each node, early implementers of the branch-and-bound method solved “relaxed” problems by treating integer variables as continuous. By doing this, the resulting relaxed problem was often a linear program that could be solved by existing codes. The key to branch-and-bound efficiency is to reduce the number of subsets that must be visited and to be able to create “strong” bounds. Early adopters realized this and those same issues are faced today by current users of the method. We will have more to say on this issue later in the chapter.

In spite of the fact that branch-and-bound can be painfully slow as a solution method for discrete optimization problems, it is still often applied as the technique of choice for these problems. Discrete optimization problems generally have locally optimal solutions and so sensible search methods are necessary to explore the solution space for a globally optimal solution. Branch-and-bound is such a method since it provides a means of exploring various subregions of the feasible set of solutions in an organized manner.

In this chapter, we give an overview of the use of branch-and-bound to solve two prototypical location problems: the quadratic assignment problem QAP and the uncapacitated facility location problem UFLP. Our focus will be on the early applications of branch-and-bound to these problems via a critical review of two papers from the 1960s. In providing these reviews we attempt to replicate the authors’ thought process in the development of the reported solution method.

The remainder of this chapter is organized as follows. Section 13.2 discusses the work of Gavett and Plyter (1966) on the quadratic assignment problem, following which we discuss advancements in the application of branch-and-bound to the problem as well as special cases of the problem solvable in polynomial time. Section 13.3 is dedicated to the uncapacitated facility location problems where we first review the work of Efroymson and Ray (1966) on this problem. We then follow this review with a discussion of further work on the problem, and special cases solvable in polynomial time. Branching strategies for branch-and-bound methods are discussed in Sect. 13.4, and concluding remarks are offered in Sect. 13.5.

2 Gavett and Plyter (1966): The Quadratic Assignment Problem

The Quadratic Assignment Problem was formulated by Koopmans and Beckman (1957) over 50 years ago. The motivating and most popular application of the quadratic assignment problem is the facility layout problem of assigning n facilities to n locations where one and only one facility can be assigned to each location. Thus, there are n! possible assignments. The cost of an assignment depends on both the distance between each pair of locations, and the traffic intensity between facilities assigned to those locations. The objective is to find a minimal-cost solution among the n! possible assignments. One of the earliest exact methods for solving it was the branch–and-bound approach given in the paper of Gavett and Plyter (1966). Herein we review their approach.

2.1 Solving the Quadratic Assignment Problem via Branch-and-Bound

To formally pose the quadratic assignment problem as an optimization problem, let A = $[{a_{j\ell}}]$denote a matrix of distances between locations j and $\ell$ for j, $\ell$= 1, …, n. Also, let B = [b _ik] denote a matrix of rates at which material is transferred (traffic intensity) between facilities i and k where i, k = 1, …, n. Letting p = (p ₁, p ₂, …, p _n) denote a permutation of 1, 2, …, n and letting P _n denote the set of all permutations on {1, 2, …, n}, we can state the quadratic assignment problem as follows:

$$ Q\!A\!P \!:{\rm{Min}}\;\left\{ \sum {a_{j\ell } b_{p_jp_\ell }} \!:p \in P_n \quad{\rm{for}}\;j,\ell = 1,2,\dots,n\right\} $$

(13.1)

In addition to facility location, there are many applications of the quadratic assignment problem in the literature. These include backboard wiring, economic problems, scheduling, the design of typewriter keyboards and control panels, archeology, statistical analysis, and reaction chemistry. For a further discussion see, for example, Loiola et al. (2007).

Consider the following simple example from Gavett and Plyter of 4 facilities to be assigned to 4 locations:

$$ {\rm{\bf A = }}\left[ {\begin{array}{*{20}c} 0 & 6 & 7 & 2 \\ 6 & 0 & 5 & 6 \\ 7 & 5 & 0 & 1 \\ 2 & 6 & 1 & 0 \\ \end{array}} \right]\;{\rm{and}}\quad{\rm{\bf B = }}\left[ {\begin{array}{*{20}c} 0 & {10} & {20} & 5 \\ {18} & 0 & 9 & 4 \\ 5 & 6 & 0 & 8 \\ 8 & 0 & {15} & 0 \\ \end{array}} \right]. $$

Assigning the facilities 3, 1, 2 and 4 to the respective locations 1, 2, 3, 4 results in a total cost of 523. A better solution is assigning the facilities 2, 4, 3, 1 to the respective locations 1, 2, 3, 4 for a total cost of 403. With only 4 facilities/locations in this example, there are only 4! = 24 possible assignments and hence the problem is readily solvable (indeed, it is easy to verify that 403 is the minimal cost). However, with even modest values of n (e.g., n = 25) the number of permutations quickly becomes disturbingly large. The challenge is how to efficiently find an optimal solution to such problems. Following up on the work of Little et al. (1963) on applying branch-and-bound to the traveling salesman problem, Gavett and Plyter showed how branch-and-bound could be used to solve this problem.

The authors assume that the matrix A is symmetric (so that the distance from location j to $\ell$ equals the distance from $\ell$ to j ). In this case (13.1) can be simplified as follows:

$$ \begin{aligned} & {\rm{Min}}\Big\{ \sum {a_{j\ell } (b_{p_j p_\ell } } + b_{p_\ell p_j } ):p \in P_n \quad \\ & \;\;\qquad {\rm{for}}\!\;j = {\rm{1,2,}} \ldots , \!\; n\;{\rm{and}}\;l = j + 1, \ldots \!,\,n \Big\} \end{aligned} $$

(13.2)

For a given permutation, observe that the objective in (13.2) is simply the sum of the products of distances ${a_{j\ell}}$ between pairs of locations and the total traffic intensity $({b_{{p_j}{p_\ell }}} + {b_{{p_\ell }{p_j}}})$ between facilities assigned to them. Clearly, an ideal solution would match high intensities with small distances and low intensities with high distances. Doing this among permutations P _n can be difficult. However, as Gavett and Plyter noticed, the problem is easy to solve by expanding the permutations to match pairs of locations with pairs of intensities. Observe that the number of pairs of n locations is simply the combination of n locations taken 2 at a time, namely N = n(n − 1)/2.

Let {α ₁, α ₂, …, α _N} be the set of distances between pairs of locations. Thus α _r = ${a_{j\ell}}$ for some pair (j, $\ell$) of locations. Also let {b ₁, b ₂, …, b _N} be the set of traffic intensities between pairs of facilities so that b _t = b _ik + b _ki for some pair (i, k) of facilities. Finally, let P _N be the set of permutations on {1, 2, …, N}. With this notation, Gavett and Plyter’s relaxed problem is

$$ {\rm{Min}}\left\{ {\sum\limits_{r = 1}^N {{\alpha _r}} {\beta _{p(r)}}\!:p \in {P_N}} \right\} $$

(13.3)

The matching in (13.3) of location pairs with facility pairs is sometimes referred to as “pair-assignment;” see, e.g., Pierce and Crowston (1971).

As suggested by Conway and Maxwell (1961) and independently established by Gilmore (1962), Gavett and Plyter prove that given two vectors of the same size, if the objective is to sort entries of the vectors so that the dot product is minimized, the solution is found by sorting one vector in nonincreasing order and the other in nondecreasing order. Thus, a permutation minimizes (13.3) when it corresponds to matching sorted elements of {α ₁, α ₂, …, α _N} with reversely sorted elements of {b ₁, b ₂, …, b _N}. In the example this corresponds to matching location pairs (1,3), (1,2), (2,4), (2,3), (1,4), and (3,5) respectively with traffic intensities of facility pairs (2,4), (1,4), (2,3), (3,4), (1,3), and (1,2) for an optimal value of 389 in (13.3). Note that this is not a feasible solution to (13.2) since matching the location pairs (1,3) and (1,2) respectively with the facility pairs (2,4) and (1,4) means that location 1 must correspond to facility 4. However, the location pair (1,4) matching with the facility pair (1,3) is inconsistent with location 1 corresponding to facility 4. This is not surprising since P _N is generally much larger than P _n. In the example, the number of permutations in P _n is 24 while the number in P_N is 720. While each permutation in P _n corresponds to one in P _N, the converse is not true. Thus, as we have seen, an optimal solution to (13.3) may not be admissible in that it may not correspond to a feasible solution in (13.2).

Given an efficient way to solve the relaxed problem (13.3), Gavett and Plyter turn their attention to using the branch-and-bound approach from Little et al. (1963) to solve (13.2). To relate the problem to this approach, they first define an [N × N]-dimensional cost matrix C of elements α _rb _t whose rows correspond to location pairs {α ₁, α ₂, …, α _N} sorted by decreasing distances and whose columns correspond to facility pairs {b ₁, b ₂, …, b _N} sorted by increasing intensities. Thus, in the example, the [6 × 6]-dimensional matrix C is shown in Table 13.1.

Table 13.1 The cost matrix C

By construction, observe that the elements of C are nondecreasing across each row and are nonincreasing down each column. Also, observe that the optimal solution to (13.3) above corresponds to the diagonal of C with the sum of the diagonal elements being the optimal value of (13.3).

A primary difference between the matrix C in the quadratic assignment problem vs. the matrix considered by Little et al. is its interpretation. In Little et al., the element c _ij denotes the cost from i to j, whereas in Gavett and Plyter the element is the cost of assigning a location pair with a traffic intensity pair. In both cases, the relaxed problem is an assignment problem where each row will be assigned to exactly one column and where each column will be assigned to exactly one row. Little et al. point out that one could solve the assignment problem for the original cost matrix C and reduce the matrix by the cost of the optimal assignment. However, rather than doing this, they present a simple reduction technique to give a nonoptimal bound: reduce C by subtracting the smallest element in each row from the elements in the row, and then subtract the smallest element in each column from the elements in the column in the resulting matrix. All elements of the reduced matrix will be nonnegative. Thus, the sum of the reducing constants is a lower bound, since the cost of any permutation in C will differ from the cost under the reduced C by the sum and since the reduced matrix is nonnegative. Applying this technique to the quadratic assignment problem, the reducing constant (minimal element) of each row is simply its first element (which respectively are 28, 24, 24, 20, 8, 4). After subtracting these from their respective rows, we obtain the matrix

$$ \left[ {\begin{array}{*{20}c} 0 & {63} & {77} & {133} & {147} & {168} \\ 0 & {54} & {66} & {114} & {126} & {144} \\ 0 & {54} & {66} & {114} & {126} & {144} \\ 0 & {45} & {55} & {95} & {105} & {120} \\ 0 & {18} & {22} & {38} & {42} & {48} \\ 0 & 9 & {11} & {19} & {21} & {24} \\ \end{array}} \right] $$

Now, the reducing constants for each column are simply the minimal element in the column (which respectively are 0, 9, 11, 19, 21, 24). After subtracting these from their respective columns, we obtain the reduced matrix

$$ \left[ {\begin{array}{*{20}c} 0 & {54} & {66} & {114} & {126} & {144} \\ 0 & {45} & {55} & {95} & {105} & {120} \\ 0 & {45} & {55} & {95} & {105} & {120} \\ 0 & {36} & {44} & {76} & {84} & {96} \\ 0 & 9 & {11} & {19} & {21} & {24} \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}} \right] $$

Since by construction all elements of this reduced matrix are nonnegative, the sum of the reduced constants (namely, 192) is a lower bound. Of course, this lower bound is not nearly as good as the lower bound of 389, which as noted previously is the optimal cost value for the assignment problem. In the case of the traveling salesman problem Little et al. observed that the advantage of finding an optimal solution to the assignment problem in comparison to their simple reduction technique was mixed in terms of their computational results. The challenge tackled by Gavett and Plyter was to find for the case of the relaxed quadratic assignment problem an efficient method of obtaining an optimal basic feasible solution to the assignment problem (namely having zeroes along the diagonal of the reduced matrix and having nonnegative elements everywhere else). Their approach for doing this, which they called successive reduction, can be viewed as the primary technical contribution of their paper.

The successive reduction technique works as follows. Starting with the matrix C, the diagonal element in each column is subtracted from all other elements in its respective column. Then the smallest element in each row is subtracted from other elements in its row. After at most N repetitions of these two reductions, the desired reduced matrix is obtained.

We illustrate with the example. In the first iteration, the column reducing constants (namely 28, 78, 90, 115, 50, 28) are the diagonal elements of the original matrix C. Subtracting these from its respective column yields the matrix

$$ \left[ {\begin{array}{*{20}c} 0 & {13} & {15} & {46} & {125} & {168} \\ { - 4} & 0 & 0 & {23} & {100} & {140} \\ { - 4} & 0 & 0 & {23} & {100} & {140} \\ { - 8} & { - 13} & { - 15} & 0 & {75} & {112} \\ { - 20} & { - 52} & { - 60} & { - 69} & 0 & {28} \\ { - 24} & { - 65} & { - 75} & { - 92} & { - 25} & 0 \\ \end{array}} \right] $$

The row reducing constants are the respectively minimal elements in the rows (namely 0, -4, -4, -15, -69, -92). Subtracting these from the corresponding rows yields the matrix

$$ \left[ {\begin{array}{*{20}c} 0 & {13} & {15} & {46} & {125} & {168} \\ 0 & 4 & 4 & {27} & {104} & {144} \\ 0 & 4 & 4 & {27} & {104} & {144} \\ 7 & 2 & 0 & {15} & {90} & {127} \\ {49} & {17} & 9 & 0 & {69} & {97} \\ {68} & {27} & {17} & 0 & {67} & {92} \\ \end{array}} \right] $$

Observe that the matrix above is nonnegative and the sum of the reducing constants give a lower bound of 205.

In the second iteration, the column reducing constants are (0, 4, 4, 15, 69, 92), yielding the matrix

$$ \left[ {\begin{array}{*{20}c} 0 & 9 & {11} & {31} & {56} & {76} \\ 0 & 0 & 0 & {12} & {35} & {52} \\ 0 & 0 & 0 & {12} & {35} & {52} \\ 7 & { - 2} & { - 4} & 0 & {21} & {35} \\ {49} & {13} & 5 & { - 15} & 0 & 5 \\ {68} & {23} & {13} & { - 15} & { - 2} & 0 \\ \end{array}} \right] $$

and the row reducing constants are (0, 0, 0, -4, -15, -15), yielding the matrix

$$\left[ {\begin{array}{*{20}c} 0 & 9 & {11} & {31} & {56} & {76} \\ 0 & 0 & 0 & {12} & {35} & {52} \\ 0 & 0 & 0 & {12} & {35} & {52} \\ {11} & 2 & 0 & 4 & {25} & {39} \\ {64} & {28} & {20} & 0 & {15} & {20} \\ {83} & {38} & {28} & 0 & {13} & {15} \\ \end{array}} \right]$$

The sum of all reducing constants from the first and second iterations yields a new lower bound of 355. Subsequent iterations proceed similarly with a nonnegative matrix at each iteration (as given in Gavett and Plyter) and with a lower bound given by the sum of the new and previous reducing constants. The reducing constants and lower bounds are given in Table 13.2.

Table 13.2 Gavett and Plyter’s reduction constants and lower bounds for each iteration

Why does successive reduction work? At a technical level, the method iteratively reduces C in a way that adds zeroes in the diagonal and sub-diagonal elements, increases the sum of the reducing constants, and ends each iteration with a nonnegative matrix (so that the sum of the reducing constants is a lower bound).

At a broader level, a key to understanding successive reduction (as well as the simple reduction proposed by Little et al.) is the dual to the assignment problem. To illustrate, we now consider the dual to the example assignment problem; see, e.g., Bazaraa and Jarvis (1977):

$$ {\rm{Max}}\;{\mkern 1mu} {u_{\rm{1}}} + {u_{\rm{2}}} + {u_{\rm{3}}} + {u_{\rm{4}}} + {u_{\rm{5}}} + {u_{\rm{6}}} + {v_{\rm{1}}} + {v_{\rm{2}}} + {v_{\rm{3}}} + {v_{\rm{4}}} + {v_{\rm{5}}} + {v_{\rm{6}}} $$

s.t.

Observe that Little et al.’s simple reduction technique solves the first column and the last row of inequalities above as equations with v ₁ = 0. This gives the dual solution u = (28, 24, 24, 20, 8, 4) and v = (0, 9, 11, 19, 21, 24). Using the fact that the coefficients of C result from products of increasing intensities across the columns and decreasing distances across the rows, it is straightforward to see that the solution is dual feasible and therefore by duality gives a lower bound (namely, 192). Thus, Little et al.’s technique is simply one way to find a dual feasible solution, and hence a lower bound.

Gavett and Plyter’s method essentially generates a sequence of at most N dual feasible solutions where each component of a solution is the sum of the corresponding reducing constants at its iteration. In particular, for our example it yields the dual solutions given in Table 13.3.

Table 13.3 Dual feasible solutions and lower bounds for each iteration

Hence, Gavett and Plyter’s technique is a way of optimally solving the dual problem in at most N iterations. It is just one of a number of possible ways of solving the dual problem of the relaxation of the quadratic assignment problem. Indeed, a simpler method than the successive reduction technique is to solve the inequalities along the diagonal and sub-diagonal (denoted above with a border) as equations and get the dual solution (with u ₁ = 0) in just one iteration. Using the monotonic properties of C, it is straightforward to show that the solution obtained by doing this is dual optimal.

As for branching, Gavett and Plyter use the same framework (and even the same notation) as Little et al. with some minor modifications. Like Little et al., at each step “certain assignments are eliminated corresponding to pattern restrictions on the cost matrix. In the traveling salesman problem, this restriction involves eliminating subtours conflicting with already selected cities. In the facility-location problem QAP, this restriction means applying the labels associated with a selected element to eliminate other elements in the C matrix that would produce an unacceptable assignment at a future branch.”

2.2 Alternative Branch-and-Bound Approaches to the Quadratic Assignment Problem

As previously noted, Gavett and Plyter (1966) used a pair-assignment formulation together with a row and column reduction technique to compute lower bounds at nodes of the branch-and-bound tree. A similar approach using only a column-reduced matrix was proposed independently by Land (1963); see, e.g., Pierce and Crowston (1971) for further discussion. While Gavett and Plyter’s reduction technique gave an easy-to-compute optimal solution to the pair-assignment problem, this solution is often infeasible to the original quadratic assignment problem, resulting in a relatively weak bound; see, e.g., Christofides and Gerrard (1981). In their branching strategy, Gavett and Plyter implemented restrictions on branching variables in order to prevent multiple assignments, etc. These restrictions were computationally advantageous since the number of nodes in the branch-and-bound tree could be reduced through their use. Nevertheless, according to Burkard and Cela (1998), numerical results show that pair-assignment algorithms are outperformed by single-assignment algorithms.

Single-assignment strategies relate facilities directly to locations. The earliest strategies of this type were introduced by Gilmore (1962) and Lawler (1963). In his paper, Gilmore outlines an enumeration algorithm to solve the quadratic assignment problem, making use of lower bounds on the objective function. Also, he suggests two methods for computing lower bounds on partial permutations. As previously noted, one method uses the fact that a lower bound on the product of two given vectors of the same size can easily be determined by sorting them in opposite orders of magnitude and then taking the product of these sorted vectors. The other suggested method involves solving a linear assignment problem LAP. Lawler, on the other hand, used an integer linear program to compute lower bounds with n ⁴ + n ² variables {y _ijkl} and {x _ij} and 2n + n ⁴ + 1 constraints:

$$ M\!I\!L\!P \!:{\rm{Min}}\sum\limits_{i,j,k,l} {{c_{ijk\ell }}{y_{ijk\ell }}}$$

$$ {\rm{s}}.{\rm{t}}.{\mkern 1mu} \sum\limits_j {{x_{ij}} = 1,{\mkern 1mu} i = 1, \ldots ,n}\;\; {\mkern 1mu} {x_{ij}} = {\rm{1}},{\mkern 1mu} i = {\rm{1}}, \ldots ,n $$

$$ \sum\limits_i {{x_{ij}} = 1,{\mkern 1mu} {\mkern 1mu} j = 1,\ldots,n}$$

$$ \sum\limits_{i,j,k,\ell } {{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {y_{ijk\ell }} = {n^2}}$$

$$ {x_{ij}} + {x_k}_{\rm{l}} - {\rm{2}}{y_{ijk}}_{\rm{l}} \ge 0;\quad i,j,k,l = {\rm{1}},{\rm{2}}, \ldots ,n $$

$$ {x_{ij}} = 0\;{\rm{or}}\;{\rm{1}},\quad i,j = {\rm{1}}, \ldots ,n $$

$$ {y_{ijkl}} = 0\;{\rm{or}}\;{\rm{1}},\quad i,j,k,l = {\rm{1}}, \ldots ,n, $$

where c _ijkl is the joint cost of assigning entity i to location j and entity k to location $\ell .$ Lower bounds are created at partial assignment nodes by solving O(n ²) linear assignment problems and then using the resulting objective function values as coefficients in a master LAP. Lawler acknowledges that his bounding technique is similar to that of Gilmore. The resulting bounds created are often cited as benchmarks in other research efforts regarding the quadratic assignment problem. As stated by Loiola et al. (2007), “the QAP lower bound presented by Gilmore and Lawler is one of the best known. Its importance is due to its simplicity and its low computational cost.”

However, researchers have realized that the simplicity of computing the Gilmore and Lawler bound comes at a cost, as the bound is often not very tight for large instances of the quadratic assignment problem. Since the publication of the Gilmore-Lawler bound, research efforts have been directed toward finding improved bounds.

An obvious approach for obtaining lower bounds is to make use of the linear programming relaxation of the mixed integer linear program and its dual linear program (see for example, Assad and Xu (1985), Adams and Johnson (1994), Ramachandran and Pekny (1998), and Karisch et al. (1999). Using ideas from Drezner (1995), Resende et al. (1995) implemented an interior point algorithm to solve a relaxation of the mixed integer program.

A different formulation of the quadratic assignment problem has led to the generation of other bounding methods. Often, as in Gavett and Plyter, the coefficient c _ijkl is the product of b _ik (the flow or traffic between entity i, and entity k) and a _jl (the distance between locations j and l). With B the [n × n]-dimensional flow matrix and A the [n × n]-dimensional matrix, a trace formulation of the problem is

$$ T\!F \!:{\rm{min}} \!\; tr({\bf{BXA}}{{\bf{X}}^t}), $$

$$ {\rm{s}}.{\rm{t}}.\,{\bf\;{X}} \in {S_n}, $$

where tr(M) is the trace of matrix M and S _n is the set of permutation matrices. Letting O _n represent the set of orthogonal matrices, it follows (since every permutation matrix is an orthogonal matrix) that a relaxation of the problem TF is

$$ T\!F\!R:{\rm{min}} \!\; tr({\bf{BXA}}{{\bf{X}}^t}), $$

$$ {\rm{s}}.{\rm{t}}.\,{\bf\;{X}} \in {O_n}. $$

The solution to the relaxation TFR is found by computing the eigenvalues of both matrices B and A, sorting one vector in nondecreasing order, the other in nonincreasing order, and then taking the product of the two resulting vectors. Unfortunately, the resulting eigenvalue bound has proven to be somewhat weak, but has been improved by enforcing additional constraints. For example, Hadley et al. (1992) enforce constraints on row and column sums resulting in a projected eigenvalue bound. Sometimes their bound was better than that by Gilmore and Lawler, and sometimes not.

Anstreicher and Brixius (2001) take a different approach by convexifying the quadratic objective function while making use of the derivation of the projected eigenvalue bound. Their formulation also makes use of optimal solutions of a semdefinite programming (SDP) problem related to the eigenvalue bound. They show that their bound is at least as good as the projected eigenvalue bound. Also, they have found that the value of their bound appears to increase much faster in comparison as branching occurs. This latter attribute is obviously very important in a branch-and-bound framework.

Use of this bound led to the first solution of several large benchmark problems, including the notorious “Nug 30” problem from Nugent et al. (1986). A nice summary of advances in quadratic assignment problem research as of the early 2000s can be found in Anstreicher (2003).

Recently, reformulation-linearization (RL) has been applied to the quadratic assignment problem to compute lower bounds. This technique involves multiplying equality constraints and nonnegativity constraints by product factors of the variables (reformulation). Then, each nonlinear term is replaced by a single variable, resulting in a mixed zero-one linear integer program (linearization). Reformulation creates redundant constraints, and different formulations are possible depending upon the product factors chosen in this step. As described by Adams et al. (2007) a level-1 reformulation (RLT-1) of the quadratic assignment problem is developed by multiplying each equality constraint and each nonnegativity constraint by each of the n ² variables. For a level-2 reformulation (RLT-2), each constraint is multiplied by the product of two variables again creating redundant constraints. As before, reformulation is followed by linearization through substitution. Even higher levels of reformulation and linearization are possible through the use of higher level product forms, resulting in improved bounds, but at the cost of even larger zero-one linear programs. The resulting optimization problems can be quite large, but have been shown to provide relatively tight bounds. Adams et al. (2007) used Lagrangean relaxation and dual ascent in a branch-and-bound framework to solve problems up to size n = 30 from Nugent et al. (1986) Although they found that their method required lower bound calculations at fewer nodes than competitive methods, computing each bound required a large amount of RAM. They cite a future research challenge as one of finding ways to reduce the RAM requirement.

Also recently, additional attention has focused on a semidefinite programming relaxation of the quadratic assignment problem, see Zhao et al. (1998) and Rendl and Sotirov (2007), as well as a reformulation-linearization semidefinite programming relaxation (also called a lift-and-project relaxation), see Burer and Vandenbussche (2006) and Lovasz and Schrijver (1991) for details. Interestingly, the equivalence between these two relaxations for the quadratic assignment problem was recently shown by Povh and Rendl (2009). Using a bundle method to solve the resulting problem, Rendl and Sotirov in 2003 obtained the tightest lower bounds at that time for a large number of test problems. More recently, Burer and Vandenbussche (2006) used an augmented Lagrangian method and derived even tighter bounds on a number of test problems. Exploiting a special structure in the data matrices of certain quadratic assignment problems, de Klerk and Sotirov (2008) have found even tighter lower bounds than Burer and Vandenbussche on some problems.

Loiola et al. (2007) provide a recent survey on the quadratic assignment problem, including a discussion on different approaches used to solve the problem. In particular, the paper includes data on lower bound values found and run times of several competing methods, including those mentioned above, applied to classical test problems.

2.3 Special Cases of the Quadratic Assignment Problem that are Solvable in Polynomial Time

We now briefly review some of the work that considers special cases of the quadratic assignment problem with particular emphasis on cases that can be solved in polynomial time. Burkard et al. (1997) considered the special case, in which c _ijkl is the product of the flow between facilities i and k, and the distance between locations j and l. They showed that if 2n numbers b _i ^r, b _i ^c, i = 1, …, n exist and can be associated with the rows and columns of the flow matrix such that b _ik = b _i ^r + b _k ^c for all i and k, then the problem is reducible to the linear assignment problem and therefore is solvable in polynomial time. The result is also true if the distance matrix can be decomposed in a similar manner. Ergodan (2006) shows that this result can be generalized to a broader class of quadratic assignment problems that are “additively decomposed.”

Ergodan also considers “multiplicative decomposition” and has the following result. Suppose there exists {v _ij: i, j = 1, …, n} where ${c_{ijk\ell}}={v_{ij}}\,{v_{k\ell}},$ for all i, j, k, $\ell .$ Then if the optimal objective function value of the linear assignment problem with coefficients {v _ij} is nonnegative, then the linear assignment problem solves the corresponding quadratic assignment problem.

Ergodan and Tansel (2006) consider the case where the n-node flow graph has a path structure (it has no cycles and every node has a degree of 0, 1, or 2) and the n by n distance matrix is induced by a grid graph in the following sense. With rc = n for two positive integers r and c, let G _rc be the undirected grid graph with rc nodes, where the nodes are arranged in r rows and c columns, and where the arc set consists of arcs connecting adjacent nodes in the same row, or adjacent nodes in the same column. Define D _ab as the [n × n]-dimensional matrix of shortest path distances in G _ab. Then if the distance matrix A of the quadratic assignment problem is identical to hD _ab for some positive h, D is said to be induced by a grid graph. For this special structure, Erdogan and Tansel show that the quadratic assignment problem is solvable in O(n) time.

For information on other special structures that lead to polynomial-time solvability, see Erdogan (2006).

3 Efroymson and Ray (1966): The Uncapacitated Facility Location Problem

Also in the early 1960s there was considerable research interest in another problem known today as the Uncapacitated Facility Location Problem (UFLP). Our purpose here is to report on perhaps the earliest published use of the branch-and-bound technique to solve the problem exactly. We will explain how branch-and-bound was used in the paper by Efroymson and Ray (1966). The problem setting involves several “demand points” (customers) requiring service from one or more potential “plant sites.” There is a given supply cost between a given demand point and potential plant site that will be incurred if the plant is opened and the demand is serviced from the plant. In addition, there is a fixed cost to open each plant.

3.1 Solving the Uncapacitated Facility Location Problem via Branch-and-Bound

To formally pose the uncapacitated facility location problem as an optimization problem, suppose there are n customer locations j = 1, …, n and m potential plants i = 1, …, m. The following mixed integer program is a prototypical formulation of the problem:

$$ U\!F\!L\!P\!:{\rm{Min\;Z}} = \sum\limits_{i,j} {{c_{ij}}{x_{ij}}}+ \sum\limits_i {{f_i}{y_i}}$$

(13.4)

$$ {\rm{s}}{\rm{.t}}{\rm{.}}\,\sum\limits_i {{x_{ij}} = 1,j = 1, \ldots ,n}$$

(13.5)

$$ x_{ij} \le y_i \;\forall i,j $$

(13.6)

$$ {x_{ij}} \ge 0\;\forall i,j $$

(13.7)

$$ {y_i} = 0{\mkern 1mu} \;{\rm{or}}\;{\mkern 1mu} {\rm{1}}\;\forall i $$

(13.8)

where we define the parameters

c _ij::

the cost to service all of customer j’s demand from plant i

f _i::

the nonnegative cost of opening plant i

and the variables

x _ij::

the fraction of customer j’s demand satisfied by plant i, and

y _i =:

1 if plant i is open, and 0 otherwise.

Thus, the decision problem is to decide which plants to open (which y _i values to set to one) and which open plant(s) will service each customer. The overall objective is to minimize total cost. Note that the allocation variables x _ij are continuous and take on values between zero and one. This is why c _ij represents the cost of servicing all demand and so c _ijx _ij denotes proportional costing. In many applications, c _ij is determined by a transportation cost per unit multiplied by total demand of customer j. Finally, constraint (13.6) forces plant i to be open whenever x _ij > 0 for some j. There are many applications of this classical location problem and we outline two of these in what follows.

Krarup and Bilde (1977) describe an application in manufacturing called the dynamic economic lot size problem. A manufacturer of a single product needs to develop a production plan for the next n months in order to satisfy demand for the product in each of these months. Producing the product in month i incurs a fixed setup cost f _i as well as a per-unit manufacturing cost p _i. Demand for the product in month j is denoted as d _j, and d _j can be satisfied by production in month j and/or some earlier month. However, units produced earlier than needed incur a holding cost, where r _i is the per unit cost of holding one unit from month i to month i + 1. Define c _ij as the cost of manufacturing and (if necessary) holding all of month j’s demand when production occurs in month i $\le$ j. Thus,

$$ {c_{ij}} = \left\{ {\begin{array}{*{20}{l}}{{d_j}({p_i}+\sum\limits_{t = i}^j {{r_t}} ),{\mkern 1mu}{\mkern1mu}\quad{\rm{for}}{\mkern 1mu} {\mkern 1mu} i <j}\\{{d_j}{p_i}{\mkern1mu} {\mkern 1mu} {\mkern 1mu} {\mkern1mu}{\mkern 1mu} {\mkern1mu} {\mkern 1mu} {\mkern 1mu} {\mkern1mu}{\mkern 1mu} {\mkern1mu} {\mkern 1mu} {\mkern 1mu} {\mkern1mu}{\mkern 1mu} {\mkern1mu} {\mkern 1mu} {\mkern 1mu} {\mkern1mu}{\mkern 1mu} {\mkern1mu} \qquad \;\!\qquad{\rm{for}}{\mkern1mu}{\mkern 1mu} i = j}\\ {\infty{\mkern 1mu} {\mkern 1mu}{\mkern1mu} {\mkern 1mu} {\mkern 1mu}{\mkern 1mu} {\mkern 1mu}{\mkern1mu} {\mkern 1mu} {\mkern 1mu}{\mkern 1mu} {\mkern 1mu}{\mkern1mu} {\mkern 1mu} {\mkern1mu}{\mkern 1mu} {\mkern 1mu}{\mkern1mu} {\mkern 1mu} {\mkern1mu} {\mkern 1mu} {\mkern 1mu}{\mkern1mu} {\mkern 1mu} {\mkern1mu} {\mkern 1mu}\;\;\quad\qquad\quad{\rm{for}}{\mkern 1mu} {\mkern 1mu} i>j}\\\end{array}} \right. $$

Note that if i = j, then no holding cost is incurred. Also units produced in month i cannot be used to satisfy demand in some earlier month. However, if it is possible to backorder demand, then c _ij for j < i could be finite, but most likely would involve a per-unit (and per-period) backorder cost. Letting y _i = 1 if and only if production occurs in month i, and x _ij as the fraction of month j’s demand produced in month i, the uncapacitated facility location problem is solved to minimize total setup, manufacturing, and holding cost over the n-month planning horizon.

In the days before electronic funds transfer, the time to clear a check often depended on which bank the check was drawn on, and the location of the recipient of the check. After all, checks were often delivered by the postal service. Thus, a company might want to maximize the total funds that are in transit. However, maintaining an account at a given bank is not costless. With c _ij as the “dollar days” (float) in transit from bank i to customer j and f _i the cost to maintain an account at bank i, the firm is faced with the problem of maximizing $\sum\nolimits_{i,j} {{c_{ij}}{x_{ij}}}- \sum\nolimits_i {{f_i}{y_i}}$ subject to the constraints (13.5)–(13.8). Note that we are maximizing a modified version of (13.4), but structurally the problems are the same. Cornuejols et al. (1990) call this problem the Bank Account Location Problem. A mirror image of this problem is called the Lock Box Problem, where a firm collecting funds wishes to minimize “float.” For more on the above problem see also Cornuejols et al. (1977).

Efroymson and Ray recognized that practical instances of the uncapacitated facility location problem might have several thousand rows and columns and that contemporary integer programming techniques could not hope to solve such large problems in a reasonable amount of time. They therefore sought methods to solve the overall problem via a sequence of smaller subproblems.

Note that for fixed values of the y _i variables {$y'_i$, i = 1, …, n}, where at least one $y'_i$ = 1, an optimal x-vector can be found easily by setting, for each value of $j,{\rm{ }}x_{ij} = {\rm{1 \;\!if }}\;\!c_{ij} = {\rm{min }}\{ c_{ij} :y'_i = {\rm{1}}\} .$ In other words, for each j, find the smallest c _ij over those plants i for which the corresponding y variable is set to one. An efficient solution method is to find a means of computing good y-vectors that will eventually lead to an optimal y-vector. Combining the above observation with the fact that the solution to a linear programming relaxation of an mixed integer program creates a lower bound to it (given a minimization objective), Efroymson and Ray made extensive use of the linear program LPR defined below.

Let N _k be the set of indices of those plants that can supply customer k and P _i be the set of indices of those customers that can be supplied from plant i, where n _i is the number of elements in P _i. Note that N _k might be all plants and P _i might be all customers, but practical considerations often prohibit some links. With these definitions, consider the following linear program:

$$ L\!P\!R \!:{\rm{Min}}{\mkern 1mu} {Z_L} = \sum\limits_{i,j} {{c_{ij}}{x_{ij}}}+ \sum\limits_i {{f_i}{y_i}}$$

(13.9)

$$ {\rm{s}}.{\rm{t}}.{\mkern 1mu} \sum\limits_{i \in {N_j}} {{x_{ij}} = 1,\;j = 1,\ldots,n}$$

(13.10)

$$\sum\limits_{j \in {P_i}} {{x_{ij}} \le {n_i}{y_{i,}},\;i = 1, \ldots ,m}$$

(13.11)

$$ {x_{ij}} \ge 0\;\forall i,j $$

(13.12)

$$ {y_i} = 0\;{\mkern 1mu} {\rm{or}}\;{\mkern 1mu} {\rm{1}}\;\forall i = {\rm{1}}, \ldots ,m $$

(13.13)

Efroymson and Ray made use of the LPR formulation in their branch-and-bound method. Since UFLP has both continuous and integer variables, it is natural to branch on the zero-one variables y. Thus, at some node in the branch-and-bound tree, some of the y variables may be set to zero (their indices collected in a set labeled K ₀), some may be set to one (their indices are included in a set labeled K ₁), while the status of some of the remaining variables y has not yet been decided. We denote this latter set of indices as K ₂.

A simple procedure can be used to solve the problem LPR without the use of an linear programming solver. The authors observed that the optimal allocation variables $\{ x_{ij}^*\}$ and corresponding allocation costs {AC _j*} could be constructed as shown in Algorithm 1.

The optimal y variables for those plants with indices in K ₂ are then computed as ${y_i}* = \left( {{\rm{1}}/{n_i}} \right)\sum\limits_{j \in {P_i}{\rm{ }}} {x_{ij}^*}$. The optimal objective function value at the node, accounting for those plants i Î K ₁ that are fixed open is then $Z_L^* = \sum\limits_{i \in {K_1}} {{f_i}}+ \sum\limits_{j = 1}^m {AC_j^*}$.

The above procedure solves LPR because relation (13.11) will hold as an equation at an optimal solution. Thus, those y _i variables i Î K ₂ can be removed from (13.9) by substitution. Using the above ideas, LPR can be solved by finding the minimum entry in each column of a [(|K ₁| + |K ₂|) × m]-dimensional matrix. Note that the value $Z_L^*$ can often be a fairly weak lower bound on UFLP at the current node. This is especially true when the number of customers actually served by plant i, i Î K ₂, is considerably smaller than n _i. When this occurs, only a fraction of the full cost f _i of opening the plant is accounted for. Realizing this fact, Efroymson and Ray developed “simplification rules,” i.e., conditions that can be used to either optimally fix the values of some members of K ₂ in all solutions that emanate from the current node, or to reduce n _i.

The first rule is to set y _i   =   1, i Î K ₂ if it is known that the net savings in allocation costs with this plant open is at least as large as the fixed cost to open the plant. For any j, if plant i, i Î K ₂ is not open, then c _~j º min{c _{k j}: k Î K ₁  È K ₂, k ¹ i} is the minimum possible cost to serve demand j by either a plant k, k Î K ₁ that is fixed open, or some other plant k Î K ₂ that might be opened. But then if c _~j − c _ij > 0, opening plant i would certainly provide an allocation cost savings to serve demand j. If the sum of these savings over all demands is at least as large as f _i, it is optimal to open plant i. More formally, let

$$ \Delta _{ij}^o \equiv {\rm{max}}\{ ({\rm{min}}\{ {c_{kj}}:k \in {K_{\rm{1}}} \cup {K_{\rm{2}}},k \ne i\}- {c_{ij}}),{\rm{ }}0\}$$

(13.14)

Rule 1: If $\sum\limits_j {\Delta _{ij}^o}> {f_i},$ set y_i   =   1.

On the other hand, if the net savings in allocation costs with plant i open is known to be no more that the cost to open the plant, then set y _i   =   0. To implement this rule, restrict k to be in K ₁ in (13.14) and define $\Delta _{ij}^c$ to be the computed value. Then,

Rule 2: If $\sum\limits_j {\Delta _{ij}^c}\le {f_i}$, set y _i   =   0.

The final simplification provided by Efroymson and Ray involves the reduction of n _i. Note that reducing n _i. can provide a stronger lower bound at the node. Suppose that j is currently in the set P _i. If for some open plant k we find that c _kj £ c _ij, then demand j will be no worse off by eliminating plant i as a potential server of j’s demand, i.e., we can safely eliminate index j from the set P _i, thereby reducing |P _i| by 1. More formally,

Rule 3: Let J(i) º {j Î P _i: min {c _kj : k Î K ₁} - c _ij £ 0}. Eliminate J(i) from P _i and reduce n _i by |J(i)|.

Algorithm 1: Solution Algorithm for the LPR Problem

Step 1: :

Find AC _j* º min{min {c _ij: i Î K ₁}, min{c _ij + f _i/n _i:

i Î K ₂} for j = 1, …, n.

Step 2: :

Set x _ij* = 1 for that value of i that attains AC _j* in Step 1, and $x_{ij}^*$ = 0 otherwise.

3.2 Alternative Branch-and-Bound Approaches to the Uncapacitated Facility Location Problem

Perhaps the best-known contribution to solution methods for the uncapacitated facility location problem is by Erlenkotter (1978). His approach involves working with the dual problem, solving a reduced nonlinear form of the dual heuristically through ascent and adjustment of the dual variables. The result of this method is the DUALOC algorithm that is frequently cited in the literature. Bilde and Krarup’s (1977) method is similar to Erlenkotter’s and was developed at approximately the same time. The ascent/adjustment method often produces an optimal dual solution that can possibly be used to construct an optimal primal solution. If not, the dual objective function value can be effectively used in a branch-and-bound algorithm to solve the uncapacitated facility location problem.

Another approach is to strengthen the lower bounds created by the linear programming relaxation of UFLP. One way to do this is to find inequalities to add as constraints to the linear program which cut off portions of the linear programming polyhedron that are known to not contain an optimal solution to the problem. These added constraints are often called valid inequalities and have been studied by many researchers. In particular, it is of value to eliminate extreme points that correspond to fractional solutions, since such solutions are infeasible to the uncapacitated facility location problem.

Cho et al. (1983a) study the issue of generating so-called facet inequalities that describe the integer polyhedron of UFLP. Such an approach has great value since the integer polyhedron is contained in the linear programming polyhedron. The authors state:

This approach deserves attention since facets are the “strongest cutting planes.” One can thus reasonably expect to improve computational results for any solution method which is based on linear programming even if one can identify only a subset of these facets.

They make use of a node-packing reformulation of the uncapacitated facility location problem, and are able to characterize all facets for the case of three plants (m = 3) and several destinations. In a companion paper, Cho et al. (1983b) identify all facets for the case of three customers (n = 3) and several plants.

Goldengorin et al. (2003) use a pseudo-Boolean polynomial-based representation of UFLP to solve the problem. Their algorithm, called branch-and-peg, uses rules to determine (before branching) whether a plant will (or will not) be located at certain sites in the current subproblem under examination. This “pegging” operation is applied to each subproblem and reduces its size. The authors report that on a number of problems solved, branch-and-peg took on average less than 10% of the execution time of branch-and-bound when the transportation matrix was dense.

Beltran-Royo et al. (2007) apply a concept called Semi-Lagrangean Relaxation to UFLP. The idea is to dualize the equality constraints (13.5) to form the dual function, but then add the constraints $\sum\nolimits_i {{x_{ij}} \le 1,{\mkern 1mu} {\mkern 1mu} j = 1,\ldots,n}$ to the dual problem. Adding the constraints increases the lower bound when the subproblem is solved to optimality. Unfortunately, the resulting subproblem is NP-hard, but the authors found that often the subproblems are smaller in dimension that the original primal problem. In those instances, they used CPLEX to solve the dual problem.

In a recent paper, Hansen et al. (2007) use a three-phase approach to solve large instances of UFLP. A key feature of their method is the use of variable neighborhood search (VNS). The idea of variable neighborhood search is to explore the neighborhood of a current solution. Once a neighborhood structure is defined, a distance function must be developed that describes the dissimilarity of two solutions. Then, for a given solution, points in the k-th neighborhood can be identified. Variable neighborhood search consists of the repetitive sequence of three basic steps that are shown in Algorithm 2.

There are three phases to their overall approach to solving unconstrained facility location problems. These phases integrate variable neighborhood search as a key ingredient. The procedure can be described as shown in Algorithm 3.

Algorithm 2: Variable Neighborhood Search: A Generic Algorithm

Step 1: :

Identify a (perturbed) solution in the k-th neighborhood of an incumbent. This step is frequently referred to as “shaking”).

Step 2: :

Perform a local search from the perturbed solution.

Step 3: :

Move to an improved solution.

Algorithm 3: Solving UFLP with Variable Neighborhood Search

Phase 1: :

Apply variable neighborhood search directly to UFLP to find a good primal solution. This step provides an upper bound of the problem.

Phase 2: :

Find an exact solution to the dual of the linear programming relaxation of UFLP. Variable neighborhood search is also used in this phase of this approach. The dual solution provides a lower bound.

Phase 3: :

A branch-and-bound procedure is then implemented making use of the upper and lower bounds from Phases 1 and 2. With their method, the authors reported success in solving very large problem instances.

3.3 Special Cases of the Uncapacitated Facility Location Problem that are Solvable in Polynomial Time

In addition to research efforts to improve bounds for the uncapacitated facility location problem, another research focus on the problem has been to identify special cases that can be solved to optimality in polynomial time. Kolen (1982) observed that UFLP could be transformed to an equivalent covering problem. Then, if the covering matrix of the resulting problem is totally balanced, it can be transformed through row and column operations into standard greedy form. (A totally balanced zero-one matrix contains no square submatrix with row and column sums equal to two, and such a matrix is in standard greedy form if it does not contain a submatrix of the form $\left[ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 0 \\ \end{array}} \right]$. Hoffman et al. (1985) give a polynomial time algorithm for this transformation.) When this can be done, Kolen shows that this covering problem can be solved in polynomial time, see also Kolen and Tamir (1990).

Jones et al. (1995) identified another class of uncapacitated facility location problems, where not every instance fits the Kolen framework but that can still be solved to optimality in polynomial time. An instance is in this class if facility and demand point indices can be ordered so that the following holds:

• (a) Continuity: If j, $\ell$ÎP _i, then k ÎP_i where j < k «$\ell .$

• (b) Cascading: For all i < t, min{j: j Î P_i} $\le$ min{j: j Î P_t}, and max{j: j Î P_i} £ max{j: j Î P_t}.

• (c) Monotonicity: For all j, if i, t Î N_j, and if c _ij £ c _tj, then c _ik £ c _tk for all k where i, t Î N _k.

In addition to giving an O(nm) algorithm for such instances, the authors identify several problems that satisfy the conditions (a), (b) and (c). These problems include the tool selection problem of Daskin et al. (1990), a substitutable inventory problem, a stochastic demand problem, the discrete lot sizing problem discussed by Wagner and Whitin (1958), and a facility location problem on the line.

4 Branching Strategies in Branch-and-Bound Procedures

For the most part, in this chapter we have focused on the “bound” part of branch-and-bound methods for the two location problems considered, because bounding techniques by their very nature need to be problem dependent. Nevertheless, our chapter would not be complete without at least a brief discussion of what seem to be some promising areas of research in the “branch” part of branch-and-bound procedures. These ideas can be applied to any mixed integer programming problem and thus are not restricted to location problems. Two key references for these ideas are Linderoth and Savelsberg (1999), and Achterberg et al. (2005).

As mentioned in the introduction to this chapter, the branch-and-bound process is most easily envisioned via a tree, where the top node of the tree is the original problem, and various branches are created through partitioning the set of feasible solutions to the problem. The “deeper” one is in the tree, the more options there are for selecting the next node for partitioning of the subset of solutions represented by that node. A significant amount of research has taken place regarding the node to be selected for partitioning, as well as how to perform the partition. In what follows, we will continue to assume that the original problem is one of minimization.

Regarding node selection, a popular method is to choose the node that has the smallest lower bound, where this bound is often found via linear programming relaxation. This method, when applied in its purest sense, is often called best-bound (or breadth-first) search. Another method, called depth-first search, is to continue searching down the tree until a feasible solution is found. Other methods include estimating the value of the best feasible integer solution obtainable from a given node in the tree, or combining depth first search early in the process and breadth-first search methods later in the process.

As described by Linderoth and Savelsberg, one way to partition the feasible region represented by a given node is to select a single variable that does not take on an integer value in the linear programming relaxation solution, but must be integer in an over-all optimal solution; then create two subregions by constraining this variable with an upper bound and a lower bound (they call this variable dichotomy). Below we discuss some methods for determining the variable to be “dichotomized.” Another method is applicable when certain generalized upper bounding constraints are present in the original problem. The generalized upper bounding dichotomy is a means of partitioning by bounding the sum of different subsets of the variables to create different subregions.

Returning to variable dichotomy, there remains the issue of variable selection. Some authors have tested the use of “pseudocosts,” i.e., estimates of changes in the objective function value when a variable is rounded up or rounded down. The estimates are usually created by using the objective function values of the corresponding linear programming relaxations. Average pseudocosts for a given variable can also be determined by gathering “local” pseudocosts at several nodes and computing the mean of the set. However they are computed, these pseudocosts can be used to help select the partitioning variable.

Another promising approach is called “strong branching,” which involves testing the set (or a subset of) the fractional variable candidates to find those that appear to give the best progress before actually branching on any of them. “Full strong branching” involves all fractional variables and thus it may be computationally prohibitive to solve all the corresponding linear programming problems to optimality. Thus, some authors have considered testing just a subset of these variables and not solving the linear programs to optimality, instead performing a limited number of dual simplex pivots. Hybridized versions of these techniques are also possible.

Both Linderoth and Savelsberg (1999), and Achterberg et al. (2005) provide results on computational testing of the above ideas applied to a number of mixed integer programming problems as well as references to the work of others.

5 Conclusions

Herein we reviewed the use of branch-and-bound in solving exactly two important location problems, the quadratic assignment problem and the uncapacitated facility location problem. Our focus was on the early application of branch-and-bound to these problems via a critical review of two classical papers from the 1960s, namely Gavett and Plyter (1966) on the quadratic assignment problem and Efroymson and Ray (1966) on the uncapacitated facility location problem. In providing these reviews we attempted to replicate the authors’ thought processes in the development of the reported solution method and to discuss how these papers set the stage for subsequent research.

The quadratic assignment problem is generally recognized as one of the most difficult combinatorial optimization problems. After an initial lull of research activity in this problem (until the mid-1970s), research on this topic has exploded. In spite of this activity, however, an exact solution to the problem has remained elusive for modest and large size problems. Yet recently, significant results have been obtained; see, e.g., Adams et al. (2007), Anstreicher (2003), Burer and Vandenbussche (2006), De Klerk and Sotirov (2008, 2009), and Rendl and Sotirov (2007). The research activity and the results are nicely summarized in the comprehensive review paper of Loiola et al. (2007). The result of this research has been better lower bounds and an approximate doubling in the size of problems that can be solved exactly in the last 10 years (from about n = 15 to about 30). Unfortunately, n = 30 is still a relatively small problem. In practice, this means that heuristic and metaheuristic approaches are needed to attempt to solve the problem. Again, see Loiola et al. (2007) for an excellent review.

In contrast, much progress has been made in solving the uncapacitated facility location problem. As noted herein, large instances of the UFLP can now be solved; see, e.g., Beltran-Royo et al. (2007) and Hansen et al. (2007).