Bifurcations and state changes in the human alpha rhythm: Theory and experiment

Abstract

Despite many decades investigating scalp recordable 8–13-Hz (alpha) electroencephalographic activity, no consensus has yet emerged regarding its physiological origins nor its functional role in cognition. Here we outline a detailed, physiologically meaningful, theory for the genesis of this rhythm that may provide important clues to its functional role. In particular we find that electroencephalographically plausible model dynamics, obtained with physiological admissible parameterisations, reveals a cortex perched on the brink of stability, which when perturbed gives rise to a range of unanticipated complex dynamics that include 40-Hz (gamma) activity. Preliminary experimental evidence, involving the detection of weak nonlinearity in resting EEG using an extension of the well-known surrogate data method, suggests that nonlinear (deterministic) dynamics are more likely to be associated with weakly damped alpha activity. Thus rather than the “alpha rhythm” being an idling rhythm it may be more profitable to conceive it as a readiness rhythm.

6.1 Introduction

The alpha rhythm is arguably the most ubiquitous rhythm seen in scalp-recorded electroencephalogram (EEG). First discovered by Hans Berger in the 1920s [27] and later confirmed by Adrian and Mathews in the early 1930s [1], it has played a central role in phenomenological descriptions of brain electrical activity in cognition and behavior ever since. While the definition of classical alpha is restricted to that 8–13-Hz oscillatory activity recorded over the occiput, which is reactive to eyes opening and closing, it is now widely acknowledged that activity in the same frequency range can be recorded from multiple cortical areas. However, despite decades of detailed empirical research involving the relationship of this rhythm to cognition, we remain essentially ignorant regarding the mechanisms underlying its genesis and its relevance to brain information processing and function [74].

Broadly speaking we are certain of only two essential facts: first, alpha activity can be recorded from scalp; and second, it bears some relationship to brain function. However a raft of recent modeling work suggests that alpha may be conceived as a marginally stable rhythm in the Lyapunov sense, and hence represents a brain state which can be sensitively perturbed by a range of factors predicted to also include afferent sensory stimuli. In this view, which we will elaborate on in some detail, the alpha rhythm is best conceived as a readiness rhythm. It is not a resting or idling rhythm, as originally suggested by Adrian and Mathews [1], but instead represents a physiologically meaningful state from which transitions can be made from or to. This perspective echos that of EEG pioneer Hans Berger [27]:

I also continue to believe that the alpha waves are a concomitant phenomenon of the continuous automatic physiological activity of the cortex.

This chapter is divided into three main sections: The first section gives a succinct overview of the alpha rhythm in terms of phenomenology, cerebral extent and mechanisms postulated for its genesis. It concludes by arguing that its complex features and patterns of activity, its unresolved status in cognition, and the considerable uncertainty still surrounding its genesis, all necessitate developing a more mathematical approach to its study. The second section provides an overview of our mean-field approach to modeling alpha activity in the EEG. Here we outline the constitutive equations and discuss a number of important features of their numerical solutions. In particular we illustrate how model dynamics can switch between different, but electroencephalographically meaningful, states. The third and final section outlines some preliminary evidence that such switching dynamics can be identified in scalp recordings using a range of nonlinear time-series analysis methods.

6.2 An overview of alpha activity

Between 1926 and 1929 Hans Berger laid the empirical foundations for the development of electroencephalography in humans. In the first of a number of identically titled reports [27], Berger described the alpha rhythm, its occipital dominance, and its attenuation with mental effort or opened eyes. This, and the subsequent reports, evinced virtually no interest from the neurophysiological community until Edgar Douglas Adrian (later Lord Adrian) and his colleague Bryan Mathews reproduced these results in a public demonstration that in addition revealed how easy the alpha rhythm was to record.

Following its demonstration by Adrian and Mathews [27], interest in the alpha rhythm and electroencephalography in general accelerated, to the point that considerable funding was devoted to its investigation. However, by the 1950s much of the early promise–-that EEG research would elucidate basic principles of higher brain function–-had dissipated. Instead, a much more pragmatic assessment of its utility as a clinical tool for the diagnosis of epilepsy prevailed. By the 1970s, rhythmicity in the EEG had been effectively labeled an epiphenomenon, assumed to only coarsely relate to brain function. However, the temporal limitations of functional magnetic resonance imaging and positron emission tomography have in the last decades renewed interest in its genesis and functional role.

6.2.1 Basic phenomenology of alpha activity

Classically, the term “alpha rhythm” is restricted to EEG activity that fulfills a number of specific criteria proposed by the International Federation of Societies for Electroencephalography and Clinical Neurophysiology (IFSECN) [32]. The most important of these are: the EEG time-series reveal a clear 8–13-Hz oscillation; this oscillation is principally located over posterior regions of the head, with higher voltages over occipital areas; it is best observed in patients in a state of wakeful restfulness with closed eyes; and it is blocked or attenuated by attentional activity that is principally of a visual or mental nature. However, alpha-band activity is ubiquitously recorded from the scalp with topographically variable patterns of reactivity. A slew of studies have revealed that the complex distribution of oscillations at alpha frequency have different sources and patterns of reactivity, suggesting that they subserve a range of different functional roles. Indeed W. Grey Walter, the pioneering British electroencephalographer, conjectured early on that “there are many alpha rhythms”, see [70]. Because the original IFSECN definition of alpha rhythm does not extend to these oscillations, they are typically referred to as alpha activity [15].

To date, two types of nonclassical alpha have been unequivocally identified. The first is the Rolandic (central) mu rhythm , first described in detail by Gastaut [25]. It is reported as being restricted to the pre- and post-central cortical regions, based on its pattern of blocking subsequent to contralateral limb movement and/or sensory activity. Like alpha activity in general, the mu rhythm does not appear to be a unitary phenomenon. For example, Pfurtscheller et al. [61] have observed that the mu rhythm is comprised of a great variety of separate alpha activities. The other well-known nonclassical alpha activity is the third rhythm (also independent temporal alphoid rhythm or tau rhythm) . It is hard to detect in scalp EEG unless there is a bone defect [28], but is easily seen in magnetoencephalogram (MEG) recordings [77]. While no consensus exists regarding its reactivity or function, it appears related to the auditory cortex, as auditory stimuli are most consistently reported to block it [50,70]. There have also been other demonstrations of topographically distinct alpha activity, whose status is much less certain and controversial. These include the alphoid kappa rhythm arising from the anterior temporal fossae, which has been reported to be non-specifically associated with mentation [36], and a 7–9-Hz MEG rhythm arising from second somatosensory cortex in response to median nerve stimulation [49].

Because historically the most common method of assessing the existence of alpha activity has been counting alpha waves on a chart, incorrect impressions regarding the distribution and neuroanatomical substrates of the various alpha rhythms are likely [55]. Thus the current nomenclature has to be viewed as somewhat provisional. Nevertheless, the global ubiquity of alpha activity and its clear associations with cognition suggest that understanding its physiological genesis will contribute greatly to understanding the functional significance of the EEG . This possibility was recognised by the Dutch EEG pioneer Willem Storm van Leeuwen who is cited in [4] as commenting:

If one understands the alpha rhythm, he will probably understand the other EEG phenomena.

6.2.2 Genesis of alpha activity

To date, two broad approaches have emerged for explaining the origin of the alpha rhythm and alpha activity. The first approach conceives of alpha as arising from cortical neurons being paced or driven at alpha frequencies: either through the intrinsic oscillatory properties of other cortical neurons [44,71], or through the oscillatory activity of a feed-forward subcortical structure such as the thalamus [30,31]. In contrast, the second approach assumes that alpha emerges through the reverberant activity generated by reciprocal interactions of synaptically connected neuronal populations in cortex, and/or through such reciprocal interactions between cortex and thalamus.

While Berger was the first to implicate the role of the thalamus in the generation of the alpha rhythm [27], it was the work of Andersen and Andersson [2] that popularised the notion that intrinsic thalamic oscillations, communicated to cortical neurons, are the source of the scalp-recorded alpha rhythm. Their essential assumption was that barbiturate-induced spindle oscillations recorded in the thalamus of the cat were the equivalent of the alpha oscillations recorded in humans. However, the notion that spindle oscillations are the source of alpha activity has not survived subsequent experimental scrutiny [74]. Spindle oscillations only occur during anesthesia and the retreat into sleep, whereas alpha oscillations occur most prominently during a state of wakeful restfulness. Further, while the frequency of spindle oscillations and alpha activity overlap, spindles occur as groups of rhythmic waves lasting 1–2 s recurring at a rate of 0.1–0.2 Hz, whereas alpha activity appears as long trains of waves of randomly varying amplitude. A range of other thalamic local field oscillations with frequencies of approximately 10 Hz have been recorded in cats and dogs [13,14,30,31], and have been considered as putative cellular substrates for human alpha activity. Nevertheless, there remains considerable controversy regarding the extent and mode of thalamic control of human alpha activity [70].

Indeed, there are good reasons to be suspicious of the idea that the thalamus is the principal source of scalp-recorded alpha oscillations. First, thalamocortical synapses are surprisingly sparse in cortex. Thalamocortical neurons project predominantly to layer IV of cerebral cortex, where they are believed to synapse mainly on the dendrites of excitatory spiny stellate cells. A range of studies [6,12,57,58] have revealed that only between 5–25% of all synapses terminating on spiny stellate cells are of thalamic origin. Averaged over the whole of cortex, less than 2–3% of all synapses can be attributed to thalamocortical projections [10]. Second, recent experimental measurements reveal that the amplitude of the unitary thalamocortical excitatory postsynaptic potential is relatively small, of the order of 0.5 mV, on its own insufficient to cause a postsynaptic neuron to fire [12]. This raises the question whether weak thalamocortical inputs can establish a regular cortical rhythm even in the spiny stellate cells, which would then require transmission to the pyramidal cells, whose apical dendrites align to form the dipole layer dominating the macroscopic EEG signal. Third, coherent activity is typically stronger between cortical areas than between cortical and thalamic areas [47,48], suggesting cortical dominance [74]. Fourth, isolated cerebral cortex is capable of generating bulk oscillatory activity at alpha, beta and gamma frequencies [19,37,76]. Finally, pharmacological modulation of alpha oscillatory activity yields different results in thalamus and cortex. In particular, low doses of benzodiazepines diminish alpha-band activity but promotes beta-band activity in EEG recorded from humans, but in cat thalamus instead appear to promote lower frequency local-field potential activity by enhancing total theta power [30,31].

For these, and a variety of other reasons [55], it has been contended that alpha activity in the EEG instead reflects the dynamics of activity in distributed reciprocally-connected populations of cortical and thalamic neurons. Two principal lines of evidence have arisen in support of this view. First, empirical evidence from multichannel MEG [16,83] and high density EEG [55] has revealed that scalp-recorded alpha activity arises from a large number or continuum of equivalent current dipoles in cortex. Secondly, a raft of physiologically plausible computational [38] and theoretical models [40,54,66,80], developed to varying levels of detail, reveal that electroencephalographically realistic oscillatory activity can arise from the synaptic interactions between distributed populations of excitatory and inhibitory neurons.

6.2.3 Modeling alpha activity

The staggering diversity of often contradictory empirical phenomena associated with alpha activity speaks against the notion of finding a simple unifying biological cause. This complexity necessitates the use of mathematical models and computer simulations in order to understand the underlying processes. Such a quantitative approach may help address three essential, probably interrelated, questions regarding the alpha rhythm and alpha activity. First, can a dynamical perspective shed light on the functional roles of alpha and its attenuation (or blocking)? While over the years a variety of theories and hypotheses have been advanced, all are independent of any physiological mechanism accounting for its genesis. The most widespread belief has been that the alpha rhythm has a clocking or co-ordinating role in the regulation of cortical neuronal population dynamics, see for example Chapter 11 of [70]. This simple hypothesis is probably the reason that the idea of a subcortical alpha pacemaker has survived despite a great deal of contradictory empirical evidence. The received view on alpha blocking and event-related desynchronisation (ERD), is that they represent the electrophysiological correlates of an activated, and hence more excitable, cortex [59]. However, this view must be regarded as, at best, speculative due to the numerous reports of increased alpha activity [70] in tasks requiring levels of attention and mental resource above a baseline that already exhibits strong alpha activity.

Second, what is the relationship between alpha and the other forms of scalp-recordable electrical activity? Activity in the beta band (13–30 Hz) is consistently linked to alpha-band activity. For instance, blocking of occipital alpha is almost always associated with corollary reductions in the amplitude of beta activity [60]. Further, peak occipital beta activity is, on the basis of large cross-sectional studies involving healthy subjects, almost exactly twice the frequency of peak occipital alpha, in addition to exhibiting significant phase coherence [52]. Significant phase correlation between alpha and gamma ($>30$ Hz) activity has also been reported in EEG recorded from cats and monkeys [67]. Less is known about the connection to the low-frequency delta and theta rhythms.

Finally, what is the link between activity at the single neuronal level and the corresponding large-scale population dynamics? Can knowledge of the latter enable us to make inferences regarding the former, and can macroscopic predictions be deduced from known microscopic or cellular level perturbations? This becomes particularly pertinent for attempts to understand the mesoscopic link between cell (membrane) pharmacology and physiology, and co-existing large-scale alpha activity [20].

6.3 Mean-field models of brain activity

Broadly speaking, models and theories of the electroencephalogram can be divided into two complementary kinds. The first kind uses spatially discrete network models of neurons with a range of voltage- and ligand-dependent ionic conductances. While these models can be extremely valuable, and are capable of giving rise to alpha-like activity [38], they are limited since the EEG is a bulk property of populations of cortical neurons [45]. Further, while a successful application of this approach may suggest physiological and anatomical prerequisites for electrorhythmogenesis, it cannot provide explicit mechanistic insight due to its own essential complexity. In particular, a failure to produce reasonable EEG/electrocorticogram (ECoG) does not per se suggest which additional empirical detail must be incorporated. A more preferable approach exists in the continuum or mean-field method [33,40,54,66,80]. Here it is the bulk or population activity of a region of cortex that is modeled, more optimally matching the scale and uncertainties of the underlying physiology. Typically the neural activity over roughly the extent of a cortical macrocolumn is averaged.

However three general points need to be noted regarding the continuum mean-field approach and its application to modeling the EEG. First, in general, all approaches dynamically model the mean states of cortical neuronal populations, but only in an effective sense. Implicitly modeled are the intrinsic effects of non-neuronal parts of cortex upon neuronal behavior, e.g., glia activity or the extracellular diffusion of neurotransmitters. In order to treat the resulting equations as closed, non-neuronal contributions must either project statically into neuronal ones (e.g., by changing the value of some neuronal parameter) or be negligible in the chosen observables (e.g., because their time-scale is slower than the neuronal dynamics of interest). Where this cannot be assumed, one must “open” the model equations by modifying the neuronal parameters dynamically.

Second, intrinsic parts or features of the brain that are not modeled (e.g., the thalamus or the laminarity of cortex) or extrinsic influences (e.g., drugs or sensory driving) likewise must be mapped onto the neuronal parameters. One may well question whether any modeling success achieved by freely changing parameters merely indicates that a complicated enough function can fit anything. There is no general answer to this criticism, but the following Ockhamian guidelines prove useful: the changes should be limited to few parameters, there should be some reason other than numerical expediency for choosing which parameters to modify, the introduced variations should either be well understood or of small size relative to the standard values, and the observed effect of the chosen parameter changes should show some stability against modifications of other parameters. If systematic tuning of the neuronal parameters cannot accommodate intrinsic or extrinsic contributions, then the neuronal model itself needs to be changed.

Third, the neuronal mean-fields modeled generally match the limited spatial resolution of functional neuroimaging, since they average over a region C surrounding a point $\textbf{x}_\mathrm{cort}$ on cortex¹: $\underline{f}\equiv f\left(\textbf{x}_\mathrm{cort},t\right)=1/C\times\int_C d\textbf{x}^{\prime} f\left(\textbf{x}^{\prime},t\right)$. In the foreseeable future images of brain activity will not have spatial resolutions better than 1–2 $\mathrm{mm}^2$, about the size of a cortical macrocolumn containing $T=10^6$ neurons. Temporal coherence dominates quickly for signals from that many neurons. A signal from N coherent neurons is enhanced linearly $\sim N=p\times T$ over that of a single neuron, whereas for M incoherent neurons enhancement is stochastic $\sim\sqrt{M}=\sqrt{(1-p)\times T}$. $p=1\%$ coherent neurons thus produce a 10 times stronger signal than the 99% incoherent neurons. If p is too low, then the coherent signal will be masked by incoherent noise. In the analysis of experimental data, such time-series are typically discarded.

A mean-field prediction hence need not match all neuronal activity. It is sufficient if it effectively describes the coherent neurons actually causing the observed signal. Neurons in strong temporal coherence are likely of similar kind and in a similar state, thus approximating them by equations for a single “effective” neuron makes sense. Other neurons or cortical matter influence the coherent dynamics only incoherently, making it more likely that disturbances on average only result in static parameter changes. A crucial modeling choice is hence the number of coherent groups within C, since coherent groups will not “average out” in like manner. Every coherent neural group is modeled by equations describing its separate characteristic dynamics, which are then coupled to the equations of other such groups according to the assumed connectivity. For example, the Liley model in Fig. 6.1 shows two different C as two columns drawn side by side. We hence see that, per C, it requires equations for one excitatory group and one inhibitory group, respectively, which will then be coupled in six ways (four of which are local).

The construction of a mean-field model requires the specification of three essential structural determinants: (i) the number of coherent neuronal populations modeled; (ii) the degree of physiological complexity modeled for each population; and (iii) the connectivity between these populations. While the majority of mean-field theories of EEG model the dynamics of at least two cortical neuronal populations (excitatory and inhibitory), details of the topology of connectivity can vary substantially. Figure 6.1 illustrates the connectivity of a number of competing modeling approaches.

Fig. 6.1

Schematic outline of the connection topologies of a number of mean-field approaches. “E” stands for excitatory, “I” for inhibitory neuronal populations. Open circles represent excitatory connections, filled circles inhibitory ones.

6.3.1 Outline of the extended Liley model

The theory of Liley et al [18,40,43] is a relatively comprehensive model of the alpha rhythm, in that it is capable of reproducing the main spectral features of spontaneous EEG in addition to being able to account for a number of qualitative and quantitative EEG effects induced by a range of pharmacological agents, such as benzodiazepines and a range of general anesthetic agents [7,39,42,75].

Like many other models, the Liley model considers two (coherent) neuronal populations within C, an excitatory one and an inhibitory one. These two populations are always indicated below by setting the subscript $k=e$ and $k=i$, respectively. In the absence of postsynaptic potential (PSP) inputs $\underline{I}$, the mean soma membrane potentials $\underline{h}$ are assumed to decay exponentially to their resting value $h^\mathrm{r}$ with a time constant $\tau$:

$$\tau_k\frac{\partial}{\partial t} \underline{h_k} \:=\: h^\mathrm{r}_k-\underline{h_k} +\frac{h^\mathrm{eq}_{ek}-\underline{h_k}}{\left|h^\mathrm{eq}_{ek}-h^\mathrm{r}_k\right|}\times\underline{I_{ek}} +\frac{h^\mathrm{eq}_{ik}-\underline{h_k}}{\left|h^\mathrm{eq}_{ik}-h^\mathrm{r}_k\right|}\times\underline{I_{ik}}\;.$$

((6.1))

Double subscripts indicate first source and then target, thus for example $\underline{I_{ei}}$ indicates PSP inputs from an excitatory to an inhibitory population. Note that PSP inputs, which correspond to transmitter activated postsynaptic channel conductance, are weighted by the respective ionic driving forces $h^\mathrm{eq}_{jk}-\underline{h_k}$, where $h^\mathrm{eq}_{ek,ik}$ are the respective reversal potentials. All these weights are normed to one at the relevant soma membrane resting potentials.

Next consider four types ($k=e,i$) of PSP inputs:

$$\left(\frac{\partial}{\partial t}+\gamma_{ek}\right)\left(\frac{\partial}{\partial t}+\tilde{\gamma}_{ek}\right) \underline{I_{ek}}=\Gamma_{ek}\underbrace{\gamma_{ek} \exp\left(\tilde{\gamma}_{ek}\delta_{ek}\right)}_{=\tilde{\gamma}_{ek} \exp\left(\gamma_{ek}\delta_{ek}\right)} \times\left[N^\beta_{ek} \underline{S_e}+\underline{p_{ek}}+\underline{\Phi_{ek}}\right]\;,\\$$

((6.2))

$$\left(\frac{\partial}{\partial t}+\gamma_{ik}\right)\left(\frac{\partial}{\partial t}+\tilde{\gamma}_{ik}\right) \underline{I_{ik}}=\Gamma_{ik}\underbrace{\gamma_{ik} \exp\left(\tilde{\gamma}_{ik}\delta_{ik}\right)}_{=\tilde{\gamma}_{ik} \exp\left(\gamma_{ik}\delta_{ik}\right)} \times\left[N^\beta_{ik} \underline{S_i}+\underline{p_{ik}}\right]\;.$$

((6.3))

The terms in the square brackets correspond to different classes of sources for incoming action potentials: local $\underline{S}$, extra-cortical $\underline{p}$, and cortico-cortical $\underline{\Phi}$. Only excitatory neurons project over long distances, thus there is no $\underline{\Phi_{ik}}$ in Eq. (6.3). However, long-range inhibition can still occur, namely by an excitation of an inhibitory populations via $\underline{\Phi_{ei}}$.

For a single incoming Dirac impulse $\delta(t)$, the above equations respond with

$$R(t)=\Gamma\gamma \exp\left(\tilde{\gamma}\delta\right)\times \frac{\exp\left(-\gamma t\right)-\exp\left(-\tilde{\gamma}t\right)}{\tilde{\gamma}-\gamma}\Theta(t)\;,$$

((6.4))

where $\Theta$ is the Heaviside function. Here, $\delta$ is the rise-time to the maximal PSP response:

$$\delta=\frac{\ln\tilde{\gamma}-\ln\gamma}{\tilde{\gamma}-\gamma} \quad\Longrightarrow R(t=\delta)=\Gamma\;.$$

((6.5))

$R(t)$ describes PSPs from the “fast” neurotransmitters AMPA/kainate and GABA${}_\mathrm{A}$, respectively. Sometimes instead the simpler “alpha form”² is used:

$$R_0(t)=\Gamma\gamma\exp(1)\times t \exp\left(-\gamma t\right)\Theta(t) \quad\Longrightarrow R_0(t=\delta_0=1/\gamma)=\Gamma\;.$$

((6.6))

Note that as $\tilde{\gamma}\rightarrow\gamma$: $R\rightarrow R_0$. Equation (6.4) must be invariant against exchanging $\tilde{\gamma}\leftrightarrow\gamma$, see Eqs (6.2) and (6.3), since the change induced by $\tilde{\gamma}\neq\gamma$ cannot depend on naming the decay constant values. In the “alpha form”, the time at which the response decays again to $\Gamma/e$ is coupled to the rise-time: $\zeta_0=-W_{-1}\left(-\frac{1}{{\rm e}^2}\right)\times\delta_0\simeq 3.1462/\gamma$, with the Lambert W function. Anaesthetic agents can change the decay time of PSPs independently and hence require the biexponential form [7]:

$$\tilde{\gamma}\simeq\gamma: \zeta= -W_{-1}\left(-\frac{1}{{\rm e}^2}\right)\times\delta+ \mathcal{O}\left(\left|\tilde{\gamma}-\gamma\right|^2\right)\;, \tilde{\gamma}\gg\gamma: \zeta\simeq\frac{\tilde{\gamma}/\gamma}{\tilde{\gamma}-\gamma}\;.$$

((6.7))

In [7] further results were derived for the specific parametrisation $\tilde{\gamma}=\exp(\varepsilon)\gamma$.

If time delays for local connections are negligible, then the number of incoming action potentials will be the number of local connections $N^\beta$ times the current local firing rate $\underline{S}$, see Eqs (6.2) and (6.3). Assume that threshold potentials in the neural mass are normally distributed with mean $\mu$ and standard deviation $\sigma$. Then the fraction of neurons reaching their firing threshold $h^\mathrm{th}$ is

$$\int_{-\infty}^{\underline{h}} dh^\mathrm{th}\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(h^\mathrm{th}-\mu)^2}{2\sigma^2}\right) =\frac{1}{2}\left[1+\mathrm{erf}\left(\frac{\underline{h}-\mu}{\sqrt{2}\sigma}\right)\right]\;.\vspace*{2pt}$$

((6.8))

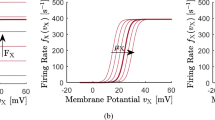
We approximate $(1+\mathrm{erf}\,x)/2\simeq [1+\exp(-2 x)]^{-1}$ and associate the theoretical limit of infinite $\underline{h}$ not with excitation block but with the maximal mean firing rate $S^\mathrm{max}$:

$$\underline{S_k}=S_k^\mathrm{max}\left[1+\exp\left(-\sqrt{2}\frac{\underline{h_k}-\mu_k}{\sigma_k}\right)\right]^{-1}\;.\vspace*{2pt}$$

((6.9))

By construction, this is a good approximation for regular $\underline{h}$ but will fail for unusually high mean potentials. Note that Eq. (6.9) reduces to $\underline{S_k}=S_k^\mathrm{max}\Theta(\underline{h}-\mu)$ for $\sigma\rightarrow 0$.

Next we consider extra-cortical sources $\underline{p}$. Unless some of these inputs are strongly coherent (e.g., for sensory input), their average over a region will be noise-like even if the inputs themselves are not. Our ansatz is hence

$$\underline{p_{ek}}=\mathcal{L}\left[\underline{\mathrm{rand}_n}\left(\bar{p}_{ek},\Delta p_{ek}\right)\right]+\underline{p_{ek}^\mathrm{coh}}\;,\vspace*{24pt}\\$$

((6.10))

$$\underline{p_{ik}}=\mathcal{L}\left[\underline{\mathrm{rand}_n}\left(\bar{p}_{ik},\Delta p_{ik}\right)\right]+\underline{p_{ik}^\mathrm{coh}}\;,\vspace*{2pt}$$

((6.11))

with spatiotemporal “background noise” potentially overlayed by coherent signals. The noise is normally distributed with mean $\bar{p}$ and standard deviation $\Delta p$, and shaped by some filter function $\mathcal{L}$. Since neurons cannot produce arbitrarily high firing frequencies, $\mathcal{L}$ should include a lowpass filter. In practice, we often set $\underline{p_{ik}}\equiv 0$, since likely extracortical projections are predominantly excitatory. Further, for stochastic driving noise in $\underline{p_{ee}}$ alone is sufficient. We take $\underline{p^\mathrm{coh}}\equiv 0$ unless known otherwise. In particular we do not assume coherent thalamic pacemaking. However, the $\underline{p^\mathrm{coh}}$ provide natural ports for future extensions, e.g., an explicit model of the thalamus could be interfaced here.

An “ideal” ansatz for cortico-cortical transmission is given by

$$\mathcal{G}_{ek}(r,t)=\frac{N^{\alpha}_{ek}}{2\pi}\tilde{\Lambda}_{ek}^2\times \exp\left(-\tilde{\Lambda}_{ek}r\right)\times \delta\left(t-\frac{r}{\tilde{v}_{ek}}\right)\;,$$

((6.12))

where r measures distances along cortex. With this Green’s function, impulses would propagate distortion-free and isotropically at velocity $\tilde{v}$. The metrics of connectivity are seen to be

$$n^{\alpha}_{ek}(r)= \int^{\infty}_{0}dt\,\mathcal{G}_{ek}(r,t) =\frac{N^{\alpha}_{ek}}{2\pi}\tilde{\Lambda}_{ek}^2\times \exp\left(-\tilde{\Lambda}_{ek}r\right)\;, \int^{\infty}_{0}dr\,2\pi r\,n^{\alpha}_{ek}(r)=N^{\alpha}_{ek}\;,$$

((6.13))

and thus the $N^{\alpha}_{ek}$ long-range connections per cortical neuron are distributed exponentially with a characteristic distance $\tilde{\Lambda}_{ek}$. One can Fourier transform Eq. (6.12)

$$\mathcal{G}_{ek}(k,\omega) =\frac{N^{\alpha}_{ek}\tilde{v}^2_{ek}\tilde{\Lambda}_{ek}^2\left({\rm i}\omega+\tilde{v}_{ek}\tilde{\Lambda}_{ek}\right)} {\left[\left({\rm i}\omega+\tilde{v}_{ek}\tilde{\Lambda}_{ek}\right)^2+\tilde{v}_{ek}^2 k^2\right]^{3/2}} \equiv\frac{\mathcal{N}(k,\omega)}{\mathcal{D}(k,\omega)}\;,\vspace*{4pt}$$

((6.14))

and write $\mathcal{N}\underline{\phi}=\mathcal{D}\underline{S}$ with ${\rm i}\omega\rightarrow\partial/\partial t$ and $k^2\rightarrow -\nabla^2$ to obtain an equivalent PDE. Unfortunately this $\mathcal{D}$ is non-local (i.e., evaluating this operator with a finite difference scheme at one discretization point would require values from all points over the domain of integration). By expanding for large wavelengths $2\pi/k$: $\mathcal{D}(k,\omega)\simeq({\rm i}\omega+\tilde{v}_{ek}\tilde{\Lambda}_{ek}) [({\rm i}\omega+\tilde{v}_{ek}\tilde{\Lambda}_{ek})^2+\frac{3}{2}\tilde{v}_{ek}^2 k^2]$, and with $v\equiv\sqrt{3/2}\tilde{v}$, $\Lambda\equiv\sqrt{2/3}\tilde{\Lambda}$, we obtain an inhomogeneous two-dimensional telegraph (or: transmission line) equation [40,66]:

$$\left[\frac{1}{v_{ek}^2}\frac{\partial^2}{\partial t^2}+\frac{2\Lambda_{ek}}{v_{ek}}\frac{\partial}{\partial t} -\nabla^2+\Lambda_{ek}^2\right]\underline{\Phi_{ek}}=N^\alpha_{ek}\Lambda_{ek}^2\underline{S_e}\;,\vspace*{6pt}$$

((6.15))

where the forcing term is simply the firing $\underline{S}$ of the sources.

Note that Eq. (6.15) is a special case. If we substitute

$$\underline{\Phi_{ek}}={\rm e}^{-\Lambda vt}\underline{\varphi_{ek}}\quad\Longrightarrow \left[\frac{1}{v_{ek}^2}\frac{\partial^2}{\partial t^2}-\nabla^2\right]\underline{\varphi_{ek}}={\rm e}^{\Lambda vt}N^\alpha_{ek}\Lambda_{ek}^2\underline{S_e}\;,\vspace*{4pt}$$

((6.16))

then $\underline{\varphi}$ obeys an inhomogeneous wave equation. (Equation (6.16) corrects a sign error in Eq. (61) of Ref. [66], which is likely to have influenced their numerical results.)

The impulse response is hence that of the 2-D wave equation multiplied by an exponential decay:

$$\mathcal{G}_{ek}(r,t)=\frac{N^{\alpha}_{ek}}{2\pi}\Lambda_{ek}^2\times \exp\left(-\Lambda_{ek}v_{ek}t\right)\times\frac{\Theta\left(t-r/v_{ek}\right)}{\sqrt{t^2-r^2/v_{ek}^2}}\;.\vspace*{2pt}$$

((6.17))

We can compare with (6.12) to see the effects of the approximation: Impulse propagation is now faster $v=\sqrt{3/2}\tilde{v}$ and distorted by a brief “afterglow” $\sim 1/\sqrt{t-r/v}$. Connectivity $n^{\alpha}_{ek}(r)=N^{\alpha}_{ek}\Lambda_{ek}^2/(2\pi)\times \mathrm{K}_0(\Lambda_{ek}r)$ follows now a zeroth-order modified Bessel function of the second kind. Compared to Eq. (6.13), it is now radially weaker for $1.0\lesssim r\tilde{\Lambda}\lesssim 4.9$, and stronger otherwise.

This completes our description of the extended Liley model: Eqs (6.1), (6.2), (6.3), and (6.15) determine its spatiotemporal dynamics, (6.9) computes local firing rates, whereas (6.10) and (6.11) define the external inputs. An important feature of this model is that there are no “toy parameters” in the constitutive equations, i.e., every parameter has a biological meaning and its range can be constrained by physiological and anatomical data. All model parameters could depend on the position on cortex or even become additional state variables, e.g., $\mu\rightarrow\mu(\textbf{x}_\mathrm{cort})\rightarrow\underline{\mu}$. The only exceptions are the parameters of Eq. (6.15), since the equation is derived assuming globally constant parameters. However, this mathematical restriction can be loosened somewhat [17,65].

6.3.2 Linearization and numerical solutions

Linearization investigates small disturbances around fixed points of the system, i.e., around state variables $\underline{\textbf{z}}=\textbf{z}^*$ which are spatiotemporally constant solutions of the PDEs. For hyperbolic fixed points (i.e., all eigenvalues have nonzero real part), the Hartman–Grobman theorem states that a linear expansion in $\underline{\textbf{z}}$ with $\underline{\textbf{z}}=\textbf{z}^*+\underline{\textbf{z}}$ will capture the essential local dynamics. Thus we define a state vector

$$\underline{\textbf{z}}\equiv\left(\underline{h_e},\underline{h_i},\underline{I_{ee}},\underline{I_{ei}},\underline{I_{ie}},\underline{I_{ii}},\underline{\Phi_{ee}},\underline{\Phi_{ei}}\right)^T\;,$$

((6.18))

and rewrite Eqs (6.10) and (6.11) with $\underline{p}\equiv\bar{p}+\underline{P}$, setting $\underline{P}\equiv 0$ for now. Then the fixed points are determined by

$$\begin{aligned}h_k^*&=h^\mathrm{r}_k +\frac{h^\mathrm{eq}_{ek}-h_k^*}{\left|h^\mathrm{eq}_{ek}-h^\mathrm{r}_k\right|} I_{ek}^* +\frac{h^\mathrm{eq}_{ik}-h_k^*}{\left|h^\mathrm{eq}_{ik}-h^\mathrm{r}_k\right|} I_{ik}^*\quad Phi_{ek}^*=N^\alpha_{ek}S_k^*=\frac{N^\alpha_{ek}S_k^\mathrm{max}}{1+\exp\left(-\sqrt{2}\frac{h_k^*-\mu_k}{\sigma_k}\right)}\;,\\ I_{ek}^*&=\Gamma_{ek} \frac{{\rm e}^{\tilde{\gamma}_{ek}\delta_{ek}}}{\tilde{\gamma}_{ek}} \left[N^\beta_{ek} S_e^*+\bar{p}_{ek}+\Phi_{ek}^*\right]\;,\quad I_{ik}^*=\Gamma_{ik} \frac{{\rm e}^{\tilde{\gamma}_{ik}\delta_{ik}}}{\tilde{\gamma}_{ik}} \left[N^\beta_{ik} S_i^*+\bar{p}_{ik}\right]\end{aligned}$$

((6.19))

which immediately reduces to just two equations in $h_e^*$ and $h_i^*$. If multiple solutions exist, we define a “default” fixed point $\textbf{z}^{*,r}$ by choosing the $h_e^*$ closest to rest $h_e^\mathrm{r}$.

We use the following ansatz for the perturbations

$$\underline{\textbf{z}}\equiv\textbf{a}\times\exp\left(\lambda t\right)\times\exp\left({\rm i}\textbf{k}\cdot\textbf{x}_\mathrm{cort}\right)\;,$$

((6.20))

and expand linearly in components $[\textbf{a}]_m$. For example, the equation for $\underline{\Phi_{ee}}$ becomes

$$\left(\frac{1}{v_{ee}^2}\lambda^2+\frac{2\Lambda_{ee}}{v_{ee}}\lambda+k^2+\Lambda_{ee}^2\right)[\textbf{a}]_7 =N_{ee}^\alpha\Lambda_{ee}^2 \frac{S_e^\mathrm{max}\sqrt{2}\upsilon}{\sigma_e(1+\upsilon)^2}[\textbf{a}]_1\;,$$

((6.21))

with $\upsilon\equiv\exp[-\sqrt{2}(h_e^*-\mu_e)/\sigma_e]$. Treating all PDEs in a similar fashion, we end up with an equation set

$$\sum_j\textsf{B}_{ij}(\lambda,k)[\textbf{a}]_j=0,\quad\mathrm{with} i,j=1,\ldots,8\;.$$

((6.22))

In matrix notation $\textsf{B}(\lambda,k)\textbf{a}=0$. Nontrivial solutions exist only for

$${\mathcal E}(\lambda,k)\equiv \textrm{det}\, \textsf{B}(\lambda,k) = 0 \;.$$

((6.23))

However, searching for roots $\lambda(k)$ of Eq. (6.23) is efficient only in special cases. Instead, introduce auxiliary variables $\underline{Z}_{\,9,\ldots,14}=\partial \underline{Z}_{\,3,\ldots,8}/\partial t$, with $\underline{Z}_{\,9,\ldots,14}^*=0$, to eliminate second-order time derivatives. Our example (6.21) becomes

$$[\textbf{a}]_{15}=\lambda [\textbf{a}]_7\;, \left(\frac{1}{v_{ee}^2}\lambda+\frac{2\Lambda_{ee}}{v_{ee}}\right)[\textbf{a}]_{15}+\left(k^2+\Lambda_{ee}^2\right)[\textbf{a}]_7 =N_{ee}^\alpha\Lambda_{ee}^2 \frac{S_e^\mathrm{max}\sqrt{2}\upsilon}{\sigma_e(1+\upsilon)^2}[\textbf{a}]_1\;.$$

((6.24))

Treating all PDEs likewise, we can write a new but equivalent form

$$\sum_j\textsf{B}_{ij}(\lambda,k)[\textbf{a}]_j=\sum_j\left[\textsf{A}_{ij}(k)-\lambda \delta_{ij}\right][\textbf{a}]_j=0,\quad\mathrm{with} i,j=1,\ldots,14\;,\vspace*{4pt}$$

((6.25))

with the Kronecker $\delta_{ij}$. In matrix notation $\textsf{A}(k)\textbf{a}=\lambda\textbf{a}$, hence $\lambda(k)$ solutions are eigenvalues. Powerful algorithms are readily available to solve (6.25) as

$$\sum_l\textsf{A}_{il}\textsf{R}_{lj}=\lambda_j\textsf{R}_{ij}\;, \sum_l\textsf{L}_{il}\textsf{A}_{lj}=\lambda_i\textsf{L}_{ij}\;, \lambda_j \sum_l\textsf{L}_{il}\textsf{R}_{lj}=\lambda_i\sum_l\textsf{L}_{il}\textsf{R}_{lj},\vspace*{4pt}$$

((6.26))

with $i,j,l=1,\ldots,14$, and all quantities are functions of k. The $\lambda_j$ denote 14 eigenvalues with corresponding right $[\textbf{r}_j]_i=\textsf{R}_{ij}$ (columns of $\textsf{R}$) and left $[\textbf{l}_j]_i=\textsf{L}_{ji}$ (rows of $\textsf{L}$) eigenvectors. The third equation in (6.26) implies orthogonality for non-degenerate eigenvalues $\sum_l\textsf{L}_{il}\textsf{R}_{lj}=\delta_{ij} n_j$. In this case one can orthonormalize $\textsf{L}\textsf{R}=\textsf{R}\textsf{L}=\mathbb{1}$. For spatial distributions of perturbations, different $k\/$-modes will generally mix quickly with time.

For numerical simulations one can model the cortical sheet as square, connected at the edges to form a torus, and discretize it $N\times N$ with sample length d _s [7,9]. Time then is also discretized $t=n t_s$ with $n=0,1,\ldots$ We substitute Euler forward-time derivatives and five-point Laplacian formulae, and solve the resulting algebraic equations for the next time-step. The five-point Laplacian is particularly convenient for parallelization [7], since only one-point-deep edges of the parcellated torus need to be communicated between nodes. The Euler-forward formulae will converge slowly $\mathcal{O}(t_s^2,d_s^2)$ but robustly, which is important since the system dynamics can change drastically for different parameter sets. The Courant–Friedrichs–Lewy condition for a wave equation, cf Eq. (6.16), is simply $t_s < d_s/(\sqrt{2}v)$. If we consider a maximum speed of $v = 10$ m/s, and a spatial spacing of $d_s=$ mm for Eq. (6.15), then $t_s < 7.1\times 10^{-5}$ s. In practice, we choose $t_s=5\times 10^{-5}$s. We initialize the entire cortex to its (default) fixed point value $\textbf{z}(\textbf{x}_\mathrm{cort})=\textbf{z}^*$ at $t=0$. For parameter sets that have no fixed point in physiological range, we instead set $h_e(\textbf{x}_\mathrm{cort})=h_e^r$ and $h_i(\textbf{x}_\mathrm{cort})=h_i^r$, and other state variables to zero. Sometimes it is advantageous to have no external inputs: then any observed dynamics must be self-sustained. In this case some added spatial variation in $h_e(\textbf{x}_\mathrm{cort})$ helps to excite $k\neq 0$ modes quickly.

6.3.3 Obtaining physiologically plausible dynamics

For “physiological” parameters, a wide range of model dynamics can be encountered. However, proper parameterisations should produce electroencephalographically plausible dynamics. In general, two approaches can be employed to generate such parameter sets. The first is to fit the model to real electroencephalographic data. However, there is still considerable uncertainty regarding the reliability, applicability and significance of using experimentally obtained data for fitting or estimating sets of ordinary differential equations [79]. Alternatively one can explore the physiologically admissible multi-dimensional parameter space in order to identify parameter sets that give rise to “suitable” dynamics, e.g., those showing a dominant alpha rhythm.

With regard to the extended Liley model outlined in the previous section, one could stochastically or heuristically explore the parameter space by solving the full set of spatiotemporal equations. However, the computational costs of this approach are forbidding at this point in time. Alternatively, the parameter space of a simplified model, e.g., spatially homogeneous without the Laplacian in Eq. (6.15), can be searched. This can provide sufficient simulation speed gains to allow iterative parameter optimization. Finally, if the defining system can be approximated by linearization, then one can estimate the spatiotemporal dynamics merely from the resulting eigensystem. Such an analysis is exceedingly rapid compared with the direct solution of the equations. One can then simply test parameter sets randomly sampled from the physiologically admissible parameter space. Thus, for example [7] shows how one can model plausible EEG recorded from a single electrode: the power spectrum, $S(\omega)$, can be estimated for subcortical noise input $\hat{\underline{\textbf{p}}}$ by

$$S(\omega)= \frac{1}{2\pi}\int\,dk\;k\left|\Psi(k) \left\{\textsf{R}\cdot\mathrm{diag}\left[\frac{1}{i\omega-\lambda_{n}(k)}\right]\cdot\textsf{L}\cdot\hat{\underline{\textbf{p}}}\right\}_{1}\right|^{2}\;,$$

((6.27))

and then evaluated for physiological veracity. The left and right eigen-matrices, $\textsf{L}$ and $\textsf{R}$, are defined in Eq. (6.26), here $\textsf{L}\textsf{R}=\mathbb{1}$ and $\Psi(k)$ is the electrode point-spread function. The obvious drawback is that nonlinear solutions of potential physiological relevance will be missed. However, as will be illustrated in the next section, “linear” parameter sets can be continued in one- and two-dimensions to reveal a plethora of electroencephalographically plausible nonlinear dynamical behavior.

6.3.4 Characteristics of the model dynamics

Numerical solutions to Eqs (6.1–6.15) for a range of physiologically admissible parameter values reveal a large array of deterministic and noise-driven dynamics, as well as bifurcations, at alpha-band frequencies [8,18,40,43]. In particular, alpha-band activity appears in three distinct dynamical scenarios: as linear noise-driven, limit-cycle, or chaotic oscillations. Thus this model offers the possibility of characterizing the complex changes in dynamics that have been inferred to occur during cognition [79] and in a range of central nervous system diseases, such as epilepsy [46]. Further, our theory predicts that reverberant activity between inhibitory neuronal populations is causally central to the alpha rhythm, and hence the strength and form of inhibitory $\rightarrow$ inhibitory synaptic interactions will be the most sensitive determinants of the frequency and damping of emergent alpha-band activity. If resting eyes-closed alpha is indistinguishable from a filtered random linear process, as some time-series analyses seem to suggest [72,73], then our model implies that electroencephalographically plausible “high quality” alpha ($Q>5$) can be obtained only in a system with a conjugate pair of weakly damped (marginally stable) poles at alpha frequency [40].

Numerical analysis has revealed regions of parameter space where abrupt changes in alpha dynamics occur. Mathematically these abrupt changes correspond to bifurcations, whereas physically they resemble phase transition phenomena in ordinary matter. Figure 6.2 displays such a region of parameter space for the 10-dimensional local reduction of our model ($\Phi_{ek}=0$). Variations in $\langle\underline{p_{ee}}\rangle$ (excitatory input to excitatory neurons) and $\langle\underline{p_{ei}}\rangle$ (excitatory to inhibitory) result in the system producing a range of dynamically differentiated alpha activities. If $\langle\underline{p_{ei}}\rangle$ is much larger than $\langle\underline{p_{ee}}\rangle$, a stable equilibrium is the unique state of the EEG model. Driving the model in this state with white noise typically produces sharp alpha resonances [40]. If one increases $\langle\underline{p_{ee}}\rangle$, this equilibrium loses stability in a Hopf bifurcation and periodic motion sets in with a frequency of about 11 Hz. For still larger $\langle\underline{p_{ee}}\rangle$ the fluctuations can become irregular and the limiting behavior of the model is governed by a chaotic attractor. The different dynamical states can be distinguished by computing the largest Lyapunov exponent (LLE), which is negative for equilibria, zero for (quasi)-periodic fluctuations, and positive for chaos. Bifurcation analysis [81] indicates that the boundary of the chaotic parameter set is formed by infinitely many saddle–node and period-doubling bifurcations, as shown in Fig. 6.2(a). All these bifurcations converge to a narrow wedge for negative, and hence unphysiological, values of $\langle\underline{p_{ee}}\rangle$ and $\langle\underline{p_{ei}}\rangle$, literally pointing to the crucial part of the diagram where a Shilnikov saddle–node homoclinic bifurcation takes place.

Fig. 6.2

[Color plate] (a) The largest Lyapunov exponent (LLE) of the dynamics of a simplified local model ($\Phi_{ek}=0$) for a physiologically plausible parameter set exhibiting robust (fat-fractal) chaos [18]. Superimposed is a two parameter continuation of saddle–node and period-doubling bifurcations. The leftmost wedge of chaos terminates for negative values of the exterior forcings, $\langle\underline{p_{ee}}\rangle$ and $\langle\underline{p_{ei}}\rangle$. (b) Schematic bifurcation diagram at the tip of the chaotic wedge. bt = Bogdanov–Takens bifurcation, gh = generalized Hopf bifurcation, and SN = saddle node. Between $\mathrm{t}_1$ and $\mathrm{t}_2$ multiple homoclinic orbits coexist and Shilnikov’s saddle–node bifurcation takes place. (c) Schematic illustration of the continuation of the homoclinic orbit between points n₁ and t_1. (Figure adapted from [81] and [18].)

Figure 6.2(b) shows a sketch of the bifurcation diagram at the tip of the wedge: the blue line with the cusp point c separates regions with one and three equilibria, and the line of Hopf bifurcations terminates on this line at the Bogdanov—Takens point bt. The point gh is a generalised Hopf point, where the Hopf bifurcation changes from sub- to super-critical. The green line which emanates from bt represents a homoclinic bifurcation , which coincides with the blue line of saddle—node bifurcations on an open interval, where it denotes an orbit homoclinic to a saddle node. In the normal form, this interval is bounded by the points $\mbox{{\bf n}}_1$ and $\mbox{{\bf n}}_2$, at which points the homoclinic orbit does not lie in the local center manifold. While the normal form is two-dimensional and only allows for a single orbit homoclinic to the saddle—node equilibrium, the high dimension of the macrocolumnar EEG model ($\Phi_{ek}=0$) allows for several orbits homoclinic to the saddle—node. If we consider the numerical continuation of the homoclinic along the saddle—node curve, starting from $\mbox{{\bf n}}_1$ as shown in Figure 6.2(b), it actually overshoots $\mbox{{\bf n}}_2$ and folds back at $\mbox{{\bf t}}_1$, where the center-stable and center-unstable manifolds of the saddle node have a tangency. In fact, the curve of homoclinic orbits folds several times before it terminates at $\mbox{{\bf n}}_2$. This creates an interval, bounded by $\mbox{{\bf t}}_1$ and $\mbox{{\bf t}}_2$, in which up to four homoclinic orbits coexist–-signaling the existence of infinitely many periodic orbits, which is the hallmark of chaos.

It is important to understand that in contrast to the homoclinic bifurcation of a saddle focus, commonly referred to as the Shilnikov bifurcation , this route to chaos has not been reported before in the analysis of any mathematical model of a physical system. While the Shilnikov saddle node bifurcation occurs at negative, and thus unphysiological, values of $\langle\underline{p_{ee}}\rangle$ and $\langle\underline{p_{ei}}\rangle$, it nevertheless organizes the qualitative behavior of the EEG model in the biologically meaningful parameter space. Further, it is important to remark that this type of organization persists in a large part of the parameter space: if a third parameter is varied, the codimension-two points c, bt and gh collapse onto a degenerate Bogdanov—Takens point of codimension three, which represents an organizing center controling the qualitative dynamics of an even larger part of the parameter space.

Parameter sets that have been chosen to give rise to physiologically realistic behavior in one domain, can produce a range of unexpected, but physiologically plausible, activity in another. For example, parameters were chosen to accurately model eyes-closed alpha and the surge in total EEG power during anesthetic induction [7]. Among other conditions, parameter sets were required to have a sharp alpha resonance ($Q>5$) and moderate mean excitatory and inhibitory neuronal firing rates $<20/$s. Surprisingly, a large fraction of these sets also produced limit cycle (nonlinear) gamma band activity under mild parameter perturbations [8]. Gamma band ($>30$ Hz) oscillations are thought to be the sine qua non of cognitive functioning. This suggests that the existence of weakly damped, noise-driven, linear alpha activity can be associated with limit cycle 40-Hz activity, and that transitions between these two dynamical states can occur. Figure 6.3 illustrates a bifurcation diagram for one such set (column 11 of Table V in [7], see also Table 1 in [8]) for the spatially homogeneous reduction $\nabla^2 \rightarrow 0$ of Eq. (6.15). The choice of bifurcation parameters is motivated by two observations: (i) differential increases in $\Gamma_{ii,ie}$ have been shown to reproduce a shift from alpha to beta band activity, similar to what is seen in the presence of low levels of $\mbox{GABA}_\text{A}$ agonists such as benzodiazepines [42]; and (ii) the dynamics of linearized solutions for the case when $\nabla^2 \neq 0$ are particularly sensitive to variations of parameters affecting inhibitory$\rightarrow$inhibitory neurotransmission [40], such as $N^{\beta}_{ii}$ and $\langle\underline{p_{ii}}\rangle$.

Fig. 6.3

6.3 Partial bifurcation diagram for the spatially homogeneous model, $\nabla^2\rightarrow 0$ in Eq. (6.15), as a function of scaling parameters k and r, defined by $\Gamma_{ie,ii} \rightarrow r\Gamma_{ie,ii}$ and $N^{\beta}_{ii}\rightarrow kN^{\beta}_{ii}$, respectively. Codimension-two points have been labeled fh for fold-Hopf, gh for generalized Hopf, and bt for Bogdanov—Takens. The right-most branch of Hopf points corresponds to emergence of gamma frequency ($\approx 37$ Hz) limit-cycle activity via subcritical Hopf bifurcation above the point labeled gh. A homoclinic doubling cascade takes place along the line of homoclinics emanating from bt. Insets on the left show schematic blowups of the fh and bt points. Additional insets show time-series of deterministic (limit-cycle and chaos) and noise-driven dynamics for a range of indicated parameter values.

Fig. 6.4

Numerical solutions of 2-D model equations (Sect. 3.1) for a human-sized cortical torus with $k = 1$ and $r = 0.875$ (see Fig. 6.3). Here, $\underline{h_e}$ is mapped every 60 ms (grayscale: $-$76.9 mV black to $-$21.2 mV white). For $r = 0.875$, linearization becomes unstable for a range of wavenumbers around $0.6325/$cm. Starting from random $\underline{h_{e}}$, one initially sees transient spatially-organized alpha oscillations ($t = 0$, starting transient removed) from which synchronized gamma activity emerges. Gamma-frequency spatial patterns, with a high degree of phase correlation (“gamma hotspots”) form with a frequency consistent with the predicted subcritical Hopf bifurcations of the spatially homogeneous equations, compare Fig. 6.3. (Figure reproduced from [8].)

Specifically, Fig. 6.3 illustrates the results of a two-parameter bifurcation analysis for changes in the inhibitory PSP amplitudes via $\Gamma_{ie,ii} \rightarrow r\Gamma_{ie,ii}$ and changes in the total number of inhibitory$\rightarrow$inhibitory connections via $N^{\beta}_{ii}\rightarrow kN^{\beta}_{ii}$. The parameter space has physiological meaning only for positive values of r and k. The saddle—node bifurcations of equilibria have the same structure as for the 10-dimensional homogeneous reduction discussed previously, in that there are two branches joined at a cusp point. Furthermore, we have two branches of Hopf bifurcations, the one at the top being associated with the birth of alpha limit cycles and the other with gamma limit cycles. This former line of Hopf points enters the wedge-shaped curve of saddle—nodes of equilibria close to the cusp point and has two successive tangencies in fold-Hopf points (fh). The fold-Hopf points are connected by a line of tori. The same curve of Hopf points ends in a Bogdanov—Takens (bt) point, from which a line of homoclinics emanate. Contrary to the previous example, this line of homoclinics does not give rise to a Shilnikov saddle—node bifurcation. Instead it gives rise to a different scenario leading to complex behavior (including chaos) , called the homoclinic doubling cascade.

In this scenario, a cascade of period-doubling bifurcations collides with a line of homoclinics. As a consequence, not only are infinitely many periodic orbits created, but so are infinitely many homoclinic connections [56]. All these periodic and homoclinic orbits coexist with a stable equilibrium. The second line of Hopf bifurcations in the gamma frequency range ($>30$ Hz) does not interact with the lines of saddle nodes in the relevant portion of the parameter space. Both branches of Hopf points change from super- to subcritical at gh around $r^* = 0.27$, so that bifurcations are “hard” for $r>r^*$ in either case. These points are also the end points of folds for the periodic orbits, and the gamma frequency ones form a cusp (cpo) inside the wedge of saddle—nodes of equilibria.

Because the partial bifurcation diagram of Fig. 6.3 has necessarily been determined for the spatially homogeneous model equations, it will not accurately reflect the stability properties of particular spatial modes (nonzero wavenumbers) in the full set of model 2-D PDEs. For example, at the spot marked “Fig 4” in Fig. 6.3, for wavenumbers around 0.6325/cm the eigenvalues of the corresponding alpha-rhythm are already unstable, implying that these modes have undergone transition to the subcritical gamma-rhythm limit cycle . If one starts a corresponding numerical simulation with random initial h _e , but without noise driving, one finds that there is, at first, a transient organization into alpha-rhythm regions of a size corresponding to the unstable wavenumber (graph labeled “0 ms” in Fig. 6.4). The amplitude of these alpha-oscillations grows, and is then rapidly replaced by “gamma hotspots”, which are phase synchronous with each other (graphs up to “480 ms” in Fig. 6.4). It may be speculated from a physiological perspective that the normal organization of the brain consists of regions capable of producing stable weakly-damped alpha-oscillations for all wavenumbers, but, due to variations in one or more bifurcation parameters, is able to become critical at a particular wavenumber, thereby determining, in some fashion, the spatial organization of the subsequently generated coherent gamma-oscillations. However, the influences of noisy inputs (and environments), inhomogeneous neuronal populations, and anisotropic connectivity, are likely to be significant for actual transitions, and require further study.

6.4 Determination of state transitions in experimental EEG

Our theoretical analysis so far suggests that cortex may be conceived as being in a state of marginal linear stability with respect to alpha activity, which can be lost by a range of perturbations and replaced by a rapidly emerging ($\approx$ 150 ms) spatially synchronized, nonlinear, oscillatory state. It is therefore necessary to examine real EEG for evidence of transitions between noise-driven linear and nonlinear states. While the theory of nonlinear, deterministic dynamical systems has provided a number of powerful methods to characterize the dynamical properties of time-series, they have to be applied carefully to the dynamical characterization of EEG, where any deterministic dynamics are expected to be partly obscured by the effects of noise, nonstationarity and finite sampling. For such weakly nonlinear systems, the preferred approach to characterizing the existence of any underlying deterministic dynamics has been the surrogate data method [34].

In this approach a statistic, $\lambda$, which assigns a real number to a time-series and is sensitive to deterministic structure, is computed for the original time-series, $\lambda_0$, and compared to the distribution of values, $\{\lambda_i\}$, obtained for a number of suitably constructed “linear” surrogate data sets. Then one estimates how likely it is to draw $\lambda_0$ from the distribution of values obtained for the surrogates $\{\lambda_{i}\}$. For example, if we have reason to believe that $\lambda$ is normally distributed, we estimate its mean $\overline{\lambda}$ and variance $\sigma^2_\lambda$. Then if $|\lambda_0-\overline{\lambda}| <2\sigma_{\lambda}$, we would not be able to reject the null hypothesis $H_{0}$ that $\lambda_0$ was drawn from $\{\lambda_{i}\}$ at the $p = 0.05$ level for a two-tailed test. Typically though, there is no a priori information regarding the distribution of $\{\lambda_{i}\}$, and hence a rank-based test is generally used.

However, rejection of the null hypothesis in itself does not provide unequivocal statistical evidence for the existence of deterministic dynamics. In particular, nonstationarity is a well-known source of false rejections of the linear stochastic null hypothesis . To deal with this, two general strategies are employed. First, the null hypothesis is evaluated on time-series segments short enough to be assumed stationary, but long enough to allow the meaningful evaluation of the nonlinear statistic. Second, if some measure of stationarity can be shown to be equivalent in the original and surrogate data time-series, then it may be assumed that nonstationarity is an insignificant source of false positives.

6.4.1 Surrogate data generation and nonlinear statistics

The features that the “linear” surrogate data sets must have depend on the null hypothesis that is to be tested. The most common null hypothesis is that the data comes from a stationary, linear, stochastic process with Gaussian inputs. Therefore almost all surrogate data generation schemes aim to conserve linear properties of the original signal, such as the auto- and cross-spectra. The simplest method of achieving this is by phase randomisation of the Fourier components of the original time-series. However, such a simple approach results in an unacceptably high level of false positives, because the spectrum and amplitude distribution of the surrogates has not been adequately preserved. For this reason a range of improvements to the basic phase-randomised surrogate have been developed [69]. Of these, the iterated amplitude-adjusted FFT surrogate (IAFFT) seems to provide the best protection against spurious false rejections of the linear stochastic null hypothesis [34].

A large number of nonlinear test statistics are available to evaluate time-series for evidence of deterministic/nonlinear structure using the surrogate data methodology. The majority of these quantify the predictability of the time-series in some way. While there is no systematic way to choose one statistic over another, at least in the analysis of EEG the zeroth-order nonlinear prediction error (0-NLPE) seems to be favored. Indeed, Schrieber and Schmitz [68], by determining the performance of a number of commonly used nonlinear test statistics, concluded that the one-step-ahead 0-NLPE gave consistently good discrimination power even against weak nonlinearities. The idea behind the NLPE is relatively simple: delay-embed a time-series $x_{n}$ to obtain the vectors $\textbf{x}_n = (x_{n-(m-1)\tau},x_{n-(m-2)\tau},\ldots,x_{n-\tau},x_n)$ in $\mathbb{R}^m$, and use the points closer than $\epsilon$ to each $\textbf{x}_N$, i.e., $\textbf{x}_{m}\in\mathcal{U}_{\epsilon}(\textbf{x}_N)$, to predict $\textbf{x}_{N+1}$ as the average of the $\{\textbf{x}_{m+1}\}$. Formally [34]

$$\hat{x}_{N+1} = \frac{1}{|\mathcal{U}_{\epsilon}(\textbf{x}_{N})|}\sum_{\textbf{x}_{m}\in\mathcal{U}_{\epsilon}(\textbf{x}_N)}x_{m+1}\;,$$

((6.28))

where $|\mathcal{U}_{\epsilon}(\textbf{x}_{N})|$ is the number of elements in the neighborhood $\mathcal{U}_{\epsilon}(\textbf{x}_{N})$. The one-step-ahead 0-NLPE is then defined as the root-mean-square prediction error over all points in the time-series, i.e, $\lambda^\mathrm{NLPE} = \sqrt{\langle(\hat{x}_{N+1}-x_{N+1})^2\rangle}$.

Other nonlinear statistics include the correlation sum, the maximum likelihood estimator of the Grassberger—Procaccia correlation dimension $\mbox{D}_2$, and a variety of higher-order autocorrelations and autocovariances. Of the latter, two are of particular note due to their computational simplicity and their applicability to short time series. These are the third-order autocovariance, $\lambda^\mathrm{C3}(\tau) = \langle x_nx_{n-\tau}x_{n-2\tau}\rangle$, and time-reversal asymmetry, $\lambda^\mathrm{TREV}(\tau) = \langle (x_n-x_{n-\tau})^3\rangle/\langle (x_n-x_{n-\tau})^2\rangle$.

6.4.2 Nonlinear time-series analysis of real EEG

The surrogate data method has produced uncertain and equivocal results for EEG [72]. An early report, using a modified nonlinear prediction error [73], suggested that resting EEG contained infrequent episodes of deterministic activity. However, a later report [26], using third-order autocovariance and time-reversal asymmetry, revealed that in a significant fraction (up to 19.2%) of examined EEG segments, the null hypothesis of linearity could not be rejected. Therefore, depending on the nonlinear statistic used, a quite different picture regarding the existence of dynamics of deterministic origin in the EEG may emerge. Thus attempts to identify transitions between putatively identified linear and nonlinear states using surrogate data methods will need to use a range of nonlinear discriminators.

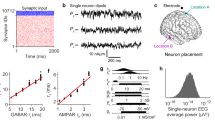
Figure 6.5 shows a subset of the results obtained from a multivariate surrogate data based test of nonlinearity for eyes-closed resting EEG recorded from a healthy male subject. The important points to note are: (i) the fraction of epochs tentatively identified as nonlinear is small for all nonlinear statistics; (ii) temporal patterns of putatively identified nonlinear segments differ depending on the nonlinear statistic used; and (iii) the power spectra of nonlinear segments are associated with a visible sharpening of the alpha resonance for all nonlinear statistical discriminators. It is this latter feature that is of particular interest to us. It suggests, in the context of our theory, that the linear stochastic system underlying the generation of the alpha activity has become more weakly damped and is thus more prone to being “excited” into a nonlinear or deterministic state.

Because we theoretically envision a system intermittently switching between linear and deterministic (nonlinear) states there is a reduced need to identify the extent to which nonstationarity acts as a source of false positives in our surrogate data nonlinear time-series analysis. For if our system switches between linear and nonlinear states on a time-scale less than the length of the interval over which nonlinearity is characterized, deterministic dynamics and nonstationarity necessarily co-exist.

Thus this preliminary experimental evidence, involving the detection of weak nonlinearity in resting EEG using an extension of the well-known surrogate data method, suggests that nonlinear (deterministic) dynamics are more likely to be associated with weakly damped alpha activity and that either a dynamical bifurcation has occurred or is more likely to occur.

Fig. 6.5

Nonlinear surrogate data time-series analysis of parieto-occipitally recorded EEG from a healthy male subject. Left-hand panels show the temporal sequence of putatively identified nonlinear 2-s EEG segments for channel P4 for three nonlinear discriminators: $\lambda^\mathrm{NLPE}$, $\lambda^\mathrm{C3}$ and $\lambda^\mathrm{TREV}$. Right-hand panels show the corresponding averaged power spectra for segments identified as nonlinear, compared with the remaining segments. Three-hundred seconds of artifact-free 64-channel (modified-expanded 10–20 system of electrode placement; linked mastoids) resting eyes-closed EEG was recorded, bandpass filtered between 1 and 40 Hz and sampled at 500 Hz. EEG was then segmented into contiguous multichannel epochs of 2-s length from which multivariate surrogates were created. $H_{0}$ (data results from a Gaussian linear stochastic process) was then tested for each channel at the $p = 0.05$ level using a nonparametric rank-order method together with a step-down procedure to control for familywise type-I error rates. Power spectra were calculated using Hamming-windowed segments of length 1000.

6.5 Discussion

We have outlined a biologically plausible mean-field approximation of the dynamics of cortical neural activity which is able to capture the chief properties of mammalian EEG. Central to this endeavor has been the modeling of human alpha activity, which is conceived as the central organizing rhythm of spontaneous EEG.

A great deal of modern thinking regarding alpha activity in general, and the alpha rhythm in particular, has focused on its variation during task performance and/or stimulus presentation, and therefore attempts to describe its function in the context of behavioral action or perception. These attempts to characterize alpha activity in terms of its psychological correlates, together with its inevitable appearance in scalp-recorded EEG has meant that specific research aimed at understanding this oscillatory phenomenon is more the exception than the rule. In a prescient review regarding electrical activity in the brain, W. Grey Walter in 1949 [82], whilst talking about spontaneous activity, remarked:

The prototype in this category, the alpha rhythm, has been seen by every electroencephalographer but studied specifically by surprisingly few.

While we have proposed a theory for the dynamical genesis of alpha activity, and via large-scale parameter searches established plausible physiological domains that can produce alpha activity, we do not understand the basis for the parameterizations so found. Our theory suggests that the reason human alpha activity shows complex and sensitive transient behavior is because it is readily perturbed from a dynamical state of marginal linear stability. It is therefore not inconceivable that the system producing alpha activity has, through as yet unknown mechanisms, a tendency to organize itself into a state of marginal stability. This line of thinking relates in a general form to the ideas of self-organized criticality [5], especially in the context of the near $1/f$ distribution of low-frequency power reported in EEG [62] ECoG [22] and MEG recordings [53].

Our view of electrorhythmogenesis and brain functioning emphasizes the self-organized structure of spontaneous neural dynamics as active (or ready) and chiefly determined by the bulk physiological properties of cortical tissue, which is perturbed or modulated by a variety of afferent influences arising from external sources and/or generated by other parts of the brain. Alpha activity is hypothesised to be the source of this self-organizing process, providing the background dynamical state from which transitions to emergent, and thus information creating, nonlinear states are made. In a general sense then, alpha activity provides ongoing dynamical predicates for subsequently evoked activity. Such an approach is not uncommon among neurophysiologists who have emphasized the importance of ongoing neural dynamics in the production of evoked responses, see for example [3]. Indeed, this point was highlighted early on by Donald O. Hebb [29]:

Electrophysiology of the central nervous system indicates in brief that the brain is continuously active, in all its parts, and an afferent excitation must be superimposed on an already existent excitation. It is therefore impossible that the consequence of a sensory event should often be uninfluenced by the pre-existent activity.

6.5.1 Metastability and brain dynamics

Although early attempts to dynamically describe brain function sought to prescribe explicit attractor dynamics to neural activity, more recent thinking focuses on transitory nonequilibrium behavior [63]. In the context of the mesoscopic theory of alpha activity presented here, it is suggested that these transient states correspond to coherent mesoscopic gamma oscillations arising from the bifurcation of noise-driven marginally stable alpha activity.

From a Hebbian perspective , such a bifurcation may represent the regenerative activation of a cell assembly through the mutual excitation of its component neurons. However, Hebb’s original notion of a cell assembly did not incorporate any clear mechanism for the initiation or termination of activity in cell assemblies. As originally formulated, Hebbian cell assemblies could only generate run-away excitation due to the purely excitatory connections among the assembly neurons. In the theory presented here, the possibility arises that the initiation and termination of cell assembly activity (assuming it corresponds to synchronized gamma band activity) might occur as a consequence of modulating local reverberant inhibitory neuronal activity through either disinhibition (variations in $\langle p_{ii}\rangle$) or transient modifications in inhibitory$\rightarrow$inhibitory synaptic efficacy ($N^{\beta}_{ii}$, $\Gamma_{ii}$) [8]. Because local inhibition has been shown to be a sensitive determinant of the dynamics of emergent model alpha activity [40], it may be hypothesized that it is readily influenced by the relatively sparse thalamocortical projections.

Given that neuronal population dynamics have been conceived as evolving transiently, rarely reaching stability, a number of authors have opted to describe this type of dynamical regime as metastability [11,21,23,35,64]. Common to many of these descriptions is an ongoing occurrence of transitory neural events, or state transitions, which define the flexibility of cognitive and sensori-motor function. Some dynamical examples include the chaotic itinerancy of Tsuda [78], in which neural dynamics transit in a chaotic motion through unique attractors (Milnor), or the liquid-state machine of Rabinovich et al [63], where a more global stable heteroclinic channel is comprised of successive local saddle states. More specific neurodynamical approaches include the work of Kelso [35], Freeman [21] and Friston [24].

In developing mathematical descriptions of metastable neural dynamics, many of the models are often sufficiently general to allow for a standard dynamical analysis and treatment. For this reason, much of the dynamical analysis of EEG has focused on the identification of explicit dynamical states. However attempts to explore the attractor dynamics of EEG have produced at best equivocal results, suggesting that such simplistic dynamical metaphors have no real neurophysiological currency. Modern surrogate data methods have revealed that normal spontaneous EEG is only weakly nonlinear [72], and thus more subtle dynamical methods and interpretations, motivated by physiologically meaningful theories of electrorhythmogenesis, need to be developed.