Abstract
We review a method to construct \(\mathrm{{G}}_2\)-instantons over compact \(\mathrm{{G}}_2\)-manifolds arising as the twisted connected sum of a matching pair of Calabi-Yau 3-folds with cylindrical end, based on the series of articles [16, 24, 32, 33] by the author and others. The construction is based on gluing \(\mathrm{{G}}_2\)-instantons obtained from holomorphic bundles over such building blocks, subject to natural compatibility and transversality conditions. Explicit examples are obtained from matching pairs of semi-Fano 3-folds by an algorithmic procedure based on the Hartshorne-Serre correspondence.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
This text addresses the existence problem of \(\mathrm{{G}}_2\)-instantons over twisted connected sums, as formulated by the author and Walpuski in [32], and the production of the first examples to date of solutions obtained by a nontrivially transversal gluing process [24]. It is aimed at graduate students and researchers in nearby areas who might be interested in a condensed exposition of the main results spread over my articles [16, 24, 32, 33] with Walpuski, Menet et al. and Menet-Nordström. By no means should this survey convey the impression that the subject is somehow closed or even in its best notational setup; indeed there is much ongoing work on this topic. A number of important questions remain open and the most impressive expected results in this theory are surely still ahead of us.
Recall that a \(\mathrm{{G}}_2\)-manifold \((X,g_{\phi })\) is a Riemannian 7-manifold together with a torsion-free \(\mathrm{{G}}_2\)-structure, that is, a non-degenerate closed 3-form \(\phi \) satisfying a certain non-linear partial differential equation; in particular, \(\phi \) induces a Riemannian metric \(g_\phi \) with \(\mathrm {Hol}(g_{\phi })\subset \mathrm{{G}}_2\) [18, Part I]. A \(\mathrm{{G}}_2\)-instanton is a connection A on some G-bundle \(E\rightarrow X\) such that \(F_A\wedge *\phi =0\). Such solutions have a well-understood elliptic deformation theory of index 0 [30], and some form of ‘instanton count’ of their moduli space is expected to yield new invariants of 7-manifolds, much in the same vein as the Casson invariant and instanton Floer homology from flat connections on 3-manifolds [10, 12]. While some important analytical groundwork has been established towards that goal [35], major compactification issues remain and this suggests that a thorough understanding of the general theory might currently have to be postponed in favour of exploring a good number of functioning examples. This article proposes a method to construct such examples.
Readers interested in a more detailed account of instanton theory on \(\mathrm{{G}}_2\)-manifolds are kindly referred to the introductory sections of [32, 33] and works cited therein.
An important method to produce examples of compact \(\mathrm{{G}}_2\)-manifolds with \(\mathrm {Hol}(g)=\mathrm{{G}}_2\) is the twisted connected sum construction, suggested by Donaldson, pioneered by Kovalev [21] and later extended and improved by Kovalev–Lee [20] and Corti–Haskins–Pacini-Nordström [6]. Here is a brief summary of this construction: A building block consists of a projective 3-fold Z and a smooth anti-canonical K3 surface \(\Sigma \subset Z\) with trivial normal bundle (cf. Definition 2.10). Given a choice of hyperkähler structure \(\left( \omega _I,\omega _J,\omega _K\right) \) on \(\Sigma \) such that \([\omega _I]\) is the restriction of a Kähler class on Z, one can make \(V:=Z\setminus \Sigma \) into an asymptotically cylindrical (\(\mathrm {ACyl}\)) Calabi–Yau 3-fold, that is, a non-compact Calabi–Yau 3-fold with a tubular end modelled on \(\mathbb {R}_+\times \mathbb {S}^1\times \Sigma \), see Haskins–Hein–Nordström [13]. Then \(Y:= \mathbb {S}^1\times V\) is an \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifold with a tubular end modelled on \(\mathbb {R}_+\times T^2\times \Sigma \).
When a pair \((Z_\pm ,\Sigma _\pm )\) of building blocks matches ‘at infinity’, in a suitable sense, one can glue \(Y_\pm \) by interchanging the \( \mathbb {S}^1\)-factors. This yields a simply-connected compact 7-manifold Y together with a family of torsion-free \(\mathrm{{G}}_2\)-structures \((\phi _T)_{T \ge T_0}\), see Kovalev [21, Sect. 4]. From the Riemannian viewpoint \((Y,\phi _T)\) contains a “long neck” modelled on \([-T,T]\times T^2\times \Sigma _+\); one can think of the twisted connected sum as reversing the degeneration of the family of \(\mathrm{{G}}_2\)-manifolds that occurs as the neck becomes infinitely long. In [5, 6, 21], building blocks Z are produced by blowing up Fano or semi-Fano 3-folds along the base curve \(\mathscr {C}\) of an anticanonical pencil (cf. Proposition 4.6). By understanding the deformation theory of pairs \((X,\Sigma )\) of semi-Fanos X and anticanonical K3 divisors \(\Sigma \subset X\), one can produce hundreds of thousands of pairs with the required matching (see Sect. 4.3).
This construction raises a natural programme in gauge theory, aimed at constructing \(\mathrm{{G}}_2\)-instantons over compact manifolds obtained as a TCS, originally outlined in [30]. If \((Z,\Sigma )\) is a building block and \(\mathcal {E}\rightarrow Z\) holomorphic bundle such that \(\mathcal {E}|_\Sigma \) is stable, then \(\mathcal {E}|_\Sigma \) carries a unique ASD instanton compatible with the holomorphic structure [9]. In this situation \(\mathcal {E}|_V\) can be given a Hermitian–Yang–Mills (HYM) connection asymptotic to the ASD instanton on \(\mathcal {E}|_\Sigma \) [33, Theorem 58], whose pullback over V to \( \mathbb {S}^1\times V\) is a \(\mathrm{{G}}_2\)-instanton, i.e., a connection A on a G-bundle over a \(\mathrm{{G}}_2\)-manifold such that \(F_A\wedge \psi =0\) with \(\psi :=*\phi \). It is possible to glue a hypothetical pair of such solutions into a \(\mathrm{{G}}_2\)-instanton over the compact twisted connected sum, provided a number of technical conditions are met (cf. Theorem 3.1).
However, the hypotheses of our \(\mathrm{{G}}_2\)-instanton gluing theorem are rather restrictive and it is not immediate to obtain suitable holomorphic bundles \(\mathcal {E}_\pm \rightarrow Z_\pm \) over the matching blocks. In particular, a transversality condition over the K3 surface \(\Sigma _\pm \) ‘at infinity’ requires some more thorough understanding of the deformation theory of data \((Z_\pm , \Sigma _\pm , \mathcal {E}_\pm )\). Assuming the so-called rigid case in which the instantons that are glued are isolated points in their moduli spaces, Walpuski [39] was able to exhibit one such example, by a different systematic approach.
Finally, in [24], we use the Hartshorne-Serre construction (cf. Theorem 4.1) to obtain families of bundles over the building blocks. Our method allows one to generate a large number of examples for which the gluing is nontrivially transversal (see Sect. 4.4.1). These are particularly relevant, because they open the possibility of obtaining a conjectural instanton number on the \(\mathrm{{G}}_2\)-manifold X as a genuine Lagrangian intersection within the moduli space \(\mathscr {M}_{S_+}\) over the K3 cross-section along the neck, which can be addressed by enumerative methods in the future.
2 Background on \(\mathrm{{G}}_2\)-Geometry
Let us recall some \(\mathrm{{G}}_2\)-trivia, following the exposition in [31, 33]; of course the immortal introductory references for the topic are [3, 17, 29]. Recall that a \(\mathrm{{G}}_2\)-structure on an oriented smooth 7-manifold Y is a smooth 3-form \(\phi \in \Omega ^{3}\left( Y\right) \) such that, at every point \(p\in Y\), one has \(\phi _{p}=r_{p}^{*}\left( \phi _{0}\right) \) for some frame \(r_{p}:T_{p}Y\rightarrow \mathbb {R}^{7}\) and (with the sign conventions of [29])
with
Moreover, \(\phi \) determines a Riemannian metric \(g(\phi )\) induced by the pointwise inner-product
under which \(*_\phi \phi \) is given pointwise by
Such a pair \(\left( Y,\phi \right) \) is a \(\mathrm{{G}}_2\)-manifold if \(\mathrm{{d}}\phi =0\) and \(\mathrm{{d}}*_{\phi }\phi =0\). Notice that the co-closed condition is nonlinear in \(\phi \), since the Hodge star depends on the metric and hence on \(\phi \) itself.
2.1 Gauge Theory on \(\mathrm{{G}}_2\)-Manifolds
The \(\mathrm{{G}}_2\)-structure allows for a 7-dimensional analogue of conventional Yang-Mills theory, yielding a notion analogous to (anti-)self-duality for 2-forms. Working in \(\mathbb {R}^7\) under the usual identification between 2-forms and matrices, we have \(\mathfrak {g}_{2}\subset \mathfrak {so}\left( 7\right) \simeq \Lambda ^{2}\), so we define \(\Lambda _{14}^{2}:= \mathfrak {g}_{2}\) and \(\Lambda _{7}^{2}\) its orthogonal complement in \(\Lambda ^{2}\):
It is easy to check that \(\Lambda _{7}^{2}=\left\langle e_1\lrcorner \phi _0,\dots ,e_7\lrcorner \phi _0 \right\rangle \), hence the orthogonal projection onto \(\Lambda _{7}^{2}\) in (2.4) is given by
in the sense that [3, p. 541]
Furthermore, since (2.4) splits \(\Lambda ^2\) into irreducible representations of \(\mathrm{{G}}_2\), a little inspection on generators reveals that \(\left( \Lambda ^{2}\right) _{^{\;7}_{14} }\) is respectively the \(_{+1}^{-2}-\)eigenspace of the \(\mathrm{{G}}_{2}\)-equivariant linear map
2.1.1 Yang-Mills Formalism on \(\mathrm{{G}}_2\)-Manifolds
Consider now a G-bundle \(E\rightarrow Y\) over a compact \(\mathrm{{G}}_2\)-manifold \(\left( Y,\phi \right) \); the curvature \(F:=F_{A} \) of some connection A decomposes according to the splitting (2.4):
where \(\mathfrak {g}_{E}\) denotes the adjoint bundle associated to E. The \(L^2\)-norm of \(F_{A}\) is the Yang-Mills functional, which therefore has two corresponding components:
It is well-known that the values of \(\mathscr {Y}\left( A\right) \) can be related to a certain characteristic class of the bundle E, given (up to choice of orientation) by
Using the property \(d\phi =0\), a standard argument of Chern–Weil theory [26] shows that the de Rham class \(\left[ \mathop {\mathrm {tr}}\nolimits \left( F_{A}^{2}\right) \wedge \phi \right] \) is independent of A, thus the integral is indeed a topological invariant. The eigenspace decomposition of \(T_{\phi }\) implies (up to a sign)
and combining with (2.6) we get
Hence \(\mathscr {Y}\left( A\right) \) attains its absolute minimum at a connection whose curvature lies either in \(\Omega _{7}^{2}(Y,\mathfrak {g}_{E})\) or in \(\Omega _{14}^{2}(Y,\mathfrak {g}_{E})\). Moreover, since \(\mathscr {Y}\ge 0\), the sign of \(\kappa (E)\) obstructs the existence of one type or the other, so we fix \(\kappa (E)\ge 0\) and define \(\mathrm{{G}}_2\)-instantons as connections with \( F\in \Omega _{14}^{2}(Y,\mathfrak {g}_{E})\), i.e., such that \(\mathscr {Y}(A)=\kappa (E)\). These are precisely the solutions of the \(\mathrm{{G}}_2\)-instanton equation:
or, equivalently,
If instead \(\kappa (E)\le 0\), we may still reverse orientation and consider \( F\in \Omega _{14}^{2}(Y,\mathfrak {g}_{E})\), but then the above eigenvalues and energy bounds must be adjusted accordingly, which amounts to a change of the \((-)\) sign in (2.7b).
2.1.2 The Chern–Simons Functional \(\vartheta \)
It was pointed out by Simon Donaldson and Richard Thomas in their seminal article on gauge theory in higher dimensions [12] that, formally, \(\mathrm{{G}}_2\)-instantons are rather similar to flat connections over 3-manifolds; in particular, they are critical points of a Chern–Simons functional and there is hope that counting them could lead to a enumerative invariant for \(\mathrm{{G}}_2\)-manifolds not unlike the Casson invariant for 3-manifolds, see [11, Sect. 6] and [38, Chap. 6]. Although this interpretation has no immediate bearing on the remainder of this material, let us briefly review the basic formalism, from a purely motivational perspective.
Given a bundle over a compact 3-manifold, with space of connections \(\mathscr {A}\) and gauge group \(\mathscr {G}\), the Chern–Simons functional is a multi-valued real function on the quotient \(\mathscr {B}=\mathscr {A}/\mathscr {G}\), with integer periods, whose critical points are precisely the flat connections [8, Sect. 2.5]. Similar theories can be formulated in higher dimensions in the presence of a suitable closed differential form [12, 34]; e.g. on a \(\mathrm{{G}}_2\)-manifold \((Y,\phi )\), the coassociative \(4-\)form \(\psi :=*\phi \) allows for the definition of a functional of Chern–Simons type.Footnote 1 Its ‘gradient’, the Chern–Simons 1-form, vanishes precisely at the \(\mathrm{{G}}_2\)-instantons, hence it detects the solutions to the Yang-Mills equation [8]. The explicit case of \(\mathrm{{G}}_2\)-manifolds, which we now describe, was examined in some detail in [30, 31].
The space \(\mathscr {A}\) of connections on \(E\rightarrow Y\) is an affine space modelled on \(\Omega ^{1}\left( \mathfrak {g}_{E}\right) \) so, fixing a reference connection \(A_{0}\in \mathscr {A}\),
and, accordingly, vectors at \(A\in \mathscr {A}\) are 1-forms \(a,b,\dots \in T_A\mathscr {A}\simeq \Omega ^{1}\left( Y,\mathfrak {g}_{E}\right) \) and vector fields are maps \(\alpha ,\beta ,\dots :\mathscr {A}\rightarrow \Omega ^{1}\left( Y,\mathfrak {g}_{E}\right) \). In this notation we define the Chern–Simons functional by
fixing \(\vartheta \left( A_0\right) =0\). This function is obtained by integration of the Chern–Simons \(1-\)form
It is straightforward to check that the co-closedness condition \(\mathrm{{d}}*\phi =0\) implies that the \(1-\)form (2.8) is closed, so the procedure doesn’t depend on the path \(A\left( t\right) \). Since \(\mathscr {A}\) is contractible, by the Poincaré Lemma \(\rho \) is the derivative of some function \(\vartheta \), and by Stokes’ theorem \(\rho \) vanishes along \(\mathcal {G-}\)orbits \(\mathop {\mathrm {im}}\mathrm{{d}}_{A} \simeq T_{A}\left\{ \mathcal {G}.A\right\} \). Thus \(\rho \) descends to the quotient \(\mathscr {B}\) and so does \(\vartheta \), at least locally. Since \(*\phi \) is not, in general, an integral class, the set of periods of \(\vartheta \) is actually dense; however, as long as our interest remains in the study of the moduli space \(\mathcal {M}=\mathrm {Crit}(\rho )\) of \(\mathrm{{G}}_2\)-instantons, there is no worry, for the gradient \(\rho =\mathrm{{d}}\vartheta \) is unambiguously defined on \(\mathscr {B}\).
2.2 Analysis on Manifolds with Tubular Ends
In order to get some more depth into the instanton gluing process of Theorem 3.1, we will need some general results from linear analysis on asymptotically cylindrical manifolds (cf. Definition 2.3).
Definition 2.1
A manifold with tubular end \((M,X, \pi )\) is given by a smooth manifold M with a distinguished compact submanifold-with-boundary \(M_0\subset M\), a Riemannian manifold X, and a diffeomorphism
The complement \(M_\infty :=M\setminus M_0\) is called the tubular end, \(\pi \) is the tubular model and X is the asymptotic cross-section.Footnote 2
Of course one could in principle consider, analogously, manifolds with any number of tubular ends but, in the context of \(\mathrm{{G}}_2\)-manifolds, the Ricci-flat geometry constrains that number to one:
Theorem 2.2
([28, Theorem 1]) If a connected and orientable manifold M with k tubular ends admits a Ricci-flat metric, then \(k\le 2\). Moreover \(k=2\) if, and only if, M is a cylinder.
2.2.1 Geometric Structures on Manifolds with Cylindrical End
On a manifold with tubular end \((M,X, \pi )\), we have the following natural maps on differential forms (which clearly extend to any tensor fields):

By slight abuse of notation, given \(\sigma _{\infty }\in \Omega ^{\bullet }(X)\), we will also denote by \(\sigma _{\infty }\) its pullback to the product under \(\mathbb {R}_{+}\times X\xrightarrow [{}]{p_2} X\). Denoting by t the coordinate function on \(\mathbb {R}\), we adopt the following notation for asymptotic behaviour:
-
\(\sigma \overset{\delta }{\rightsquigarrow }\sigma _\infty \), if \(\vert \nabla ^{k}(\pi _{*}\sigma -\sigma _\infty )\vert \le O(e^{-\delta t})\), \(t\in \mathbb {R}_{+}\), \(\forall k\ge 0\), for a given \(\delta >0\).
-
\(\sigma \rightsquigarrow \sigma _\infty \), if \(\exists \delta >0\) such that \(\sigma \overset{\delta }{\rightsquigarrow }\sigma _\infty \).
Whenever \(\sigma \rightsquigarrow \sigma _\infty \), \(\sigma \) is said to be asymptotically translation-invariant and \(\sigma _\infty \) is its asymptotic limit.
Definition 2.3
A manifold with tubular end \((M,X,\pi )\) is said to be asymptotically cylindrical ( \(\mathrm {ACyl}\) ) if M is also a Riemannian manifold and its metric \(g_M\) is asymptotic to the natural cylindrical metric on the tubular model: \(g_M\rightsquigarrow g_X+\mathrm{{d}}t^2\). In this case, we will call the map \(\pi : M_\infty \rightarrow \mathbb {R}_+\times X\) the cylindrical model.
Let \(E_\infty \rightarrow X\) be a Riemannian vector bundle. By slight abuse of notation we also denote by \(E_\infty \) its pullback to \(\mathbb {R}_+\times X\). For \(k\in \mathbb {N}_0\), \(\alpha \in (0,1)\) and \(\delta \in \mathbb {R}\) we define
denoting by \(C^{k,\alpha }_\delta (X,E_\infty )\) the respective closure of \(C^\infty _0(X,E_\infty )\). We set \(C^\infty _\delta :=\bigcap _{k} C^{k,\alpha }_\delta \).
Similarly, a Riemannian vector bundle \(E\rightarrow M\) over an \(\mathrm {ACyl}\) manifold \((M,X,\pi )\) is said to be asymptotic to \(E_\infty \rightarrow X\) if there is a bundle isomorphism \(\bar{\pi }: E|_{M_\infty } \rightarrow E_\infty \) covering \(\pi \) such that the push-forward of the metric on E is asymptotic to the metric on \(E_\infty \) in the \(C^\infty _\delta \) tubular norm above (for some \(\delta >0\)). Denote by \({t: M\rightarrow [1,\infty )}\) a smooth positive function which agrees with \(t\circ \pi \) on \(\pi ^{-1}([1,\infty )\times X)\), and define
denoting by \(C^{k,\alpha }_\delta (M,E)\) the respective closure of \(C^\infty _0(M,E)\).
Finally, a connection \(A\in \mathscr {A}(E)\) is said to be asymptotic to \(A_\infty \in \mathscr {A}(E_\infty )\) if \((A-\bar{\pi }^*A_\infty )\rightsquigarrow 0\) (the difference of two connections being a 1-form). We also denote by \(A_\infty \) its pullback to \(E_\infty \rightarrow \mathbb {R}_+\times X\).
2.2.2 Asymptotically Translation-Invariant Operators on ACyl Manifolds
Let us briefly review some spectral theory for elliptic operators on sections of vector bundles over an \(\mathrm {ACyl}\) manifold M with asymptotic cross-section X. The primary references for the material in this section are Maz’ya–Plamenevskiĭ [25] and Lockhart–McOwen [22].
Let \(F\rightarrow X\) be a Riemannian vector bundle, and let \({D: C^\infty (X,F)\rightarrow C^\infty (X,F)}\) be a linear self-adjoint elliptic operator of first order. The operator
extends to a bounded linear operator \({L_{\infty ,\delta }: C^{k+1,\alpha }_\delta (X,F)\rightarrow C^{k,\alpha }_\delta (X,F)}\).
Theorem 2.4
([25, Theorem 5.1]) \(L_{\infty ,\delta }\) is invertible if and only if \(\delta \notin \mathrm {spec}(D)\).
Indeed, elements \(a\in \ker L_\infty \) can be expanded in terms of the \(\delta \)-eigensections of D, see [8, Sect. 3.1]:
Now let \(E\rightarrow M\) be a (Riemannian) vector bundle asymptotic to F and consider an elliptic operator
asymptotic to \(L_\infty \), that is, such that the coefficients of L are asymptotic to the coefficients of \(L_\infty \). The operator L extends to a bounded linear operator \({L_\delta : C^{k+1,\alpha }_{\delta }(M,E)}{\rightarrow C^{k,\alpha }_{\delta }(M,E)}\).
Proposition 2.5
([13, Proposition 2.4]) If \(\delta \notin \mathrm {spec}(D)\), then \(L_\delta \) is Fredholm.
Elements in the kernel of L still have an asymptotic expansion analogous to (2.9). We need the following result which extracts the constant term of this expansion.
Proposition 2.6
([32, Prop. 3.5]) There is a constant \(\delta _0>0\) such that, for all \(\delta \in [0,\delta _0]\), one has \(\ker L_\delta = \ker L_0\) and there is a linear map \({\iota : \ker L_0 \rightarrow \ker D}\) such that
In particular,
2.3 Twisted Connected Sums
An important method to produce examples of compact 7-manifolds with holonomy exactly \(\mathrm G_2\) is the twisted connected sum (TCS) construction [5, 6, 21]. It consists of gluing a pair of asymptotically cylindrical (\(\mathrm {ACyl}\)) Calabi–Yau 3-folds obtained from certain smooth projective 3-folds called building blocks (see Definition 2.7). Combining results of Kovalev and Haskins–Hein–Nordström, each matching pair of building blocks yields a one-parameter family of closed \(\mathrm{{G}}_2\)-manifolds.
A building block \((Z,\Sigma )\) is given by a projective morphism \(\zeta : Z\rightarrow \mathbb {P}^1\) such that \(\Sigma :=\zeta ^{-1}(\infty )\) is a smooth anticanonical K3 surface, under some mild topological assumptions (see Definition 2.10); in particular, \(\Sigma \) has trivial normal bundle. Choosing a convenient Kähler structure on Z, one can make \(V:=Z\setminus \Sigma \) into an \(\mathrm {ACyl}\) Calabi–Yau 3-fold (cf. Definition 2.9), that is, a non-compact Calabi–Yau manifold with a tubular end modelled on \(\mathbb {R}_+\times \mathbb {S}^1\times \Sigma \) [6, Theorem 3.4]. Then \(\mathbb {S}^1\times V\) is an \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifold (cf. Definition 2.15) with a tubular end modelled on \(\mathbb {R}_+\times \mathbb {T}^2\times \Sigma \).
Definition 2.7
(cf. [6, Definition 3.9]) Let \(Z_\pm \) be complex 3-folds, \(\Sigma _\pm \subset Z_\pm \) smooth anticanonical K3 divisors and  Kähler classes. We call a matching of
Kähler classes. We call a matching of  and
and  a diffeomorphism \({\mathfrak {r}}:{\Sigma _+ \rightarrow \Sigma _-}\) such that
a diffeomorphism \({\mathfrak {r}}:{\Sigma _+ \rightarrow \Sigma _-}\) such that  and
and  have type \((2,0) + (0,2)\).
have type \((2,0) + (0,2)\).
Given a pair of building blocks \((Z_\pm ,\Sigma _\pm )\), a set of matching data is a collection \( \mathbf{{m}}=\{\left( \omega _{I,\pm },\omega _{J,\pm },\omega _{K,\pm }\right) ,{\mathfrak {r}}\} \) consisting of a choice of hyper-Kähler structures on \(\Sigma _\pm \) such that  is the restriction of a Kähler class on \(Z_\pm \) and a matching \({{\mathfrak {r}}: \Sigma _+\rightarrow \Sigma _-}\) such that
is the restriction of a Kähler class on \(Z_\pm \) and a matching \({{\mathfrak {r}}: \Sigma _+\rightarrow \Sigma _-}\) such that
In this case \((Z_\pm ,\Sigma _\pm )\) are said to match via \(\mathbf{{m}}\) and \({\mathfrak {r}}\) is called a hyper-Kähler rotation (see Remark 2.12 below).
Identifying a matching pair \((Z_\pm ,\Sigma _\pm )\) of building blocks by the hyper-Kähler rotation between the K3 surfaces ‘at infinity’, the corresponding pair \(\mathbb {S}^1 \times V_\pm \) of \(\mathrm {ACyl}\) \(\mathrm G_2\)-manifolds is truncated at a large ‘neck length’ T and, intertwining the circle components in the tori \(\mathbb {T}^2_\pm \) along the tubular end, glued to form a compact 7-manifold (Fig. 1)
For large enough \(T_0\), this twisted connected sum Y carries a family of \(\mathrm G_2\)-structures \(\{\phi _T\}_{T\ge T_0}\) with \(\mathrm {Hol}(\phi _T)=\mathrm G_2\) [6, Theorem 3.12]. The construction is summarised in the following statement.
Theorem 2.8
([6, Corollary 6.4]) Given a matching pair of building blocks \((Z_\pm , \Sigma _\pm )\) with Kähler classes  such that
such that  , there exists a family of torsion-free \(G_{2}\)-structures \(\left\{ \phi _{T}:T\gg 1\right\} \) on the closed 7-manifold \(Y = Z_+\#_{\mathfrak {r}}Z_-\).
, there exists a family of torsion-free \(G_{2}\)-structures \(\left\{ \phi _{T}:T\gg 1\right\} \) on the closed 7-manifold \(Y = Z_+\#_{\mathfrak {r}}Z_-\).
2.3.1 ACyl Calabi–Yau 3-folds from Building Blocks
The twisted connected sum in Theorem 2.8 is based on gluing \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifolds, which arise as the product of an \(\mathrm {ACyl}\) Calabi-Yau 3-fold with \( \mathbb {S}^1\). Let us review how to produce these from building blocks.
Definition 2.9
Let \((V,\omega ,\Omega )\) be a Calabi–Yau 3-fold with tubular end and asymptotic cross-section \(\Sigma \times \mathbb {S}^1\) given by a hyper-Kähler surface \((\Sigma ,\omega _I,\omega _J,\omega _K)\). Then V is called an asymptotically cylindrical Calabi-Yau 3-fold ( \(\mathrm {ACylCY}^3\) ) if
where t and \(\alpha \) denote the respective coordinates on \(\mathbb {R}_+\) and \( \mathbb {S}^1\).
Numerous examples of \(\mathrm {ACylCY}^3\) can be obtained from the following ingredients:
Definition 2.10
(Corti–Haskins–Nordström–Pacini [5, Definition 5.1]) A building block is a smooth projective 3-fold Z together with a projective morphism \({\zeta : Z\rightarrow \mathbb {P}^1}\) such that the following hold:
-
The anticanonical class \(-K_Z\in H^2(Z)\) is primitive.
-
\(\Sigma :=\zeta ^{-1}(\infty )\) is a smooth K3 surface and \(\Sigma \sim -K_Z\).
-
Identifying \(H^{2}(\Sigma ,\mathbb {Z})\) with the K3 lattice (i.e. choosing a marking for \(\Sigma \)), the following embedding is primitive:
$$ N:=\mathop {\mathrm {im}}(H^{2}(Z,\mathbb {Z})\rightarrow H^{2}(\Sigma ,\mathbb {Z}))\hookrightarrow H^2(\Sigma ) $$ -
The groups \(H^{3}(Z,\mathbb {Z})\) and \(H^{4}(Z,\mathbb {Z})\) are torsion-free.
In particular, building blocks are simply-connected [5, Sect. 5.1].
Remark 2.11
The existence of the fibration \({\zeta : Z\rightarrow \mathbb {P}^1}\) is equivalent to \(\Sigma \) having trivial normal bundle. This is crucial because it means that \(Z\setminus \Sigma \) has a cylindrical end, given by an exponential radial coordinate in a tubular neighbourhood of \(\Sigma \). The last two conditions in the definition of a building block are not essential; they are meant to facilitate the computation of certain topological invariants.
Remark 2.12
Given a matching \({\mathfrak {r}}\) between a pair of building blocks  , one can make the choices in the definition of the \(\mathrm {ACyl}\) Calabi-Yau structure so that \({\mathfrak {r}}\) becomes a hyper-Kähler rotation (cf. Definition 2.7) of the induced hyper-Kähler structures [6, Theorem 3.4 & Proposition 6.2].
, one can make the choices in the definition of the \(\mathrm {ACyl}\) Calabi-Yau structure so that \({\mathfrak {r}}\) becomes a hyper-Kähler rotation (cf. Definition 2.7) of the induced hyper-Kähler structures [6, Theorem 3.4 & Proposition 6.2].
In his original work, Kovalev [21] used building blocks arising from Fano 3-folds by blowing-up the base-locus of a generic anti-canonical pencil. This method was extended to the much larger class of semi Fano 3-folds (a class of weak Fano 3-folds) by Corti–Haskins–Nordström–Pacini (see Proposition 4.6 below). Kovalev–Lee [20] construct building blocks starting from K3 surfaces with non-symplectic involutions, by taking the product with \(\mathbb {P}^1\), dividing by \(\mathbb {Z}_2\) and blowing up the resulting singularities. In every instance, one obtains an \(\mathrm {ACylCY}^3\) by the following theorem:
Theorem 2.13
([13, Theorem D]) Let \((Z,\Sigma )\) be a building block and let \((\omega _I,\omega _J,\omega _K)\) be a hyper-Kähler structure on \(\Sigma \). If \([\omega _I]\in H^{1,1}(\Sigma )\) is the restriction of a Kähler class on Z, then there is an asymptotically cylindrical Calabi–Yau structure \((\omega ,\Omega )\) on \(V:=Z\setminus \Sigma \) with asymptotic cross section \((\Sigma ,\omega _I,\omega _J,\omega _K)\).
Remark 2.14
This result was first claimed by Kovalev in [21, Theorem 2.4]; see the discussion in [13, Sect. 4.1].
2.3.2 Gluing ACyl \(\mathrm{{G}}_2\)-Manifolds
We may now describe the gluing of matching pairs of \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifolds, obtained from \(\mathrm {ACylCY}^3\) given by Theorem 2.13.
Definition 2.15
Let \((Y,\phi )\) be a \(\mathrm{{G}}_2\)-manifold with tubular end and asymptotic cross-section given by a compact Calabi–Yau 3-fold \((W,\omega ,\Omega )\). Then Y is called asymptotically cylindrical ( \(\mathrm {ACyl}\) ) if
where t denotes the coordinate on \(\mathbb {R}_+\).
Taking the product of an \(\mathrm {ACylCY}^3\) \((V,\omega ,\Omega )\) with \( \mathbb {S}^1\), with coordinate \(\beta \), yields an \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifold
with asymptotic cross section
Let \(V_\pm \) be a matching pair of \(\mathrm {ACylCY}^3\) with asymptotic cross section \(\Sigma _\pm \) and suppose that \({{\mathfrak {r}}: \Sigma _+\rightarrow \Sigma _-}\) is a hyper-Kähler rotation. A pair of \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifolds \((Y_\pm ,\phi _\pm )\) with asymptotic cross sections \((W_\pm ,\omega _\pm ,\Omega _\pm )\) as above is said to match if there exists a diffeomorphism
such that
Remark 2.16
If q did not interchange the \( \mathbb {S}^1\)-factors, then Y would have infinite fundamental group and, hence, could not carry a metric with holonomy equal to \(\mathrm{{G}}_2\) [17, Proposition 10.2.2].
Let \((Y_\pm ,\phi _\pm )\) be a matching pair of \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifolds. For fixed \(T\ge 1\), define
and denote by \(Y_T\) the compact 7-manifold obtained by gluing \(Y_\pm \) together at neck length T via Q:
Fix a non-decreasing smooth cut-off function \({\chi : \mathbb {R}\rightarrow [0,1]}\) with \(\chi (t)=0\) for \(t\le 0\) and \(\chi (t)=1\) for \(t\ge 1\). Define a 3-form \(\tilde{\phi }_T\) on \(Y_T\) by
on \(Y_{T,\pm }\). If \(T\gg 1\), then \(\tilde{\phi }_T\) defines a closed \(\mathrm{{G}}_2\)-structure on \(Y_T\). Clearly, all the \(Y_T\) for different values of T are diffeomorphic; hence, we often drop the T from the notation. The \(\mathrm{{G}}_2\)-structure \(\tilde{\phi }_T\) is not torsion-free yet, but can be made so by a small perturbation:
Theorem 2.17
([21, Theorem 5.34]) In the above situation there exist a constant \(T_0\ge 1\) and, for each \(T\ge T_0\), a 2-form \(\eta _T\) on \(Y_T\) such that \(\phi _T:=\tilde{\phi }_T+\mathrm{{d}}\eta _T\) defines a torsion-free \(\mathrm{{G}}_2\)-structure and for some \(\delta >0\)
In summary, the TCS Theorem 2.8 is established by the following procedure. For any building block \((Z,\Sigma )\), the noncompact 3-fold \(V := Z \setminus \Sigma \) admits \(\mathrm {ACyl}\) Ricci-flat Kähler metrics (Theorem 2.13) hence an \(\mathrm {ACylCY}^3\) structure whose asymptotic limit defines a hyper-Kähler structure on \(\Sigma \). Given a matching pair of such Calabi-Yau manifolds \(V_\pm \), one can apply Theorem 2.17 to glue \( \mathbb {S}^1 \times V_\pm \) into a closed manifold Y with a 1-parameter family of torsion-free \(\mathrm{{G}}_{2}\)-structures [6, Theorem 3.12].
3 The \(\mathrm{{G}}_2\)-Instanton Gluing Theorem
Let A be an ASD instanton on a \(\mathbf{{P}}U(n)\)-bundle F over a Kähler surface \(\Sigma \). The linearisation of the instanton moduli space \(\mathcal {M}_{\Sigma }\) near A is modelled on the kernel of the deformation operator
Let \(\mathcal {F}\) be the corresponding holomorphic vector bundle (cf. Donaldson–Kronheimer [10]), and denote by f the Hitchin–Kobayashi isomorphism:
Theorem 3.1
([32, Theorem 1.2]) Let \(Z_{\pm }\) ,\(\Sigma _{\pm }\),  , \({\mathfrak {r}}\), X and \(\phi _T\) be as in Theorem 2.8. Let \(\mathcal {E}_{\pm } \rightarrow Z_{\pm }\) be a pair of holomorphic vector bundles such that the following hold:
, \({\mathfrak {r}}\), X and \(\phi _T\) be as in Theorem 2.8. Let \(\mathcal {E}_{\pm } \rightarrow Z_{\pm }\) be a pair of holomorphic vector bundles such that the following hold:
- Asymptotic stability:
-
\(\mathcal {E}_{\pm }|_{\Sigma _{\pm }}\) is \(\mu \)-stable with respect to
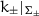 . Denote the corresponding ASD instanton by \(A_{\infty ,\pm }\).
. Denote the corresponding ASD instanton by \(A_{\infty ,\pm }\). - Compatibility:
-
There exists a bundle isomorphism \(\overline{{\mathfrak {r}}}:\mathcal {E}_{+}|_{\Sigma _{+}}\rightarrow \mathcal {E}_{-}|_{\Sigma _{-}}\) covering the hyper-Kähler rotation \({\mathfrak {r}}\) such that \(\overline{{\mathfrak {r}}}^{*} A_{\infty ,-}=A_{\infty ,+}\).
- Inelasticity:
-
There are no infinitesimal deformations of \(\mathcal {E}_{\pm }\) fixing the restriction to \(\Sigma _{\pm }\):
$$\begin{aligned} H^{1}(Z_{\pm },\mathscr {E}{} \textit{nd}_{0}(\mathcal {E}_{\pm })(-\Sigma _{\pm }))=0. \end{aligned}$$(3.2) - Transversality:
-
If \(\lambda _{\pm }:=f_\pm \circ \mathrm{{res}}_\pm : H^{1}(Z_{\pm },\mathscr {E}{} \textit{nd}_{0}(\mathcal {E}_{\pm }))\rightarrow H^{1}_{A_{\infty ,\pm }}\) denotes the composition of restrictions to \(\Sigma _{\pm }\) with the isomorphism (3.1), then the image of \(\lambda _{+}\) and \(\overline{{\mathfrak {r}}}^{*}\circ \lambda _{-}\) intersect trivially in the linear space \(H^{1}_{A_{\infty ,+}}\):
$$\begin{aligned} \mathop {\mathrm {im}}(\lambda _{+})\cap \mathop {\mathrm {im}}(\overline{{\mathfrak {r}}}^{*}\circ \lambda _{-})=\left\{ 0\right\} . \end{aligned}$$(3.3)
Then there exists a U(r)-bundle E over Y and a family of connections \(\left\{ A_{T}\ :\ T\gg 1\right\} \) on the associated \(\mathbf{{P}}U(r)\)-bundle, such that each \(A_{T}\) is an irreducible unobstructed \(G_{2}\)-instanton over \((Y,\phi _{T})\).
The asymptotic stability assumption guarantees finite energy of Hermitian bundle metrics on \(\mathcal {E}_\pm |_{V_\pm }\) (see [33, Sect. 2.2]), which are equivalent to asymptotically translation-invariant HYM connections \(A_\pm \rightsquigarrow A_{\infty ,\pm }\), under the Chern correspondence (cf. Theorem 3.15). The maps \(\lambda _+\) and \(\overline{{\mathfrak {r}}}^{*}\circ \lambda _{-}\) can be seen geometrically as linearisations of the natural inclusions of the moduli of asymptotically stable bundles \(\mathcal {M}_{Z_\pm }\) into the moduli of ASD instantons \(\mathcal {M}_{\Sigma _+}\) over the K3 surface ‘at infinity’, and we think of \(H^{1}_{A_{\infty ,+}}\) as a tangent model of \(\mathcal {M}_{\Sigma _+}\) near the ASD instanton \(A_{\infty ,+}\). Then the transversality condition asks that the actual inclusions intersect transversally at \(A_{\infty ,+}\in \mathcal {M}_{\Sigma _+}\). That the intersection points are isolated reflects that the resulting \(\mathrm G_2\)-instanton is rigid, since it is unobstructed and the deformation problem has index 0.
Remark 3.2
If \(H^1(\Sigma _+,{\mathcal {E}} nd_0(\mathcal {E}_+|_{\Sigma _+}))=\{0\}\), then (3.3) is vacuous. If, moreover, the topological bundles underlying \(\mathcal {E}_\pm \) are isomorphic, then the existence of \(\bar{\mathfrak {r}}\) is guaranteed by [15, Theorem 6.1.6].
Furthermore, condition (3.2) yields a short exact sequence, which is self-dual under Serre duality:
This implies [36, p. 176 ff.] that each
is a complex Lagrangian subspace with respect to the complex symplectic structure induced by \(\Omega _\pm :=\omega _{J,\pm }+i\omega _{K,\pm }\) or, equivalently, Mukai’s complex symplectic structure on \(H^1(Z_\pm ,{\mathcal {E}} nd_0(\mathcal {E}_\pm ))\). Under the assumptions of Theorem 3.1 the moduli space \(\mathscr {M}_{\Sigma _+}\) of holomorphic bundles over \(\Sigma _+\) is smooth near \([\mathcal {E}_+|_{\Sigma _+}]\) and so are the moduli spaces \(\mathscr {M}_{Z_\pm }\) of holomorphic bundles over \(Z_\pm \) near \([\mathcal {E}_\pm ]\). Locally, \(\mathscr {M}_{Z_\pm }\) embeds as a complex Lagrangian submanifold into \(\mathscr {M}_{\Sigma _\pm }\). Since \({\mathfrak {r}}^*\omega _{K,-}=-\omega _{K,+}\), both \(\mathscr {M}_{Z_+}\) and \(\mathscr {M}_{Z_-}\) can be viewed as Lagrangian submanifolds of \(\mathscr {M}_{\Sigma _+}\) with respect to the symplectic form induced by \(\omega _{K,+}\). Equation (3.3) asks for these Lagrangian submanifolds to intersect transversely at the point \([\mathcal {E}_+|_{\Sigma _+}]\). If one thinks of \(\mathrm{{G}}_2\)-manifolds arising via the twisted connected sum construction as analogues of 3-manifolds with a fixed Heegaard splitting, then this is much like the geometric picture behind Atiyah–Floer conjecture in dimension three [2].
In Sect. 4, we will review a constructive method to obtain explicit examples of such instanton gluing in many interesting cases.
3.1 Hermitian Yang-Mills Connections on ACyl CY 3-Folds
Suppose \((W,\omega ,\Omega )\) is Calabi–Yau 3-fold and \((Y:=\mathbb {R}\times W,\phi :=\mathrm{{d}}t\wedge \omega +\mathop {\mathrm {Re}}\Omega )\) is the corresponding cylindrical \(\mathrm{{G}}_2\)-manifold. In this section we relate translation-invariant \(\mathrm{{G}}_2\)-instantons over Y with Hermitian–Yang–Mills connections over W.
Definition 3.3
Let \((W,\omega )\) be a Kähler manifold and let E be a \({\mathbf{{P}}\mathrm{{U}}}(n)\)-bundle over W. A connection \(A\in \mathscr {A}(E)\) on E is Hermitian–Yang–Mills (HYM) connection if
Here \(\Lambda \) is the dual of the Lefschetz operator \(L:=\omega \wedge \cdot \).
Remark 3.4
Instead of working with \({\mathbf{{P}}\mathrm{{U}}}(n)\)-bundles, one can also work with \(\mathrm{{U}}(n)\)-bundles and instead of the second part of (3.4) require that \(\Lambda F_A\) be equal to a constant. These view points are essentially equivalent.
Remark 3.5
By the first part of (3.4) a HYM connection induces a holomorphic structure on E. If W is compact, then there is a one-to-one correspondence between gauge equivalence classes of HYM connections on E and isomorphism classes of polystable holomorphic bundles \(\mathcal {E}\) whose underlying topological bundle is E, see Donaldson [9] and Uhlenbeck–Yau [37].
On a Calabi–Yau 3-fold, (3.4) is equivalent to
hence, using \(*(\mathrm{{d}}t\wedge \omega +\mathop {\mathrm {Re}}\Omega )=\frac{1}{2}\omega \wedge \omega -\mathrm{{d}}t\wedge \mathop {\mathrm {Im}}\Omega \) one easily derives:
Proposition 3.6
([33, Proposition 8]) Denote by \({\pi _W: Y\rightarrow W}\) the canonical projection. A is a HYM connection if and only if \(\pi _W^*A\) is a \(\mathrm{{G}}_2\)-instanton.
In general, if A is a \(\mathrm{{G}}_2\)-instanton on a G-bundle E over a \(\mathrm{{G}}_2\)-manifold \((Y,\phi )\), then the moduli space \(\mathcal {M}\) of \(\mathrm{{G}}_2\)-instantons near [A], i.e., the space of gauge equivalence classes of \(\mathrm{{G}}_2\)-instantons near [A] is the space of small solutions \((\xi ,a)\in \left( \Omega ^0\oplus \Omega ^1\right) (Y,{\mathfrak {g}}_E)\) of the system of equations
modulo the action of \(\Gamma _A\subset \mathscr {G}\), the stabiliser of A, assuming either that Y is compact or appropriate control over the growth of \(\xi \) and a. The infinitesimal deformation theory of [A] is governed by that equation’s linearisation operator
Definition 3.7
A is called irreducible and unobstructed if \(L_A\) is surjective.
If A is irreducible and unobstructed, then \(\mathcal {M}\) is smooth at [A]. If Y is compact, then \(L_A\) has index zero; hence, is surjective if, and only if, it is invertible; therefore, irreducible and unobstructed \(\mathrm{{G}}_2\)-instantons form isolated points in \(\mathcal {M}\). If Y is non-compact, the precise meaning of \(\mathcal {M}\) and \(L_A\) depends on the growth assumptions made on \(\xi \) and a and \(\mathcal {M}\) may very well be positive-dimensional.
Proposition 3.8
If A is HYM connection on a bundle E over a \(\mathrm{{G}}_2\)-manifold \(Y:=\mathbb {R}\times W\) as in Proposition 3.6, then the operator \(L_{\pi _W^*A}\) defined in (3.5) can be written as
where
and \({D_A: \left( \Omega ^0\oplus \Omega ^0\oplus \Omega ^1\right) (W,{\mathfrak {g}}_E) \rightarrow \left( \Omega ^0\oplus \Omega ^0\oplus \Omega ^1\right) (W,{\mathfrak {g}}_E)}\) is defined by
Definition 3.9
Let A be a HYM connection on a \({\mathbf{{P}}\mathrm{{U}}}(n)\)-bundle E over a Kähler manifold \((W,\omega )\). Set
\(\mathcal {H}^0_A\) is called the space of infinitesimal automorphisms of A and \(\mathcal {H}^1_A\) is called the space of infinitesimal deformations of A.
Remark 3.10
If W is compact, then \(\mathcal {H}^i_A\cong H^i(W,{\mathcal {E}} nd_0(\mathcal {E}))\) where \(\mathcal {E}\) is the holomorphic bundle induced by A.
Proposition 3.11
If \((W,\omega ,\Omega )\) is a compact Calabi–Yau 3-fold and A is a HYM connection on a G-bundle \(E\rightarrow W\), then
where \(D_A\) is as in (3.6).
3.2 Gluing \(\mathrm{{G}}_2\)-Instantons over ACyl \(\mathrm{{G}}_2\)-Manifolds
Definition 3.12
Let \((Y,\phi )\) be an \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifold and let A be a \(\mathrm{{G}}_2\)-instanton on a G-bundle over \((Y,\phi )\) asymptotic to \(A_\infty \). For \(\delta \in \mathbb {R}\) we set
where \({\underline{a}}=(\xi ,a)\in \left( \Omega ^0\oplus \Omega ^1\right) (Y,{\mathfrak {g}}_E)\). Set \(\mathcal {T}_A:=\mathcal {T}_{A,0}\).
Proposition 3.13
([32, Propositions 3.22, 3.23]) Let \((Y,\phi )\) be an \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifold and let A be a \(\mathrm{{G}}_2\)-instanton asymptotic to \(A_\infty \). Then there is a constant \(\delta _0>0\) such that for all \(\delta \in [0,\delta _0]\), \(\mathcal {T}_{A,\delta }=\mathcal {T}_A\) and there is a linear map \({\iota : \mathcal {T}_{A} \rightarrow \mathcal {H}^0_{A_\infty }\oplus \mathcal {H}^1_{A_\infty }}\) such that
In particular, \( \ker \iota =\mathcal {T}_{A,-\delta _0}.\)
Furthermore,
and, if \(\mathcal {H}^0_{A_\infty }=0\), then \(\mathop {\mathrm {im}}\iota \subset \mathcal {H}^1_{A\infty }\) is Lagrangian with respect to the symplectic structure on \(\mathcal {H}^1_{A_\infty }\) induced by \(\omega \).
Assume we are in the situation of Proposition 3.13; if moreover \(\ker \iota =0\) and \(\mathcal {H}^0_{A_\infty }=0\), then one can show that the moduli space \(\mathcal {M}_Y\) of \(\mathrm{{G}}_2\)-instantons near [A] which are asymptotic to some HYM connection is smooth. Although the moduli space \(\mathcal {M}_W\) of HYM connections near \([A_\infty ]\) is not necessarily smooth, formally, it still makes sense to talk about its symplectic structure and view \(\mathcal {M}_Y\) as a Lagrangian submanifold. The following theorem shows that transverse intersections of a pair of such Lagrangians give rise to \(\mathrm{{G}}_2\)-instantons.
Theorem 3.14
([32, Theorem 3.24]) Let \((Y_\pm ,\phi _\pm )\) be a pair of \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifolds that match via \({f: W_+\rightarrow W_-}\). Denote by \((Y_T,\phi _T)_{T\ge T_0}\) the resulting family of compact \(\mathrm{{G}}_2\)-manifolds arising from the construction in Sect. 2.3.2. Let \(A_\pm \) be a pair of \(\mathrm{{G}}_2\)-instantons on \(E_\pm \) over \((Y_\pm ,\phi _\pm )\) asymptotic to \(A_{\infty ,\pm }\). Suppose the following hold:
-
There is a bundle isomorphism \({\bar{f}: E_{\infty ,+}\rightarrow E_{\infty ,-}}\) covering f such that \(\bar{f}^*A_{\infty ,-}{=}A_{\infty ,+}\),
-
The maps \({\iota _\pm : \mathcal {T}_{A_\pm }\rightarrow \ker D_{A_{\infty ,\pm }}}\) constructed in Proposition 3.13 are injective and their images intersect trivially
$$\begin{aligned} \mathop {\mathrm {im}}\left( \iota _+\right) \cap \mathop {\mathrm {im}}\left( \bar{f}^*\circ \iota _-\right) =\{0\} \subset \mathcal {H}^0_{A_{\infty ,+}}\oplus \mathcal {H}^1_{A_{\infty ,+}}. \end{aligned}$$(3.7)
Then there exists \(T_1\ge T_0\) and for each \(T\ge T_1\) there exists an irreducible and unobstructed \(\mathrm{{G}}_2\)-instanton \(A_T\) on a G-bundle \(E_T\) over \((Y_T,\phi _T)\).
Sketch of Proof
One proceeds in three steps. We first produce an approximate \(\mathrm{{G}}_2\)-instanton \(\tilde{A}_T\) by an explicit cut-and-paste procedure. This reduces the problem to solving the non-linear partial differential equation
for \(a\in \Omega ^1(Y_T,{\mathfrak {g}}_{E_T})\) and \(\xi \in \Omega ^0(Y_T,{\mathfrak {g}}_{E_T})\) where \(\psi _T:=*\phi _T\). Under the hypotheses of Theorem 3.14 one can solve the linearisation of (3.8) in a uniform fashion. The existence of a solution of (3.8) then follows from a simple application of Banach’s fixed-point theorem.\(\square \)
3.3 From Holomorphic Bundles over Building Blocks to \(\mathrm{{G}}_2\)-Instantons over ACyl \(\mathrm{{G}}_2\)-Manifolds
We now briefly explain how one may deduce Theorem 3.1 from Theorem 3.14.
Let \((V,\omega ,\Omega )\) be an \(\mathrm {ACylCY}^3\) with asymptotic cross-section \((\Sigma ,\omega _I,\omega _J,\omega _K)\). The following theorem can be used to produce examples of HYM connections A on a \({\mathbf{{P}}\mathrm{{U}}}(n)\)-bundle \(E\rightarrow V\) asymptotic to an ASD instanton \(A_\infty \) on a \({\mathbf{{P}}\mathrm{{U}}}(n)\)-bundle \(E_\infty \rightarrow \Sigma \) (here, by a slight additional abuse, we denote by \(E_\infty \) and \(A_\infty \) their respective pullbacks to \(\mathbb {R}_+\times \mathbb {S}^1\times \Sigma \)). Hence, by taking the product with \( \mathbb {S}^1\), it yields examples of \(\mathrm{{G}}_2\)-instantons \(\pi _V^*A\) asymptotic to \(\pi _\Sigma ^*A_\infty \) over the \(\mathrm {ACyl}\) \(\mathrm{{G}}_2\)-manifold \( \mathbb {S}^1\times V\). Denote the canonical projections in this context by
Theorem 3.15
([33, Theorem 59] & [19, Theorem 1.1]) Let Z and \(\Sigma \) be as in Theorem 2.13 and let \((V:=Z\setminus \Sigma ,\omega ,\Omega )\) be the resulting \(\mathrm {ACylCY}^3\). Let \(\mathcal {E}\) be a holomorphic vector bundle over Z and let \(A_\infty \) be an ASD instanton on \(\mathcal {E}|_\Sigma \) compatible with the holomorphic structure. Then there exists a HYM connection A on \(\mathcal {E}|_V\) which is compatible with the holomorphic structure on \(\mathcal {E}|_V\) and asymptotic to \(A_\infty \).
Remark 3.16
The last assertion of the exponential decay \(A\rightsquigarrow A_\infty \) is claimed in [33, Theorem 59] but its proof in that reference is not satisfactory. That part of the theorem is essentially superseded by [19, Theorem 1.1], which additionally extends this existence result to singular \(\mathrm{{G}}_2\)-instantons, obtained from asymptotically stable reflexive sheaves, following in spirit the argument in the compact case, by [4].
This together with Theorem 3.14 and the following result immediately implies Theorem 3.1.
Proposition 3.17
([32, Proposition 4.3]) In the situation of Theorem 3.15, suppose \(H^0(\Sigma ,{\mathcal {E}} nd_0(\mathcal {E}|_\Sigma ))=0\). Then
and, for some small \(\delta >0\), there exist injective linear maps \( \kappa _-\) and \(\kappa \) such that the following diagram commutes:

Sketch of Proof
Equation (3.9) is a direct consequence of \(\mathcal {H}^0_{A_\infty }=0\). If A is a HYM connection asymptotic to \(A_\infty \) over an \(\mathrm {ACylCY}^3\) then there exists a \(\delta _0>0\) such that, for all \(\delta \le \delta _0\),
with \(D_A\) as in (3.6). Furthermore, there exists \(\delta _1>0\) such that, for all \(\delta \le \delta _1\), one has \(\mathcal {H}^0_{A,\delta }=0\) and
where \(\mathcal {H}^i_{A,\delta }:=\left\{ \alpha \in \mathcal {H}^i_A : \alpha \overset{\delta }{\rightsquigarrow }0 \right\} \).\(\square \)
4 Transversal Examples via the Hartshorne-Serre Correspondence
In [5, 6, 21], building blocks Z are produced by blowing up Fano or semi-Fano 3-folds along the base curve \(\mathscr {C}\) of an anticanonical pencil (see Proposition 4.6). By understanding the deformation theory of pairs \((X,\Sigma )\) of semi-Fanos X and anticanonical K3 divisors \(\Sigma \subset X\), one can produce hundreds of thousands of pairs with the required matching (see Sect. 4.3). In order to apply Theorem 3.1 to produce \(\mathrm G_2\)-instantons over the resulting twisted connected sums, one first requires some supply of asymptotically stable, inelastic vector bundles \(\mathcal {E}\rightarrow X\). Moreover, to satisfy the hypotheses of compatibility and transversality, one would in general need some understanding of the deformation theory of triples \((X, \Sigma , \mathcal {E})\). In this Sect. I outline our approach in [24] to the problem of production of ingredients, in the form of gluable pairs of holomorphic bundles over building blocks.
The Hartshorne-Serre construction generalises the correspondence between divisors and line bundles, under certain conditions, in the sense that bundles of higher rank are associated to subschemes of higher codimension. We recall the rank 2 version, as an instance of Arrondo’s formulationFootnote 3 [1, Theorem 1]:
Theorem 4.1
Let \(\mathscr {S}\subset Z\) be a local complete intersection subscheme of codimension 2 in a smooth algebraic variety. If there exists a line bundle \(\mathcal {L}\rightarrow Z\) such that
-
\(H^2(Z,\mathcal {L}^*)=0\),
-
\(\wedge ^2\mathcal {N}_{\mathscr {S}/Z}=\mathcal {L}|_\mathscr {S}\), where \(\mathcal {N}_{\mathscr {S}/Z}\) denotes the normal bundle of \(\mathscr {S}\) in Z.
then there exists a rank 2 holomorphic vector bundle \(\mathcal {F}\rightarrow Z\) such that
-
1.
\(\wedge ^2\mathcal {F}=\mathcal {L}\),
-
2.
\(\mathcal {F}\) has one global section whose vanishing locus is \(\mathscr {S}\).
We will refer to such \(\mathcal {F}\) as the Hartshorne-Serre bundle obtained from \(\mathscr {S}\) (and \(\mathcal {L}\)).
Using the Hartshorne-Serre construction, we can systematically produce families of bundles over the building blocks, which, in favourable cases, are parametrised by the building block’s blow-up curve \(\mathscr {C}\) itself. This perspective lets us understand the deformation theory of the bundles very explicitly, and it also separates the latter from the deformation theory of the pair \((X,\Sigma )\). We can therefore first find matchings between two semi-Fano families using the techniques from [6], and then exploit the high degree of freedom in the choice of the blow-up curve \(\mathscr {C}\) (see Lemma 4.7) to satisfy the compatibility and transversality hypotheses.
4.1 A Detailed Example
As a proof of concept, we will henceforth walk through the process of construction of examples, with the particular pair adopted in [24]:
Example 4.2
The product \(X_+=\mathbb {P}^1\times \mathbb {P}^2\) is a Fano 3-fold. Let \(\left| \Sigma _{0},\Sigma _{\infty }\right| \subset \left| -K_{X_+}\right| \) be a generic pencil with (smooth) base locus \(\mathscr {C}_+\) and \(\Sigma _+\in \left| \Sigma _{0},\Sigma _{\infty }\right| \) generic. Denote by \(r_+:Z_+\rightarrow X_+\) the blow-up of \(X_+\) in \(\mathscr {C}_+\), by \(\widetilde{\mathscr {C}_+}\) the exceptional divisor and by \(\ell _+\) a fibre of \(p_{1}:\widetilde{\mathscr {C}_+}\rightarrow \mathscr {C}_+\). The proper transform of \(\Sigma _+\) in \(Z_+\) is also denoted by \(\Sigma _+\), and \((Z_+,S_+)\) is a building block by Proposition 4.6. For future reference, we fix classes
NB.: Clearly \(-K_{X_+}\) is very ample, thus also \(-K_{X_+|\Sigma _+}\), so \(X_+\) lends itself to application of Lemma 4.7.
Example 4.3
A double cover \(\pi :X_-\overset{2:1}{\longrightarrow } \mathbb {P}^1\times \mathbb {P}^2\) branched over a smooth (2, 2) divisor D is a Fano 3-fold. Let \(\left| \Sigma _{0},\Sigma _{\infty }\right| \subset \left| -K_{X_-}\right| \) be a generic pencil with (smooth) base locus \(\mathscr {C}_-\) and \(\Sigma _-\in \left| \Sigma _{0},\Sigma _{\infty }\right| \) generic. Denote by \(r_-:Z_-\rightarrow X_-\) the blow-up of \(X_-\) in \(\mathscr {C}_-\), and by \(\widetilde{\mathscr {C}_-}\) the exceptional divisor. The proper transform of \(\Sigma _-\) in \(Z_-\) is also denoted by \(\Sigma _-\), and \((Z_-,S_-)\) is a building block by Proposition 4.6. For future reference, we fix classes
and
where x is a point.
In that context, the existence of solutions satisfying the hypotheses of the TCS \(\mathrm{{G}}_2\)-instanton gluing theorem takes the following form:
Theorem 4.4
([24, Theorem 1.3]) There exists a matching pair of building blocks \((Z_\pm , \Sigma _\pm )\), obtained as \(Z_\pm =\mathrm {Bl}_{\mathscr {C}_\pm }X_\pm \) for \(X_+=\mathbb {P}^1\times \mathbb {P}^2\) and the double cover \(X_-\overset{2:1}{\longrightarrow }\mathbb {P}^1\times \mathbb {P}^2\) branched over a (2, 2) divisor, with rank 2 holomorphic bundles \(\mathcal {E}_\pm \rightarrow Z_\pm \) satisfying the hypotheses of Theorem 3.1.
Here’s a sketch of the procedure leading to Theorem 4.4:
-
We construct holomorphic bundles on building blocks from certain complete intersection subschemes, via the Hartshorne-Serre correspondence (Theorem 4.1), as well as two families of bundles \(\{\mathcal {F}_{\pm }\rightarrow X_\pm \} \), over the particular blocks of Theorem 4.4, that are conducive to application of Theorem 3.1.
-
Then, in Sect. 4.5, we focus on the moduli space \(\mathscr {M}_{\Sigma _+,\mathcal {A}_+}^{s}(v_{\Sigma _+})\) of stable bundles on \(\Sigma _+\), where the problems of compatibility and transversality therefore “take place”. Here \(X_+=\mathbb {P}^1\times \mathbb {P}^2\), \(\Sigma _+ \subset X_+\) is the anti-canonical K3 divisor and, for a smooth curve \({\mathscr {C}}_+ \in |{-}K_{X_+|\Sigma _+}|\), the block \(Z_+ := {\text {Bl}}_{{\mathscr {C}}_+} X_+\) is in the family obtained from Example 4.2.
It can be shown that \(\mathscr {M}_{\Sigma _+,\mathcal {A}_+}^{s}(v_{\Sigma _+})\) is isomorphic to \(\Sigma _+\) itself, and that the restrictions of the family of bundles \(\mathcal {F}_+\) correspond precisely to the blow-up curve \(\mathscr {C}\). Now, given a rank 2 bundle \(\mathcal {F}_+\rightarrow Z_+\) such that \(\mathcal {G}:= \mathcal {F}_{+|\Sigma _{+}} \in \mathscr {M}^{s}_{\Sigma _{+},\mathcal {A}_{+}}(v_{\Sigma _+})\), the restriction map
$$\begin{aligned} \mathrm{{res}}\, : H^1\left( Z_+, \mathscr {E}{} \textit{nd}_0(\mathcal {F}_+)\right) \rightarrow H^1(\Sigma _+, \mathscr {E}{} \textit{nd}_0(\mathcal {G})) \end{aligned}$$(4.1)corresponds to the derivative at \(\mathcal {F}_+\) of the map between instanton moduli spaces. Combining with Lemma 4.7, which guarantees the freedom to choose \(\mathscr {C}_+\) when constructing the block \(Z_+\) from \(\Sigma _+\), one has:
Theorem 4.5
([24, Theorem 1.4]) For every \(\mathcal {G} \in \mathscr {M}_{\Sigma _+,\mathcal {A}_+}^{s}(v_{\Sigma _+})\) and every line \(V \subset H^1(\Sigma _+, \mathscr {E}{} \textit{nd}_0(\mathcal {G}))\), there is a smooth base locus curve \(\mathscr {C}\in |{-}K_{X_+|\Sigma _+}|\) and an exceptional fibre \(\ell \subset \widetilde{\mathscr {C}}\) corresponding by Hartshorne-Serre to an inelastic vector bundle \(\mathcal {F}_+ \rightarrow Z_+\), such that \(\mathcal {F}_{+|\Sigma _+} = \mathcal {G}\) and the restriction map (4.1) has image V.
-
Let \({\mathfrak {r}}: \Sigma _+ \rightarrow \Sigma _-\) be a matching between \(X_+=\mathbb {P}^1\times \mathbb {P}^2\) and \(X_-\overset{2:1}{\longrightarrow }\mathbb {P}^1\times \mathbb {P}^2\). Then for any \(\mathcal {F}_- \rightarrow Z_-\) as above we can (up to a twist by holomorphic line bundles \(\mathcal {R}_\pm \rightarrow Z_\pm \)) choose the smooth curve \(\mathscr {C}_+ \in |{-}K_{X_+ | \Sigma _+}|\) in the construction of \(Z_+\) so that there is a Hartshorne-Serre bundle \(\mathcal {F}_+\rightarrow Z_+\) that matches \(\mathcal {F}_-\) transversely. Then the bundles \(\mathcal {E}_\pm :=\mathcal {F}_\pm \otimes \mathcal {R}_\pm \) satisfy the gluing hypotheses of Theorem 3.1.
4.2 Building Blocks from Semi-Fano 3-Folds and Twisted Connected Sums
For all but 2 of the 105 families of Fano 3-folds, the base locus of a generic anti-canonical pencil is smooth. This also holds for most families in the wider class of ‘semi-Fano 3-folds’ in the terminology of [5], i.e. smooth projective 3-folds where \(-K_X\) defines a morphism that does not contract any divisors. We can then obtain building blocks using [6, Proposition 3.15]:
Proposition 4.6
Let X be a semi-Fano 3-fold with \(H^{3}(X,\mathbb {Z})\) torsion-free, \(|\Sigma _{0},\Sigma _{\infty }{|}\subset |-K_{X}|\) a generic pencil with (smooth) base locus \(\mathscr {C}\), \(\Sigma \in |\Sigma _{0},\Sigma _{\infty }|\) generic, and Z the blow-up of X at \(\mathscr {C}\). Then \(\Sigma \) is a smooth K3 surface, its proper transform in Z is isomorphic to \(\Sigma \), and \((Z,\Sigma )\) is a building block. Furthermore
-
1.
the image N of \(H^{2}(Z,\mathbb {Z})\rightarrow H^{2}(\Sigma ,\mathbb {Z})\) equals that of \(H^{2}(X,\mathbb {Z})\rightarrow H^{2}(\Sigma ,\mathbb {Z})\);
-
2.
\(H^{2}(X,\mathbb {Z})\rightarrow H^{2}(\Sigma ,\mathbb {Z})\) is injective and the image N is primitive in \(H^{2}(\Sigma ,\mathbb {Z})\).
Let us notice for later use that, whenever \(-K_X|_\Sigma \) is very ample, it is possible to ‘wiggle’ a blow-up curve \(\mathscr {C}\) so as to realise any prescribed incidence condition \((x,V)\in T\Sigma \). This fact will play an important role in the transversality argument in Sect. 4.5.
Lemma 4.7
([24, Lemma 2.5]) Let X be a semi-Fano, \(\Sigma \in |{-}K_X|\) a smooth K3 divisor, and suppose that the restriction of \(-K_X\) to \(\Sigma \) is very ample. Then given any point \(x \in \Sigma \) and any (complex) line \(V \subset T_x \Sigma \), there exists an anticanonical pencil containing \(\Sigma \) whose base locus \(\mathscr {C}\) is smooth, contains x, and \(T_x \mathscr {C}= V\).
Finally, note that if \(X_\pm \) is a pair of semi-Fanos and \({\mathfrak {r}}: \Sigma _+ \rightarrow \Sigma _-\) is a matching in the sense of Definition 2.7, then \({\mathfrak {r}}\) also defines a matching of building blocks constructed from \(X_\pm \) using Proposition 4.6. Thus given a pair of matching semi-Fanos we can apply Theorem 2.8 to construct closed \(\mathrm{{G}}_{2}\)-manifolds, but this still involves choosing the blow-up curves \(\mathscr {C}_\pm \).
4.3 The Matching Problem
We now explain in more detail the argument of [6, Sect. 6] for finding matching building blocks \((Z_\pm , \Sigma _\pm )\). The blocks will be obtained by applying Proposition 4.6 to a pair of semi-Fanos \(X_\pm \), from some given pair of deformation types \(\mathcal {X}_\pm \).
A key deformation invariant of a semi-Fano X is its Picard lattice \(\mathrm{{Pic}}(X) \cong H^2(X; \mathbb {Z})\). For any anticanonical K3 divisor \(\Sigma \subset X\), the injection \(\mathrm{{Pic}}(X) \hookrightarrow H^2(\Sigma ;\mathbb {Z})\) is primitive. The intersection form on \(H^2(\Sigma ;\mathbb {Z})\) of any K3 surface is isometric to \(L_{K3} := 3\mathrm{{U}}\oplus 2\mathrm{{E}}_8\), the unique even unimodular lattice of signature (3, 19). We can therefore identify \(\mathrm{{Pic}}(X)\) with a primitive sublattice \(N \subset L_{K3}\) of the K3 lattice, uniquely up to the action of the isometry group \(O(L_{K3})\) (this is usually uniquely determined by the isometry class of N as an abstract lattice).
Given a matching \({\mathfrak {r}}:\Sigma _+ \rightarrow \Sigma _-\) between anticanonical divisors in a pair of semi-Fanos, we can choose the isomorphisms \(H^2(\Sigma _\pm ;\mathbb {Z}) \cong L_{K3}\) compatible with \({\mathfrak {r}}^*\), hence identify \(\mathrm{{Pic}}(X_+)\) and \(\mathrm{{Pic}}(X_-)\) with a pair of primitive sublattices \(N_+, N_- \subset L_{K3}\). While the \(O(L_{K3})\) class of \(N_\pm \) individually depends only on \(X_\pm \), the \(O(L_{K3})\) class of the pair \((N_+, N_-)\) depends on \({\mathfrak {r}}\), and we call \((N_+, N_-)\) the configuration of \({\mathfrak {r}}\). Many important properties of the resulting twisted connected sum only depend on the hyper-Kähler rotation in terms of the configuration.
Given a configuration \(N_+, N_- \subset L_{K3}\), let
We say that the configuration is orthogonal if \(N_\pm \) are rationally spanned by \(N_0\) and \(R_\pm \) (geometrically, this means that the reflections in \(N_+\) and \(N_-\) commute). Given a pair \(\mathcal {X}_\pm \) of deformation types of semi-Fanos, then there are sufficient conditions for a given orthogonal configuration to be realised by some matching [6, Proposition 6.17],
Proposition 4.8
i.e., so that there exist \(X_{\pm }\in \mathcal {X}_{\pm }\), \(\,\Sigma _{\pm }\in |{-}K_{X_{\pm }}|\), and a matching \({\mathfrak {r}}:\Sigma _{+}\rightarrow \Sigma _{-}\) with the given configuration.
Now consider the problem of finding matching bundles \(\mathcal {E}_\pm \rightarrow Z_\pm \) in order to construct \(\mathrm G_2\)-instantons by application of Theorem 3.1. For the compatibility hypothesis it is obviously necessary that Chern classes match:
Identifying \(H^2(\Sigma _+; \mathbb {Z}) \cong L_{K3} \cong H^2(\Sigma _-; \mathbb {Z})\) compatibly with \({\mathfrak {r}}^*\), this means we need
Hence, if \(N_0\) is trivial, both \(c_1(\mathcal {E}_{\pm |\Sigma _\pm })\) must also be trivial, which is a very restrictive condition on our bundles. To allow more possibilities, we want matchings \({\mathfrak {r}}\) whose configuration \(N_+, N_- \subset L_{K3}\) has non-trivial intersection \(N_0\).
Table 4 of [7] lists all 19 possible such matchings with Picard rank 2, among which we can find the pair of building blocks of Examples 4.2 and 4.3, coming from the Fano 3-folds \(X_+=\mathbb {P}^1\times \mathbb {P}^2\) and the double cover \(X_-\overset{2:1}{\longrightarrow }\mathbb {P}^1\times \mathbb {P}^2\) branched over a (2, 2) divisor. Several other choices would be possible to produce examples of \(\mathrm G_2\)-instantons.
4.4 Hartshorne-Serre Bundles over Building Blocks
4.4.1 The General Construction Algorithm
Let X be a semi-Fano 3-fold and \((Z,\Sigma )\) be the block constructed as a blow-up of X along the base locus \(\mathscr {C}\) of a generic anti-canonical pencil (Proposition 4.6). In [24, Sect. 3.1] a general approach is provided for making the choices of \(\mathcal {L}\) and \(\mathscr {S}\) in Theorem 4.1, in order to construct a Hartshorne-Serre bundle \(\mathcal {F}\rightarrow Z\) which, up to a twist, yields the bundle \(\mathcal {E}\) meeting the requirements of Theorem 3.1. The approach may be summarised as follows:
Summary 4.9
Let \((Z_\pm ,\Sigma _\pm )\) be the building blocks constructed by blowing-up \(N_\pm \)-polarised semi-Fano 3-folds \(X_\pm \) along the base locus \(\mathscr {C}_\pm \) of a generic anti-canonical pencil (cf. Proposition 4.6). Let \(N_{0}\subset N_\pm \) be the sub-lattice of orthogonal matching, as in Sect. 4.3. Let \(\mathcal {A}_\pm \) be the restriction of an ample class of \(X_\pm \) to \(\Sigma _\pm \) which is orthogonal to \(N_{0}\). We look for the Hartshorne-Serre parameters \(\mathscr {S}_\pm \) and \(\mathcal {L}_\pm \) of Theorem 4.1, where \(\mathscr {S}_+=\ell \) is an exceptional fibre in \(Z_+\), \(\mathscr {S}_-\) is a genus 0 curve in \(Z_-\) and \(\mathcal {L}_\pm \rightarrow Z_\pm \) are line bundles such that:
-
1.
\(c_{1}(\mathcal {L}_\pm ) \in N_{0} \mod 2\mathrm{{Pic}}(\Sigma _\pm )\);
-
2.
\(c_{1}(\mathcal {L}_{\pm |\Sigma _\pm })\cdot \mathcal {A}_\pm >0\);
-
3.
\(\chi (\mathcal {L}^*_{\pm })\le 0\);
-
4.
\(c_{1}(\mathcal {L}_+)\cdot \mathscr {S}_+=-1\) and \((S_--c_1(\mathcal {L}_-))\cdot \mathscr {S}_-=2\);
-
5.
\(c_{1}(\mathcal {L}_{+|\Sigma _+})^{2}=-4\) and \(\Sigma _-\cdot \mathscr {S}_- -\frac{1}{4}c_{1}(\mathcal {L}_{-|\Sigma _-})^{2}=2\);
Finally, among candidate data satisfying these constraints, inelasticity must be arranged “by hand’.
The reader who would like to construct other examples might follow this 4-step programme:
- Step 1.:
-
Find two matching \(N_\pm \)-polarized semi-Fano 3-folds \(X_\pm \) such that:
-
(i)
there exists \(x\in N_+\) such \(x^2=-4\) (or more generally \(x^2=2k-6\), for a moduli space \(\mathscr {M}^{s}_{\Sigma ,\mathcal {A}}(v)\) of dimension 2k).
-
(ii)
there exists a primitive element \(y\in N_0\) such that \(y^2\le -8\) and 4 divides \(y^2\).
- Step 2.:
-
Find \(\mathcal {L}_\pm \) and \(\mathscr {S}_-\) which verify the conditions of Summary 4.9 (perhaps with a computer).
- Step 3.:
-
The following must be checked by ad-hoc methods:
-
1.
\(H^2(\mathcal {L}^*_\pm )=0\), for the Hartshorne-Serre construction (Theorem 4.1);
-
2.
divisors with small slope do not contain \(\mathscr {S}\), for asymptotic stability ([16, Proposition 10]);
-
3.
\(h^1(\mathcal {L}^*)=h^1(\mathcal {F})=0\) and the dimensional constraint (4.2) for your choice of \(\dim \mathscr {M}^{s}_{\Sigma ,\mathcal {A}}(v)\), corresponding to inelasticity (Proposition 4.15).
- Step 4.:
-
Conclude with similar arguments to Sect. 4.5.
4.4.2 Construction of \(\mathcal {F}_+\) over \(X_+=\mathbb {P}^1\times \mathbb {P}^2\) and \(\mathcal {F}_-\) over \(X_-\overset{2:1}{\longrightarrow }\mathbb {P}^1\times \mathbb {P}^2\)
In view of the constraints in Summary 4.9, we apply Theorem 4.1 to \(Z_+=\mathrm {Bl}_\mathscr {C}X_+\) as above, obtained by blowing up \(X_+=\mathbb {P}^1\times \mathbb {P}^2\) from Example 4.2, with parameters
Proposition 4.10
([24, Propositions 3.5, 4.4, 5.7]) Let \((Z_+,\Sigma _+)\) be a building block as in Example 4.2, \(\mathscr {C}\) a pencil base locus and \(\ell \subset Z_+\) an exceptional fibre of \(\widetilde{\mathscr {C}}\rightarrow \mathscr {C}\). There exists a rank 2 asymptotically stable and inelastic Hartshorne-Serre bundle \(\mathcal {F}_+\rightarrow Z_+\) obtained from \(\ell \) such that
-
1.
\(c_{1}(\mathcal {F}_+)=-\Sigma _+-G_++H_+\), and
-
2.
\(\mathcal {F}_+\) has a global section whose vanishing locus is a fibre \(\ell \) of \(p_1:\widetilde{\mathscr {C}}\rightarrow \mathscr {C}\).
Similarly, one applies Theorem 4.1 to the building block \(Z_-\) obtained by blowing up \(X_-\overset{2:1}{\longrightarrow }\mathbb {P}^1\times \mathbb {P}^2\), from Example 4.3, with
Proposition 4.11
([24, Propositions 3.9, 4.5, 5.8]) Let \((Z_-,\Sigma _-)\) be a building block provided in Example 4.3 and \(\mathscr {S}\) a line of class \(h_-\). There exists a rank 2 Hartshorne-Serre bundle \(\mathcal {F}_-\rightarrow Z_-\) obtained from \(\mathscr {S}\) such that:
-
1.
\(c_{1}(\mathcal {F}_-)=G_-\), and
-
2.
\(\mathcal {F}_-\) has a global section whose vanishing locus is \(\mathscr {S}\), where \(\left[ \mathscr {S}\right] =h_-\).
Remark 4.12
In order to check the stability of Hartshorne-Serre bundles over \(\Sigma _\pm \), we use a tailor-made instance [16, Proposition 10] of a more general Hoppe-type stability criterion for holomorphic bundles over so-called polycyclic varieties, whose Picard group is free Abelian [16, Corollary 4].
In the context above, the moduli spaces of the stable bundles \(\mathcal {F}_{\pm |\Sigma _\pm }\) have the ‘minimal’ positive dimension, for transversal intersection to occur:
Proposition 4.13
Let \((Z_\pm ,\Sigma _\pm )\) be the building block provided in Examples 4.2 and 4.3, and let \(\mathcal {F}_\pm \rightarrow Z_\pm \) be the asymptotically stable bundles constructed in Propositions 4.10 and 4.11. Let \(\mathscr {M}^{s}_{\Sigma _\pm ,\mathcal {A}_\pm }(v_\pm )\) be the moduli space of \(\mathcal {A}_\pm \)-stable bundles on \(\Sigma _\pm \) with Mukai vector \(v_\pm =v(\mathcal {F}_{\pm |\Sigma _\pm })\). We have:
Recall that (see eg. [14]) that the Mukai vector of a vector bundle \(\mathcal {F}\rightarrow \Sigma \) on a K3 surface is defined as
with \(\chi (\mathcal {F})=\frac{c_{1}(\mathcal {F})^2}{2}+2\mathop {\mathrm {rk}}\nolimits \mathcal {F}-c_{2}(\mathcal {F})\).
4.4.3 Inelasticity of Asymptotically Stable Hartshorne-Serre Bundles
These results hold for general building blocks and may be of independent interest. Recall that a bundle \(\mathcal {F}\) over a building block \((Z,\Sigma )\) is inelastic if
This condition means that there are no global deformations of the bundle \(\mathcal {F}\) which maintain \(\mathcal {F}_{|\Sigma }\) fixed at infinity. The following characterisation of inelasticity, in the case of asymptotically stable bundles, relates the freedom to extend \(\mathcal {F}\) and the dimension of the moduli space \(\mathscr {M}^{s}_{\Sigma ,\mathcal {A}}(v_\mathcal {F})\). The proof uses Serre duality and Maruyama’s characterisation of the moduli space of stable bundles over a polarised K3 surface [23, Proposition 6.9].
Proposition 4.14
Let \((Z,\Sigma )\) be a building block and \(\mathcal {F}\) an asymptotically stable bundle on Z. Let \(\mathscr {M}^{s}_{\Sigma ,\mathcal {A}}(v)\) be the moduli space of \(\mathcal {A}\)-\(\mu \)-stable bundles on \(\Sigma \) with Mukai vector \(v=v(\mathcal {F}_{|\Sigma })\). Then \(\mathcal {F}\) is inelastic if and only if
For Hartshorne-Serre bundles of rank 2 satisfying certain topological hypotheses, we may express the half-dimension of the moduli space in terms of the construction data:
Proposition 4.15
Let \((Z,\Sigma )\) be a building block, and let \(\mathcal {F}\rightarrow Z\) be an asymptotically stable Hartshorne–Serre bundle obtained from a genus 0 curve \(\mathscr {S}\subset Z\) and a line bundle \(\mathcal {L}\rightarrow Z\) as in Theorem 4.1. Let \(\mathscr {M}^{s}_{\Sigma ,\mathcal {A}}(v)\) be the moduli space of \(\mathcal {A}\)-\(\mu \)-stable bundles on \(\Sigma \) with Mukai vector \(v=v(\mathcal {F}_{|\Sigma })\). We assume:
-
1.
\(H^1(\mathcal {L}^*)=0\),
-
2.
\(H^1(\mathcal {F})=0\).
Then \(\mathcal {F}\) is inelastic if and only if
4.5 Proof of Theorem 4.5
Let \(X_+=\mathbb {P}^1\times \mathbb {P}^2\) as in Example 4.2, and \(\Sigma _+ \subset X_+\) be a smooth anti-canonical K3 divisor. For suitable choices of polarisation \(\mathcal {A}_+\) on \(\Sigma _+\) and Mukai vector \(v_{\Sigma _+}\), the associated moduli space \(\mathscr {M}^{s}_{\Sigma _+,\mathcal {A}_+}(v_{\Sigma _+})\) of (rank 2) \(\mathcal {A}_+\)-stable bundles is 2-dimensional. For a smooth curve \(\mathscr {C}\in |{-}K_{X_+|\Sigma _+}|\), let \(Z_+ := \text {Bl}_{\mathscr {C}} X_+\) be the building block resulting from Proposition 4.6. Then, for each exceptional fibre \(\ell \subset \widetilde{\mathscr {C}}\), the Mukai vector
has the property that, given a bundle \(\mathcal {F}_+\rightarrow Z_+\) as in Proposition 4.10 with \((\mathop {\mathrm {rk}}\nolimits \mathcal {F}_+, c_{1}(\mathcal {F}_+),c_{2}(\mathcal {F}_+))=v_{Z_+}\), the restriction to \(\Sigma _+\) has Mukai vector \(v_{\Sigma _+}\), so \(\mathcal {G} := \mathcal {F}_{+|\Sigma _+} \in \mathscr {M}^{s}_{\Sigma _+,\mathcal {A}_+}(v_{\Sigma _+})\). Thus the Hartshorne-Serre construction yields a family of asymptotically stable vector bundles \(\{(\mathcal {F}_+)_p\rightarrow Z_+ \mid p \in \mathscr {C}\}\) with
parametrised by \(\mathscr {C}\) itself.
One crucial feature of the building block obtained from \(X_+=\mathbb {P}^1\times \mathbb {P}^2\) is the fact that the moduli space of bundles over the anti-canonical K3 divisor \(\Sigma _+\) is actually isomorphic to \(\Sigma _+\) itself:
Proposition 4.16
([24, Lemma 4.7 & Proposition 4.8]) For each \(p\in \Sigma _+\), there exists an \(\mathcal {A}_+\)-\(\mu \)-stable and rank 2 Hartshorne-Serre bundle \(\mathcal {G}_p\rightarrow \Sigma _+\) obtained from p. The induced map
is an isomorphism of K3 surfaces.
Now let \(\mathcal {G} \in \mathscr {M}_{\Sigma _+,\mathcal {A}_+}^{s}(v_{\Sigma _+})\) and \(V \subset H^1(\Sigma _+, \mathscr {E}{} \textit{nd}_0(\mathcal {G}))\). From Proposition 4.16, there is \(p\in \Sigma _+\) such that \(\mathcal {G}=\mathcal {G}_p\) and let \(V'=(\mathrm{{d}}g)_p ^{-1}(V)\). Since \({-}K_{X_+|\Sigma _+}\) is very ample (see Example 4.2), Lemma 4.7 allows the choice of a smooth base locus curve \(\mathscr {C}\in |{-}K_{X_+|\Sigma _+}|\) such that \(p\in \mathscr {C}\) and \(T_p \mathscr {C}= V'\). By Proposition 4.10, we can find a family \(\{(\mathcal {F}_+)_q\rightarrow Z \mid q \in \mathscr {C}\}\) of holomorphic bundles parametrised by \(\mathscr {C}\), with prescribed topology (4.3) and \((\mathcal {F}_{+|\Sigma })_q=\mathcal {G}_q\) . Such a bundle \(\mathcal {F}_+\) has therefore all the properties claimed in Theorem 4.5.
Corollary 4.17
([24, Cor. 6.1]) In the context of Example 4.2, for every bundle \(\mathcal {G} \in \mathscr {M}_{\Sigma _+,\mathcal {A}_+}^{s}(v_{\Sigma _+})\) and every complex line \(V \subset H^1(\Sigma _+, \mathscr {E}{} \textit{nd}_0(\mathcal {G}))\), there are a smooth curve \(\mathscr {C}_+ \in |{-}K_{X_+|\Sigma _+}|\) and an asymptotically stable and inelastic vector bundle \(\mathcal {E}_+ \rightarrow Z_+\) such that \(\mathcal {E}_{+|\Sigma _+} = \mathcal {G}\) and \(\mathrm{{res}}\, : H^1(Z_+, \mathscr {E}{} \textit{nd}_0(\mathcal {E}_+)) \rightarrow H^1(\Sigma _+, \mathscr {E}{} \textit{nd}_0(\mathcal {G}))\) has image V.
Let
Corollary 4.18
([24, Cor. 6.2]) In the context of Example 4.3, there exists a family of asymptotically stable and inelastic vector bundles \(\{\mathcal {E}_- \rightarrow Z_-\}\), parametrised by the set of the lines in \(X_-\) of class \(h_-\), such that \(\mathcal {E}_{-|\Sigma _-}\in \mathscr {M}_{\Sigma _-,\mathcal {A}_-}^{s}(v_{\Sigma _-})\).
We fix a representative \(\mathcal {E}_- \rightarrow Z_-\) in the family of holomorphic bundles from Corollary 4.18, to be matched by a bundle \(\mathcal {E}_+ \rightarrow Z_+\) given by Corollary 4.17, so that asymptotic stability and inelasticity hold from the outset.
It remains to address compatibility and transversality. Since the chosen configuration for \({\mathfrak {r}}\) ensures that \({\mathfrak {r}}^*\) identifies the Mukai vectors of \(\mathcal {E}_{\pm |\Sigma _\pm }\), it induces a map \(\bar{{\mathfrak {r}}}^* :\mathscr {M}_{\Sigma _-,\mathcal {A}_-}^{s}(v'_{\Sigma _-})\rightarrow \mathscr {M}_{\Sigma _+,\mathcal {A}_+}^{s}(v'_{\Sigma _+})\). In particular, the target moduli space is 2-dimensional, by Proposition 4.13, and \({\mathfrak {r}}^* (\mathop {\mathrm {im}}\mathrm{{res}}_-)\) is 1-dimensional, since the bundles \(\{\mathcal {E}_-\}\) are parametrised by lines of fixed class \(h_-\). So indeed we apply Corollary 4.17 with \(\mathcal {G}= \bar{{\mathfrak {r}}}^* (\mathcal {E}_{-|\Sigma _-})\) and any choice of a direct complement subspace V such that
Denoting by \(\mathcal {M}_{\Sigma _\pm }(v)\) the moduli space of ASD instantons over \(\Sigma _\pm \) with Mukai vector v, the maps \(f_\pm \) (cf. (3.1)) in Theorem 3.1 are the linearisations of the Hitchin-Kobayashi isomorphisms
Therefore, our bundles \(\mathcal {E}_\pm \) indeed satisfy \(A_{\infty ,+}=\bar{{\mathfrak {r}}}^* A_{\infty ,-}\) for the corresponding instanton connections. Moreover, by linearity, \(\lambda _+(H^1(Z_+, \mathscr {E}{} \textit{nd}_0(\mathcal {E}_+)))\) is transverse in \(T_{A_{\infty ,+}} \mathcal {M}_{\Sigma _+}(v_{\Sigma _+}')\) to the image of the real 2-dimensional subspace \(\lambda _-(H^1(Z_-,\mathscr {E}{} \textit{nd}_0(\mathcal {E}_-))) \subset T_{A_{\infty ,-}} \mathcal {M}_{\Sigma _-}(v_{\Sigma _-}')\) under the linearisation of \(\bar{{\mathfrak {r}}}^*\).
Notes
- 1.
In fact only the condition \(\mathrm{{d}}\psi =0\) is required, so the discussion extends to cases in which the \(\mathrm{{G}}_2\)-structure is not necessarily torsion-free.
- 2.
The reader interested in analysis on tubular manifolds will find a thorough and very useful toolbox in [27].
- 3.
For a thorough justification of this choice of reference for the correspondence, see the Introduction section of Arrondo’s notes.
References
Arrondo, E. (2007). A home-made Hartshorne-Serre correspondence. Revista Matematica Complutense, 20, 423–443.
Atiyah, M. (1988). New invariants of \(3\)- and \(4\)-dimensional manifolds, The mathematical heritage of Hermann Weyl (pp. 285–299). Durham, NC, 1987.
Bryant, R. (1985). Metrics with holonomy \({\rm {G}}_{2}\) or Spin(7). Lecture Notes in Mathematics, 1111, 269–277.
Bando, S., & Siu, Y. T. (1994). Stable sheaves and Einstein-Hermitian metrics. Geometry and Analysis on Complex Manifolds, 39, 39–50.
Corti, A., Haskins, M., Nordström, J., & Pacini, T. (2013). Asymptotically cylindrical Calabi-Yau 3-folds from weak Fano 3-folds. Geometry and Topology, 17(4), 1955–2059.
Corti, A., Haskins, M., Nordström, J., & Pacini, T. (2015). \({\rm {G}}_{2}\)-manifolds and associative submanifolds via semi-Fano 3-folds. Duke Mathematical Journal, 164(10), 1971–2092.
Crowley, D., & Nordström, J. (2014). Exotic \(G_{2}\)-manifolds. arXiv:1411.0656 [math.AG].
Donaldson, S. K. (2002). Floer homology groups in Yang-Mills theory. Cambridge Tracts in Mathematics (Vol. 147). Cambridge: Cambridge University Press. With the assistance of Furuta, M. & Kotschick, D.
Donaldson, S. K. (1985). Anti self-dual Yang-Mills connections over complex algebraic surfaces and stable vector bundles. Proceedings of the London Mathematical Society, 50(1), 1–26.
Donaldson, S. K. (1990). Polynomial invariants for smooth four-manifolds. Topology, 29(3), 257–315.
Donaldson, S. K., & Segal, E. (2011). Gauge theory in higher dimensions, II. Surveys in Differential Geometry, 16, 1–41.
Donaldson, S. K., & Thomas, R. P. (1996). Gauge theory in higher dimensions, The geometric universe Oxford, 1998, pp. 31–47.
Haskins, M., Hein, H.-J., & Nordström, J. (2015). Asymptotically cylindrical Calabi-Yau manifolds. Journal of Differential Geometry, 101(2), 213–265.
Huybrechts, D., & Lehn, M. (2010). The geometry of moduli spaces of sheaves (2nd ed.). Cambridge: Cambridge Mathematical Library.
Huybrechts, D., & Lehn, M. (1997). The geometry of moduli spaces of sheaves. Aspects of Mathematics, E31, Friedr. Braunschweig: Vieweg & Sohn.
Jardim, M., Menet, G., Prata, D. M., & Sá Earp, H. N. (2017). Holomorphic bundles for higher dimensional gauge theory. Bulletin of the London Mathematical Society, 49(1), 117–132.
Joyce, D. D. (2000). Compact manifolds with special holonomy. Oxford Mathematical Monographs. Oxford: Oxford University Press.
Joyce, D. D. (1996) Compact Riemannian 7-manifolds with holonomy \({\rm {G}}_{2}\). I, II. Journal Differential Geometry, 43(2), 291–328, 329–375.
Jacob, A. & Walpuski, T. (2016). Hermitian Yang-Mills metrics on reflexive sheaves over asymptotically cylindrical Kähler manifolds. arXiv:1603.07702v1 [math.DG].
Kovalev, A., & Lee, N.-H. (2011). K3 surfaces with non-symplectic involution and compact irreducible \({\rm {G}}_{2}\)-manifolds. Mathematical Proceedings of the Cambridge Philosophical Society, 151(2), 193–218.
Kovalev, A. (2003). Twisted connected sums and special Riemannian holonomy. Journal für die reine und angewandte Mathematik, 565, 125–160.
Lockhart, R. B., & McOwen, R. C. (1985). Elliptic differential operators on noncompact manifolds. Scuola Normale Superiore di Pisa, Classe di Scienze (4), 12(3), 409–447.
Maruyama, M. (1978). Moduli of stable sheaves ii. Journal of Mathematics of Kyoto University, 18, 557–614.
Menet, G., Nordström, J., & Sá Earp, H.N. (2017). Construction of \({\rm {G}}_{2}\)-instantons via twisted connected sums. arXiv:1510.03836 [math.AG]. To appear in Mathematical Research Letters.
Maz’ya, V. G., & Plamenevskiĭ, B. A. (1978). Estimates in \(L_{p}\) and in Hölder classes, and the Miranda-Agmon maximum principle for the solutions of elliptic boundary value problems in domains with singular points on the boundary. Mathematische Nachrichten, 81, 25–82.
Milnor, J. W., & Stasheff, J. D. (1974). Characteristic classes. Princeton: Princeton University Press.
Pacini, T. (2012). Desingularizing isolated conical singularities: Uniform estimates via weighted sobolev spaces. arXiv:1005.3511v3. To appear in Communications in Analysis and Geometry.
Salur, S. (2006). Asymptotically cylindrical ricci-flat manifolds. Proceedings of the American Mathematical Society, 134(10), 3049–3056.
Salamon, S. (1989). Riemannian geometry and holonomy groups. Pitman Research Notes in Mathematics Series (Vol. 201).
Sá Earp, H. N. (2009). Instantons on \({\rm {G}}_{2}\)-manifolds. Ph.D. Thesis.
Sá Earp, H. N. (2014). Generalised Chern-Simons theory and \({\rm {G}}_{2}\)–instantons over associative fibrations. SIGMA - Symmetry, Integrability and Geometry: Methods and Applications, 10(083).
Sá Earp, H. N. (2015). \({\rm {G}}_{2}\)-instantons over asymptotically cylindrical manifolds. Geometry and Topology, 19(1), 61–111.
Sá Earp, H. N., & Walpuski, T. (2015). \(\rm {G}_2-\)instantons over twisted connected sums. Geometry & Topology, 19(3), 1263–1285.
Thomas, R. (1997). Gauge theories on Calabi-Yau manifolds. D. Phil. thesis, University of Oxford.
Tian, G. (2000). Gauge theory and calibrated geometry. I. Annals of Mathematics (1), 151(1), 193–268.
Tyurin, A. (2012) Vector bundles, Universitätsverlag Göttingen. In Fedor Bogomolov, Alexey Gorodentsev, Victor Pidstrigach, Miles Reid and Nikolay Tyurin (Eds.), Collected works (Vol. I, p. 330).
Uhlenbeck, K. K., & Yau, S-T. (1986). On the existence of Hermitian-Yang-Mills connections in stable vector bundles. Communications on Pure and Applied Mathematics, 39(S1), S257–S293.
Walpuski, T. (2013). \({\rm {G}}_{2}\)–instantons on generalised Kummer constructions. Geometry and Topology, 17(4), 2345–2388.
Walpuski, T. (2016). \({\rm {G}}_{2}\)-instantons over twisted connected sums: an example. Mathematical Research Letters, 23(2), 529–544. arXiv:1505.01080.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Science+Business Media, LLC, part of Springer Nature
About this chapter
Cite this chapter
Sá Earp, H. (2020). Current Progress on \(\mathrm{{G}}_2\)-Instantons over Twisted Connected Sums. In: Karigiannis, S., Leung, N., Lotay, J. (eds) Lectures and Surveys on G2-Manifolds and Related Topics. Fields Institute Communications, vol 84. Springer, New York, NY. https://doi.org/10.1007/978-1-0716-0577-6_14
Download citation
DOI: https://doi.org/10.1007/978-1-0716-0577-6_14
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-0716-0576-9
Online ISBN: 978-1-0716-0577-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


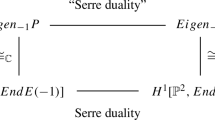


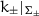 . Denote the corresponding ASD instanton by
. Denote the corresponding ASD instanton by