Chance-Constraint-Based Heuristics for Production Planning in the Face of Stochastic Demand and Workload-Dependent Lead Times

Abstract

While the problem of planning production in the face of uncertain demand has been studied in various forms for decades, there is still no completely satisfactory solution approach. In this chapter we propose several heuristics based on chance-constrained models for a simple single stage single product system with workload-dependent lead times, which we compare to two-stage and multi-stage stochastic programing formulations. Exploratory computational experiments show promising performance for the heuristics, and raise a number of interesting issues that arise in comparing solutions obtained by the different approaches.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In today’s global supply chains, effective coordination of operations across space and time is vital to capital-intensive industries like semiconductor manufacturing with short product life cycles and rapidly changing market conditions. However, despite the fact that problems related to the planning of production and inventories have been the stock in trade of industrial engineering and operations research for the last five decades, a comprehensive solution to the problem as faced in industry is still unavailable [65]. Current research has followed the basic paradigms of deterministic mathematical programing and stochastic inventory models, resulting in highly compartmentalized streams of research that each focus on certain aspects of the problem at the expense of others. In particular, the problem of planning production releases and allocating production capacity among different products has ignored the nonlinear congestion effects induced by capacitated resources subject to queueing, and has been treated in isolation from the problem of maintaining service levels in the face of stochastic demand.

This work is motivated by two basic limitations of the mathematical programing models used for production planning in both industrial practice and academia. The first of these is that the vast majority of these models fail to capture the nonlinear relationships between work in process inventories (WIP), cycle times, and work releases. Queueing models of production systems [17, 52] show that cycle times increase nonlinearly with resource utilization, which in turn is determined by the release plan produced by the planning system. Capital-intensive industries such as semiconductor manufacturing, with long, complex production processes, must run at high utilization to be profitable. Under these conditions small fluctuations in utilization may cause large changes in cycle times, rendering the effects of this dependence important to effective planning.

In addition to this nonlinear dependence, uncertain demand is a fact of life in most supply chains, requiring the deployment of safety stocks to ensure desired customer service levels. The production of these safety stocks, in turn, requires the release of additional work, affecting cycle times, and hence the work release and capacity allocation decisions made by planning models. It is thus notable that the planning of safety stocks [43, 107] has largely been addressed separately from capacity allocation, presumably due to the motivation for much inventory research arising from retail and distribution applications.

The large size and stochastic nature of industrial supply chain planning problems renders their exact solution computationally prohibitive. Thus industrial practice requires efficient approximations with reliable solution quality. However, when approximations are proposed, assessing the quality of their solutions is fraught with all the difficulties encountered in evaluating the quality of heuristic solutions for deterministic optimization problems [92]. There is thus a need to develop exact solution methods to provide insight into the structure of optimal solutions, as well as benchmarks against which different approximation methods can be compared and assessed.

This, in turn, presents additional complications. Problems of production planning and control in the face of stochastic demand admit several different formulations that often have quite different assumptions, advantages and drawbacks. Inventory and queueing models [107], for instance, tend to produce optimal solutions under steady-state conditions, but have difficulty in addressing transient solutions. Conventional mathematical programing models [103] solve a deterministic approximation to the actual stochastic problem, sometimes with inventory targets based on off-line analysis included as constraints. Stochastic dynamic programming models, including Markov decision processes [89], give state-based reactive decision rules that do not directly consider information about future demand that may be available. Stochastic programing [12] and chance-constrained models [87] make different assumptions about recourse actions that can result in subtle theoretical and practical difficulties.

A conclusive, unifying solution to these complex issues is clearly a long way in the future. Our objective in this chapter is more modest and exploratory in nature. We consider a simple single-stage single product production-inventory system subject to workload-dependent lead times and stochastic demand. We then develop a number of alternative formulations for this system, including two different chance-constrained models, a two-stage stochastic programing model, and a multi-stage stochastic programing approach. The multistage stochastic programing model is the only one of these that has potential to yield an exact solution, and that conditional upon the choice of scenarios; the other three are heuristics. We compare the solutions obtained from these different models by subjecting them to a simulation of uncertain demand realizations. Our exploratory computational experiments suggest that when parameters are appropriately chosen, heuristics based on chance constrained models may provide near-optimal solutions that are competitive with those from much larger stochastic programing models, although the stochastic programing models consider a very limited number of scenarios. Our results suggest a number of directions for future work on improving the heuristics, and further experimentation aimed at elucidating the strengths and limitations of the chance constraint-based heuristics.

2 Previous Related Work

A comprehensive review of the literature on production planning under uncertainty is clearly beyond the scope of this chapter. Instead, we briefly review the literature most relevant to this paper. Overviews of the production planning domain are given by de Kok and Fransoo [27], Voss and Woodruff [103] and Missbauer and Uzsoy [78].

Most deterministic production planning models establish optimal production, inventory and release levels over a given finite planning horizon to meet the total demand [16, 45, 50]. The planning horizon is divided into discrete periods during which production and demand rates are assumed to be constant; the capacity of the system is represented by the number of hours available on key resources in a planning period; and the production, inventory, WIP and demand associated with a period are treated as continuous quantities. These models allocate capacity to products to optimize a specified objective and satisfy aggregate constraints representing system capacity and dynamics. However, models of this type are subject to the utilization-lead time dependence discussed in Sect. 1. The estimates of cycle times used in planning models are referred to as lead times.

The most common approximation in both the research literature and industrial practice is to treat lead times as a fixed, exogenous quantity independent of resource load. The Material Requirements Planning (MRP) approach [82] uses fixed lead times in its backward scheduling step to determine job releases. Several authors have suggested ways of adapting MRP to uncertain demand. Meal [73] and Grubbstrom [39] derive component plans with safety stocks in the MRP records. Miller [75] proposes hedging of the master schedule to provide safety stocks within the system. However, all these approaches assume fixed exogenous lead times.

Another common approach to production planning under fixed lead times and deterministic demand is the use of linear(LP) and integer programing(IP) models, of which a wide variety exist [42, 56, 103]. These represent capacity as a fixed upper bound on the number of hours available at the resource in a period, and model input and output time lags between stages. However, these time lags are independent of workload.

Several authors have proposed enhanced models that address the dependency between lead times and resource utilization to some degree. Lautenschlager and Stadtler [69] suggest a model where the production in a given period becomes available over several future periods. Voss and Woodruff [103] propose a nonlinear model where the function linking lead time to workload is approximated as a piecewise linear function. Kekre et al. [63] and Ettl et al. [31] take a similar approach, adding a convex term representing the cost of carrying WIP as a function of workload to the objective function. Graves [37], Karmarkar [61], Missbauer [76], Anli et al. [2] and Asmundsson et al. [5, 4] use nonlinear clearing functions to model the dependency between workload and lead times. Several related models are proposed in the recent book by Hackman [41]. Pahl et al. [83] and Missbauer and Uzsoy [78] review production planning models with load-dependent lead times. We shall discuss clearing functions, which are used in the models in this chapter, more extensively in the next section.

Another approach to modeling the operational dynamics of the system has been the use of detailed simulation or scheduling models in the planning process. Dauzere-Peres and Lasserre [26] use a scheduling model to check whether the plans their IP model develops are feasible. Other approaches use simulation models in the same manner, e.g., Pritsker and Snyder [88]. The use of simulation or scheduling models captures the operational dynamics of the system correctly. However, this approach does not scale well, since simulation models of large systems are time-consuming to run and analyze. An innovative approach to integrating simulation and LP is that of Hung and Leachman [53]. Given initial lead-time estimates, an LP model for production planning is formulated and solved. The resulting plan is fed into a simulation model to estimate the lead-times the plan would impose on a real system. If these lead-times do not agree with those used in the LP, the LP is updated with the new lead-time estimates and resolved. This iteration is repeated until convergence. Similar models have been proposed by others [6, 18, 19, 66, 95]. However, the convergence of these methods is not well understood [55, 57]. The computational burden of the simulation runs required is also a significant disadvantage for large systems such as those encountered in semiconductor manufacturing.

Stochastic inventory models seek an optimal inventory policy (when to order, and how much to order) for individual items in the face of different environmental conditions (e.g. demand patterns, modes of shipment from suppliers) and constraints (e.g. supply restrictions, budget limitations, and desired customer service levels). Much of the work in this area [54, 59, 101, 102] is in the context of ordering from suppliers, modeling demand carefully but treating supply as known and unlimited, generally with a fixed lead time. Many subsequent papers have addressed variations of this basic problem [46, 47, 107]. However, the vast majority assume that a supplier can supply any amount of material within the specified lead time, i.e., has unlimited capacity.

Federgruen and Zipkin [32, 33] consider the capacitated inventory problem with uncertain demand and explore the optimality of “modified” base stock policies when the cost for the single period is convex in the base stock level. Tayur [99] extends this work by discussing the computation of the optimal base stock level. However, these models use simple capacity constraints that ignore the dependency between load and lead times. Ciarallo et al. [23] describe the structure of optimal policies for problems with uncertain production capacity and a time-stationary demand distribution. Anupindi et al. [3] provide bounds and heuristics for the problem with nonstationary demand and stochastic lead times, where the lead time distribution is stationary over time.

The idea of combining inventory and queueing models has attracted attention from many researchers [17, 52, 91]. Zipkin [106] develops a queueing framework to analyze supply chains facing a stationary demand distribution and where a (Q, r) policy is used to release units onto the shop floor. Ettl et al. [31] develop an optimization model combining queueing and inventory models to set base-stock levels for a multi-item batch production system facing non-stationary demands. Liu et al. [71] extend this approach.

One of the most popular frameworks for planning under uncertainty is stochastic programing [12, 58, 87]. Uncertainty is represented by using a number of discrete scenarios to represent possible future states, which allows stochastic linear programs to be modeled as large linear programing problems. Constraints are formulated requiring that an optimal solution be feasible for all scenarios, and the objective function is usually to minimize the expected value of the specified objective function. A number of authors have formulated production planning problems as multi-stage stochastic linear programs (M-SLPs) [48, 85], but the approach presents challenges.

A significant difficulty of M-SLPs is that the problem size tends to grow exponentially with the number of possible realizations (scenarios) of uncertain parameters, requiring solution methods that exploit their special structure. The scenario-based structure of M-SLPs makes decomposition methods attractive. Most decomposition methods exploit convexity of the recourse function to use outer linearization. Commonly used methods include Dantzig-Wolfe decomposition (inner linearization) and Benders decomposition (outer linearization), which decompose the large-scale problem into a master problem and several independent subproblems. Dantzig-Wolfe decomposition adds new columns to the master problem based on the suproblem solutions [25]. Benders decomposition, on the other hand, proceeds by adding new constraints (supporting hyperplanes known as optimality cuts) that are computed using dual solutions to the subproblems (e.g., Lasdon [68]).

Van Slyke and Wets [100] extended Benders’ decomposition to solve two-stage stochastic linear programs (2-SLPs) via the L-Shaped Method. M-SLPs are much more challenging computationally than 2-SLPs. An extension of the L-shaped method to more than two stages, called nested decomposition, was first proposed by Louveaux [72] for multi-stage quadratic programs and by Birge [11] for multi-stage linear programs. The algorithm generates cuts for an ancestor scenario problem that has feasible completion in all descendant scenarios. As in the L-shaped method, nested decomposition achieves outer linearization by generating feasibility and optimality cuts until it converges to an optimal solution. A number of different strategies have been used to select the next subproblem for deterministic problems. Numerical experiments by Gassmann [35] found that the fast-forward-fast-back procedure of Wittrock [105] outperforms other strategies.

There have been recent attempts to model production planning problems using robust optimization approaches [7, 10]. Leung et al. [70] develop a robust optimization model to solve the aggregate production planning problem. Raa and el-Aghezzaf [90] use robust optimization to obtain a dynamic planning strategy for the stochastic lot-sizing problem.

Chance constrained programing dates back to the work of Charnes and Cooper [20, 21, 22]. A more recent overview of these methods is given by Prékopa [87]. In chance constrained programing, constraints can be violated with a specified probability, which is quite useful to model, for instance, service levels in supply chain problems [40]. Continuous probability distributions are often assumed on the uncertain parameters. This approach achieves a substantial decrease in the size of the model, and avoids the problem of defining the penalty function. However, it fails to capture the cost consequences of constraint violations, which can result in anomalous behavior [14].

Given that exact solutions to stochastic optimization problem are computationally challenging, a number of approaches to obtain solutions via decision rules have been proposed. These approaches classify decision variables according to whether they are implemented before (first stage decisions), or after (second stage decisions) an outcome of the random variable(s) is observed. However, in the decision rule-based approach, the second stage recourse decisions are determined by a rule that incorporates both the first stage decisions and the observed outcomes. A commonly encountered example of such a rule that is in fact optimal in form is the well-known base stock policy for inventory systems with unlimited capacity, deterministic replenishment lead time and linear holding and backorder costs. However, as pointed out by Garstka and Wets [34], the decision rule approach assumes a specific form for the optimal solution to the stochastic program. Since very few multistage stochastic programs yield a closed-form characterization of the optimal solution, solutions obtained assuming decision rules cannot be guaranteed to be optimal in the vast majority of cases.

A well-known family of decision rules are the Linear Decision Rules, where the second stage recourse decision is a linear function of the first stage decision variables and the observed outcomes. The pioneering Linear Decision Rule (LDR) was developed by Holt, Modigliani, Muth and Simon (HMMS) in the mid 1950s [49, 51]. Extensions to this rule have been proposed by several authors [8, 28, 36, 44, 84]. While the HMMS model and its variations incorporate demand uncertainty, these models treat capacity, specifically workforce levels, as a decision variable that can be varied continuously, which avoids the problem of workload-dependent lead times encountered under fixed capacity limits. In addition, the specific quadratic form of the objective function adopted allows the construction of a deterministic equivalent that simply replaces each random variable with its expectation. However, it is well known that this approach does not yield optimal solutions in general.

In summary, a variety of models have been proposed that address the issues of workload-dependent lead times and demand uncertainty separately at best, and in many cases do not address either. The LP and MRP approaches do not address workload-dependent lead times, and generally ignore stochastic demand. Most inventory models focus on modeling demand, with simple models of replenishment that do not consider workload-dependent lead times. The combined queueing-inventory models capture the interaction between workload-dependent lead times and inventory levels correctly, but assume specific inventory policies of the order up to type, and make different assumptions about the representation of a production unit. Stochastic programing approaches are hampered by their exponentially growing computational burden as the number of products and planning periods (stages) increase. Our heuristics, in contrast, consider non-stationary demand distributions to provide production plans over a finite planning horizon, taking available information about future demand into account. The work in this paper is an initial step in assessing the performance of this approach.

In the next section we present an overview of the clearing function concept that we use to develop a LP model that addresses the load dependent lead time and demand uncertainty aspects simultaneously for a single-product supply chain.

3 Clearing Function Basics

Clearing functions (CF) [37, 61, 78, 98], express the expected throughput of a capacitated resource over a given period of time as a function of some measure of WIP level at the resource over that period, which in turn, is determined by the average resource utilization over the period. We shall use the term “WIP” and the generic variable W to denote any reasonable measure of WIP level over a planning period.

To motivate the use of a nonlinear CF, it is helpful to begin with a single resource that can be modeled as a G/G/1 queueing system in steady state. The expected number in system (i.e., expected WIP) for a single server is given by Medhi [74] as:

$$ W = {\frac{(c_a^2 + c_s^2)}{2}}{\frac{\rho^{2}}{(1-\rho)}} + \rho $$

where $c_{a}$ and $c_{s}$ denote the coefficients of variation of service and interarrival times, respectively and $\rho$ the utilization of the server. Setting $c=(c_{a}^{2}+c_{s}^{2})/2$ and rearranging (1) we obtain a quadratic in W whose positive root yields the desired $\rho$ value. Solving for $\rho$ with $c>1$, we obtain

$$ \rho ={\frac{\sqrt{(W+1)^{2} +4W(c^2-1)} - (W+1)}{2 (c^2 -1)}} $$

which has the desired concave form. When $0\leq c <1$, the other root of the quadratic will always give positive values for $\rho.$ When $c\mathop{=}1$, the expression simplifies to yield $\rho\mathop{=} W/(1+W)$, again of the desired concave form. If we use utilization as a surrogate for output, we see that for a fixed c value, utilization, and hence throughput, increase with WIP but at a declining rate. Utilization, and hence output, is decreasing in c due to variability in service and arrival rates.

Figure 1, derived from Karmarkar [61], depicts several examples of CFs considered in the literature, where X denotes the expected throughput in a planning period. The horizontal line $X\mathop{=}C$ represents a fixed upper bound on output over the period, but without a lead-time constraint it implies that production can occur without any WIP in the system if work input and production are synchronized. This approach is implemented in most LP models but is supplemented with a fixed lead time as described above. The linear CF of Graves [37] is represented by the $X\mathop{=}W/L$ line, which implies a lead time of L periods that is maintained independently of the WIP level. If a fixed lead time is maintained up to a certain maximum output, we have $X\mathop{=}\text{min}\{W/L, C \}.$ When the parameters of the Graves CF are set such that the lead time is equal to the average processing time, with no queueing delays at all, we obtain the line $X\mathop{=}W/p$, where p denotes the average processing time. Assuming that lead time is equal to the average processing time up to a maximum output level gives the “Best Case” model $X\mathop{=} \text{min} \{W/p, C\}$ of Hopp and Spearman [52]. The workload-independent fixed lead time in most LP models differs from the linear CF of Graves in that the former does not link output to WIP, while the latter does [81]. The CF always lies below the $X\mathop{=}W/p\;\hbox{and}\;X\mathop{=}C$ lines. For most capacitated production resources subject to congestion, limited capacity leads to a saturating (concave) shape of the CF, for which Asmundsson et al. [4] and Selçuk et al. [96] provide analytical support.

Fig. 1

Examples of CFs (Karmarkar [61])

Several authors discuss the relationship between throughput and WIP levels in the context of queueing analysis, focusing on the long-run steady-state expected throughput and WIP levels. Agnew [1] studies this behavior in the context of optimal control policies. Spearman [97] presents an analytic congestion model for a family of closed production systems that describes the relationship between throughput and WIP. Srinivasan et al. [98] derives the CF for a closed queueing network with a product form solution. Asmundsson et al. [4, 5] and Missbauer [77] study the problem of estimating CFs from experimental data, obtained either from industry or simulation models. Missbauer and Uzsoy [78] review the state of the art in this area.

An important advantage of CFs for our purposes is their ability to reflect different sources of variability in the production process. In queueing terms, this is accomplished by basing the CF on the effective processing time at the resources, which includes the effects of detractors such as uncertain yield, machine failures and setups, as discussed in Chap. 8 of Hopp and Spearman [52]. The manner in which these effects change the shape of the CF is described in Asmundsson et al. [4]. When the CFs are estimated from empirical data, the effects of the variability induced by detractors are present in the data to which the CF is fit, again capturing their effects.

Hence, given the current research on the derivation of CFs using both analytical and empirical approaches, in this chapter we shall proceed on the assumption that adequate methods of estimating CFs for different production systems will emerge from ongoing work. We focus on using CFs to develop production models that consider stochastic demand and the nonlinear relationship between workload and cycle in an integrated manner. We introduce our approach in the next section.

4 A Deterministic Model Based on Clearing Functions

In this section we develop a LP model for aggregate planning under the effects of congestion and demand uncertainty. We begin with a basic formulation prevalent in the literature, discuss its weaknesses, and use these to motivate our formulations, drawing heavily on the exposition in Bookbinder and Tan [15]. While there are clearly many formulations in the literature that capture additional aspects such as multiple stages, alternative production paths, etc., our focus is to find computationally tractable formulations that allow us to treat both the nonlinear dynamics of utilization and lead times and the stochastic nature of the demand as endogenous to the model. Hence to isolate these aspects of the problem for study, we focus on a single-stage single product system. The quantity of raw material released into the system in each time period is the key decision variable in our models. These releases are then converted into output according to different mechanisms defined by the models considered, which will be discussed as we proceed.

Consider the production planning problem for such a single stage production system producing a single product. The planning horizon is divided into T discrete periods of equal length. Demand in each period is assumed to be stochastic with known cumulative distribution function (CDF), and independent of demand in other periods. Service level requirements to be met are prespecified, and are thus treated as a constraint. We consider the simple objective of minimizing the sum of expected costs of holding finished goods inventory (FGI) and work in process (WIP) over the planning horizon. Following the literature, we do not consider the cost of stockouts in the objective function because we assume that the service level requirements are sufficiently high that the cost of stockouts is negligible. This assumption will be relaxed in our computational experiments. Clearly far more elaborate objective functions are possible, but our emphasis is on representation of production capacity and demand uncertainty.

To describe the models used in this paper we use three different classes of variables:

Decision or Control Variables: These variables represent the primary management decisions in a plan. In order to be implementable, a plan must specify either specific values for these variables, or specific rules by which they can be computed with the information available at the time a decision must be made.

State Variables: These variables define the behavior of the system, and their values are determined by the constraints determining the operational dynamics of the system and the values of the decision variables. These variables may be either deterministic or random.

Parameters: These are external inputs to the system and are prespecified in the model. We will assume these are always deterministic.

The notation used in the formulations is given below. We use a bold font, e.g., X, for a random variable and a normal font, e.g., X, for a deterministic variable.

• $R_{t}:$ Planned quantity of product released into the system during period t

• $X_{t}:$ Planned production quantity during period t

• ${\mathbf I}_{\mathbf t}:$ Inventory on hand at the end of period t. The initial inventory on hand at the start of period 1 will be denoted by $I_{0}.$

• $h_{t}:$ Unit inventory holding cost for period t

• $C_{t}:$ Capacity, e.g., total number of machine hours available, in period t

• $\alpha:$ Specified service level

• $G_{[t,t+k]}:$ CDF of cumulative demand from period t to period $t+k$

• ${\mathbf D}_{\mathbf t}:$ Demand during period t. Throughout this paper we shall assume the demand in each period t to be normally distributed with known mean $\mu_{\hbox{t}}$ and standard deviation $\sigma_{t}.$ In our experiments we will assume demands are independent by time periods. However, the models presented remain valid for correlated demands as long as the variance-covariance matrix is known, or can be estimated with reasonable accuracy.

• $L_{t}:$ Average lead time in period t. For simplicity of exposition in presenting the models in this section we shall assume these are integer multiples of the planning period length. Fractional $L_{t}$ values can be accommodated in a straightforward manner.

4.1 Basic Formulation

Most chance-constrained production planning models in the literature are similar to that of Bookbinder and Tan [15] given below; a slightly different version is given in Johnson and Montgomery [56]. Our model incorporates the following constraints:

• Releases

Since the lead time is $L_{t}$ in period t, whatever is released into the system in period t is converted to output and available for consumption in period $t + L_{t}.$ Hence the relationship between release quantities and output is given by

$$ R_{t}=X_{t+L_{t}},\;\text{for}\;\text{all}\;t=1,\ldots,T-L_{t} $$

The primary decision variable is the amount of work $R_{t}$ released in period t, which must be specified at the start of the planning horizon. Hence both releases and production are deterministic. Note that the $X_{t}\;\hbox{and}\;R_{t}$ variables are redundant, and the formulation can be written with only one of these two sets of variables.

In this model, work that is released into the production system at time t is in WIP for $L_t$ periods until it emerges as finished product. Most LP models do not explicitly represent this quantity, or assign it a cost in the objective function, but it can easily be estimated for any period t as the difference between the cumulative releases and output up to a given period t.

• Inventory balance

The finished goods inventory on hand at the end of period t, ${\mathbf I}_{\mathbf t}$, is a random variable for which the relationship

$$ {\mathbf I}_{\mathbf t} = {\mathbf I}_{\mathbf {t}-1}+ X_{t} - {\mathbf D}_{\mathbf t} $$

holds for each time period t. Taking the expectation and repetitive substitution yields

$$\begin{aligned} E[{\bf I}_{\bf t}]=E[{\bf I}_{{\bf t-1}}]+X_t -E[{\bf D}_{\bf t}]=&I_0 +\sum_{i=1}^t {X_i } -\sum_{i=1}^t {E[{\bf D}_i ]}\\ =&I_0 +\sum_{i=1}^t {X_i } -\sum_{i=1}^t {\mu _i },\;{\text{for all}}\; {\it t} = 1,\ldots,{\it T}. \end{aligned} $$

All terms in this expression are now deterministic.

• Capacity

$$ X_t\leq C_t ,\;{\text{for all}}\; t = 1,\ldots,T. $$

Service level: This constraint requires that the service level, defined by the probability of ${\mathbf I}_{\mathbf t}< 0$, i.e., a stockout occurring, be less than $(1-\alpha)$, implying

$$ P\{{\mathbf I}_{\mathbf t} \geq 0\}\geq \alpha \Rightarrow P\left\{I_0 +\sum_{i=1}^t {X_i } \geq \sum_{i=1}^t {{\mathbf D}_{\mathbf i} } \right\}\geq \alpha ,\;{\text{for all}}\;{\it t} = 1,\ldots,{\it T}. $$

The service level measure fits the chance constraint approach well, since the latter allows constraints to be violated with a certain probability. However, it does not capture the degree to which the constraint is violated. Hence a production plan that has stockouts in many periods, but falls short by a very small fraction of the demand in each period, will appear to have a poor service level. To this end, we use the fill rate, the fraction of total period demand met from inventory, as another performance measure in our computational experiments. The basic formulation is summarized in Table 1, using the production variables $X_{t}.$

Table 1 Basic formulation

While the basic formulation is intuitive, it suffers from the following disadvantages:

• It ignores the effects of loading on WIP and lead times in a capacitated system [4, 5, 37, 60] by considering lead times to be fixed exogenous values.

• It assumes that safety stock must be held in finished goods inventory, based on the demand for each individual period. This is adequate when the lead times of the production system, which correspond to the replenishment time of the finished goods inventory, do not exceed one period, as in the models of Bookbinder and Tan [15] and Johnson and Montgomery [56]. However, if lead times span multiple periods, this becomes problematic. It is well known in the inventory literature [24] that in the presence of nonzero lead times the optimal policy in many cases, and a good heuristic in many more, is to set the inventory position, the sum of on-hand inventory and outstanding orders, to the desired percentile of the demand over the lead time (e.g., [29]). Hence this formulation fails to recognize that WIP can serve some of the function of safety stock [38], and hence might hold more finished goods inventory than required to maintain a given service level. We shall assume a replenishment policy of this form, which is not optimal for the production system we consider, in developing our heuristics.

  In the production-inventory context of this paper, outstanding orders are represented by material that has been released into the production line but has not yet emerged as finished goods, i.e., WIP [38]. The inventory position, which will be an important quantity for our development in the rest of this paper, will be defined in more detail in the following section.

• The model makes all decisions for the entire planning horizon at the beginning of the horizon, before any of the demands become known, and does not provide a way to use information as it becomes available. In other words, there is no recourse action.

In the rest of this section we extend this formulation to address these issues.

4.2 Development of Integrated Model

An elegant way of capturing the effect of capacity loading on WIP and lead times in production planning models is the use of clearing functions (CFs) as discussed in Sect. 3. Recall that up to this point all variables are deterministic except the inventory levels ${\mathbf I}_{\mathbf t}.$ Hence, incorporating CFs in the model requires:

• Introduction of WIP balance equations. If $W_{t}$ is defined to be the WIP at a given time t, then the WIP balance equations are given as $W_{t} = W_{t-1} + R_{t} - X_{t}$ for all periods $t = 1,\ldots,T.$ We treat $R_{t }$as a deterministic decision variable that is specified at the start of the planning horizon by solution of the planning model, and cannot be modified as uncertainty is realized.

• Replacing the original capacity constraint with a set of linear inequalities that represent the outer linearization of the original CF [4, 5]. The set of inequalities representing the CF is given by $X_{t} \leq a_{k} W_{t-1}+ b_{k}$, for all periods $t = 1,\ldots,T$ and line segments $k = 1,\ldots,n$ used to outer linearize the CF.

The use of CFs to represent the capacity of the production system takes a more complex view of the relationship between the planned release quantity $R_{t}$ in period t and the planned output $X_{t}$ of the system in that period. The releases in a period determine the planned WIP level $W_{t}$ at the end of the period, together with the linearized CF represented by the constraints above, determines the planned system output $X_{t+1}$ in the next period The release variables $R_{t}$ are defined such that releases are made at the end of period t, and hence cannot contribute to output during period t. This is necessary because in later models, our linear decision rule observes the realization of the random demand ${\mathbf D}_{\mathbf t}$ in period t to determine the releases $R_{t}$ at the end of period t. This definition, together with the definition of the CF and the WIP balance equations, is thus internally consistent.

In inventory theory an optimal or near-optimal policy, when there is no fixed ordering cost and shortage and holding costs are linear, is to maintain the inventory position, the sum of on-hand and on-order inventory, at a critical fractile of the demand over the replenishment lead time [24]. Hence if ${\mathbf I} {\mathbf P}_{\mathbf t}$ denotes the inventory position at the end of period t, we have ${\mathbf I} {\mathbf P}_{\mathbf t}\mathop{=} W_{t} + {\mathbf I}_{\mathbf t},\;\hbox{where}\;W_{t}$ represents orders that have been released to production but not yet completed. This analogy with inventory models suggests a service level constraint requiring a probability $\upalpha\;\hbox{that}\;{\mathbf I}{\mathbf P}_{\mathbf t}$ is at least as great as the demand over the replenishment lead time [38]. Assuming this replenishment lead time, corresponding to the cycle time of the production system under study, is known to be $L_t$periods in period t, we have

$$ P\left\{{\mathbf {IP}}_{\mathbf t} \geq \sum_{i=t+1}^{t+L_t } {{\mathbf D}_i }\right \}\geq \alpha \Rightarrow P\left\{{\mathbf I}_{\mathbf t} +W_t \geq \sum_{i=t+1}^{t+L_t } {{\mathbf D}_i }\right \}\geq \upalpha . $$

The $L_{t}$ parameters on the right hand sides of our chance constraints define the distribution of the lead time demand that will be used to set safety stock levels. Noting that

$$ {\bf I}_{\bf t} =I_0 +\sum_{i=1}^t {X_i } -\sum_{i=1}^t {{\bf D}_i }\;\hbox{and} $$

$$ W_t =W_0 +\sum_{i=1}^t R_i-\sum_{i=1}^t X_i $$

we obtain

$$ {\bf IP}_t ={\bf I}_{\bf t} +W_t =(I_0 +W_0 )+\sum_{i=1}^t R_i-\sum_{i=1}^t {\bf D}_i. $$

The chance constraint is now of the form

$$ \begin{aligned} P\{{\bf IP}_t \geq 0\}\geq \alpha &\Rightarrow P\left\{I_0 +W_0 +\sum_{i=1}^t {R_i } -\sum_{i=t+1}^{t+L_t } {{\bf D}_i } \geq \sum_{i=1}^t {{\bf D}_i }\right \}\geq \upalpha \\ & \Rightarrow \hbox{ }P\{I_0 +W_0 +\sum_{i=1}^t {R_i } \geq \sum_{i=1}^{t+L_t } {{\bf D}_i } \}\geq \upalpha . \end{aligned} $$

Following the approach of Charnes and Cooper [22] the deterministic equivalent of the service level constraint can be written as

$$ I_0 +W_0 +\sum_{i=1}^T R_i \geq G_{[1,t+L_t ]}^{-1} (\upalpha ),\;{\text{for all}}\;t = 1,\ldots,T. $$

where $G_{[1,\;t]}(\cdot)$ denotes the cumulative distribution function (CDF) of the cumulative demand random from periods 1 to t,

Replacing the probabilistic service level constraint with its deterministic equivalent yields the Zero-Order Inventory Position (ZOIP) formulation shown in Table 2. This formulation embodies a service level constraint on inventory position and a zero order decision rule where all decision variables are specified irrevocably at the start of the planning horizon.

It is important to note that there are two different lead times at work in the ZOIP model. The first of these is the estimated replenishment lead time $L_{t}$ used to establish the inventory position required to approximately achieve the desired service levels. The second lead time in question is that realized in the production system, the time required for work released into the system to become available as finished product. The workload-dependent nature of this realized lead time is explicitly represented by the clearing function, whose effectiveness for this purpose we have demonstrated in prior work [4, 5]. Ideally, the two lead times should be equal, with the replenishment lead time used for setting inventory targets matching that realized by the production system in the face of the release schedule recommended by the model. In other words, in an ideal situation the $L_{t}$ should be an output of the model. This would require us to estimate $L_{t}$ using Little’s Law as ($W_{t}+ W_{t-1})/2 X_{t}$ assuming the planning periods are long enough for the law to apply; for the shorter periods some transient version of Little’s Law such as those discussed by Bertsimas and Mourtzinou [9], Whitt [104] and Riaño [95] would be required. Even the use of the classical stationary version of Little’s Law yields a highly nonlinear constraint. Hence for the sake of tractability we treat the replenishment lead time $L_{t}$ on the right hand side of the chance constraints as an exogenous parameter, which reduces the right hand sides to constants that can be precomputed easily. Our model thus captures workload-dependent lead times correctly in defining the relationship between releases $R_{t}$, planned WIP level $W_{t-1}$, and expected output $X_{t}$, but uses an exogenous parameter to approximate the distribution of the lead time demand, which will be used to set the safety stocks. Computational experiments indicate that the realized lead time may deviate somewhat from the exogenously assumed value used to establish the chance constraints when used in this manner, but results are still favourable over base stock type models that do not consider clearing functions [94].

Table 2 ZOIP formulation

A full resolution of this issue appears to be challenging, and must be left for future research. A promising approach is to use an iterative scheme, where we solve the ZOIP model using an initial set of lead time estimates to obtain a release plan, i.e., a set of $R_{t}$ values. These $R_{t}$ values are then used to compute the resulting state variables $X_{t}, W_{t},\;\hbox{and}\;I_{t}$, from which a new set of $L_{t}$ values can be estimated as $L_{t}\mathop{=} W_{t} /X_{t}.$ These new $L_{t}$ values are then substituted into the model and the process is repeated until convergence is, hopefully, achieved. Orcun et al. [79] have implemented this procedure with favourable results, but formal analysis of its convergence remains for future work.

Up to this point we have developed a formulation that combines the modeling of congestion and lead times in the production system with the explicit representation of random demand using chance constraints. We now move on to adding flexibility to the decision mechanism by utilizing information as it becomes available.

4.3 A Linear Decision Rule

So far our formulations have zero order static decision rules, where the values of all decision variables are determined at the beginning of the time horizon and there is no recourse action after the outcomes are observed. We now follow Charnes and Cooper [22] and propose a linear decision rule to introduce flexibility in the decision mechanism, recalling that this approach does not yield an optimal solution. Since the releases are the decision variables in the CF formulations, the decision rule is based on releases.

We use a simple rule closely following that described in Johnson and Montgomery [56] that allows the releases to be modified as uncertain demand is observed, rendering them random variables. We define auxiliary variables $Y_{t}$ that represent the change in planned inventory position from period $t-1$ to period t, implying that ${\mathbf R}_{\mathbf t}= Y_{t}+{\mathbf D}_{\mathbf t}.\;\hbox{Thus}\;Y_{t}$ represents the amount of work released in period t over and above that necessary to replenish the inventory position after that period’s demand has been withdrawn; note that it may be negative, if demand is decreasing in a given time interval. This decision rule thus represents a base stock policy, and it is straightforward to show that $Y_{t}= IP_{t}- IP_{t-1}$ for specified values of ${\mathbf {IP}}_{\mathbf t}\;\hbox{and}\;{\mathbf {IP}}_{\mathbf {t}-1}.$ Our heuristic establishes chance constraints that set the planned inventory position at the end of period t, $\hbox{IP}_{\hbox {t}}$, to a percentile of the lead time demand distribution as described below. The releases ${\mathbf R}_{\mathbf t}$ are now random variables derived from the $Y_{t}$ and the realized demand ${\mathbf D}_{\mathbf t}.$ Thus the WIP variables ${\mathbf W}_{\mathbf t}$ are now also random. Since the production ${\mathbf X}_{\mathbf t}$ in a given period depends on the realized WIP level ${\mathbf W}_{\mathbf{t}-1}$ at the start of that period, ${\mathbf X}_{\mathbf t}$ is also a random variable. We have the relation

$$ \begin{aligned} E[W_t ]&=E[{\mathbf W}_{t-1} +{\mathbf R}_t -{\mathbf X}_t ]=E[{\mathbf W}_{t-1} +Y_t +{\mathbf D}_t -{\mathbf X}_t ] \\ & =W_0 +\sum_{i=1}^t {(Y_i } +\mu _i -{\mathbf X}_i ) \end{aligned} $$

Since the release quantities are now random variables, there exists a possibility that they may be negative. To prevent this, we use the chance constraint

$$ P\{{\mathbf R}_{\mathbf t} \geq 0\}\approx 1\Rightarrow P\{Y_t +{\mathbf D}_{\mathbf t} \geq 0\}\approx 1\Rightarrow Y_t + D_t^{\min} \geq 0 , $$

where $D_t^{\min}$ is a value of demand in period t such that the probability of demand falling below this level is deemed by management to be extremely small. This is clearly an approximation when demand follows a distribution with unbounded support, like the normal distribution we assume, and is unlikely to be binding except when there is a very sudden, large decline in demand from one period to another.

We again define the event of a stockout as the event that the total lead time demand exceeds the inventory position ${\mathbf I}{\mathbf P}_{{\mathbf t}} = {\mathbf W}_{{\mathbf t}} + {\mathbf I}_{\bf t}$, yielding the chance constraint

$$ W_0 +I_0 +\sum_{i=1}^t Y_i \geq G_{[t+1,t+L_t]}^{-1} (\alpha ) . $$

Since releases, WIP and production are all interrelated, all decision variables are now random variables except the $Y_{t}$, creating difficulties in establishing a tractable formulation. Hence for tractability in the solution procedure, we will assume that the production variables $X_{t}$ and the auxiliary variables $Y_{t }$ are determined at the start of the planning horizon, with the ${\mathbf W}_{\bf t}, {\mathbf I}_{\bf t},\;\hbox{and}\;{\mathbf D}_{\bf t}$ remaining as random variables. The assumption here is that when a production target $X_{t}$ is in danger of not being met, the system will take extraordinary measures to meet it, such as running an extra shift or buying from an outside source. The cost of this is not captured in the models, but is, of course, considered in our computational experiments, where we assume the production system has no outside recourse when planned production levels cannot be achieved. This ensures that all models are treated similarly in the computational experiments. Incorporating this rule in the ZOIP formulation gives us our final Dynamic Inventory Position (DYNIP) formulation summarized in Table 3.

Table 3 DYNIP formulation

The models presented above have been analyzed by Ravindran et al. [93]. They compare the performance of the ZOIP and DYNIP models with a static base stock policy and find that DYNIP performs significantly better in terms of backorders. They also analyze the structure of optimal solutions to the model under the linear clearing function of Graves. These results indicate that the ZOIP model will overstock consistently, while DYNIP will not.

5 Stochastic Programing Models

For comparison with the chance constrained models, we develop two different stochastic programing models along with their implementation strategies. We first present a two-stage stochastic programing model. A multi-stage stochastic programing formulation is also presented along with static and dynamic implementation strategies.

5.1 The Two-Stage Model (2-SP)

As in the rest of the paper, we assume the primary source of uncertainty is the demand in each period, and consider the simple objective of minimizing the sum of expected WIP holding, FGI holding and backorder costs over the planning horizon of T periods. We assume that the demand evolves as a discrete time stochastic process with a finite probability space. This information structure can be interpreted as a scenario tree, where the nodes in stage tof the tree constitute the states of the world that can be distinguished by information available up to period t. The size of the scenario tree is clearly exponential in the number of periods T, and depends on the number of possible demand realizations considered at each stage.

The computational burden of any model based on scenario trees will rapidly become impractical. Therefore even for relatively small problem instances used to benchmark our heuristics, some means of reducing the size of the scenario tree must be devised. To this end, we shall follow Escudero et al. [30] and consider a two-stage formulation which consists of specifying a number of scenarios $\xi$ composed of demand realizations for all periods. The first-stage problem involves deciding the production, release, and planned WIP levels for all periods, regardless of the state of the world. The second stage determines the FGI and backlog levels at the end of each period subject to the realized state. Thus the $X_{t}, R_{t},\;\hbox{and}\;W_{t}$ variables are only indexed by time periods (since they do not change with the realized state) while FGI variables $I^{\xi}_{t}$ and backorder $B^{\xi}_{t}$ at the end of period are indexed by the scenario $\xi.$ The model can be stated as follows:

$$ \text{Min} \sum\limits_{t=1}^{T} h_{t}W_{t}+E_{\xi}[Q(X_{t}, \xi)] $$

subject to

$$ W_{t} = W_{t-1} +R_{t}- X_{t}\quad{\text{for all}}\; t = 1,\ldots,T $$

$$ X_{t}\leq f(W_{t}),\;{\text{for all}}\;t =1,\ldots,T $$

$$ X_{t}, R_{t}, W_{t}\geq 0\;{\text{for all}}\;t = 1,\ldots,T $$

where $Q(X_{t},\xi)$ denotes the recourse function which is defined as

$$ Q(X_t ,\xi )=\min \sum_{t=1}^T {(h_t } I_t^\xi +b_t B_t^\xi ) $$

subject to

$$ I_{t}^{\xi}-B_{t}^{\xi}=I_{t-1}^{\xi}-B_{t-1}^{\xi}+X_{t}-D_{t}^{\xi}, \;{\text{for all}}\;t=1,\ldots,T $$

$$ I_{t}^{\xi}-B_{t}^{\xi}\geq0,\;{\text{for all}}\;t=1,\ldots,T $$

Unlike DYNIP, this model assumes no recourse for the $R_{t}$ variables. In fact under the two-stage model the first stage decision variables $X_{t}, R_{t},\;\hbox{and}\; W_{t}$ are determined at the beginning of the planning horizon, while the second stage problem simply computes the realized FGIs and backorders after demands are realized. This model has the advantage that the size of the model grows linearly with the number of scenarios considered, and that it has complete recourse, in that all first-stage decisions are feasible for the second stage. The disadvantage is that it does not allow recourse action to be taken as demand is realized, placing it on a par with the ZOIP model in this regard.

In order to determine a 2-SP production planning strategy, one has to generate multiple scenarios, each consisting of demand realizations for periods $1, \ldots, T$. The 2-SP model is then solved and the optimal decisions $(R^{\ast}_{t},X^{\ast}_{t},W^{\ast}_{t}), t = 1,\ldots,T$ yield a production plan that is completely defined at the beginning of the planning horizon.

5.2 The Multi-Stage Model (M-SP)

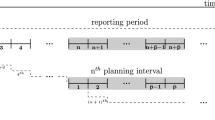
A natural extension of the two-stage model is to allow recourse actions as demand is observed. This is accomplished by representing the demand process $\{D_{t}\}$ as a scenario tree. Each node n in the tree represents a demand realization in the corresponding period $t(n)$ with a probability $q_{n}$. The root node $(n\!\! =\!\!1)$ of the tree represents the current demand, i.e. $D_{1}.$ Node a(n) is the direct ancestor of node n. The direct descendants of node n are called the children of node n. The subtree with root node n is denoted by $T(n).$ A path from the root node to a node n describes one realization of the stochastic process from the present (period 1) to period $t(n).$ The set of all the nodes on this path is denoted as $P(n).$ A full evolution of the demand process over the entire planning horizon, i.e., the path from the root node to a leaf node, is called a scenario.

The scenario tree representation of the demand process is an approximation of the actual demand distribution due to its use of a finite number of possible demand outcomes in each period. Also, generally the size of scenario tree increases exponentially with increasing time horizon. The cumulative demand, production, and releases for the partial realization of the demands represented by a path from the root node 1 to a node n in the tree are given by

$$ D(1,n)=\sum\nolimits_{m \in P(n)}D_{m} $$

$$ X(1,n)=\sum\nolimits_{m \in P(n)}X_{m} $$

$$ R(1,n)=\sum\nolimits_{m \in P(n)}R_{m} $$

The stochastic programing formulation of the production planning problem with congestion is given by the following model:

(MSP):

$$ \begin{array}{lll} \hbox{min} & \sum_{n\in T(1)} q_{n}[h_{t(n)}(I_{n}+W_{n})+b_{t(n)}B_{n}]&\\ \hbox{s.t.}& W_{n}=W_{0}-X(1,n)+R(1,n)&\\&I_{n}=I_{0}+X(1,n)-D(1,n)+B_{n}&\forall n\\ &X_{n}\leq f(W_{a(n)})&\forall n\\ &R_{n},\;X_{n},\;I_{n},\;W_{n},\;B_{n}\geq0&\forall n \end{array} $$

The objective in the M-SP model is to minimize the expected cost over the planning horizon, which includes the present cost determined by the root node decisions and the expected future cost. In any given period t, the release, WIP, and production can be determined before the knowledge of demand, and are hence called first-stage decisions. On the other hand inventory and backorder are recourse decisions because they depend on the first-stage decisions as well as the realization of the uncertain parameter (demand). In our implementation, the constraints related to the clearing function are piecewise linearized as in Asmundsson et al. [4] for computational convenience.

The MSP model has considerable similarities to the Model Predictive Control approach deployed in the engineering disciplines. The similarities between control theoretic and mathematical programing approaches were noted early on by Kleindorfer et al. [67] and their application to supply chain management problems has been discussed by Kempf [64].

5.3 Implementation Strategies for the M-SP Model

Based on the multi-stage stochastic programming model (M-SP) we develop two production planning strategies to satisfy future demand over the planning horizon. The first strategy is a static strategy (MSP) and the second is a dynamic strategy (MSP-DYN).

5.3.1 A Static Strategy (MSP)

MSP is a static strategy, which specifies completely the release, production, and WIP decisions for all future periods at the beginning of the planning horizon. Once demands are realized, the FGI and backorders can be determined and the performance of the solution evaluated, in a manner similar to that used for ZOIP. The primary difference between ZOIP and MSP lies in the manner they model the uncertainty in the demand process. ZOIP assumes a known demand distribution in each period, and establishes constraints that may be violated with a prespecified probability. MSP, on the other hand, captures the uncertainty of demand through a limited number of demand values in each period. Another important difference between ZOIP and MSP is that ZOIP assumes no recourse action is possible as uncertain demand is revealed.

In order to determine the MSP strategy, i.e., the production planning decisions for all periods, we follow the procedure below. Note that all the steps are performed at the beginning of the planning horizon.

For $t=1$, we construct a scenario tree $T(1)$, set the first period demand to the current demand and the initial inventories to some preset initial values, then solve the MSP model. We obtain the optimal production decisions for all the nodes in the tree, i.e., $(R_{n},X_{n},W_{n})^{\ast}$. However we only save the root node decisions, which correspond to the decisions to be implemented in period 1, $(R_{1},X_{1},W_{1})^{\ast}$, under the MSP strategy. Also, $(I_{1},W_{1})^{\ast}$ serve as initial inventories for the next period.

For $t=2$, we construct a scenario tree $T(2)$ over the periods $2,\ldots,T$, set the root node demand to $\mu_{2}$ and solve the M-SP. Here $\mu_{2}$ is the forecast of period 2 demand available to us in the beginning of the planning horizon.

The root node optimal decisions are recorded as $(R_{2}, X_{2}, W_{2})^{\ast}$ and will be implemented in the second period under the MSP strategy. Repeat the same for $t= 3,\ldots,T.$ The optimal decisions $(R_{t}, X_{t}, W_{t})^{\ast},\;t = 1,\ldots,T$ constitute the MSP production plan that is completely defined at the beginning of the planning horizon.

5.3.2 A Dynamic Strategy (MSP-DYN)

As pointed out in Powell et al. [86], a model is dynamic if “it incorporates explicitly the interaction of activities over time”. A model is applied dynamically if “the model is solved repeatedly as new information is received”. Under this definition, DYNIP is a dynamic model, while MSP-DYN presented below is a model applied dynamically.

In the MSP-DYN, the multi-stage SP model is applied dynamically over the planning horizon and only the decisions of the first period are implemented. As new information about demand becomes available the model is resolved and the release, production, and WIP decisions are made. Therefore, at the beginning of the planning horizon only period 1 decisions are known and future decisions will only be determined once the corresponding demand is realized. More specifically, we proceed as follows:

For the current period, $t=1$, we construct a scenario tree $T(1)$, set the first period demand to the current demand and the initial inventories to some pre-set initial values, then solve the MSP model. We obtain the optimal production decisions for the root node decisions to be implemented in period 1, $(R_{1}(D_{1}), X_{1}(D_{1}), W_{1}(D_{1}))^{\ast}\cdot (I_{1}, W_{1})^{\ast}$ serve as initial inventories for the next period.

The current period is $t=2$, the demand of period 2 is now realized and corresponds to the root node demand in a scenario tree to be constructed for periods $2,\ldots,T.$ The MSP model is solved and the root node decisions $(R_{2}(D_{2}), X_{2}(D_{2}), W_{2}(D_{2}))^{\ast}$ are implemented. This process is repeated for $t=3,\ldots,T.$ At the end of the planning horizon the values $(R_{t}(D_{t}), X_{t}(D_{t}), W_{t}(D_{t}))^{\ast},\; \hbox{for}\;t = 1,\ldots,T$ constitute the MSP-DYN production plan.

6 Computational Experiments

In this section, we present a computational study where we compare the performance of the ZOIP, DYNIP, 2-SP, MSP, and MSP-DYN models considering various demand profiles and based on Fill Rate and Inventory Position. The former is a proxy for the level of customer service provided, while the latter serves as a proxy for the average inventory holding cost, considering both WIP and finished goods inventory levels. The models have been implemented in GAMS and solved using CPLEX 11.0. We begin by discussing the experimental design and then present the results and analysis.

Demand Profiles: Demand is forecasted over a horizon of three months, each consisting of four working weeks ($T = 12$ weeks). Demand in each period is independent and normally distributed. However, the means and variances of demand are allowed to vary across periods. Three possible levels of mean demand in a given month are considered: H ($\hbox{High} =140$), M ($\hbox{Medium} = 100$), and L ($\hbox{Low} = 60$). Based on these levels, seven demand profiles are constructed by considering different levels for each month (i.e., four week subinterval): LLL, MMM, HHH, LMH, HML, LHL, and HLH. For example, demand profile LMH represents an increasing monthly demand, where demand from week 1 to week 4 is 60, from week 5 to week 8 is 100, and from week 9 to week 12 is 140. These profiles show how the mean values of the demand distributions vary over the planning horizon. In all these profiles, we assume a constant coefficient of variation $\rho _t =\sigma _t /\mu _t =0.25$ for the demand distributions in every period. This yields very small probability of negative demands; in the few cases in our experiments in which they arose, negative demands were set to zero.

In order to implement the stochastic programs 2-SP and M-SP, scenario trees based on the various demand profiles must be constructed. For the 2-SP model, three scenarios are considered, Low, Medium, and High, with demand in each period t is set to each of the values $\mu _t-\sigma _t , \mu _t$, and $\mu _t+\sigma _t$, respectively. The probabilities of the three demand realizations are assumed to be 0.25, 0.5, and 0.25, respectively. This is clearly a limited representation of the demand uncertainty, and we shall return to this issue in our discussion of our computational results.

In the case of the M-SP model, successive stochastic programs (one in each period) have to be solved in order to obtain a production plan for the entire horizon. Therefore, in each period t a binary scenario tree starting from period t up to the end of the horizon is constructed. In each period we consider two possible demand realizations, Low Demand ($\mu_{t}-\sigma_{t}$) and High Demand ($\mu_{t}+\sigma_{t}$), with equal probabilities. Thus in any given period t, a M-SP is formulated and solved with a scenario tree containing $2^{T-t+1}-1$ nodes and $2^{T-t}$ scenarios (number of leaf nodes).

The capacity of the production system is represented by a clearing function which captures the effect of congestion as discussed in Sect. 3. Following Karmarkar [61], we assume the form of the clearing function to be

$$ f(W)={\frac{K_{1}W}{K_{2}+W}}, $$

where $K_{1}=200$ is the production capacity, and $K_{2}=80$ measures the curvature of the CF.

The resulting CF is shown in Fig. 2. Our piecewise linearization of this CF is given in Table 4.

Fig. 2

Clearing function used in experiments

Table 4 Clearing function approximation

There are clearly many specific issues involved in the estimation and piecewise linearization of CFs which are beyond the scope of this paper. These issues have been discussed extensively in Missbauer and Uzsoy [78]; specific approaches are illustrated in Asmundsson et al. [4], Missbauer [77], and Selcuk et al. [96], among others. Extensive experimentation in the course of this work has shown that the specific manner in which an appropriately fitted CF is piecewise linearized does not have much effect on the quality of the resulting production plans, although it does affect the estimates of the dual prices obtained for the associated constraints [62]. Since the primary purpose of this paper is to compare the solutions obtained from different formulations of the production planning problem with stochastic demand, all the models compared use the same piecewise linearized function. Hence the quality of the fit of the CF is not a factor in this study.

The values of $L_{t}$, i.e. the lead times in period $t=1,..,T$ used in the formulations were chosen to be the same for all periods. This value, based on Little’s Law, was chosen to be $L=W/\mu$, where $\mu$ is the average of all the demand means over the planning horizon and W the WIP value corresponding to a throughput of $\mu$ on the CF. This represents the behavior of a practitioner establishing a model based on historical data. The choice of values for $I_{0}$ and $W_{0}$ can be arbitrary, but the values we use are those recommended by Graves [38], setting $W_{0}=L\mu$, and $I_{0}=z_{\alpha}\sigma \surd L.$

To compare the performance of the production planning models, ZOIP, DYNIP, 2-SP, and M-SP (including the MSP and MSP-DYN strategies) we evaluate their optimal production plans in the face of simulated demand scenarios. For each demand profile, the evaluation procedure is as follows:

$\user2{\it For\, ZOIP,\, 2\hbox{-}SP,}\; \user2{\it and\, MSP}$

• ${\rm Step\,1}:$ Solve the four models for each demand profile and obtain the optimal values of the variables $(R_{t}, X_{t}, W_{t})$ for all periods to be specified at the beginning of the horizon before any actual demand has been observed, i.e. the first stage decision variables. These constitute the optimal production plan.

• ${\rm Step \,2}:$ Generate $N=100$ demand scenarios from the normal distribution for each period and simulate the production plans for the models for each scenario. For each scenario a realization of inventories and backorders is obtained.

• ${\rm Step \,3}:$ Compute the performances for each model i.e., average and variance of backorders, fill rate, inventory position, and holding cost.

$\user2{\it For\, DYNIP }$

• ${\rm Step} \,1:$ Solve the model for each demand profile and obtain the optimal values of the variable $Y_{t}$ for all periods to be specified at the beginning of the horizon before any actual demand has been observed, i.e. the first stage decision variables.

• ${\rm Step\,2}:$ Generate $N=100$ demand scenarios. For each scenario, once demand is realized in a given period, the corresponding (R, X, W) are determined and hence, the inventory and backlogs can be computed.

• ${\rm Step\,3}:$ Compute the performances for each model i.e., average and variance of backorders, fill rate, inventory position, and holding cost.

$\user2{\it For\, MSP\hbox{-}DYN }$

• ${\rm Step\,1}:$ Generate 100 demand scenarios. For each scenario, once demand is realized in a given period t, solve a M-SP model for the periods $t, \ldots, T$ and implement the first period decisions, i.e., the (R, X, W) are determined as well as the ending inventory (I) and backlogs (B).

• ${\rm Step\,2}:$ Compute the performances for each model i.e., average and variance of backorders, fill rate, inventory position, and holding cost.

Since the chance constrained models ZOIP and DYNIP and the stochastic programing models 2SP, MSP and MSP-DYN use rather different modeling assumptions, care must be exercised when making comparisons. The chance constrained models assume a form for the demand distribution in each period, and do not consider shortage costs. However, it can be argued that an implicit judgement on the relative magnitude of holding and shortage costs is made in the specification of the required service level $\alpha$, which also serves as the probability of constraint violation. The chance constrained models do not specify any particular recourse action when constraints are violated; in our computational experiments we assume any missed demands can be backlogged. We thus consider three levels of the service level in our experiments: 90, 95 and 99.9%.

The stochastic programs, on the other hand, do not represent the demand distribution in a closed form. Instead, they use a discrete set of scenarios of outcomes to represent the uncertain nature of demand. Hence the effectiveness of these models is clearly linked to the number and degree of representativeness of the scenarios used to obtain the solutions. Another interesting issue is that stochastic programing models provide, by their nature, values for the decision variables corresponding to first stage decisions that must be made at the present time, as well as decision variables corresponding to each of the scenarios considered. However, since the scenarios considered in the model represent only a sample of possible realizations of the demand process, it is highly likely that in the future we will face a demand realization that does not match any of the scenarios used in obtaining them unless the stochastic program is solved on a rolling horizon basis. Since the size of the formulation to be solved for the stochastic programs is directly driven by the number of scenarios considered, this raises some interesting questions.

The performance of the stochastic programs (2-SP, MSP and MSP-DYN) is mainly affected by the magnitude of the backorder cost relative to the holding cost. We assume a unit production cost of $c\mathop{=}\$100{,}$ and set the holding cost to $h= 0.2\, c\,$ and consider three levels for b the backorder cost: 0.5c, c, and 4c.

7 Results of Experiments

In order to facilitate a fair comparison between the different models, we have taken the approach of multiobjective optimization. The solution produced by any model represents a tradeoff between shortage and holding costs as that model perceives them, subject to the specific parameter settings used. The issue is further complicated by the different definitions of shortage that are possible. The chance constrained models require the specification of a maximum stockout probability. However, there is clearly a practical difference between a solution that stocks out by a large amount in one period, and one that stocks out by very small amounts in several.

We shall thus examine the issue in stages. We shall first consider the tradeoff between average inventory position, defined as the total finished goods and work in process inventory, and the fill rate, which is the fraction of demand in each period met from inventory. We shall then examine the difference between the planned and realized service levels in the chance constraint models, and also explore their sensitivity to errors in the estimation of the demand distributions used.

7.1 Inventory Position-Fill Rate Tradeoff

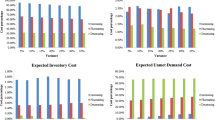
In order to examine the performance of the different models in terms of their tradeoff between inventory position and fill rate, we shall compute the scaled inventory position for each algorithm under each of our seven demand configurations. Let ${\it IP}(i,k)$ denote the average inventory position realized under model i under demand configuration k. Then we define the Scaled ${\it IP}(i,k) = {\it IP}(i,k)/\text{min}_{j}\{{\it IP}(j,k)\}.$ This quantity indicates the level of inventory position of a given model relative to the model with the lowest average inventory position obtained by any model for that demand configuration.

Figure 3 depicts the tradeoff between the models based on average performance across all demand configurations. The fill rate is plotted on the horizontal axis and the scaled inventory position on the vertical. Since we want fill rate to be high, and scaled IP to be low, the efficient frontier is to the bottom right of the plots.

Fig. 3

Average performance of models over all demand configurations

Figure 3 yields a number of interesting insights. The ZOIP model is completely dominated, as we would expect. This is due to its complete lack of a recourse action, leaving it unable to react to the realized demand after it is observed. In particular, this leaves the model unable to react to demand that is lower than expected, causing it to overstock by a significant amount, as indicated by Ravindran et al. [93]. The two-stage stochastic program 2SP is also dominated. The efficient frontier is made up entirely of DYNIP and the static multistage model MSP, while the dynamic implementation of the M-SP, MSP-DYN, is also dominated.

Two salient features emerge from these results. The first and most encouraging from our perspective is the excellent performance of DYNIP. This model is highly competitive at service levels of 0.90 and 0.95, although it is dominated for a service level of 0.999. The relatively small difference in fill rate between the three service levels suggests that the model overstocks to some degree. There are two possible reasons for this behavior. One is that the assumptions of the chance constrained model are violated in the simulations we use, constituting an interesting direction for future work in understanding the sources of this behavior. Another possibility is that the lead time estimate used to set the safety stock levels is too high. The success of DYNIP over ZOIP is due to its incorporation of a dynamic recourse action—it can modify releases based on observed demand in the past, while ZOIP fixes all decisions at the start of the planning horizon; note that ZOIP and DYNIP use the same information about the demand process.

The comparison between DYNIP and MSP is more interesting. The results indicate that DYNIP obtains the same performance as MSP for a specific choice of service levels corresponding to a choice of parameters for MSP lying between $b=100$ and $b=400.$ Given the very limited recourse action incorporated in DYNIP, this seems surprising at first sight; one would expect MSP to perform considerably better. However, we need to bear in mind that DYNIP is using a complete characterization of the demand distribution in each period, while MSP characterizes the demand uncertainty through the use of scenarios. Thus the number and choice of scenarios is critical for the MSP to obtain a good solution.

However, this is also where the size of the competing formulations needs to be taken into account. For a planning horizon of T periods, the DYNIP model requires $O(T)$ decision variables and constraints. Assuming two possible realizations for demand in each period as we do in this study, the scenario tree for MSP has $O(2^{T-1})$ nodes, implying that number of decision variables for what is a minimal amount of information on demand uncertainty. These results hold out the encouraging possibility that a minimal number of well-chosen scenarios may be sufficient for a stochastic program to make near-optimal decisions. However, the sheer size of the scenario trees required to model an industrial problem with multiple products, each with their own different demand processes, suggests that scaling conventional stochastic programing models up to solve industrial-sized problems poses substantial challenges.

Another interesting observation from Fig. 3 is the fact that the static MSP outperforms the dynamic version, MSP-DYN. The latter differs from the former in that the M-SP model is resolved at each period in the planning horizon, using the information from the realized demand in previous periods. Hence the recourse action taken at each period is to resolve the M-SP in the light of previously realized demand.

This result is particularly interesting since implementation on a rolling horizon or dynamic basis has been held up as a solution to the problem of uncertain demand in production planning for decades; the assumption is that only the decisions in the next period matter, and as long as we can revise decisions in the light of observed information we can obtain good results. However, some recent results suggest that our faith in this insight may be misplaced, at least under some circumstances. Orcun and Uzsoy [80] have shown that when the planning model does not accurately represent the behavior of the production system under study, rolling horizon implementations can result in undesirable oscillatory behavior similar to the nervousness discussed in the Material Requirements Planning (MRP) literature (e.g., [13]). What is striking in this case is that the extremely simple recourse action used in DYNIP yields just as good results as the far more sophisticated recourse action in MSP-DYN. This may well be due in part to the very limited demand information used in M-SP, as discussed above, which could potentially be remedied by including additional scenarios in the M-SP model. However, this would come at the cost of increasing the size of an already very large model. It is important to note that in the current experiments, the planning horizon T is fixed and does not recede into the future, which will cause ending effects to arise in decisions towards the end of the planning horizon. In particular, the limited planning horizon may cause the models to take decisions that are very good within the current horizon, but have very unfavorable consequences outside the current planning horizon. This issue clearly needs to be more carefully examined in future work.

7.2 Effect of Estimation Errors

In order to further explore the performance of DYNIP relative to MSP, we conducted two additional experiments in which the mean of the demand distribution used in the DYNIP models are perturbed by a random error uniformly distributed between 0 and 0.2 times the mean, representing a situation where demand is systematically overestimated. Our second case represents the case when demand is underestimated, represented by an error uniformly distributed between $-0.2$ and 0. The standard deviations are subjected to a random error uniformly distributed between $-0.2$ and 0.2. The purpose of this experiment is to examine the sensitivity of DYNIP to errors in the estimation of the demand distributions used.

The results of these experiments are shown in Fig. 4. The suffix “H” denotes the results for the case with overestimated demand, and “L” for the case with underestimated demand. The results for MSP are included for comparison. The results are quite intuitive. The impact of errors in demand estimation increases with the required service level. When $\alpha=0.90$, the scaled IP varies between 1.12 and 1.21; for $\alpha=0.95$, from 1.14 to 1.24; and for $\alpha=0.999$, from 1.3 to 1.47. The changes in fill rate are all less than 1%. The MSP results are dominated except for MSP-4.0, which achieves a higher service level than DYNIP-0.999 and DYNIP-0.999-H with lower inventory position. These results together suggest that DYNIP is relatively robust to errors in demand estimation, while at the same time supporting the earlier evidence that it tends to overstock relative to the desired service level.

Fig. 4

Sensitivity of DYNIP to errors in demand estimation

The tradeoff between fill rate and scaled IP for the individual demand configurations was also examined, although detailed results are not presented for brevity. Comparing the HHH, LLL and MMM results indicates that for LLL and MMM, DYNIP dominates MSP, while for HHH MSP enters the efficient frontier, obtaining slightly lower fill rates with substantially lower inventory position than MSP, although DYNIP-0.90 and DYNIP-0.95 remain on the efficient frontier. In all demand configurations except HML, DYNIP is represented in the efficient frontier; in that configuration MSP dominates all the DYNIP models, obtaining both higher fill rate and lower inventory position. Interestingly, the converse is true for the LHL configuration, where MSP is dominated by the DYNIP models.

Taken as a whole, these results suggest that DYNIP is at least a contender as a solution technique for the planning problem considered in this paper. While it exhibits some weaknesses in the face of high demand variability, its performance appears to be relatively robust to errors in the estimation of the demand distributions it uses, and it consistently achieves a position on the efficient frontier of the fill rate—inventory position tradeoff. It appears to have a tendency to overstock, which is likely due to the discrepancy between the assumptions of the model and the environment in which the simulations take place.

Table 5 Realized fill rates and service levels

7.3 Service Level-Fill Rate Comparison

An interesting comparison that sheds some additional light on the behavior of the different models is to compare the average service levels and fill rates. The entries in Table 5 are computed by taking the average over all periods in each realization, and then taking the grand average of these over all realizations of a specific demand configuration. It is immediately apparent that the service levels realized by DYNIP are higher than the planned service levels, resulting in even higher fill rates. The reason for this behavior is very likely that the lead time being used to compute the inventory targets is higher than the average lead time that is realized in the simulations. Interestingly, even though the same lead time parameters are used in the ZOIP model, ZOIP’s service level is markedly worse than that of DYNIP. ZOIP and DYNIP appear to perform better when the demand distribution is time-stationary (demand configurations LLL, MMM, and HHH) than when it is not. In contrast, MSP maintains a consistent level of fill rate across all scenarios. The fact that the fill rate is consistently higher than the service level for the chance constrained models (ZOIP and DYNIP) suggests that even though stockouts occur, the amount of the stockout is quite modest in most cases.

8 Conclusions and Future Directions

Acknowledging at the outset the exploratory nature of this chapter, our results raise some interesting issues. Planning procedures with recourse (MSP, MSP-DYN and DYNIP) consistently outperform those without recourse (ZOIP and 2SP) as one would expect. However, the performance of DYNIP suggests that when appropriately parameterized it may be able to compete effectively, in terms of producing near-optimal solutions in reasonable CPU time, with far larger multi-stage stochastic programing models that employ a limited number of scenarios to capture demand uncertainty—at least under certain conditions. It also appears to be relatively robust to errors in estimation of the demand distribution used to construct the model. On the other hand, the MSP model appears to be able to produce good solutions with a minimal number of demand scenarios, considering only two possible values in each planning period. Even so, the MSP approach results in very large models relative to DYNIP. Finally, a dynamic, rolling horizon implementation of MSP yielded no apparent advantage over the static procedure. This finding is interesting in itself, since a rolling implementation is widely held to be the remedy for demand uncertainty.

Given the limited number of experiments carried out, these findings raise more questions than they answer, suggesting several directions for future work to clarify or confirm these findings. Clearly future work needs to focus on procedures with recourse, such as MSP and DYNIP. The reason why DYNIP appears to consistently overstock needs to be understood, and methods found to alleviate this issue if possible. It may be as simple as setting the lead time parameter used to compute the inventory targets more accurately, but it may also be related to the fact that the assumptions used in developing the model are violated in the experimental environment. If the latter is the case, careful mathematical analysis must be carried out to reveal the reason, and suggest an approach to correct the problem. The sensitivity of DYNIP to errors in estimating the demand distributions, and approaches for using it in the face of very limited demand information also need to be explored.

The MSP model used in this work highlights the primary issue with multistage stochastic programing when applied to production planning: the size of the scenario tree grows very rapidly, resulting in very large formulations even when a very limited number of different demand realizations are considered in each period. There needs to be a systematic investigation of how many scenarios need to be considered to provide a reasonably good solution (however that is to be defined, which is another complex issue), and possible solution methods that will allow a scaling up of these approaches to problems of industrial size.

Finally, as we have noted in our analysis, the chance constrained and stochastic programing models make quite different assumptions in formulating the models. The chance constrained models ignore shortage costs, and require a specified stockout probability. The stochastic programing models require a number of scenarios that describe the demand uncertainty and explicit holding and shortage costs. These different assumptions have been shown in the literature to lead to paradoxical behavior for the chance constrained models under certain circumstances, such as a negative value of the expected value of perfect information [14]. While the mathematical existence of such behavior is well documented, it may yet remain the case that chance constrained models, when appropriately formulated and parameterized, can provide effective heuristics for the problem of production planning under uncertain demand.