Deformation and Fatigue of Solders

Abstract

Cyclic load generally leads to mechanical failure of a material. In cyclic load, the load applied to a specimen varies in time and magnitude. This variation of load and time can be regular or stochastic. The effect of purely stochastic variations cannot be predicted; thus, the analysis of a cyclic load is done by simplifications trying to find a regular pattern in the load/time history. For the degradation behaviour, it makes a difference whether a specimen is subject to a slow variation of the load or to a rapid one. The two load regimes are assigned as low-cycle fatigue and high-cycle fatigue, respectively. In low-cycle fatigue, the time in each cycle allows the material to deform plastically, usually by creep. This means in low-cycle fatigue, the failure is triggered by deformation. High-cycle fatigue on the other hand does not leave enough time for relaxation. Local defects lead to local stress concentration above the yield strength, which causes the defect to grow with each cycle. In other words, high-cycle fatigue is stress driven. Usually, in high-cycle fatigue, the number of cycles to failure is above 10⁵ cycles. In reality, it is quite common that both kinds of fatigue are present, which makes testing for cyclic load quite complex.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In this chapter, a brief introduction in the definition of cyclic load as well as in the deformation mechanisms and their corresponding degradation mechanisms is given. For more in-depth information, there is ample literature available.

1.1 Deformation

1.1.1 Time-Independent Deformation

Every material deforms if stress is applied. The deformation can be either elastic, which means that the deformation is reversible as soon as the load is removed or instantaneous plastic if the stress is above the so-called yield stress.

The elastic deformation has its origin in the stretching of interatomic bonds.

The bonds are a combination of attractive and repulsive forces with the net force being zero when the bond is at equilibrium. Clearly, when the atoms are far apart, the attractive part must dominate and when they are very close together, the repulsive part is greater; both contributions decay away as the separation increases. The combination of attractive and repulsive forces manifest in the general atomic force (F)–atomic spacing (r) graph (Fig. 1.1).

Fig. 1.1

Atomic force–atomic spacing graph

A tensile force will lengthen the interatomic bonds and will be opposed by the attractive part of the interatomic force. As soon as the minimum of the F–r graph is reached, the external force will dominate and the bond will break.

This behaviour can be illustrated with a spring. As a load is applied, the spring extends following a linear law

$$ F = C \cdot \Updelta l $$

(1.1)

F load, C spring constant, Δl deformation.

In construction materials, this relationship is expressed as

$$ \sigma = E \cdot \varepsilon $$

(1.2)

σ stress, E modulus of elasticity or Young’s modulus, ε strain or under shear load.

$$ \tau = G \cdot \gamma $$

(1.3)

τ shear stress, G shear modulus, γ shear strain.

The elastic deformation is principally time independent. This means the specimen deforms as soon as a load is applied.

As soon as the spring is stretched above a certain amount, it will relax the maximum elastic amount but also the spring will show a remaining deformation if the load is removed. This behaviour is visible in most metals. If a metal is strained more than 0.5%, the stress–strain behaviour is clearly no more a straight line but a curve and a not-recoverable deformation called plastic deformation takes place. The plastic deformation is caused by the movement of crystal layers above each other. As soon as a certain stress is exceeded, dislocations in the crystal lattice will be activated to move through the crystal lattice and thus two plains of atoms are moving across each other. The point where the elastic deformation gradually merges to the plastic deformation is called the proportional limit. However, this point cannot be defined precisely. To overcome this problem, a line with the same slope as the elastic line is drawn, originating from a given strain, usually 0.2%. The intersection of this line with the curved line of the stress–strain diagram is called the yield strength (Fig. 1.2).

Fig. 1.2

Definition of yield strength

1.1.2 Time-Dependent Deformation

There is also a time-dependent elastic deformation. This means that under a constant load, a material deforms and after the load is removed, the deformation goes back to 0 over time. This behaviour is called anelastic deformation.

If a material under load experiences an elevated temperature, time-dependent plastic deformation takes place, which means that the material shows an ongoing deformation under constant load. This deformation is called creep.

In contrast to the spring example, a material that creeps can be compared with a wet chewing gum. If one applies a constant load to such a specimen, it will constantly deform until it breaks. Varying the load results in differences in the deformation rate. The heavier the load, the faster the chewing gum deforms. If the specimen is cooled down, the deformation will come to an end as soon as the chewing gum is frozen.

How fast a material deforms if a certain load is applied depends on how close it is to its solidus temperature. How close the temperature of the application is to the solidus temperature is expressed with the homologues temperature

$$ T_{\text{H}} = {\frac{{T_{\text{A}} }}{{T_{\text{S}} }}} $$

(1.4)

T _A temperature of application (K), T _S temperature of solidus (K).

Note that absolute temperatures in Kelvin are to be used.

As soon as a material surpasses a T _H of 0.5, creep becomes an important part of the deformation history.

In creep, two deformation mechanisms are dominant: grain boundary sliding and dislocation creep. In grain boundary sliding (GBS), the crystals that make up the metal slide above each other along their grain boundaries. Since the grains fit only in one configuration, they have to move on complex paths combining rotation and lateral movement in all three dimensions to come around each other. As soon as the stress applied exceeds a certain value, dislocations will start to glide through the grains (DC), thus deforming the grains. Again in both cases the deformation causes microvoids to form that have to be filled up by diffusion.

Thus, GBS occurs if low stress results in a slow deformation, DC is the dominant deformation mechanism if large stress is applied to a specimen.

In reality, GBS and DC never occur on their own. Also, with a low overall stress that would activate GBS only, local stress build-up can cause local DC.

In contrast to the elastic deformation, creep is time dependent as already mentioned earlier. Thus, the load does not cause a certain deformation but a deformation rate.

$$ F = f\left( {{\frac{\Updelta l}{\Updelta t}}} \right) $$

(1.5)

F force, Δl elongation, Δt time; or as stress–strain.

$$ \sigma = f(\dot{\varepsilon }) $$

(1.6)

σ normal stress, $\dot{\varepsilon }$ strain rate; or under shear load

$$ \tau = f(\dot{\gamma }) $$

(1.7)

τ shear stress, $\dot{\gamma }$ shear strain rate.

This means the more load one applies to a specimen, the faster it deforms, and the longer one waits, the more the specimen deforms; in other words, every deformation can be achieved with every load—it is just a question of time. Thus, it is senseless to speak of a yield strength when characterising soft solder: Since Creep is the main deformation mechanism in soft solders due to their high homologues temperature even at room temperature (Table 1.1), everydeformation rate will result in another yield strength.

Table 1.1 T_H at 20°C of some soft solder alloys

If a creep test is done, where a constant load is applied to the specimen and the deformation is monitored, one sees that the strain often varies over time (Fig. 1.3). After an initial elastic deformation, primary creep with a varying strain rate takes place followed by a regime with mostly constant creep rate called secondary creep. In the end, the creep rate starts to increase due to damage in the material until the specimen fails.

Fig. 1.3

Creep behaviour with constant load

If the creep rate of metals is plotted against the stress applied in a double logarithmic plot, one sees that over a limited interval, the measurement points are located on a straight line.

Norton [1] surveyed creep in steel and described the nearly linear relationship of the secondary creep in the double logarithmic plot with

$$ \dot{\gamma } = A\left( {{\frac{\tau }{G}}} \right)^{n} \exp \left[ {\frac{Q}{RT}} \right] $$

(1.8)

$\dot{\gamma }$ creep rate, A constant, τ shear stress, G shear modulus, n exponent, Q activation energy, R gas constant, T temperature in K

where τ is normalised with the shear modulus G in order to eliminate the units of τ and an Arrhenius term is used to account for the influence of the temperature.

However, in solder, over an extended measurement range of stress vs. strain rate, one sees that the measurement points are no more located on a straight line (Fig. 1.4).

Fig. 1.4

Measurement of creep of SnPb₃₆Ag₂ at room temperature

Several models have been used to describe this behaviour.

A very popular model is the approach of Garofalo [2] who approximated the curve where the points are located with a sinh-relationship:

$$ \dot{\gamma } = C_{1} \left[ {\sinh \left( {C_{2} \tau } \right)} \right]^{n} $$

(1.9)

$\dot{\gamma }$ creep rate, C ₁, C ₂ constant, τ shear stress, n exponent.

Another possibility has been proposed by Hart [3] who treated the system of grain boundary sliding (GBS) and matrix creep (MC which is the same as DC) with a rheological analogue (Fig. 1.5). Hart modelled GBS with a linear viscous law and MC by a power law.

Fig. 1.5

Analogous model of Hart

The system of Fig. 1.5 can be modelled with

$$ \sigma = \sigma_{0} \left[ {y + \left( {1 - y} \right)Z} \right]\dot{\varepsilon }^{\mu } $$

(1.10)

σ stress, $\dot{\varepsilon }$ strain rate, σ₀ material constant, μ material constant, y parameter for the grain size; with

$$ Z = {\frac{{\sigma_{\text{b}} }}{{\sigma_{\text{m}} }}} $$

(1.11)

σ_b stress in the grain boundaries, σ_m stress in the matrix.

Another constitutive equation proposed by Weber and Grossmann [4] models the deformation behaviour of soft solder as the sum of the two deformation mechanisms GBS and DC, both expressed with a Norton equation:

$$ \dot{\gamma } = A\left( {{\frac{\tau }{G}}} \right)^{n} \exp \left[ {{\frac{{ - Q_{\text{GBS}} }}{RT}}} \right] + B\left( {{\frac{\tau }{G}}} \right)^{m} \exp \left[ {{\frac{{ - Q_{\text{DC}} }}{RT}}} \right] $$

(1.12)

$\dot{\gamma }$ strain rate, τ shear stress, G dynamic shear modulus, Q _GBS activation energy GBS, Q _DC activation energy DC, n exponent GBS, m exponent DC.

1.2 Degradation Due to Cyclic Load

1.2.1 Definition of a Cyclic Load

A regular cyclic load is defined by its stress amplitude σ_a, its mean stress σ_m as well as the upper stress level σ_u, the lower stress level σ_l and the period of a cycle t (Fig. 1.6) with

$$ \sigma_{\text{a}} = \sigma_{\text{u}} - \sigma_{\text{l}} $$

(1.13)

σ_a stress amplitude, σ_u upper stress level, σ_l lower stress level or with the stress quotient R:

$$ R = {\frac{{\sigma_{\text{l}} }}{{\sigma_{\text{u}} }}} $$

(1.14)

σ_l lower stress level, σ_u upper stress level; and

$$ f = \frac{1}{t} $$

(1.15)

f frequency, t time for 1 period.

Fig. 1.6

Definition of a cyclic load

A cyclic load can be single-levelled with σ_m and σ_a constant or multi-levelled with varying σ_m and σ_a. The frequency f is rarely varied since if f is varied, the evaluation of the resistance of a material against fatigue becomes multidimensional and extremely complex.

1.2.2 Fatigue Testing

The resistance of a material against cycle fatigue is evaluated by cyclic fatigue testing with two kind of testing set-up: In one set-up, σ_m is held constant and σ_a varies and in the second set-up, both, σ_m and σ_a, are varied.

1.2.2.1 σ_m Constant, σ_a Varying

Usually σ_m is 0, which means that the specimen encounters cyclic tensile and compressive stress. By varying σ_a, the average number of cycles to failure (N _f) is determined for each level of σ_r (Fig. 1.7). The resulting curve of N _f = f·(σ_a) is called Wöhler’s curve.

Fig. 1.7

Determination of Wöhler’s curve [5]

Of course there is a considerable spread in the measurements of Wöhler’s curve. Thus, the failure probability has to be included in the measurements to describe the resistance of a material against high-cycle fatigue (Fig. 1.8).

Fig. 1.8

Wöhler’s curve of an Al-alloy with σ_m = 0 with the probability of occurrence as free parameter [6]

1.2.2.2 σ_m and σ_a Varying

If both parameters are varied, there are 2 ways to look at the results. The straightforward one is to draw the average Wöhler’s curve for various σ_m in one diagram (Fig. 1.9).

Fig. 1.9

Wöhler’s curve for varying σ_m with σ_m1 > σ_m2 > σ_m3 [6]

The other possibility is to fix a desired N _f for a specimen and plot the σ_a and σ_m combinations leading to this particular N _f in the Haigh diagram (Fig. 1.10).

Fig. 1.10

Haigh diagram for a given N _f [6]

1.2.3 Brittleness

The brittleness of a material is measured in the Charpy test with an impact tester where a pendulum hits a specimen that bears a notch (Fig. 1.11). The geometry of the specimen and the notch are standardised in EN10045.

Fig. 1.11

Charpy test

The energy loss of the pendulum given by the difference of height between the starting position and the end position of the pendulum (H–h) is a measure for the brittleness of the specimen. A ductile material will absorb more kinetic energy than a brittle material and thus h will be smaller if a ductile material is tested than for a brittle material. The brittleness of a material depends on the crystal structure, on grain size and on shape and size of particles to name a few influencing factors. Whether a material is brittle or not depends also on its temperature. Many materials show a transformation from ductile to brittle as a function of temperature called the transition temperature.

This transition from brittle to ductile is influenced by the crystal lattice. Cubic face-centred (fcc) materials such as Pb, Al or Cu retain their plasticity at low temperature where cubic body-centred materials such as Fe, Cr or W show a clear transition temperature (Fig. 1.12).

Fig. 1.12

Transition of some materials [7]

Various parameters influence the brittleness of solder, as discussed in Chap. 2.

There seems to be no widely accepted parameter or index (in ASTM, or ASM or Mil Handbook standards or elsewhere) for distinguishing brittleness from ductile failure. The best statement might come from the qualitative guidance offered by Charpy impact toughness measurements (either as a function of temperature or strain rate), where failures below the transition toughness level are considered as generally brittle and those above that as ductile. For tensile tests, it is common to report failure strains, and let readers make the judgement in the context it was presented. In industry, anything below a few % failure strain such as 5 or 10% (from a room temperature tension test, for example) would be considered to be brittle. Thus, there can be an “arbitrary” industry basis, with some understandable justification, to call a material brittle for failure strains less than a few percent.

Regarding shear failure strains, it is difficult to apply such a definition. Microscopically, some single crystals of ductile metals will fail by pure shear along slip planes when suitably oriented in tension tests, but in shear, they can exhibit very large strain to fracture, often like 20, 50%, due to accumulation of sliding on planes across the gage section.

On the other hand, under biaxial pure shear load, one could have a material fail with an overall strain at rupture above 10%. However, taking the strain to failure in either stress direction, it could be that in one direction high strain occurs thus being characterised as ductile failure while in the other direction the material deforms only a few per cent and should be declared as brittle

1.2.4 Modes of Fatigue

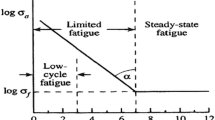
In Wöhlers curve, three areas can be identified (Fig. 1.13). On the left side, one can see that the stress applied has nearly no influence on N _f. Degradation in this area appears early and is called low-cycle fatigue (LCF). In order to have a more precise definition, it is common sense that failures below 5 × 10⁴ are assigned to LCF. If a specimen fails, later it is attributed to high-cycle fatigue (HCF). Some materials, such as steel, show a fatigue limit, a stress level below which no failures occur which is assigned as infinite life. This limit is not easy to determine because the limit occurs at low stress levels where tests usually run for a long time and where it is difficult to distinguish between a slow degradation and a real fatigue limit.

Fig. 1.13

Zones in Wohlers curve

1.2.4.1 Low-Cycle Fatigue

As already mentioned, in LCF, the stress amplitude applied has no direct influence on N_f. This is due to the fact that in LCF, the degradation is strain driven. Be it time-independent or time-dependent strain. In slow cycles where time-dependent deformation takes place, not only the stress applied to a specimen has to be considered but also the time (the frequency) is important. This applies specially to ductile materials such as solder where creep is essential.

Each cycle will leave some microvoids because the grains only fit in one configuration and every plastic deformation due to GBS will cause voids due to the geometric mismatch. Along the grain boundaries, atoms will diffuse from areas with compressive stress to the voids and fill them up. The longer one waits, the more atoms will diffuse into the voids, and the higher the temperature, the faster the diffusion takes place. However, usually the cycle will be reversed before the voids are totally filled up, thus leaving a microvoid. With every cycle, new microvoids form and coalescent to large defects. The larger the deformation per cycle is, the larger are the microvoids that form. This means that in LCF, a degradation field develops where microvoids coalesce during the cyclic load to crack like separations. This degradation field corresponds to the strain filed in a material which means that degradation due to LCF can form locally in a volume. The occurrence of local degradation is well visible in lead-free solder after thermal cycling (Fig. 1.14).

Fig. 1.14

Degraded solder joint made of SnAg_3.5Cu_0.7 after 4,000 thermal cycles (−20°C/+120°C)

The degradation due to LCF has been modelled by Coffin and Manson with

$$ N_{\text{f}} \cdot \varepsilon_{\text{pl}}^{\alpha } = C $$

(1.16)

N _f number of cycles to failure, ε_pl plastic deformation per cycle, α degradation exponent, C constant as well as by Morrow with

$$ N_{\text{f}} \cdot E^{\beta } = C $$

(1.17)

N _f number of cycles to failure, E _pl strain energy per cycle, β degradation exponent, C constant.

The strain energy can be derived from the area in the stress–strain hysteresis, which occurs in a material under cyclic load with plastic deformation. The main difference of the two models is the fact that in the Coffin–Manson approach, only the strain is the driving force for the degradation. The model of Morrow assumes that also the stress applied influences the degradation. With the approach of Morrow, this means in practical applications that short thermal cycles (e.g. in an accelerated test with steep temperature ramps and large temperature excursion) with large stress but small strain result in an equivalent degradation as in a slow cycle with reduced temperature excursion which, due to creep, will induce large strain with small stress because the area in the stress–strain hysteresis is the same in both cases. The Coffin Manson approach restricts the possibility of accelerated testing since in any test, the cycles must be long enough to allow the material to creep. Generally, it does not make a big difference which of the two models is used. Since it is easier do determine the strain per cycle than the strain energy, the Coffin–Manson relationship is more popular than Morrows equation. Assuming total relaxation during each thermal cycle in the solder joint of an electronic component, the strain can be estimated by:

$$ \varepsilon_{\text{pl}} = {\frac{{\Updelta \alpha \cdot \Updelta \vartheta \cdot l_{0} }}{d}} $$

(1.18)

Δα difference of the coefficients of thermal expansion between the component and the PCB, Δϑ temperature swing, l ₀ half-length of the component, d thickness of solder gap.

Of course this is only an estimate. The deformation field can only be determined with FEM simulation as it is outlined in Chap. 3. However, also the simulation has its limitations. It shows the deformation field for a given idealised geometry only. In reality, the geometry and also the structure of the solder, which influences the creep behaviour of the solder, change continuously as the degradation evolves. And, due to differences in the geometry and in the structure of the solder joints, the degradation evolves different in each joint. The consequence is evident in a component with two connectors such as a chip resistor. One of the solder joints will degrade faster than the other. This means that over time, the load-bearing area of one joint becomes smaller than the one of the other joint, which again means that in the end of the process, the weaker joint only will be deformed and degrade. As a consequence, in Eq. (1.18), the full length of the component has to be used for l₀ instead of its half-length.

However, for a first approximation of the live time of a solder joint, one can say that the estimate as shown above is often precise enough despite its shortcomings.

1.2.4.2 High-Cycle Fatigue

HCF is stress driven in contrast to LCF. If a load is applied to a homogeneous specimen, the stress is evenly distributed. However, if the bearing cross-section of the specimen contains a discontinuity, stress amplification at the tip will occur (Fig. 1.15). The maximum stress occurring at the tip can be calculated with

$$ \sigma_{\max } = 2\sigma_{0} \sqrt {{\frac{a}{\rho }}} $$

(1.19)

σ_max maximum stress, σ₀ average stress, a length of discontinuity, ρ radius of discontinuity.

Fig. 1.15

Local overstress due to a discontinuity [6]

Due to a certain plasticity in metals, σ_max is transformed to strain in a limited zone around the tip. The radius of this zone depends on the mechanical properties of the material. In a brittle material, the radius ρ is smaller than in a ductile material and because of the term 1/ρ, σ_max becomes infinite if ρ is converging to 0, independently of the applied load. This maximum stress can be high enough to break up the bonds of the atoms that are right at the end of the tip. As a result, a crack will grow as long as a positive load is applied in a cycle even if the load is far below the yield strength of the material. In other words, the more brittle a material is, the more HCF becomes a thread. The progress of a crack due to high-cycle fatigue can be seen on the surface of a rupture. From an initial site, the stair-like striations indicate the path of the fatigue until the bearing area is so small that the yield strength of the material is exceeded and a forced rupture occurs (Fig. 1.16).

Fig. 1.16

High-cycle fatigue damage

Because in the HCF zone, the Wöhler curve is very close to a straight line, the degradation has been modelled by Basquin with

$$ \sigma \cdot N_{\text{f}}^{\alpha } = C $$

(1.20)

σ stress amplitude, N _f number of cycles to failure, α degradation exponent, C constant.

Generally, high-cycle fatigue is not a concern for solder joints, since due to the ductility of the material, the critical radius will never converge to 0. With SnPb solder also the brittle interfaces with intermetallic compounds which are prone to high-cycle fatigue rarely see enough load to exhibit failure due to rapid cycling. Usually the leads of components fail before the solder joint shows significant degradation.

Lead-free solders on the other hand show some properties that make the occurrence of high-cycle fatigue in the solder joint more probable:

• The lower creep rate of lead-free solder causes larger stress in the intermetallic compound, thus provoking high-cycle fatigue in the interface of the solder with the substrate.

• Lead-free solder containing Ag shows a clear transition temperature as shown at IMEC with a mini-Charpy tester on specimen measuring 10 × 10 × 55 mm (Fig. 1.17). The outcome of the investigation was that SnPb shows a gradual transition below −20°C. The Sn–Cu alloys show a clear transition between −140 and −120°C. The most interesting result was that Sn–Ag shows a transition temperature depending on the amount of Ag in the alloy. The alloy with 5% Ag had its transition between −60 and −20°C, which is in the range technical applications with lead-free solder are subject to.

  Fig. 1.17

  

  Transition of solders [8]

The same damaging characteristic as in high-cycle fatigue (incremental growth of a crack due to local overstress in brittle materials) has been observed in tests on lead-free solders but the number of cycles to failure is not necessarily >10⁵ cycles as expected in high-cycle fatigue. Thus, in solder joints, it might be more appropriate to talk about stress-induced fatigue rather than high-cycle fatigue.

This means that in certain mission profiles, high-cycle fatigue in lead-free solder might become important:

• Low temperature

• High Ag content

• Fast alternating load such as bending of a PCB due to vibration or drop. Tony Mattila at HUT Helsinki found that a PCB starts to vibrate after impact in a drop test with bending modes occurring at various natural frequencies of the specimen [9]. This is discussed in depth in Chap. 9.

1.2.4.3 More than One Degradation Mechanism

Of course usually more than one degradation mechanisms occur in a material in real-field applications. As it is implied in Eq. (1.12), GBS and DC are always effective in varying proportions. But also HCF and LCF might occur under combined vibration and thermal cycle load in a temperature range close to the transition temperature where creep is active. This has been modelled by Miner and Palmgren with

$$ \sum\limits_{i = 1}^{n} {{\frac{{n_{i} }}{{N_{{{\text{f}}i}} }}} = 1} \;{\text{at failure}} $$

(1.21)

n _i number of cycles with degradation mechanism i, N _fi number of cycles to failure with degradation mechanism i.

For the special case where different degradation mechanisms are active in one load cycle, Eq. (1.21) can be modified as proposed by Halford and Manson:

$$ \sum\limits_{i = 1}^{n} {{\frac{{f_{i} }}{{N_{{{\text{f}}i}} }}} = {\frac{1}{{N_{\text{f}} }}}} $$

(1.22)

f _i fraction of a cycle with degradation mechanism i, N _f number of cycles all mechanisms combined.

In [10], it has been shown in a joined work between CRF and IMEC within the EC-IMECAT project that a combined load of temperature cycling and vibration, as encountered in automotive applications, has a more severe effect on the degradation of a solder joint than the same stress history applied sequentially, incorporating a considerable amount of stress-induced fatigue.