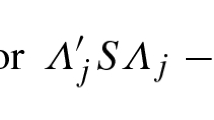Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The currently dominant, myopic approach to statistical analysis in psychology is based on analysis of inter-individual variation. Differences between subjects drawn from a population of subjects provide the information to make inferences about states of affairs at the population level. For instance, the factor structure of a personality test is determined by drawing a random sample of subjects from the population of interest, estimating the item correlation matrix by pooling across the scores of sampled subjects, and generalizing the results of the ensuing factor analysis to the population of subjects.

Pooling across subjects is the hall-mark of analyses of inter-individual variation. Such pooling implies that the individuality of each subject in the population is immaterial to the statistical analysis—subjects in a homogeneous population are considered to be exchangeable like atoms in a homogeneous gas, constituting replications of each other. Accordingly, the population is conceived of as a set of statistical atoms or clones in which the variation between atoms (inter-individual variation) has the same (factor) structure as the variation of each atom in time (intra-individual variation).

This perspective underlying analyses of inter-individual variation would seem to imply that results which hold in a homogeneous population also apply to each of the individual subjects making up this population. That is, the variation between subjects at each point in time has to be qualitatively and quantitatively the same as the variation which characterizes the life trajectory of each individual subject. Therefore results obtained in analyses of inter-individual variation can be, and abundantly are, applied to assess, counsel and treat individual subjects.

It has been shown recently (Molenaar, 2004), however, that in general the inferred states of affairs at the population level, as determined in analyses of inter-individual variation, do not apply at the level of intra-individual variation characterizing the life trajectories of individual subjects making up the population. This is a direct consequence of general mathematical theorems—the so-called classical ergodic theorems—which have far-reaching implications for the way in which psychological processes have to be analyzed.

These theorems, which are heuristically described below, imply the necessity of using alternative approaches for the analysis of intra-individual variation, based on single-subject and replicated time series analysis. Next an overview is presented of dynamic factor models for the analysis of multivariate time series and the various ways to fit these models to the data. Some persistent misunderstandings in the recent literature on dynamic factor analysis will be addressed and an illustrative empirical application of factor analysis of mood change during pregnancy data is presented. The next topic is innovative—a new dynamic factor model for the analysis of multivariate time series having time-varying statistical characteristics is introduced and applied to simulated data. In the closing section future extensions of dynamic factor analysis are outlined.

12.1 The Classical Ergodic Theorems

The standard approach to statistical analysis in psychology is to draw a random sample of subjects from a presumably homogeneous population of subjects, analyze the structure of inter-individual variation in this sample, and then generalize the results thus obtained to the population. Such analysis of inter-individual variation underlies all known statistical techniques, like analysis of variance, regression analysis, factor analysis, multilevel modeling, mixture modeling, etc. Consequently the standard approach to psychological data analysis aims to describe the state of affairs at the population level, not at the level of individual subjects. Accordingly, the individuality of each of the persons in the sample and population is deemed immaterial: the subjects are considered to be replications devoid of individuality. This is expressed by the assumption that subjects are homogeneous in all respects relevant to the analysis. This essential homogeneity assumption allows for the averaging (pooling) of the scores of the sampled subjects in the determination of statistics (e.g., means, variances, correlations, model parameters) to be generalized to the population.

However, the standard approach based on analysis of inter-individual variation is incorrect if a psychological process under investigation does not obey stringent conditions (Molenaar, 2004). The proof is based on the classical ergodic theorems; theorems of extreme generality which apply to all measurable processes irrespective of their content (cf. Choe, 2005, for a modern proof of the first ergodic theorem of Birkhoff). The conditions concerned are specified at the close of this section.

To appreciate the far-reaching implications of the classical ergodic theorems, it is helpful to first characterize the elementary methodological situation in psychological measurement. Instead of postulating an abstract population of subjects, consider an ensemble of actually existing human subjects whose measurable psychological processes are functions of time and place (the basic Kantian dimensions of phenomenological reality).

To simplify the following discussion, without affecting its generality, the focus will be on time as the basic dimension along which psychological processes are evolving. The ensuing basic scientific representation of a human subject in psychology therefore is a high-dimensional dynamic system, the output of which consists of a set of time-dependent processes. The system includes important functional subsystems such as the perceptual, emotional, cognitive, and physiological systems, as well as their dynamic interrelationships. The complete set of measurable time-dependent variables characterizing the system’s behavior can be represented as the coordinates of a high-dimensional space which will be referred to as the behavior space. The behavior space contains all the scientifically relevant information about a person (cf. De Groot, 1954).

Within the behavior space, inter-individual variation is defined as follows:

  1. (i)

    select a fixed subset of variables;

  2. (ii)

    select one or more fixed time points as measurement occasions,

  3. (iii)

    determine the variation of the scores on the selected variables at the selected time points by pooling across subjects.

Analysis of inter-individual variation thus defined is called R-technique by Cattell (1952).

In contrast, intra-individual variation is defined as follows:

  1. (i)

    select a fixed subset of variables;

  2. (ii)

    select a fixed subject;

  3. (iii)

    determine the variation of the scores of the single subject on the selected variables by pooling across time points.

Analysis of intra-individual variation thus defined is called P-technique by Cattell (1952).

With these preliminary specifications in place, the following heuristic description of the content of the classical ergodic theorems can be given. These theorems detail the conditions that must be met in order to generalize from analyses of inter-individual variation to analyses of intra-individual variation, and vice versa.

The conditions of the ergodic theorems are twofold. First, a process has to be stationary, meaning that the mean function must be constant in time (without trends or cycles) and the sequential dependence must be constant in time (with constant variance and sequential correlations depending only upon the relative distance between time points; cf. Hannan, 1970).

Second, each person in the population must obey the same dynamics. If a dynamic process obeys both conditions, it is called ergodic; if one or both conditions are violated, it is called non-ergodic. For ergodic processes, lawful relationships between inter- and intra-individual variation exist, but for non-ergodic processes these relationships do not exist. Put another way, if the conditions of ergodicity are violated, no a priori relationship exists between results obtained in an analysis of inter-individual variation (R-technique) and results obtained in an analogous analysis of intra-individual variation (P-technique).

The consequences of the classical ergodic theorems affect all psychological statistical methodology (e.g., Molenaar, Huizenga, & Nesselroade, 2003; Borsboom, 2005). Because “development” generally implies that some kind of growth or decline occurs, developmental processes are almost always non-stationary and are, therefore, non-ergodic. Generally, developmental scientists consider change that occurs in average or mean levels of a process. However, change may also occur in variances or sequential dependencies over time.

12.2 Overview of Dynamic Factor Modeling

Dynamic factor analysis is factor analysis of single-subject multivariate time series. It constitutes a generalization of Cattell’s P-technique (Cattell, 1952) in that it takes account of lead-lag patterns in the dynamic relationships between latent factor series and observed series. In contrast, P-technique involves straightforward application of standard factor analysis to multivariate time series without accommodation of lead-lag sequential dependencies; the reader is referred to Molenaar and Nesselroade (2008) for further discussion of the domain of application of P-technique.

In what follows, bold face lower case letters denote vectors; bold face upper case letters denote matrices; an apostrophe attached to vectors or matrices denotes transposition. Let \({\mathbf{y}}({\text{t}}) = [{\text{y}}_1 ({\text{t}}),\,\,{\text{y}}_2 ({\text{t}}),\,\,...,\,{\text{y}}_{\rm p} ({\text{t}})]\)¢ be a p-variate time series, \({\text{p}} \geqslant 1\), observed at equidistant time points \({\text{t}} = 1,\,\,2,...,{\text{T}}\). The mean of y(t) at each time point t is: \({\text{E}}[{\mathbf{y}}({\text{t}})] = {{\boldsymbol{\mu} }}({\text{t}})\). Considered as function of t, μ(t) denotes the p-variate mean function (trend) of y(t). If \({{\boldsymbol{\mu} }}{\text{(t)}} = {{\boldsymbol{\mu} }}\), i.e., if the mean function is constant in time, then y(t) has a stationary mean function. The sequential covariance of y(t) between a given pair of time points t1 and t2 is defined as: \({\boldsymbol{\Sigma }}({\text{t}}_{\text{1}} ,\,\,{\text{t}}_{\text{2}} ) = {\rm cov} [{\mathbf{y}}({\text{t}}_{\text{1}} ),\,\,{\mathbf{y}}({\text{t}}_{\text{2}} )^{\prime}]\). Considered as function of 2-D time, \(\boldsymbol{\Sigma} ({\text{t}}_1 ,\,\,{\text{t}}_2 )\) denotes the (p,p)-variate covariance function of y(t). If \(\boldsymbol{\Sigma}(\text{t}_{1},\,\,{\text{t}}_{\text{2}})\) only depends upon the relative time difference \({\text{t}}_1- \,\,{\text{t}}_2= {\text{u}}\), i.e., \({\boldsymbol{\Sigma }}({\text{t}}_1 ,\,\,{\text{t}}_2 ) = {\boldsymbol{\Sigma }}({\text{t}}_1- {\text{t}}_2 ) = {\boldsymbol{\Sigma }}({\text{u}}),\,\,{\text{u}} = 0,\,\, \pm 1,\,... \pm {\text{T}} - 1\), then y(t) has stationary covariance function depending only on lag u. If both the mean function and covariance function of y(t) are stationary then y(t) is called a weakly stationary p-variate time series.

In the first publication on dynamic factor analysis in psychology the following model for weakly stationary multivariate Gaussian series was considered (Molenaar, 1985):

$$ {{\bf y}}({\rm{t}}) = \boldsymbol{\mu} + \boldsymbol{\Lambda} (0){{\boldsymbol{\eta}}}({\rm{t}}) + \boldsymbol{\Lambda} (1){\boldsymbol{\eta}}({\rm{t}} - 1) + ... + \boldsymbol{\Lambda} ({\rm{s}}){{\boldsymbol{\eta}}}({\rm{t}} - {\rm{s}}) + {{\boldsymbol{\varepsilon} }}({\rm{t}}) $$
(1a)

where y(t) is an observed p-variate time series, η(t) is a latent q-variate factor series and e(t) is a p-variate measurement error series. Because our main interest is not in the constant mean function μ, it is conveniently assumed that μ =  0. Then all time series in (1a), y(t), η(t), and e(t), are zero mean weakly stationary.

The L(u), \({\text{u}} = 0,\,\,1,...,{\text{s}}\), are (p,q)-dimensional matrices of lagged factor loadings, where s is the maximum lag. These lagged factor loadings allow for the possibility that the realization of the latent factor series η(t) at each time t not only has an instantaneous effect on y(t), but also may have delayed effects at later time points \(\ {\rm{t}} + 1,\,...,\,{\rm{t}} + {\rm{s}} \). The linear combination \(\ \boldsymbol{\Lambda} (0)\boldsymbol{\eta} ({\rm{t}}) + \boldsymbol{\Lambda} (1)\boldsymbol{\eta} ({\rm{t}} - 1) + \cdots + \boldsymbol{\Lambda} ({\rm{s}})\boldsymbol{\eta} ({\rm{t - s}}) \) is called a convolution.

For later reference the limiting case of (1a) is considered in which s = 0, i.e., the case in which there are no lagged factor loadings:

$$ {\bf{y}}({\rm{t}}) = \boldsymbol{\Lambda} (0){\boldsymbol{\eta}}({\rm{t}}) + {\boldsymbol{\varepsilon}}({\rm{t}}) $$
(1b)

Equation (1b) is a special instance of (1a). It has been assigned several labels, including state-space model (e.g., Molenaar 1985) and process factor model (e.g., Browne & Nesselroade, 2005). In what follows (1b) will be referred to as a state-space model. As will be explained shortly, (1b) has a special property not shared by (1a).

The dynamic factor model (1a) was inspired by Brillinger’s (1975) principal component analysis of multivariate weakly stationary time series. It differs from Brillinger’s approach in a number of respects, perhaps the most important of which is that in (1a) the convolution of lagged factor loadings and latent factor series is finite and only depends at each time point t upon earlier realizations \( {{\boldsymbol{\eta} }}({\rm{t}}),\,\,...,\,\,{{\boldsymbol{\eta} }}({\rm{t}} - {\rm{s}}) \) of the latent factor series, whereas in Brillinger’s model this convolution is infinite and also depends upon future realizations \( {{\boldsymbol{\eta} }}({\rm{t}} + 1),\,\,{{\boldsymbol{\eta} }}({\rm{t}} + 2) \), …. Another important difference relates to the statistical characteristics of the measurement error series in each of the two models.

To complete the definition of the dynamic factor model under consideration, the covariance functions of the time series occurring in (1a)–(1b) have to be specified. Let diag-A denote a square diagonal matrix A (all off-diagonal elements being zero). Then the covariance functions associated with the right-hand side of (1a) are:

$$ \begin{array}{l} {\rm{cov}}[{{\boldsymbol{\varepsilon} }}({\rm{t}}),\,\,{{\boldsymbol{\varepsilon} }}({\rm{t}} - {\rm{u}})'] = {\rm diag} - \boldsymbol{\theta} ({\rm{u}});\,{\rm{u}} = 0, \pm 1,... \\ {\rm{cov}}[{{\boldsymbol{\eta}}}({\rm{t}}),\,{{\boldsymbol{\eta} }}({\rm{t}} - {\rm{u}})'] = {{\boldsymbol{\Psi} }}({\rm{u}}) = 0, \pm 1,... \\ \end{array} $$
(1c)

The first equation of (1c) defines the covariance function of the measurement error process. The univariate measurement error process ek(t) associated with the kth observed univariate series yk(t), k Î {1,…,p], is allowed to have nonzero sequential covariance: cov\( [{{\boldsymbol{\varepsilon} }}_{\rm k} ({\rm{t}}),\,\,{{\boldsymbol{\varepsilon} }}_{\rm k} ({\rm{t}} - {\rm{u}})] \ne 0 \) for "u. However, measurement error processes ek(t) and em(t) associated with different observed univariate series yk(t) and \( {\rm{y}}_{\rm m} ({\rm{t}}),\,\,{\rm{k}} \ne {\rm{m}}\, \notin \,\,\{ 1,\,...,{\rm{p}}] \), are assumed to be uncorrelated at all lags u: cov\( [{{\boldsymbol{\varepsilon} }}_{\rm k} ({\rm{t}}),\,\,{{\boldsymbol{\varepsilon} }}_{\rm m} ({\rm{t}} - {\rm{u}})] = 0 \) for "u. The second equation in (1c) defines the covariance function of the latent factor series.

Some intricacies associated with (1) It was proven in Molenaar (1985) that under certain conditions the covariance function of the latent factor series defined in (1c) is not identifiable. That means that under certain conditions the variances and sequential covariances in \({{\boldsymbol{\Psi} }}({\text{u}}),\,\,{\text{u}} = 0,\,\, \pm 1,...,\) cannot be estimated, but have to be fixed a priori. The conditions concerned are twofold. Firstly, the maximum lag s of the matrices of factor loadings \( \boldsymbol{\Lambda} ({\rm{u}}),\,{\rm{u}} = 0,\,\,1,\ldots, \)s, has to be larger than zero: s > 0. Secondly, all factor loadings in \( \boldsymbol{\Lambda} ({\text{u}}),\,{\text{u}} = 0,\,\,1,..., \)s, should be free parameters. That is, the dynamic factor model should be exploratory, having no a priori pattern of fixed factor loadings.

If both these conditions obtain then the covariance function of the latent factor series has to be fixed a priori. Ψ(u), u = 0, ± 1,…, then can be fixed at any possible covariance function without affecting the goodness of fit of the model. In Molenaar (1985) the simplest covariance function for η(t) was chosen: cov\([{{\boldsymbol{\eta} }}({\text{t}}),\,\,{{\boldsymbol{\eta} }}({\text{t}} - {\text{u}})] = \delta ({\text{u}}){\mathbf{l}}_{\rm q} \), where d(u) is the Kronecker delta \( ({\rm{\delta }}({\rm{u}}) = 1) \) if \( {\rm{u}} = 0;\,\,{{\delta }}({\rm{u}}) = 0 \) if \({\text{u}} \ne 0\)) and I q is the (q,q)-dimensional identity matrix. This particular choice implies that the latent factor series lacks instantaneous as well as sequential dependencies. Accordingly, η(t) can be conceived of as a sequence of random shocks, often referred to in the engineering literature as a white noise sequence. But quite other choices are possible (cf. Molenaar & Nesselroade, 2001).

If the dynamic factor model is confirmatory, i.e., if an a priori pattern of fixed factor loadings has been specified in L(u), u = 0,1,…,s, then the covariance function of the latent factor series is identifiable. Also if s = 0, i.e., if the state space model (1b) applies, then the covariance function of the latent factor series is identifiable. In these cases Y(u), \({\text{u}} = 0,\,\, \pm 1,\,...,\) can be freely estimated or, alternatively, a parametric time series model for η(t) (and hence for it covariance function) can be considered. For instance, the latent factor series η(t) can be represented by a vector autoregression: \( {{\boldsymbol{\eta} }}({\rm{t}}) = {\bf{B}}{{\boldsymbol{\eta} }}({\rm{t}} - 1) + \boldsymbol{\zeta} ({\rm{t}}) \), where B is a (q,q)-dimensional matrix of regression coefficients and z(t) is a q-variate white noise sequence.

Given that for the state-space model (1b) the covariance function (or a parametric time series model) of the latent factor series always is identifiable, it would seem rational to restrict attention to this type of model. At least for exploratory dynamic factor analyses, this would preclude the need to have to arbitrarily fix Y(u), u = 0,±1,…, which is necessary in such applications of (1a). However, it can be shown that for certain types of psychological time series the state-space model is too restrictive. In particular when the effect of η(t) on y(t) is delayed, the state space model will be inappropriate. For these time series one needs the general dynamic factor model (1a) in which s > 0. Such delays occur, for instance, in multi-lead EEG registrations of electro-cortical brain fields caused by a finite set of underlying neural sources. The activity of the neural sources is represented by the latent factor series η(t) and the EEG registrations by the manifest series y(t). The effects of each neural source travel with finite speed along long-range axons to their target regions. Because target regions are located at different distances from a given neural source and the effects of a volley of action potentials of a neural source on the ongoing activity of target areas take time to dissipate, the relationships between η(t) and y(t) will show complex patterns of delays.

But the pattern of delayed relationships between the latent factor series and the observed series does not have to be complex in order to invalidate the state space model (1b). This will be illustrated with data simulated with the following simple dynamic 1-factor model. Let y(t) be a 5-variate time series and η(t) a univariate latent factor series. Let L(0) = [1.0, 0.9, 0.8, 0.7, 0.6]¢ and L(1) = [0, -0.5, 0, 0, 0]¢. Hence s = 1. Notice that all elements of L(1) are zero, except the lagged loading on \({\text{y}}_2 ({\text{t}}):\lambda _2 (1) =- 0.5\). Hence there only is a simple delayed effect of η(t) on y2(t). Let all measurement errors be white noise series having variance equal to \( {{\theta }}_{\rm{k}} (0) = 0.5{\rm{,}}\,\,{\rm{k}} = 1,\,...,5 \). The autoregressive model for the univariate latent factor series is: \( {{\eta }}({\rm{t}}) = 0.7{{\eta }}({\rm{t}} - 1) + \zeta ({\rm{t}}) \), where the variance of the white process noise is var\([\zeta ({\text{t}})] = 1.0\).

A 5-variate time series of length T = 400 has been generated. Although the simulation model almost is a state-space model (save for one delayed factor loading \(\lambda _2 (1) =- 0.5)\), the state-space model (1b) with univariate state process η(t) does not fit the data. Using a window width of 5 (cf. Molenaar, 1985), chi-square = 751.95, degrees of freedom = 313, prob. = 0.0; non-normed fit index = 0.93; comparative fit index = 0.93. The non-normed fit index and the comparative fit index should have values larger than 0.95 for acceptable model fits. In contrast, the general dynamic 1-factor model (1a) with s = 5 yields an acceptable fit: chi-square = 235.78, degrees of freedom = 295, prob. = 1.0; non-normed fit index = 1.0; comparative fit index = 1.0.

Alternative ways to fit (1) Analysis of stationary multivariate Gaussian time series based on the dynamic factor model (1) can proceed in various ways:

  1. 1)

    Based on the sequential covariance function, arranged in a so-called block-Toeplitz matrix (see Molenaar, 1985, for a detailed description). This can be carried out by means of commercially available structural equation modeling software. Browne and Zhang (2005, 2007) provide an alternative method for fitting a dynamic factor analysis model to a sequential autocorrelation function. Their approach, implemented in the DyFA computer program, does not use a block-Toeplitz matrix in the estimation process. It fits the model directly to the autocorrelation function without duplicating the constituent autocorrelation matrices to form a block-Toeplitz matrix. The DyFa program can be downloaded from: http://faculty.psy.ohio-state.edu/browne/software.php

  2. 2)

    Based on Expectation-Maximization of the raw data likelihood associated with state-space models (1b), where the latent factor series is estimated by means of the recursive Kalman filter (Expectation Step) and the parameters are estimated by means of multivariate regression (Maximization Step). See Hamaker, Dolan, and Molenaar (2005); Hamaker, Nesselroade, and Molenaar (2007) for applications; the software used in these applications can be obtained from: http://users.fmg.uva.nl/cdolan/

  3. 3)

    In the frequency domain, after discrete Fourier transformation. This yields a set of frequency-dependent complex-valued factor models that can subjected to standard ML factor analysis (Molenaar, 1987). The software for dynamic factor analysis in the frequency domain can be obtained from the first author. Special nonlinearly constrained variants of this approach have been developed for the purpose of neural source estimation in brain imaging (Grasman, Huizenga, Waldorp, Böcker, & Molenaar, 2005). The software concerned can be obtained from: http://users.fmg.uva.nl/rgrasman/

  4. 4)

    Rewriting the model as a state-space model, with extended state containing not only the latent factor series but also the unknown parameters. This results in a nonlinear state-space model for which the extended Kalman filter is used to estimate the extended state, including the parameters. This will be discussed further in a later section.

12.2.1 Application in Replicated Time Series Design

Dynamic factor analysis constitutes a generalization of Cattell’s P-technique (Cattell, Cattell, & Rhymer, 1947). P-technique involves application of the standard factor model to the zero-lag covariance matrix ∑(0) of an observed multivariate time series (cf. Jones & Nesselroade, 1990), whereas dynamic factor modeling involves analysis of the observed series’ complete sequential covariance function \(\boldsymbol{\Sigma} ({\text{u}}),\,{\text{u}} = 0,\,\, \pm 1\), …. Excellent recent discussions and illustrations of dynamic factor analysis of psychological time series can be found in Browne and Nesselroade (2005); Browne and Zhang (2007); Ferrer and Nesselroade (2003); Ferrer (2006); Hamaker, Dolan, and Molenaar, (2005); Kim, Zhu, Chang, Bentler, and Ernst (2007); Mumma (2004); Nesselroade, McArdle, Aggen, and Meyers (2002); Sbarra and Ferrer (2006); Shifren, Hooker, Wood, and Nesselroade (1997); and Wood and Brown (1994). Dynamic factor modeling is increasingly prominent in econometrics, see for instance Forni, Hallin, Lippi, and Reichlin (2005); Stock and Watson (2005).

In this section an innovative application of dynamic factor analysis will be presented using multivariate time series data of multiple subjects and performing new types of statistical tests to uncover nomothetic relationships underlying idiographic observations. It concerns a multi-subject dynamic factor analysis of mood change during pregnancy data is presented, using the block-Toeplitz approach introduced in Molenaar (1985). A complete description of the data is given in Lebo and Nesselroade (1978). Here only part of the data will be analyzed (we thank Dr. Michael Lebo for making the data available). Only the data of three of the five subjects will be analyzed. Moreover, only five items will be selected: Enthusiastic, Energetic, Active, Peppy, and Lively. Keeping the same numbering of subjects as in Lebo and Nesselroade (1978), the length of this 5-variate observed time series (daily measurements) is T = 112 for Subject 1, T = 110 for Subject 3, and T = 103 for Subject 5.

State space models (1b) with 2-variate latent factor series are fitted to the data of the three subjects, using the block-Toeplitz correlation matrix approach with window width of 2 (cf. Molenaar, 1985). A window width of 2 implies that the covariance function of the latent factor series can be estimated up to lag \( \pm 1\): cov\([{{\boldsymbol{\eta} }}({\text{t}}),\,{{\boldsymbol{\eta} }}(\text{t} - \text{u})^{\prime}] = \Psi ({\text{u}}),\,\,{\text{u}} = 0,\, \pm 1\). No equality constraints across subjects are imposed on the (5,2)-D matrices of factor loadings. The subject-specific patterns of free and fixed factor loadings in L(0) were determined in preliminary confirmatory oblique P-technique analyses. The measurement errors are assumed to lack sequential dependencies. No equality constraints across subjects are imposed on the zero lag covariance matrices cov\( [{{\boldsymbol{\varepsilon} }}({\rm{t}}),\,\,{{\boldsymbol{\varepsilon} }}({\rm{t}})'] = {\rm{diag}} - \Theta (0) \) of the measurement errors. In contrast, it is assumed that the sequential correlation function of the bivariate latent factor series, cor\( [{{\boldsymbol{\eta} }}({\rm{t}}),\,{{\boldsymbol{\eta} }}({\rm{t - u}})'] = \boldsymbol{\Psi} ({\rm{u}}),\,\,{\rm{u}} = 0,\, \pm 1 \), is invariant across the three subjects.

Notice that the state-space models specified above are partly subject-specific and partly invariant across subjects. No equality constraints across subjects have been imposed on the factor loadings and measurement error variances, hence ∧(0) and diag-Θ(0) are subject-specific. But the sequential correlation function of the latent factor series \(\Psi ({\text{u}}),\,\,{\text{u}} = 0,\, \pm 1\), is constrained to be invariant across the three subjects. This pattern of subject-specific factor loadings and measurement error variances in combination with invariant sequential correlation function of the latent factor series implements the new definition of measurement equivalence proposed in Nesselroade, Gerstorf, Hardy, and Ram (2007). Whereas traditional definitions of measurement equivalence require that at least the matrices of factor loadings are invariant across subjects, it is argued by Nesselroade et al. (2007) that factor loadings should be allowed to be subject-specific while correlations among factor series should be invariant across subjects.

The overall fit of the state-space models to the replicated 5-variate time series is excellent: chi-square = 114.40, degrees of freedom = 129, prob. = 0.82; non-normed fit index = 1.0; comparative fit index = 1.0. Hence the assessments of the three subjects can be considered measurement equivalent in the sense of Nesselroade et al. (2007). For Subject 1 η1(t) has significant positive factor loadings on Enthusiastic, Energetic, Active, and Lively, whereas η1(t) has zero loading on Peppy. For this subject η2(t) has unit loading on Peppy (no measurement error) and significant loading of 0.30 on Energetic. For Subject 2 η1(t) has significant positive factor loadings on Enthusiastic, Energetic, Active and Lively, whereas η1(t) has zero loading on Peppy. For this subject η2(t) has unit loading on Peppy (no measurement error) and significant loadings of 0.26 on Enthusiastic and 0.24 on Lively. Finally, for Subject 3 η1(t) has significant positive factor loadings on Energetic, Active, Peppy and Lively, whereas η1(t) has zero loading on Enthusiastic. For this subject η2(t) has unit loading on Enthusiastic (no measurement error) and a significant loading of 0.17 on Lively.

Given that η1(t) has significant positive factor loadings on four of the five items for each subject and following Lebo and Nesselroade (1978), this factor series can be interpreted as Energy. Interpretation based on the pattern of factor loadings associated with η2(t) also is unambiguous for Subjects 1 and 3—this factor series has unit loading on Peppy in combination with zero measurement error variance. Hence η2(t) for Subjects 1 and 3 could be interpreted as Peppy. But for Subject 5 η2(t) has unit loading on Enthusiastic in combination with zero measurement error variance. According to this pattern of factor loadings, η2(t) for Subject 5 should be interpreted as Enthusiastic. It therefore is problematic to assign an interpretation to η2(t) which is invariant across the three subjects, at least if this interpretation is based on the patterns of subject-specific factor loadings.

An alternative way of assigning interpretations to η1(t) and η2(t) follows from a suggestion which is more in line with the basic tenet of the new definition of measurement equivalence of Nesselroade et al. (2007). Instead of considering patterns of factors loadings, interpretations of η1(t) and η2(t) are based on the sequential correlation function of the latent factor series. Nesselroade (2007, p. 258) also suggests this alternative way of interpreting factor series, in that “… invariance might be sought at the process level by focusing on patterns of auto- and cross-regression of latent factors, for example, in individual level dynamic factor models”. The estimated sequential correlation function \(\Psi ({\text{u}}),\,\,{\text{u}} = 0,\, \pm 1\) of the latent factor series η(t), assumed to be invariant across the three subjects, has significant zero lag correlation: est.-cor\( [{{\boldsymbol{\eta} }}_1 ({\rm{t}}),\,\,{{\boldsymbol{\eta} }}_2 ({\rm{t}})] = 0.69 \). Also the autocorrelation of η1(t) at lag \( \pm 1\) is significant: est.-cor\( [{{\boldsymbol{\eta} }}_1 ({\rm{t}}),\,\,{{\boldsymbol{\eta} }}_2 ({\rm{t}} \pm 1)] = 0.19 \). The remaining elements of est.\( - {{\boldsymbol{\Psi} }}( \pm 1)\) are not significant. Consequently, η1(t) has a certain degree of stability (i.e., significant autocorrelation) and can be interpreted as Stable Energy, whereas η2(t) resembles a white noise sequence and can be interpreted as Unstable Energy.

In conclusion of this section, it has been shown that using the multi-group option in commercially available structural equation modeling software, in combination with the block-Toeplitz matrix approach introduced in Molenaar (1985), it is possible to test for equivalences across different subjects using data obtained in a replicated time series design. In this approach different subjects constitute different “groups”. In this way it is possible to detect nomothetic relationships based on idiographic data, or stated otherwise, to detect inter-individual relationships based on intra-individual variation. This approach has been illustrated by implementing the new definition of measurement equivalence proposed by Nesselroade et al. (2007). But it can be applied in many other situations, including testing for measurement equivalence according to the traditional definitions.

12.3 Nonstationary Dynamic Factor Analysis

To reiterate, the two criteria for ergodicity are stationarity in time and homogeneity across subjects. In the previous application we focused on testing for homogeneity of the sequential correlations function across three subjects. Now we turn to a consideration of stationarity; the other criterion for ergodicity. A new approach is presented to test for stationarity and model nonstationary processes. The new approach is based on a state-space model with arbitrarily time-varying (nonstationary) parameters. The model concerned is:

$$ \begin{gathered}{\mathbf{y}}({\text{t}}) =\boldsymbol{\Lambda} [\boldsymbol{\theta} ({\text{t}})]{{\boldsymbol{\eta} }}({\text{t}}) + {\mathbf{v}}({\text{t}}) \hfill \\{{\boldsymbol{\eta}}}({\text{t + 1}}) = {\text{\bf B}}[\boldsymbol{\theta} (t)]{{\boldsymbol{\eta} }}({\text{t}}) + \boldsymbol{\zeta} ({\text{t + 1}}) \hfill \\\boldsymbol{\theta} ({\text{t + 1}}) = \boldsymbol{\theta} ({\text{t}}) + \boldsymbol{\zeta} ({\text{t + 1}}) \hfill \\ \end{gathered}$$
(2a)

In (2a) y(t) denotes the observed p-variate time series; η(t) the q-variate latent factor series (state process). The first equation of (2a) shows that factor loadings in L[q(t)] depend upon a time-varying parameter-vector q(t). The second equation describes the time evolution of the state process η(t); the autoregressive weights in B[q(t)] depend upon q(t) and therefore can be arbitrarily time-varying. The third equation in (2a) describes the time-dependent variation of the unknown parameters. The r-variate parameter vector process q(t) obeys a random walk with Gaussian white noise innovations x(t). The covariance functions associated with (2a) are given in (2b):

$$\begin{array}{rcl} {\rm cov}[{\bf v}({\rm t}),\,{\bf v}({\rm t} - {\rm u})^{\prime}] &= &\delta({\rm u}){\rm diag} - {\Xi} \\ {\rm cov}[{\zeta} ({\rm t}),\,\,{\zeta} ({\rm t} - {\rm u})^{\prime}] & =& \delta({\rm u}){\rm diag} - {\Psi} \\ {\rm cov}[{\zeta} ({\rm t}),\,{\zeta} ({\rm t} - {\rm u})^{\prime}] &=& \delta({\rm u}){\rm diag}-{\Phi}\end{array}$$
(2b)

To fit the state-space model with time-varying parameters to an observed multivariate time series, use is made of a combination of the second and fourth estimation techniques mentioned at the end of section "Some intricacies associated with (1)". That is, a combination of the EM algorithm and the extended Kalman filter/smoother. First, an extended state process is defined. The extended state process consists of the original latent factor series and the time-varying parameter process: \( {\bf{x}}({\rm{t}})' = [{{\boldsymbol{\eta} }}({\rm{t}}) + {{\boldsymbol{\theta} }}({\rm{t}})'] \). Then, using the extended state process x(t), (2a) is rewritten as the following nonlinear state-space model:

$$ \begin{gathered}{\mathbf{y}}({\text{t}}) = {\mathbf{h}}{\text{[x(t),}}\,{\text{t]}} + {\mathbf{v}}{\text{(t)}} \hfill \\{\mathbf{x}}({\text{t + 1}}) = {\mathbf{f}}{\text{[}}{\mathbf{x}}{\text{(t),}}\,\,{\text{t]}} + {\mathbf{w}}{\text{(t)}} \hfill \\ \end{gathered}$$
(3)

The vector-valued nonlinear functions h[x(t),t] and f[x(t),t] consist of products of the entries of x(t). The (q + r)-dimensional innovations process w(t) is defined as the composition of the innovation processes \(\zeta ({\rm t})\) and \( \zeta ({\rm{t}}):\,{\bf{w}}({\rm{t}}'\, = [\zeta ({\rm{t}})',\,\,\zeta ({\rm{t}})'] \).

In Fig. 12.1 an illustrative result is shown of an application of this new technique to a simulated time series. A 4-variate time series has been generated by means of the state-space model with time-varying parameters. The model has a univariate latent state process (q = 1). The autoregressive coefficient \( {\bf{B}}[{{\theta }}({\rm{t}})] = {\rm{b}}({\rm{t}}) \) in the true process model for the latent state [second equation in (2a)] increases linearly from 0.0 to 0.9 over the observation interval comprising T = 100 time points. Depicted is the estimate of this autoregressive coefficient b(t) obtained by means of (3). It is clear that the estimated trajectory closely tracks the true time-varying path of this parameter.

Fig. 12.1
figure 1

EKFIS estimate of time-varying coefficient b(t) in the autoregressive model for the latent factor scores

Full size image

12.4 Discussion and Conclusion

The future of dynamic factor analysis is challenging because of the necessity to focus on the structure on intra-individual variation in the study of nonergodic psychological processes. This necessity follows directly from the classical ergodic theorems. In case subjects are heterogeneous with respect to a particular psychological process, that is, in case person-specific dynamics describe the intra-individual variation of this process, one can only obtain valid information about such non-ergodic process by means of dedicated time series analysis. In a similar vein, in case a psychological process is nonstationary, like developmental and learning processes, but also many clinical and biomedical processes, one also can only obtain valid information about such a nonergodic process by means of dedicated time series analysis.

The implications of the classical ergodic theorems have a very broad impact, not only in psychometrics and psychology but also in the biological and medical sciences. They imply that growth processes as well as disease processes have to be analyzed in organism-specific and patient-specific ways, focusing on the intra-individual variation concerned. We presently are involved in a series of pilot studies using stochastic person-specific control of day-today intra-individual variation in disease processes such as asthma, diabetes, and daily stress. In these projects dynamic factor analysis of non-stationary time series is used to track momentary changes in a disease process as function of medication dose, environmental, emotional and contingent stressors. Then, using predictive control methods based on the fitted time-varying state-space patient models, optimal medication dose is determined at each point in time in a patient-specific way. It is known that the effects of medication, in particular for diabetes and asthma, are patient-specific. Dynamic factor analysis of nonstationary multivariate time series is excellently equipped to accommodate substantial patient-specific reactions to medication and counteract the occurrence of contingent disturbances occurring under normal daily life circumstances.