Performance Analysis of an M/E _k /1 Queue with Balking and Two Service Rates Based on a Single Vacation Policy

Abstract

In this chapter, we present an analysis for an M/E _k /1 queue with balking and two service rates based on a single vacation policy. Customers are served at two different rates depending on the number of customers in the system. If customers on arrival find other customers in the system, they either decide to enter the queue or balk with a constant probability. The server takes a single vacation when the system becomes empty. We first formulate a quasi birth-and-death process for the queueing system. Then, we obtain the equilibrium condition of the system. By using the matrix-geometric solution method, we obtain the matrix-geometric form solution for the steady-state probability vectors. The computation of the boundary steady-state probability vectors is also discussed. Then, we derive explicitly performance measures of the system. Based on this performance analysis, we develop a cost model to determine numerically the system's optimal cost and optimal critical value. Finally, we perform a sensitivity analysis through numerical experiments.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

In this chapter, we consider an M/E _k /1 queueing system with balking and two service rates based on a single vacation policy. Customers are served at two different rates depending on the number of customers in the system. If customers on arrival find other customers in the system, they either decide to enter the queue or balk with a constant probability. Balking is not only a common phenomenon in queues arising in daily activities, but is also found in applications in communication systems, production line systems, and in various machine interference or repair models (see, e.g., [1], [2], and references therein).

The queueing systems with balking, or reneging, or both have been studied by many researchers. Haight [3] was the first person who considered an M/M/1 queue with balking. An M/M/1 queue with customer reneging was also proposed by Haight [4]. The combined effects of balking and reneging in an M/M/1 queue with limited waiting room and unlimited waiting room have been investigated by Ancker and Gafarian [5], [6]. They obtained the steady-state probabilities and some performance measures of the system such as the mean number of customers in the queue, the mean number of customers in the system, and the mean rate of customer loss.

Abou-El-Ata [7] extended the model in [5] to study a state-dependent M/M/1/N queue with reneging and a general balk function, where the server has two service rates depending on the number of customers in the system. They obtained the transient solution of the state probabilities. Al-Seedy [8] extended the model in [7] to a state-dependent M/E _k /1/N queue with balking. By solving the steady-state probability-difference equations, Al-Seedy [8] obtained some iterative expressions of the steady-state probabilities. A state-dependent M/M/1 queue with balking was studied by Al-Seedy and Kotb [9]. Recently, Yue, Li, and Yue [10] extended the model in [8] to a state-dependent M/E _k 1 queueing system with balking. They formulated a quasi birth-and-death (QBD) process, and obtained the steady-state probability vector and some performance measures of the system.

Similarly, queueing models with vacations have been studied by many researchers and have been found to be applicable in analyzing numerous real-world queueing situations such as flexible manufacturing systems, service systems, and telecommunication systems. Excellent surveys of queueing systems with server vacations can be found in the paper by Doshi [11] and the book by Takagi [12]. However, most of the research works on queueing systems with balking have not considered server vacations. There were only a few papers that we know of that considered queueing systems with balking and server vacations (see, e.g., [1], [13], and [14]). In this chapter, we study an M/E _k /1 queueing system with balking and single vacations.

The rest of this chapter is organized as follows. In Sect. 6.2, we formulate a QBD process and obtain the equilibrium condition for the system. In Sect. 6.3, by using a matrix-geometric solution method, we derive the explicit expression for the steady-state probability vector. We also discuss the computation of the boundary steady-state probability vectors. In Sect. 6.4, we derive explicitly some performance measures of the system such as the expected number of the customers in the system, the expected number of customers in the queue, and the mean balking rate of the system. Based on this performance analysis, we develop a cost model to determine numerically the optimal cost and optimal critical value of the system.

In Sect. 6.5, we perform sensitivity analysis through numerical experiments. Conclusions are given in Sect. 6.6.

System Model and Equilibrium Condition

In this chapter, we consider an M/E _k /1 queueing system with balking and two service rates based on a single vacation policy.

System Model

The assumptions of the system model are as follows:

• (1) Customers arrive according to a Poisson process with arrival rate λ. There is one server in the system. If customers on arrival find other customers in the system, they either decide to enter the queue with a probability β or balk with a probability 1 —β.

• (2) Customers are served on a First-Come First-Served (FCFS) basis. Once service commences, it always proceeds to completion. The service times are assumed to be distributed according to an Erlang distribution with mean kμ, _n ; that is, the service time is made up of k independent and identical exponential stages, each with mean 1/¼ _n , given by

  $$\mu _n = \left\{{\begin{array}{l} {\mu _1,n = 1,2, \cdots,r} \\ {\mu _2,n = r + 1,r + 2,\ldots.} \\ \end{array}} \right.$$

  This means that the server at each service stage has two rates, say “slow and fast,” depending on the number of customers n in the system. When the number of customers n in the system is less than or equal to the critical value r, the server has a slow service rate μ₁; otherwise, the server has a fast service rate μ ₂ (0 < μ ₁ < μ ₂ < ∞).

• (3) When the system is empty, the server goes on a vacation. If the server returns from a vacation to find customers waiting, it begins to serve those waiting customers; otherwise, the server is idle and begins serving whenever customers arrive. This type of vacation is called “single vacation”. The server's vacation time follows an exponential distribution with the vacation rate η(η > 0).

• (4) The interarrival times, service times, and vacations are mutually independent.

Equilibrium Condition

In the following, we first formulate a QBD process. Then, we provide the equilibrium condition of the system.

Let N(t) denote the number of customers in the system at time t, and let J(t) denote the service stage for the customer being served at time t (t ≥ 0). A customer goes into the first stage of the service, then progresses through the remaining stages, and must complete the last stage. Let J(t) = 0, if the server goes on vacation at time t; J(t) = i, if the server is servicing the customer and the customer goes into the ith service stage at time t; and J(t) = − 1, if the server is idle at time t. The state space of the two-dimensional process {(N(t),J(t)); t ≤ 0} is given by

$$S = \left\{{\left({0,j} \right);j = - 1,0} \right\} \cup \left\{{\left({i,j} \right);i = 0,1, \ldots,j = 1,2, \ldots,k} \right\}.$$

.

All states of this two-dimensional process are labeled in lexicographic order as follows:

$$(0,0);(0, - 1); (1,0), (1,1),\ldots, (1,k);(2,0), (2,1),\ldots, (2,k);\ldots$$

By probability analysis, the process {(N(t),J(t)); t ≤ 0} has the following infinitesimal generator.

where

$${\bf{B}}_0 = \left({\begin{array}{*{20}c} {- \left({\lambda + \eta} \right)} \\ 0 \\ \end{array}\begin{array}{*{20}c} \eta \\ {- \lambda} \\ \end{array}} \right),{\bf{C}}_0 = \left({\begin{array}{*{20}c} \lambda \\ 0 \\ \end{array}\begin{array}{*{20}c} 0 \\ \lambda \\ \end{array}\begin{array}{*{20}c} 0 \\ 0 \\ \end{array}\begin{array}{*{20}c} \ldots \\ \ldots \\ \end{array}\begin{array}{*{20}c} 0 \\ 0 \\ \end{array}} \right),$$

where B ₀ is a 2 ×2 matrix, C ₀ is a 2 × (k+ 1) matrix, A ₀ is a (k+ 1) × 2 matrix, and the other matrices are (k+ 1) × (k+ 1) matrices.

From the book written by Neuts [15], we know that {(N(t),J(t));t ≤ 0} is aQBD process. Let H = A ₂ + B ₂ + C ₁, then H can be given by

It is readily known that H is an irreducible generator. Let π = (π₀,π₁,…,π _k ) be a (k +1) -dimensional row vector of the steady-state probability of H. Then, π satisfies the linear equations: πH = 0 and πe = 1, where e=(1,1,…,1)isa column vector with (k+ 1) elements. Solving the linear equations, we get

$$\pi _0 = 0,\,\pi _i = \frac{1}{k},\,i = 1,2, \ldots,k.$$

(6.1)

By Theorem 3.1.1 in [15], the equilibrium condition of the system is given by πA ₂e s> πC ₁e. Substituting π with (6.1), we then have the equilibrium condition for the system given by

$$\frac{{k\beta \lambda}}{{\mu _2}} < 1.$$

(6.2)

Steady-State Probability Vector

From the discussion in Sect. 6.2, we know that the steady-state probability vector of Q exists under the equilibrium condition given by (6.2). In this section, we derive the explicit expression for the steady-state probability vector.

Let X = (X ₀,X _1,… X _r,X _r+1,…), where X ₀ = (x ₀,x _…1) is a row vector with two elements, and X _i= (x _{i 0} , x _{i 1} , x _{i 2} , …, x _ik ) is a row vector with (k + 1) elements, i= 1,2,….By applying the matrix-geometric solution method, the stationary probability vector is given by

$${\bf{X}}_i = {\bf{X}}_r {\bf{R}}^{i - r},\,i = r,r + 1, \ldots,$$

(6.3)

where R is the minimal nonnegative solution to the equation R ² A ² + RB ² + C ¹ =0, and the boundary steady-state probability vectors X ⁰, X ¹,…, X ^r are given by solving the following equations:

$${\bf{X}}_0 = {\bf{B}}_0 + {\bf{X}}_1 {\bf{A}}_0 = {\bf{0}},$$

(6.4)

$${\bf{X}}_0 {\bf{C}}_0 + {\bf{X}}_1 {\bf{B}}_1 + {\bf{X}}_2 {\bf{A}}_1 = {\bf{0}},$$

(6.5)

$${\bf{X}}_i {\bf{C}}_1 + {\bf{X}}_{i + 1} {\bf{B}}_1 + {\bf{X}}_{i + 2} {\bf{A}}_1 = {\bf{0}},\,i = 1,2, \ldots,r - 2,$$

(6.6)

$${\bf{X}}_{r - 1} {\bf{C}}_1 + {\bf{X}}_r \left({{\bf{B}}_1 + {\bf{RA}}_2} \right) = {\bf{0}},$$

(6.7)

$$x_0 + x_{- 1} + \mathop \sum \limits_{i = 1}^{r - 1} {\bf{X}}_i {\bf{e}} + {\bf{X}}_r \left({{\bf{I}} - {\bf{R}}} \right)^{- 1} {\rm{e}} = 1,$$

(6.8)

where e= (1,1,…1) is a column vector with (k+ 1) elements. In order to solve (6.4)−(6.8), we define the following matrices:

$${\bf{M}}_r = {\bf{I}},$$

(6.9)

$${\bf{M}}_{r - 1} = \frac{1}{{\beta \lambda}}\left({{\bf{B}}_1 + {\bf{RA}}_2} \right),$$

(6.10)

$${\bf{M}}_{r - 1} = \frac{1}{{\beta \lambda}}\left({{\bf{M}}_{i + 1} {\bf{B}}_1 + {\bf{M}}_{i + 2} {\bf{A}}_1} \right),\,i = 1,2, \ldots,r - 2,$$

(6.11)

$${\bf{M}}_0 = - \left({{\bf{M}}_1 {\bf{B}}_1 + {\bf{M}}_2 {\bf{A}}_1} \right),$$

(6.12)

where I is the (k+ 1) ×; (k+ 1) identity matrix.

Let ε1 = (1,0,0,…,0) and ε₂ = (0,1,0,…,0) be column vectors with (k+ 1) elements, respectively. Let B~₀ = (ε₁, ε₂)B ₀ be the (k+1) ×; (k+ 1) matrix. We have the following theorem.

Theorem 6.1. The solutions of (6.4)–6.8) are given by

$${\bf{X}}_i = {\bf{X}}_r {\bf{M}}_i,\,i = 1,2, \ldots,r,$$

(6.13)

$$x_0 = \frac{1}{\lambda}{\bf{X}}_r {\bf{M}}_0 \varepsilon _1,$$

(6.14)

$$x_{- 1} = \frac{1}{\lambda}{\bf{X}}_r {\bf{M}}_0 \varepsilon _2,$$

(6.15)

and X _r satisfies the following equations:

$${\bf{X}}_r \left({\frac{1}{\lambda}{\bf{M}}_0 {\bf{\tilde{B}}}_0 + {\bf{M}}_1 {\bf{A}}_1} \right) = 0,$$

(6.16)

$${\bf{X}}_r \left[{\frac{1}{\lambda}{\bf{M}}_0 \left({\varepsilon _1 + \varepsilon _2} \right) + \mathop \sum \limits_{i = 1}^{r - 1} {\bf{M}}_r {\bf{e}} + \left({{\bf{I}} - {\bf{R}}} \right)^{- 1} {\bf{e}}} \right] = 1.$$

(6.17)

Proof. Note that C ₁ is invertible and ${\bf{C}}_1^{- 1} = 1/\left({\beta \lambda} \right)$ I. We have from (6.7) that

$${\bf{X}}_{r - 1} = {\bf{X}}_r {\bf{M}}_{r - 1}.$$

(6.18)

This indicates that (6.13) holds for i = r− 1. It is obvious that (6.13) holds for i = r. Suppose that (6.13) holds for i = k + 2, k + 1; then we have from (6.6) that

$$\begin{array}{rl} {\bf{X}}_k & = - \left({{\bf{X}}_{k + 1} {\bf{B}}_1 + {\bf{X}}_{k + 2} {\bf{A}}_1} \right){\bf{C}}_1^{- 1} \\ {} & = - \frac{1}{{\beta \lambda}}{\bf{X}}_r \left({{\bf{M}}_{k + 1} {\bf{B}}_1 + {\bf{M}}_{k + 2} {\bf{A}}_1} \right) \\ {} & = {\bf{X}}_r {\bf{M}}_k. \\ \end{array}$$

(6.19)

Thus, by the inductive method, we conclude that (6.13) holds for i = 1,2,.…r. From (6.5), we have

$$\begin{array}{rl} {\bf{X}}_0 {\bf{C}}_0 & = - {\bf{X}}_r \left({{\bf{M}}_1 {\bf{B}}_1 + {\bf{M}}_2 {\bf{A}}_1} \right) \\ {} & = {\bf{X}}_r {\bf{M}}_0.\\ \end{array}$$

(6.20)

Note that C ₀ε₁ = (λ,0) and C ₀ε₂ = (0,λ) are column vectors with two elements, respectively, we get (6.14) and (6.15). Substituting (6.14) and (6.15) into (6.4) and (6.8), we get (6.16) and (6.17).

In general, it is difficult to give an exact expression of R except for a few special cases. However, the matrix R can be approximately calculated by the following iterative procedure:

• (1) R(0) = 0,

• (2) ${\bf{R}}\left({n + 1} \right) = - \left({{\bf{C}}_1 + {\bf{R}}^2 \left(n \right){\bf{A}}_2} \right){\bf{B}}_2^{- 1},\,\;\;n \ge 0.$

The proof of the convergence for this iterative algorithm is given in [15]. The matrix in the above algorithm exists, and can be explicitly given by

where a = − 1/(βλ + η) and b = − 1/(βη +μ₂).

Performance Measures and Cost Model

In this section, we give some useful performance measures of the system. Based on these performance measures, we develop a cost model to determine the optimal critical value to minimize the total expected cost per unit time.

Performance Measures

Using the steady-state probability vector X presented in Sect. 6.3, we can obtain some performance measures of the system.

Theorem 6.2.

(1) The expected number of customers in the queue is given by

$${\bf{E}}\left[ {N_q} \right] = {\bf{X}}_r \left\{{\mathop \sum \limits_{n = 1}^{r - 1} n{\bf{M}}_{n + 1} + {\bf{R}}\left[ {\left({r - 1} \right)\left({{\bf{I}} - {\bf{R}}} \right)^{- 1} + \left({{\bf{I}} - {\bf{R}}} \right)^{- 2}} \right]} \right\}{\bf{e}}.$$

(6.21)

(2) The expected number of customers in the system is given by

$${\bf{E}}\left[ N \right] = {\bf{X}}_r \left\{{\mathop \sum \limits_{n = 1}^r n{\bf{M}}_n + {\bf{R}}\left[ {r\left({{\bf{I}} - {\bf{R}}} \right)^{- 1} + \left({{\bf{I}} - {\bf{R}}} \right)^{- 2}} \right]} \right\}{\bf{e}}.$$

(6.22)

(3) The mean balking rate of the system is given by

$$BR = \left({1 - \beta} \right)\lambda \left({1 - {\bf{X}}_0 {\bf{e}}} \right),$$

(6.23)

where e = (1,1,…, 1) is a column vector with(k+ 1) elements.

(4) The probability that the server is busy is given by

$$P_B = {\bf{X}}_r \left\{{\mathop \sum \limits_{n = 1}^{r - 1} {\bf{M}}_n + \left({{\bf{I}} - {\bf{R}}} \right)^{- 1}} \right\}\delta,$$

(6.24)

where δ = (0,1,…1) is a column vector with (k+ 1) elements.

(5) The probability that the server goes on vacation is given by

$$P_V = 1 - P_B - x_{- 1}.$$

(6.25)

(6) The probability that the server is idle is given by

$$P_I = x_{- 1}.$$

(6.26)

Proof. The expected number of customers in the queue is given by

$${\bf{E}}\left[ {N_q} \right] = \mathop \sum \limits_{n = 1}^\infty \mathop \sum \limits_{i = 0}^k nx_{n + 1,i} = \mathop \sum \limits_{n = 1}^{r - 1} n{\bf{X}}_r {\bf{M}}_{n + 1} {\bf{e}} + \mathop \sum \limits_{n = r}^\infty n{\bf{X}}_r {\bf{R}}^{n - r + 1} {\bf{e}}.$$

(6.27)

Hence, we obtain (6.21) by a summation of series. The expected number of customers in the system is given by

$${\bf{E}}\left[ {N_q} \right] = \mathop \sum \limits_{n = 1}^\infty \mathop \sum \limits_{i = 0}^k nx_{n,i} = \mathop \sum \limits_{n = 1}^r n{\bf{X}}_r {\bf{M}}_n {\bf{e}} + \mathop \sum \limits_{n = r + 1}^\infty n{\bf{X}}_r {\bf{R}}^{n - r} {\bf{e}}.$$

(6.28)

Hence, we get (6.22) by a summation of series. Using the concept of Ancker and Gafarian [5], the average balking rate of the system is given by

$$BR = \mathop \sum \limits_{n = 1}^\infty \left({1 - \beta} \right)\lambda {\bf{X}}_n {\bf{e}} = \left({1 - \beta} \right)\lambda \left({1 - {\bf{X}}_0 e} \right).$$

(6.29)

The processes of the proofs for (6.24)–(6.26) are obvious, hence the proofs for (6.24)–(6.26) have been omitted. ?

Cost Model

In this subsection, we develop a steady-state expected cost function where the critical value r is a decision variable. Our objective is to determine the critical value r to minimize the total expected cost per unit time.

Let C ₁ be the cost per unit time when there are customers waiting for service, C ₂ be the cost per unit time when the server is busy, C ₃ be the cost per unit time when the server goes on vacation, C ₄ be the lost cost per unit time when customers balk, and C ₅ be the cost per unit time when the server is idle.

According to the definition of each of the cost parameters listed above, the total expected cost function per unit time is given by

$$F\left(r \right) = C_1 E\left[ {N_q} \right] + C_2 P_B + C_3 P_V + C_4 PB + C_5 P_I,$$

(6.30)

where E[N _q ], P _B , P _V , BR, and P _I are given in (6.21) and (6.23)–(6.26). The first item is the cost incurred by the customer's waiting. The fourth item is the cost incurred by the loss of a customer. The second, the third, and the last items are the costs incurred by the server.

Sensitivity Analysis

In this section, we perform a sensitivity analysis on the optimal critical value r * and its expected cost F(r*) based on changes in values of the system parameters such as the arrival rate λ, the slow service rate μ₁, the fast service rate μ₂, the vacation rate 7η, and the entering probability β. Let the distribution of the service time be a two-stage Erlang distribution, and the employed cost parameters C ₁ = 150, C ₂ = 250, C ₃ = 200, C ₄ = 300 and C ₅ = 100. The numerical results of the optimal critical value r* and its expected minimum cost F(r*) are illustrated in Figs. 6.1–6.5.

Fig 6.1

Optimal critical value r* and optimal cost F(r*) versus arrival rate γ for μ₁ = 0.2, μ₂ = 0.8, η = 0.5, and β = 0.5.

Fig 6.2

Optimal critical value r* and optimal cost F(r*) versus slow service rate γ₁ for γ = 0.1, μ₂ = 0.8, η = 0.5, and β = 0.5.

Fig 6.3

Optimal critical value r* and optimal cost F(r*) versus fast service rate μ₂ for γ = 0.1, μ₁ = 0.2, η = 0.5, and β = 0.5.

Fig 6.4

Optimal critical value r* and optimal cost F(r*) versus fast vacation rate η for γ = 0.1, μ₁ = 0.2, μ₂ = 0.8, and β = 0.5.

Fig 6.5

Optimal critical value r* and the optimal cost F(r*) versus the probability β for γ = 0.1, μ₁ = 0.2, μ₂ = 0.8, and η = 0.5.

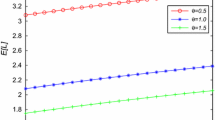
In Fig. 6.1, we fix μ₁ = 0.2, μ2 = 0.8, η = 0.5, and β = 0.5, and display the optimal critical value r* as well as its expected minimum cost F(r*) by varying the arrival rate λ. Figure 6.1 shows that: (i) the optimal critical value r* decreases as λ increases from 0.05 to 0.1, and it does not change at all when λ varies from 0.1 to 0.3; (ii) the minimum expected cost F(r*) increases as λ increases. Intuitively, λ affects r* slightly and affects F(r*) significantly.

In Fig. 6.2, we fix λ = 0.1,μ₂ = 0.8, η = 0.5, and β3 = 0.5, and display the optimal critical value r* as well as its expected minimum cost F(r*) by varying the slow service rate μ₁. Figure 6.2 shows that: (i) the optimal critical value r* increases as μ₁ increases; (ii) its minimum expected cost F(r*) decreases as μ₁ increases. Intuitively, μ₁ affects r* and F(r*) significantly.

In Fig. 6.3, we fix λ = 0.1, μ₁ = 0.2, η = 0.5, and β = 0.5, and display the optimal critical value r* as well as its expected minimum cost F(r*) by varying the fast service rate μ₂. Figure 6.3 shows that: (i) the optimal critical value r* decreases as μ₂ increases from 0.3 to 0.5, whereas it does not change at all when μ₂ varies from 0.5 to 0.8; (ii) the minimum expected cost F(r*) rarely changes when μ₂ varies from 0.3 to 0.8. Intuitively, μ₂ affects r* slightly and affects F(r*) rarely.

In Fig. 6.4, we fix λ = 0.1, μ₁ = 0.2, μ₂ = 0.8, and β = 0.5, and display the optimal critical value r* as well as its expected minimum cost F(r*) by varying the vacation rate λ. Figure 6.4 shows that: (i) the optimal critical value r* changes slightly when η varies from 0.1 to 0.8; (ii) the minimum expected cost F(r*) decreases slightly as η increases. Intuitively, η affects r* and F(r*) slightly.

In Fig. 6.5, we fix λ = 0.1, μ₁ = 0.2, μ₂ = 0.8, and η = 0.5, and display the optimal critical value r* and its expected minimum cost F(r*) by varying the entering probability β. Figure 6.5 shows that: (i) the optimal critical value r* does not change at all when β varies from 0.3 to 0.8; and (ii) the minimum expected cost F(r*) increases slightly as β increases. Intuitively, the optimal critical value r* and its expected minimum cost F(r*) are insensitive to changes in β.

It appears from Figs. 6.1–;6.5 that: (a) λ affects r* slightly, and affects F(r*) significantly; (b) μ₁ affects r* and F(r*) significantly; and (c) the optimal critical value r* and its expected minimum cost F(r*) are insensitive to changes in μ₂, η, andβ.

Conclusions

We considered an M/Ek/1 queueing system with balking and two service rates based on a single vacation policy. By using a matrix-geometric solution, we obtained the matrix solution of the steady-state probability distribution and the explicit expressions for some performance measures of the system. Based on these performance measures, we developed a cost model to determine the optimal critical value to minimize the total expected cost per unit time. Furthermore, we performed sensitivity analysis for the optimal critical value and its expected minimum cost with various parameters.