Keywords

1 From Replication to Fitness Landscapes

1.1 The Quasispecies

The interplay of replication, selection, and mutation is the basis of Darwinian evolution . Replication can be interpreted as an autocatalytic chemical reaction that, in the simplest case, is of the form

$$ {\mathbf{A}} + {\mathbf{Y}} {\mathop{\longrightarrow}\limits^{k}}2{\mathbf{Y}} , $$
(1)

where A is the substrate that is used as building material for the autocatalyst Y that is required as template for its own formation. Mutation in the form of imprecise, or error-prone, reproduction represents the universal kind of variation, which occurs in all organisms and can be sketched by a single overall reaction step:

$$ {\mathbf{A}} + {\mathbf{Y}}{\mathop{\longrightarrow}\limits^{k_{xy}}}{\mathbf{Y}} + {\mathbf{X}}. $$
(2)

Here, the mutant is denoted by X, and the rate parameters k and k xy refer to two parallel reaction channels. Reaction rates depend explicitly on the type y of the replicator Y. These rate differences are the basis for selection due to the fact that the different templates compete for the common resource A.

In the case of RNA or protein molecules, y is simply the nucleotide sequence of the molecule Y. The production of a variant X from Y, in the simplest model, occurs with a probability \( q_{xy} : = {\mathbb{P}}[{\mathbf{Y}} \to {\mathbf{X}}] \), while Y undergoes the copying reaction with a rate \( k_{0} ({\mathbf{Y}}) = \alpha f(y) \), where \( \alpha : = [{\mathbf{A}}] \) is the concentration of the building material A. Adding an unspecific outflow from the system, we arrive at a

$$ \frac{{{\text{d}}[x]}}{{{\text{d}}t}} = \sum\limits_{y} q_{xy} \alpha f(y)[y] - \varphi [x] $$
(3)

The dynamics of this system is thus described by two ingredients: the rate of copying of each type, f(x), usually referred to as its fitness, and the probabilities of specific copying errors q xy . The specific form of the flux φ plays little role for the overall dynamics as long as it is small enough not to completely drain all the replicating material from the system (Happel and Stadler 1999). In the simplest case, we may assume that the total concentration of all replicating types as well as the concentration of the building material is kept constant. This model, known as constant organization , yields the famous quasispecies equation as follows:

$$ \frac{{{\text{d}}[x]}}{{{\text{d}}t}} = \sum\limits_{y} q_{xy} f(y)[y] - \varphi [x]\quad {\text{with}}\quad \varphi = \sum\limits_{x,y} q_{xy} f(y)[y] $$
(4)

i.e., φ equals the total production of replicating types.

Since the molecular types x and y are sequences, the most common model assumes that \( \left( {\begin{array}{*{20}c} {q_{xy} = } \\ {ndp^{d} } \\ \end{array} } \right) \) where n is the sequence length, d = d xy is the number of sequence positions in which x and y differ, n is the common length of both sequences, and p is the probability of a point mutation, i.e., the exchange of a single letter, per copying event. Nearly all work on the quasispecies model has used this mutation model (Eigen 1971; Eigen et al. 1989; Eigen and Schuster 1977). Conceptually, it can be simplified further by ignoring the small probabilities of multiple mutations, simply setting \( q_{xy} = 0 \) if \( x \ne y \) differ by more than a single mutation. Sequences are “easily accessible,” i.e., adjacent, if they differ by a single (point) mutation only. This arranges the set X of sequences as the vertices of a graph, which is usually referred to as the sequence space \( (X,\tau ) \). The symbol τ denotes the accessibility structure, which here is just the edge set of graph but may, in general, be a more complicated topological structure (Flamm et al. 2007). Together with the fitness function \( f:X \to {\mathbb{R}} \), that sequence space forms the fitness landscape \( (X,\tau ,f) \).

The dynamics of a population evolving according to Eq. (4) is governed by the underlying fitness landscape . Its stationary solution

$$ \sum\limits_{y} q_{xy} f(y)[y] = \varphi [x] $$
(5)

determines the equilibrium distribution of the variants in an evolved population. In the limit of small mutation rates, where \( q_{xy} \approx 1 - pa_{xy} \) with \( a_{xy} = 1 \), if x and y are adjacent and \( p \ll 1 \), one can show that [x] is concentrated around the fitness maximum (Eigen 1971). Chapters 1, 4, and 5 in this book are concerned with the relationships of the fitness landscape (X, τ, f) and the structure of the resulting quasispecies.

1.2 Molecular Replicators

A variety of in vitro systems embody self-replication of RNA or DNA. Although template-instructed ligation can also be achieved without enzymes, these are restricted to short and usually specialized sequences (Lee et al. 1996; von Kiedrowski 1986). All copy reactions of interestingly long and diverse templates known today, however, require elaborate enzymes.

The earliest system studied in detail was based on the RNA-dependent RNA polymerase of the bacteriophage Qβ , a Levivirus. Extensive studies on the reaction kinetics of this system (Biebricher and Eigen 1988) demonstrated that the kinetic data are consistent with a many-step reaction mechanism describing the stepwise addition of nucleotides. It can be coarse-grained to a Michaelis–Menten-like overall reaction of the form

$$ {\mathbf{A}} + {\mathbf{Y}} + {\mathbf{E}}{ \leftrightharpoons }{\mathbf{A}} + {\mathbf{Y}} \cdot {\mathbf{E}} \to {\mathbf{Y}} \cdot {\mathbf{E}} \cdot {\mathbf{X}}{ \leftrightharpoons }{\mathbf{Y}} \cdot {\mathbf{E}} + {\mathbf{X}} $$
(6)

that still explains the observed three distinct regimes: exponential growth a low [Y], linear growth for intermediate replicator concentrations, and saturation by product inhibition at high concentrations. The rate constants depend strongly on the sequence of the template Y since Qβ replicase is well adapted to recognize the genomic RNA of the Qβ phage and to discriminate it from host cell sequences. Affinity to the replicase thus is an important determinant of fitness in in vitro evolution experiments with this system. Manipulation of the environment in this experimental setup has lead to the selection of widely different RNA molecules with surprising properties. SV11, for instance, is replicated from an extremely stable metastable conformation of the RNA (Biebricher and Luce 1992); a “drug-addicted” RNA was obtained in Kramer et al. (1974) by adding the intercalating dye ethidium bromide.

Enzymes that replicate nucleic acid templates effectively independent of their sequence have evolved in particular for genomic DNA templates. The discovery of the DNA polymerase chain reaction (PCR) (Mullis et al. 1986) was a milestone toward sequence independent amplification of DNA sequences in vitro. It requires, however, higher temperatures to separate the two strands of the double helical product. Since the product of template-directed replication or ligation is invariably a double strand, product inhibition cannot be entirely avoided in most systems. The simplest replication system is thus better described by

$$ {\mathbf{A}} + {\mathbf{Y}} + {\mathbf{E}} \to {\mathbf{E}} + {\mathbf{Y}} \cdot {\mathbf{Y}}\quad {\text{and}}\quad {\mathbf{Y}} \cdot {\mathbf{Y}}{ \leftrightharpoons }2{\mathbf{Y}} $$
(7)

Under the “quasi-steady state” approximation (Segel and Slemrod 1989), this model follows a modified kinetics (Wills et al. 1998)

$$ \frac{{{\text{d}}[x]}}{{{\text{d}}t}} = [x]\left( {f(x)\psi (\beta (x)[x]c) - \varphi } \right) $$
(8)

where f(x) is the fitness measures at infinite dilution, i.e., for a total concentration of replicating material \( c \to 0 \), \( \beta (x) \) is a constant derivable from the microscopic rate constants that describes the strength of product inhibition, and \( \psi (u) = 2(\sqrt {u + 1} - 1)/u \) is a function that decays like the square root of its argument. It reduces to the simple case for \( \beta (x) \to 0 \). A wide range of related mechanisms of template-directed ligation, including an experimentally studied systems based on DNA triple helices (Li and Nicolaou 1994), and the membrane-anchored mechanism suggested for the “Los Alamos Bug” artificial protocell project (Rasmussen et al. 2003) follow the same effective kinetic law. An approximation that replaces \( \psi (u) \) by \( \sqrt u \) was considered in Szathmáry and Gladkih (1989).

In contrast to the quasispecies-like models, which (apart from the mutant cloud around the “master sequence”) effectively lead to “survival of the fittest ” at least for small mutation rates, there is no selection in the parabolic growth model (Varga and Szathmáry 1997; Wills et al. 1998). More general systems with product inhibition, however, allow for cooperation of all replicators whose fitness exceeds a certain concentration-dependent threshold, which can be computed explicitly (Wills et al. 1998). Most of the experimental systems of self-replicating polymers without enzyme fall into this class, see, e.g., Plöger and Kiedrowski (2014) for a recent peptide nucleic acid system. Unless product inhibition is too strong (or concentrations become too large), these systems show selection by “extinction of the unfittest ” rather than survival of the fittest. So far, their population-level dynamics have not been explored for complex, realistic fitness landscapes.

Several enzymatic systems have been well established to amplify nucleic acid sequences, most famously the PCR (Erlich 1989). Here the product inhibition problem is solved by “thermal cycling,” i.e., a periodic increase in temperature to release product bound in duplices. An isothermal version based on T7 polymerase is the 3SR reaction (Fahy et al. 1991). A recently introduced alternative is the isothermal multiple displacement amplification (IMDA) (Luthra and Medeiros 2004). A common theme in these technologically highly relevant systems is that templates are amplified nearly independently of their sequence. This enables among other applications high-throughput DNA sequencing as well as artificial selection (Systematic Evolution of Ligands by EXponential Enrichment (SELEX)) (Ellington and Szostak 1990; Tuerk and Gold 1990). In the latter, amplification is alternated by an assay that enriches RNA or DNA molecules with desired properties, thereby effectively implementing a user-defined fitness landscape. This allowed the creation of RNA and DNA sequences with a surprisingly wide variety of both binding and enzymatic properties. A detailed mathematical analysis of the SELEX procedure and its convergence properties can be found in Levine and Nilsen-Hamilton (2007).

1.3 Quantifying Natural Fitness Landscapes

Since the volume of sequence space increases exponentially with sequence length, it has long been impossible to obtain a comprehensive picture of fitness landscapes. Nevertheless, early attempts to empirically chart at least a neighborhood of the optimal or native sequence date back almost two decades (Aita et al. 2002; Aita et al. 2000; Hayashi et al. 2006; Reetz and Sanchis 2008).

The situation has changed with the advent of micro-arrays and then deep sequencing technologies. At least for very small model systems, it has become possible to measure the relative abundance of a very large number of sequences. Comparing the sequence distribution p(x) with the distribution in the initial pool p 0(x) immediately yields the estimated

$$ f(x) \approx p(x)/p_{0} (x){\kern 1pt}. $$
(9)

It is worth noting that the fitness function cannot be inferred from the equilibrium quasispecies distribution since the latter is usually concentrated around the fittest member of the population, making it impossible to obtain data for more distant parts of the landscape.

Micro-arrays have provided a convenient means of measuring the fitness of larger samples in parallel (Lauring and Andino 2011). Instead of measuring fitness directly from an adapting population, equilibrium parameters such as RNA-protein binding constants also have been measured using micro-arrays (Rowe et al. 2010). Various sources of bias deriving from the ligation and sequencing steps must be measured and taken into account in the practical analysis of HTS-based surveys of landscapes, see, e.g., Jimenez et al. (2013) for details. Earlier work still targeted particular regions in sequence space. The fitness of all possible individual point mutants of a nine-amino acid region of yeast Hsp90 was determined in Hietpas et al. (2011). Pitt and Ferré d’Amaré (2010) mutagenized an artificial RNA ligase ribozyme and estimated the fitness in the neighborhood of the original ligase sequence from a reselected variant pool.

Various interpolation and machine learning schemes have been proposed to estimate the structure of fitness landscapes from sparse data (Romero et al. 2013; Woo and Reifman 2014). The issue, however, remains a difficult one and the problem is far from being solved. Most geometric and topological characteristics of the inferred fitness landscape, such as the number of monotonically increasing paths between ancestral and derived genotypes, the prevalence of sign epistasis, and the number of local fitness maxima, are distorted in the inferred landscape (Otwinowski and Plotkin 2014).

Most recently, small systems have been investigated in their entirety. An example is a survey the space of 24-mers selected for GTP binding (Jimenez et al. 2013), see also Athavale et al. (2014) for a recent review.

Empirical landscapes seem to differ substantially between different biological systems. DNA-protein binding landscapes (Rowe et al. 2010) have been found to be rugged, with many local optima. Protein landscape, on the other hand, seems to be at least locally smooth, “Mt. Fuji-like” (Aita et al. 2000; Lobkovsky et al. 2011) consistent with computational prediction from simple computational models (Babajide et al. 1997; Chan and Bornberg-Bauer 2002). Similar structures are observed for viral fitness landscapes, both experimentally (Lauring and Andino 2011; Woo and Reifman 2014) and in computational models (Kouyos et al. 2012). For RNA landscapes , however, there is an apparent discrepancy between the observed very rugged landscapes and the computationally predicted landscape structure (Athavale et al. 2014). We return to this issue in some detail in the next section.

A promising alternative to exhaustively covering sequence space is to associate fitness with a low-dimensional phenotype . Acevedo et al. (2014), for instance, mapped thousands of measured fitness values of mutants onto three-dimensional structures of viral proteins to explore the structure–function relationships.

1.4 Computer Models of RNA Evolution

RNA has turned out to be a particularly fruitful model to study fitness landscapes in computational models of evolution. On the one hand, it is intriguing catalytic activities and its crucial involvement in the core information metabolism of modern life forms, having lead up to the RNA world hypothesis of pre-biotic evolution (Gilbert 1986), justify detailed studies. On the other hand, nucleic acid structures have specific feature, not shared by polypeptides, which make them computationally tractable at a convenient coarse-grained resolution.

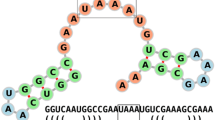
Nucleobases interact specifically through hydrogen bonding in a manner that established simple combinatorial rules of complementary base pairing (GC, AU, and GU). Paired bases form regular helical structures stabilized by π-electron interactions whose energetics are nearly perfectly additive in terms of the contributions of adjacent base pairs. The resulting secondary structures shown in Fig. 1 are thus matchings in the graph theoretical sense, which are further restricted by the non-crossing rule that excludes so-called “pseudoknots.” These simplifications result in the combinatorial model of RNA secondary structures in which the folding problem, i.e., the prediction of structure from sequence, can be solved efficiently and completely by means of dynamic programming (Zuker and Stiegler 1981). This simple model, which has been parameterized by careful thermodynamic measurements (Turner and Mathews 2010), has proved its practical relevance in thousands of applications ranging from explaining and organizing structural features of RNAs to the prediction of effects of mutations and wholesale design of functional RNAs. Far from perfect, it nevertheless captures most of the energetics of RNA folding , it describes key features of RNA folding kinetics, and it explains many of the evolutionary patterns observed in RNA. We refer to a recent book on RNA bioinformatics for details on applications and limits of the model (Gorodkin and Ruzzo 2014).

Fig. 1
figure 1

RNA folding in a nutshell. Top Folding of the yeast tRNA-Phe. The secondary structure can be computed with little effort, while the 3D structure (shown here is the PDB crystal structure 5TNA) is not easily accessible by computational methods alone. Below The algorithm of RNA folding consists of fairly simple recursion relations that construct the energy (or partition function) of a substructure on a sequence interval from i to j from smaller components. An arbitrary structure (F) begins with either an unpaired base • or a substructure enclosed by a base pair (C). In both cases, it then continues with a correspondingly shorter unconstrained structure. The second line describes the decomposition of base pair enclosed structure (C) into the three major loop types: hairpin loops, interior loops (including stacked base pairs, k = i + 1 and l = j – 1), and multi-branch loops. The last three lines correspond to the recursion for multi-branch loops, see Lorenz et al. (2011); Zuker and Stiegler (1981) for details. For each possible decomposition step, the energy of the l.h.s. structure is the sum of the energies of the r.h.s. components. These recursions require quadratic memory and cubic time in terms of the input sequence length, providing a highly efficient and exact solution of the RNA folding problem

Full size image

Instead we concentrate here on a different aspect which was explored in substantial detail almost a quarter of a century ago (Schuster et al. 1994). The efficiency of structure prediction has made it feasible to explore the sequence-structure map of RNA as a proxy for genotype–phenotype maps . Starting from the insight that genotype (sequence) is acted upon by mutation and other genetic operators while the phenotype (structure) is subject to selection, it is appealing to model biologically relevant fitness landscapes as compositions

$$ f(x) = \phi (\varPhi (x)) $$
(10)

where \( \varPhi :X \to {\mathbb{P}} \) is the genotype–phenotype map and \( \phi :{\mathbb{P}} \to {\mathbb{R}} \) is a fitness function that evaluates the phenotypes \( y \in {\mathbb{P}} \) rather than the genotype. In the case of RNA secondary structures, \( \varPhi \) is simply RNA folding as implemented, e.g., by the ViennaRNA package (Lorenz et al. 2011) and \( {\mathbb{P}} \) denotes the set of RNA secondary structures. In many circumstances, the properties of \( f:X \to {\mathbb{R}} \) are essentially determined already by the genotype–phenotype map \( \varPhi \), as in the case of RNA secondary structures.

Extensive computational studies (Fontana et al. 1991; Fontana et al. 1993; Fontana and Schuster 1998; Fontana et al. 1993; Gruener et al. 1996a, 1996b) showed the following:

  1. 1.

    A large fraction of point mutations are neutral in RNA molecules in the sense that the mutation does not change the base pairing pattern (secondary structure) of the ground state structure.

  2. 2.

    The pre-image \( \varPhi^{ - 1} (y) \), i.e., the sequences folding into a common RNA structure y, is to a first approximation homogeneously distributed among the sequences C(y) that satisfy the base pairing constraints imposed by y. Note that \( \varPhi^{ - 1} (y) \subseteq C(y) \).

  3. 3.

    As a consequence of the high degree of neutrality (1) and the approximate homogeneity (2), there are extensive so-called “neutral networks” of sequences folding into the same ground state structure. These neutral networks “percolate” through sequence space and contain neutral paths that connect sequences without detectable sequence similarity.

  4. 4.

    The neutral networks tend to be connected or at least to decompose into only a small number of very large components.

  5. 5.

    The intersection theorem (Reidys et al. 1997) guarantees that the sets \( C(y^{{\prime }} ) \) and \( C(y^{{\prime \prime }} ) \) of sequences that are compatible with two arbitrary structures \( y^{{\prime }} \) and \( y^{{\prime \prime }} \) have non-empty intersection.

  6. 6.

    The neutral networks \( \varPhi^{ - 1} (y^{{\prime }} ) \) and \( \varPhi^{ - 1} (y^{{\prime \prime }} ) \) therefore come very close to each other, and the distance of an arbitrary sequence x 0 to a sequence \( x \in \varPhi^{ - 1} (y) \) folding into y is determined essentially by the violations of the base pairing constraints in x 0 only. This property is known as shape space covering.

This rather special structure of the RNA folding map implies a diffusion-like behavior of evolving populations of RNA molecules in sequence space, which conforms to Kimura’s neutral theory (Huynen et al. 1996; Kimura 1983). It also implies constant rates of encountering novel variants along evolutionary trajectories (Huynen 1996). Thus, it explains the punctuated-equilibrium -like dynamics of RNA evolution characterized by long phases of diffusion on neutral networks interrupted by intermittent bursts of adaptive evolution when fitter mutants are encountered at the fringes of the neutral network (Huynen et al. 1996).

A beautiful illustration of these properties of the RNA folding map is the construction of a bistable ribozyme (Schultes and Bartel 2000): A single RNA folds into either of two evolutionarily unrelated ribozyme structures and catalyzes the corresponding reactions. Nevertheless, the bistable sequence has neighbors that are efficient catalysts for only one of the two alternative reactions and that are connected by neutral paths of the corresponding wild-type ribozyme.

Recent empirical work on very small RNA fitness landscapes defined by aptamer binding affinities, on the other hand, seems to be at odds with these observations and rather indicates as rugged structure without extensive paths (Athavale et al. 2014). The empirical aptamer binding landscape, however, focussed on the small subsequence actually involved in binding. This is indeed expected to be dominated by a few peaks corresponding to the best-binding motives. It forms a low-dimensional subspace that constrains the RNA molecules to those that have the binding motive but does not speak to the landscape defined by the large rest of the molecule. Computational studies indeed have shown that small sequence motives (as models of active sites or binding pockets) can be constrained without affecting the overall structure of the RNA folding map.

A different line of evidence for (nearly) neutral paths in RNA fitness landscapes comes from the comparative analysis homologous RNAs. Here we often observe a strong conservation of secondary structure while the sequence may have diverged already to beyond the detection limit (Torarinsson et al. 2006). Computational surveys with different methods have provided good evidence that this is not at all a rare phenomenon: More than 10 % of mammalian genomes are under stabilizing selection for RNA secondary structure elements, but more than 85 % of these elements are essentially unconstrained at sequence level (Smith et al. 2013). This provides a rather direct way to observe diffusive evolution on neutral networks.

2 Autocatalytic Networks

2.1 The Bioinformatics of RNA–RNA Interactions

Specific interactions among distinct RNA molecules are readily established by complementary base pairing, i.e., using the same principles that lead to the formation of intramolecular secondary structures. Conceptually straightforward (but computationally at times difficult) extensions of the secondary structure model thus also incorporate RNA–RNA interaction s. Since there is no local difference between intermolecular and intramolecular base pairs, even the same energy parameters can be used. For an in-depth discussion, we refer to Backofen (2014) for a recent review. An important issue is the concentration dependence. In thermodynamic equilibrium, setting is expressed as

$$ \frac{[AB]}{[A][B]} = K_{AB} = \frac{{Z_{AB}^{{\prime }} }}{{Z_{A} Z_{B} }} $$
(11)

where [A], [B], and [AB] are the concentrations of monomers of two types of RNAs and their dimer, respectively. The key observation is that the equilibrium constant \( K_{AB} \) can be computed directly from the sequences using the partition function versions of RNAfold \( (Z_{A} ,Z_{B} ) \) and RNAcofold or RIP (Z AB ). The correct partition function for the duplex can be expressed as \( Z_{AB}^{{\prime }} = (Z_{AB} - Z_{A} Z_{B} )e^{ - \beta e} \), where Z AB is the partition function computed directly by a cofolding approach, which also contains non-interacting conformations, and e is an initialization energy parameter capturing the additional entropic effects of forming a duplex (Bernhart et al. 2006; Dimitrov and Zuker 2004).

RNA–RNA interactions by means of canonical base pairing play an important role in post-transcriptional regulation. For example, the interaction of microRNAs with messenger RNAs and of small nucleolar RNAs with ribosomal RNAs is of this type. Similarly, it is the preferred mode of action of bacterial small RNAs. Of course, product inhibition in model systems of replicating nucleic acids is also owed to RNA–RNA binding in trans.

2.2 Replicator Networks

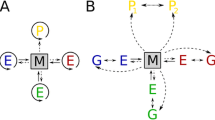
Eigen and Schuster noticed already in the late 1970s that systems of replicating molecules behave qualitatively different depending on whether the catalyst E in Eq. (7) is considered part of the environment or whether the replicators also catalyze their—or each other’s—replication (Eigen and Schuster 1979). The net reaction of such a system can be abstracted in the form

$$ {\mathbf{A}} + 2{\mathbf{Y}}{\mathop{\longrightarrow}\limits^{k}3}{\mathbf{Y}} $$
(12)

for a single self-replicator with perfect accuracy and

$$ {\mathbf{A}} + {\mathbf{Y}} + {\mathbf{Z}}{\kern 1pt} \mathop{\longrightarrow}\limits^{{q_{xy} k_{yz} }}{\mathbf{Y}} + {\mathbf{Z}} + {\mathbf{X}} $$
(13)

in the general case of cross-catalysis with imperfect copying. As in the quasispecies model, Y is the template, X, which may coincide with Y, is the product of the copy reaction, and Z is the ribozyme catalyst. The kinetic constants k yz describe the rate of copying template Y by catalyst Z. Again q xy is the mutation probability of producing the offspring X from the template Y.

The construction of an RNA replicase ribozyme that is capable of copying a broad range of templates, including itself, has been an open problem for decades, ever since the discovery that RNA molecules have catalytic activities akin to proteins. As proof of principle, an RNA ligase ribozyme (Paul and Joyce 2002) was obtained in 2002, the first RNA replicase followed in 2009 (Lincoln and Joyce 2009), and was improved stepwise (Ferretti and Joyce 2013). Earlier this year, Roberson and Joyce finally described a self-replicating ribozyme that can sustain exponential growth (Robertson and Joyce 2014). It also copies a partner ribozyme so that the coupled system is capable of Darwinian evolution. Autocatalytic self-replicators of this type are in principle capable of open-ended Darwinian evolution. Experimental exploration of the test tube models of a hypothetical RNA world comprising autonomous interacting self-replicating RNAs thus is becoming feasible.

The dynamics of such a system can again be derived from the reaction mechanism under the assumption of mass action kinetics. In the simplest instantiation, it is of the form (Stadler and Schuster 1992)

$$ \frac{{{\text{d}}[x]}}{{{\text{d}}t}} = \underbrace {{[x]\left( {\sum\limits_{z} k_{xz} [z] - \varphi } \right)}}_{\text{selection}} + \underbrace {{\sum\limits_{y,z} \left( {q_{xy} k_{y} z[y][z] - q_{yx} k_{xz} [y][z]} \right)}}_{\text{mutation}} $$
(14)

Constant organization is enforced by balancing the flux with the net production in the system, i.e., \( \varphi = \sum\nolimits_{xz} k_{xz} [x][z] \), independent of the choice of the mutation rates q xy . In the absence of mutation, \( p \to 0 \), the second term, which is proportional to the mutation rate p, vanishes. The remaining dynamical systems are known as the (quadratic) replicator equation (Schuster and Sigmund 1983). Maybe the most famous special case is the hypercycle model (Eigen and Schuster 1979). Second-order replicator equation also serves as a canonical model in game dynamics, and they are equivalent to the Lotka–Volterra equations, one of the first models of predator–prey interactions. They admit a rich mathematical theory with warrants books entirely dedicated to their analysis (Hofbauer and Sigmund 1998). More realistic reaction mechanisms again include variable levels of product inhibition . As in the quasispecies case, they are dominated by product inhibition for large total concentrations and eventually lead to global coexistence, i.e., the absence of selection. For moderate concentrations, however, complex dynamics described effectively by the catalyzed replication prevails Stadler et al. (2000).

2.3 Evolution of Autocatalytic Networks

Comparably, little is known about the evolution of sequences of autocatalytic networks. In Stadler (2002), the diffusion (in sequence space) of a population of interacting replicators has been studied. A major issue in models of this type is the assignment of the reaction rates k xy as a function of sequences of template and catalyst. This problem is analogous to the assignment of fitness values to individual sequences in the quasispecies equation. It is even more challenging, however, since (1) we now have a quadratic number of coefficients to determine and (2) virtually nothing is known about the sequence dependence of the catalytic capabilities of nucleic acids. Very simple minimal models thus have been used: In Stadler (2002), k xy is assumed to be dependent on the Hamming distance of x and y. In Forst (2000) and later in Stephan-Otto Attolini and Stadler (2006), the reaction rates were assumed to depend on the interaction structure of x and z as computed by RNAcofold. Neutrality in the interaction structure, i.e., of RNAcofold (x, z) w.r.t. mutation in either x or y, is important for evolvability in sequence space as well as the persistence of the population (Stephan-Otto Attolini and Stadler 2006). It remains unknown, however, whether this type of model is realistic even in a statistical sense. One would assume that the catalytic activity of a catalyst z on a template z depends on local interactions close to the processive site rather than on a conserved global structure.

2.4 Distributed Autocatalysis

Macromolecules that are directly self-replicating, i.e., that can copy a template including a second copy of themselves, are certainly the conceptually simplest building blocks of a self-propagating system. Since it has remained open for a long time whether RNA replicase enzymes can be constructed, alternative architectures have been explored at least theoretically. Assuming that copy machines are infeasible, systems of chemical reactions have been studied in which some of the chemical species also act as catalysts. Seminal work in this direction includes Stuart Kauffman’s string concatenation model (Kauffman 1986) or Walter Fontana’s artificial chemistry based on the lambda calculus (Fontana and Buss 1994). The key question is then to characterize closed, self-maintaining sets that collectively behave as an autocatalyst. Despite substantial progress in the mathematical and computational analysis of this class of models (Hordijk et al. 2012, 2014; Smith et al. 2014), it remains unclear whether and how they may have played a role in the origin of life. For example, it can be shown that in large chemical systems with n distinct molecular species, each molecule must catalyze \( \propto \log n \) reaction in order to make it likely to find a collective autocatalytic set (Hordijk et al. 2011). At present, no plausible material instantiation appears to be known, and it remains to be seen whether the required abundance and specificity of catalytic activities are realistic for some kind of chemistry.