General Computational Algorithms for Ab Initio Crystal Structure Prediction for Organic Molecules

Abstract

The prediction of the possible crystal structure(s) of organic molecules is an important activity for the pharmaceutical and agrochemical industries, among others, due to the prevalence of crystalline products. This chapter considers the general requirements that crystal structure prediction (CSP) methodologies need to fulfil in order to be able to achieve reliable predictions over a wide range of organic systems. It also reviews the current status of a multistage CSP methodology that has recently proved successful for a number of systems of practical interest. Emphasis is placed on recent developments that allow a reconciliation of conflicting needs for, on the one hand, accurate evaluation of the energy of a proposed crystal structure and on the other hand, comprehensive search of the energy landscape for the reliable identification of all low-energy minima. Finally, based on the experience gained from this work, current limitations and opportunities for further research in this area are identified. We also consider issues relating to the use of empirical models derived from experimental data in conjunction with ab initio CSP.

1 Introduction

Crystalline organic materials play an important role in many high-value manufacturing sectors such as the pharmaceutical, agrochemical and fine chemicals industries. For instance, the majority of active pharmaceutical ingredients (APIs) are produced and delivered as solids [1]. The propensity of medium-size organic molecules to crystallize in multiple forms (“polymorphs”) leads to significant challenges for the industry as differences in crystal structure can lead to large changes in physical properties such as solubility, dissolution rate and mechanical strength. These variations affect both manufacturing process and product effectiveness, and the appearance of a new, more stable, crystal structure of a given API can have wide-ranging effects on the availability and economic value of a drug [2]. As a result, the crystalline structure of an API has become a key element of patent protection and regulatory approval.

Given the practical importance of polymorphism and its intrinsic scientific interest, much research effort has been devoted towards increased understanding of this phenomenon and converting this understanding into methodologies for crystal structure prediction (CSP). Five blind tests for CSP have been organised by the Cambridge Crystallographic Data Centre (CCDC) since 1999 [3], providing useful benchmarks and helping to identify areas where improvements and further research are needed. While the blind tests are based on a relatively small set of compounds, the publications summarising their results [3–7] provide some evidence of progress in the development of increasingly reliable methodologies. Of particular note is the growing ability to predict the solid state behaviour of molecules of size, complexity and characteristics that are relevant to the pharmaceutical industry [8–10].

1.1 Definition and Scope of the CSP Problem

The central problem of CSP can be summarised as follows:

Given the molecular diagrams for all chemical species (neutral molecule(s) or ions) in the crystal, identify the thermodynamically most stable crystal structure at a given temperature and pressure, and also, in correct order of decreasing stability, other (metastable) crystal structures that are likely to occur in nature.

From a thermodynamic point of view, the most stable crystal structure is that with the lowest Gibbs free energy at the given temperature and pressure and, where relevant, at the given composition (crystal stoichiometry). The other structures of interest are normally metastable structures with relatively low free energy values. Mathematically, all these structures correspond to local minima of the Gibbs free energy surface, with the global (i.e. lowest) minimum determining the most stable structure.

The scope of the CSP methodology presented in this chapter includes both single-component crystals and co-crystals, hydrates, solvates and salts. It is applicable to flexible molecules of a size typical of “small molecule” pharmaceuticals (i.e. up to several hundred daltons) and to crystals in all space groups, without restriction on the number of molecules in the asymmetric unit (any Z′ > 0). Examples of such systems are presented in Fig. 1.

Fig. 1

Examples of systems of interest to current CSP methodologies. (a) “Molecule XX”, fifth CCDC blind test target [4] (benzyl-(4-(4-methyl-5-(p-tolylsulfonyl)-1,3-thiazol-2-yl)phenyl)carbamate). (b) Bristol-Myers Squibb’s BMS-488043 [11] (1-[4-(benzoyl)piperazin-1-yl]-2-(4,7-dimethoxy-1H-pyrrolo[5,4-c]pyridin-3-yl)ethane-1,2-dione). (c) Pfizer’s Axitinib anti-cancer drug [12] (N-methyl-2-[[3-[(E)-2-pyridin-2-ylethenyl]-1H-indazol-6-yl]sulfanyl]benzamide). (d) (R)-1-phenyl-2-(4-methylphenyl)ethylammonium-(S)-mandelate salt [13]. (e) Progesterone-pyrene (2:1) co-crystal [14]

1.2 Requirements for General CSP Methodologies

In this chapter we are interested in CSP methodologies that can be applied reliably in a systematic and standardised manner across the wide range of systems defined above. Based on the experience of the last two decades of activity in CSP, but also from other areas of model-based science and engineering, this translates into certain key requirements:

• A reliable CSP methodology must be based on automated algorithms, with minimal need for user intervention beyond the specification of the problem to be tackled. This in turn limits the scope for reliance on previous experience and/or similarities with other systems, which in any case can lead to erroneous results as small changes in molecular structure can result in significant changes in the crystal energy landscape [15], including the number of local minima and the detailed geometry of the crystal packing. Statistical analysis of experimental evidence, such as that contained in the Cambridge Structural Database (CSD), does not always provide reliable guidance and sometimes leads to potentially relevant stable/metastable crystal structures being missed. In past blind tests [7], this was one of the stated reasons for failing to produce successful matches to experimental crystal structures.

• It must have a consistent, fundamental physical basis that can be applied uniformly to wide classes of systems. In our experience, “special tricks” (e.g. case-by-case adjustments of intermolecular interactions), whilst sometimes successful at reproducing known experimental structures for specific molecules, lead to limited predictive capability. They also sometimes obscure the real issues that need to be addressed, acting as an obstacle to gaining the understanding that is necessary for the advancement of the field.

• It must produce consistently reliable solutions, e.g. as judged in terms of its ability to reproduce experimental evidence for different systems, predicting all known polymorphs with low energy ranking. However, such an assessment is complicated by the practical unfeasibility of conducting exhaustive experimental “polymorph screening” programs. While it is always possible to recognise that a CSP approach has failed to identify an experimental structure or to find its correct stability rank, it is harder to draw conclusions when it predicts structures that have not been observed experimentally [16, 17].

• It must take advantage of current state-of-the-art computer hardware and software within practicable cost. There is little benefit in a computationally efficient CSP methodology that is capable of producing results within minutes on a desktop computer if it fails to identify significant low-energy structures. While there is certainly a higher cost in securing access to advanced distributed computing hardware, this is usually negligible compared to the cost of a missed polymorph.

Current methodologies for crystal structure prediction pay varying degrees of attention to the above requirements. In any case, the blind test papers and several recent reviews provide a good overview of current thinking and of the tools that have been developed [18–25].

1.3 The CrystalPredictor and CrystalOptimizer Algorithms

As much of the relevant background is readily available elsewhere, our focus in this chapter is to provide a coherent overview of a CSP methodology that we have been developing over the past 15 years in the Centre for Process Systems Engineering at Imperial College London. Consistent with the principles outlined above, our methodology, algorithms and workflow have been heavily influenced by a systems engineering background and have drawn on experience in developing algorithms and implementing them in large software codes in other areas. We aim to provide a CSP algorithm designer’s perspective, setting out the general considerations that need to be taken into account in a manner that can hopefully be of value to designers of future algorithms. The approach presented is one concrete example of what can be achieved given current constraints on underlying software infrastructure (e.g. for quantum-mechanical (QM) calculations) and on computing hardware.

Our work has focused on two general-purpose algorithms and codes, namely CrystalPredictor [26, 27] which performs a global search of the crystal energy landscape, and CrystalOptimizer [28] which performs a local energy minimisation starting from a given structure. Over the last few years, these algorithms have been applied both by us and more extensively by others to a relatively wide variety of systems including single compound crystals [15, 29–36], co-crystals [14, 37–39], including chiral co-crystals [40, 41], hydrates and solvates [42, 43]. The codes have also been used separately, e.g. Gelbrich et al. [44] report a recent application of CrystalOptimizer to the study of four polymorphs of methyl paraben.

The CrystalPredictor algorithm has been in use since the third blind test [4–6], while CrystalOptimizer has been available only since the latest (fifth) blind test [4], where it was applied successfully to the prediction of the crystal structure of target molecule XX [9], one the largest and most flexible molecules considered in a blind test to date. Both codes have been evolving continually in terms both of the range of systems to which they are applicable and of their computational efficiency.

1.4 Structure of Chapter

Section 2 of this chapter reviews the main considerations that need to be taken into account in the design of CSP algorithms. Based on this background, Sect. 3 provides a description of the key elements of our methodology in its most recent form. Finally, Sect. 4 seeks to draw some general conclusions based on the experience gathered from a fairly consistent application of this methodology across a relatively wide range of systems over the last few years. In particular, we consider the limitations of our current approach and identify areas of further work that are needed to address them. We also consider issues relating to the use of empirical models derived from experimental data in conjunction with ab initio CSP.

2 Key Considerations in the Design of CSP Algorithms

2.1 Mathematical Formulation of the CSP Problem

A crystal formed from one or more chemical species is a periodic structure defined in terms of its space group, the size and shape of the unit cell, the numbers of molecules of each species within the unit cell and the positions of their atoms. For example, Fig. 2 shows the unit cell of crystalline Form II of piracetam ((2-oxo-1-pyrrolidinyl)acetamide). In this case, there is only one molecule per unit cell, and the crystal structure is also characterised by the Cartesian coordinates of the atoms within this cell. For the purposes of this chapter, we are interested in systems that extend practically infinitely in each direction and are free of all defects.

Fig. 2

Lattice vectors (a, b, c) and angles (α, β, γ) defining the unit cell in the Form II crystal of piracetam [45]

The crystal structures of practical interest are those which are stable or metastable at the given temperature, pressure and composition; as such they correspond to local minima in the free energy surface with relatively low values of the Gibbs free energy, G, which can be expressed as:

$$ \min G=U+ pV- TS $$

(1)

where U denotes the internal energy of the crystal, p the pressure, V the volume, T the temperature and S the entropy on a molar basis. The minimisation is carried out with respect to the variables defining the crystal structure as listed above.

The entropic contribution −TS is typically omitted in the context of CSP as it is difficult to compute reliably and at low computational cost for systems of practical interest. The magnitude of this term is expected to be small compared to the enthalpic contribution at the relatively low temperatures of interest [46]; on the other hand, omission of the term is often cited as one of the possible reasons for failing to predict experimentally observed structures accurately. In any case, any predictions made by CSP methodologies making use of this simplification in principle relate to a temperature of 0 K.

The work term +pV is also often omitted from the free energy expression. It is worth mentioning that, in contrast to the –TS term, this term can be computed with negligible cost, and is sometimes important for predictive accuracy at high pressures.

Based on the above approximations, the energy function used to judge stability of a crystal structure is usually reduced to the lattice internal energy U, typically computed with reference to the gas-phase internal energy U ^gas _i of the crystal’s constituents i:

$$ \min \Delta G\cong U-{\displaystyle \sum_i{x}_i{U}_i^{\mathrm{gas}}} $$

(2)

where x _i is the molar fraction of chemical species i in the crystal structure. Posing the CSP problem in this manner reduces it to two important sub-problems, namely the accurate computation of this energy for a proposed crystal structure and the reliable identification of all local minima, or at least those with relatively low energy values. We consider these in more detail in the two sections below.

2.2 Accurate Computation of Lattice Energy

In principle the lattice energy can be computed through QM computations, as is the case in periodic solid-state density functional theory approaches, e.g. [47, 48]. However, such an approach is computationally very demanding, to an extent that may currently limit its applicability with respect to the size of the system to which it can be applied successfully; its theoretical rigour is also somewhat compromised by the need to use an empirical model of dispersion interactions. The alternative is the “classical” approach to computing lattice energy which distinguishes intramolecular and pair-wise intermolecular contributions, with the latter being further divided into repulsive, dispersive and electrostatic terms. Moreover, starting with a reference unit cell, one has to add up the interactions of its molecules with those in all other cells within an infinite periodic structure.

Most organic molecules of interest to CSP have a non-negligible degree of molecular flexibility which allows them to deform in the closely packed crystalline environment. In turn, the deformation induces changes to their intramolecular energy, but also to two other aspects that affect intermolecular interactions within the crystal, namely the relative positioning of the atoms in the molecule and their electronic density field. Overall, then, stable/metastable crystal structures represent a trade-off between the increase in intramolecular energy caused by deformations from in vacuo conformations and the overall energy decrease due to attractive and repulsive intermolecular interactions. This is illustrated in Fig. 3 for xylitol (1,2,3,4,5-pentapentanol) using a model that includes separate contributions to the lattice energy from the intra- and intermolecular interactions (cf. Sect. 3). Intramolecular forces tend to favour larger values of the torsions in the range considered (cf. Fig. 3d where the minimum energy point occurs at the top right corner). On the other hand, intermolecular forces drive torsion angle H1-O1-C1-C2 to a low value, and torsion angle O1-C1-C2-C3 towards an intermediate value of approximately 180° (cf. Fig. 3c where the minimum energy point is near the middle of the left vertical axis). These opposite effects are of similar magnitudes, resulting in the torsions adopting intermediate values in the experimentally observed conformation (cf. Fig. 3b).

Fig. 3

Effect of conformational flexibility on the energetics of xylitol. (a) Molecular conformation of xylitol in the experimental crystal structure [49], with blue arrows denoting the two torsional angles being considered here. (b) Lattice energy map as a function of the two angles. (c) Intermolecular energy map. (d) Intramolecular energy map. The open circle on each map denotes the values of the torsions in the experimentally observed crystal

The classical approach to lattice energy computation is common to most current CSP approaches. Notwithstanding the approximations that are already inherent in the classical calculations, what is not always appreciated is the very significant extent to which even relatively small inaccuracies in them affect the quality of crystal structure predictions, especially when considering relative stability rankings as a measure of success. Potential pitfalls include:

• Inaccuracies in Intramolecular Energy Calculation

These may arise either from failing to take account of all the conformational degrees of freedom that are substantially affected by the crystalline environment, or from approximations in the calculation of the intramolecular energy for a given conformation (e.g. via the use of inappropriate empirical force fields).

• Inaccuracies in Pairwise Intermolecular Interactions—Electrostatic Contributions

Analysis of blind test results (for example for Molecule VIII [19]) indicates that partial charges do not provide a sufficiently accurate representation of the electrostatic field, and one has to resort to more complex alternatives such as off-centre charges [50] or distributed multipoles [51, 52]. These classical electrostatic descriptions are often derived from gas-phase isolated-molecule QM calculations and therefore ignore the effects of polarisability, which can sometimes lead to inaccurate ranking, especially for polar crystals. Approaches aiming to address this issue include the use of gas-phase calculations on dimers [53], or of continuum polarisable models for the isolated-molecule calculations [54]. Developments in more accurate atom-atom potentials also hold promise in this area [55, 56].

• Inaccuracies in Pairwise Intermolecular Interactions—Dispersion/Repulsion Contributions

Given the difficulty in their ab initio computation, the contributions of repulsion/dispersion interactions are usually computed via empirical potentials fitted to experimental data [57–63]. A potential pitfall in this context is that the values of the repulsion/dispersion potential parameters derived from such an exercise depend on what other terms are included in the lattice energy (e.g. intramolecular and/or intermolecular electrostatic contributions) and on precisely how each such term is computed (e.g. whether electrostatic contributions are accounted for in terms of partial charges or distributed multipoles, and the level of theory employed in the QM isolated-molecule calculations used to derive these partial charges/multipoles). For example, the commonly used parameters from [60, 61, 63] were estimated assuming perfectly rigid molecules, with electrostatic interactions computed via atomic charges derived from HF/6-31G** QM calculations. Therefore, these parameter values are not necessarily consistent with more recent CSP techniques that take account of molecular flexibility and/or employ distributed multipoles derived from QM computations at much higher levels of theory.

• Errors in Summation of Intermolecular Interactions Over Infinite Periodic Structures

The importance of efficiently and accurately computing these summations is generally well understood, and techniques such as Ewald summations [64] are routinely used to calculate conditionally convergent electrostatic sums such as charge–charge interactions. However, the quality of practical implementations varies widely. For example, cut-off distances for determining which terms to include in these summations are often set to inappropriately low values, and/or are applied to distances between centres of mass (rather than individual atoms) of the molecules involved – even when the size of the molecule is a significant fraction of the cut-off distance itself; in the latter case, at least some of the terms omitted from the summation relate to pairs of atoms that are much closer to each other than centre-of-mass distances suggest.

2.3 Identification of Local Minima on the Lattice Energy Surface

Addressing the issues identified above is clearly important for ensuring an accurate calculation of the lattice energy. The next area of concern is ensuring that the crystal structures predicted are local minima on the energy surface. This may not be the case if the optimisation algorithm used for energy minimisation converges to points that are not true local minima. Such failures may be caused by using algorithms, such as simplex [65], which do not make use of the values of the partial derivatives of the energy with respect to the crystal structure decision variables, and consequently exhibit slow convergence. More recent work had tended to avoid this problem by using gradient-based optimisation algorithms [66]; nevertheless, failure may still occur because of inaccurate values of these partial derivatives (e.g. when they are approximated via finite difference perturbations).

Ensuring that any crystal structures obtained are true local minima does not necessarily guarantee that all such structures of practical relevance are identified. The standard approach for identifying multiple local minima is based on generating a large number of structures which are used as initial points for local energy minimisation along the lines described above. Mathematically, it can be shown that such an approach is guaranteed to identify all local minima provided an infinite number of initial points are generated in a manner that sufficiently covers the space of decision variables. The more practical question is how many structures need to be generated in order to provide a reasonably high probability of identification of all structures of interest. Some relevant insight is provided in Fig. 4 which shows the local minima identified during the global search phase for the ROY molecule [36]. Even for such a relatively small molecule, there are several thousands of local minima, many hundreds of which would be of interest as potential starting points for a refinement using a more accurate lattice energy model. Given that there is currently no technique which can selectively and directly identify only relatively low-energy structures, it seems that the desired degree of reliability in CSP can be achieved only by generating very large numbers (in the order of tens or hundreds of thousands) of candidates.

Fig. 4

Local minima of lattice energy surface for ROY molecule (5-methyl-2-[(2-nitrophenyl)amino]-3-thiophenecarbonitrile, [67]) identified by global search. (a) Energy vs density diagram; each point corresponds to a unique local minimum on the lattice energy surface. (b) Cumulative number of unique local minima identified vs energy difference from the global minimum

Insufficient exploration of the space of possible crystal structures may also arise in more subtle ways as a result of the introduction of artificial constraints during the global search. A common pitfall is to base the search on a finite number of rigid molecular conformations generated a priori by fixing some of the key flexible degrees of freedom (e.g. torsion angles) to specific sets of values. This “multiple rigid-body searches” approach avoids the need to handle molecular flexibility during the global search. However, whilst this approach can be successful in specific cases (cf. the “RCM” algorithm reported in [9]), its outcome is highly dependent upon the specific choice and indeed the total number of rigid structures tested; for highly flexible molecules, comprehensive coverage of the crystal structure space may be achievable only via a very large number of global searches, each based on a different rigid conformation. Moreover, taken together, these rigid-body global searches may result in many more unique structures than a single flexible search: two or more neighbouring but ostensibly distinct local minima may relax into a single one if the molecules are allowed to deform continuously under the intermolecular forces exerted on them. Not taking advantage of this relaxation effect during the global search stage invariably results in a higher number of structures that need to be analysed at the refinement stage, and consequently a higher computational load.

2.4 Implications for CSP Algorithm Design

The analysis presented above suggests that taking shortcuts in the accurate calculation and minimisation of crystal energy in an attempt to reduce computational complexity may be detrimental to the quality of the prediction, as are attempts to sample only a small part of the decision space (e.g. by using only hundreds or thousands of initial points in the global search). Such “savings” may prove highly counter-productive in applications (e.g. in the pharmaceutical industry) where failing to identify a low-energy polymorph or identifying too many fictitious ones can have serious implications. Accordingly, one needs to aim for algorithms that attempt to maximise reliability of prediction within currently available computational power.

The challenge for the CSP algorithm designer is how to reconcile the need for very accurate evaluation of energy and its partial derivatives for the purposes of local minimisation of lattice energy, with the extremely large number of such minimisations that have to be carried out during the search for low-energy structures. A practical way of achieving this is via a two-stage procedure where the global search is performed using a relatively simpler and computationally less expensive energy model. This allows a much smaller number of promising structures to be identified which can then serve as starting points for refinement via local minimisation using a more detailed model.

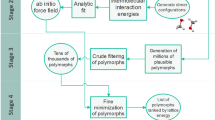
The two-stage approach to ab initio CSP is illustrated schematically in Fig. 5. It takes as input the stoichiometry of the crystalline phase and the molecular connectivity diagrams for the relevant chemical species, and produces as output the crystal structure with the lowest (globally minimum) lattice energy as well as other crystal structures that correspond to local lattice energy minima with energy values close to the global minimum.

Fig. 5

Multistage approach for CSP, illustrated for molecule BMS-488043 (cf. Fig. 1b)

In practice it is usually necessary to have an additional “Stage 0” dedicated to the study of each individual species in order to:

• Identify important aspects of its molecular flexibility (e.g. the set of torsional angles that are likely to undergo significant deformation in the crystalline environment, and the likely range of any such deformation).

• Determine an appropriate level of theory of QM calculations (e.g. via comparison with any available experimental data on its gas-phase conformation or any already known polymorphs for crystals formed by it).

In some CSP methodologies the information necessary for computing intramolecular energy and/or intermolecular electrostatic contributions during Stages 1 and 2 is also generated via QM calculations during this Stage 0. Alternatively, these QM calculations may be performed “on-the-fly” when necessary during Stages 1 and 2 (see Sect. 3.3).

The multistage approach to CSP has been widely adopted [18, 25, 38, 68] and has been successfully used in the blind tests of crystal structure prediction [3–7, 9]. Its success hinges on the hypothesis that relatively simple models of the energy surface can provide energy minima whose geometry is in reasonably good agreement with that of energy minima on a more accurate surface – even if the actual energy values differ significantly, in both absolute and relative terms, between the simpler and the more rigorous models. The approach comes with its own potential pitfalls: for example, using too simplistic an energy model at the global search phase may result in some of the structures of interest either being missed altogether or being ranked so high in crystal energy that they are not selected for subsequent refinement. Therefore, the global search phase also exhibits an accuracy vs computational cost trade-off, and the way the balance between these two is struck differs significantly between algorithms.

3 The CrystalPredictor and CrystalOptimizer CSP Algorithms

The CrystalPredictor and CrystalOptimizer algorithms (cf. Sect. 1.3) are aimed, respectively, at the global search and refinement stages of the general methodology described in Fig. 5. They are designed to be applicable to crystal structures which belong, in principle,¹ to any space group and which involve any number of chemical species of the same or different types within the asymmetric unit.

Based on the analysis presented in Sect. 2, and in order to ensure the maximum degree of consistency between the two algorithms, their overall design philosophy can be summarized as follows:

• In CrystalOptimizer, use the highest degree of accuracy in lattice energy computation that can be practically deployed at the refinement stage.

• In CrystalPredictor, apply the above subject to the minimal set of simplifications that are necessary to accommodate the additional computational complexity of the global search.

Inevitably, the practical implications of these general principles have been changing over the years, reflecting advances in our ability to describe efficiently and accurately various terms in the energy function. In this section we discuss the current state of the algorithms and their implementation in computer code.

3.1 Molecular Descriptions

The description of the molecular conformation is a key element of any CSP methodology. In CrystalPredictor and CrystalOptimizer each chemical entity in the crystal is assumed to be flexible with respect to all conformational degrees of freedom (CDFs), including torsion angles, bond angles and bond lengths.

In general, we divide the CDFs into two different sets²:

• The independent CDFs, θ, are those which are affected directly by intermolecular interactions in the crystalline environment.

• The dependent CDFs, $\overline{\theta}$, always assume values that minimise the intramolecular energy of an isolated molecule for given values of θ; therefore $\overline{\theta}=\overline{\theta}\left(\theta \right)$.

By spanning the whole range from an empty set θ (i.e. a rigid molecule calculation) to an empty set $\overline{\theta}$ (i.e. a fully atomistic computation), the above partitioning provides a mechanism for adjusting the number of degrees of freedom that have to be manipulated during the energy minimisation (see Sect. 3.2). More specifically, it allows us to employ different degrees of molecular flexibility between the global search and refinement stages.

In earlier applications of our CSP methodology, θ would typically include only the more flexible torsion angles while $\overline{\theta}$ would comprise the remaining torsion angles, as well as bond angles and lengths. However, with increasing computational capability and more efficient ways of computing intramolecular energy contributions (see Sect. 3.3), one can afford to shift the balance from $\overline{\theta}$ to θ, taking direct account of a wider range of torsion angles and even some bond angles, especially during the refinement stage. A number of examples employing extended sets of independent CDFs θ, including fully atomistic computations, were reported in [28].

3.2 The Lattice Energy Minimisation Problem

The lattice energy minimisation problem is formulated in terms of the following independent decision variables:

• The unit cell lattice lengths and angles, collectively denoted by X

• The positions of the centres of mass and the orientation of the chemical entities within the unit cell, collectively denoted by β

• The independent CDFs, θ, of the chemical entities

As already mentioned, the dependent CDFs $\overline{\theta}$ can be computed as functions of the independent ones, i.e. $\overline{\theta}\left(\theta \right)$ via minimisation of the intramolecular energy, i.e.

$$ \overline{\theta}\left(\theta \right)= \arg \min {}_{\overline{\theta}}{U}^{\mathrm{intra}}\left(\overline{\theta},\theta \right) $$

(3)

carried out as an isolated-molecule QM calculation. The latter also produces the information necessary for deriving an appropriate finite-dimensional description Q(θ) of the molecule's electrostatic field in terms of charges or distributed multipoles [52, 69]. The CDFs θ and $\overline{\theta}$ can also be used in conjunction with the molecular positioning variables β to determine the Cartesian coordinates Y of all atoms within a central unit cell, i.e. $Y=Y\left(\theta, \overline{\theta},\beta \right)$. Finally, Y together with the unit cell parameters X determines the atomic positions in all periodic images of the central unit cell, which are required for the calculation of intermolecular energy contributions.

Overall, the lattice energy minimisation problem in both CrystalPredictor and CrystalOptimizer is formulated mathematically as³

$$ { \min}_{X,\beta, \theta }\ U\left(X,\beta, \theta \right)\equiv \Delta {U}^{\mathrm{intra}}\left(\theta, \overline{\theta}\right)+{U}^e\left(Q,Y,X\right)+{U}^{\mathrm{rd}}\left(Y,X\right) $$

(4)

where ΔU ^intra represents the intramolecular energy contribution (after subtraction of the gas-phase internal energy of the chemical species in the crystal) and U ^e and U ^rd represent the intermolecular electrostatic and repulsion/dispersion contributions. Note that, in the interests of clarity, the above expression does not show explicitly the direct and indirect functional dependence of the quantities $\overline{\theta},Q,Y$ on the independent decision variables X, β, θ.

3.3 Accounting for Molecular Flexibility During Lattice Energy Minimisation

The evaluation of the intramolecular contribution $\Delta {U}^{\mathrm{intra}}\left(\theta, \overline{\theta}\right)$ in the above objective function can be done via a standard QM minimisation of configurational energy at given (fixed) values of θ. In general, such isolated-molecule calculations can provide the accuracy required for modelling the deformation of the molecular structure and energy within the crystal [70], although neglecting intramolecular dispersion can lead to inaccuracies for highly flexible molecules [71].

In principle this QM calculation could be embedded directly within the overall energy minimisation algorithm, as implemented in the DMAFlex algorithm [72]. This has the added advantage of also producing consistent values of the dependent CDFs $\overline{\theta}$, thereby allowing correct evaluation of atomic positions Y within the central unit cell, and consequently of the interatomic distances that are needed for the correct calculation of intermolecular contributions U ^e and U ^rd at each iteration. It also allows the derivation of consistent electrostatic descriptions Q which are also needed for the accurate evaluation of the intermolecular electrostatic contributions, U ^e.

The obvious difficulty that arises from embedding an expensive QM calculation within an iterative optimisation procedure is one of computational cost, and this severely limits the number of independent CDFs that can be handled in practice. An alternative would be to replace the QM calculations by molecular mechanics intramolecular potentials (cf. the use of the DREIDING and COMPASS potentials in the RCM approach reported in [9]). Such techniques can approximate the effects of θ on ΔU ^intra to a varying degree of accuracy; however, they do not take account of the secondary effects on intermolecular contributions arising from the effects of θ on $\overline{\theta}$ and Q. Overall, there is some doubt regarding the suitability of such models for CSP [19, 68].

A different way of addressing the above difficulties is via the use of pre-constructed interpolants for ΔU ^intra (and, in principle, $\overline{\theta}$ and Q) based on a multi-dimensional grid of values of θ. An example of such an approach was the restricted multidimensional Hermite interpolants used in earlier versions of CrystalPredictor [27]. However, the size of the required grid effectively imposed a limit on the number of independent CDFs that could be handled to typically 3–6 torsion angles depending on the complexity of the molecule(s) under consideration. For molecules exhibiting higher degrees of flexibility, one had to resort to artificial approximations, such as grouping the flexible torsion angles into multiple, supposedly non-interacting groups, and then constructing the interpolants using QM calculations based on surrogate simpler molecules, each involving a different group of torsions. For example, in the case of molecule XX of the fifth blind test, the six flexible torsion angles considered during the global search were decomposed into two “independent” groups (of three angles each) located at either end of the molecule; the QM calculations were then performed using two simpler surrogate molecules derived from the original molecule (cf. Sect. 2.1 in [9]). While in this case the global search was ultimately successful in identifying a structure corresponding to the experimentally observed crystal, in general such an approach is cumbersome, involves elements of subjective judgment and may not be applicable in cases where the torsion angles interact more closely with each other; all these factors make it less than ideal, especially in the context of the general principles and requirements set out in Sect. 1.2.

In view of the above, the approach used in the most recent versions of our algorithms is based on Local Approximate Models (LAMs) [28]. LAMs are essentially multidimensional quadratic Taylor expansions of the functions $\Delta {U}^{\mathrm{intra}}\left(\theta \right)\equiv { \min}_{\overline{\theta}}{U}^{\mathrm{intra}}\left(\overline{\theta},,,\theta \right)-{U}^{\mathrm{gas}}$ and $\overline{\theta}\left(\theta \right)\equiv \arg \min {}_{\overline{\theta}}{U}^{\mathrm{intra}}\left(\overline{\theta},,,\theta \right)$, and multidimensional linear Taylor expansions of the functions ${Q}^{*}\left(\theta \right)\equiv Q\left(\overline{\theta},,,\theta \right)$. As their name implies, they are local approximations constructed around certain points θ ^[1], θ ^[2], θ ^[3] … in the space of the independent CDFs θ. Because of the continuity and differentiability of the functions $\Delta {U}^{\mathrm{intra}}\left(\theta \right),\overline{\theta}\left(\theta \right),{Q}^{*}\left(\theta \right)$, each LAM can be guaranteed to be accurate within a required tolerance within a finite non-zero volume surrounding the point at which it was derived. Consequently, in principle the entire θ-domain of interest can be covered with a finite number of LAMs. In practice the range of applicability of LAMs for each molecule of interest is determined based on test calculations at Stage 0 of the methodology of Fig. 5.

The use of LAMs can provide accurate values of ΔU ^intra(θ), $\overline{\theta}\left(\theta \right)$ and Q*(θ) for the computation of the lattice energy function at minimal cost. It may also potentially improve the performance of the optimisation algorithm as LAMs are not subject to the numerical noise that may arise because of the iterative nature of the QM calculations. However, certain adjustments need to be made to the optimisation algorithm to account for the discontinuities that may arise as the iterates move from one LAM to a neighbouring one.

LAMs were originally introduced in the context of CrystalOptimizer [28]. In this case the θ-domain of interest cannot normally be determined a priori, and therefore the sequence of Taylor expansion points θ ^[1], θ ^[2], θ ^[3] … is determined “on-the-fly” during the optimisation iterations. This is illustrated schematically in Fig. 6 for a hypothetical molecule involving two independent CDFs, θ ₁ and θ ₂. Once a LAM is derived, it is kept in memory even if the optimisation iteration moves out of its range of applicability; this allows the LAM to be re-used should the optimisation iterates return to within range at a later state of the optimisation iterations (cf. the green point in Fig. 6). Moreover, at the end of the calculation, the relevant QM results that have been used to derive LAMs are stored in persistent storage (“LAM databases”), thereby allowing them to be re-used in future CSP calculations involving this particular molecule.

Fig. 6

Use of LAMs during lattice energy minimisation by CrystalOptimizer for a molecule involving two independent CDFs θ ₁ and θ ₂. The points and solid arrows indicate the progress of the optimisation iterations in the two-dimensional [θ ₁, θ ₂] domain. Large red circles indicate points at which new LAMs have to be derived, while the smaller circles indicate other iterates at which an existing LAM can be used. The dashed rectangles indicate the limits of applicability of each LAM; these are usually expressed in terms of ranges ± Δθ which are established at Stage 0 of the procedure in Fig. 5

The introduction of LAMs in CrystalOptimizer over the last 3 years has significantly increased the range of molecular flexibility that can be handled from only a few (typically no more than six) torsional angles to large numbers of torsion and bond angles and indeed all the way to fully atomistic calculations [28]. For example, the successful prediction of molecule XX in the fifth blind test involved treating 14 torsion angles and 5 bond angles as independent CDFs (cf. the “FCC” approach reported in [9]).

The benefits realized from the use of LAMs in CrystalOptimizer and also the experience gained with the application of earlier versions of CrystalPredictor to the global searches undertaken in the context of the fifth blind test [4, 9] and other challenging systems [36] have motivated the introduction of LAMs in CrystalPredictor [27]. In this case, the θ-domain of interest is known a priori since the global search algorithm (see Sect. 3.5.3) will, by design, cover the entire allowable space of θ, as well as those of the other optimisation decision variables X and β. Therefore, in this case there is no advantage in computing the LAMs on-the-fly during the search; instead, it is more efficient to compute them before the start of the global search based on a regular grid, as illustrated in Fig. 7.⁴ This recent development has made it possible to consider much higher degrees of molecular flexibility during the global search without the need for ad hoc approximations such as the molecular decomposition described earlier.

Fig. 7

LAMs for use by global search in CrystalPredictor for a molecule involving two independent CDFs θ ₁ and θ ₂. LAMS are derived at points (indicated by the large red circles) placed on a regular grid defined over the θ-domain of interest [θ ₁ ^min,θ ₁ ^max] × [θ ₂ ^min,θ ₂ ^max]. The dashed rectangles indicate the limits of applicability of each LAM; these are usually expressed in terms of ranges ± Δθ which are established at Stage 0 of the procedure in Fig. 5

3.4 Intermolecular Contributions to the Lattice Energy

Both CrystalPredictor and CrystalOptimizer calculate the intermolecular electrostatic contributions to the lattice energy using finite representations of the electrostatic potential determined via isolated-molecule QM computations (cf. Sect. 3.3). The main difference between the two codes is in the form of this finite representation. In the interest of computational efficiency during the global search, CrystalPredictor employs simple charges located at the atomic positions. On the other hand, in order to ensure higher accuracy during the crystal structure refinement stage, CrystalOptimizer makes use of distributed multipoles, placing an expansion comprising charge, dipole, quadrupole, octupole and hexadecapole terms at each atomic position. The expansion is derived directly from the isolated molecule wavefunction [52] using the GDMA [69] program. Distributed multipole moments have been shown to be successful in predicting the highly directional (anisotropic) lone-pair interactions, π–π stacking in aromatic rings and hydrogen bond geometries in molecular organic crystals [73–75].

CrystalPredictor and CrystalOptimizer employ empirical isotropic potentials for the computation of repulsion/dispersion contributions to the lattice energy. The energy contribution arising from a pair of atoms (i,i′) located at a distance r from each other is given by the Buckingham potential [76]:

$$ {U}_{i{i}^{\prime }}(r)={A}_{i{i}^{\prime }}{e}^{-{B}_{i{i}^{\prime }}r}-\frac{C_{i{i}^{\prime }}}{r^6} $$

(5)

where ${A}_{i{i}^{\prime }},{B}_{i{i}^{\prime }},{C}_{i{i}^{\prime }}\kern0.5em$ are given parameters. For atoms of the same type (i.e. i = i′), the values of the latter are taken from [62]; for unlike pairs (i′ ≠ i), they are computed via the combining rules:

$$ {A}_{i{i}^{\prime }}=\sqrt[2]{A_{ii}{A}_{i^{\prime }{i}^{\prime }}};\kern1em {B}_{i{i}^{\prime }}=\frac{B_{ii}+{B}_{i^{\prime }{i}^{\prime }}}{2};\kern1em {C}_{i{i}^{\prime }}=\sqrt[2]{C_{ii}{C}_{i^{\prime }{i}^{\prime }}} $$

(6)

The summations of intermolecular atom-atom interactions between the central unit cell and its neighbouring cells are handled via a combination of direct and Ewald [64] summations.

3.5 The Global Search Algorithm in CrystalPredictor

CrystalPredictor performs a global search by generating very large numbers of structures, each one of which may be used as an initial guess for a local minimisation of the lattice energy function (cf. Sect. 3.2). The key aspects of this algorithm are described below.

3.5.1 Exploitation of Space Group Symmetry

Physically, any crystal structure will have to belong to one of the 230 crystallographic space groups. For a given space group, only a subset of the optimisation decision variables X, β, θ may be independent, while the rest can be determined via space group symmetry relations. In practical terms this means that the global search for this particular space group only needs to explore the space of the independent subset, thereby improving the coverage of the decision space that can be achieved with any given number of candidates.

In its current implementation, CrystalPredictor generates candidate structures in 59 space groups chosen among those most frequently encountered in the CSD. The total number of structures to be generated is specified by the user, and so is the distribution of these structures among the 59 space groups. Typical choices include the numbers of structures generated being either the same for all space groups, or in direct proportion to the space groups’ frequency of occurrence in the CSD.

3.5.2 Search Domains for Conformational Variables

The domain of independent CDFs θ (cf. Sect. 3.2) that needs to be searched is an important aspect of the global search algorithm given the complexity and cost associated with handling the effects of these variables on both intramolecular and intermolecular energy contributions (cf. Sect. 3.3). For example, the size of the domain [θ ₁ ^min, θ ₁ ^max] × [θ ₂ ^min, θ ₂ ^max] illustrated in Fig. 7 directly determines the number of LAMs that are needed to cover it, which is an important consideration given the fact that the construction of each LAM requires a computationally expensive isolated-molecule QM calculation.

In view of the above, establishing appropriate ranges of the independent CDFs for each chemical entity that appears in the crystal is an important part of the preliminary conformational analysis carried out at Stage 0 of the algorithm of Fig. 5. Typically, this involves varying each independent CDF θ around its value in the in vacuo conformation of the molecule while keeping all other θ constant at their in vacuo values. The variations that are assumed to be relevant for CSP purposes are those which increase intramolecular energy by up to a given threshold (typically +20 kJ/mol) from its minimum value at the in vacuo conformation.

Overall, the above procedure establishes the range of interest for each independent CDF θ _i in terms of lower and upper bounds [θ _i ^min,θ _i ^max] . The θ-domain of interest is assumed to be the Cartesian product [θ ₁ ^min,θ ₁ ^max] × [θ ₂ ^min,θ ₂ ^max] × [θ ₃ ^min,θ ₃ ^max] × … . Theoretically, the one-dimensional scans used to determine this could result in inadvertently excluding certain combinations of multiple θ _i that would result in intramolecular energy increases below the specified threshold. However, this has not been found to be a problem in practice; this may be a result of setting the threshold at a conservatively high value.

It is worth noting that, in some cases, the values of interest may belong to multiple ranges that are disjoint from each other, e.g. [a, b] and [c, d] with c > b. In such cases, the CrystalPredictor global search is applied separately to each range. If more than one independent CDF has multiple ranges, then the search needs to be applied to each combination of the ranges of these CDFs.

3.5.3 Generation of Candidate Structures

An important decision in any global search algorithm is the precise way in which candidate points are generated over the space of independent variables being searched. Typical choices include creating points on a uniform grid in multidimensional space, or as random samples from a uniform probability distribution (the Monte–Carlo approach). CrystalPredictor [26, 27] makes use of deterministic low-discrepancy sequences [77]. These normally lead to better coverage of the search space for any given number of points being generated.

By way of illustration, Fig. 8 shows 225 points being placed on a two-dimensional search space according to the 3 schemes mentioned above. By construction, the low-discrepancy sequence approach (cf. Fig. 8c) places each new point so as to maximise a measure of distance from all previous points; this leads to better coverage of the domain than that achievable using random samples (cf. Fig. 8b). Moreover, the projection of each point onto each of the axes corresponds to a distinct value of each decision variable, i.e. no two points in the low-discrepancy sequence in Fig. 8c have the same abscissa or ordinate; in practical terms this means that the search samples 225 distinct values of each variable in the search space, as compared with only 15 distinct values in the uniform grid case of Fig. 8a. A further advantage of low-discrepancy sequences over uniform grids is that the final number of candidate points does not have to be decided a priori. Should the initial search be deemed to be insufficient for whatever reason, more points can be added and optimally placed with respect to all previously generated points.

Fig. 8

Different schemes for candidate point generation during global search. (a) Uniform grid. (b) Random points drawn from uniform probability distributions. (c) Low-discrepancy sequences

3.5.4 Local Minimisation of Lattice Energy

The crystal structures generated by the approach described in Sect. 3.5.3 are used as starting points for minimisation of the lattice energy function. In practice, before doing this, CrystalPredictor applies a pre-screening based on density, lattice energy and steric hindrance criteria, aimed at eliminating from further consideration any structures that are clearly unrealistic.

The minimisation of lattice energy, subject to the symmetry constraints determined by the space group currently under consideration (cf. Sect. 3.5.1) and simple bounds on the decision variables, is performed via a sequential quadratic programming (SQP) algorithm [66]. For efficiency and robustness, the algorithm makes use of exact first-order derivatives of the objective function and the constraints, determined via analytical differentiation and application of the chain rule on the dependent quantities $\overline{\theta}\left(\theta \right),Q\left(\theta \right),Y\left(\theta, \overline{\theta},\beta \right)$.

The CrystalPredictor code is designed to use distributed computing environments involving arbitrarily large numbers of processors for the simultaneous minimisation of multiple structures.

3.5.5 Post-Processing of Generated Structures

The successful execution of CrystalPredictor typically results in a large number of structures, each of which is a local minimum of the lattice energy within a given space group. Given the even larger number of initial candidate structures that are generated and minimised, not all of these final structures will be unique. Accordingly, CrystalOptimizer applies a clustering step intended to remove any duplicate structures among the final set based on their lattice energy, density and interatomic distances.

Finally, because of the space group symmetry constraints, it is possible that a structure is a local minimum only with respect to the space group under which it was generated but only a saddle point as far as the lattice energy surface is concerned. This is assessed by generating the corresponding Hessian matrix of the lattice energy via centered finite differences and evaluating its eigenvalues. For a true local minimum, all of these have to be positive; if the Hessian is found to have one or more zero or negative eigenvalues, then a small perturbation is applied to this structure and it is then used as a starting point for a lattice energy minimisation without any space symmetry constraints. This leads to a lower-energy structure that is a true local minimum on the lattice energy surface.

3.6 Crystal Structure Refinement Via CrystalOptimizer

The crystal structures of lowest energy determined at the end of the CrystalPredictor global search stage (cf. Sect. 3.5.5) are selected for refinement by CrystalOptimizer using a more detailed model of lattice energy. One common criterion for determining whether a given structure is to be refined is based on the difference between the structure’s lattice energy and the globally minimum lattice energy determined during the search, with typical cut-off points being placed at around +10–20 kJ/mol. Alternatively, a fixed number of structures (e.g. the lowest 1,000) may be chosen for refinement. Inevitably, there is a degree of subjective judgment in both of the above criteria, the overall objective being to apply refinement to the minimum possible number of structures but without leaving out any polymorphs that are likely to occur in nature. In general, the number of structures that need to be refined becomes lower as more physical detail is added to the lattice energy computation during the global search.

At the fundamental level, CrystalOptimizer employs a very similar lattice energy description as CrystalPredictor with two important differences:

• Molecular flexibility: both algorithms employ the concept of partitioning CDFs into independent θ and dependent $\overline{\theta}$ (cf. Sect. 3.1) and the LAMs described in Sect. 3.3. However, in order to achieve higher accuracy, CrystalOptimizer calculations typically involve more independent and fewer dependent CDFs. Because of the use of LAMs, the incremental computational cost is usually acceptable, especially given the relatively few structures that have to be refined.

• Intermolecular electrostatic interactions: as has already been stated, CrystalPredictor uses atomic charges while CrystalOptimizer employs distributed multipole expansions.

At the implementational level, the minimisation of lattice energy in CrystalOptimizer is unconstrained: there is little advantage in explicitly enforcing space group symmetry constraints in order to reduce the number of independent decision variables during the optimisation. The space groups of the final structures can be determined by a posteriori analysis using tools such as PLATON [78].

Finally, CrystalOptimizer poses the lattice energy minimisation as a bilevel optimisation problem of the form

$$ { \min}_{\theta}\left(\Delta {U}^{\mathrm{intra}}\left[\theta, \overline{\theta}\left(\theta \right)\right]+{U}_{*}^{\mathrm{inter}}\left[\theta, \overline{\theta}\left(\theta \right),Q\left(\theta \right)\right]\right) $$

(7)

where the function U ^inter_* is the intermolecular energy corresponding to the minimum lattice energy crystal incorporating rigid molecule(s) described by CDFs $\theta, \overline{\theta}$ and distributed multipole expansions Q, i.e.

$$ {U}_{*}^{\mathrm{inter}}\left[\theta, \overline{\theta},Q\right]\equiv { \min}_{X,\beta}\left({U}^e\left[Q,Y\left(\theta, \overline{\theta},\beta \right),X\right]+{U}^{\mathrm{rd}}\left[Y\left(\theta, \overline{\theta},\beta \right),X\right]\right). $$

(8)

Thus, the bilevel optimisation problem comprises:

• An outer optimisation problem in the independent CDFs θ

• An inner optimisation problem in the unit cell parameters X and molecular positioning variables β.

CrystalOptimizer employs a quasi-Newton algorithm for the solution of the outer problem, and the DMACRYS code [79, 80] for the solution of the inner problem. The partial derivatives of the function U ^inter_* are obtained via centered finite differences.

The application of the refinement algorithm to the structures selected at the end of the global search stage may result in the same structure being generated more than once. This often arises because the additional molecular flexibility taken into account by CrystalOptimizer allows two or more structures identified by CrystalPredictor as being distinct to relax into the same structure. Accordingly, a clustering algorithm based on the root mean square deviation in the 15-molecule coordination sphere [81] is applied to eliminate any crystallographically identical structures. This finally leaves the list of distinct structures that are reported to the user in ascending order of lattice energies as potential polymorphs.

4 Concluding Remarks

The methodology presented in this chapter is applicable to the prediction of a wide range of crystal structures of organic molecules, including those involving highly flexible molecules and containing multiple molecules (of the same or different types) or ions in the asymmetric unit.

Based on a two-stage global search/refinement approach, the methodology incorporates some major recent advances such as the use of low-discrepancy sequences for the systematic coverage of the space of decision variables during the global search, the efficient and accurate handling of molecular flexibility during both the global search and the refinement stages via LAMs and the accurate description of electrostatic interactions via distributed multipole expansions at the refinement stage. The CrystalPredictor and CrystalOptimizer codes are based on a careful implementation of these ideas, together with efficient numerical optimisation algorithms and exploitation of modern distributed computing resources.

4.1 Predictive Performance of CSP Methodology

There is currently a growing body of experience (cf. the references mentioned in Sect. 1.3) on the performance of these codes on a range of systems; some of this experience has been gained under blind test conditions. It may be worth noting in this context that, as the codes have been evolving over the last decade, results reported in different publications may have been obtained with different versions. However, an improvement in applicability and predictive accuracy is clearly discernible over this period, and we have now reached a point where, for example, we can usefully study molecules of relevance to the pharmaceutical or agrochemical industries.

Although the predictive performance of the methodology varies from one case to another, we believe the following statements to be a fair general representation of the current state of the technology to the extent that this has been explored both by us and by others:

• [S1] Experimentally observed crystal structures are generally identified successfully.

• [S2] In general, the accuracy of structure reproduction is reasonably good for crystals involving a single chemical species, and less good for co-crystals, salts and hydrates.

• [S3] Experimentally observed structures are generally predicted to have low rank (i.e. high relative stability).

• [S4] For systems where multiple crystal structures have been identified experimentally (cf. the ROY molecule [36]), the predicted stability ranking is not always correct.

• [S5] Low-energy structures that have not (yet) been identified experimentally are often also reported, and some of them may be more stable than the experimentally observed ones.

4.2 Errors and Approximations in CSP Methodology

At the fundamental level, our CSP approach incorporates a number of approximations, including:

• The use of a lattice enthalpy⁵ criterion, i.e. the omission of entropic contributions from the Gibbs free energy.

• The separation of lattice energy into intramolecular and intermolecular electronic and repulsive/dispersive contributions.

• The calculation of the intermolecular contributions as sums of pairwise interactions.

• The use of finite descriptions of electronic charge density based on isolated molecule calculations, and not taking account of polarisability effects.

• The use of empirical isotropic repulsion/dispersion potentials.

At a less fundamental, but potentially also important, level the application of the methodology to a particular system may be subject to practical limitations relating to:

• The level of theory of QM calculations that can be employed for a given chemical species within practical computational limits.

• The partitioning between independent and dependent CDFs.

• The use of empirical repulsion/dispersion potential parameters that were estimated from experimental data using molecular descriptions and lattice energy models which were different to those used by our methodology (e.g. in accounting for molecular flexibility, in the description of electrostatic interactions, and in the QM level of theory); we shall return to consider this issue in more detail in Sect. 4.4.

4.3 The Free Energy Residual Term

Mathematically, we can summarize the discussion of Sect. 4.2 via the following expression for the Gibbs free energy, G, of the crystal structure:

$$ G(x)=\widehat{G}\kern-0.2em (x)+\mathcal{E}(x) $$

(9)

where x is the set of variables defining the crystal structure, $\widehat{G}$ is the free energy approximation that is computed⁶ by a CSP methodology and $\mathcal{E}$ is a residual term that combines the errors from all the approximations, both physical and mathematical/numerical, listed in Sect. 4.2.

To date we have not reached firm conclusions regarding the relative importance of these approximations in the context of our methodology and their relation to observations [S1]–[S5]. However, some of these factors (e.g. the effects of polarisability or of anisotropic repulsion/dispersion interactions) have been studied in the CSP literature, and it would be useful to repeat this type of analysis with the more detailed energy model presented here. From the general mathematical and algorithmic perspectives:

• [S1] indicates that the molecular representations (e.g. in terms of flexibility), the nature and extent of the global search and the criteria used for selecting the crystal structures to be refined are generally satisfactory.

• [S2] suggests that, at least for crystals comprising single chemical species and notwithstanding the various approximations listed in Sect. 4.2, the local minima of the computed lattice energy function are close to true minima of the Gibbs free energy. Thus, the local sensitivities (gradients) of the residual term $\mathcal{E}$ with respect to the variables x are likely to be significantly smaller than the gradients of the computed free energy $\widehat{G}$, i.e.:

$$ \left\Vert \frac{\partial \mathcal{E}}{\partial x}\right\Vert \ll \left\Vert \frac{\partial \widehat{G}}{\partial x}\right\Vert \Rightarrow \frac{\partial G}{\partial x}\approx \frac{\partial \widehat{G}}{\partial x}. $$

(10)

On the other hand, the term $\frac{\partial \mathcal{E}}{\partial x}$ may be more significant for crystals involving multiple types of chemical species.

• [S4] indicates that the errors $\mathcal{E}$ depend on the variables x to an extent sufficient to alter the relative stability order of two crystal structures x ₁ and x ₂, both of which correspond to local minima, i.e. $\widehat{G}\kern-0.2em \left({x}_1\right)<\widehat{\mathrm{G}}\kern-0.2em \left({x}_2\right)$ while G(x ₁) > G(x ₂).

One practical implication of the above analysis is that, at least in some cases, it may be useful to:

• 1. Use our CSP methodology as a way of identifying, with reasonable accuracy, a small number n of (likely) stable structures x _k ,  k = 1, …, n, and their corresponding energy values ${\widehat{G}}_k$.

• 2. Keep these structures fixed at the values x _k and apply to them more computationally demanding calculations in order to compute more accurate values ${\widehat{G}}_k^{\prime }$.

• 3. Re-rank the structures x _k according to the new values ${\widehat{G}}_k^{\prime }$.

Overall, such a procedure may lead to a more accurate ranking of structures x _k ,  k = 1, …, n at a relatively moderate cost and without actually introducing additional complex calculations within the optimisation carried out at the refinement stage. Examples of a posteriori calculations that could be applied at step 2 include QM calculations at very high levels of theory, and the use of harmonic approximation techniques for estimating the entropic contributions to the free energy [82].

4.4 Combining Experimental Information and Ab Initio CSP

The free energy residual term $\mathcal{E}$ also provides a useful way of thinking about the potential role of experimental information and empirical models derived from it in CSP. We note that any method for constructing an ab initio approximation of free energy, irrespective of its accuracy, is likely to have a non-zero residual, $\mathcal{E}$, and this will inevitably lead to non-zero deviations between predictions and available experimental data. Therefore, a more accurate estimate of the free energy may be achievable by assuming an empirical parameterized functional form, $\mathcal{E}\left(x,\alpha \right)$, i.e.

$$ G(x)=\widehat{G}\kern-0.2em (x)+\mathcal{E}\left(x,\alpha \right) $$

(11)

and then using the experimental data to estimate the parameters α so as to minimise some measure of the deviation between data and predictions.

In fact, the use of empirical “repulsion/dispersion” potentials (cf. Sect. 3.4) may be interpreted as one example of the introduction of a residual term. In particular, equations (5) and (6) essentially define the functional form of a parameterized residual function $\mathcal{E}\left(x,\alpha \right)$, where the set of parameters α comprises the interaction parameters A _ii , B _ii and C _ii for pairs of atoms of type i. Interestingly, the analysis presented above indicates that:

• Albeit ostensibly intended to account for repulsion/dispersion interactions, this residual term actually acts as an all-purpose “garbage bin”, attempting to capture all errors and approximations listed in Sect. 4.2, some of which may be at least as important as repulsion/dispersion.

• The values of the parameters α obtained by any experimental data fitting procedure will depend on the form of the computed energy term $\widehat{G}\kern-0.2em (x)$ used for this procedure; using them in conjunction with a different $\widehat{G}\kern-0.2em (x)$ is, to say the least, questionable.

• If the above considerations are not taken into account properly, the use of more sophisticated calculations⁷ in an attempt to mitigate the effects of some of the approximations listed in Sect. 4.2 may be ineffective or even counterproductive. For example, employing higher levels of theory in QM calculations may sometimes lead to a worse quality of predictions.

Finally, it could be argued that the immediate objective of introducing any empirical function $\mathcal{E}\left(x,\alpha \right)$ should be to improve CSP accuracy for a specific system of interest. Therefore it would make sense to estimate the parameters α using experimental data that are more directly relevant to the system of interest, in conjunction with the same model $\widehat{G}\kern-0.2em (x)$ as the one that will be used for carrying out the CSP. Examples of appropriate experimental data would include already resolved polymorphs for the same system, or indeed structures in the CSD arising from similar molecules. We note that such an approach would be substantially different to the common practice of using information in the CSD to provide qualitative guidance as to likely high-level features (e.g. packing motifs) in crystal structures; instead, parameter estimation would extract quantitative lower-level information on energetic contributions that would complement the ab initio computed energy $\widehat{G}\kern-0.2em (x)$ in the context of formal CSP algorithms. We believe that this area, and the fundamental and practical challenges associated with it, constitute a fruitful subject for further research.