Dispersion Corrected Hartree–Fock and Density Functional Theory for Organic Crystal Structure Prediction

Abstract

We present and evaluate dispersion corrected Hartree–Fock (HF) and Density Functional Theory (DFT) based quantum chemical methods for organic crystal structure prediction. The necessity of correcting for missing long-range electron correlation, also known as van der Waals (vdW) interaction, is pointed out and some methodological issues such as inclusion of three-body dispersion terms are discussed. One of the most efficient and widely used methods is the semi-classical dispersion correction D3. Its applicability for the calculation of sublimation energies is investigated for the benchmark set X23 consisting of 23 small organic crystals. For PBE-D3 the mean absolute deviation (MAD) is below the estimated experimental uncertainty of 1.3 kcal/mol. For two larger π-systems, the equilibrium crystal geometry is investigated and very good agreement with experimental data is found. Since these calculations are carried out with huge plane-wave basis sets they are rather time consuming and routinely applicable only to systems with less than about 200 atoms in the unit cell. Aiming at crystal structure prediction, which involves screening of many structures, a pre-sorting with faster methods is mandatory. Small, atom-centered basis sets can speed up the computation significantly but they suffer greatly from basis set errors. We present the recently developed geometrical counterpoise correction gCP. It is a fast semi-empirical method which corrects for most of the inter- and intramolecular basis set superposition error. For HF calculations with nearly minimal basis sets, we additionally correct for short-range basis incompleteness. We combine all three terms in the HF-3c denoted scheme which performs very well for the X23 sublimation energies with an MAD of only 1.5 kcal/mol, which is close to the huge basis set DFT-D3 result.

1 Introduction

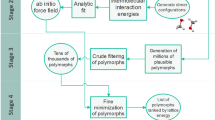
Aiming at organic crystal structure prediction, two competing requirements for the utilized theoretical method exist. On the one hand, the calculation of crystal energies has to be accurate enough to distinguish between different polymorphs. This involves an accurate account of inter- as well as intramolecular interactions in various geometrical situations. On the other hand, each single computation (energy including the corresponding derivatives for geometry optimization or frequency calculation) has to be fast enough to sample all space groups under consideration (and possibly different molecular conformations) in a reasonable time [1–5]. Typically, one presorts the systems with a fast method and investigates the energetically lowest ones with a more accurate (but more costly) method. For the inclusion of zero point vibrational energy (ZPVE) contributions a medium quality level is often sufficient. A corresponding algorithm is sketched in Fig. 1. The generation of the initial structure (denoted as sample space groups) is an important issue, but will not be discussed in this chapter. Here we focus on the different electronic structure calculations, denoted by the quadratic framed steps in Fig. 1. We present dispersion corrected Density Functional Theory (DFT-D3) as a possible high-quality method with medium computational cost and dispersion corrected Hartree–Fock (HF) with semi-empirical basis error corrections (HF-3c) as a faster method with medium quality.

Fig. 1

A typical crystal structure prediction algorithm [1]. First, the optimum electronic crystal energy E _el is calculated with a fast, medium quality method. Second, the more costly second derivatives for the electronically lowest structures in a certain energy interval (Δ) are calculated to get the zero point vibrational energy E _ZPVE. Finally, the electronic energy E ^'_el is re-calculated for the energetically lowest structures in a (different) energy interval (Δ′) with a more accurate method. The data from step two can be finally used also to estimate thermal and entropic corrections

Density Functional Theory (DFT) is the “work horse” for many applications in chemistry and physics and still an active research field of general interest [6–9]. In many covalently bound (periodic and non-periodic) systems, DFT provides a very good compromise between accuracy and computational cost. However, common generalized gradient approximated (GGA) functionals are not capable of describing long-range electron correlation, a.k.a. the London dispersion interaction [10–13]. This dispersion term can be empirically defined as the attractive part of the van der Waals-type interaction between atoms and molecules that are not directly bonded to each other. For the physically correct description of molecular crystals, dispersion interactions are crucial [14, 15]. In the last decade, several well-established methods for including dispersion interactions into DFT were developed. For an overview and reviews of the different approaches, see, e.g., [16–25] and references therein. Virtual orbital dependent (e.g., random phase approximation, RPA [26]) and fragment based (e.g., symmetry adapted perturbation theory, SAPT [27]) methods are not discussed further here because they are currently not routinely applicable to larger molecular crystals. For the alternative combination of accurate molecular quantum chemistry calculations for crystal fragments with force-fields and subsequent periodic extension see, e.g., [28, 29].

Here we focus on the atom-pairwise dispersion correction D3 [30, 31] coupled with periodic electronic structure theory. The D3 scheme incorporates non-empirical, chemical environment-dependent dispersion coefficients, and for dense systems a non-additive Axilrod–Teller–Muto three-body dispersion term. We present the details of this method in Sect. 2.1. Compared to the self-consistent solution of the Kohn–Sham (KS) or HF equations, the calculation of the D3 dispersion energy requires practically no additional computation time. Although it does not include information about the electron density, it provides good accuracy with typical deviations for the asymptotic dispersion energy of only 5% [19]. The accuracy for non-covalent interaction energies with current standard functionals and D3 is about 5–10%, which is also true for small relative energies [32]. Therefore, it is an ideal tool to fulfill fundamental requirements of crystal structure prediction. We evaluate the DFT-D3 scheme with huge plane-wave basis sets in Sect. 2.2 and compare it to competing pairwise-additive methods, which partially employ electron density information.

Because the calculation of the DFT or HF energy is the computational bottle-neck, a speed-up of these calculations without losing too much accuracy is highly desirable. The computational costs mainly depend on the number of utilized single particle basis functions N with a typical scaling behavior from N ² to N ⁴. The choice of the type of basis functions is also an important issue. Bulk metals have a strongly delocalized valence electron density and plane-wave based basis sets are probably the best choice [33]. In molecular crystals, however, the charge density is more localized and a typical molecular crystal involves a lot of “vacuum.” For plane-wave based methods this can result in large and inefficient basis sets. In a recently studied typical organic system (tribenzotriquinacene, C₂₂H₁₆), up to 1.5 × 10⁵ projector augmented plane-wave (PAW) basis functions must be considered for reasonable basis set convergence [34]. For this kind of system, atom-centered Gaussian basis functions as usually employed in molecular quantum chemistry could be more efficient. However, small atom-centered basis sets strongly suffer from basis set errors (BSE), especially the basis set superposition error (BSSE) which leads to overbinding and too high computed weight densities (too small crystal volumes) in unconstrained optimizations. Because different polymorphs often show various packings with different densities, correcting for BSSE is mandatory in our context. In order to get reasonable absolute sublimation energies and good crystal geometries, these basis set errors must be corrected. A further problem compared to plane-wave basis sets is the non-orthogonality of atom-centered basis functions which can lead to near-linear dependencies and bad self-consistent field (SCF) convergence. We have recently mapped the standard Boys and Bernardi correction [35], which corrects for the BSSE, onto an atom-pairwise repulsive potential. It was fitted for a number of typical Gaussian basis sets and depends otherwise only on the system geometry and is therefore denoted gCP [36]. Analytic gradients are problematic in nearly all other counterpoise schemes, but are easily obtained for gCP. For the calculation of second derivatives, analytic first derivatives are particularly crucial. Periodic boundary conditions are included and the implementation has been tested in [37].We present the gCP scheme here together with an additional short-range basis (SRB) incompleteness correction in Sect. 3.1. In Sect. 3.2 the combination of small (almost minimal) basis set DFT and HF, dispersion correction D3, geometrical counterpoise correction gCP, and short-range incompleteness correction SRB is evaluated for typical molecular crystals. The plane-wave, large basis PBE-D3 results are briefly discussed and used for comparison.

2 Dispersion Corrected Density Functional Theory

2.1 London Dispersion Correction

At short inter-atomic distances, standard density functionals (DF) describe the effective electron interaction rather well because of their deep relation to the corresponding electron density changes. Long-range electron correlation cannot be accurately described by the local (or semi-local) DFs in inhomogeneous materials. To describe this van der Waals (vdW)-type interaction, one can include non-local kernels in the vdW-DFs as pioneered by Langreth and Lundquist [38, 39] and later improved by Vydrov and van Voorhis (VV10 [25]). For the total exchange-correlation energy E _xc of a system, the following approximation is employed in all vdW-DF schemes:

$$ {E}_{\mathrm{xc}}={E}_{\mathrm{X}}^{\mathrm{GGA}}+{E}_{\mathrm{C}}^{\mathrm{GGA}}+{E}_{\mathrm{c}}^{\mathrm{NL}}, $$

(1)

where standard exchange (X) and correlation (C) components (in the semi-local generalized gradient approximation GGA) are used for the short-range parts and E ^NL_c represents the non-local correlation term describing the dispersion energy. In the vdW-DF framework it takes the form of a double-space integral:

$$ {E}_{\mathrm{c}}^{\mathrm{NL}}=\frac{1}{2}{\displaystyle \iint \rho \left(\mathbf{r}\right){\Phi}^{\mathrm{NL}}\left(\mathbf{r},{\mathbf{r}}^{\mathbf{\prime}}\right)\rho \left({\mathbf{r}}^{\mathbf{\prime}}\right){d}^3r{d}^3{r}^{\mathit{\prime}}.} $$

(2)

The electron density ρ at positions r and r ′ is correlated via the integration kernel Φ^NL(r,r′). It is physically approximated by local approximations to the frequency dependent dipole polarizability α(r,ω). The VV10 kernel has been successfully used in various molecular applications [40–43] by us but is not discussed further in this work.

The famous Casimir–Polder relationship [44] connects the polarizability with the long-range dispersion energy, which scales as C ₆ = R ⁶ where R is the distance between two atoms or molecules. The corresponding dispersion coefficient C ^AB₆  for interacting fragments A and B is given by

$$ {\mathrm{C}}_6^{\mathrm{A}\mathrm{B}}=\frac{3}{\pi }{\displaystyle {\int}_0^{\infty }{\boldsymbol{\alpha}}^{\mathrm{A}}\left(\boldsymbol{i}\boldsymbol{\omega } \right){\boldsymbol{\alpha}}^{\mathrm{B}}\left(\boldsymbol{i}\boldsymbol{\omega } \right)d\boldsymbol{\omega}, } $$

(3)

where α ^A(iω) is the averaged dipole polarizability at imaginary frequency ω. In vdW-DF (but not in DFT-D3) dispersion can be calculated self-consistently and changes the density in turn. Because this change is normally insignificant [25, 38, 40], E ^NL_c is typically added non-self-consistently to the SCF-GGA energy. The main advantage of vdW-DF methods is that dispersion effects are naturally included via the system electron density. Therefore, they implicitly account for changes in the dispersion coefficients due to different “atoms-in-molecules” oxidation states in a physically sound manner. The disadvantage is the raised computational cost compared to pure (semi-)local DFs.

By treating the short-range part with DFs and the dispersion interaction with a semi-classical atom-pairwise correction, one can combine the advantages of both worlds. Semi-classical models for the dispersion interaction like D3 show very good accuracy compared to, e.g., the VV10 functional [43, 45] for very little computational overheads, particularly when analytical gradients are required.

The total energy E _tot of a system can be decomposed into the standard, dispersion-uncorrected DFT/HF electronic energy E _DFT/HF and the dispersion energy E _disp:

$$ {E}_{\mathrm{tot}}={E}_{\mathrm{DFT}/\mathrm{HF}}+{E}_{\mathrm{disp}}. $$

(4)

We use our latest first-principles type dispersion correction DFT-D3, where the dispersion coefficients are non-empirically obtained from a time-dependent, linear response DFT calculation of α ^A(iω). The dispersion energy can be split into two- and three-body contributions E _disp = E ⁽²⁾ + E ⁽³⁾:

$$ {E}^{(2)}=-\frac{1}{2}{\displaystyle \sum_{n=6,8}{\displaystyle \sum_{\mathrm{A}\ne \mathrm{B}}^{\mathrm{atom}\;\mathrm{pairs}}{\displaystyle \sum_{\mathbf{T}}{s}_n\frac{C_{\mathrm{n}}^{\mathrm{A}\mathrm{B}}}{\left\Vert {\mathbf{r}}_{\mathrm{B}}-{\mathbf{r}}_{\mathrm{A}}+\mathbf{T}\right\Vert +f{\left({R}_0^{\mathrm{A}\mathrm{B}}\right)}^n}}}} $$

(5)

$$ {E}^{(3)}=\frac{1}{6}{\displaystyle \sum_{\mathrm{A}\ne \mathrm{B}}^{\mathrm{a}\mathrm{tom}\;\mathrm{pairs}}{\displaystyle \sum_{\mathbf{T}}\frac{C_9^{\mathrm{A}\mathrm{BC}}\left(3 \cos {\boldsymbol{\theta}}_{\mathrm{a}} \cos {\boldsymbol{\theta}}_{\mathrm{b}} \cos {\boldsymbol{\theta}}_{\mathrm{c}}+1\right)}{r_{\mathrm{A}\mathrm{BC}}^9\cdot \left(1+6\left({r}_{\mathrm{A}\mathrm{BC}}/{R}_0\right)-\alpha \right)}.}} $$

(6)

Here, C ^AB_n denotes the averaged (isotropic) nth-order dispersion coefficient for atom pair AB, and R _A/B are their Cartesian positions. The real-space summation over all unit cells is done by considering all translation invariant vectors T inside a cut-off sphere. The scaling parameter s6 equals unity for the DFs employed here and ensures the correct limit for large interatomic distances, and s8 is a functional-dependent scaling factor. The rational Becke and Johnson damping function f(R ^ab₀ ) is [46]

$$ f\left({R}_0^{\mathrm{ab}}\right)={a}_1{R}_0^{\mathrm{ab}}+{a}_2,\kern0.36em {R}_0^{\mathrm{ab}}=\sqrt{\frac{C_8^{\mathrm{ab}}}{C_6^{\mathrm{ab}}}}. $$

(7)

The dispersion coefficients C ^AB₆ are computed for molecular systems with the Casimir–Polder relation (3).We use the concept of fractional coordination numbers (CN) to distinguish the different hybridization states of atoms in molecules in a differentiable way. The CN is computed from the coordinates and does not use information from the electronic wavefunction or density but recovers basic information about the bonding situation of an atom in a molecule, which has a dominant influence on the C ^AB₆ coefficients [30]. The higher order C ₈ coefficients are obtained from the well-known relation [47]

$$ {C}_8=\frac{3}{2}{C}_6\frac{\left\langle {r}^4\right\rangle }{\left\langle {r}^2\right\rangle }. $$

(8)

With the recursion relation ${C}_{i+4}={C}_{i\mathit{\hbox{-}}2}\left(\frac{C_{i+2}}{C_i}\right)$ and ${C}_{10}=\frac{49}{40}\frac{C_8^2}{C_6}$, one can in principle also generate higher orders, but terms above C ₁₀ do not improve the performance of the D3 method. The three parameters s ₈, a ₁, and a ₂ are fitted for each DF on a benchmark set of small, non-covalently bound complexes. This fitting is necessary to prevent double counting of dispersion interactions at short range and to interpolate smoothly between short- and long-range regimes. These parameters are successfully applied to large molecular complexes and to periodic systems [45, 48]. In the non-additive Axilrod–Teller–Muto three-body contribution (6) [30, 49], r _ABC is an average distance in the atom-triples and θ _a/b/c are the corresponding angles. The dispersion coefficient C ^ABC₉ describes the interaction between three virtually interacting dipoles and is approximated from the pairwise coefficients as

$$ {C}_9^{\mathrm{AB}\mathrm{C}}=-\sqrt{C_6^{\mathrm{AB}}{C}_6^{\mathrm{AC}}{C}_6^{\mathrm{BC}}}. $$

(9)

The applicability of this atom-pairwise dispersion correction with three-body corrections in dense molecular systems was shown in a number of recent publications [16, 50, 51].

For early precursors of DFT-D3 also in the framework of HF theory, see [52–56]. Related to the D3 scheme are approaches that also compute the C₆ coefficients specific for each atom (or atom pair) and use a functional form similar to (5). A system dependency of the dispersion coefficients is employed by all modern DFT-D variants. We explicitly mention the works of Tkatchenko and Scheffler [57, 58] (TS. “atom-in-molecules” C₆ from scaled atomic volumes), Sato et al. [59] (use of a local atomic response function), and Becke and Johnson [46, 60, 61] (XDM utilizes a dipole-exchange hole model). The TS and XDM methods are used routinely in solid-state applications [62–65].

2.2 Evaluation of Dispersion Corrected DFT

2.2.1 X23 Benchmark Set

A benchmark set for non-covalent interactions in solids consisting of 21 molecular crystals (dubbed C21) was compiled by Johnson [24]. Two properties for benchmarking are provided: (1) thermodynamically back-corrected experimental sublimation energies and (2) geometries from low-temperature X-ray diffraction. The error of the experimental sublimation energies was estimated to be 1.2 kcal/mol [66]. Recently, the C21 set was extended and refined by Tkatchenko et al. [67]. The X23 benchmark set (16 systems from [67] and data for 7 additional systems were obtained from these authors) includes two additional molecular crystals, namely hexamine and succinic acid. The molecular geometries of the X23 set are shown in Fig. 2. The thermodynamic back-correction was consistently done at the PBE-TS level. Semi-anharmonic frequency corrections were estimated by solid state heat capacity data. Further details of the back-correction scheme are summarized in [67] The mean absolute deviation (MAD) between both data sets is 0.55 kcal/mol. Because the X23 data seem to be more consistent, we use these as a reference. If we take the standard deviation (SD) between both thermodynamic corrections as statistical error measure, the total uncertainty of the reference values is about 1.3 kcal/mol. In the following, all sublimation energies and their deviations consistently refer to one molecule (and not the unit cell).

Fig. 2

Geometries of the 23 small organic molecules in the X23 benchmark set for non-covalent interactions in solids. Hydrogen atoms at carbons are omitted for clarity. Carbons are denoted by dark gray balls, hydrogens are light gray, oxygens are red, and nitrogens are light blue

The calculations are carried out with the Vienna Ab-initio Simulation Package VASP 5.3 [68, 69]. We utilize the GGA functional PBE [70] in combination with a projector-augmented plane-wave basis set (PAW) [71, 72] with a huge energy cut-off of 1,000 eV. This corresponds to 200% of the recommended high-precision cut-off. We sample the Brillouin zone with a Γ-centered k-point grid with four k-points in each direction, generated via the Monkhorst–Pack scheme [73]. To simulate isolated molecules in the gas phase, we compute the Γ-point energy of a single molecule in a large unit cell (minimum distance between separate molecules of 16 Å, e.g., adamantine is calculated inside a 19 × 19 × 19 × ų unit cell). In order to calculate the sublimation energy, we optimize the single molecule and the corresponding molecular crystal. The unit cells are kept fixed at the experimental values. The atomic coordinates are optimized with an extended version of the approximate normal coordinate rational function optimization program (ANCOPT) [74] until all forces are below 10⁻⁴ Hartree/Bohr. We compute the D3 dispersion energy in the Becke–Johnson damping scheme with a conservative distance cut-off of 100 Bohr. The three-body dispersion energy is always calculated as a single-point on the optimized PBED3/1,000 eV structure. The results for X23 are summarized in Table 1. Figure 3 shows the correlation between experimental sublimation energies and the calculated values on the PBE/1,000 eV, PBE-D3/1,000 eV, and PBE-D3/1,000 eV+E ⁽³⁾ levels. The uncorrected functional yields unreasonable results. Because of the missing dispersion interactions, the attraction between the molecules is significantly underestimated, which results in too small sublimation energies. Some systems are not bound at all on the PBE/1,000 eV level. For PBE-D3 all results are significantly improved. The MAD is exceptionally low and drops below the estimated experimental error of 1.3 kcal/mol. The mean deviation of +0.4 kcal/mol indicates a slight overbinding on the PBE-D3/1,000 eV level. The three-body dispersion correction is always repulsive and therefore decreases the sublimation energy. At the PBE-D3/1,000 eV+E ⁽³⁾ level the MAD and SD is slightly raised but these changes are within the uncertainty of the reference data and hence we cannot draw definite conclusions about the importance of three-body dispersion effects from this comparison. Because inclusion of three-body dispersion has been shown to improve the description of binding in large supramolecular structures [45] and is not spoiling the results here, we recommend that the term is always included. However, the many-body effect (i.e., adding E ⁽³⁾ to the PBE-D3 data) is smaller than found in recent studies by another group [58, 75] employing a general many-body dispersion scheme. We compare our results to the pairwise dispersion corrections XDM and TS and show the normal error distributions in Fig. 4. The XDM model works reasonably well with an MAD of 1.5 kcal/mol, while the TS scheme is significantly overbinding with an MAD of 3.5 kcal/mol. The overbinding of the TS model is partially compensated by large many-body contributions and the MAD on the PBE-MBD level drops to 1.5 kcal/mol. A remarkable accuracy with an MAD of 0.9 kcal/mol was reported with the hybrid functional PBE0-MBD [67, 76]. The XDM model works slightly better in combination with the more repulsive B86b functional. However, the mean deviation of –0.5 kcal/mol and –0.3 kcal/mol reveals a systematic underbinding of the XDM method consistent with results for supramolecular systems (ER Johnson (2013), Personal Communication). This will lead to a worse result when a three-body term is included.

Table 1 Mean absolute deviation (MAD), mean deviation (MD), and standard deviation (SD) of the calculated, zero-point exclusive sublimation energy from reference values for the X23 test set. The energies and geometries refer to the PBE/1,000 eV, PBE-D3/1,000 eV, PBE-D3/1,000 eV+E ⁽³⁾ levels. Values for the XDM and TS method are taken from [24] and the data for 16 systems on the PBE-MBD level from [67]. Negative MD values indicate systematic underbinding

Fig. 3

Correlation between experimental and PBE computed sublimation energy with and without dispersion correction. The gray shading along the diagonal line denotes the experimental error interval. All energies are calculated on optimized structures but with experimental lattice constants

Fig. 4

Deviations between experimental and theoretical sublimation energies for the X23 set. We convert the statistical data into standard normal error distributions for visualization. The gray shading denotes the experimental error interval. The quality of the theoretical methods decreases in the following order: PBE-D3/1,000 eV, PBE-XDM/1,088 eV, and PBE-TS/1,088 eV

As a further test we investigate the unit cell volume for the same systems. We perform a full geometry optimization and compare with the experimental low-temperature X-ray structures. The unit cell optimization is done with the VASP quasi-Newton optimizer with a force convergence threshold of 0.005 eV/A°. Without dispersion correction, too large unit cells are obtained. On the PBE/1,000 eV level, the volumes of the orthorhombic systems are overestimated by 9.7%. We compare the theoretical zero Kelvin geometries with low-temperature X-ray diffraction data at approximately 100 K. Therefore, the calculated values should always be smaller than the measured ones due to thermal expansion effects. After applying the D3 correction, the unit cells are systematically too small by 0.8% which is reasonable considering typical thermal volume expansions assumed to be approximately 3%. In passing it is noted that the geometries of isolated organic molecules are systematically too large in volume by about 2% with PBE-D3 [77], which is consistent with the above findings. In summary, PBE-D3 or PBE-D3 + E ⁽³⁾ provide a consistent treatment of interaction energies and structures in organic solids. Screening effects on the dispersion interaction as discussed in [58, 75] seem to be unimportant in the D3 model.

2.2.2 Structure of Tribenzotriquinazene (TBTQ)

As an example for a larger system where London dispersion is even more important, we re-investigate the recently studied tribenzotriquinacene (TBTQ) compound [34] which involves π-stacked aromatic units. We utilized the GGA functionals PBE [70] and RPBE [78], a PAW basis set [71, 72] with huge energy cut-off of 1,000 eV within the VASP program package. The crystal structures of TBTQ and its centro-methyl derivate (Me-TBTQ) was measured and a space group R3m was found for both TBTQ and Me-TBTQ. However, a refined analysis revealed the true space group of TBTQ to be R3c (an additional c-glide plane), while the space group of Me-TBTQ is confirmed. The structure in Fig. 5 shows the tilting between neighboring TBTQ layers. With dispersion corrected DFT (PBE-D3/1,000 eV), we were able to obtain all subtle details of the structures as summarized in Table 2. The unusual packing induced torsion between vertically stacked molecules was computed correctly as well as an accurate stacking distance. The deviations from experimental unit cell volumes of 1.4% for TBTQ and 1.5% for Me-TBTQ are within typical thermal volume expansions. The agreement between theory and experiment is excellent but necessitated a huge basis set with 1.46 × 10⁵ plane-wave basis functions. A calculation of the crystal structure of Me-TBTQ on the same theoretical level confirms the measured untilted stacking geometry.

Fig. 5

X-Ray (left) and PBE-D3/1,000 eV (middle) crystal structure of TBTQ. The computed structure was obtained by an unconstrained geometry optimization [34]. The right figure highlights the analyzed geometry descriptors

Table 2 Comparison of experimental X-ray and computed PBE-D3/1,000 eV structures. The first block corresponds to the TBTQ crystal, the second to the Me-TBTQ crystal. As important geometrical descriptors the vertical stacking distance R, the tilting angle Θ, and the unit cell volume Ω are highlighted

The dispersion correction is also crucial for the correct description of the sublimation energy. For PBE negative values (no net bindings) are obtained. On the PBE-D3 level reasonable ZPVE-exclusive sublimation energies of 35 and 29 kcal/mol are calculated, which fit the expectations for molecules of this size. In Fig. 6 we show the potential energy surface (PES) with respect to the vertical stacking distance for Me-TBTQ. In addition to the PBE functional, we applied the Hammer et al. modified version, dubbed RPBE [78], to investigate the effect of the short-range correlation kernel. For each point, we perform a full geometry optimization with a fixed unit cell geometry. The curves for both uncorrected functionals show no significant minimum in agreement with the wrong sign of the sublimation energy. Furthermore, we see significant deviation between the two functionals, i.e., PBE is much less repulsive than RPBE. With the inclusion of the D3 correction the differences between both functionals diminishes nicely and the PES are nearly identical. This is a strong indication that the D3 correction provides a physically sound description of long- and medium-range correlation effects. In fact, RPBE-D3 reproduces the equilibrium structure even slightly better than PBED3. This confirms previous observations from different groups that dispersion corrections are ideally coupled to inherently more repulsive (semi-local) functionals [19, 79, 80].

Fig. 6

Dependence of the cohesive energy E _coh per molecule on the vertical cell parameter c (the dashed line denotes the experimental value). The results refer to the PBE and RPBE functional with a PAW basis set and an energy cut-off of 1,000 eV. The cell parameters a and b are fixed to their experimental value. For each point we perform a full geometry optimization with a fixed unit cell geometry. The asymptotic energy limit c → ∞ corresponds to the interaction in one Me-TBTQ layer, approximated by a large distance of 15 Å

3 Dispersion Corrected Hartree–Fock with Basis Set Error Corrections

3.1 Basis Set Error Corrections

The previously presented results were obtained with huge plane-wave basis sets and these DFT calculations are rather costly. It seems hardly possible to use fewer plane-wave functions, because the stronger oscillating functions are necessary to describe the relatively localized electron density in molecular crystals. A significant reduction of basis functions seems only possible with atom centered functions, i.e., Gaussian atomic orbitals (AO). In contrast to plane-waves, however, small AO basis sets suffer greatly from basis set incompleteness errors, especially the BSSE. Semi-diffuse AOs can exhibit near linear dependencies in periodic calculations and the reduction of the BSSE by systematic improvement of the basis is often not possible. A general tool to correct for the BSSE efficiently in a semi-empirical way was developed in 2012 by us [36]. Recently, we extended the gCP denoted scheme to periodic systems and tested its applicability for molecular crystals [37].

Additionally, the basis set incompleteness error (BSIE) becomes crucial when near minimal basis sets are used. For a combination of Hartree–Fock with a MINIX basis (combination of valence scaled minimal basis set MINIS and split valence basis sets SV, SVP as defined in [81]), dispersion correction D3, and geometric counterpoise correction gCP, we developed a short-ranged basis set incompleteness correction dubbed SRB. The SRB correction compensates for too long covalent bonds. These are significant in an HF calculation with very small basis sets, especially when electronegative elements are present. The HF-D3-gCP-SRB/MINIX method will be abbreviated HF-3c in the following. The HF method has the advantage over current GGA functionals that it is (one-electron) self interaction error (SIE) free [82, 83]. Further, it is purely analytic and no grid error can occur. The numerical noise-free derivatives are important for accurate frequency calculations. In contrast to many semi-empirical methods, HF-3c can be applied to almost all elements of the periodic table without any further parameterization and the physically important Pauli-exchange repulsion is naturally included. Here, we extend the HF-3c scheme to periodic systems and propose its use as a cheap DFT-D3 alternative or for crosschecking of DFT-D3 results.

The corrected total energy E ^{HF − 3c}_tot is given by the sum of the HF energy E ^HF/MINIX, dispersion energy E ^D3_disp , BSSE correction E ^gCP_BSSE , and short-ranged basis incompleteness correction E _SRB:

$$ {E}_{\mathrm{tot}}^{\mathrm{HF}-3\mathrm{c}}={E}^{\mathrm{HF}/\mathrm{MINIX}}+{E}_{\mathrm{disp}}^{\mathrm{D}3}+{E}_{\mathrm{BSSE}}^{\mathrm{gCP}}+{E}_{\mathrm{SRB}}. $$

(10)

The form of the first term E ^D3_disp is already described in Sect. 2.1. For the HF-3c method the three parameters of the damping function s ₈, a ₁, and a ₂ were refitted in the MINIX basis (while applying gCP) against reference interaction energies [84] and this is denoted D3(refit). The second correction, namely the geometrical counterpoise correction gCP [36, 37], depends only on the atomic coordinates and the unit cell of the crystal. The difference in atomic energy e ^miss_A between a large basis (def2-QZVPD [85]) and the target basis set (e.g., the MINIX basis) inside a weak electric field is computed for free atoms A. The e ^miss_A term measures the basis incompleteness and is used to generate an exponentially decaying, atom-pairwise repulsive potential. The BSSE energy correction E ^gCP_BSSE EgCP BSSE reads

$$ {E}_{\mathrm{B}\mathrm{SSE}}^{\mathrm{gCP}}=\frac{\boldsymbol{\sigma}}{2}{\displaystyle \sum_{\mathrm{A}\ne \mathrm{B}}^{\mathrm{atom}\;\mathrm{pairs}}{\displaystyle \sum_{\mathbf{T}}{e}_{\mathrm{A}}^{\mathrm{miss}}\frac{ \exp \left(-\boldsymbol{\alpha} \cdot \left\Vert {\mathbf{r}}_{\mathrm{B}}-{\mathbf{r}}_{\mathrm{A}}+\mathbf{T}\right\Vert \boldsymbol{\beta} \right)}{\sqrt{S_{\mathrm{A}\mathrm{B}}\cdot {N}_{\mathrm{B}}^{\mathrm{virt}}}},}} $$

(11)

with Slater-type overlap integral S _AB, number of virtual orbitals on atom B in the target basis set N ^virt_B  , and basis set dependent fit parameters σ , α, and β. The Slater exponents of s- and p-valence orbitals are averaged and scaled by a fourth fit parameter η to get a single s-function exponent. For each combination of Hamiltonian (DFT or HF) and basis set, the four parameters were fitted in a least-squares sense against counterpoise correction data obtained by the Boys–Bernardi scheme [35].

Systematically overestimated covalent bond lengths for electronegative elements

are corrected by the third term E _SRB:

$$ {E}_{\mathrm{SRB}}=-\frac{s}{2}{\displaystyle \sum_{\mathrm{A}\ne \mathrm{B}}^{\mathrm{atom}\;\mathrm{pairs}}{\displaystyle \sum_{\mathbf{T}}{\left({Z}_{\mathrm{A}}{Z}_{\mathrm{B}}\right)}^{3/2} \exp \left(-\gamma {\left({R}_{\mathrm{A}\mathrm{B}}^{0,\mathrm{D}3}\right)}^{3/4}\left\Vert {\mathbf{r}}_{\mathrm{B}}-{\mathbf{r}}_{\mathrm{A}}+\mathbf{T}\right\Vert \right).}} $$

(12)

We use the default cut-off radii R ^0,D3_AB as determined ab initio for the D3 dispersion correction and Z_A/B are the nuclear charges. The parameters s and γ were determined by fitting the HF-3c total forces against B3LYP-D3/def2-TZVPP [86] equilibrium structures of 107 small organic molecules. Altogether, the HF-3c method consists of nine empirically determined parameters, three for the D3 dispersion, four in the gCP scheme, and two for the SRB correction. The HF-3c method was recently tested for geometries of small organic molecules, interaction energies and geometries of non-covalently bound complexes, for supramolecular systems, and protein structures [81], and good results superior to traditional semi-empirical methods were obtained. In particular the accurate non-covalent HF-3c interactions energies for a standard benchmark [84] (i.e., better than with the “costly” MP2/CBS method and close to the accuracy of DFT-D3/“large basis”) are encouraging for application to molecular crystals.

3.2 Evaluation of Dispersion and Basis Set Corrected DFT and HF

We evaluate the basis corrections gCP and SRB by comparison with reference sublimation energies for the X23 benchmark set, introduced in Sect. 2.2. We calculate the HF and DFT energies with the widely used crystalline orbital program CRYSTAL09 [87, 88]. In the CRYSTAL code, the Bloch functions are obtained by a direct product of a superposition of atom-centered Gaussian functions and a k dependent phase factor. We use raw HF, the GGA functional PBE [70], and the hybrid GGA functional B3LYP [89, 90]. The Γ-centered k-point grid is generated via the Monkhorst–Pack scheme [73] with four k-points in each direction. The large integration grid (LGRID) and tight tolerances for Coulomb and exchange sums (input settings. TOLINTEG 8 8 8 8 16) are used. The SCF energy convergence threshold is set to 10⁻⁸ Hartree. We exploit the polarized split-valence basis set SVP [91] and the near minimal basis set MINIX. The atomic coordinates are optimized with the extended version of the approximate normal coordinate rational function optimization program (ANCOPT) [74].

Mean absolute deviation (MAD), mean deviation (MD), and standard deviation (SD) of the sublimation energy for the X23 test set and for the subset X12/Hydrogen (systems dominated by hydrogen bonds) are presented in Table 3. The dispersion and BSSE corrected PBE-D3-gCP/SVP and B3LYP-D3-gCP/SVP methods yield good sublimation energies with MADs of 2.5 and 2.0 kcal/mol, respectively. The artificial overbinding of the gCP-uncorrected DFT-D3/SVP methods is demonstrated by the huge MD of 8.5 kcal/mol for PBE and 10.1 kcal/mol for B3LYP. Adding the three-body dispersion energy changes the MADs for D3-gCP to 2.9 and 1.7 kcal/mol, respectively. As noted before [37], the PBE functional with small basis sets underbinds hydrogen bonded systems systematically. The HF-3c calculated sublimation energies are of very good quality with an MAD of 1.7 and 1.5 kcal/mol without and with three-body dispersion energy, respectively, which is similar to the previous PBE-D3/1,000 eV results. Considering the simplicity of this approach, this result is remarkable. The MD is with 0.6 and –0.2 kcal/mol, respectively, also very close to zero. This indicates that, with the three correction terms, most of the systematic errors of pure HF are eliminated. For hydrogen bonded systems the MAD is only slightly higher, which indicates an overall consistent treatment. To analyze the HF-3c method in more detail, we investigate the different energy contribution to the sublimation energy on the optimized HF-3c structures as shown in Fig. 7.

Table 3 Mean absolute deviation (MAD), mean deviation (MD), and standard deviation (SD) of the computed sublimation energy with respect to experimental reference data for the X23 test set and for the subset X12/Hydrogen dominated by hydrogen bonds. We compare the HF-3c method with gCP corrected PBE-D3/SVP and B3LYP-D3/SVP methods. For PBE/SVP level, we also give deviations to the corresponding large plane-wave basis set values in parentheses

Fig. 7

Correlation between experimental sublimation energy and HF results with subsequent addition of the three corrections. All sublimation energies are calculated on optimized HF-3c structures for experimental lattice constants. The gray shading along the diagonal line denotes the experimental error interval

Plain HF is not capable of describing the intermolecular attraction in the crystals and has the largest MAD of 11.3 kcal/mol. The only significant physical attraction between the molecules arises in hydrogen bonded systems which are dominated by electrostatics which is properly described by HF. By inclusion of dispersion, the MAD drops to 6.3 kcal/mol on the HF-D3(refit)/MINIX level, but the sublimation energy is significantly overestimated. This too strong attraction can be efficiently and accurately corrected with the gCP scheme. The MAD on the HF-D3(refit)-gCP/MINIX level is 1.6 kcal/mol and very similar to the MAD of the full HF-3c method. This demonstrates that the SRB correction mainly affects geometries as intended. Because the energy decomposition analysis is done for fixed geometries, we cannot investigate the importance of the E _SRB contribution in more detail. In conclusion, the computationally very cheap HF-3c method provides encouraging energies. However, for a few systems we encounter convergence problems of the SCF procedure with the CRYSTAL09 code. This can be sometimes avoided with tighter tolerances for Coulomb and exchange integral sums with the side effect of increased computational cost. Zero point vibrational energies are not analyzed here, but numerically stable second energy derivatives of HF-3c were reported in [81].

4 Conclusions

We have presented and evaluated dispersion corrected Hartree–Fock and Density Functional Theories for their potential application to computed organic crystals and their properties. For a correct description of molecular crystals, semi-local (hybrid) density functionals have to be corrected for London dispersion interactions. A variety of modern DFT-D methods, namely D3, TS/MBD, and XDM, can calculate sublimation energies of small organic crystals with errors close to the experimental uncertainty. For the X23 test set we found that the D3 scheme gives the best performance of the tested additive dispersion corrections with an MAD of 1.1 kcal/mol, which is well below the estimated error range of 1.3 kcal/mol. In the DFT-D3 scheme the three-body dispersion energy corrections are approximately 5% of the sublimation energy. The finding that the method, which has been developed originally for molecules and molecular complexes, can be applied without further, solid-state specific modifications is encouraging. It was furthermore shown that DFT-D3 can calculate the π-stacking of tribenzotriquinacene and its centro-methyl derivative with all subtle geometry details. This example demonstrates that larger molecules routinely considered in organic chemistry can also be treated accurately in their solid state by DFT based methods.

In addition to these calculations with huge plane-wave based basis sets, we exploited Gaussian atom-centered orbitals. We demonstrated the large basis set errors on the DFT-D3/SVP and HF-D3/MINIX levels and presented and evaluated two semi-empirical basis set corrections. The resulting DFT-D3-gCP/SVP and HF-3c methods perform well and the MAD of 1.5 kcal/mol (with three-body dispersion) for HF-3c is especially remarkable. However, the SCF convergence with unscreened Fock-exchange is sometimes problematic and, despite a larger basis being used, the PBE-D3-gCP/SVP calculations converge faster and yield an acceptable MAD of 2.5 kcal/mol for the X23 sublimation energies.

In Fig. 8 we summarize the results of the various theoretical methods for the X23 benchmark set by converting the statistical data into standard normal distributions. The best results are calculated with the D3 dispersion corrected PBE functional in a huge PAW basis set. HF-3c + E ⁽³⁾ and PBE-D3-gCP/SVP can also be recommended.

Fig. 8

Deviations between experimental and theoretical sublimation energies for the X23 set. We convert the statistics into standard normal error distributions for visualization. The gray shading denotes the experimental error interval. The quality of the theoretical methods decreases in the following order. PBED3/1,000 eV, HF-3c+E ⁽³⁾, PBE-D3-gCP/SVP, PBED3/ SVP, and PBE/1,000 eV

In future work the description of energy rankings of polymorphs on the different theoretical levels has to be investigated systematically. Furthermore, coupling of the D3 dispersion correction to different GGA, meta-GGA, and hybrid GGA functionals might provide even better performance. In any case, the future for fully quantum chemical based first principles crystal structure prediction seems bright.