The Influence of the Thermoelastic Instability on the Wear of Composite Brake Discs

Abstract

In the paper, the initiation of thermoelastic instability under unsteady friction of anisotropic disc samples is considered. This process takes place during the operation of high-load braking systems in aviation and railway transport, special-purpose clutches for vehicles, and in other mechanisms. The instability leads to overheating of the friction surfaces, increased wear, and instability of the friction torque. The mutual influence of wear, friction-induced heating, and elastic deformations of the friction surface is modeled by a finite difference method. The process of friction and wear of discs is studied, taking into account the history of a series of braking actions. The annular pattern of the surface pressure and temperature distribution is considered and the influence of the emerging instability on the wear of the disc surface is determined.

INTRODUCTION

Thermoelastic instability under friction occurs due to the positive feedback between local contact pressure on the friction surface and the temperature in this area of the contact surface. This feedback occurs because the local friction-induced heating of the friction surface causes local thermal expansion, which leads to an increase in the contact pressures in the region under consideration. The local increase in the contact pressures results, in turn, in a local increase in the friction-induced heating. In most friction assemblies, the positive feedback mechanism is compensated for by the negative feedback as a consequence of the heat removal from the locally heated regions due to the thermal conductivity of the material and more intense wear of the regions with the increased contact pressure (running-in of the friction surfaces). The effect of the thermoelastic instability manifests itself in tribological systems with a high friction-induced heat flux on the friction surface, primarily in braking system of different kinds. In classical works by Barber [1], the initiation of the thermoelastic instability along the sliding direction as a result of small perturbations in the distribution of contact pressures and temperatures is considered. Such instability develops very quickly and leads to instability of the friction process. For this reason, in Barber’s models the wear of the friction surfaces is neglected and only the conditions for the origination of a process of this kind are considered. This model, with slight modifications, is suitable for a wide range of tribological joint configurations [2, 3]. Another line of developments related to this phenomenon is the thermoelastic instability at the macrolevel of nominally flat rubbing surfaces of different materials that exhibit different thermal properties [4‒6]. In later works, the influence of the wear on the initiation of the thermoelastic instability is investigated and three-dimensional configurations of the contact pressure distribution under instability are simulated by numerical methods [7]. Studies show that the instability under friction of brake disks may develop in the form of so-called “hot bands” [8]. The distribution of the surface temperatures and pressures is symmetrical to the rotation axis of the disk and no vibrations, acoustic emissions, or instability of the friction process at the macrolevel occurs in this case. In [9], the instability of this kind is studied under friction of clutch disks, taking the linear wear into account in the formulation that does not consider the history of the disk. Experimental studies [10], however, show that, in aircraft braking systems, an axisymmetric instability takes place with a development time commensurate with the duration of a singular braking action. This allows for the operation of the brakes under such conditions, but can considerably affect the wear of the brake disks and does not allow neglecting the previous operation of the brakes.

The aim of this work is to model the process of the dynamic wear of high-load discs of composite materials considering the mutual influence of the friction-induced heating, wear, and history of the preceding friction cycles.

FORMULATION OF THE PROBLEM

In this work, the friction of a pair of discs of a composite (anisotropic) material is investigated in a multidisc braking system used in aircraft, high-speed trains, and some types of clutches. Let us consider a pair of contacting discs, a rotating and a fixed one (Fig. 1), manufactured of equal materials. The discs with a thickness 2h have an inner radius R₁ and an outer radius R₂. The properties of the disc material are thought to be homogeneous and transversely anisotropic. The axis of anisotropy is parallel to the rotation axis of the disc. We assume that the conditions on the friction surfaces from different sides of each disc are equal and, during the friction, the disc remains symmetrical with respect to its median plane, which is perpendicular to the rotation axis.

Fig. 1.

Schematic of the friction of a disc pair.

Then, considering the friction surface between a pair of discs, we assume that the planes of their symmetry remain flat during friction and all conditions such as the temperature, stresses, and strains remain symmetrical with respect to the above planes in every disc. This also implies the symmetry of the conditions in the contacting discs with respect to the plane of friction. Furthermore, we consider that, under friction, the conditions of the axial symmetry with respect to the rotation axis hold true. Then, each of the discs can be considered to be a layer with a thickness h and a width R₂ – R₁ that rests on a rigid base (the plane of symmetry) on which no displacements occur and that does not transfer heat. Such a formulation can also be applied to modeling the work of inertia friction machines, where a pair of disc samples mounted in rigid heat-insulated flat holders interacts, e.g., the IM-58 friction test machine. Let us introduce polar coordinates with the 0z axis that coincide with the axis of rotation of the discs and the origin of the coordinates at the intersection of the rotation axis with the contact plane of the discs. The discs are compressed by an external force P and slide against each other at an angular velocity ω . We assume that in the course of a single braking action, the angular velocity drops to zero according the linear law

$$\omega \left( t \right) = {{\omega }_{0}} - \frac{{{{\omega }_{0}}}}{{{{t}_{{{\text{br}}}}}}}t,$$

(1)

where ω₀ is the initial rotational velocity and t_br is the time of braking.

Then, the sliding velocity on the friction surface has the form

$$V\left( {r,t} \right) = 2\pi \omega \left( t \right)r = 2\pi \omega {{{\kern 1pt} }_{0}}\left( {1 - \frac{t}{{{{t}_{{{\text{br}}}}}}}} \right)r.$$

(2)

We consider the material of the discs to be elastic and describable by a one-dimensional Winkler model. Then, the normal displacements of the friction surface under elastic deformations have the form

$${{u}_{E}}\left( {r,t} \right) = \frac{{p\left( {r,t} \right)h}}{{{{E}_{z}}}},$$

(3)

where p(r, t) is the pressure on the contact surface of two discs and E_z is Young’s modulus of the material of the disc in the direction of the 0z axis.

The interaction between the discs results in the wear of their working surfaces. The rate of the wear u_W(r, t) is described by the formula

$$\frac{{\partial {{u}_{W}}\left( {r,t} \right)}}{{\partial t}} = {{K}_{W}}{{\left( {\frac{{p\left( {r,t} \right)}}{{\tilde {p}}}} \right)}^{\alpha }}V\left( {r,t} \right),$$

(4)

where K_W , $\tilde {p}$, and α are the wear coefficients of the material of the discs.

During the friction, the friction surface and the material of the discs are heated under the influence of the friction-induced heat flux q(r, t) as:

$$q\left( {r,t} \right) = \frac{1}{2}\mu p\left( {r,t} \right)V\left( {r,t} \right),$$

(5)

where μ is the coefficient of friction between the discs. The heating of the discs results in the thermal expansion of the latter. The normal displacements u_T(r, t) of the surface under the influence of the temperature field can be presented in a 1D model in the form

$${{u}_{T}}\left( {r,t} \right) = {{a}_{z}}\mathop \smallint \limits_0^h T\left( {z,r,t} \right)dz,$$

(6)

where T(r, z, t) is the temperature of the material of the disc and a_z is the linear expansion coefficient of the material in the direction of the 0z axis.

The temperature of the material of the disc can be found from the heat conduction equation as follows:

$${{\lambda }_{r}}\frac{{{{\partial }^{2}}T}}{{\partial {{r}^{2}}}} + {{\lambda }_{z}}\frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}} = c\rho \frac{{\partial T}}{{\partial t}},$$

(7)

where λ_r and λ_z are the heat conduction coefficients of the disc in the directions r and z; c is the heat capacity of the material, and ρ is the density of the material. We use the conditions of the heat insulation at the face ends of the layer and its base as the boundary conditions for Eq. (8) as follows:

$${{\left. {\frac{{\partial T}}{{\partial r}} = 0} \right|}_{{r = {{R}_{1}},~r = {{R}_{2}}}}},\,\,\,\,~{{\left. {\frac{{\partial T}}{{\partial z}} = 0} \right|}_{{z = h}}}~.$$

(8)

The condition of the heat insulation on the base of the layer ensues from the fact that this is the plane of symmetry of the disc; the heat exchange on the face ends of the disc can be neglected owing to an insignificant rate of cooling the material by air compared with the rate of the friction-induced heating and considering the short duration of the friction process.

On the friction surface, we obtain the boundary condition of the friction-induced heating as:

$${{\left. {\frac{{\partial T}}{{\partial z}} = - \frac{{q\left( {r,t} \right)}}{{{{\lambda }_{z}}}}} \right|}_{{z = 0}}}.$$

(9)

At the initial point of time (the beginning of the braking), the temperature of the disc is considered equal to zero.

Let Ω be the contact area of the disc surfaces. Then, considering the conditions on the contact surface at z = 0, the following system can be obtained:

$$\left\{ {\begin{array}{*{20}{c}} {{{u}_{E}}\left( {r,t} \right) + {{u}_{W}}\left( {r,t} \right) - {{u}_{T}}\left( {r,t} \right) = {{u}_{\Delta }}\left( t \right),\,\,\,\,r \in \Omega } \\ {{{u}_{G}}\left( {r,t} \right) + {{u}_{W}}\left( {r,t} \right) - {{u}_{T}}\left( {r,t} \right) = {{u}_{\Delta }}\left( t \right),\,\,\,\,r \notin \Omega ,} \end{array}} \right.$$

(10)

where u_Δ(t) is the convergence of the friction surface and the plane of symmetry of the disc and u_G(r, t) is the half gap between the friction surfaces, which, in the absence of the contact between the latter, is taken with the negative sign. In this case,

$${{u}_{E}}\left( {r,t} \right) \geqslant 0,\,\,\,\,{{u}_{G}}\left( {r,t} \right) \leqslant 0.$$

(11)

From the equilibrium reasons, we obtain

$$2\pi \mathop \smallint \limits_{{{R}_{1}}}^{{{R}_{2}}} p\left( {r,t} \right)rdr = P.$$

(12)

Considering that R₂ – R₁ ⪡ R₁, Eq. (12) can be rewritten in the form

$$\mathop \smallint \limits_{{{R}_{1}}}^{{{R}_{2}}} p\left( {r,t} \right)dr = \frac{P}{{\pi \left( {{{R}_{1}} + {{R}_{2}}} \right)}} = P{\kern 1pt} '.$$

(13)

Considering the distribution functions of pressures p(r, t) and temperatures T(z, r, t) as unknown quantities, we can obtain the following system of integral–differential equations by substituting Eqs. (3)–(6) into the first equation of (10) and using Eq. (7)

$$\left\{ \begin{gathered} \frac{{p\left( {r,t} \right)h}}{{{{E}_{z}}}} + \mathop \smallint \limits_0^t {{K}_{W}}{{\left( {\frac{{p\left( {r,t} \right)}}{{\tilde {p}}}} \right)}^{\alpha }}V\left( {r,\tau } \right)d\tau \hfill \\ - \,\,{{a}_{z}}\mathop \smallint \limits_0^h T\left( {r,z,t} \right)dz = {{u}_{\Delta }}\left( t \right),\,\,\,\,r \in \Omega \hfill \\ {{\lambda }_{r}}\frac{{{{\partial }^{2}}T}}{{\partial {{r}^{2}}}} + {{\lambda }_{z}}\frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}} = c\rho \frac{{\partial T}}{{\partial t}}. \hfill \\ \end{gathered} \right.$$

(14)

The boundary conditions for the system have the form:

$$\left\{ \begin{gathered} T\left( {r,z,0} \right) = 0 \hfill \\ {{\left. {\frac{{\partial T}}{{\partial r}} = 0} \right|}_{{r = {{R}_{1}},~r = {{R}_{2}}}}},~\,\,\,\,{{\left. {\frac{{\partial T}}{{\partial z}} = 0} \right|}_{{z = h}}} \hfill \\ ~{{\left. {\frac{{\partial T}}{{\partial z}} = - \frac{\mu }{{2{{\lambda }_{z}}}}p\left( {r,t} \right)V\left( {r,t} \right)} \right|}_{{z = 0}}} \hfill \\ \mathop \smallint \limits_{{{R}_{1}}}^{{{R}_{2}}} p\left( {r,t} \right)dr = P{\kern 1pt} '. \hfill \\ \end{gathered} \right.$$

(15)

METHOD OF SOLUTION

System (14) can be solved by a finite-difference method. To do this, let us introduce the discretization by the coordinates (r, z, t) in the sections $r \in \left[ {{{R}_{1}},{{R}_{2}}} \right],z \in \left[ {0,h} \right],t \in \left[ {0,{{t}_{{{\text{br}}}}}} \right]$ with increments (Δr, Δz, and Δt), respectively (Fig. 2). The functions p(r, t) and T(z, r, t) are searched for at the points

$$\begin{gathered} {{r}_{i}} = {{R}_{1}} + i\Delta r,\,\,\,\,i = 0...I,\,\,\,\,I = \frac{{{{R}_{2}} - {{R}_{1}}}}{{\Delta r}}, \\ {{z}_{j}} = j\Delta z,\,\,\,\,j = 0...J,\,\,\,\,J = \frac{h}{{\Delta z}}, \\ {{t}_{n}} = n\Delta t,\,\,\,\,n = 0...N,\,\,\,\,N = \frac{{{{t}_{{{\text{br}}}}}}}{{\Delta t}}. \\ \end{gathered} $$

(16)

Fig. 2.

Discretization of the finite-difference solution scheme.

We designate the function p(r_i, t_n) by $p_{i}^{n}$ and the function T(r_i, z_j, t_n) by $T_{{i,j}}^{n}$ (Fig. 2).

We replace heat conduction equation (14.2) by the explicit difference scheme as:

$$\left\{ \begin{gathered} {{\lambda }_{r}}\frac{{T_{{i + 1,j}}^{n} - 2T_{{i,j}}^{n} + T_{{i - 1,j}}^{n}}}{{{{\Delta }}{{r}^{2}}}} \hfill \\ + \,\,{{\lambda }_{z}}\frac{{T_{{i,j + 1}}^{n} - 2T_{{i,j}}^{n} + T_{{i,j + 1}}^{n}}}{{{{\Delta }}{{z}^{2}}}} = c\rho \frac{{T_{{i,j}}^{{n + 1}} - T_{{i,j}}^{n}}}{{{{\Delta }}t}}~ \hfill \\ i = 1...I - 1,\,\,\,\,j = 1...J - 1,\,\,\,\,~n = 0...N - 1. \hfill \\ \end{gathered} \right.$$

(17)

Boundary condition (15.2) in the difference form is

$$\left\{ \begin{gathered} T_{{0,j}}^{{n + 1}} = T_{{1,j}}^{{n + 1}},\,\,\,\,T_{{N,j}}^{{n + 1}} = T_{{N - 1,j}}^{{n + 1}} \hfill \\ j = 0...J,\,\,\,\,n = 0...N - 1 \hfill \\ \frac{{T_{{i,0}}^{{n + 1}} - T_{{i,1}}^{{n + 1}}}}{{{{\Delta }}z}} = \frac{\mu }{{2{{l}_{z}}}}p_{i}^{{n + 1}}V({{r}_{i}},{{t}_{{n + 1}}}) \hfill \\ T_{{i,J}}^{{n + 1}} = 2T_{{i,J - 1}}^{{n + 1}},\,\,\,\,i = 0...I,\,\,\,\,~n = 0...N - 1. \hfill \\ \end{gathered} \right.$$

(18)

Equation (14.1) in the difference form is written as

$$\frac{{hp_{i}^{n}}}{{{{E}_{z}}}} + u_{{Wi}}^{n} - {{a}_{z}}{{\Delta }}z\mathop \sum \limits_{j = 1}^J T_{{i,j}}^{n} = u_{\Delta }^{n},\,\,\,\,{{r}_{i}} \in {{\Omega }}{\text{,}}$$

(19)

where $u_{{Wi}}^{n}$ is the wear of the friction surface, which can be calculated by the formula

$$u_{{Wi}}^{n} = {{K}_{W}}{{\Delta }}t\mathop \sum \limits_{\eta = 1}^n {{\left( {\frac{{p_{i}^{\eta }}}{{\tilde {p}}}} \right)}^{\alpha }}\theta \left( {p_{i}^{n}} \right)V\left( {{{r}_{i}},{{t}_{n}}} \right).$$

(20)

Boundary condition (15.3) in the difference form takes the form

$${{\Delta }}r\mathop \sum \limits_{i = 1}^I p_{i}^{{n + 1}} = P{\kern 1pt} '.$$

(21)

The accumulative average wear per one braking action can be found by the formula

$${{U}_{W}} = \frac{{\sum\limits_{i = 0}^I {u_{{Wi}}^{N}} }}{I}.$$

(22)

The solution was performed according the following calculation scheme:

(0) At the initial point of time, the temperature distribution $T_{{i,j}}^{0}$ was set by boundary conditions (15.1) and the wear $u_{{Wi}}^{0}$ is thought to be equal to zero.

(1) We determine the convergence $u_{\Delta }^{{n + 1}}$ and the contact area Ω by the method of successive approximations so that equalities (19) and (21) are met in the following way:

(a) we find $\bar {p}_{i}^{{n + 1}}$ for the subsequent $\bar {u}_{\Delta }^{{n + 1}}$ by formula (19);

(b) if $\bar {p}_{i}^{{n + 1}} \leqslant 0$, then ${{r}_{i}} \notin {{\Omega }}$, as follows from the second equation of (10) and Eq. (11);

(c) we check condition (21) for all ${{r}_{i}} \in {{\Omega }}$. If the load proves to be below $P{\kern 1pt} '$, we increase $\bar {u}_{\Delta }^{{n + 1}}$; otherwise, we decrease $\bar {u}_{\Delta }^{{n + 1}}$;

(d) if the difference between the obtained load and the set one is above 0.01%, we return to step (a).

(2) Having obtained $u_{\Delta }^{{n + 1}}$ and the corresponding Ω from (19), we obtain the new distribution of the pressures $p_{i}^{{n + 1}}$.

(3) According to the known distribution of the contact pressures, we find the temperature distribution $T_{{i,j}}^{{n + 1}}$ in the following time step by formula (17).

(4) We find the wear at the next time step as

$$u_{{Wi}}^{{n + 1}} = u_{{Wi}}^{n} + {{K}_{W}}{{\Delta }}t{{\left( {\frac{{p_{i}^{{n + 1}}}}{{\tilde {p}}}} \right)}^{\alpha }}\theta \left( {p_{i}^{{n + 1}}} \right)V\left( {{{r}_{i}},{{t}_{{n + 1}}}} \right).$$

(23)

(5) We go to item (1) and the new time step.

Due to a nonuniform pressure distribution during the friction process, the wear over the radius of the disc will also be distributed nonuniformly ($u_{{Wi}}^{N} \ne {\text{const}}$) upon the completion of the braking cycle; therefore, a relief is formed on the disc that will determine the pressure distribution during the subsequent braking actions. To take this factor into account when modeling a series of several braking actions, it is necessary to assume the initial wear at point 0 to be equal to the wear after the preceding braking action.

RESULTS AND DISCUSSION

In Fig. 3, the predicted wear of the friction surface of a full-size aviation brake disc is shown upon a series of six braking actions. The parameters of the material and the friction process are presented in Table 1. They correspond to the parameters of a composite material manufactured by JSC Rubin Aviation Corporation based on the Zoltek 1400 carbon fiber and a pitch-based carbon matrix. It can be seen from Fig. 3 that, upon the first several running-in braking actions—two actions in this case; however, the duration of the running-in varies depending on the parameters of the material and braking—the shape of the surface changes cyclically in the course of a two-deceleration cycle. Thus, the braking actions can be divided into “even” and “odd” ones with different alternating temperature and contact pressure distributions.

Fig. 3.

Linear wear u_W (mm) vs. radial coordinate r (mm) (the shape of the worn-out surface of a full-size disc) for six consecutive braking actions.

Table 1.   Parameters of the material and friction process used in the calculations

In Fig. 4, the time evolution of the temperature on the friction surface is shown at the same point of the disc surface (r = R₁ + (R₂ – R₁)/3) during the third to sixth braking actions (after the running-in). It can be seen from the graph that the maximum temperature during the “even” braking actions is significantly lower than that during the “odd” ones. This effect can be observed experimentally, for example, by controlling the temperature by a thermocouple under the friction surface [10] (the experiments were conducted at JSC Rubin on inertia friction test machines).

Fig. 4.

Temperature T (°C) at a fixed point of the friction surface vs. time t (s) for the 3rd, 4th, 5th, and 6th braking actions.

The modeling of the friction for samples with other linear dimensions yields absolutely different results. A standard sample for friction testing on the IM-58 friction test machine was considered under conditions, namely, the average specific load, the average initial sliding velocity, and the deceleration time, completely similar to those applied in the previous test. Owing to a significantly narrower friction area—12 mm against 60 mm for the full-size disc—there is not enough time for the thermal instability to develop and the conditions such as the temperature, pressure, and wear remain almost the same on the entire friction surface.

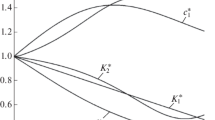
The influence of the thermoelastic instability on the wear of the discs under friction is an especially topical issue. In Fig. 5, the average wear per braking action is shown for the above modeled series of braking actions of the full-size disc and the small sample tested on the IM-58 machine. The wear of the small sample that did not develop instability under friction not only became more stable from braking to braking but was almost 2.5 times lower under the same conditions, namely, the average specific load, the initial linear sliding velocity, the deceleration time, the thickness of the disc plus all parameters of the material including the wear coefficients. The cause of this phenomenon is the significant nonlinearity of the dependence of the wear rate of the material under investigation (Zoltek 1400) on the contact pressure (the wear coefficient α = 2.5). For the materials with a linear dependence of the wear rate on the contact pressure (α = 1), the average wear per braking action depends only on the average specific load, initial velocity, and deceleration time. The wear of such a material is insensitive to the developing thermoelastic instability under a weak effect of the temperature at the contact point on the wear rate. At α > 1, the average wear per braking action increases with the pressure distribution pattern deviating from the uniform pattern (a detailed deduction is provided in [10]).

Fig. 5.

(1) Average linear wear per one braking action U_W (mm) for six consecutive braking actions of a full-size disc and (2) a small IM-58 sample.

In Table 2, the experimentally measured wear of the material under modeling, Zoltek 1400, and the ADF-OS material, which demonstrates a linear dependence of the wear rate on the contact pressure (the wear coefficient α = 1), is presented. The results for the material under modeling are in very good agreement with the predicted results, whereas the material with the wear coefficient α = 1, as shown above, demonstrates the same result in both the presence of the thermoelastic instability (full-size discs) and the absence of the latter (small samples).

Table 2.   Experimentally measured wear of carbon composites under friction of small disc samples and full-size brake discs

The conducted studies suggest that, to assess the lifetime of high-load brake discs, it is necessary to establish how the friction parameters, primarily the contact pressure, influence the wear rate of the material, i.e., to establish the local law of wear. Without doing this, the wear of the discs cannot be predicted in the case when inhomogeneous conditions arise on the friction surface. It has been shown that the history of a brake disc’s operation can determine to a great extent both the distribution patterns of the contact pressures and temperatures and the average wear per braking action. The constructed model allows for the determination of the conditions suitable for investigation of frictional materials and for the prediction of the behavior of these materials in high-load tribological systems. The model constructed in this work is in good agreement with experimental data and allows for the description of the dynamic friction process and wear of high-load composite discs considering the mutual influence of the friction-induced heating, wear, and the history of the previous friction cycles.

CONCLUSIONS

The frictionally induced thermoelastic instability can make a significant contribution to the wear of tribological assemblies with high frictional heat release density on the friction surface. In this work, we consider patterns of friction that occur in operating aviation brake systems and in friction tests of the corresponding materials on friction test machines. It is shown that, owing to the thermoelastic instability, the wear may differ under similar friction conditions by more than two times. Furthermore, it is shown that the change in the wear rate of the material depends primarily on the power-law wear rate and may not be observed at all in materials of some kinds. Comparison with experimental data shows both qualitative and quantitative adequacy of the model to the observed phenomena. The thermoelastic instability causes considerable difficulties in correctly assessing the wear resistance of the material by a model experiment method. A paradoxical situation may arise when friction tests conducted under equal averaged conditions such as specific load, sliding time and velocity, and configuration of the samples (disc–disc in this case) yield different wear rates of the material. To adequately study and predict the wear resistance of materials under such conditions, it is necessary to determine the wear coefficients correctly in an experiment with a uniform distribution of the contact pressures, temperatures, and wear over the friction surface, e.g., in annular samples with a narrow friction path. After that, using the model constructed in this work, it is possible to assess the parameters of friction and wear of a tribological system of the disc–disc configuration.

NOTATION

${{R}_{{{\kern 1pt} 1}}}$ inner disc radius

${{R}_{2}}$ outer disc radius

h half disc thickness

ω rotational speed of the disc

ω₀ initial rotational speed of the disc

V sliding velocity

r radial coordinate

t time coordinate

z axial coordinate

${{t}_{{{\text{br}}}}}$ deceleration duration

P disc compression force

$P{\kern 1pt} '$ specific disc compression force

p contact pressure

${{u}_{E}}$ displacement of the friction surface under elastic deformations

u_T displacement of the friction surface under temperature deformations

u_W linear wear of the surface

u_G half of the gap between the friction surfaces

u_Δ convergence of the friction surface and the disc symmetry plane

${{U}_{W}}$ average linear wear per braking action

q friction-induced heat flux on the friction surface

$\rho$ density of the material

c heat capacity of the material

${{\lambda }_{z}}$ thermal conductivity in the axial direction

${{\lambda }_{r}}$ thermal conductivity in the radial direction

${{a}_{z}}$ thermal expansion coefficient

$\mu$ friction coefficient

${{K}_{E}}$ compliance coefficient

E_z Young’s modulus of the material along the 0z axis

${{K}_{W}}$ wear coefficient of the material

α power-law wear parameter

$\tilde {p}$ wear unit parameter

Ω contact area of the disc

Δr, Δz, Δt discretization steps in variables r, z, and t, respectively

i, j, and n variables of discretization by variables r, z, and t, respectively

I, J, and N discretization ranges by variables r, z, and t, respectively

$p_{i}^{n},$ $T_{{i,j}}^{n},$ and $u_{\Delta }^{n}$ discretized variables p, T, and u_Δ, respectively