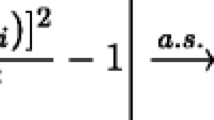Face Recognition Based on the Coefficient Tree for Three Scale Wavelet Transformation

Abstract—A new method for face recognition is presented in the paper. The new method based on the coefficient tree for three-scale wavelet transformation is presented for solving a problem on feature separation. The hidden Markov model is used for classifying face image features.

INTRODUCTION

In crowded modern towns, it becomes necessary to ensure security. This problem correlates with the problem of face recognition and it is one of the main practical problems whose solution contributes to the development of the theory of pattern recognition [1]. This field appeared at the beginning of the 1980s, but its active development started in the 1990s, when information retrieval systems for face recognition and personal identification were created.

The process of person recognition is based on face recognition according to their images and consists in comparing the image with the features of facial images in a database. The process of face recognition can be separated into three main stages (Fig. 1) [2]: to detect faces in images, to separate features (specificities), and to classify features.

Fig. 1.

Block diagram of face recognition.

For solving the problem on detecting faces in images, we present an algorithm based on the Viola-Jones procedure [3], which is the most popular among similar methods [4] and is characterized by high speed and acceptable accuracy. The Viola-Jones face detector is based on the main three ideas [5]: to present the image integrally; to generate a classifier by using an adaptive boosting algorithm (AdaBoost); and to use a procedure for combining classifiers into a cascade structure. These ideas make it possible to generate a robust face detector able to operate in online mode [6].

The experimental simulation for face recognition is performed in the Python 3.5 environment. Data set FaceWarehouse: http://gaps-zju.org/facewarehouse/, 150 people, for each person, 24 images in a natural background, among which 10 images are for training the model of the person, and 14 other images for face recognition. It is known that for face recognition using neural networks, a good deal of training data is required. On the other hand, in practice, in training the model for face recognition, it is not always necessary to have large volumes of training data; the application of neural networks for face recognition leads to retraining. The procedure presented in our paper can solve this problem. Faces in a database are very different over race, age, and sex. For each person in the database, there are different facial expressions with illumination and contrast features, which is useful for verifying that the algorithm is not sensitive to these factors, but has a great ability to generalize. All face images are separated with the help of the Viola-Jones procedure. Fig. 2

Fig. 2.

Face images obtained using the Viola-Jones method: (a) training images; (b) images for testing. Faces detection in images.

Image features are separated into global and local. The essence of the algorithm for early face recognition is as follows: to separate and classify global features. There are two algorithms for face recognition using global features: Eigenface and Fisherface. Algorithm Eigenface uses the principal component method for face recognition. Algorithm Fisherface – is the method of linear discriminant analysis [7]. Algorithms for recognizing global features are sensitive to image illumination and contrast and to facial expression. Therefore, if the environment changes, the reliability and accuracy of face recognition decreases.

Face recognition algorithms based on local image features are generated to overcome these disadvantages. The best known are as follows:

1. Histogram of Oriented Gradients (HOG) [8], the main idea of the algorithm for forming the HOG descriptor is as follows: the object in image area can be described by edge directions or by the distribution of brightness gradients.

2. Local Binary Patterns (LBP) [9], which is a description of the neighborhood of the image pixel in binary form.

3. SIFT (scale-invariant feature transform, (SIFT) descriptor [10], this descriptor searches the reference points and generates a feature vector.

4. An improved version and combination of reference points detector FAST and binary descriptors BRIEF (oriented FAST and rotated BRIEF, ORB) [11], which describes function points by using a binary string based on FAST and BRIEF algorithms.

Figure 3 depicts the local features of face images, which are not sensitive to illumination variation, contrast and face expression. All of them are characterized by one common disadvantage: the dimensionality of feature vectors is too high (for HOG the dimensionality is 291 060, for LBP-27000, for SIFT-15744, and for ORB-5280), which does not contribute to a later classification of features.

Fig. 3.

Different known local features: (a) initial face image with resolution of 180 × 150; (b) HOG features (dimensionality is 291 060; (c) original LBP features (vicinity radius r = 2, number of points N = 8, dimensionality 27 000); (d) improved LBR features (vicinity radius r =2, number of points N = 8, dimensionality 27 000); (e) SIFT features (dimensionality is 15 744); (f) ORB features (dimensionality is 5280).

In the paper, we present the procedure for extracting image features on the basis of a tree of coefficients for a three-scale wavelet transform, which not only preserves the characteristics of the methods that use global features, but has advantages intrinsic to the methods based on local features.

The final step in face recognition is the classification of the features using an already trained classifier such as Random Forests (RFs) [12], Support Vector Machines, (SVMs) [13], or Adaptive Boosting, (AdaBoost) [14]. These three classifiers are the most usable and most accurate. It has been proved [15] that the RF method results in retraining for classification in the presence of noise, and in addition, there is no visual presentation of the decision-making process and it is difficult to interpret the solutions. For the SVM method, there are not enough parameters for tuning and when we fix the core, the only one varying parameter is the error coefficient C, and the model is trained more slowly. Very often Adaptive Boosting causes cumbersome compositions consisting of hundreds of algorithms. For such compositions, it is impossible to perform proper interpretations; they require large amounts of memory to store the basic algorithms and a significant time for calculation of classifications.

In our paper, we use a Hidden Markov Model (HMM), which is a powerful technique for classifying the features of different objects; it is characterized by a simple mathematical structure, high efficiency and recognition accuracy, and needs a short training time.

TREE OF COEFFICIENTS FOR A THREE-SCALE WAVELET TRANSFORM

According to the theory of wavelet analysis, any square-integrable function $f\left( x \right)$ can be restored with the help of an inversion formula [16]:

$$f\left( x \right) = C_{\psi }^{{ - 1}}\mathop \smallint \limits_{ - \infty }^\infty \mathop \smallint \limits_{ - \infty }^\infty \left\langle {f\left( x \right),{{\psi }^{{a,b}}}\left( x \right)} \right\rangle {{\psi }^{{a,b}}}\left( x \right)\frac{{dadb}}{{{{a}^{2}}}},$$

((1))

where ${{\psi }^{{a,b}}}\left( x \right) = {{\left| a \right|}^{{ - 1/2}}}\psi \left( {\frac{{x - b}}{a}} \right)$ is the set of wavelet functions, operation $\left\langle {,~} \right\rangle$ means scalar product in space ${{L}^{2}}$ and $a,b$ are shift and compression parameters with the restriction $a \ne 0$. Constant $C_{\psi }^{{ - 1}}$ depends only on ${{\psi }^{{a,b}}}\left( x \right)$ and is determined by the following formula:

$${{C}_{\psi }} = 2\pi \mathop \smallint \limits_{ - \infty }^\infty {{\left| {\hat {\psi }\left( \xi \right)} \right|}^{2}}{{\left| \xi \right|}^{{ - 1}}}d\xi ,$$

((2))

where $~\hat {\psi }\left( \xi \right)$ is the Fourier transformation for the wavelet function.

Let us introduce a concept of 2D discrete wavelet transform for Daubechies function $f\left( {x,y} \right)$ [17] with dimensionality of $M \times N$:

$${{W}_{\varphi }}\left( {{{j}_{0}},m,n} \right) = \frac{1}{{\sqrt {MN} }}\mathop \sum \limits_{x = 0}^{M - 1} \mathop \sum \limits_{y = 0}^{N - 1} f\left( {x,y} \right){{\varphi }_{{{{j}_{0}},m,n}}}\left( {x,y} \right),$$

((3))

$$W_{\psi }^{i}\left( {j,m,n} \right) = \frac{1}{{\sqrt {MN} }}\mathop \sum \limits_{x = 0}^{M - 1} \mathop \sum \limits_{y = 0}^{N - 1} f\left( {x,y} \right)\psi _{{j,m,n}}^{i}\left( {x,y} \right)~{\text{,}}~~~~~~i = \left\{ {H,V,D} \right\},$$

((4))

where ${{W}_{\varphi }}\left( {{{j}_{0}},m,n} \right)$ characterizes the approximation coefficients for function $f\left( {x,y} \right)$ in scale ${{j}_{0}}$, where ${{j}_{0}}$ is the arbitrary initial scale; $W_{\psi }^{i}\left( {j,m,n} \right)$ are wavelet transform coefficients, where $~i = \left\{ {H,V,D} \right\}$ (H are coefficients for horizontal, V–vertical, and D–diagonal details for scales $j \geqslant {{j}_{0}}$). Let us calculate the approximation coefficients ${{W}_{\varphi }}\left( {{{j}_{0}},m,n} \right)$ in fourth, third and second scales (in this case ${{j}_{0}} = 4,3,2$), as it is shown in Fig. 4.

Fig. 4.

Approximation coefficients under different scales: (a) in 4th scale (resolution is 15 × 14); (b) in 3rd scale (resolution is 30 × 28); (c) in 2nd scale (resolution is 60 × 56);

According to the theory of fast wavelet transformation, the high-scale approximation coefficients are obtained by low-pass filtering and sparse sampling of the approximation coefficients in a neighboring low scale. Let us use the bilinear interpolation so that the total number of low-scale approximation coefficients is exactly twice the number of high-scale approximation coefficients in the long and wide directions.

The correlation between approximation coefficients in the neighboring three scales can be established as is shown in Fig. 5.

Fig. 5.

The structure of coefficient tree for three-scale wavelet transform.

For each approximation coefficient in the fourth scale, it is possible to generate a 21-dimensional vector using the coefficient tree structure for a three-scale wavelet transform. Hereby, we obtain a 21-dimensional tensor corresponding to the approximation coefficients in the 4-th scale in Fig. 6 and the dimensionality of image features is $15 \times 14 \times 21 = 4410$.

Fig. 6.

21-dimensional feature tensor corresponding to the approximation coefficients in 4th order scale.

HIDDEN MARKOV MODEL

The hidden Markov process is an arbitrary process, which at each moment of time $t \in \left\{ {1,...,T} \right\}$ is in one of the states $s \in \left\{ {{{S}_{1}},...,{{S}_{N}}} \right\}$ and transits to the new state according to transition probabilities [18]. These states are hidden from the observer and are seen only in several patterns, which are a sequence of observations generated in the hidden states. Figure 7 depicts a simple hidden Markov model (HMM) with three hidden states:

Fig. 7.

Hidden Markov model.

The hidden Markov model is described by a matrix of transition probabilities, a matrix of observed symbols and by initial state probabilities [19]: $\lambda = \left( {A,B,{\Pi }} \right)$, whose definitions are presented below:

The matrix of transition probabilities $A = \left\{ {{{a}_{{ij}}}} \right\},~\,\,i,j = 1, \ldots ,N,$ the transition probability ${{a}_{{ij}}} = P\{ {{q}_{t}} = {{S}_{j}}|{{q}_{{t - 1}}} = {{S}_{i}}\}$, $N$ is the number of hidden states in the model, $S$ are hidden states $S = \left\{ {{{S}_{1}},{{S}_{2}}, \ldots ,{{S}_{N}}} \right\}$, ${{q}_{t}}$ is the hidden state at time $t$ (${{q}_{t}} \in S,1 \leqslant t \leqslant T$) and $T$ is the length of the observed sequence. The restrictions:

$$\left\{ {\begin{array}{*{20}{c}} {0 \leqslant {{a}_{{ij}}} \leqslant 1} \\ {\mathop \sum \limits_{j = 1}^N {{a}_{{ij}}} = 1} \end{array}} \right..$$

((5))

The matrix of observed sequence probabilities is written as follows: $B = \{ {{b}_{j}}\left( {{{o}_{t}}} \right)\} ,~j = 1, \ldots ,N$, where ${{b}_{j}}\left( {{{o}_{t}}} \right) = P\{ {{o}_{t}}|{{q}_{t}} = {{S}_{j}}\}$, where ${{o}_{t}}$ is a symbol observed at the time $t = 1, \ldots ,T.$

The vector of initial state probabilities ${\Pi } = \left\{ {{{\pi }_{i}}} \right\}$, $i = 1, \ldots ,N$, where ${{\pi }_{i}} = P\left\{ {{{q}_{1}} = {{S}_{i}}} \right\}$, and ${{q}_{1}}$ is the hidden state at the initial time.

HIDDEN MARKOV MODEL TRAINING AND FACE RECOGNITION IMPLEMENTATION

The process of model training and face recognition includes the following steps:

Step 1. To separate features of face images using the coefficients tree for three-scale wavelet transforms as an observed sequence $O$.

Step 2. To de-correlate features with the help of Principal Component Analysis (PCA).

Step 3. To generate a general model $\lambda = \left( {A,B,{\Pi }} \right)$, to determine the number of hidden states $N$, for initial state probabilities ${\Pi } = \left\{ {{{\pi }_{i}}} \right\}$ we determine ${{\pi }_{1}} = 1,\,\,{{\pi }_{i}} = 0\,~\left( {i \ne 1} \right)$, for the matrix of transition probabilities $A = \left\{ {{{a}_{{ij}}}} \right\}$ we determine ${{a}_{{ij}}} = 1~\left( {i = j} \right),\,\,{{a}_{{ij}}} = 0\,~\left( {i \ne j} \right)$, the matrix of observed sequences probabilities $B = \{ {{b}_{j}}\left( {{{o}_{t}}} \right)\}$ [20]:

$${{b}_{j}}\left( {{{o}_{t}}} \right) = \mathop \sum \limits_{k = 1}^M {{c}_{{jk}}}{{\left( {2\pi } \right)}^{{ - N/2}}}{{\left| {{{{\Sigma }}_{{jk}}}} \right|}^{{ - 1/2}}}{\text{exp}}{\kern 1pt} {\kern 1pt} [ - {{\left( {{{o}_{t}} - {{\mu }_{{jk}}}} \right)}^{T}}\Sigma _{{jk}}^{{ - 1}}({{o}_{t}} - {{\mu }_{{jk}}})]/2,$$

((6))

where $M$ is the dimensionality of the observation alphabet, ${{c}_{{jk}}}$ is the ith weight coefficient for the mix of normal distributions in $j$th hidden state, ${{\mu }_{{jk}}}$ and ${{{\Sigma }}_{{jk}}}$ are the mean value and the covariation matrix of the $k$th mixture component in the $j$th hidden state, $j = 1, \ldots ,N,k = 1, \ldots ,M$:

$${{\mu }_{{jk}}} = {{\left( {\mathop \sum \limits_{t = 1}^{{{E}_{{jk}}}} o_{t}^{{\left( {j,k} \right)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\mathop \sum \limits_{t = 1}^{{{E}_{{jk}}}} o_{t}^{{\left( {j,k} \right)}}} \right)} {{{E}_{{jk}}}}}} \right. \kern-0em} {{{E}_{{jk}}}}},$$

((7))

$${{{\Sigma }}_{{jk}}} = {{\left[ {\mathop \sum \limits_{t = 1}^{{{E}_{{jk}}}} \left( {o_{t}^{{\left( {j,k} \right)}} - {{\mu }_{{jk}}}} \right){{{\left( {o_{t}^{{\left( {j,k} \right)}} - {{\mu }_{{jk}}}} \right)}}^{T}}} \right]} \mathord{\left/ {\vphantom {{\left[ {\mathop \sum \limits_{t = 1}^{{{E}_{{jk}}}} \left( {o_{t}^{{\left( {j,k} \right)}} - {{\mu }_{{jk}}}} \right){{{\left( {o_{t}^{{\left( {j,k} \right)}} - {{\mu }_{{jk}}}} \right)}}^{T}}} \right]} {{{E}_{{jk}}}}}} \right. \kern-0em} {{{E}_{{jk}}}}},$$

((8))

where ${{E}_{{jk}}}$ is the length of the observed sequence, respectively, of the kth component of the normal distribution mixture in the j-th hidden state, and $o_{t}^{{\left( {j,k} \right)}}$ are the corresponding observed data.

Figure 8а depicts the result of reducing the dimensionality of the 21-dimensional tensor to three. Let us divide each image in the feature tensor into several parts according to the number of hidden states ($N = 5$). The area marked by the dashed line in Fig. 8b corresponds to the observed sequence of the first hidden state.

Fig. 8.

(a) 3D feature tensor, dimensionalities are reduced by PCA method; (b) feature segmentation according to the number of hidden states (N = 5).

Step 4. To train the model using the Baum-Welch algorithm [21], from which we obtain the model ${{\lambda }_{1}} = \left( {{{A}_{1}},{{B}_{1}},{{{\Pi }}_{1}}} \right)$ corresponding to the first person.

Step 5. To repeat steps 2, 3 and 4, and we obtain the trained models for all faces.

Step 6. To separate features of face image ${{O}_{k}}$ in the test base using the coefficient tree for the three-scale wavelet transform and the PCA method. We calculate the probability $P({{O}_{k}}|{{\lambda }_{i}})$ that the model ${{\lambda }_{i}}$ generates ${{O}_{k}}$. If the nth model ${{\lambda }_{n}}$ is characterized by the highest probability of generating sequence ${{O}_{k}}$, assign the corresponding image to the nth person. A block diagram for face recognition using the hidden Markov model is shown in Fig. 9.

Fig. 9.

Block diagram of face recognition by hidden Markov model.

Figure 10 depicts the accuracy of face recognition when varying the number of hidden states $S$ and the dimensionality of feature tensor $K$.

Fig. 10.

Recognition accuracy when varying the hidden states and dimensionalities of feature tensor.

Axis x in Fig. 10 characterizes the dimensionality of feature tensor $K$, axis y shows percentages. Line $\cdot \cdot * \cdot \cdot$ shows the accuracy of face recognition when the number of hidden states is three, line $- {\text{o}}$ corresponds to the case when the number of hidden states is four, line $- \triangleright$ corresponds to the case when the number of hidden states is five, line $- \blacksquare$ corresponds to the case when the number of hidden states is six. It is seen that if the number of hidden states is five, and the dimensionality of the feature tensor is three, the accuracy of face recognition is maximal at 95.71%.

WEIGHT FUNCTION OF A 2D NORMAL DISTRIBUTION

For each coefficient in the fourth scale with resolution of $15 \times 14$ there is a 21-dimensioal vector. Any point in 4-th scale corresponds to a 21-dimensional vector. Let us fill all 21-dimensional data in a $5\,~ \times ~\,5$ square (Fig. 11). Numbers in the square indicates the point’s level in the coefficient tree of the wavelet transform. Values of four points in the square corner can be calculated by means of bilinear interpolation. Let us assume that all surrounding points introduce a contribution to this area, the nearer to the center, the higher the contribution, and the weight coefficients of the contribution are determined by a function of a 2D normal distribution:

$$f\left( {x,y} \right) = \frac{{{{{\left( {1 - \rho _{{xy}}^{2}} \right)}}^{{ - \frac{1}{2}}}}}}{{2\pi {{\sigma }_{x}}{{\sigma }_{y}}}}{\text{exp}}\left\{ { - \frac{1}{{2\left( {1 - \rho _{{xy}}^{2}} \right)}}\left[ {\frac{{{{{\left( {x - {{\mu }_{x}}} \right)}}^{2}}}}{{\sigma _{x}^{2}}} - {{\rho }_{{xy}}}\frac{{2\left( {x - {{\mu }_{x}}} \right)\left( {y - {{\mu }_{y}}} \right)}}{{{{\sigma }_{x}}{{\sigma }_{y}}}} + \frac{{{{{\left( {y - {{\mu }_{y}}} \right)}}^{2}}}}{{\sigma _{y}^{2}}}} \right]} \right\},$$

((9))

where, ${{\rho }_{{xy}}}$ is the correlation coefficient of $x$ and $y$, μ_x, $~{{\mu }_{y}}$—the mathematical expectations, and $~{{\sigma }_{x}},{{\sigma }_{y}}$ are variances. We determine ${{\rho }_{{xy}}} = 0,~~{{\mu }_{x}} = {{\mu }_{y}} = 0,~{{\sigma }_{x}} = {{\sigma }_{y}} = \sigma$. If condition $\left( {6\sigma + 1} \right)\left( {6\sigma + 1} \right) = 5 \times 5$ is true, the sum of all weight coefficients is equal to unity, and $\sigma = 0.67$. Figure 12 depicts the weight function.

Fig. 11.

Position of 21-dimensional feature tensor in 5 × 5 square.

Fig. 12.

2D weight function.

If the weighted features are used for training models, the accuracy of face recognition increases. Figure 13 depicts the recognition accuracy under different numbers of hidden states and different numbers of training images.

Fig. 13.

Accuracy of face recognition when varying hidden states and the number of training images.

In Fig. 13, axis x depicts the number of training face images $K$, axis y depicts the recognition percentage. Line $\cdot \cdot * \cdot \cdot$ is the accuracy of face recognition when the number of hidden states $S$ is three, line $- {\text{o}}$ corresponds to the case when the number of hidden states is four, line $- \triangleright$ corresponds to the case when the number of hidden states is five, line $- \blacksquare$ corresponds to the case when the number of hidden states is six. It is seen that the recognition accuracy increases if the number of training face images increases, and when $K = 10$ and $S = 5$, the accuracy of face recognition is maximal at 98.57%.

COMPARISION WITH OTHER ALGORITHMS

Table 1 depicts the accuracy of face recognition by different algorithms.

Table 1.   Accuracies of face recognition by different algorithms

WF – Wavelet Features.

WC – Weighted Coefficients.

Multi-NN – Multilayer Neural Network (network parameters: 4 layers, 1200 neurons/layer, Dropout 0.2).

CNN – Convolutional Neural Network (network parameters: 7 layers with regularization L2, two 32 × 3 × 3 convolutional layers, two 64 × 3 × 3 convolutional layers).

From the table it is seen that since the number of training models is small, the model of convolutional neural network is retrained and the recognition accuracy for testing is very unstable. Maximal recognition accuracy obtained in numerous experiments is 99.14%, and minimal recognition accuracy is 96.43%.

In reality, the data volume used for training is insufficient and it is easy to trigger retraining when using a convolutional neural network, as shown in Table 1. For face recognition with small samples, the procedure presented in this paper has advantages in training speed and recognition accuracy. Table 2 depicts the time needed for training for different algorithms. It is seen that the CMM method is characterized by the shortest time for model training, 351.5 ms, and the CNN method is characterized by the highest time for training, 1323.7 s, with video card GT650M; if super video card Tesla P100 is used, the time for model training decreases to 228.6 s.

Table 2. Time for model training for different algorithms

CONCLUSIONS

The new method for face recognition based on a coefficient tree for a three-scale wavelet transform and on a hidden Markov model (HMM) is presented in the paper. The wavelet transform and the weight function of a 2D normal distribution are used sequentially for extracting features. The hidden Markov model is used for comparing features.

The presented procedure is used for simpler models (with respect to other methods). It is characterized by the following advantages:

(1) The dimensionality of image features is lower.

(2) It is not necessary to retrain the model if new samples are added, i.e., only the new samples are trained individually.

(3) The training rate increases.

(4) The accuracy of face recognition is higher.

As a result of the experiment, we found that: if the bio-orthogonal wavelet set bior 1.3 is used, the accuracy of face recognition is 98.57%, if the number of hidden states is five, and the number of training images is ten.

For this method the time required for recognizing an image feature of each model is 0.12 ms with processor Intel Core i7-3630QM @ 2.40 GHz, meaning that the recognition rate is acceptable if the total number of models is less than 1000. Since each model is independent, the present method can be used in the majority of practical applications, if parallel calculation is possible.