The Role of the Shell Structure in the Formation of Surface Tension in Atomic Nuclei

Abstract

The surface tension coefficients $\sigma$ of even–even nuclei with $10<A<212$ were estimated by using their dependence on the nuclear rigidity. The values of the nuclear rigidity were calculated based on the data on the mean squared deformation of nuclei. The correlation of the values of $\sigma$ with the structure of the neutron and proton subshells was investigated. The connection of the surface tension with the nuclear deformation was revealed.

INTRODUCTION

An important role of surface tension in nuclei in forming their properties was shown at the dawn of nuclear physics during the creation of the liquid drop model of the nucleus [1]. Despite the fact that the connection between the surface tension and Coulomb interaction of nucleons with the shape of nuclei has been established, the quantitative estimation of the properties of the nuclear surface is one of the relevant problems of nuclear physics.

N. Bohr and his collaborators revealed the connection between the surface tension coefficient of atomic nuclei and their rigidity [2, 3], i.e., the characteristic that determines the collective oscillations of nuclei. The collective quadruple oscillations of the surface of even–even nuclei is the principal mode of excitation of these nuclei at low energies. The collective quadruple oscillations of nuclei are responsible for the formation of the lower excited states of even–even nuclei; in this case, the potential energy of collective oscillations of such nuclei is a function of the nucleus rigidity.

The following relationship occurs between the rigidity $C$ of an even–even nucleus with respect to quadruple oscillations and the value of its surface tension coefficient [3]:

$$C=4R^{2}\sigma-\frac{3Z^{2}e^{2}}{10\pi R}.$$

(1)

In the theory of collective oscillations (see, for instance, [4]), the relationship between the rigidity $C$ in the ground state and the energy of the lowest $2^{+}$ level of an even–even nucleus and its mean squared deformation $\beta$ is proved to be:

$$C=\frac{5E(2^{+})}{2\beta^{2}}.$$

Table 1 The surface tension coefficients $\sigma$ (MeV/fm${}^{2}$) of nuclei with ($12\leq A\leq 40$)

In review [5], the results of a series of experimental and theoretical studies are presented; the aim of these studies was to determine the mean squared deformation of nuclei $\beta$ in the ground states. (The evaluation is possible owing to the fact that there is a relation between the probability of transitions $2^{+}\rightarrow 0^{+}$ and this quantity.) In [6] the references are given to the refined results for the probability of transitions $2^{+}\rightarrow 0^{+}$.

These data have allowed calculation of the rigidities of even–even nuclei [7]. These results demonstrated the strong dependence of the values of $C$ on the shell structure of nucleus.

The connection between the rigidity and surface tension has made it possible to estimate the surface tension coefficients $\sigma$ for the majority of even–even nuclei [8]. The data [9, 10] on the radii of nuclei were used in the calculations.

The results obtained in [8] revealed that the values of $\sigma$ are very different: they range from $\sigma\sim 0.8{-}1.1$ MeV/fm${}^{2}$ for deformed nuclei up to $\sigma\sim 30$ MeV/fm${}^{2}$ for even isotopes of lead.

This study is devoted to investigation of the influence of the shell structure on the surface tension of even–even nuclei.

What factors determine the degree of accuracy of the performed estimations of the surface tension coefficients? Since the estimations of $\sigma$ are performed based on calculations of the rigidities of nuclei with respect to the quadruple collective oscillations, which, in their turn, are based on the results of calculations of the values of the mean squared deformations $\beta$, the accuracy of the values of $\sigma$ presented above cannot be higher than the accuracy of the estimations of $\beta$ [5, 6].

The second significant factor that influences the accuracy of estimation of the surface tension coefficients of nuclei is the necessity of using experimental data on the radii of nuclei. The relationship between the surface tension and rigidity in formula (1) involves the radius of the nucleus as a characteristic of the spatial distribution of nucleons. The problem of the comparative quantities of the neutron and proton distributions in nuclei has been discussed in the scientific literature (see, for example, [11–13]). In particular, the relationship between the exceedance of the neutron radius over the proton radius and the parameters of the so-called ‘‘pygmy’’ resonance [14] is of great interest. However, the mass distribution is known for a small number of nuclei; therefore, in the calculations discussed in this study the charge radii of nuclei are used if necessary.

Last, the estimates presented in this paper are based on the connection between the surface tension and the rigidity of nuclei; here, the calculation of rigidities was carried out only for quadruple oscillations of the surface of nuclei. Despite the fact that these oscillations are dominant in the collective excitations [4], the collective oscillations of other types may also cause effects on the properties of the nuclear surface.

These factors make it possible to estimate that the accuracy of calculations of the surface tension coefficients of even–even nuclei is not higher than $15{-}20\%$.

Table 2 The surface tension coefficients $\sigma$ (MeV/fm${}^{2}$) of nuclei with ($40\leq A\leq 66$)

1 THE SURFACE TENSION IN NUCLEI WITH $12<A\leq 40$

The results of estimation of the surface tension coefficients in light nuclei with the nucleon number $A\leq 40$ are presented in Table 1.

The calculations of the surface tension coefficients $\sigma$ [7] of even–even nuclei have shown a dominant role of the filling of neutron shells and subshells in formation of high values of $\sigma$. For example, adding a neutron pair to the ‘‘magic’’ nucleus ${}^{16}$O leads to a significant decrease in the surface tension coefficient. However, the analysis of the situation with light nuclei (Table 1) points to a more complicated character of this dependence. Adding a pair of neutrons to the nucleus ${}^{12}$C results in a sharp increase in $\sigma$ in the ${}^{14}$C nucleus; here, the surface tension coefficient in this nucleus exceeds its value in the double ‘‘magic’’ ${}^{16}$O nucleus.

Low values of the surface tension coefficients are characteristic of the atomic nuclei deformed in the ground state. (${}^{20}$Ne, ${}^{22}$Ne, and ${}^{24}$Mg are deformed nuclei, which is proved by the presence of rotational bands in their spectra). It should be noted that theoretical calculations of excited states, for example, the giant dipole resonance in such nuclei, can be successful only provided that the real structure of the ground states of nuclei is considered. Such a consideration can be performed when constructing the basic configurations of the problem based on the information on the experimental ‘‘hole’’ state distribution, which is realized in the ‘‘particle–final nucleus state’’ theoretical approach [15, 16]. Since the state distribution of nucleus (A-1) in the nucleon pickup reaction contains information on the real shape of the target nucleus, the use of this spectroscopy when constructing the basic configurations of the problem on resonance excitations of nucleus have made it possible, in particular, to obtain a realistic picture of the cross sections of excitation of the deformed ${}^{24}$Mg nucleus [17, 18].

Adding a pair of neutrons to the nucleus ${}^{28}$Si significantly increases the surface tension coefficient (Table 1). This effect may be a consequence of the fact that the surface of the nucleus ${}^{30}$Si is formed by two completely filled $(1d_{5/2})^{6}(2s)^{2}$ neutron subshells. The calculations of the isovector dipole excitations in the nuclei ${}^{28}$Si and ${}^{30}$Si [19], based on the use of spectroscopy of the direct neutron pickup reactions, have shown that a satisfactory description of the giant resonances in the nucleus ${}^{28}$Si is reached based on the assumption that the shape of this nucleus is deformed, i.e., not spherical. The resonance excitations of this nucleus is significantly influenced by the deformation of its shape from a sphere, which is a consequences of a relatively low value of $\sigma$.

2 THE SURFACE TENSION IN THE NUCLEI WITH $40\leq A\leq 66$

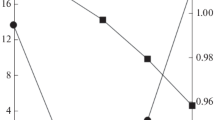
The influence of the shell structure on the surface tension is the most pronounced in the even isotopes of calcium. Comparison of the values obtained with the shell structure of the investigated even–even nuclei has revealed a dominant effect of the structure of neutron shells on the surface tension of the nucleus (Table 2 and Fig. 1).

For even–even isotopes of calcium, the surface tension coefficients are maximum for the ${}^{40}$Ca and ${}^{48}$Ca nuclei.

Fig. 1

The values of $\sigma$ and $r_{0}$ for isotopes of Ca.

Fig. 2

The values of $\sigma$ and $r_{0}$ for isotopes of Ti.

Subsequent adding of neutron pairs $(1f_{7/2})^{2}$ to ${}^{42}$Ca, ${}^{44}$Ca, and ${}^{46}$Ca leads to lower values of $\sigma$ than that of the ‘‘double magic’’ ${}^{40}$Ca nucleus; here, simultaneously the value of parameter $r_{0}$ decreases. Filling of neutron subshells $(1d_{3/2})^{4}(1f_{7/2})^{8}$ in ${}^{48}$Ca implies the maximum value of $\sigma$ for all investigated nuclei except for two even isotopes of lead. The parameter $r_{0}$ riches its minimum in the ${}^{48}$Ca nucleus.

Since the nucleon density of nuclei is inversely proportional to the third degree of the parameter $r_{0}=R_{ch}A^{-1/3}$, a decrease in its values corresponds to compression of the proton component of the nuclear matter. The correlation of the high values of rigidity and the minima in the charge density distribution in the atomic nucleus is a consequence of the influence of the surface tension on the shape and sizes of the nucleus. An increase in the surface tension coefficient leads to an increase in the pressure $p$ to the sphere with the radius $R$, which is described by the ‘‘classical’’ Laplace formula $p={2\sigma/R}.$ An increase in the surface tension and an increase in the pressure on the nucleus related to it, despite the weak compressibility of nuclear matter, leads to the minimum values of parameter $r_{0}$ for charge radii; i.e., to compression of the proton component of nuclear matter.

The estimations of the surface tension coefficients in even isotopes of titanium have shown that adding of a proton pair to the neutron structure $(1d_{3/2})^{4}(1f_{7/2})^{n}$ of the double ‘‘magic’’ ${}^{48}$Ca nucleus abruptly reduces the values of $\sigma$:$\sigma({}^{50}{\textrm{Ti}})/\sigma({}^{48}{\textrm{Ca}})\approx 0.17$ (Table 2 and Figs. 1, 2).

The distribution of the surface tension coefficients in the even isotopes of the nuclei of Cr, Fe, Ni, and Zn is shown in Fig. 3. The maxima of $\sigma$ correspond to the ‘‘magic’’ numbers of neutrons $N=28$ and $N=40$. It is also seen in Fig. 3 that there is an influence of the filling of proton shells and subshells on the value of surface tension.

3 THE SURFACE TENSIONS IN NUCLEI WITH $68\leq A\leq 96$

An interesting example of the influence of the filling of neutron shells on surface tension is even isotopes of zirconium (Fig. 4, Table 3).

The ${}^{90}$Zr nucleus with a filled neutron subshell $(1g_{9/2})^{10}$ has a value of $\sigma$ approximately by 5 times higher than that of the ${}^{88}$Zr nucleus and approximately by 3 times higher than that of the ${}^{92}$Zr nucleus with the surface-neutron configuration $(1g_{9/2})^{10}(2d_{5/2})^{2}$. However, the surface tension of the ${}^{96}$Zr nucleus with closed neutron configurations $(1g_{9/2})^{10}(2d_{5/2})^{6}$ proves to be close to $\sigma$ of the ‘‘double magic’’ ${}^{90}$Zr nucleus. (The closeness of the properties of ${}^{96}$Zr and those of ‘‘magic’’ nuclei was pointed out for the first time in [19].) The minimum values of parameter $r_{0}$ are also characteristic of the ${}^{90}$Zr and ${}^{96}$Zr isotopes with the maximum values of $\sigma$ (Fig. 4).

Fig. 3

The coefficients $\sigma$ for isotopes of Cr, Fe, Ni, and Zn.

Fig. 4

The coefficients $\sigma$ and the values of $r_{0}$ for the even isotopes of Zr.

4 THE SURFACE TENSION IN NUCLEI WITH $96\leq A\leq 150$

The results of calculations of the surface tension coefficients in the nuclei with the number of nucleons $96\leq A\leq 150$ are shown in Tables 4 and 5.

It is characteristic for the nuclei of this group to have relatively moderate fluctuations of the surface tension coefficient within the limits of four isotopes of one chemical element. For example, for tin ($Z=50$), the variations of the values of $\sigma$ for isotopes with the number of neutrons $N=66{-}72$ do not exceed $2.5\%$. The variations of the surface tension are relatively moderate also in the even isotopes of molybdenum ($Z=42$) and tellurium ($Z=52$), as well as in some other elements. A peculiarity of such elements is a large number of stable isotopes; for instance, tin ($Z=50$) has 10 stable isotopes. The maximum values of $\sigma$ in the nuclei belonging to the group with $96\leq A\leq 150$ are reached in barium (${}^{138}$Ba) and cerium (${}^{140}$Ce), i.e., in the nuclei with a ‘‘magic’’ number of neutrons $N=82$.

5 THE SURFACE TENSION IN NUCLEI WITH $152\leq A\leq 182$

This group of even–even nuclei differs from the nuclei above by low values of surface tension coefficients; here, for the nuclei with $Z=64{-}72$, the variations of $\sigma$ do not exceed $20\%$. A feature of the excitation spectra of these nuclei is their well pronounced rotational bands; the measurements of the quadruple moments for the odd isotopes of this group also point out to a high level of deformations.

6 THE SURFACE TENSION IN NUCLEI WITH $184\leq A\leq 210$

Table 3 The surface tension coefficients $\sigma$ (MeV/fm${}^{2}$) of nuclei with $68\leq A\leq 96$

Table 4 The surface tension coefficients $\sigma$ (MeV/fm${}^{2}$) of nuclei with $96\leq A\leq 122$

Table 5 The surface tension coefficients $\sigma$ (MeV/fm${}^{2}$) of nuclei with $124\leq A\leq 150$

Table 6 The surface tension coefficients $\sigma$ (MeV/fm${}^{2}$) of nuclei with $152\leq A\leq 182$

Table 7 The surface tension coefficients $\sigma$ (MeV/fm${}^{2}$) of nuclei with $184\leq A\leq 210$

For the nuclei with the number of nucleons from 182 to 194, the surface tension coefficient monotonously grows with growing $A$. In the even isotopes of mercury, the growth rate of $\sigma$ with adding of a pair of neutrons increases and reaches 3.3 MeV/fm${}^{2}$ for the ${}^{204}$Hg isotope. It should be noted that the estimations of parameter $r_{0}$ of the isotopes of mercury have shown that it decreases as the number of neutrons grows (Fig. 5).

The most pronounced influence of the shell structure on the surface tension of heavy stable nuclei manifests itself in the isotopes of mercury and lead: the surface tension coefficient $\sigma$ increases more then by three times in the case of adding a pair of protons $(3s)^{2}$ to the ${}^{204}$Hg nucleus and formation of a ‘‘magic’’ number of protons 82. The filling of a neutron shell of lead up to $N=126$ results in a still sharper growth of $\sigma$ (Fig. 6).

Fig. 5

The coefficients $\sigma$ and the values of $r_{0}$ for the even isotopes of Hg.

Fig. 6

The coefficients $\sigma$ and parameters $r_{0}$ for isotopes of Pb.

CONCLUSIONS

It follows from the presented tables of the surface tension coefficients of even–even atomic nuclei that the maximum values of $\sigma$ belong, as expected, to the double ‘‘magic’’ nuclei: ${}^{40}$Ca, ${}^{48}$Ca, ${}^{90}$Zr, and ${}^{208}$Pb. However, a relatively low value of $\sigma$ for ${}^{16}$O and, in addition, the fact that the surface tension of the ${}^{14}$C nucleus exceeds $\sigma$(${}^{16}$O) (Table 1) were unexpected.

The largest values of the surface tension coefficients for other even–even nuclei with numbers of nucleons close to each other are characteristic of those nuclei with the ‘‘magic’’ numbers of protons whose shell structure corresponds to two subsequently filled neutron subshells. These are ${}^{48}$Ca, ${}^{96}$Zr, and, especially, ${}^{210}$Pb. The particular properties of such nuclei are related to their so-called ‘‘neutron skin’’ [13, 14].

Adding a pair of neutrons to the structure of a ‘‘nonmagic’’ even–even nucleus leads, as a rule, to an increase in the surface tension and formation of a shell closed with respect to neutrons. Such a situation is characteristic of the following pairs: ${}^{36}$Ar${}_{18}{-}{}^{38}$Ar${}_{20}$, ${}^{48}$Ti${}_{26}{-}{}^{50}$Ti${}_{28}$, ${}^{34}$S${}_{18}{-}{}^{36}$S${}_{20}$, and ${}^{136}$Ba${}_{80}{-}{}^{138}$Ba${}_{82}$. However, the surface tension increases when adding a pair of neutrons in other cases as well, for example, for ${}^{82}$Kr${}_{46}{-}{}^{84}$Kr${}_{48}$, ${}^{110}$Cd${}_{62}{-}{}^{112}$Cd${}_{64}$. A subsequent increase in the coefficient $\sigma$ occurs also when adding neutron pairs in the tellurium isotopes ${}^{126}$Te${}_{74}{-}{}^{128}$Te${}_{76}{-}{}^{130}$Te${}_{78}$ (Table 5).

Adding of a pair of neutrons to a subshell that is closed with respect to neutrons leads, as a rule, to an decrease in coefficient $\sigma$. Examples of such cases are the following pairs:

${}^{16}$O${}_{8}{-}{}^{18}$O${}_{10}$, ${}^{38}$Ar${}_{20}{-}{}^{40}$Ar${}_{22}$, ${}^{40}$Ca${}_{20}{-}{}^{42}$Ca${}_{22}$, ${}^{90}$Zr${}_{50}{-}{}^{92}$Zr${}_{52}$, ${}^{140}$Ce${}_{82}{-}{}^{142}$Ce${}_{84}$.

Adding a pair of protons to a nucleus with a ‘‘magic’’ number of protons also leads to a decrease in the surface tension coefficient. This result is obtained by comparing coefficients $\sigma$ in the nuclei ${}^{18}$O–${}^{20}$Ne, ${}^{48}$Ca–${}^{50}$Ti, ${}^{90}$Zr–${}^{92}$Mo, ${}^{96}$Zr–${}^{98}$Mo.

If adding a pair of protons to a nucleus leads to formation of a subshell closed with respect to protons, as a rule, the coefficient $\sigma$ exhibits considerable growth: $\sigma({}^{54}\text{Fe})<\sigma({}^{56}\text{Ni})$. If adding a pair of protons forms a ‘‘double magic’’ nucleus, the growth of surface tension is especially significant. Such conclusions are made based on comparison of the surface tension coefficient in the nuclei ${}^{38}$Ar–${}^{40}$Ca, ${}^{88}$Sr–${}^{90}$Zr.

The sharpest increase in $\sigma$ (by more than by 5 times!) as a result of adding of a pair of protons occurs for the nuclei ${}^{204}$Hg–${}^{206}$Pb.

The tendencies above in the change in the surface tension coefficients when adding a pair of neutrons or protons are valid in most cases; however, they are not absolute! Exceptions to this rule are of particular interest.

As an example, adding a pair of neutrons to the ${}^{70}$Ge nucleus with formation of ${}^{72}$Ge, i.e., a nucleus with a ‘‘magic’’ number of neutrons $N=40$, is accompanied by a decrease in the surface tension coefficient (Table 3).

The most paradoxical fact revealed in the investigation of surface tension in the even–even nuclei is the situation with the lightest nuclei: adding a pair of protons to the nucleus of ${}^{14}$C with $\sigma$ = 5.5 MeV/fm${}^{2}$ leads to a double ‘‘magic’’ ${}^{16}$O nucleus with a significantly lower value of the surface tension coefficient $\sigma$ (Table 1).

An appropriate interpretation of the peculiarities of the changes in the surface tension coefficients in the process of filling nuclear shells requires a deeper study of the nucleon–nucleon and nucleon–cluster interactions.