1 INTRODUCTION

CNTs possess excellent electrical, mechanical and thermal characteristics and can be considered as a great reinforcement material in multifunctional composites and high performance structures. Therefore, the research on CNTs has been in progress in the last few years.

The dynamic properties of CNTs have been widely investigated in structural analyses,and have become vital components of various engineering applications. Recently, many dynamic researches have been carried out on carbon nanotubes reinforced composites (CNTRC). Gholami et al. [1] examine the impact of initial geometric imperfection on the nonlinear dynamical characteristics of functionally graded carbon nanotube-reinforced composite rectangular plates. By use of the first-order shear deformation theory of shells, Mohammadimehr et al. [2] analyzed the bending and free vibration of a rotating sandwich cylindrical shell with nanocomposite core and piezoelectric layers subjected to thermal and magnetic fields. Civalek et al. [3] used discrete singular convolution method to present the numerical solution and modeling of free vibrations of annular sector plate of CNTRC. Nonlinear vibration of CNTRC plates exposed to the parametric and forced excitations was improved by Guo et al. [4]. Jorge et al. [5] investigated a 3D multiscale finite element (FE) model and exploited dynamic response of polymer material reinforced with CNTs. In view of Donald shell theory and the effective model of multi-walled CNTs, Wang et al. [6] provided an analytical method for studying the dynamic stability of composites reinforced with multi-walled CNTs. Moumen et al. [7] investigated polymer composite impact responses with random distributions of CNTs. Mohandes et al. [8] evaluated free vibration behavior of a thin cylindrical shells made of single-walled CNTs reinforced fiber-metal composite. Fiorenzo et al. [9] investigated stability and thermoelastic vibrations of CNTRC structures in thermal environments. Thai et al. [10] analyzed free vibration and bending of CNTRC plates. Considering agglomeration effect of CNTs, Kamarian et al. [11] studied free vibration behavior of CNTRC conical shells. Vinyas [12] studied effect of free vibrations of CNTs reinforced inclined and magneto-electro- elastic rectangular plates by FE method.

However, weak interface of matrix and CNTs limits the use of CNTs in nanocomposites. Subsequently, functionally graded FG-CNTRC emerged and gained considerable research interest. Shen [13] investigated non-linear bending of single-walled CNT-reinforced functionally gradient nanocomposite plates and discovered that strength bonding interface could be enhanced by using gradient distribution of CNT in the matrix. Dynamic behaviors of FG-CNTRC shells were exploited by some researcher [14] using a linear discrete dual-controller FE model. Jiao et al. [15] applied a semi-analytical method and addressed dynamic buckling of cylindrical shells made of FG-CNTRC exposed to dynamic displacement loading. Chakraborty et al. [16] applied semi-analytical method to examine vibration and stability of CNTs reinforced FG laminated composite cylindrical shells. Zhao [17] used modified Fourier series of field variables and exploited free vibrations behavior of FG-CNTRC truncated conical plates under general boundary conditions. Qin et al. [18] provides a general method for analyzing effect of free vibration of rotating cylindrical shells made of FG-CNTRC under arbitrary boundary conditions. Mirzaei et al. [19] used Donnell kinematics assumption and first-order shear deformation shell theory (FSDT) to deal with free vibration of single-walled CNTRC plates. Moradi et al. [20] adopted a mesh-free method and dynamically analyzed SWCNT reinforced nanocomposite cylinder under an impact load. Heshmati et al. [21] employed Timoshenko beam theory (TBT) to discuss dynamic responses of nanocomposite beams made of FG multi-walled CNT polystyrene under multiple moving loads. Using semi-analytical method, Zhong et al. [22] discussed the vibrations of sector, circular and annular plates made of FG-CNTRC with arbitrary boundary conditions. Nguyen et al. [23] developed a novel technique for investigating nonlinear and vibration dynamic responses of imperfect double curved shallow shells made of FG-CNTRC., Fantuzzi et al. [24] used non-uniform rational B-spline curves and researched free vibration of FG-CNT structures with arbitrary shape. Adopting first-order beam theory and improved Fourier series, Shi et al. [25] obtained semi-analytical solutions for in-plane free vibrations of circular arches made of FG-CNTRC under elastic constraints. Chakraborty et al. [26] analyzed the vibration and stability of CNTs reinforced FG laminated composite cylindrical shells through semi-analytical method.

As technology and science improves, novel intelligent structures, including FG-CNTRC components combined with piezoelectric sensors or actuators, have attracted more and more attention from the scientific community. These structures are actually critical due to their relation with thermal stress control, transportation engineering, structural health monitoring and structural vibration control. A few research works have been conducted on dynamic and static behaviors of FG-CNTRC structures containing surface-bonded PL. Rafiee et al. [27] used von Kármán geometric non-linearity and FSDT and investigated non-linear dynamic stabilities of imperfect piezoelectric plates made of FG-CNTRC. Applying Hamilton’s principle and classical plate theory, Rezaee et al. [28] illustrated non-linear stability and vibrations of simply supported (SS) FG rectangular plates attached by PLs. According to first order shear deformation plate theory, Kiani [29] evaluated free vibration of CNTRC plates bonded with PLs at both top and bottom surfaces. Alibeigloo et al. [30] used state space method along radial direction and gave the thermo-electro- elasticity solution of FG-CNTRC cylindrical shells bonded with PL. Ansari et al. [31] put forward an theoretical solution for nonlinear post-buckling of functionally graded carbon nanotube reinforced composite shells with piezoelectric layers. Employing generalized differential quadrature and Navier methods, Hamed et al. [32] evaluated buckling and free vibration of fast rotating CNT reinforced cylindrical piezoelectric shells. Utilizing Galerkin’s method and Airy’s stress function, Ninh et al. [33] exploited torsional post-buckling of the piezoelectric FG-CNTRC shells. Rafiee et al. [34] applied Euler–Bernoulli beam theory (EBBT) and von Kármán geometric nonlinearity and presented nonlinear thermal bifurcation buckling behavior of CNTRC beams with PLs bonded their surface. Using Flügge-Lur’e-Bryrne theory, Ninh [35] investigated the nonlinear vibration of the full-filled fluid shell through the Galerkin method. Nonlinear dynamics of the conveying-fluid toroidal shell segments made of functionally graded (FG) grapheme nanoplatelets (GNPs) with piezoelectric layers are studied by Ninh [36]. Adopting an analytical approach, Tien [37] researched nonlinear vibration of functionally graded carbon nanotube–reinforced polymer plate subjected to electro–thermo–mechanical loads resting on elastic foundations. But so far, research on bifurcation and chaos of FG-CNTRC shells containing PL has not been reported in printed publication. Bifurcation is defined that the qualitative behavior of a dynamic system changes fundamentally with the change of its parameters. Chaos is a periodic long-term behavior in a deterministic system, which is sensitive to initial conditions. When the system is in bifurcation or chaos state, the noise, stability, and reliability of the system will be seriously affected, which will directly lead to the damage of the structure.

With this in mind, we plan to research the bifurcation and chaos of FG-CNTRC cylindrical shell containing PL under electro-thermo-mechanical loads. Employing variational principle, equations of nonlinear motion of shells were gained. Through the introduction of additional state variable and Galerkin method, the equations of nonlinear motion were converted to FNODE and were resolved employing fourth order Runge-Kutta approach. The obtained numerical results were graphically depicted which showed the influences of distribution pattern of CNTs, temperature, volume fraction and voltage on bifurcation and chaos of piezoelectric FG-CNTRC shells.

2 THEORETICAL FORMULATIONS

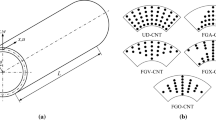
Figure 1 depicts a CNT-reinforced cylindrical shell in a typical coordinate system (x, y, z). R is middle surface radius of shell, L is length and h is thickness with two PLs bonded to the surface with thickness hp. H is total thickness of shell. As can be seen in Fig. 1, CNT reinforcement can be uniformly distributed (UD) or FG along the thickness including FG-X and FG-O. Furthermore, shells were under uniform temperature rise \(\Delta T\), applied voltage V and transverse dynamic load \(q(x,y,t)\).

Fig. 1.
figure 1

CNTRC cylindrical shell integrated by PLs.

Full size image

2.1 Material Froperties of FG-CNTRC

The CNTRC is obtained by mixing an isotropic matrix and SWCNT. According to mixture rule, effective material characteristics of CNTRC shells was stated as [13]

$${{E}_{{11h}}} = {{\eta }_{1}}{{V}_{{CN}}}E_{{11}}^{{CN}} + V_{m}^{{}}E_{{}}^{m},\quad \frac{{{{\eta }_{2}}}}{{{{E}_{{22h}}}}} = \frac{{{{V}_{{CN}}}}}{{E_{{22}}^{{CN}}}} + \frac{{V_{m}^{{}}}}{{E_{{}}^{m}}},\quad \frac{{{{\eta }_{3}}}}{{{{G}_{{12h}}}}} = \frac{{{{V}_{{CN}}}}}{{G_{{12}}^{{CN}}}} + \frac{{V_{m}^{{}}}}{{G_{{}}^{m}}},$$
(1)

where \(G_{{12}}^{{CN}}\) and \(E_{{11}}^{{CN}},E_{{22}}^{{CN}}\) are shear and Young’s moduli of CNT, respectively, and Gm and Em are the properties of corresponding isotropic matrices. To take into account scale-dependent material characteristics, ηj \((j = 1,2,3)\), the efficiency parameters of CNT, obtained through matching CNTRC effective properties from the rule of mixture with those from MD simulations, were introduced. \({{V}_{{CN}}}\) and \(V_{m}^{{}}\) are CNT volume fractions and matrix, respectively.

Uniform and two FG CNT distributions along the thickness were assumed to be:

$$\left\{ {\begin{array}{*{20}{c}} {{{V}_{{CN}}} = V_{{CN}}^{*}{\text{ }}\left( {UD - CNTRC} \right)} \\ {{{V}_{{CN}}} = 2\left( {1 - \frac{{2\left| z \right|}}{h}} \right)V_{{CN}}^{*}{\text{ }}\left( {FGO - CNTRC} \right)} \\ {{{V}_{{CN}}} = 2\left( {\frac{{2\left| z \right|}}{h}} \right)V_{{CN}}^{*}{\text{ }}\left( {FGX - CNTRC} \right)} \end{array} } \right.,$$
(2)

where

$$V_{{CN}}^{*} = \frac{{{{W}_{{CN}}}}}{{{{W}_{{CN}}} + ({{\rho }^{{CN}}}{\text{/}}{{\rho }^{m}}) - ({{\rho }^{{CN}}}{\text{/}}{{\rho }^{m}}){{W}_{{CN}}}}}$$
(3)

and \({{W}_{{CN}}}\) is CNT mass fraction, and ρm and ρCN are matrix and CNT mass densities, respectively.

Mass density and Poisson’s ratio were calculated by

$${{{v}}_{{12h}}} = V_{{CN}}^{*}{v}_{{12}}^{{CN}} + V_{m}^{{}}{v}_{{}}^{m},\quad {{\rho }_{h}} = {{V}_{{CN}}}{{\rho }^{{CN}}} + V_{m}^{{}}\rho _{{}}^{m},$$
(4)

where \({v}_{{12}}^{{CN}}\) and \({v}_{{}}^{m}\) are CNT and matrix Poisson’s ratio, respectively.

Thermal expansion coefficients along transverse and longitudinal directions were expressed as

$${{\alpha }_{{11h}}} = {{V}_{{CN}}}\alpha _{{11}}^{{CN}} + V_{m}^{{}}\alpha _{{}}^{m},$$
$${{\alpha }_{{22h}}} = (1 + {v}_{{12}}^{{CN}}){{V}_{{CN}}}\alpha _{{22}}^{{CN}} + (1 + {v}_{{}}^{m})V_{m}^{{}}\alpha _{{}}^{m} - {{{v}}_{{12h}}}{{\alpha }_{{11h}}},$$
(5)

where \(\alpha _{{11}}^{{CN}},\alpha _{{22}}^{{CN}}\) and αm are CNT and matrix thermal expansion coefficients, respectively.

2.2 Displacement Field Model

Assuming that \(\bar {u},{\bar {v}},\bar {w}\) are the displacements along axes x, y, z respectively, and \(u,{v}\), w are their corresponding mid-plane displacements, piezoelectric shell displacement field were written as

$$\begin{gathered} \bar {u}(x,y,z,{\kern 1pt} t) = u(x,y,t) - z{{w}_{{,x}}}(x,y,t), \\ {\bar {v}}(x,y,z,{\kern 1pt} t) = {v}(x,y,t) - z{\kern 1pt} {{w}_{{,y}}}(x,y,t), \\ \bar {w}(x,y,z,{\kern 1pt} t) = w(x,y,t). \\ \end{gathered} $$
(6)

In view of the von Kármán-Donnell shell theory, relationships of nonlinear strain-displacements for piezoelectric shell are

$${{\bar {\varepsilon }}_{x}} = {{\varepsilon }_{x}} + z{{\kappa }_{x}}\quad {{\bar {\varepsilon }}_{y}} = {{\varepsilon }_{y}} + z{{\kappa }_{y}}\quad {{\bar {\varepsilon }}_{{xy}}} = {{\varepsilon }_{{xy}}} + z{{\kappa }_{{xy}}},$$
(7)

where \(\varepsilon _{x}^{{}},\varepsilon _{y}^{{}},\varepsilon _{{xy}}^{{}}\) are strain on middle surface and \({{\kappa }_{x}},{{\kappa }_{y}},{{\kappa }_{{xy}}}\) are the middle surface curvatures, and

$$\begin{gathered} \varepsilon _{x}^{{}} = u_{{,x}}^{{}} + \frac{1}{2}w_{{,x}}^{2},\quad \varepsilon _{y}^{{}} = {v}_{{,y}}^{{}} - \frac{w}{R} + \frac{1}{2}w_{{,y}}^{2}{\kern 1pt} ,\quad \varepsilon _{{xy}}^{{}} = u_{{,y}}^{{}} + {v}_{{,x}}^{{}} + {{w}_{{,x}}}{{w}_{{,y}}}, \\ {{\kappa }_{x}} = - {{w}_{{,xx}}},\quad {{\kappa }_{y}} = - {{w}_{{,yy}}},\quad {{\kappa }_{{xy}}} = - 2{{w}_{{,xy}}}. \\ \end{gathered} $$
(8)

2.3 Constitutive Equations

Under thermal, electrical and mechanical loadings, the constitutive equations of CNT-reinforced cylindrical shell containing PL was written as

$$\sigma _{i}^{{}} = {{Q}_{{ij}}}({{\bar {\varepsilon }}_{j}} - {{\alpha }_{j}}\Delta T) - e_{{ik}}^{T}{{E}_{k}}\quad (i,j = 1,2, \cdots 6,k = 1,2,3),$$
(9)

where, \({{e}_{{ik}}}\), \({{\alpha }_{\kappa }}\) and \({{E}_{\kappa }}\)represent piezoelectric constants, thermal expansion coefficient and electric field, respectively. \({{Q}_{{ij}}}\) if stiffness of plane stress-reduced expressed as

$${{Q}_{{11}}} = {{Q}_{{11h}}} = \frac{{{{E}_{{11h}}}}}{{1 - {v}{}_{{12h}}{v}{}_{{21h}}}},\quad {{Q}_{{12}}}\, = \,{{Q}_{{12h}}}\, = \,\frac{{{v}{}_{{12h}}{{E}_{{12h}}}}}{{1 - {v}{}_{{12h}}{v}{}_{{21h}}}},\quad {{Q}_{{22}}} = {{Q}_{{22h}}} = \frac{{{{E}_{{22h}}}}}{{1 - {v}{}_{{12h}}{v}{}_{{21h}}}},\quad {{Q}_{{66}}} = {{Q}_{{66h}}} = {{G}_{{12h}}},$$
(10)

for the FG-CNTRC, and

$${{Q}_{{11}}} = {{Q}_{{11p}}} = {{Q}_{{22}}} = {{Q}_{{22p}}} = \frac{{{{E}_{{11p}}}}}{{1 - {v}_{p}^{2}}},\quad {{Q}_{{12}}} = {{Q}_{{12h}}} = \frac{{{v}{}_{p}{{E}_{{11p}}}}}{{1 - {v}_{p}^{2}}},\quad {{Q}_{{66}}} = {{G}_{{12p}}} = \frac{{{{E}_{{11p}}}}}{{2\left( {1 + {{{v}}_{p}}} \right)}}$$
(11)

for the PL.

By assuming the application of only electric-field component \({{E}_{z}}\) on inner and outer surfaces of cylindrical shells along thickness and \({{E}_{z}}\) and V to be electric-field intensity and electric voltage, respectively, following equation was written

$${{E}_{z}} = V{\text{/}}{{h}_{p}}.$$
(12)

2.4 Governing Equations

For CNT-reinforced cylindrical shells with PL, total potential energy Π was stated as

$$\Pi = K - U + \Gamma $$
(13)

in which K means the kinetic energy, U means the strain energy and Γ means the work done by the transverse dynamic load.

Dynamic governing equations of structure can be reduced using the variational principle (\(\delta \Pi = 0\)) as

$$\begin{gathered} {{N}_{{x,x}}} + {{N}_{{xy,y}}} = ({{\rho }_{h}}h + 2{{\rho }_{p}}{{h}_{p}}){{u}_{{,tt}}}, \\ {{N}_{{xy,x}}} + {{N}_{{y,y}}} = ({{\rho }_{h}}h + 2{{\rho }_{p}}{{h}_{p}}){{{v}}_{{,tt}}}, \\ {{M}_{{x,xx}}} + 2{{M}_{{xy,xy}}} + {{M}_{{y,yy}}} + {{N}_{y}}{\text{/}}R + {{N}_{x}}{{w}_{{,xx}}} + 2{{N}_{{xy}}}{{w}_{{,xy}}} + {{N}_{y}}{{w}_{{,yy}}} + q = ({{\rho }_{h}}h + 2{{\rho }_{p}}{{h}_{p}}){{w}_{{,tt}}}, \\ \end{gathered} $$
(14)

where

$$\left\{ {\begin{array}{*{20}{c}} {{{N}_{x}}} \\ {{{N}_{y}}} \\ {{{N}_{{xy}}}} \\ {{{M}_{x}}} \\ {{{M}_{y}}} \\ {{{M}_{{xy}}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{A}_{{11}}}}&{{{A}_{{12}}}}&{{{A}_{{16}}}}&{{{B}_{{11}}}}&{{{B}_{{12}}}}&{{{B}_{{16}}}} \\ {{{A}_{{12}}}}&{{{A}_{{22}}}}&{{{A}_{{26}}}}&{{{B}_{{12}}}}&{{{B}_{{22}}}}&{{{B}_{{26}}}} \\ {{{A}_{{16}}}}&{{{A}_{{26}}}}&{{{A}_{{66}}}}&{{{B}_{{16}}}}&{{{B}_{{26}}}}&{{{B}_{{66}}}} \\ {{{B}_{{11}}}}&{{{B}_{{12}}}}&{{{B}_{{16}}}}&{{{D}_{{11}}}}&{{{D}_{{12}}}}&{{{D}_{{16}}}} \\ {{{B}_{{12}}}}&{{{B}_{{22}}}}&{{{B}_{{26}}}}&{{{D}_{{12}}}}&{{{D}_{{22}}}}&{{{D}_{{26}}}} \\ {{{B}_{{16}}}}&{{{B}_{{26}}}}&{{{B}_{{66}}}}&{{{D}_{{16}}}}&{{{D}_{{26}}}}&{{{D}_{{66}}}} \end{array}} \right\}\left\{ {\begin{array}{*{20}{c}} {{{\varepsilon }_{x}}} \\ {{{\varepsilon }_{y}}} \\ {{{\varepsilon }_{{xy}}}} \\ {{{\kappa }_{x}}} \\ {{{\kappa }_{y}}} \\ {{{\kappa }_{{xy}}}} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {N_{x}^{T}} \\ {N_{y}^{T}} \\ {N_{{xy}}^{T}} \\ {M_{x}^{T}} \\ {M_{y}^{T}} \\ {M_{{xy}}^{T}} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {N_{x}^{P}} \\ {N_{y}^{P}} \\ {N_{{xy}}^{P}} \\ {M_{x}^{P}} \\ {M_{y}^{P}} \\ {M_{{xy}}^{P}} \end{array}} \right\}.$$
(15)

In the above equation, superscripts “P” and “T” denote electric and thermal loads, respectively, and \({{A}_{{ij}}},{{B}_{{ij}}},{{D}_{{ij}}}\) are stretching, stretching–bending coupling and bending stiffness coefficients, respectively, stated as

$$\left( {{{A}_{{ij}}},{{B}_{{ij}}},{{D}_{{ij}}}} \right) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} {{{Q}_{{ijh}}}(1,z,{{z}^{2}})} dz + \int\limits_{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}}^{{H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}} {{{Q}_{{ijp}}}(1,z,{{z}^{2}})} dz + \int\limits_{ - {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}}^{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0em} 2}} {{{Q}_{{ijp}}}(1,z,{{z}^{2}})} dz{\text{ }}\left( {i,j = 1,2,6} \right)$$
(16)

The resultant moment, electrical force and thermal are defined as

$$\left\{ {\begin{array}{*{20}{c}} {N_{x}^{T}}&{M_{x}^{T}} \\ {N_{y}^{T}}&{M_{y}^{T}} \\ {N_{{xy}}^{T}}&{M_{{xy}}^{T}} \end{array}} \right\} = \int\limits_{ - h/2}^{h/2} {\left[ {\begin{array}{*{20}{c}} {{{Q}_{{11h}}}}&{Q_{{12h}}^{{}}}&0 \\ {Q_{{12h}}^{{}}}&{Q_{{22h}}^{{}}}&0 \\ 0&0&{Q_{{66h}}^{{}}} \end{array}} \right]} \left\{ \begin{gathered} {{\alpha }_{{11h}}} \\ {{\alpha }_{{22h}}} \\ 0 \\ \end{gathered} \right\}(1,z)\Delta Tdz$$
$$ + \int\limits_{h/2}^{H/2} {\left[ {\begin{array}{*{20}{c}} {{{Q}_{{11p}}}}&{Q_{{12p}}^{{}}}&0 \\ {Q_{{12p}}^{{}}}&{Q_{{22p}}^{{}}}&0 \\ 0&0&{Q_{{66p}}^{{}}} \end{array}} \right]} \left\{ \begin{gathered} {{\alpha }_{{11p}}} \\ {{\alpha }_{{22p}}} \\ 0 \\ \end{gathered} \right\}(1,z)\Delta Td + \int\limits_{ - H/2}^{ - h/2} {\left[ {\begin{array}{*{20}{c}} {{{Q}_{{11p}}}}&{Q_{{12p}}^{{}}}&0 \\ {Q_{{12p}}^{{}}}&{Q_{{22p}}^{{}}}&0 \\ 0&0&{Q_{{66p}}^{{}}} \end{array}} \right]} \left\{ \begin{gathered} {{\alpha }_{{11p}}} \\ {{\alpha }_{{22p}}} \\ 0 \\ \end{gathered} \right\}(1,z)\Delta Td$$
$$\left\{ {\begin{array}{*{20}{c}} {N_{x}^{p}}&{M_{x}^{p}} \\ {N_{y}^{p}}&{M_{y}^{p}} \\ {N_{{xy}}^{p}}&{M_{{xy}}^{p}} \end{array}} \right\} = \int\limits_{h/2}^{H/2} {\left[ {\begin{array}{*{20}{c}} 0&0&{{{e}_{{31}}}} \\ 0&0&{{{e}_{{32}}}} \\ 0&0&0 \end{array}} \right]} \left\{ \begin{gathered} 0 \\ 0 \\ {{E}_{z}} \\ \end{gathered} \right\}(1,z)dz + \int\limits_{ - H/2}^{ - h/2} {\left[ {\begin{array}{*{20}{c}} 0&0&{{{e}_{{31}}}} \\ 0&0&{{{e}_{{32}}}} \\ 0&0&0 \end{array}} \right]} \left\{ \begin{gathered} 0 \\ 0 \\ {{E}_{z}} \\ \end{gathered} \right\}(1,z)dz.$$
(17)

In the case of axisymmetry, the circumferential displacement \({v}\) is zero, and \(u,w\) is a function of only x. Therefore, second equation in (14) is balanced automatically and could be left out. Considering Eqs. (8) and (15), and using the following dimensionless parameters,

$$\xi = \frac{x}{L},\quad W = \frac{w}{H},{\kern 1pt} \quad U = \frac{u}{L},\quad Q = \frac{{q{{L}^{4}}}}{{A_{{22}}^{{}}{{H}^{3}}}},\quad \lambda = \frac{L}{H}{\kern 1pt} ,{\kern 1pt} \quad K = \frac{{{{L}^{2}}}}{{RH}},\quad \tau = \frac{t}{{{{L}^{2}}}}\sqrt {A_{{22}}^{{}}{{H}^{2}}{\text{/}}({{\rho }_{h}}h + 2{{\rho }_{p}}{{h}_{p}})} $$
(18)

the nonlinear dynamic equations of axisymmetric CNT-reinforced cylindrical shells with PL under electro-thermo-mechanical loadings were expressed as

$$S_{{11A}}^{{}}{{U}_{{,\xi \xi }}} - S_{{12A}}^{{}}\frac{K}{{{{\lambda }^{2}}}}{{W}_{{,\xi }}} + S_{{11A}}^{{}}\frac{1}{{{{\lambda }^{2}}}}{{W}_{{,\xi }}}{{W}_{{,\xi \xi }}} - S_{{11B}}^{{}}\frac{1}{{{{\lambda }^{2}}}}{{W}_{{,\xi \xi \xi }}} = \frac{{S_{{22A}}^{{}}}}{{{{\lambda }^{2}}}}{{U}_{{,\tau \tau }}}$$
$$\begin{gathered} - \frac{1}{{12}}S_{{11D}}^{{}}{{W}_{{,\xi \xi \xi \xi }}}\, + \,\left[ {S_{{11A}}^{{}}{{\lambda }^{2}}{{U}_{{,\xi }}} + \frac{{S_{{11A}}^{{}}}}{2}W_{{,\xi }}^{2}\, - \,S_{{12A}}^{{}}KW\, - \,S_{{11B}}^{{}}{{W}_{{,\xi \xi }}}\, - \,{{\lambda }^{2}}\frac{{N_{x}^{T} + N_{x}^{p}}}{H}} \right]{{W}_{{,\xi \xi }}}\, + \,S_{{12A}}^{{}}K{{\lambda }^{2}}{{U}_{{,\xi }}} + \frac{{S_{{12A}}^{{}}K}}{2}W_{{,\xi }}^{2} \\ - \,\,S_{{22A}}^{{}}K_{{}}^{2}{{W}_{{}}} - {{\lambda }^{2}}K\frac{{N_{y}^{T} + N_{y}^{p}}}{H} - S_{{12B}}^{{}}(1 + {{\lambda }^{2}})K{{W}_{{,\xi \xi }}} + S_{{11B}}^{{}}({{\lambda }^{2}}{{U}_{{,\xi \xi \xi }}} + W_{{,\xi \xi }}^{2}) + {{W}_{{,\xi }}}{{W}_{{,\xi \xi \xi }}} + S_{{22A}}^{{}}Q = S_{{22A}}^{{}}{{W}_{{,\tau \tau }}}, \\ \end{gathered} $$
(19)

where \(S_{{ijA}}^{{}} = A_{{ij}}^{{}}{\text{/}}{{H}_{{}}},S_{{ijB}}^{{}} = B_{{ij}}^{{}}{\text{/}}H_{{}}^{2},S_{{ijD}}^{{}} = D_{{ij}}^{{}}{\text{/}}(H_{{}}^{3}{\text{/1}}2)\).

Assuming simply supported conditions for both shell ends, the following dimensionless boundary conditions were obtained

$$\begin{gathered} {{N}_{\xi }}(0) = 0,\quad W(0) = 0,\quad W{{,}_{{\xi \xi }}}(0) = 0{\kern 1pt} , \hfill \\ {\kern 1pt} {{N}_{\xi }}(1) = 0,{\kern 1pt} \quad {\kern 1pt} W(1) = 0,\quad W{{,}_{{\xi \xi }}}(1) = 0{\kern 1pt} , \hfill \\ \end{gathered} $$
(20)

where

$${{N}_{\xi }} = \left[ {{{S}_{{11A}}}\left( {{{U}_{{,\xi }}} + \frac{1}{{2{{\lambda }^{2}}}}W_{{,\xi }}^{2}} \right) - {{S}_{{12A}}}\frac{K}{{{{\lambda }^{2}}}}W - S_{{11B}}^{{}}\frac{1}{{{{\lambda }^{2}}}}{{W}_{{,\xi \xi }}} - \frac{{N_{x}^{T} + N_{x}^{p}}}{H}} \right..$$

3 SOLUTION APPROACH

To meet boundary conditions provided in Eq. (20), formal solution of Eq. (19) is considered to be

$$\begin{gathered} W = \sum\limits_{m = 1,3,}^\infty {{{{\tilde {w}}}_{m}}(\tau )} \sin m\pi \xi , \\ U = - \frac{1}{{2\pi }}g(\eta ){\kern 1pt} \sin 2\pi \xi + \sum\limits_{m = 1,3,}^\infty {{{{\tilde {u}}}_{m}}(\tau )} \cos m\pi \xi {\kern 1pt} , \\ \end{gathered} $$
(21)

where \(g(\eta )\) are defined as

$$g(\eta ) = \frac{1}{{2{{\lambda }^{2}}}}{{W}_{{,\xi }}}^{2} - {{\varphi }_{1}},\quad {\text{on}}\quad \xi = 0\quad {\text{and}}\quad \xi = 1,$$
(22)

and

$${{\varphi }_{1}} = \frac{{N_{x}^{T} + N_{x}^{p}}}{{{{S}_{{11A}}}H}} + \frac{{{{S}_{{12A}}}K}}{{{{S}_{{11A}}}{{\lambda }^{2}}}}W + \frac{{S_{{11B}}^{{}}}}{{{{S}_{{11A}}}{{\lambda }^{2}}}}{{W}_{{,\xi \xi }}}.$$
(23)

The dynamic load was assumed to be:

$$Q = F\sin \pi \xi ,\quad F = {{F}_{0}}\sin \omega \tau $$
(24)

In above equation, ω and F0 are the frequency and dimensionless amplitude of dynamic load, respectively.

By substituting Eq. (21) into Eq. 19), the first and second result equations are multiplied by \(\cos i\pi \xi \) and \(\sin i\pi \xi \), respectively. Then, integrating the obtained equations in the range of 0 to 1 and performing first-order Galerkin truncation, gave nonlinear ordinary differential equations by time functions \(\tilde {u}\) and \(\tilde {w}\) as

$$\begin{gathered} {{L}_{{11}}}\tilde {u} + {{L}_{{12}}}\tilde {w} + {{L}_{{13}}}{{{\tilde {w}}}^{2}} + {{L}_{{14}}} = 0, \\ {{L}_{{31}}}\tilde {w} + {{L}_{{32}}}{{{\tilde {w}}}^{3}} + {{L}_{{33}}}\tilde {u}\tilde {w} + {{L}_{{34}}}{{{\tilde {w}}}^{2}} + {{L}_{{35}}}\tilde {u} + {{L}_{{36}}} + pF = p\ddot {\tilde {w}}, \\ \end{gathered} $$
(25)

where

$$\begin{gathered} {{L}_{{11}}} = \int\limits_0^1 {{{S}_{{11A}}}{{\Lambda }_{{1,\xi \xi }}}} {{\Lambda }_{1}}d\xi , \\ {{L}_{{12}}} = \int\limits_0^1 {\left( { - {{S}_{{12A}}}\frac{K}{{{{\lambda }^{2}}}}{{\Lambda }_{{3,\xi }}} - {{S}_{{11B}}}\frac{1}{{{{\lambda }^{2}}}}{{\Lambda }_{{3,\xi \xi \xi }}}} \right)} {{\Lambda }_{1}}d\xi ,, \\ \end{gathered} $$
$$\begin{gathered} {{L}_{{13}}} = \int\limits_0^1 {\frac{{{{S}_{{11A}}}}}{{{{\lambda }^{2}}}}({{\Lambda }_{{4,\xi \xi }}} + {{\Lambda }_{{3,\xi }}}{{\Lambda }_{{3,\xi \xi }}}){{\Lambda }_{1}}} d\xi , \\ {\kern 1pt} {{L}_{{14}}} = \int\limits_0^1 {{{S}_{{11A}}}{{\Lambda }_{{6,\xi \xi }}}{{\Lambda }_{1}}} d\xi , \\ \end{gathered} $$
$${{L}_{{31}}} = \int\limits_0^1 {\left[ { - \frac{{{{S}_{{11D}}}}}{{12}}{{\Lambda }_{{3,\xi \xi \xi \xi }}} + ( - {{S}_{{11A}}}\lambda _{{}}^{2}\frac{2}{{{{\pi }^{2}}}}{{\varphi }_{2}}{{\Lambda }_{{4,\xi }}} + {{\varphi }_{2}}){{\Lambda }_{{3,\xi \xi }}} - {{S}_{{22A}}}{{K}^{2}}{{\Lambda }_{3}} - {{S}_{{12B}}}(1 + {{\lambda }^{2}})K{{\Lambda }_{{3,\xi \xi }}}} \right]} {{\Lambda }_{3}}d\xi ,$$
$$\begin{gathered} {{L}_{{32}}} = \int\limits_0^1 {\left. {{{S}_{{11A}}}\left( {{{\Lambda }_{{4,\xi }}} + \frac{1}{2}\Lambda _{{3,\xi }}^{2}} \right){{\Lambda }_{{3,\xi \xi }}}} \right]} {{\Lambda }_{3}}d\xi , \\ {{L}_{{33}}} = \int\limits_0^1 {{{S}_{{11A}}}H_{{}}^{2}{{\Lambda }_{{1,\xi }}}{{\Lambda }_{{3,\xi \xi }}}} {{\Lambda }_{3}}d\xi , \\ {{L}_{{34}}} = \int\limits_0^1 {\left( { - ({{S}_{{12A}}}K{{\Lambda }_{3}} + {{S}_{{11B}}}{{\Lambda }_{{3,\xi \xi }}}){{\Lambda }_{{3,\xi \xi }}} + \frac{{{{S}_{{12A}}}K}}{2}\Lambda _{{3,\xi }}^{2} + {{S}_{{11B}}}\Lambda _{{3,\xi \xi }}^{2} + {{\Lambda }_{{3,\xi }}}{{\Lambda }_{{3,\xi \xi \xi }}} + {{\Lambda }_{{4,\xi }}} + \frac{1}{2}\Lambda _{{3,\xi }}^{2}} \right)} {{\Lambda }_{3}}d\xi , \\ \end{gathered} $$
$$\begin{gathered} {{L}_{{35}}} = \int\limits_0^1 {({{S}_{{12A}}}K\lambda _{{}}^{2}{{\Lambda }_{{1,\xi }}} + {{S}_{{11B}}}\lambda _{{}}^{2}{{\Lambda }_{{1,\xi \xi \xi }}})} {{\Lambda }_{3}}d\xi {\kern 1pt} {\kern 1pt} , \\ {{L}_{{36}}} = \int\limits_0^1 {{{\varphi }_{3}}} {{\Lambda }_{3}}d\xi , \\ p = \int\limits_0^1 {{{S}_{{22A}}}} \Lambda _{3}^{2}d\xi . \\ \end{gathered} $$

In the above equations,

$${{\Lambda }_{1}} = \cos \pi \xi ,\quad {{\Lambda }_{3}} = \sin \pi \xi ,\quad {{\Lambda }_{4}} = - \frac{\pi }{4}\sin 2\pi \xi ,{\kern 1pt} \quad {{\Lambda }_{6}} = \frac{{{{\varphi }_{2}}}}{{2\pi }}{\kern 1pt} \sin 2\pi \xi ,$$
$$\begin{gathered} {{\varphi }_{2}} = - H(N_{x}^{T} + N_{x}^{p}), \\ {{\varphi }_{3}} = - HK(N_{y}^{T} + N_{y}^{p}). \\ \end{gathered} $$
(26)

The \(\tilde {u}\) in the first one of Eq.(25) can be solved as

$$\tilde {u} = - \frac{1}{{{{L}_{{11}}}}}({{L}_{{12}}}\tilde {w} + {{L}_{{13}}}{{\tilde {w}}^{2}} + {{L}_{{14}}}).$$
(27)

Which is expressed as

$$\tilde {u} = {{\Gamma }_{0}} + {{\Gamma }_{1}}\tilde {w} + {{\Gamma }_{2}}{{\tilde {w}}^{2}}.$$
(28)

By the substitution of Eq. (28) into second equation of Eq. (25) and bringing linear damping term \(\mu \dot {\tilde {w}}\), nonlinear governing equation only obtained by \(\tilde {w}\) for CNT-reinforced cylindrical shell containing PL was given as

$${{\varphi }_{1}}\tilde {w} + {{\varphi }_{2}}{{\tilde {w}}^{2}} + {{\varphi }_{3}}{{\tilde {w}}^{3}} + {{\varphi }_{4}} + pF - \mu \dot {\tilde {w}} = p\ddot {\tilde {w}},$$
(29)

where

$$\begin{gathered} {{\phi }_{1}} = {{L}_{{31}}} + {{L}_{{33}}}{{\Gamma }_{0}} + {{L}_{{35}}}{{\Gamma }_{1}} \\ {{\phi }_{2}} = {{L}_{{34}}} + {{L}_{{33}}}{{\Gamma }_{1}} + {{L}_{{35}}}{{\Gamma }_{2}} \\ {{\phi }_{3}} = {{L}_{{32}}} + {{L}_{{33}}}{{\Gamma }_{2}} \\ {{\phi }_{4}} = {{L}_{{36}}} + {{L}_{{35}}}{{\Gamma }_{0}} \\ \end{gathered} $$

By the introduction of state variables \({{y}_{1}}(\tau ) = \tilde {w}{\kern 1pt} {\kern 1pt} (\tau ),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{y}_{2}}(\tau ) = \dot {\tilde {w}}{\kern 1pt} {\kern 1pt} (\tau )\), Eq.(29) was transformed to the first order differential equations below

$$\begin{gathered} {{{\dot {y}}}_{1}} = {{y}_{2}}, \\ {{{\dot {y}}}_{2}} = {{p}^{{ - 1}}}{\kern 1pt} {\kern 1pt} ({{\phi }_{1}}{{y}_{1}} + {{\phi }_{2}}{\kern 1pt} y_{1}^{2} + {{\phi }_{3}}{\kern 1pt} y_{1}^{3} + {{\phi }_{4}} - \mu {{y}_{2}} + pF). \\ \end{gathered} $$
(30)

Equation (30) was resolved using fourth-order Runge-Kutta method. Then, bifurcation diagram, phase plane trajectory, Poincaré map and time course curve can also be achieved through uniting the numerical analysis method used for nonlinear dynamics.

4 NUMERICAL RESULTS AND DISCUSSION

In order to verify the current analysis, first dynamic response of FGX CNTRC cylindrical shells under impact loads is studied. Material and geometrical parameters of shells are similar to those in [38]. In Fig. 2, the obtained time histories for FGX CNTRC cylindrical shells and those obtained by Zhang et al. [38] are compared. A good agreement with 5.9% relative error is observed.

Fig. 2.
figure 2

Time histories of FGX CNTRC cylindrical shells.

Full size image

Then, the bifurcation and chaos of CNTRC shells containing PL exposed electro-thermo-mechanical loads are researched. There are simple supports at both shell ends. Geometric parameters of piezoelectric shells are R/H = 10 and L/R = 1 and external excitation frequency ω is 5. Matrix material properties are \(\rho _{{}}^{m}\) = 1150 kg/m3, \({v}_{{}}^{m} = 0.34,\) \({{E}^{{\text{m}}}} = 2.1\) GPa, \({{\alpha }^{m}} = 45 \times {{10}^{{ - 6}}}\). The material properties of the CNTs are \(\rho _{{}}^{{CN}}\) = 1400 kg/m3, \({v}_{{12}}^{{CN}} = 0.175,\) \(E_{{11}}^{{CN}} = 5.6466\) TPa, \(E_{{22}}^{{CN}} = 7.08\) TPa, \(G_{{12}}^{{CN}} = 1.9445\) TPa, \(\alpha _{{11}}^{{CN}} = 3.3484\) × 10–6/K, \(\alpha _{{22}}^{{CN}} = 5.1682 \times {{10}^{{ - 6}}}{\text{/K}}\). Efficiency parameters \({{\eta }_{i}}\) of CNT are as follows: \({{\eta }_{1}} = 0.137,{{\eta }_{2}} = 1.022,\) \({{\eta }_{3}}\) = 0.715 for the case of \(V_{{CN}}^{*} = 0.12\), and \({{\eta }_{1}} = 0.142,{{\eta }_{2}} = 1.626,{{\eta }_{3}} = 1.138\) for \(V_{{CN}}^{ * } = 0.17\), and \({{\eta }_{1}} = 0.141,{{\eta }_{2}}\) = 1.585, \({{\eta }_{3}}\, = \,1.109\) for \(V_{{CN}}^{*}\, = \,0.28\) [23]. Piezoelectric layer material properties are \(E_{{11p}}^{{}}\) = 63.0 GPa, \({{\rho }_{{\text{p}}}}\) = 7600 kg/m3, \(\alpha _{{11p}}^{{}} = \alpha _{{22p}}^{{}} = 0.9 \times {{10}^{{ - 6}}}{\text{/K,}}\) \({{\nu }_{{\text{p}}}} = 0.3\) and \({{e}_{{{\text{31}}}}} = {{e}_{{{\text{32}}}}} = 17.6\) C/m2.

The effect of distributions of CNTs on nonlinear dynamic characteristics of CNTRC cylindrical shells with piezoelectric layer is shown in Figs. 3 to 5. Given load is \(F = 494\), temperature rise \(\Delta T\) is zero, and CNTs volume fraction \(V_{{CN}}^{ * }\) is 0.17. Figures 3 to 5 show bifurcation diagram, time course curve, phase-plane trajectory and poincaré map for different distributions of CNTs. It is noteworthy that the one periodic motion is exhibited in system and there is one isolated fixed point in poincaré map for the FGX CNTRC shell (see Fig. 3); the system shows triple periodic bifurcation motions, and there were three isolated fixed points in the poincaré map for the UD-CNTRC shell (see Fig. 4); and chaotic motion is exhibited in the system and poincaré map showed fractal features similar to clouds for the FGO CNTRC shell (see Fig. 5). Based on the Figs. 3–5, the reinforcements distributed close to outer and inner surface can enhance the dynamic stability of the structure, and those distributed nearby the mid-plane contributes to weakening system stability. The difference of the matrix and the reinforcement of three distribution patterns results in the disparity of the stiffness, and the FGX pattern are more contributory to the strengthening of the structures. These results fit perfectly with the literature [39, 40].

Fig. 3.
figure 3

Nonlinear dynamic characteristics of the FGX CNTRC shells containing piezoelectric layer: (a) bifuration diagram, (b) time course curve, (c) phase-plane trajectory, (d) Poincaré map.

Full size image
Fig. 4.
figure 4

Nonlinear dynamic characteristics of the UD CNTRC shells containing piezoelectric layer: (a) Bifuration diagram, (b) Time course curve, (c) Phase-plane trajectory, (d) Poincaré map.

Full size image
Fig. 5.
figure 5

Nonlinear dynamic characteristics of the FGO CNTRC shells containing piezoelectric layer: (a) Bifuration diagram, (b) Time course curve, (c) Phase-plane trajectory, (d) Poincaré map.

Full size image

The influence of voltage on nonlinear dynamic characteristics of UD-CNTRC composite cylindrical shells containing piezoelectric layer is shown in Figs. 6, 7 and 8. Temperature rise \(\Delta T\) is zero, given load is \(F = 460\), the volume fraction of CNTs \(V_{{CN}}^{ * }\) is equal to 0.17. Figs. 7, 8 and 9 show bifurcation diagram, phase-plane trajectory, time course curve and poincaré map corresponding to different voltage. By the application of negative voltage to the shell structure, system shows one periodic motion and poincaré map exhibits one isolated fixed point (Fig. 6). By the application of zero voltage to shell structure, system shows double periodic bifurcation motion and poincaré map erxhibits two isolated fixed points (Fig. 7). By applying positive voltage to shell structure, system shows chaotic motion and poincaré map exhibits fractal features same as clouds (Fig. 8). Consequently, negative voltage improves the dynamic stability of CNTRC shells containing piezoelectric layer. This is because in such a case, the applied voltage is opposite to the polarization direction in the longitudinal axis thus makes the shell contract. The tensile stress state thus induced increases the shell stiffness. This is in contrast to the positive voltage case.

Fig. 6.
figure 6

Nonlinear dynamic characteristics of the UD-CNTRC shells containing piezoelectric layer \((V = - 100\)): (a) Bifuration diagram, (b) Time course curve, (c) Phase-plane trajectory, (d) Poincaré map.

Full size image
Fig. 7.
figure 7

Nonlinear dynamic characteristics of the UD-CNTRC shells containing piezoelectric layer \((V = 0\)): (a) Bifuration diagram, (b) Time course curve, (c) Phase-plane trajectory, (d) Poincaré map.

Full size image
Fig. 8.
figure 8

Nonlinear dynamic characteristics of the UD-CNTRC shells containing piezoelectric layer \((V = + 100\)): (a) Bifuration diagram, (b) Time course curve, (c) Phase-plane trajectory, (d) Poincaré map.

Full size image
Fig. 9.
figure 9

Comparison of the nonlinear dynamic characteristics of UD-CNTRC shells containing piezoelectric layer with different volume fraction: (a) Bifurcation diagram \(V_{{CN}}^{ * } = 0.17\), (b) Bifurcation diagram \(V_{{CN}}^{ * } = 0.28\), (c) Phase-plane trajectory \(V_{{CN}}^{ * } = 0.17\), (d) Phase-plane trajectory \(V_{{CN}}^{ * } = 0.28\), (e) Poincaré map \(V_{{CN}}^{ * } = 0.17\), (f) Poincaré map \(V_{{CN}}^{ * } = 0.28\), (g) Time course curve \(V_{{CN}}^{ * } = 0.17\), (h) Time course curve\(V_{{CN}}^{ * } = 0.28\).

Full size image

Figure 9 shows the influence of CNTs volume fraction (\(V_{{CN}}^{ * }\)) on the nonlinear dynamic characteristics of UD-CNTRC shells. In this example, voltage and temperature are zero. From Figs. 9(a)–(b), it can be shown that by increasing load, system goes through one period motion, several period bifurcation motions, one period motion, and double period bifurcation motion, and finally gets into a complex state containing multiple periodic motion, quasi-periodic motion or chaotic motion. However, CNT volume fraction being different, the two kinds of situations creates different critical loads corresponding to system entering chaotic motion and critical load enhances when volume fraction \(V_{{CN}}^{ * }\) increases.

Figures 9(c)–(h) exhibits nonlinear dynamic characteristics of UD-CNTRC shells containing piezoelectric layer under varied volume fraction as the load \({{F}_{0}} = 512\). It is witnessed that shell structure with \(V_{{CN}}^{ * } = 0.17\) shows chaotic motion while that with \(V_{{CN}}^{ * } = 0.28\) is still in double period motion. When the system occur the period motion (\(V_{{CN}}^{ * } = 0.28\)), the time history is a cyclic function depending on the time. It is presented through the curves of the deflection-velocity relation demonstrated in the phase plane are repeat and closed-form curves while the Poincaré map includes the finite regular point. For chaotic state (\(V_{{CN}}^{ * } = 0.17\)), the time history is not a cyclic line and Poincaré map appears to be a random point while the curves of the phase plane are not repeat and opened-form [41–43]. Consequently, the structure delays the multiply chaotic or periodic motions by the increase of CNTs volume fraction. In other words, increase of CNTs volume fraction stabilizes dynamic characteristics of structures, which is conducive to structure dynamic stability.

Temperature influence on the nonlinear dynamic characteristics of UD-CNTRC shells containing piezoelectric layer is exhibited in Fig. 10. CNTs volume fraction \(V_{{CN}}^{ * }\) is equal to 0.17 and the applied voltage V is zero. In Figs. 10(a)–(b), it can be shown that by increasing load, system goes through one periodic motion, several periodic bifurcation motions, one periodic motion, several periodic bifurcation motions, and eventually a complicated chaotic motion is created. However, due to different temperatures, different critical loads are created in the system entering chaotic motion. It can also be shown that by increasing temperature, critical load decreases.

Fig. 10
figure 10

Comparison of nonlinear dynamic characteristics of UD-CNTRC shells containing piezoelectric layer for different temperatures: (a) T = 0, (b) T = 200, (c) Phase-plane trajectory T = 0, (d) Phase-plane trajectory T = 200, (e) Poincaré map T = 0, (f) Poincaré map T = 200, (g) Time course curve T = 0, (h) Time course curve T = 200.

Full size image

Figs. 10(c)–(h) exhibits the nonlinear dynamic characteristics of UD-CNTRC shells containing piezoelectric layer under varied temperature as the load \({{F}_{0}} = 312\). It can be seen that the shell structure with T = 200 shows a chaotic motion, while shell structure with T = 0 still shows one periodic motion. Consequently, increase of temperature will lead to the emergence of multi-periodic or chaotic motions ahead of time. This shows that temperature increase is not conducive to dynamic stability of structure.

5 CONCLUSIONS

The bifurcation and chaos of FG-CNTRC cylindrical shell containing piezoelectric layer under electro- thermo-mechanical loadings are studied. Using variational principle, nonlinear motion equations of shells are gained and resolved using fourth order Runge-Kutta method. There are some significant results as follows:

♦ The numerical results of the dynamic response for FGX CNTRC cylindrical shells are validated very well with the previous publications.

♦ The numerical results show that decreasing voltage or temperature and increasing volume ratio delay chaotic or multiple periodic motions in FG-CNTRC shells with piezoelectric layer, resulting in the dynamic stability of the structure.

♦ Reinforcements distributed close to outer and inner surface can enhance the dynamic stability of the structure, and those distributed nearby the mid-plane contribute to weakening system stability.