1 Introduction

The thermal problem is relevant for alkali-silica reaction (ASR) development, as the temperature influences pathology development, stress developement and phase assemblage [1,2,3,4]. A temperature increase on the order of 10 \(^{\circ }\)C is reported to accelerate ASR expansion roughly threefold [5]. Along with an increase in relative humidity and alkalinity, accelerated tests for ASR generally also involve increasing the temperature to enhance reaction kinetics [5]. Higher-temperature protocols include specimen storage at 38\(^{\circ }\)C in the concrete prism test (CPT), as recommended by ASTM [6], CSA [7], and RILEM [8, 9]. Accelerated CPT is usually performed at 60\(^{\circ }\)C [10]. Several authors have adopted temperatures between and above the range of 38–60\(^\circ\)C in the study of ASR [5]. Temperature is also shown to affect remedial measures regarding ASR [11]. Chemo-thermo-mechanical analysis of ASR-affected concrete has been proposed in the literature [12,13,14,15]. In these studies, the use of thermal properties of ASR could help in increasing the precision of predictions. Furthermore, alkali-activated materials (AAM) are susceptible to form ASR products, especially high calcium AAM [16]. The quantification of the thermal and thermo-mechanical properties of ASR products, therefore, helps in predicting the behaviour of these materials.

Recent progress have been made in unveil the details of the atomic structure of ASR products. The main ASR products identified are [17]:

  • K-shlykovite (KCaSi\(_4\)O\(_8\)(OH)\(_3\)·2H\(_2\)O): crystalline products akin to the naturally occurring mineral shlykovite [18].

  • Na-shlykovite (NaCaSi\(_4\)O\(_8\)(OH)\(_3\)·2H\(_2\)O): crystalline products based on the total substitution of potassium in shlykovite structure by sodium [17, 19].

  • ASR-P1 (K\(_{0.52}\)Ca\(_{1.16}\)Si\(_4\)O\(_8\)(OH)\(_{2.84}\)·1.5H\(_2\)O): nanocrystalline products whose atomic structure can be related to defective K-shlykovite with a coherence length of a few nanometers. This product has also been reported as amorphous [20, 21] in the literature, but recent molecular simulations [22] show that defective nanocrystalline K-shlykovite reproduces available experimental X-ray diffraction patterns and pair distribution functions better. The comparison of defective nanocrystalline K-shlykovite structure with available experimental data demonstrate that ASR-P1 can be associated with the disordered/ amorphous products reported in previous studies in the literature [23,24,25]

Na- and K-rich products are the main ASR products in cement systems, as these are the primary alkalis in the pore solution of cement-based materials [26]. However, molecular simulations point out the possibility of having other alkalis (Li and Cs) substituting K counterions with no significant changes in shlykovite structure [27]. The compositional and structural differences among these products signify that variations in thermal properties are expected. The extent of these differences is yet to be quantified. Disordered solids exhibit distinctive vibrational and thermal properties compared to their fully crystalline counterparts (e.g., [28, 29]). In crystals, the vibrational density of states (VDOS) is well-described in low frequencies (up to 1 THz) by the Debye model, which states an evolution of the VDOS \(g(\omega ) \propto \omega ^2\) as the square of the angular frequency \(\omega\) [29, 30]. The absence of long-range periodicity is claimed to be responsible for the presence in non-crystalline materials of an excess contribution to the Debye model, evidenced as a peak in the reduced VDOS \(g(\omega )/\omega ^2\), termed the boson peak [29, 31]. Boson peak was identified for C–S–H [32], which is a nanocrystalline phase [33]. This observation suggests that the boson peak can be relevant for the thermal properties of both nanocrystalline and amorphous ASR products.

To the best of the authors’ knowledge, no experimental measurements have been reported in the literature for the heat capacity of ASR products to date. Estimates based on empirical laws exist for crystalline products [34]. Full classical molecular simulations have been used to calculate the heat capacity of Na- and K-shlykovite [27]. However, full classical molecular dynamics simulations are known to lead to overestimations of the heat capacity of solids (e.g., [35, 36]). Thermal expansion tensors have been computed in the same study for crystalline products with non-reactive force fields [27]. No experimental data, theoretical estimates, or empirical calculations have been proposed for the thermal conductivity and thermal expansion of all ASR products, particularly nanocrystalline and amorphous products. Molecular dynamics (MD) simulations have been successful in providing missing data on thermal properties of cement systems, including C–(A)–S–H [32, 37], portlandite [32, 38], clinker minerals [32, 39, 40], and AF-phases [41, 42]. Thermal conductivity, thermal expansion, and heat capacity have been calculated for these phases. When experimental data is available, the results computed with molecular simulations generally show good agreement with such data, which is the case of thermal conductivity of alite [40], thermal expansion and heat capacity of ettringite and metaettringite [41], and thermal properties of C–(A)–S–H [32, 37, 43]. These results build confidence in using this technique to estimate, even for the first time, thermal properties of various phases of interest in cement systems. Only recently, an atomic structure was proposed for non-crystalline products [22] (based on the ASR-P1 composition provided in [44]). The present study builds on these recent references by providing the thermal properties of ASR products.

In this work, the thermal properties of crystalline, nanocrystalline, and amorphous ASR products are computed using molecular dynamics and reactive force fields. Thermal conductivity and thermal expansion tensors are provided, highlighting anisotropy at the molecular scale. The heat capacities at constant volume and pressure are computed using a semi-classical approach, accounting for quantum corrections. Using the semi-classical simulation for heat capacity computation, we also provide the estimate for the standard entropy. Quantum corrections are also introduced for thermal conductivity. Most of the data are provided for the first time in the literature.

2 Molecular models and methods

2.1 Atomic structure and force fields

The atomic structure of (K)-shlykovite [18] is adopted for crystalline systems. Na-Shlykovite is made by substitution of K counterions by Na, as in [19, 27]. Amorphous and nanocrystalline systems were constructed in a previous work [22] based on defective K-shlykovite structure. For these system the composition reported for ASR-P1 is used as reference [44]. The final composition of these system is K\(_{0.53}\)Ca\(_{1.17}\)Si\(_4\)O\(_8\)(OH)\(_{2.83}\)·1.5H\(_2\)O. To build the ASR-P1 structures, defects were introduced randomly [22]. Four independent atomic structures with different random defects were generated and are considered here. Nanocrystalline and amorphous systems are based on these four defective structures. Amorphicity was obtained using high annealing temperature in well-established simulation protocol [45]. In all cases, unit cell is replicated 3x3x1 fold to obtain a simulation box on the order of 10 nm\(^3\).

Fig. 1
figure 1

Snapshots of the atomic structure depicting Na and K-shlykovite, and defective shlykovite with ASR-P1 composition in nanocrystalline and amorphous forms

Full size image

All simulations are run with LAMMPS [46]. ReaxFF parameters for Na/K/Si/O/H/Water systems [47], developped to the study of zeolites and already used for potassium ASR products [22], are adopted. Here, Na-shlykovite is for the first time modelled with these ReaxFF parameters. The lattice parameters obtained for the studies system are reported in Table 1. In reference [22], lattice parameters were computed in systems in which unit cell angles were kept the same as the one obtained after Shlykovite relaxation with ReaxFF. Here, the angles are also allowed to change upon NPT relaxation. The results for K-shlykovite can be compared with Zubkova et al. [18] experimental data on lattice parameters \((a, b, c, \alpha , \beta , \gamma )=\) (6.4897 Å, 6.6669 Å, 26.714 Å, 90 \(^{\circ }\), 94.697 \(^{\circ }\), 90 \(^{\circ }\)); and previous data from non-reactive MD simulations [19]: \((a, b, c, \alpha , \beta , \gamma )=\) (6.40 ± 0.04 Å, 6.90 ± 0.04 Å, 27.29 ± 0.30 Å, 90.0 ± 2.4 \(^{\circ }\), 91.6 ± 5.6 \(^{\circ }\), 90.0 ± 0.7 \(^{\circ }\)). The results for Na-shlykovite are consistent with non-reactive MD simulations [19]: \((a, b, c, \alpha , \beta , \gamma )=\) (6.35 ± 0.05 Å, 6.92 ± 0.04 Å, 24.89 ± 0.61 Å, 90.0 ± 3.8 \(^{\circ }\), 89.9 ± 3.6 \(^{\circ }\), 90.0 ± 1.0 \(^{\circ }\)). The results for ASR-P1 obtained here are consistent with the one reported in reference [22] for the systems with fixed angles. Snapshots of the atomic structures are shown in Fig. 1. As observed with simulation ussing ClayFF [19, 27], some of the Na in Na-shlykovite displace to a position closer to the Ca plan in shlykovite.

Table 1 Lattice parameters of ASR products simulated with ReaxFF at ambient conditions
Full size table

The system studied here refers to the so-called undrained conditions, i.e., when water is not allowed to exchange with an exterior reservoir (which can be the environment or larger neighboring pores). Undrained conditions are relevant for short timescales, such as fast temperature changes when no significant water content can be evacuated to reequilibrate with the new temperature (and humidity) conditions, and for moderate temperature changes. Drained properties of nanoporous hydrophilic phases like ASR products would correspond to boundary conditions in which water can exchange with the environment (e.g., by drying due to RH or temperature change). It must be noted that the saturating vapor pressure of water increases with temperature, and drained conditions in environments with available liquid water would lead to only a very slight dehydration of the nanoporous solid (water would leave the system due to the thermal expansion of a liquid being generally one order of magnitude larger than that of a solid; in the case of C–S–H, less than one water molecule per Si is lost for a variation of more than 100\(^{\circ }\)C [48]). Drained conditions with significant water loss occur only in environments in which the external vapor reservoir is kept at a partial pressure below saturating vapor pressure. In this case, significant water loss would occur when liquid water changes to vapor above boiling temperature. For the temperatures of interest in ASR accelerated protocols (up to 60 \(^{\circ }\)C, as discussed in the introduction), no significant amount of water is expected to leave the system since all is done below the boiling temperature of water under normal pressure conditions. The undrained conditions considered here are therefore relevant for the conditions observed in accelerated protocols.

In general, pressure effects should not alter significant properties of solids at the molecular scale except if pressures exceeding GPa (i.e., well above the service life conditions of concrete application) are adopted. Thus, pressure effects are not considered hereafter.

2.2 Thermal and thermo-mechanical properties from molecular simulations

Details on computing thermal properties with classical molecular dynamics simulation are recalled in this section.

2.2.1 Coefficient of thermal expansion

The thermal expansion tensor is calculated using the fluctuation-dissipation approach. In this case, it is determined using the cross fluctuations of the "enthalpy" \(H=E+PV\) (calculated using the instantaneous total energy E and instantaneous volume V but the imposed pressure P instead of the instantaneous pressure since this latter fluctuates with the barostat leading, therefore, to erroneously larger fluctuations) and the Lagrangian deformation tensor \(\epsilon _{ij}\) in the N\(\sigma\)T ensemble [49,50,51] using the following equation:

$$\begin{aligned} \alpha _{ij} = \frac{\left\langle H \epsilon _{ij} \right\rangle _{NPT} - \left\langle H \right\rangle _{NPT} \left\langle \epsilon _{ij} \right\rangle _{NPT}}{k_B T^2}, \end{aligned}$$
(1)

where \(k_B\) is the Boltzmann constant, T is the temperature, \({\textbf{I}}\) is the identity matrix, and the superscript \([\star ]^T\) denotes a matrix transpose; \(\epsilon _{ij} = \frac{1}{2} \left[ (h_{0}^{-1})^T h^T h h_{0}^{-1} - {\textbf{I}} \right]\) is the Lagrangian deformation for a generic (triclinic) system; \(\epsilon _{ij}\) is obtained from the matrices \(h_{0} = [a_0, b_0, c_0]{x, y, z}\) and \(h = [a, b, c]{x, y, z}\) associated with the metric of the reference and deformed supercell, respectively.

Simulations were performed in NPT ensemble with the Nosé-Hoover barostat applied independently along each uniaxial and tangential direction. A timestep of 0.1 fs is adopted, and six trajectories are considered in calculating the average value and standard deviations.

2.2.2 Heat capacity and entropy

Following the standard procedure for solid phases, the isochoric heat capacity is calculated accounting for quantum corrections with [52, 53]:

$$\begin{aligned}{} & {} c_{V} = \frac{C_V}{m}=\frac{3Nk_B}{m} \int _0^{\infty } \left( \frac{\hbar \omega \; n(\omega ,T)}{k_B T} \right) ^2 \nonumber \\{} & {} \quad \exp \left[ \frac{\hbar \omega }{k_B T} \right] g(\omega ) d \omega \end{aligned}$$
(2)

where \(C_V\) is the molar isochoric heat capacity (respectively, \(C_P\) is the molar isobaric heat capacity), \(3Nk_B\) is the Dulong-Petit relation, m is the total mass, \(\hbar\) is the reduced Planck constant, \(\omega\) is the angular frequency, \(n(\omega ,T) = \left[ \exp \left( \frac{\hbar \omega }{k_b T} \right) -1 \right] ^{-1}\) is Bose-Einstein distribution. In the formula above \(g(\omega )\) is the Vibrational Density of the States (VDOS) [36, 52]:

$$\begin{aligned} g(\omega ) = \frac{2}{\pi } \int _{-\infty }^{\infty } \sum _j \frac{\langle m_j {\textbf{v}}_j(t).{\textbf{v}}_j(0) \rangle }{\langle m_j {\textbf{v}}^2_j(0) \rangle } \cos \left[ \omega t \right] dt \end{aligned}$$
(3)

obtained from the mass-weighted velocity auto-correlation function (VACF) \(\langle m_j {\textbf{v}}_j(t).{\textbf{v}}_j(0) \rangle\). The estimate above is semi-classical since the VDOS is calculated using classical methods, but quantum corrections are introduced. The same approach was successfully used for the heat capacity of various solid phases in cement-based materials [32, 37, 39,40,41].

The isobaric heat capacity is calculated using anisotropic Mayer’s relation (e.g., [54]):

$$\begin{aligned} c_p - c_v = \frac{T}{\rho } \alpha _{ij} C_{ijkl} \alpha _{kl} \end{aligned}$$
(4)

where \(\rho\) is the density, and \(C_{ijkl}\) is the stiffness tensor. Details on the computation of \(C_{ijkl}\) are provided in other work [55].

The entropy S can also be calculated from the VDOS for solids by assuming harmonic oscillators with the expression (e.g., [56, 57]):

$$\begin{aligned}{} & {} S = 3Nk_B \int _0^{\infty } \left[ \frac{\hbar \omega }{k_B T} n(\omega ,T) - \ln \left[ 1 - \exp \left( \frac{-\hbar \omega }{k_B T} \right) \right] \right] \nonumber \\{} & {} \quad g(\omega ) d \omega \end{aligned}$$
(5)

This expression is consistent with \(S=\int _0^T C_v(T)/T dT\). As for \(c_V\), this estimate of entropy is semi-classical since the VDOS is computed using classical molecular simulations, but quantum corrections are introduced. Standard molar entropy \(S^0\), a crucial parameter in thermodynamic modeling, is typically determined from \(C_p\) at standard conditions (25\(^{\circ }\) and 1 bar). In this context, we approximate \(S^0\) by integrating \(C_p \approx C_v \left( \frac{C_p(T=273.15K)}{C_v(T=273.15K)}\right)\), where the term \(\left( \frac{C_p(T=273.15K)}{C_v(T=273.15~K)}\right)\) serves as an approximation for the conversion of \(C_v\) into \(C_p\).

The VACFs are calculated in an NVE run following proper equilibration in an NVT run. A timestep of 0.1 fs is adopted, and five trajectories are considered in the calculation of the average value and standard deviations. The VDOS is computed in post-processing the mass-weighted VACF by taking the Fourier transform after linearly interpolating the VACF. Numerical integration is used to get the entropy and heat capacity.

2.2.3 Thermal conductivity

Thermal conductivity tensor is computed using Green-Kubo formalism (e.g., [32, 58]):

$$\begin{aligned} \lambda _{ij} = \frac{V}{k_B T^2} \int _0^{\infty } \langle J_i(0) \otimes J_j(t) \rangle dt \end{aligned}$$
(6)

where \(\langle J_i(0) \otimes J_j(t) \rangle\) are the components of ensemble-averaged heat flux auto-correlation function (HFACF) HFACF, with \(J_i\) being heat flux; i or j representing the Cartesian directions x, y, and z; \(\otimes\) denotes the dyadic product; and V stands for the system volume. The heat flux vector \(J_i\) is calculated from the viral stress tensor \(\mathbf {\sigma }_p\) and the energy (kinetic and potential) per atom \(E_p\) with \({\textbf{J}}_p = \frac{1}{V} \left[ \sum _p E_p {\textbf{v}}_p - \sum _p \mathbf {\sigma }_p {\textbf{v}}_p \right]\), where \({\textbf{v}}_p\) is the velocity vector.

Quantum corrections are needed for the thermal conductivity for temperatures T below \(T_D\), where \(T_D\) is the Debye temperature. The Debye temperature can be estimated by (e.g., [59, 60]):

$$\begin{aligned} T_D \approx \frac{\hbar }{k_B} S_v \root 3 \of {6 \pi ^2 N/V} \end{aligned}$$
(7)

in which \(S_v\) is the sound velocity, and N/V is the number density. The volumetric sound velocity reads [61]:

$$\begin{aligned} S_v=\frac{1}{\root 3 \of {\frac{1}{3} \left( \frac{1}{S_l^3} + \frac{2}{S_t^3} \right) }} \end{aligned}$$
(8)

where the longitudinal and transverse sound velocities are, respectively, given by:

$$\begin{aligned} S_l=\sqrt{\frac{C_{11}+C_{22}+C_{33}}{3 \rho }}; \; S_t=\sqrt{\frac{C_{44}+C_{55}+C_{66}}{3 \rho }} \end{aligned}$$
(9)

both computed from the density \(\rho\), and the diagonal components of the elastic tensor in Voigt notation (The three axial components for \(S_l\), and the three shear components for \(S_t\)).

The quantum-corrected thermal conductivity can be approximated as [62]:

$$\begin{aligned} \lambda ^{corr} = \frac{C_v}{3 N k_B} \lambda ^{GK} \end{aligned}$$
(10)

where \(C_v\) is for the quantum-corrected volume heat capacity (corresponding to Eq. 2), and \(\lambda _{GK}\) is classical (Green-Kubo) thermal conductivity.

HFACF are computed in NVE runs for 5 ns; the correlations are calculated using a 10000 timestep correlation window, with input values recorded every timestep, and time window averages computed every 10000 timesteps. Before HFACF calculation, the systems were equilibrated adequately under ambient conditions using Nosé-Hoover barostat and thermostat. The linear and angular moments were zeroed during equilibration to avoid HFACF converging to non-zero values at large timescales. Average values and standard deviations are calculated based on data obtained from 4 independent trajectories.

3 Results

3.1 Coefficient of thermal expansion

The components of the thermal expansion tensor are gathered in Table 2. A larger thermal expansion is obtained in the direction perpendicular to the interlayer, as expected for systems with confined water. Anisotropy in the response decreases with nanocrystallinity and amorphicity. Thermal expansion in the interlayer plane directions increases with nanocrystallinity and amorphicity. Due to the monoclinic symmetry of shlykovite, the response along the layers’ plane directions is not expected to be the same. Still, the expansions along x and y obtained for all products are statistically indistinguishable (considering the variability/ uncertainty of our results). Off-diagonal components are larger in crystalline systems.

The volumetric thermal expansion \(\alpha _{v}=\text {Tr}(\alpha _{ij})\) is larger for Na- and K-shlykovite when compared to ASR-P1. The values for crystalline products can be compared with simulation using ClayFF [27] for which \(\alpha _{v}\) = 15.52 ± 2.96 \(\times\) 10\(^{-5}\)/K for Na-Shlykovite, and \(\alpha _{v}\) = 5.73 ± 0.70 \(\times\) 10\(^{-5}\)/K for K-Shlykovite. The results presented here are obtained with simulations with smaller timesteps and more extensive production lengths, which means they are more reliable. These new results show that thermal expansion is positive for all Cartesian directions, indicating that the previous results for Na-Shlykovite are likely related to simulation imprecision.

Table 2 Thermal expansion of ASR products (in 10\(^{-5}\)/K): Volumetric \(\alpha _{v}= \text {Tr} (\alpha _{ij})\), and components of \(\alpha _{ij}\) tensor
Full size table

These values can be compared with the volumetric thermal expansion coefficients reported for C–(A)–S–H: 1.2\(-\)6.2 \(\times\) 10\(^{-5}\)/K according to various C–(A)–S–H models and Ca/Si ratios [32, 37, 63, 64], since ASR products are also layered calcium silicate hydrates. Siliceous aggregates, clinker minerals and hydrates such as portlandite and AF-phases have volumetric thermal expansion in the range of 2−4 \(\times\) 10\(^{-5}\)/K [65]. Thermal expansion and elastic constant property mismatch between ASR products and the other phases will lead to the rise of thermal stresses in each phase with a temperature variation. These results provided here can be used in future analyses to quantify the contribution of thermal cracking in ASR development under temperature-accelerated conditions.

3.2 Heat capacity and entropy

The VDOS are shown in Fig. 2. Experimental spectra measurements such as infrared adsorption and Raman spectra can be related to the VDOS. The specific per bond frequencies for K-ASR products are already discussed in ref. [22]. The VDOS for Na-shlykovite is computed here for the first time. All VDOS exhibit zero values for frequencies above 120 THz. Identified bands (I-V) in the VDOS correspond to various vibrations: Na–O, K–O, Si–O, and Ca–O vibrations for Band I, Si–O and O–H vibrations for Bands II and III, and intramolecular water vibrations for Bands IV and V. Hydrogen vibrations play a significant role in all bands, primarily contributing to Band V. Between bands II and IV and IV and V, the VDOS vanishes. These findings align with experimental spectra from other silicates, including C–(A)–S–H [17, 32, 37, 66]. In FTIR experiments of ASR products [17], the 28–34 THz (950-1130/cm) band corresponds to asymmetric and symmetric stretching vibrations of Si–O bonds, while the 18-21 THz (600–700/cm) band relates to Si–O–Si bending. The 2400-3800/cm band signifies stretching vibrations of O-H groups in molecular water or hydroxyls, potentially associated with gel water or loosely bound water in the products [17]. ASR-P1 experiments reveal a weak hydroxyl signal, attributed to the absence of well-ordered OH-groups [17, 66]. Raman spectroscopy of ASR products identifies high-frequency symmetrical stretching vibrations of Si–O bonds (24\(-\)34.4 THz), Si–O–Si symmetrical bending vibrations (600–700/cm), and intramolecular Si-O tetrahedra vibrations (12-15 THz) in silicates and ASR products [17, 66]. Specific wavenumbers associated with polymerization levels are noted, but the precision of the VDOS results hinders such identification.

Fig. 2
figure 2

A Total VDOS per ASR product. B VDOS per species

Full size image
Table 3 Isochoric and isobaric heat capacity and standard molar entropy \(S^0\) of ASR products:
Full size table
Table 4 Calculated heat capacity \(C_p\) and standard molar entropy \(S^0\) values at 298 K and 1 bar pressure of ASR products
Full size table

The occurrence of the boson peak is evaluated in the low-frequency VDOS and the reduced VDOS \(g(\omega )/\omega ^2\) in Fig. 3. In the reduced VDOS, a Lorentzian tail was used to describe the quasi-elastic component associated with the fast relaxation process [31, 70]. This contribution was extracted from the reduced VDOS to identify the boson peak. The VDOS at the low-frequency range in Fig. 3 for ASR-P1 shows an excess in the VDOS compared to the Debye model. The reduced VDOS indicates that the boson peak for ASR products appears in the 0.5-2 THz scale. These positions of boson peaks are similar to the ones experimentally identified for vitreous silica in the frequency range \(\nu _{BP}=\omega /2\pi\) of 1–2 THz [71] and 1.5\(-\)2.8 THz [72], and in simulations on C–S–H with varying Ca/Si with frequencies in the range 1\(-\)2.5 THz [32]. The boson peak frequency \(\nu _{BP}\) is reported to increase with temperature, with the intensity of the boson peak decreasing with temperature [71]. This observation helps explain the reduced VDOS of ASR-P1. ASR-P1 amorphous systems were built based on a higher annealing temperature than the nanocrystalline system. Thus, amorphous ASR-P1 would exhibit similar features as higher temperature vitreous silica compared with the lower temperature system (ASR-P1 nanocrystalline). K-shlykovite also shows a boson peak, which can be related to the disorder induced by finite temperature and the intrinsic degree of disorder associated with confined water and counterions. Conversely, Na-shylokoite shows two less pronounced peaks in the reduced VDOS in the 0-2 THz range that can be fairly approximated as negligible effects of the boson peak.

Fig. 3
figure 3

At top, VDOS at low frequency range per ASR product. The Debye model indicating VDOS \(g(\omega ) \propto \omega ^2\) at low frequency range is shown for comparison. At bottom, reduced VDOS per ASR product

Full size image

The heat capacities of ASR products computed with the semi-classical approach are gathered in Table 3. K-shlykovite exhibits the largest heat capacity; for K products, the heat capacities increase with the disorder, as expected. Values for ASR-P1 are provided for the first time. The values reported here are almost half of the values reported for crystalline products by MD simulations with full classical approach [27] (i.e., without the quantum correction adopted here in the semi-classical approach): 1.860 ± 0.011 J/(g K) for Na-shlykovite, and 1.949 ± 0.024 J/(g K) for K-shlykovite. Full classical simulations are known to lead to overestimations of the heat capacity of solids (e.g., [35, 36]). This observation reaffirms the importance of accounting for quantum effects in the heat capacity estimates for solids.

The isobaric heat capacity can be compared with estimates provided by empirical formula. Various authors provide empirical relations also for the isobaric heat capacity (in J/(mol K)) as a function of the molar volume \(V_m\) [67,68,69].

  • \(C_p = 2.2 V_m -0.8\) [68]

  • \(C_p = 2.29 V_m\) [67]

These formulas rely on the observation that the heat capacity is strongly linearly correlated with formula volume for large sets of minerals [73]. Table 4 gathers the heat capacities obtained with different empirical formulas. Overall, the empirical formula leads to values of \(C_p\) larger than the values obtained by MD. The formula proposed by [68] leads to lower values of \(C_p\), therefore closer to the values computed by MD. Using the expression proposed by [69], the heat capacity of crystalline products was computed and used in thermodynamics calculation by [34].

The standard molar entropy of ASR products computed with the semi-classical approach are also gathered in Table 3. Empirical relations are also provided for the standard molar entropy (in J/(mol\(\cdot\)K)) as a function of the molar volume \(V_m\) [67,68,69].

  • \(S^0 = 2.10 V_m + 13\) [69]

  • \(S^0 = 2.26 V_m + 15\) [68]

  • \(S^0 = 2.08 V_m\) [67]

Again, the empirical formula also lead to values of \(S^0\) larger than the values obtained by MD, and the formula proposed by [68] is closer to the values computed by MD.

Differences in the range of tenths of J/(mol\(\cdot\)K) have been observed for both \(C_p\) and \(S^0\) in the comparison with values calculated from molecular simulations, empirical formulas, and experimental data for other minerals as well [74]. These consistent trends between MD results and empirical formulas underscore the reliability and consistency of the molecular dynamics approach, especially considering the uncertainties in calculations.

Fig. 4
figure 4

Temperature dependence of \(C_p\) and \(S^0\) obtained from semi-classical estimates from MD. The lines corresponds to the fits with Eqs. 11 and 12 with optimized parameters listed in Table 5

Full size image

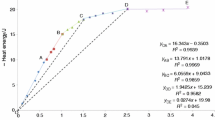
The semi-classical approach enables computing the temperature dependence of \(C_v\) and \(S^0\) from a single VDOS. Figure 4 displays the temperature dependence of \(C_p\) and \(S^0\). The MD results are fitted with the expressions (with T in Kelvins):

$$\begin{aligned} C_p(T) = a_0 +a_1 T+a_2/T^2 +a_3/\sqrt{T} +a_4 \sqrt{T} \end{aligned}$$
(11)
$$\begin{aligned} S^0(T) = b_0 +b_1 T+b_2/T^2 +b_3/\sqrt{T} +b_4 \sqrt{T} \end{aligned}$$
(12)

where \(a_i\) and \(b_i\) (\(i=0-4\)) are fitting parameters obtained from least squares fitting for each property independently. To avoid the indeterminations as \(T \rightarrow 0\), the fittings are performed from 7 K (this explains why \(a_0\) is a non-zero value). The values of the fitting parameters are listed in Table 5. The coefficient of determination of all fits were \(R^2=\) 1.00. These results can used in to describe the temperature dependence in thermodynamic modelling of ASR development.

Table 5 Fits of \(C_p(T)\) and \(S^0(T)\) obtained from MD simulations [in J/(mol\(\cdot\)K)]. The coefficient of determination of all fits were \(R^2=\) 1.00
Full size table

3.3 Thermal conductivity

Nanoacoustic parameters including sound velocities, phonon mean free path, and phonon relaxation time are calculated for each ASR products and reported in Table 6. Phonons mean free path \(l_m\) can be estimated in the framework of kinetic theory with [75]:

$$\begin{aligned} l_m=\frac{3 \lambda _v}{ \rho C_v S_v} \end{aligned}$$
(13)

In the same framework, phonons relaxation time \(\tau _m\) is [61]:

$$\begin{aligned} \tau _p=\frac{3 \lambda _v}{ \rho C_v S_v^2} \end{aligned}$$
(14)

Sound velocities are in line with values previously reported for C–S–H [76]. Phonon mean free path \(l_m\) is on the order of half of the simulation boxes used in MD simulations, suggesting that size effects should not significantly affect the results. The relaxation time is on the order of half of a picosecond.

The Debye temperatures computed for the ASR products (Table 6) are close to the ambient temperature in which the simulations were carried out. Quantum correction might, therefore, need to be included in thermal conductivity estimates. The correction \(\frac{C_v}{3 N k_B}\) used is also reported in Table 6. Table 7 shows the thermal conductivity of ASR products obtained directly from simulation with Green-Kubo formalism (\(\lambda ^{GK}\)) and the quantum-corrected values (\(\lambda ^{corr.}\)). Not accounting for the correction led to an overestimation of the thermal conductivity of approximately 40\(\%\).

Conductivity along the layer plans is larger than in the perpendicular direction for crystalline products. As already discussed in the case of thermal expansion, the monoclinic symmetry of shlykovite means that the behavior along the layers’ plan is not isotropic (therefore, xx and yy components are not expected to be the same). Still, the values obtained here are indistinguishable statistically when the computed uncertainty is accounted for. The results for amorphous products are more isotropic, as expected. Nanocrystalline ASR-P1 also shows an approximately isotropic response despite the layered structure still being present in its atomic structure. The off-diagonal components of the thermal conductivity tensor are closer to zero and can be approximated to zero, considering the standard error reported. These results mean that the frame adopted in the simulation is approximately the principal frame. The volumetric thermal conductivity (the invariant calculated as the trace of the full tensor: \(\lambda _{v}=\text {Tr}\lambda _{ij}/3\)) is close to that reported for other calcium silicate hydrates [32, 76, 77] and amorphous silica [78].

Table 6 Nanoacoustic of ASR products: sound velocities, phonon mean free path, phonon relaxation time, and Debye temperature
Full size table
Table 7 Corrected thermal conductivity of ASR products (in W/(m.K)): Volumetric \(\lambda _{v}\), and components of \(\lambda _{ij}\) tensor
Full size table

4 Conclusions

Thermal and thermo-mechanical properties of ASR products are provided through molecular simulations. The significance of this work lies in its ability to offer data on thermal properties not yet reported for ASR products, a crucial aspect for future research focusing on the role of temperature in ASR development, including accelerated tests.

The thermal properties of ASR products are comparable to those of C–S–H obtained in previous studies using atomistic simulations, highlighting the similarities in layered silicates’ properties. Anisotropy plays a significant role in the thermal expansion and conductivity of crystalline products. Nanocrystalline products exhibit marked anisotropic thermal expansion, while thermal conductivity is approximated as isotropic.

Quantum corrections are crucial for estimates of thermal properties such as heat capacity and thermal conductivity. Compared to previous simulation results [27], the heat capacity provided here based on the semi-classical approach aligns better with theoretical estimates for heat capacity. Standard molar entropy profiling also indicates that molecular simulations can be a helpful tool in providing data to complete thermodynamic tables.

Future work may focus in upscaling thermal properties to the gel scale [79], as well as simulating temperature effects coupled in both undrained and drained (i.e., coupled with drying) conditions. Even for phases like C–S–H undrained thermal properties remains unknown to date (no experimental data is known, to the best of our knowledge; and no molecular simulation have been done so far considering drained conditions). Simulating drained systems with molecular simulations requires using techniques like Grand Canonical Monte Carlo simulation [80, 81] that are computer intensive and are yet to be applied to all ASR products.