1 Introduction

Advances in concrete rheology [1] have allowed the estimation of quantitative descriptors for construction processes and the consequent constructability, in accompany with load resistance, serviceability, and durability of concrete structures. The reliable measurement [2,3,4,5] for the rheological properties of relevant freshly mixed concrete is the first task required for the purpose. There are various models to represent the behavior of fluids such as Newtonian model, Bingham model, and Herschel–Bulkley model [6, 7]. Various concrete rheometers have been recently introduced [8,9,10,11], with the yield stress and plastic viscosity of freshly mixed concrete being generally measured assuming it is a Bingham model fluid. This study also assumes it a Bingham model fluid for computational efficiency.

Nonetheless, field application of concrete rheometers is still rare and challenging due to the costly and relatively non-robust nature. Conventionally, the slump test for normally vibrated concrete or the slump flow test for self-consolidating concrete (SCC) are the most important tests for concrete quality assurance. Regulations for concrete structure construction specify the required repetitions of the slump or slump flow measurements. The evaluation of a concrete’s rheological properties using the field tests becomes promising once a correlating model between the field-test measurements and the rheological properties is found. Murata and Kikukawa [12] proposed τ y = 7.29–4.83 lnS, while Hu et al. [8] proposed τ y = ρ(30-S)/27, where τ y, S, and ρ are the yield stress in Pa, the slump in cm, and the density in kg/m3, respectively. Ferraris and de Larrard [13] updated the latter model by τ y = ρ(30-S)/34.7 + 212, thereby improving the model’s accuracy for very fluid mixtures (τ y < 500 Pa). The model for SCC was introduced by Roussel and Coussot [14, 15], where the yield stress was correlated with the slump flow of SCC. In this model, an equilibrium between the yield stress and gravity following the end slope of a mixture determined its slump flow. This analytical formulation could be also applied to the L-box test [16].

Despite the reasonable estimates obtained for SCC’s yield stress using the aforementioned models, these models suffer from a drawback because of neglecting the effect of inertia and aggregates. A fast-spreading SCC strikes the equilibrium position at the flow front. The flow velocity onset of stoppage affects the final shape (the end slope) of the slump flow spread. In addition, the mortar-phase contribution to the yield stress generally dominates that of the coarse-aggregates skeleton in SCC [17, 18], and the thickness of its slump flow spread is comparable to the coarse-aggregates size. The LCPC-box test has been proposed instead of the slump flow test to eliminate both weak points [19]. Therefore, this paper proposes a model that compensates for this test’s weaknesses. Adopting the volume-of-fluid (VOF) simulation for a single-fluid flow allows the inclusion of the inertia effect, and the valid extension to the two-phase mixture model reflects the effect of coarse aggregates. Finally, the proposed model is validated using concrete flow tests and a discussion regarding the model’s suitability for evaluating a concrete’s self-compacting ability is presented.

2 Modeling

2.1 Single-fluid simulation

First, freshly mixed concrete is assumed to be a unitary continuous fluid, where the VOF method is applied to trace the interface between the fluid and void space. The volume fraction for an Eulerian cubic element is described by the following advection equation:

$$\frac{\partial C}{\partial t} + \vec{v} \cdot \vec{\nabla }C = 0,$$
(1)

where \(\vec{v}\left( {\vec{x},t} \right)\) is the velocity field of fluid. The volume fraction of C indicates the degree of fluid filling within an element. An element is fully filled by the single fluid when C = 1 and empty when C = 0. Consequently, a continuous fluid surface can be constructed. The velocity vector field for each element is governed by the Navier–Stokes equation:

$$- \frac{1}{\rho } + \frac{\mu }{\rho }\nabla^{2} \vec{v} + \vec{g} = \frac{{{\text{D}}\vec{v}}}{{{\text{D}}t}}$$
(2)

where v is the fluid’s velocity vector, Dv/Dt indicates its material derivative, and ρ and μ are the density and shear viscosity of the fluid, respectively. The fluid is assumed to be incompressible. The gravity assigned by its acceleration of g = 9.8 m/s2 causes the fluid to flow. The scalar volume fraction and velocity vector can be obtained by combining the advection and Navier–Stokes equations. In this study, a commercial software was used for the processing (ABAQUS 6.14, Dassau System Inc.), where the VOF simulation was conducted using a finite element method that relies on a weighted residual algorithm.

The model to be simulated is the slump flow test standardized in ASTM C 1611 (Standard Test Method for Slump Flow of Self-Consolidating Concrete) and EN 12350-8 (Testing Fresh Concrete. Part 8: Self-Compacting Concrete-Slump-Flow Test). The slump flow test is conducted by (1) filling a concrete mix in an Abraham cone, and then (2) lifting the cone to allow the mix to flow under the effect of gravity. The top diameter of the Abraham cone is 100 mm, the bottom diameter is 200 mm, and the cone has a height of 300 mm. A one-fourth symmetric model is composed using 8-node hexagonal elements. The average mesh size is between 8 and 10 mm, which is small enough to have an accurate flow simulation of cement-based materials [20]. A total of 44,840 elements constructed the initial concrete cone and void space. The time increment for the flow simulation is 0.03 s. Figure 1 shows an example of the simulation results, where the contour colors indicate the reaction forces applied on each fluid element. For this example, the yield stress (τ y) and plastic viscosity (η p) were set to 75 and 100 Pa s, respectively. The density is 2400 kg/m3. Note that the surface tension effects could be negligible when the effect of viscous behavior is much higher than effects of surface tension. The shear stress at the edge of slump-flow spreading is dominated by viscous effect, e.g., yield stress, rather than surface tension of water [14].

Fig. 1
figure 1

Simulation of the slump flow

Full size image

Slump flow simulations can be represented by a spread curve plot whose abscissa and ordinate axes are time and flow front (the front end of fluid surface), respectively. The spread curves are then curve-fitted with

$$s\left( t \right) = \beta_{\ln } \cdot \ln \left( t \right) + \alpha_{\ln }$$
(3)

or

$$s\left( t \right) = \alpha_{\exp } \left( {1 - \exp \left( { - \frac{t}{{\beta_{\exp } }}} \right)} \right) + 200.$$
(4)

Both parameters (α and β) in each model function are determined by least-square fitting and can describe the spread curve within a marginal error. Investigation of various simulation results indicated that the logarithmic model function for the spread curve of a Newtonian fluid provided the highest coefficient of determination; and so did the exponential model function for a Bingham fluid.

The measures for the field test are the slump flow (the final spread, D f) and the time to reach the 500-mm-diameter spread (T 50). They need to be reported when the slump flow test is performed following ASTM C 1611 and EN 12350-8. The fitting parameters (α and β) allowed to easily determine both field-test measures. Defining a cut-off velocity (slope of the spread curve) of 2.5 mm/s effectively determined the final spread, where the value of the cut-off velocity is small enough to have apparent stop of the mini-slump flow. Tregger et al. [21] quantitatively assigned a cut-off velocity as 0.3 mm/s by image processing for the experiment and simulation of the mini-slump flow test. The cut-off velocity for the slump flow of concrete was set as approximately 10 times that of the paste test because the thickness of spreading is 10 times higher than that of mini-slump flow. All simulated spread reached the cut-off velocity within 20 s. The change of the cut-off velocity within ± 50% did not change the upper bound, 20 s, of the time for the final spread. Therefore, the slump flow (D s) from the single-fluid simulation can be simply determined by applying t = 20 s in Eq. (4):

$$D_{\text{s}} = \alpha_{\exp } \left( {1 - \exp \left( { - \frac{20}{{\beta_{\exp } }}} \right)} \right) + 200.$$
(5)

Inversion of the model functions, on the other hand, gave the corresponding value of T s. The fitting parameters for Newtonian or Bingham model fluid are separately applied to Eq. (3) or (4) to get s(t) = 500 mm:

$$T_{\text{s}} = \exp \left( {\frac{{500 - \alpha_{\ln } }}{{\beta_{\ln } }}} \right)$$
(6)

or

$$T_{s} = - \beta_{\exp } \cdot \ln \left( {1 - \frac{300}{{\alpha_{\exp } }}} \right).$$
(7)

As a result, the single-fluid simulation results can be parameterized using D s and T s, corresponding to D f and T 50, respectively, given that the yield stress and plastic viscosity of a concrete mix is provided.

2.2 Parametrization of the single-fluid simulation

The aforementioned single-fluid simulation is a costly process. For example, the simulation of the slump flow test took approximately 66.5 h to get 30 s simulation when four threads of Intel Core i5-4670 3.40 GHz are used. In order to replace the simulation by a regression model, a set of simulated data was stacked. The ranges of input variables, yield stress, and plastic viscosity were set to τ y = 0–100 Pa and η p = 50–500 Pa s. The corresponding output of D s and T s were finally obtained by a total of 46 simulations.

Non-dimensionalization of each parameter is preceded to develop a correlation between the input and output parameters. Reference values for non-dimensionalizing the output parameters are selected; in practice, their minima are D s = 500 mm and T s = 2 s. Only for the slump flow larger than 500 mm, T 50 can be defined. In addition, ACI committee 237 [22] and a European guideline [23] have reported that SCC can be called low-viscosity mix when its T 50 is smaller than 2 s. The corresponding reference value for the viscosity of Newtonian fluid models is 67.6 Pa s, and for Bingham fluid models, the correspondence is maintained if τ y < 36.7 Pa. In other words, a Bingham fluid model having yield stress less than 36.7 Pa shows the same spread curve with a Newtonian fluid model. The effect of yield stress less than 36.7 Pa is negligible. The dimensionless parameters are finally obtained as D s ′ = D s /(500 mm), T s ′ = T s /(2 s), τ y ′ = τ y/(36.7 Pa), and η p ′ = η p/(67.6 Pa s).

Figure 2 shows the correlation between the dimensionless input and output parameters. The identical relationship for the time to get 500 mm spread, T s ′ = η p ′, is found because the non-dimensionalization for T s ′ is conducted with the results of the Newtonian fluid models. T s = 0.0296η p or η p = 33.8T s can be used for this application, where the unit of each term is second or Pascal, respectively. The linearity is also found for Bingham fluid models, as shown in Fig. 3a, but the slope of each linear relationship increased with a higher yield stress. The slump flow, D s ′, have a logarithmic relationship with the viscosity, as shown in Fig. 3b. Introducing parameters a, b, and c developed the relationships

$$T_{\text{s}}^{{\prime }} = a\eta_{\text{p}}^{{\prime }}$$
(8)

and

$$D_{\text{s}}^{{\prime }} = - b\ln \left( {\eta_{\text{p}}^{{\prime }} } \right) + c.$$
(9)

The parameters depends on the yield stress of the model fluids:

$$a = k_{1} \exp \left( {k_{2} \tau_{\text{y}}^{\prime } } \right),$$
(10)
$$b = - k_{3} \tau_{\text{y}}^{{\prime }} + k_{4}$$
(11)

and

$$c = - k_{5} \tau_{\text{y}}^{\prime } + k_{6} ,$$
(12)

respectively, where the values of the k-coefficients are reported in Table 1.

Fig. 2
figure 2

Correlations for the single-fluid simulation results: a dimensionless T s and b dimensionless D s for Bingham fluid models

Full size image
Fig. 3
figure 3

Ellipsoidal cross section of concrete flow and consideration of partial segregation

Full size image
Table 1 k-coefficients for the correlation relationship
Full size table

2.3 Extension to two-phase model

The mortar phase in concrete dominantly contributes to the rheological behavior of SCC. It passes through the skeleton of highly concentrated aggregates at the end of the slump flow test. Coarse aggregates partially floating on the surface of the mix are easily observed [19]. There was a conventional research to reveal the segregation of SCC with correlating the slump flow test. The low value of time to reach final slump flow, T f, which result in high plastic viscosity result in high dynamic segregation of the mix [24]. In this case, the flow of SCC goes against the assumption of the single-fluid simulation, and a consequent update of the correlating model is required to consider such a partial segregation of aggregates.

Figure 3 illustrates a two-phase model described by coarse aggregates suspended in a mortar fluid. Under the assumption of single-fluid simulation, the mortar fluid is supposed to stay with all particles of the aggregates. However, the low-yield-stress mortar slips through the aggregates skeleton, which decreases the height (Δh s) and increases the diameter of the slump flow spread (ΔD s). The coarse aggregates break up the surface of the single fluid, here the mortar fluid. The degree of segregation is conceptually defined by θ = ∆h s/d max, where d max is the maximum aggregate size. No segregation occurs when θ = 0, while all aggregates are covered by the mortar fluid. A maximum-sized particle of aggregates is potentially released from mortar fluid if ∆h s = d max (θ = 1 refers to the onset of full segregation). The degree of segregation may be beyond the upper limit, having θ > 1 theoretically, but the case is not considered as a fully segregated concrete mix is never adopted in practice. As a result, the degree of segregation is bounded between 0 and 1.

The two-phase model extension is formulated given that the final spread of a concrete mix had an ellipsoidal cross section on its axisymmetric geometry. The ellipsoidal cross section of the single-fluid simulation, shown in Fig. 3, can be written as

$$\left( {\frac{2x}{{D_{\text{s}} }}} \right)^{2} + \left( {\frac{y}{{h_{\text{s}} }}} \right)^{2} = 1,$$
(13)

where D s is again the slump flow obtained by the single-fluid simulation and h s is the height at the center of the cross section. The volume of the concrete mix, V 0, is then calculated by integrating the cross section of the slump flow with respect to the y-axis:

$$V_{0} = \frac{\pi }{4}\mathop \int \limits_{0}^{{h_{\text{s}} }} \left( {D_{\text{s}}^{2} - \frac{{D_{\text{s}}^{2} }}{{h_{\text{s}}^{2} }}y^{2} } \right){\text{d}}y = \frac{\pi }{6}{\text{D}}_{\text{s}}^{2} h_{\text{s}} .$$
(14)

The volume of the slump cone is 5.5 × 106 mm3 and is maintained constant regardless of D s and h s.

The partial segregation of coarse aggregates lost the cover of ∆h s = θdmax, and consequently additional spread of the mortar fluid is contributed keeping V 0 constant. The volume decrease by ∆h s is then given by

$$\Delta V = \frac{\pi }{6}\left( {1 - \varphi } \right){\text{D}}_{\text{s}}^{2} \Delta h_{\text{s}} = \frac{\pi }{6}\left( {1 - \varphi } \right){\text{D}}_{\text{s}}^{2} \theta \,{\text{d}}_{\hbox{max} }$$
(15)

where φ is the volume fraction of aggregates. The slump flow, as a result, is added by the supply of the segregated volume. A proportional expression for V 0 gives the increase in the slump flow by

$$\Delta D_{s} = D_{s} \sqrt {\frac{\Delta V}{{V_{0} }}} = D_{s}^{2} \sqrt {\frac{{\pi \left( {1 - \varphi } \right)\theta {\text{d}}_{\hbox{max} } }}{{6V_{0} }}}$$
(16)

and then

$$D_{\text{f}} = D_{\text{s}} + \Delta D_{\text{s}} = D_{\text{s}} + D_{\text{s}}^{2} \sqrt {\frac{{\pi \left( {1 - \varphi } \right)\theta d_{ \hbox{max} } }}{{6V_{0} }}} .$$
(17)

The slump flow, D s, obtained by the single-fluid simulation is finally replaced by D f considering the partial segregation. Note that the time required to obtain the 500 mm slump flow spread is not disturbed by the partial segregation. Therefore, there is no difference in T 50 = T s by the two-phase extension.

On the final prediction by Eq. (17), the degree of segregation is still unknown and it should be priory determined. Its form and curvature are optimized to consider the field experience generally faced on the segregation problem: a higher fluidity of concrete mix, showing a higher slump flow, is susceptible to the aggregates segregation [22, 23]. It is finally modeled using a sigmoid function,

$$\theta = \frac{1}{{1 + \exp \left\{ { - 25\left( {D_{s}^{{\prime }} - 1.35} \right)} \right\}}}$$
(18)

where D s ′ is the dimensionless slump flow obtained by the single-fluid simulation.

2.4 Inversion of the model

The inversion of the single-fluid simulation is easily obtained using the parameterized functions of Eqs. (8) and (9). Applying the logarithmic function to Eq. (8) and eliminating ln(η p ′) from both equations give a quadratic equation with respect to the yield stress of τ y ′. The yield stress is then obtained from the following quadratic equation:

$$\tau_{\text{y}}^{\prime } = 1.66\ln T_{\text{s}}^{\prime } - 5.76 + \sqrt {2.76\left( {\ln T_{\text{s}}^{\prime } } \right)^{2} - 35.5\ln T_{\text{s}}^{\prime } + 329 - 229D_{\text{s}}^{\prime } } .$$
(19)

The plastic viscosity is also calculated directly from Eq. (8):

$$\eta_{p}^{\prime } = \frac{{T_{s}^{\prime } }}{{0.72\exp \left( {0.30\tau_{y}^{\prime } } \right)}},$$
(20)

where τ y ′ is given by Eq. (19).

Considering the partial segregation makes it difficult to use the simple inversion of the single-fluid simulation. The two-phase extension in Eq. (17) is an additional step to predict the slump flow, which does not have an analytical inversion. Instead, a nonlinear optimization can be used as pseudo-coded by Fig. 4. In this study, a generalized reduced gradient method is applied to optimize the field measurement of D f. Other inputs such as T 50 and d max are used to predict D f as formulated by Eqs. (17) and (18).

Fig. 4
figure 4

Flow chart and pseudocode for nonlinear optimization

Full size image

3 Verification

3.1 Channel flow test

The first example for the verification was the SCC flow through an open-cut channel. Three samples were used for the test. Table 2 reports the result of the slump flow test, where the samples are labeled as C1, C2, and C3. The maximum aggregate size of each mix was 25 mm for C1 and 10 mm for C2 and C3. The predicted yield stress and plastic viscosity, based on the proposed model, are also listed in the table.

Table 2 Fresh properties of the SCC samples
Full size table

The open-cut channel was fabricated to hold 100 mm × 100 mm × 1000 mm space. A cubic sample having 100 mm on each side was placed on one side. Opening a gate from a side of the cube allowed the gravity-induced flow through the 100-mm-wide channel [25]. Because the top of the channel was opened and both sides of the flow are guided, the flow simulation was accomplished with fixed boundary conditions on the bottom and both sides of the channel. Figure 5 shows the simulated spread of the channel flow, and its blue-colored elements show free surface which are applied no shear stress. The spread length was measured from one end of the channel to the edge of the spread, and the flow was recorded using a video camera. As a result, the time-spread curves were obtained as shown in Fig. 6.

Fig. 5
figure 5

The channel flow simulation

Full size image
Fig. 6
figure 6

Time-spread curves for the channel flow simulation of C1

Full size image

Results of the channel flow simulation are comparable with the experimental measurements of all 3 samples even though Fig. 6 shows the result of C1 as an example. The bounded area in the figure represents an inevitable error range caused by the tolerance of the slump flow measurement. The measurement error propagates to the predicted rheological properties, and thus, the expected range of error on the prediction can be analyzed from the tolerance for the slump flow measurement. A simple calculation that does not degrade the accuracy is conducted with derivatives of Eqs. (8) and (9):

$$\Delta \tau_{\text{y}}^{\prime } = \frac{{\Delta D_{\text{s}}^{\prime } }}{{0.019\ln \left( {\eta_{\text{p}}^{\prime } } \right) - 0.10}}$$
(21)

and

$$\Delta \eta_{\text{p}}^{{\prime }} = \frac{{\Delta T_{\text{s}}^{{\prime }} }}{{0.72\exp \left( {0.30\tau_{\text{y}}^{{\prime }} } \right)}},$$
(22)

respectively. For example, the calculated error range for SCC showing 650 mm slump flow with T 50 = 5 s are ∆τ y = ± 21.49 Pa and ∆η p = ± 35.60 Pa s, assuming that the tolerances for D s and T 50 are ± 20 mm and ± 1 s, respectively. The tolerance value is derived based on repeated measurements for the identical mixes. Note that the tolerance for quality control of an SCC mix is much wider than the specified value, i.e., ± 40 mm for the slump flow less than 550 mm and ± 65 mm for the slump flow more than 550 mm, according to ASTM C94/C94 M-16 (Standard Specification for Ready-Mixed Concrete). As a result, the simulation errors are fully covered by the measurement tolerance effect.

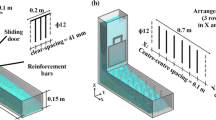
3.2 L-shaped panel filling test

Two more SCC mixes were used to verify the reliability of the correlation equations. Each mix was labeled by either L1 or L2, as listed in Table 2. In order to control its viscosity at the slump flow of 620 mm, different polycarboxylate-type admixtures were used. Therefore, L1 and L2 represented high- and low-viscosity mixes, respectively.

The testing device was an L-shaped concrete panel. The space to be filled was 100 mm thick, 240 mm wide, and 900 mm tall. Its length was also 900 mm. The column part of the transparent form with the length of 900 mm was filled with an SCC mix, and its spread caused by opening the gate to the beam section was measured. Figure 7 shows the simulated filling of the L-shaped panel. The contour color indicates the magnitude of reaction forces and moment of fluid. The reddish elements show the part under high reaction forces induced by gravitational force. The time-filling curve of each mix is shown in Fig. 8. The simulated filling of L1 and L2 showed a similar tendency while the time required to fill is different in each case: The high-viscosity mix L1 requires more time than L2. The simulation results were compatible with the measurements, and the simulation error can be covered properly considering the tolerance range previously described.

Fig. 7
figure 7

L-shape panel filling simulation

Full size image
Fig. 8
figure 8

Time-spread curves for the filling simulation

Full size image

4 Discussion

4.1 Comparison with the conventional model

The proposed model is compared with one of the conventional models. Figure 9 shows their estimation on the yield stress, where the conventional model is an analytical solution obtained by Roussel and Coussot [14]:

$$\tau_{\text{y}} = \frac{{225\rho gV_{0}^{2} }}{{128\pi^{2} R^{5} }} = \frac{4.06}{{D_{\text{f}}^{5} }}$$
(23)

where the slump flow and yield stress are used in their SI units, meter and Pascal, respectively. Each curve can be changed with the maximum size of aggregates and volume fraction of aggregates. In case of Fig. 9, the maximum size of aggregates and volume fraction of aggregates are set to 25 mm and 0.35, respectively, which are typical values for generally used SCC. The proposed model curves are developed by a coordinate transform after the slump flow in Eq. (17) is calculated for various yield stresses. The yield stress of SCC decreases with a higher slump flow. The proposed model also indicates the general trend, even though it shows T 50 dependence. A mix showing a low T 50, for example, 3 s in the figure, would have a relatively higher yield stress even if its slump flow is the same compared with the others. The fast-flowing mix pulls down an equilibrium shape at the slump flow front, as described formerly, and then redevelops an equilibrium at a further distance from the center, and the partial segregation upsizes the inertia effect (compare the dashed lines of the single-fluid simulation with the solid lines).

Fig. 9
figure 9

Comparison of the proposed model with a conventional model. Each dashed line reports a relationship without considering the partial segregation

Full size image

The value of T 50 is more affected by the plastic viscosity. A lower T 50 gives a lower plastic viscosity. The T 50 index for evaluating the viscosity of a mix [22, 23] can be replaced by the quantitative model. A low-viscosity mixes with T 50 less than 2 s have the plastic viscosity less than 75 Pa s in a serviceable range of the slump flow (approximately more than 620 mm). The plastic viscosity–T 50 relationship is also dependent on the slump flow. While having the same T 50, a mix with a lower slump flow has a lower plastic viscosity.

4.2 Comparison with the rheological measurements

The reliability of the proposed model can be confirmed by comparing the estimated results with the measurements of a commercialized rheometer. In this study, a total of 61 SCC mixes are collected, and the slump flow and T 50 are measured for each. Finally, the yield stress and plastic viscosity are measured with an ICAR rheometer (German Instruments, Inc.). The measured slump flow and T 50 are converted into the yield stress and plastic viscosity using both the current and conventional models. Figure 10a shows the yield stress comparison, where the ICAR measurements are indicated by the vertical axis. Two estimated values for a single mix (measurement) are distinguished by different colors of the points. Both models are comparably reliable, even though their estimated biases are different. Note that the measurement of a concrete rheometer can give only a relative value for the rheological properties of concrete, rather than the material properties [10, 26, 27]. For example, the measurements of a ConTec 5 viscometer (Steyputaekni ehf) are compared with those of ICAR in a previous study [26], where the correlations of the two parameters are \(\tau_{\text{y, ICAR}} = 1.75\tau_{\text{y,ConTec}}\) and \(\eta_{\text{p,ICAR}} = 0.75\eta_{\text{p,ConTec}}\) for mixes showing a slump flow of larger than 500 mm diameter. As shown in Fig. 10, the correlation between the yield stresses measured using the ICAR rheometer and estimated by the proposed model is given by \(\tau_{\text{y, ICAR}} = 0.82\tau_{\text{y}} - 13.2\) and \(\eta_{\text{p,ICAR}} = 0.57\eta_{\text{p}}\). Unfortunately, as shown in Fig. 10b, the plastic viscosity estimation showed relatively large fluctuation even though its tendency was strong. It might be considered as experiment error bound for the viscosity measurement of concrete. Considering a timed spread passage point for cement paste [28] or mortar [29] is expected to decrease the fluctuation.

Fig. 10
figure 10

Comparison with the measured rheological properties using ICAR rheometer: a yield stress estimation by the conventional and proposed models and b plastic viscosity estimation by the proposed model

Full size image

Even though the accuracy of the correlations is limited within the used rheometer model, the correlations can develop a comprehensive rheograph to evaluate the self-compacting performance of a concrete mix. The original rheograph is proposed with a set of measured yield stress and plastic viscosity using the ConTec viscometer [27]. The rheological properties are converted to results similar to those of the slump flow test. On the other hand, the European guideline [23] has also provided self-compacting ability based on the slump flow and T 50, and yield stress and plastic viscosity compatible with our results. A comprehensive rheograph is provided in Fig. 11. The rheological properties required to fill “walls and piles” and “floors and slabs” in the guideline are comparable with the SCC requirements based on the original rheograph. The recommended area of SCC comprises parts of “floors and slabs,” “walls and piles,” and “tall and slender” members.

Fig. 11
figure 11

Updated rheograph by the slump flow test results

Full size image

5 Conclusion

The slump flow test is the most widespread and important method to assess the workability of SCC. This study presents a model that can estimate a sample’s rheological properties using the slump flow test results. The proposed model is based on the VOF simulations of the slump flow test, which allows us to consider the inertia effects on the flow spread. The simulation results are parameterized using the slump flow and the elapsed time to reach a diameter of 500 mm. A two-phase extension additionally considers the partial segregation of coarse aggregates, which can form an extra spread for the VOF-simulated slump flow. Finally, numerical inversion is used to determine the yield stress and plastic viscosity of SCC, where the input variables are the maximum size and volume fraction of coarse aggregates, in addition to the slump flow test results. The channel flow and L-shaped panel filling tests are conducted to verify the model. In addition, merits of the proposed model are highlighted by comparing it with conventional models. A comprehensive rheograph is drawn using the proposed model, and the measurement incoherencies according to various concrete rheometer types are compared. As a result, on the updated rheograph the incoherent measurements of a single SCC mix indicate the same level of self-compacting ability.