1 Introduction

The analysis of complex systems based on experimentally recorded time series is typically performed using stationary or almost stationary data sets produced, e.g., by systems with slowly changing parameters, if their variation throughout the analyzed segments is treated as insignificant. Consideration of such data sets allows the use of a wide range of standard and special signal processing tools [1,2,3], assuming that the amount of data is sufficient to quantify signal properties with the required accuracy and reliably diagnose the state of the system. Depending on the signal duration and features, as well as the purpose of the study, the choice of the appropriate method is carried out. Spectral or correlation analysis, measures of complexity and predictability, along with other quantitative characteristics, make it possible to thoroughly describe the dynamics from different points of view. Diagnostics of the dynamics is often carried out by comparing several methods with the choice of the most suitable one, capable of separating the states of the system related to different functioning conditions. Although many characteristics are interrelated, different amounts of samples may be required to estimate them with the required accuracy due to distinct convergence of methods with the duration of the data.

Studying of complex systems for diagnostic purposes is not always limited to stationary dynamics. For example, important information about physiological systems can be obtained when they operate under conditions different from the baseline behavior. Changing the state of the system with subsequent restoration of its original dynamics is applied to study the adaptive capabilities. Due to this, the responses caused by functional tests, stresses, and other factors are often more informative than the purely stationary dynamics of such systems. Response characterization requires an appropriate analysis of transients, and this analysis often cannot be provided under the assumption of slowly changing parameters, i.e., the application of approaches for nonstationary signal processing becomes mandatory. Recent advances in this field include various wavelet-based methods [4,5,6,7,8,9,10], the empirical mode decomposition with the Hilbert–Huang transform [11, 12], detrended fluctuation analysis [13,14,15,16,17], etc. The ability to quantify the state of a system from short data sets is an important issue to describe the features of transient processes. The latter makes it possible not only to establish a change in the state, but also to quantify the duration of the transient process and even predict when this process will be finished.

One of the most important questions is how to determine the minimum length of a data set that can be processed to reliably diagnose the state of the system, i.e., shorter data sets will give unacceptable computational errors, while longer time series segments do not reduce the quality of diagnostics. Such a minimum duration is not a constant value and can be adjusted depending on the intensity and statistics of noise, the degree of nonstationarity associated with both the absolute changes in the control parameters and the rate of their variation. In this study, we analyze how transitions between different types of complex oscillatory behavior can be quantified based on multiresolution wavelet analysis [5]. This mathematical tool is currently widely applied to solve many scientific and technical problems, and the processing of nonstationary signals is one from them. Usually, a signal is decomposed according to a fast (pyramidal) scheme with orthogonal basic functions of the Daubechies family [4], and the standard deviations of the detail wavelet coefficients are treated as informative measures of complex signals [18, 19]. An enhanced version of the MWA method can also be applied to improve the characterization of signal features [20]. Thus, our recent studies have illustrated some advantages of enhanced versions that use cumulant analysis in wavelet space [21] or combine MWA with DFA of the detail wavelet coefficients [22].

The purpose of this study is to analyze the applicability of MWA for revealing transitions between system states and answer the question about the possibility of reducing the amount of data to determine inter-state transitions. We will consider chaos–hyperchaos transitions in the dynamics of coupled systems with self-sustained oscillations as an example of simulated data sets. Then we discuss the ability to characterize transitions between two different physiological states (wakefulness and artificial sleep) using EEG in mice. The paper is organized as follows. Section 2 briefly describes the wavelet-based multiresolution analysis and measures used to characterize distributions of detail decomposition coefficients. It also includes descriptions of the simulated and experimental data considered in this work. Section 3 contains the main results of the study of inter-state transitions at different rates of change in system parameters. The concluding remarks are summarized in Sect. 4.

2 Methods and experiments

2.1 MWA and its enhancements

Multiresolution wavelet analysis is an iterative signal decomposition procedure using filter banks constructed from two conjugate mirror filters called the scaling function \(\varphi (t)\) (low-pass filter) and the wavelet \(\psi (t)\) (high-pass filter) [23]. The filter banks are built by integer translations of \(\varphi (t)\) and \(\psi (t)\) and their dilations with the scaling factor \(2^j\):

$$\begin{aligned} \varphi _{j,l}(t)= & {} 2^{j/2}\varphi (2^j t - l), \nonumber \\ \psi _{j,l}(t)= & {} 2^{j/2}\psi (2^j t - l). \end{aligned}$$
(1)

Such a procedure is carried out for time series consisting of \(N=2^n\) samples. Each value of j is associated with distinct frequency bands (resolution levels). The signal f(t) can be decomposed at all available resolution levels or only up to some level \(j_m\)

$$\begin{aligned} f(t)=\sum _k s_{j_m,l} \varphi _{j_m,l}(t) + \sum _{j \ge j_m} \sum _l d_{j,l}\psi _{j,l}(t), \end{aligned}$$
(2)

where the sets of approximation (\(s_{j_m,l}\)) and detail coefficients (\(d_{j,l}\)) carry information about the signal in independent ranges of scales and can be used to restore the signal within the framework of iterative inverse wavelet transforms [24]. The choice of basis depends on the purpose of the study. Orthogonal wavelets of the Daubechies family are often applied with the function \(D^8\) being a good compromise between regularity and support length of \(\psi (t)\) [4].

Signal fluctuations are accompanied by fluctuations in decomposition coefficients [25, 26]. To describe their variability, the standard deviations of \(d_{j,l}\) are considered as a function of the resolution level:

$$\begin{aligned} \sigma _j=\sqrt{\frac{1}{J}\sum _{l=1}^{J}\left[ d_{j,l} - \langle d_{j,l}\rangle \right] ^2}, \langle d_{j,l} \rangle = \sum _{l=1}^{J} d_{j,l}, \end{aligned}$$
(3)

where J is the number of decomposition coefficients at the level j.

Depending on the distribution of detail coefficients, other measures can also be used for their characterization, not limited to the standard deviation or variance, which is the second cumulant of the distribution. Thus, the higher cumulants can be applied, namely the skewness (the third cumulant)

$$\begin{aligned} A_j= \frac{\mu _j^3}{\sigma _j^3},~~~~~\mu _j^3=\frac{1}{J}\sum _{l=1}^{J} \left[ d_{j,l} - \langle d_{j,l}\rangle \right] ^3 \end{aligned}$$
(4)

or excess kurtosis (the fourth cumulant)

$$\begin{aligned} E_j= \frac{\mu _j^4}{\sigma _j^4} - 3,~~~~~\mu _j^4=\frac{1}{J}\sum _{l=1}^{J} \left[ d_{j,l} - \langle d_{j,l}\rangle \right] ^4. \end{aligned}$$
(5)

In particular, the latter quantities can be informative and helpful in processing physiological time series with specific features (extreme events) and their application can outperform the approach based on standard deviations in diagnostic-related studies [21, 27]. We designate the multiresolution analysis with thorough processing of decomposition coefficients as enhanced MWA (EMWA).

2.2 Simulated data

A model of two coupled Rössler oscillators is considered to analyze chaos–hyperchaos transitions by variations in the control parameter [28, 29]. This model is described by six first-order ordinary differential equations:

$$\begin{aligned} \frac{\text {d}x_{1,2}}{\text {d}t}= & {} -\omega _{1,2}y_{1,2} - z_{1,2} + \gamma (x_{2,1}-x_{1,2}),\nonumber \\ \frac{\text {d}y_{1,2}}{\text {d}t}= & {} \omega _{1,2}x_{1,2} + a y_{1,2},\nonumber \\ \frac{\text {d}z_{1,2}}{\text {d}t}= & {} b + z_{1,2} (x_{1,2} - c), \end{aligned}$$
(6)

where the parameters \(a=0.15\), \(b=0.2\) and c govern the dynamics of each oscillatory unit, \(\gamma =0.02\) is the coupling strength, and non-identical basic frequencies \(\omega _{1,2}=1.0 \pm \Delta\) are characterized by mismatch \(\Delta =0.009\). We use the parameter c near the value \(c=7.0\), where chaotic synchronous oscillations are changed by hyperchaotic dynamics. The analysis of such transitions for the case of fast switching between the given regimes and a slower change in the parameter c is carried out based on sequences of return times into the Poincaré section \(x_2+y_1=0\).

2.3 Experimental data

The experiments were carried out on six male mice weighing 20–25 g in accordance with the Guide for the Care and Use of Laboratory Animals (2011) and the protocol approved by the Local Bioethical Commission of the Saratov State University. The animals were housed in a light–dark environment with lights on from 8:00 to 20:00 and fed ad libitum with standard rodent food and water. Cortical EEG [30, 31] (two channels, Pinnacle Technology, Taiwan) was acquired using silver electrodes. Signals were measured in awake mice and after anesthesia provoked by 4% isoflurane (i.e., in artificial sleep). The duration of the recording was 2 h with a sampling rate of 2 kHz. Artifact removal procedures [32] were performed prior the EEG data analysis.

3 Results and discussion

3.1 Chaos–hyperchaos transitions

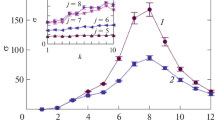
Before studying the transients between chaotic and hyperchaotic oscillations produced by the model of two interacting Rössler systems (6), let us consider what is the minimum amount of data that allows us to reliably characterize the steady-state oscillations associated with these two types of complex dynamics. Recently, we have demonstrated how these regimes can be detected and quantified based on Lyapunov exponents, a commonly used approach for diagnosing chaos–hyperchaos transitions [33]. However, this method requires rather long data sets to perform authentic estimates associated with the two largest Lyapunov exponents, and especially with the second one, the estimates of which are performed after thorough averaging over various regions of the chaotic/hyperchaotic attractor. The MWA method considered in the current study cannot recognize complex oscillations with two positive Lyapunov exponents as a hyperchaotic regime, but it can reveal different complexities of return times sequences, related to chaotic and hyperchaotic oscillations in terms of the features of the distributions of wavelet coefficients. To ensure that these two types of complex dynamics are clearly separated, Fig. 1a shows the t-values of the Student’s t test computed using sequences of detail wavelet coefficients for chaotic and hyperchaotic dynamics.

According to Fig. 1a, the best state separation is observed at the first resolution level, characterized by the standard deviation of the wavelet coefficients (\(\sigma _1\)). Here, k denotes the number of segments with a duration of 128 samples used to diagnose the analyzed types of oscillations. For any k, starting from \(k=2\), the estimated value t exceeds the critical value \(t_c\) related to the significance level \(p<0.05\). Thus, the possibility of a clear separation between the two types of dynamics is confirmed, and the question arises whether it is possible to reduce the amount of data for diagnostic purposes. To answer such a question, we performed a more careful analysis, considering segments of different lengths with different numbers of averages, and choosing \(\sigma _1\), which provided the best characterization of the states. Figure 1b illustrates that \(t > t_c\) for \(k=2\) if \(n \ge 32\), i.e., 64 return times into the Poincaré section make it possible to distinguish between chaotic and hyperchaotic oscillations. A similar analysis performed for various initial conditions and a small change in the control parameters (which does not change the type of complex dynamics under study) produces results similar to Fig. 1b, and, therefore, we can establish the minimum required amount of the data set. The results obtained refer to stationary dynamics, when any transient processes between regimes are excluded and do not affect the analysis. Taking them into account obviously affects the estimates and may require longer data sets for diagnostic purposes, especially if the transients take quite a long time compared to the duration of the signal segment used for analysis. Since the duration of the transient process is an important circumstance, we considered two cases: fast (switching between values of control parameters) and slow change (linear growth of the control parameter).

Fig. 1
figure 1

Estimates of t value of the Student’s t test for standard deviations and excess kurtosis of wavelet coefficients of simulated data sets (chaotic and hyperchaotic oscillations) for \(n=128\) and different number k of segments for averaging (a), and t values for \(\sigma _1\) and n from 16 to 128 depending on k (b). The critical values \(t_c\), related to the significance level \(p<0.05\), are shown by a black solid line. Skewness results (hereinafter) are comparable to excess kurtosis, so we do not reproduce them in the figures

Full size image

The switching case is illustrated in Fig. 2. For relatively long data sets (\(n=256\) or \(n=128\), Fig. 2a), there is no obvious problem of distinguishing between chaotic (\(i<1000\)) and hyperchaotic oscillations (\(i>1000\)) by simply introducing a threshold level related, e.g., to \(\sigma _1=0.03\). Smaller data sets (\(n=64\) or \(n=32\), Fig. 2b) give a greater variability of the estimated values of \(\sigma _1\) for hyperchaotic oscillations, and the introduction of a threshold level is less appropriate, since it will be crossed by some variations in \(\sigma _1\). To remedy this situation, running averaging can be carried out, i.e., averaging within a floating window. By choosing a window of size n, the high-frequency variations of \(\sigma _1\) can be reduced, and the obtained dependences become more suitable for distinguishing between chaotic and hyperchaotic oscillations. This averaging, however, means increasing the analyzed data set to 2n samples. In the example under consideration, authentic diagnostics for \(n\ge 128\) is provided in both cases, without averaging (Fig. 2a) and after averaging \(\sigma _1\)-values at \(n=64\) (Fig. 2c) using a window of 64 values.

Fig. 2
figure 2

Changes of \(\sigma _1\) during the transition from chaotic to hyperchaotic oscillations (the switching case) for several values of n: (a) 128 and 256, (b) 32 and 64 (without running averaging), (c) 32 and 64 after running averaging. In the latter case, the duration of the window is equal to n

Full size image

These results show that consideration of smaller parts of data with an additional running averaging procedure does not improve diagnostics compared to the case of larger data segments without averaging. Up to now, we have considered the case of purely deterministic dynamics. The presence of additive (measuring) noise does not strongly affect the results and conclusions of this study. Figure 3 compares estimates for \(n=128\) performed for the case when the variance of white noise takes values of 0, 1, and 10% of the signal range. The first two dependences are almost the same. Stronger noise (10%) leads to an increase in \(\sigma _1\)-values for both regimes, chaotic and hyperchaotic, and, therefore, the threshold value may increase, but the possibility of reliable diagnostics is kept, as well as estimates of the minimum required amount of data. We have shown that in the example under consideration, switching between regimes which produce the related transient processes, requires almost twice as much data (\(n=128\)) as compared to the case when the stationary dynamics of the model (6) is analyzed, and transients are avoided (\(n=64\)).

Fig. 3
figure 3

Changes of \(\sigma _1\) during the transition from chaotic to hyperchaotic oscillations (the switching case) for \(n=128\) and several variances of additive white noise. Noise statistics affects the \(\sigma _1\) values, but the conclusion of the study remains unchanged

Full size image

If the control parameters vary slowly, the duration of the transients increases, and the latter affects the length of the data set required to study the transitions between states. Figure 4 illustrates this case for the linear growth of the parameter c from \(c=6.9\) to \(c=7.1\) in the range \(i \in [500, 1500]\). Changes in \(\sigma _1\) in this case are more complex compared to switching of the control parameter (Fig. 2a). Before \(\sigma _1\) stabilizes at a value related to hyperchaotic dynamics, it can behave in a rather complicated way. Although near \(i=1000\) there is a rapid growth associated with the intersection of the bifurcation value of c, further variations of \(\sigma _1\) at \(n=128\) are quite strong, and a simple introduction of the threshold level, e.g., \(\sigma _1=0.03\) may lead to misinterpretations of the underlying dynamics. Here, the case \(n=256\) is more appropriate for diagnosing chaos–hyperchaos transitions. Thus, the minimum amount of the data set depends on the duration of the transients, what can be considered as an expected result. It is important, however, to note that in all the examples considered, stationary dynamics, switching, slow changes in control parameters and measurement noise, MWA analysis enables to reliably diagnose chaos–hyperchaos transitions using a relatively small amount of data.

Fig. 4
figure 4

Changes of \(\sigma _1\) during the transition from chaotic to hyperchaotic oscillations (linear growth of the control parameter) for two values of n

Full size image

3.2 EEG recordings with transitions between physiological states

The analysis of physiological processes, such as EEG recordings, allows us to consider similar cases of almost stationary dynamics, when the state of the body does not change essentially (e.g., relaxation), fast changes in dynamics (responses to sudden stimuli), or relatively slower changes when one state of the body is replaced by another one (waking and sleeping). Diagnostics of the dynamics based on relatively short signals is important not only for detecting inter-state transitions in healthy organisms, but also makes it possible to establish the development of pathological dynamics of the brain. In this study, we discuss the features of EEG signals during anesthesia. By analogy with the simulated data sets discussed in Sect. 3.1, let us start with stationary dynamics (or almost stationary, which is more appropriate for physiological processes) and compare the states of wakefulness and artificial sleep caused by anesthesia.

Fig. 5
figure 5

Estimates of t value of the Student’s t test for standard deviations and excess kurtosis of wavelet coefficients of EEG signals for \(n=128\) and different number k of segments for averaging. The critical value \(t_c\), related to the significance level \(p<0.05\), is shown by a black solid line

Full size image

Figure 5 shows the t values of the Student’s ttest computed from segments of the duration \(n=512\) (smaller segments did not provide reliable separation between states due to the rather high sampling rate, 2 kHz). According to Fig. 5, the results for standard deviations of detail wavelet coefficients and excess kurtosis are comparable, and both of these measures can be applied in this example. Reliable inter-state separation takes place at \(k>15\), i.e., the minimum duration of EEG signals for such separation approaches 4 s. For other experiments, this quantity may vary, but typically it does not exceed 10 s. Therefore, this amount of data enables diagnosing the effects of anesthesia in the dynamics of the brain. When analyzing these effects for experimental data with transient processes, the duration of the required data sets increases by a factor of 2–3, i.e., records up to 30 s should be used.

4 Conclusion

Transient processes contain important information about the dynamics of the system, which can be used to identify features of complex behavior when the system changes its state under the influence of external forces, variations in internal parameters or interactions between components. The exclusion of such information simplifies the analysis of experimental data, since a significantly wider set of signal processing tools can be applied, but this strongly reduces the possibility of studying the adaptive properties of the system. Extracting information from short data sets is a way to conduct a more thorough analysis of inter-state transitions, which is useful for characterizing the duration of the transient process and its features. Based on this ideology, here we consider the possibility of reducing the amount of data for MWA to preserve a reliable separation between different types of complex oscillations. Using the model of two interacting Rössler systems, which describes the chaos–hyperchaos transitions, we show that these changes can be detected from the sequences of return times into the Poincaré section, including about 64 samples, if transient processes are excluded from consideration. When time series contain such transients, their duration should increase, and the necessary amount of data depends on the rate of change of the parameter. Thus, for fast changes with short transients (switching the control parameter), transformations of chaotic oscillations into hyperchaotic ones and vice versa were identified by about 128 return times. For a slower change in the parameter (for example, with its linear growth), this amount of data was about twice as large as in the case of switching. Nevertheless, the possibility of using sufficiently short data segments for diagnostic purposes was confirmed. This conclusion is valid for other transitions, e.g., for transitions between synchronous and asynchronous chaotic oscillations in the model of two interacting Rössler systems (in the vicinity of the bifurcation line). Further, we have also demonstrated the ability to diagnose inter-state transitions in brain dynamics based on EEG processing. In particular, the state of artificial sleep was recognized based on segments with a duration of less than 10 s for data sets without transients and less than 30 s for EEG signals with transient processes.