Asymptotic study of the Levitron dynamics

Abstract

In the present effort, we revist the Levitron’s dynamics in the line of previous works due to Berry, Dullin and Easton, and Gans. An invariant set in the Eulerian formulation is delivered and a local study is performed which disclose the dynamics on the invariant manifold which coincides to that obtained by Dullin and Easton using the yaw–pitch–roll angles. Moreover, we extend the results of Gans, being able to determine further stable regions for the magnetic levitation of the Levitron. Symmetric and asymmetric trajectories close to an analytical solution are numerically explored. An asymptotic multiscale analysis is also carried out with the aim of studying the nonlinear interaction between the traslational and rotational modes. By recourse to a Hamiltonian approach, we provide the study of the local behavior of the Levitron near an equilibrium point of the system. Also, the existence of invariant regions in phase space corresponding to persistent levitation of the top are detected. The performed numerical studies serve to elucidate the Levitron’s behavior.

1 Introduction

The Levitron is a mechanical device conformed by a top, namely a magnetized rotationally symmetric rigid body of uniform mass that behaves as a magnetic dipole, and a base that provides a permanent magnetic field which, by interacting with the magnetic dipole, compensates the gravitational force acting on the top when put to spin over it. A diagram of the Levitron is presented in Fig. 1 where $B({{\bar{r}}})$ is the static magnetic field of the base and $\varvec{\mu }$ is the top magnetic dipole.

Magnetic levitation of spinning bodies was first explored by Roy Harrigan by means of a device consisting of a square magnetic base and a magnetic top whose volume and mass needed to be calibrated to achieve the inertial and magnetic momenta leading to its persistent magnetic levitation ([1]). The Earnshaw’s theorem [2] establishes the rules for the magnetic levitation of static dipoles, but the first theoretical approaches to the Levitron’s dynamics date from 1996 and are given in Ref. [1, 3]. Indeed, Berry [1] delivered a Hamiltonian formulation and an adiabatic theory to prove that the magnetic levitation is possible only for some ranges of the spinning rates, and his results were confirmed by recourse to both physical and numerical experiments in Ref. [3].

Later on, in the frame of a Hamiltonian approach, Dullin and Easton [4] not only studied the local behavior of the Levitron near an equilibrium point of the system, but detected invariant regions in phase space corresponding to persistent levitation of the top. Also following the guideline drew by Berry [1], Gans [5] addressed the analysis of numerical simulations by introducing dimensionless quantities. However, neither Dullin and Easton nor Gans considered the energy losses due to friction, which were considered for the first time in Ref. [6].

In the present effort, whose outline is mostly based on the works of Dullin and Easton and Gans, the equations of motion are included at length, and invariant regions in phase space as well as equilibrium solutions are thoroughly described. The numerical verification of the range for the spinning rates given in Ref. [1] is performed, a persistent levitation of the top being observed. Furthermore, to enlighten our comprehension of the nonlinear behavior of the interacting translational and rotational modes, we perform multiscale asymptotic computations which provide evidence of the nutation affecting the spinning body’s translation. Our main motivation in such a practice is to distinguish how the varying difference between the rotational and precession momenta affects at different scales. Let us notice that a similar though linear asymptotic study was addressed in Ref. [7].

Fig. 1

Diagram of the Levitron $^{\text {TM}}:\, B({{\bar{r}}})$ is the static magnetic field of the base and $\varvec{\mu }$ is the top magnetic dipole

This paper is organized as follows. First and for the sake of completeness, a Hamiltonian description of the problem (which coincides with that in Ref. [5]) is delivered in Sect. 2. The equations of motion, the adopted routine for numerical integration, as well as the invariant set and stability regions are presented in Sect. 3, 5 and 4 respectively. Symmetric and non-symmetric solutions are analyzed in Sect. 6, and the description of the phase space configuration for the equations of motion is provided in Sect. 7. The multiscale asymptotic study of the Levitron’s stability is included in Sect. 8. The final section is devoted to present the conclusions of the overall analysis.

2 Kinetic and potential energies

The kinetic energy of the Levitron can be regarded as the sum of the translational kinetic energy of its center of mass and the kinetic energy associated with its rotation.

In fact, in terms of the Eulerian angles, the total kinetic energy of the top of mass m can be recast as (see [8, 9] for details)

$$\begin{aligned} T= & {} \frac{1}{2}\bigg [m(\dot{x}^2+\dot{y}^2+\dot{z}^2)+\varTheta _1({{\dot{\theta }}}^2\nonumber \\&+{{\dot{\psi }}} ^2\sin ^2\theta )+\varTheta _2({{\dot{\phi }}}+{{\dot{\psi }}} \cos \theta )^2\bigg ], \end{aligned}$$

(1)

where $\theta$ is the tilt, $\psi$ the precession (or the latitude and the longitude of the rotation axis, respectively), and $\phi$ the rotation or spin, while the coordinates ${{\bar{r}}}=(x,y,z)$ denote the position of the top’s center of mass. Notice that due to the axial symmetry of the body, we can assume that its inertia tensor is $\varTheta =\text {diag}(\varTheta _1,\varTheta _1,\varTheta _2)$.

Meanwhile, the potential energy on a given point of the configuration space, $\varPsi ({{\bar{r}}} ,{\mathbf {R}})$, where ${{\bar{r}}}$ and ${\mathbf {R}}$ describe the translation of the top’s center of mass and its rigid rotation, respectively, involves two terms: the one associated with the gravitational force mgz, z being the height of its center of mass, and the other one due to the magnetic field of the base that interacts with the spinning top. If we denote by $\mu <0$ the magnitude of the dipole’s force, located at the center of mass of the spinning body, we have that, following [9] or [8] and being $B({{\bar{r}}})=-\nabla V({{\bar{r}}})$, the total potential energy of the Levitron reads

$$\begin{aligned} \varPsi ({{\bar{r}}},{\mathbf {R}})= & {} mgz+\mu \biggl [\sin \theta \biggl (\cos \psi \frac{\partial V}{\partial x} +\sin \psi \frac{\partial V}{\partial y}\biggl )\nonumber \\&+\cos \theta \frac{\partial V}{\partial z}\biggl ]. \end{aligned}$$

(2)

Let us notice that, accounting to the cylindrical symmetry in the top’s flight, the harmonic function $V({{\bar{r}}})$ can be written as

$$\begin{aligned} V({{\bar{r}}})=V_{0}(z)+\rho V_{1}(z)+\rho ^2 V_{2}(z)+\cdots , \end{aligned}$$

where $\rho ^2=x^2+y^2$ being $\rho \ll 1$, and for $n>0$ we have

$$\begin{aligned} V_n(z)={\left\{ \begin{array}{ll} 0&{}\text {if { n} odd,}\\ -n^{-2}V''_{n-2}(z)&{}\text {if { n} even.} \end{array}\right. } \end{aligned}$$

Using the notation

$$\begin{aligned} \varPhi _{k}(z)=\frac{\mathrm {d} ^{k}}{\mathrm {d} z^{k}}V_{0}(z), \end{aligned}$$

and being

$$\begin{aligned} R_{13}=\sin \theta \cos \psi \qquad R_{23}=\sin \theta \sin \psi \qquad R_{33}=\cos \theta ,\nonumber \\ \end{aligned}$$

(3)

the total potential energy can finally be recast as

$$\begin{aligned} \varPsi ({{\bar{r}}},{\mathbf {R}})= & {} mgz-\mu \bigg [ \frac{1}{2}\varPhi _{2}(z)(xR_{13}+yR_{23})+\big (-\varPhi _{1}(z)\nonumber \\&+\frac{1}{4}(x^{2}+y^{^2})\varPhi _{3}(z)\big )R_{33}+\cdots \bigg ]. \end{aligned}$$

(4)

The magnetic base over which the spinning top levitates can be regarded as a vertical orientated dipole distribution in the plane. If this magnetization is uniform, since the planar base of the Levitron has cylindrical symmetry, the magnetic potential over the z-axis is given by

$$\begin{aligned} V_{0}(z)=\frac{M}{4\pi }z \iint \limits _{\text {base}}\frac{l}{(l^2+z^2)^{3/2}} d\gamma dl, \end{aligned}$$

(5)

where $\gamma$ and l are the angular and radial coordinates of the base, and M is the magnetization in the z-direction (see [10]).

Though different shapes of the base have been considered along the literature (see, for instance, [1] and [4]), we work with a ring dipole of radius a, so that the integral (5) becomes

$$\begin{aligned} V_0(z)=\frac{M}{2}\frac{za}{(a^2+z^2)^{3/2}}, \end{aligned}$$

(6)

that leads to qualitative outcomes which, near the z-axis, bearly differ from those obtained with other models (as claimed in Ref. [5]).

3 Equations of motion

We deal with the dimensionless equations of motion for the spinning top, by scaling by the radius of the dipole ring a and a consistent time scale $\tau$. Therefore, following [5], we introduce:

$$\begin{aligned} x=aX,\qquad y=aY,\qquad z=aZ,\qquad t=(a/g)^{1/2}\tau , \end{aligned}$$

so that V can be written as

$$\begin{aligned}&V=\frac{M_{e}}{4\pi a^{2}}\bigg [f_{0}(Z)+(X^2+Y^2)f_{2}(Z)+O((X^2+Y^2)^2)\bigg ]\nonumber \\&\quad =:\frac{M_{e}}{4\pi a^{2}}\varPhi , \end{aligned}$$

(7)

with

$$\begin{aligned} f_{0}(Z)=\frac{Z}{(1+Z^{2})^{3/2}}, \qquad f_{2}(Z)=-\frac{3}{4}\frac{(2Z^{2}-3)Z}{(1+Z^{2})^{7/2}},\nonumber \\ \end{aligned}$$

(8)

where $M_e=2\pi M a$ is the net strength of the dipoles of the ring and a is the effective radius.

The outcoming Hamiltonian is

$$\begin{aligned} {\mathcal {H}}= & {} \frac{1}{2}\left( p_{X}^{2}+p_{Y}^{2}+p_{Z}^{2}+\frac{p_{\theta }^{2}}{A}+\frac{[p_{\psi }-p_{\phi }\cos \theta ]^{2}}{A \sin ^{2}\theta }+\frac{p_{\phi }^{2}}{C}\right) \\&-{\mathcal {M}}\left[ \sin \theta \left( \cos \psi \frac{\partial \varPhi }{\partial X}+\sin \psi \frac{\partial \varPhi }{\partial Y} \right) + \cos \theta \frac{\partial \varPhi }{\partial Z} \right] +Z, \end{aligned}$$

and the concomitant equations of motion, which have already been given in Ref. [11] and are included herein just for the sake of completeness, read

$$\begin{aligned} {\dot{X}}&=p_{X} \end{aligned}$$

(9a)

$$\begin{aligned} {\dot{Y}}&=p_{Y} \end{aligned}$$

(9b)

$$\begin{aligned} {\dot{Z}}&=p_{Z} \end{aligned}$$

(9c)

$$\begin{aligned} {\dot{\theta }}&=\frac{p_{\theta }}{A} \end{aligned}$$

(9d)

$$\begin{aligned} {\dot{\psi }}&=\frac{p_{\psi }-p_{\phi }\cos \theta }{A \sin ^{2}\theta } \end{aligned}$$

(9e)

$$\begin{aligned} {\dot{\phi }}&=-\cos \theta \cdot \frac{p_{\psi }-p_{\phi }\cos \theta }{A \sin ^{2}\theta }+\frac{p_{\phi }}{C} \end{aligned}$$

(9f)

$$\begin{aligned} \dot{p_{X}}&=2{\mathcal {M}}\left[ f_{2}(Z)\sin \theta \cos \psi +X f_{2}'(Z)\cos \theta \right] \end{aligned}$$

(9g)

$$\begin{aligned} \dot{p_{Y}}&=2{\mathcal {M}}\left[ f_{2}(Z)\sin \theta \sin \psi +Y f_{2}'(Z)\cos \theta \right] \end{aligned}$$

(9h)

$$\begin{aligned} \dot{p_{Z}}&={\mathcal {M}}\left[ 2f_{2}'(Z)\sin \theta (X \cos \psi +Y\sin \psi )\right. \nonumber \\&\quad \left. +\cos \theta (f_{0}''(Z)+(X^{2}+Y^{2})f_{2}''(Z))\right] -1 \end{aligned}$$

(9i)

$$\begin{aligned} \dot{p_{\theta }}&=-\frac{(p_{\phi }\cos \theta -p_{\psi })(p_{\psi }\cos \theta -p_{\phi })}{A\sin ^{3}\theta }\nonumber \\&+{\mathcal {M}}\left[ 2f_{2}(Z)\cos \theta (X\cos \psi +Y\sin \psi )\right. \nonumber \\&\left. \quad -\sin \theta (f_{0}'(Z)+(X^{2}+Y^{2})f_{2}'(Z)) \right] \end{aligned}$$

(9j)

$$\begin{aligned} \dot{p_{\psi }}&=2{\mathcal {M}} f_{2}(Z) \sin \theta (Y\cos \psi -X\sin \psi ) \end{aligned}$$

(9k)

$$\begin{aligned} \dot{p_{\phi }}&=0, \end{aligned}$$

(9l)

where

$$\begin{aligned} A=\frac{\varTheta _1}{ma^{2}},\qquad C=\frac{\varTheta _2}{ma^{2}}, \qquad {\mathcal {M}}=\frac{-\mu M_{e}}{4\pi mga^{4}}, \end{aligned}$$

(10)

are positive constants. Notice that both ${\mathcal {H}}$ and $p_{\phi }$ are conserved quantities.

4 Local analysis

As we have already proposed in Ref. [11], an invariant set for equations (9) is given by

$$\begin{aligned}&Inv=\{X=Y=0,\ \theta =0,\ p_{X}=p_{Y}=0,\\&p_{\theta }=0,\ p_{\psi }=p_{\phi } \}. \end{aligned}$$

Let us remark that the proof of our proposition strongly relies on the assumption that $p_\psi =p_\phi$ and that there is no tilt (i.e., $\theta = 0$). Both $\dot{p_{\theta }}$ and ${\dot{\psi }}$ are shown to be null by considering the Taylor series of $\sin \theta$ and $\cos \theta$ to conclude that $\theta =0$ is just an evitable singularity of (9) whenever the equality $p_{\psi }=p_{\phi }$ holds.

Indeed, the existence of such an invariant set allows us to compare some assumptions and results with those of previous works. In Ref. [4], for instance, the authors find the invariant set for the non-singular equations of motion which encompass the yaw–pitch–roll angles instead of our Eulerian description of the top’s motion. Notice should be taken that we are handling a different matrix ${\mathbf {R}}$ from that used in Ref. [4] and, as a consequence, we are dealing with a different magnetic potential, but we still get the invariant region which responds to the physical intuition that when the top rotates without precession, it is $p_\phi =p_\psi$, the dynamics of $\psi$ becoming irrelevant from a physical point of view. In this regard, we obtained numerical evidence that the spinning top has a stable flight whenever $p_\phi$ and $p_\psi$ are close (see [12]).

The corresponding Hamiltonian function is

$$\begin{aligned} {\mathcal {H}}_{\mathrm{Inv}}=\frac{1}{2}\left( p_{Z}^{2}+ \frac{p_{\phi }^{2}}{C}\right) -{\mathcal {M}}\left[ \frac{\partial \varPhi }{\partial Z} \right] +Z, \end{aligned}$$

(11)

and the dynamics in this region is described by

$$\begin{aligned} {\dot{Z}}&=p_{Z} \qquad \dot{p_{Z}}={\mathcal {M}} f_{0}''(Z)-1 \end{aligned}$$

(12)

$$\begin{aligned} {\dot{\phi }}&= \frac{p_{\phi }}{C} = \sigma \qquad \dot{p_{\phi }}=0. \end{aligned}$$

(13)

Notice that the equations for Z and $\phi$ are uncoupled; while the rotation rate ${\dot{\phi }}$ remains constant on the invariant set, the local dynamics of Z mimics a harmonic oscillator.

Let us now introduce through

$$\begin{aligned} V_{Inv}=-{\mathcal {M}}\left[ \frac{\partial \varPhi }{\partial Z} \right] +Z =-{\mathcal {M}} f_0'(Z)+Z, \end{aligned}$$

(14)

the potential energy onto the invariant set.

To linearize the system, we need to find the equilibrium points of (12) from

$$\begin{aligned}&{\mathcal {M}} f_{0}''(Z)-1=0 \qquad \text {with} \qquad \nonumber \\&\quad f_{0}''(Z)=-4f_{2}(Z)=\frac{3(2Z^{2}-3)Z}{(1+Z^{2})^{7/2}}, \end{aligned}$$

(15)

that is

$$\begin{aligned} f_0''(Z)=\frac{1}{{\mathcal {M}}}. \end{aligned}$$

(16)

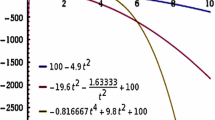
As $\mu <0$ and from definitions (10), there results $1/{\mathcal {M}}>0$. Then, Eq. (16) allows for a solution whenever

$$\begin{aligned} \frac{1}{{\mathcal {M}}}\le \max _{0\le Z <\infty } f_0''(Z), \end{aligned}$$

as shown in Fig. 2.

Fig. 2

Equilibrium points of $V_{Inv}$

The critical points of $f_0''$ (or $f_2$) are the roots of

$$\begin{aligned} 8Z^4-24Z^2+3=0, \end{aligned}$$

namely,

$$\begin{aligned} \pm \sqrt{\frac{6\pm \sqrt{30}}{4}}. \end{aligned}$$

The two positive roots correspond to a maximum and a minimum of $f_2$. On evaluating $f_0''$ in the larger root, we get that

$$\begin{aligned} \max _{0\le Z <\infty } f_0''(Z)=\frac{3\sqrt{30(6+\sqrt{30})}}{4\bigl (\frac{5}{2}+\frac{1}{4}\sqrt{30}\bigl )^{7/2}}=0.122131, \end{aligned}$$

and then, Eq. (16) admits a solution if

$$\begin{aligned} {\mathcal {M}}\ge \frac{1}{0.122131}=8.187957392. \end{aligned}$$

(17)

Therefore, the equilibrium exists over the invariant region if condition (17) is satisfied. We will show numerically that stable solutions require ${\mathcal {M}}$ to be big enough. In fact, since $f_0''$ reaches only one maximum and continues as a monotone function that decreases to zero, there are only two values that satisfy the equation for critical points, $Z_u<Z_s$ (see Fig. 2). Since these two points are critical points of the restricted potential $V_{Inv}$, they satisfy the equation

$$\begin{aligned} V_{Inv}'=-{\mathcal {M}} f_{0}''(Z)+1=0; \end{aligned}$$

$Z_u$ and $Z_s$ being the unstable and stable equilibrium points of the system (12), respectively. It is clear that $Z_u$ and $Z_s$ coincide when ${\mathcal {M}}$ equals its minimum value, that is for ${\mathcal {M}}=8.187957392$, and then, (16) determines a unique value of Z

$$\begin{aligned} Z_c=1.693848849\dots \end{aligned}$$

(18)

This result, already derived in Ref. [5], will be complemented herein and it will serve to look for stable regions of the full system. As a consequence, some differences between Gans’s and our results are observed in Sect. 6.

Let us notice that the linearized system of (12) near the point $(Z_s,0)$ corresponds to a harmonic oscillator

$$\begin{aligned} {\ddot{Z}}+ V_{Inv}''(Z_s)Z=0, \end{aligned}$$

(19)

and that in the invariant region, Z oscillates with frequency

$$\begin{aligned} \sqrt{-{\mathcal {M}} f_{0}'''(Z_{s})}. \end{aligned}$$

Therefrom, a periodic orbit in the phase space of the complete system is given by

$$\begin{aligned}&({\mathbf {q}},{\mathbf {p}})=(X,Y,Z,\theta ,\psi ,\phi ,p_X,p_Y,p_Z,p_{\theta },p_{\psi },p_{\phi })\nonumber \\&\quad =(0,0,Z_{s},0,0,\sigma t,0,0,0,0,{C\, \sigma },C\, \sigma ). \end{aligned}$$

(20)

Furthermore, the uncoupled dynamical behavior in the Z-direction follows an ordinary differential equation of the form

$$\begin{aligned} {\ddot{Z}} = \delta _1 Z + \delta _2 Z^2 + \cdots \end{aligned}$$

(21)

whose phase space, depicted in Fig. 3, reveals the existence of two fixed points in agreement with the results in Ref. [4] (see Fig. 1 therein).

In the vicinity of the elliptic point, the Levitron will vertically oscillate with a frequency close to that of its concomitant eigenvalue. Meanwhile, when approaching the separatrix corresponding to the hyperbolic point, such a frequency will tend to vanish. Outside from the libration zone, the Z dynamics is clearly unstable.

Fig. 3

Phase space corresponding to (21)

These outcomes provide us a starting point to look for invariant regions by numerical means. The fact that the system has a coordinate that behaves as a harmonic oscillator suggests that we could perturb it parametrically, thus simulating a vertical oscillation of the magnetic base, as we do in Ref. [12]. With a proper frequency, in the presence of dissipation, this parametric perturbation would counteract the effect of friction and then witness a persistent levitation of the spinning top under more realistic assumptions.

5 Numerical study: general frame and adopted numerical scheme

For our numerical study, we fixed the parameters A and C adopting, as in Ref. [5], the values

$$\begin{aligned} A=0.089,\qquad C=0.139, \end{aligned}$$

which correspond to physical measurements; the effective radius being $a=34.7\, mm$.

As in Ref. [11], we used a Runge–Kutta $7-8$ method (RK78) to cope with the integration in regions of phase space where the system (9) can turn stiff. To overcome the fact that Eq. (9e, f and j) becomes singular whenever $\theta = 0$ or $\theta =\pi$, we proceeded to control the numerators in such expressions. Thus, for instance, in the case of Eq. (9e), we fixed to zero the field entry for $\psi$ whenever it was

$$\begin{aligned} |p_\psi -p_\phi \cos \theta |\le tol. \end{aligned}$$

The same control was kept in the other two equations and the value of tol was calibrated numerically, not having found any significant difference for values lesser than 0.0001.

We verified that to have a stable flight of the spinning top $p_\phi$ and $p_\psi$ should be close (we refer the reader to [11] and [12] for a thorough study). Let us notice that our results confirmed the ones in Ref. [1], who showed that both the precession and spin rates must be comparable in order the top to have a persistent levitation. Despite the fact that the singularity requires of the extra effort needed to determine the suitable value for tol, the Eulerian angles in the singular equations of motion permit a straightforward visualization of the top’s motion in space in comparison to the yaw–pitch–roll angles used in Ref. [4].

6 Symmetric and non-symmetric solutions

For our first simulation, we adopted equal values for the angular velocities $p_\phi =p_\psi$. Numerical explorations were performed to find, as [1] did, that large spinning velocities do not stabilize the flight of the spinning top. We took as initial condition

$$\begin{aligned}&(X,Y,Z,\theta ,\psi ,\phi ,p_X,p_Y,p_Z,p_{\theta },p_{\psi },p_{\phi })\nonumber \\&\quad =(0,0,3.34,0.005, 0, 0 ,0, 0, 0, 0, 5., 5.) \end{aligned}$$

with $p_\phi =p_\psi$. For this symmetric solution, the coordinate Z evolves, as shown in Fig. 4, while the coordinates (X, Y) remain fixed at the origin.

Fig. 4

Z-coordinate in the symmetric solution

To find stable regions, we performed a thorough search for the possible values of ${\mathcal {M}}$ and $Z_s$ and found that the value ${\mathcal {M}}=11.022$ provides a somewhat major stability than the value given by Muabs (17) corresponding to (18). Indeed, such a result can be verified analytically following [5], by proposing a solution with small precession, namely:

$$\begin{aligned} {\mathbf {q}}&=(r\cos \varOmega t,r\sin \varOmega t, h, \alpha ,\varOmega t,\omega t)^T \end{aligned}$$

(22a)

$$\begin{aligned} {\mathbf {p}}&=[-r\varOmega \sin \varOmega t,r\varOmega \cos \varOmega t, 0,0,\varOmega (A\sin ^2\alpha +C\cos ^2\alpha )\nonumber \\&\quad +C \omega \cos \alpha ,C(\omega +\varOmega \alpha )]^T, \end{aligned}$$

(22b)

where only the spinning velocity $\omega$ can be freely fixed. Indeed, the values of r, $\alpha$, h, and $\varOmega$ should be taken so as (22) satisfies the equations of motion. In particular, in order the first two equations for ${\mathbf {p}}$ be verified, the condition

$$\begin{aligned} r=3\,\,\frac{{\mathcal {M}}h\sin \alpha (1+h^2)(h^2-3)}{(12h^4-63h^2+9){\mathcal {M}}\cos \alpha +2(1+h^2)^{9/2}\varOmega ^2}\nonumber \\ \end{aligned}$$

(23)

follows. As shown in [5], this expression is positive if

$$\begin{aligned} \biggl (\frac{21-\sqrt{393}}{8}\biggl )^{1/2}=0.3834<h<\sqrt{3} \end{aligned}$$

and

$$\begin{aligned} \varOmega ^2\le \,\,\frac{-{\mathcal {M}} \cos \alpha (12h^4-63h^2+9)}{2(1+h^2)^{9/2}}. \end{aligned}$$

(24)

Let us notice that in this range of h (that corresponds to the Z-coordinate of the top), the numerator as well as the first term in the denominator of (23) takes negative values. As a consequence of the other bound for the equilibrium $Z_s$ imposed by (18), we have

$$\begin{aligned} 1.693848849\dots<Z_s<\sqrt{3}=1.732050808\dots \end{aligned}$$

However, as already stated in Ref. [11] (and skipped in [5]), the equation for r is also positive whenever

$$\begin{aligned} \biggl (\frac{21+\sqrt{393}}{8}\biggl )^{1/2}=2.258988369 <h. \end{aligned}$$

Therefore, if we choose the initial condition $Z_s=3.34$, we have from (16) that ${\mathcal {M}}=11.022$. These are the final set of values that we will use in the sequel.

In the case where $p_\phi$ and $p_\psi$ are slightly different, we take the same initial conditions as in the symmetric case except for $p_\psi =5.0001$, the remaining initial conditions being $X=Y=\phi =\psi =p_X=p_Y=p_Z=p_{\theta }=0$, $Z=Z_s$, $p_\phi =5.0$, and $\theta =0.005$.

The results of the integration of (9), which yield the geometrical description of the Levitron’s dynamics, are displayed in Fig. 5 and 6 (taken from [11]), where the abrupt loss of stability can be clearly visualized. Notice that in the non-symmetric solution, the coordinates (X, Y) are no longer fixed at the origin, and the spinning top remains stable for a rather short extent of time, the flight barely surpassing the 350 time units.

Despite of the neat oscillation observed in the Z coordinate, the motion of the top’s center of mass in the (X.Y)-plane shown in Fig. 6 displays a rather chaotic nature, as confirmed by the concomitant MEGNO behavior which varies linearly with time (see [12] to disclose this argument).

Fig. 5

Time evolution of the Z-coordinate in a slightly non-symmetric solution

Fig. 6

(X, Y)-coordinates in a slightly non-symmetric solution

7 Description of the phase space configuration

At this point, it has already been stated that we are dealing with a 12-dimensional phase space when describing the motion of the spinning top, a dynamics that allows of two first integrals, namely the total energy and the momemtum $p_{\phi }$. Each one of the coordinates defining the location of the center of mass as well as the Eulerian angle $\theta$ defining the tilt and their related momemtum remain bounded as long as the Levitron flies in a stable fashion.

The dynamics obtained from initial conditions close to that of (22) exhibits both in the planes $(X,p_X)$ and $(Y,p_Y)$ an almost quasiperiodic nature but characterized by different frequencies.

This is also the case for the Z and $\theta$ variables. Therefore, the concomitant dynamics is seen to lie on a torus ${{\mathbb {T}}}^4$. On the other hand, the angles $\phi$ angles $\psi$ continue to increase, since ${\dot{p}}_{\phi }=0$ and $p_{\psi }$ remains rather close to $p_{\phi }$. Indeed, according to (9), such a similarity between both $p_{\psi }$ and $p_{\phi }$ is required in order the equations of motion remain regular for $|\theta |<< 1$. In sum, the stable dynamics of the Levitron takes place onto a nearby manifold to ${{\mathbb {T}}}^4 \times {{\mathbb {R}}}^2$.

As soon as stability is lost, the dynamics turns to be unbounded but integrable, and asymptotically tends to a parabolic trajectory due to gravity. Far from the fixed magnetic field, the top behaves as a rigid body in the absence of torques and the trajectory outcomes as the intersection between a sphere and an ellipsoid of revolution (recall that two of the moments of inertia are equal).

8 Asymptotics

For gaining some insight in the role, the variables $p_{\psi }$, $p_{\phi }$, and $\theta$ play in maintaining the nonlinear stability of the solutions of (9); we carried out an asymptotic study following [7]. Namely, we considered different scales identified by powers of a given parameter $\epsilon$ to determine the influence of each scale on the Levitron’s nonlinear stability. The first scale is related to the rotation period of the spinning top (order $\epsilon ^0$) and the second one corresponds to the period of the vertical oscillation of the top (order $\epsilon ^1$), while the third scale concerns the horizontal displacements and the top tilt. Notice should be taken however that we have adopted a different criterion for introducing the multiscale analysis than the one in Ref. [7] where the authors’ choice is based on the relative velocities in each direction.

Herein instead, we performed a multiscale analysis backed by our considering the Lagrange top dynamics in which a rigid body rotates without nutating in the first place, that is, the vertical or sleeping top, and then gradually introducing perturbations to the vertical spinning top. Accordingly, the zeroth-order scale corresponds to the situation in which the spin axis of the top is vertical and its center of mass lies on the Z-axis, not undergoing neither vertical nor horizontal displacements. The first-order scale takes into account the vertical displacements of the spinning top, for which precession and rotation may be decoupled in the absence of nutation. Therefore, up to the first-order scale, the spinning top is kept in the invariant set Inv. For the second-order scale instead, the Levitron can experience both vertical and transversal movements, as well as nutation and also precession, which can be decoupled from the top’s spin.

Therefore, our adopted asymptotic representation of the coordinates and their moments has the following form:

$$\begin{aligned}&Z=z_0+\epsilon z_1 +\epsilon ^2 z_2 p_Z=p_{z_0}+\epsilon p_{z_1} +\epsilon ^2p_{z_2}\nonumber \\&X= \epsilon ^2 x_2 p_X= \epsilon ^2p_{x_2}\nonumber \\&Y= \epsilon ^2 y_2 p_Y= \epsilon ^2p_{y_2}\nonumber \\&\theta = \epsilon ^2 \theta _2 p_{\theta }= \epsilon ^2p_{\theta _2}\nonumber \\&\psi = \psi _0+ \epsilon \psi _1 +\epsilon ^2 \psi _2 p_\psi = p_{\psi _0}+ \epsilon p_{\psi _1} +\epsilon ^2p_{\psi _2}\nonumber \\&\phi = \phi _0 + \epsilon \phi _1 +\epsilon ^2 \phi _2 p_\phi = p_{\phi _0}+ \epsilon p_{\phi _1} +\epsilon ^2p_{\phi _2}, \end{aligned}$$

(25)

where all the subindex-linked variables concern the concomitant order in the multiscale analysis.

Rewriting (9) by recourse to (25), and arranging terms according to the powers of $\epsilon$, we can obtain the equations of motion up to order $\epsilon ^n$ for $n=0,1,2$. Notice that in order the negative powers of $\epsilon$ be absent in the series, we have to fix

$$\begin{aligned} p_{\psi _0}=p_{\phi _0}\qquad \text {and} \qquad p_{\psi _1}=p_{\phi _1}, \end{aligned}$$

which are congruent with the region of phase space where the Levitron shows the more stable flights.

At order $\epsilon ^0$, the equations read

$$\begin{aligned} \begin{array}{rlp{0.5cm}rl} \dot{z}_0&{}=p_{z_0} &{} &{} {\dot{p}}_{z_0}&{}= {\mathcal {M}} [f''_0(z_0)]_0-1\\ \dot{x}_0&{}= 0 &{} &{} {\dot{p}}_{x_0}&{}=0\\ \dot{y}_0&{}= 0 &{} &{} {\dot{p}}_{y_0}&{}=0\\ {{\dot{\theta }}}_0&{}= 0 &{} &{} {\dot{p}}_{\theta _0}&{}=0\\ {{\dot{\psi }}}_0&{}=\frac{1}{A\theta _2^2}\,(p_{\psi _2}-p_{\phi _2}) &{} &{} \dot{p}_{\psi _0}&{}=0\\ &{}\quad +\frac{1}{2A}\,p_{\phi _0}&{}&{} \\ {{\dot{\phi }}}_0&{}=-\frac{1}{A\theta _2^2}\,(p_{\psi _2}-p_{\phi _2}) &{} &{} {\dot{p}}_{\phi _0}&{}=0,\\ &{}\quad -\frac{1}{2A}\,p_{\phi _0}+\frac{1}{C}\,p_{\phi _0}&{}&{}\\ \end{array} \end{aligned}$$

(26)

where $[\ \cdot \ ]_n$ stands for all the terms of order $\epsilon ^n$. It is clear that $p_{\psi _2} = p_{\phi _2}$ to avoid the singularity when $\theta _2$ is close to zero. Clearly, a solution is given by

$$\begin{aligned} z_0&=Z_c\quad \qquad p_{z_0}\qquad =0\\ \phi _0&= (\frac{-1}{2A}+\frac{1}{C})p_{\phi _0}t\quad \qquad p_{\phi _0}\qquad =\mathrm{const.} \\ \psi _0&=\frac{p_{\phi _0}}{C}t\quad \qquad p_{\psi _0}\qquad =\mathrm{const.} \end{aligned}$$

The vertical momentum $p_{z_0}$ is null, since $Z_c$ is the stable equilibrium point (18).

At order $\epsilon ^1$, we have the equations

$$\begin{aligned} \begin{array}{rlp{0.5cm}rl} \dot{z}_1&{}=p_{z_1} &{} &{} {\dot{p}}_{z_1}&{}= \omega ^2 z_1\\ \dot{x}_1&{}= 0 &{} &{} {\dot{p}}_{x_1}&{}=0\\ \dot{y}_1&{}= 0 &{} &{} {\dot{p}}_{y_1}&{}=0\\ {{\dot{\theta }}}_1&{}= 0 &{} &{} {\dot{p}}_{\theta _1}&{}=0\\ {{\dot{\psi }}}_1&{}= -\frac{1}{2A}\,p_{\phi _1} &{} &{} {\dot{p}}_{\psi _1}&{}=0\\ {{\dot{\phi }}}_1&{}=\frac{1}{A}\,p_{\phi _1} &{} &{} {\dot{p}}_{\phi _1}&{}=0\\ \end{array} \end{aligned}$$

(27)

whose solutions read

$$\begin{aligned} z_1&= A\sin (\omega t+\beta )\quad p_{z_1} =\omega A\cos (\omega t+\beta )\\ \phi _1&=-\frac{p_{\phi _1}}{2A}\,t\quad p_{\phi _1} =\mathrm{const.} \\ \psi _1&= \frac{p_{\phi _1}}{A}\,t\quad p_{\psi _1} =\mathrm{const.} \\ \end{aligned}$$

Therefore, notice should be taken that up to the first-order scale, the spinning top is kept in the invariant set Inv.

Finally, the set of equations at order $\epsilon ^2$ are

$$\begin{aligned} \begin{array}{rlp{0.05cm}rl} \dot{z}_2&{}=p_{z_2} &{} &{}{\dot{p}}_{z_2}&{}= - \omega ^2 z_2 + \frac{1}{2} f^{(iv)}_0(Z_c) z^2_1\\ \dot{x}_2&{}=p_{x_2} &{} &{} {\dot{p}}_{x_2}&{}= 2 \theta _2 \cos \psi _0 - f'''_0 \,x_2 \\ \dot{y}_2&{}=p_{y_2} &{} &{} {\dot{p}}_{y_2}&{}= 2 \theta _2 \sin \psi _0 - f'''_0 \, y_2\\ {{\dot{\psi }}}_2&{}=\frac{1}{2A}\,p_{\phi _2} &{} &{}{\dot{p}}_{\psi _2}&{}=0\\ {{\dot{\phi }}}_2&{}=-\frac{1}{2A}\,p_{\phi _2}&{} &{}{\dot{p}}_{\phi _2}&{}=0\\ &{}\quad + (p_{\psi _2} - p_{\phi _2}) &{}&{}\\ \end{array} \end{aligned}$$

(28)

$$\begin{aligned} \begin{array}{rl} {{\dot{\theta }}}_2&{}= \frac{1}{A}p_{\theta _2}\\ \\ {\dot{p}}_{\theta _2}&{}= -\frac{1}{4 A} p_{\phi _0} p_{\psi _0} \theta _2 - 2 (x_2 \cos \psi _0 + y_2 \sin \psi _0 ) - {\mathcal {M}} f'_0 \theta _2. \\ \end{array} \end{aligned}$$

At this order, we apply the Taylor expansions of $f_0$ and $f_2$ with $z=Z_c +\epsilon z_1+\epsilon ^2 z_2$ to obtain

$$\begin{aligned} \begin{array}{rl} f'_0(z)&{}=f'_0(Z_c)+f''_0(Z_c)\;\;\epsilon z_1\\ f''_0(z)&{}= \frac{1}{{\mathcal {M}}}+f'''_0(Z_c) \;\;\epsilon z_1\\ \end{array} \end{aligned}$$

and, renaming ${\mathcal {M}} f'''_0(Z_c)=-\omega ^2$, there results

$$\begin{aligned} 4 f'_2(z)= & {} -f'''_0(z)=-f'''_0(Z_c)-f^{iv}_0(Z_c)\;\;\nonumber \\ \epsilon z_1= & {} \frac{\omega ^2}{{\mathcal {M}}}-f^{(iv)}_0(Z_c)\;\;\epsilon z_1. \end{aligned}$$

(29)

Therefore, the terms $[f'_2]_n$, $[f_2]_n$ and $[f'_0]_n$ in the asymptotic equations of motion can easily be computed.

Fig. 7

Numerical solution of (28) in the $(x_2,y_2)$ plane for the adopted parameter values $\mu =-32.75$, $a=0.089$, and $p_{\psi _0}=100$

Fig. 8

The maximum amplitude onto the horizontal plane is depicted in red versus $p_{\psi _0}$ (represented in the horizontal axis); the vertical axis on the left corresponding to $\log (R(T))$, with $R=|x_2| + |y_2|$

According to the asymptotic theory, in order the solutions of the original Eq. (9) be either periodic or quasiperiodic, the solutions of the equations at any order in $\epsilon$ have to be bounded. Since the equations obtained at order $\epsilon ^2$ admit no analytic solutions, we are compelled to numerically integrate (28). The outcoming trajectory in the $(x_2,y_2)$ plane seems to be bounded as Fig. 7 shows (compare with Fig. 11 in Ref. [13]).

The solutions of the asymptotic equations (26), (27), and (28) are consistent with those solutions obeying some kind of symmetry such as those of (12) or the one given by (22). Since ${\dot{p}}_{\psi _i}={\dot{p}}_{\phi _i}=0$ for $i=0,1,2,3$, setting $p^2_{\phi _2} = -4 A {\mathcal {M}} f'_0$, we get ${\mathcal {M}} f'_0 f'''_0 +1 =0$ and the concomitant value of $Z_c$ as well as the limiting value $r>\sqrt{x^2_2 + y^2_2}\;\;$ verifying $r={2\alpha }\big /{(\varOmega ^2 +f'''_0)}$, with $\alpha$ given in (22).

Equations (28) provide a linear system for $(x_2,y_2,z_2,\theta _2,\psi _2,\phi _2)$ and their related momenta, which depends on time through $\psi _0$ that evolves linearly with time, which should be addressed by means of the Floquet theory. The $z_2$ variable is the solution of a driven linear equation. Nonetheless, as in Ref. [4], we could consider that $\psi _0$ is constant in the invariant set and thus obtain a reduced autonomous linear system by putting aside the equations for $z_2$, $\phi _2$ and their momenta. Then, the reduced system reads

$$\begin{aligned} \begin{array}{c} {\dot{W}} = D W \\ \\ W=(x_2,y_2,\theta _2,\psi _2,p_{x_2},p_{y_2},p_{\theta _2},p_{\psi _2})^T, \\ \end{array} \end{aligned}$$

the matrix D being

$$\begin{aligned} D= \left( \begin{array}{cccccccc} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{A} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\frac{1}{2A} -1 \\ -f_0''' &{} 0 &{} 2\cos \phi _0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -f_0''' &{}2\sin \phi _0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -2\cos \psi _0 &{} -2\sin \psi _0 &{} -\frac{p_{\phi _0}p_{\psi _0}}{4A} - Mf_0' &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) , \end{aligned}$$

so that it can be written in the fashion

$$\begin{aligned} D=\left( \begin{array}{cc} {{{\mathcal {O}}}} &{} {{{\mathcal {I}}}} \\ {{{\mathcal {D}}}} &{} {{{\mathcal {O}}}} \\ \end{array} \right) \end{aligned}$$

with ${{{\mathcal {O}}}}$ and ${{{\mathcal {I}}}}$ denoting the $4 \times 4$ null and (after the due distance and time rescaling) identity matrices, respectively, and ${{{\mathcal {D}}}}$ is the antisymmetric matrix

$$\begin{aligned} {{{\mathcal {D}}}}=\left( \begin{array}{cccc} \alpha &{} 0 &{} \beta &{} 0 \\ 0 &{} \alpha &{} \gamma &{} 0 \\ -\beta &{} -\gamma &{} \delta &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) \end{aligned}$$

with $\alpha =-f_0'''$, $\beta =2\cos \psi _0$, $\gamma =2\sin \psi _0$ and $\delta =-\frac{p_{\phi _0} p_{\psi _0}}{4A} - Mf_0'$. The corresponding eigenvalues are

$$\begin{aligned} \lambda _1^2=0 ,\;\; \lambda _2^2=\alpha ,\;\; \lambda _{3,4}^2 = \frac{\alpha + \delta }{2} \pm \frac{1}{2} \sqrt{(\alpha - \delta )^2 - 16 }, \end{aligned}$$

and stability takes place for $\alpha < 0$ and $\lambda _{3,4}^2 < 0$, i.e., $|\alpha -\delta | > 16$, $\alpha +\delta < 0$ and $|\alpha +\delta | > \frac{1}{2}\sqrt{(\alpha -\delta )^2 - 16}$.

Moreover, if $\psi _0$ is a linear function of time, from Floquet’s theory, we know that the sum of the Floquet exponents vanishes, since the trace of D is null.

Let us notice that, as $\delta$ depends on $p_{\psi _0}$ and $p_{\psi _0}=p_{\phi _0}$, whenever $p_{\psi _0}$ tends to 0 stability is lost (as it can be observed in the forthcoming Fig. 8).

Let us now consider two further terms in the expansion for $p_{\psi }$, namely

$$\begin{aligned} p_\phi = p_{\phi _0}+\epsilon p_{\phi _1} +\epsilon ^2 p_{\phi _2} +\epsilon ^3 p_{\phi _3} + \epsilon ^4 p_{\phi _4}, \end{aligned}$$

in (25); such a practice leads us to ${\dot{p}}_{\psi _i}=0$ for $i=0,3$, and, consequently, to ${p}_{\psi _i}={p}_{\phi _i}$ for $i=0,3$. Nonetheless, $\psi _4$ is no longer constant, but evolves according to

$$\begin{aligned} {\dot{p}}_{\psi _4} = {\mathcal {M}} \theta _2 (3600 z^2_0 - 72)\,\left( y_2 \,\cos \psi _0 -x_2 \,\sin \psi _0\right) , \end{aligned}$$

and $p_{\psi _4}$ departs from $p_{\phi _4}$ which continues to be a constant of motion at this order. Due to the quasi–oscillatory behavior of coordinates $x_2$ and $y_2$ shown in Fig. 7, we could conclude that $p_{\psi _4}$ beholds a quasiperiodic nature. Let us notice that it is necessary to go as far as the fourth power in the parameter to detect a slight variation in $p_{\psi }$.

Let us remark then that in our asymptotic study, we obtain $p_{\psi _i}=p_{\phi _i}, \; i=0,1,2,3,$ which guarantees the regular and bounded behavior of the equations of motion up to such an order (we refer to [12] for a detailed analysis of the $|p_{\psi } - p_{\phi }|$ behavior as $\theta \rightarrow 0$, which should remain bounded in order the equations of motion be stable). Indeed, it is not up to the fourth order that the momentum $p_{\psi _4}$ is decoupled from $p_{\phi _4}$.

After some numerical exploration, we disclose $p_{\psi _0}$ to be the main bifurcation parameter for (28), which besides is equal to $p_{\phi _0}$. In fact, the numerical integration allows for the computation of $R(t)=|x_2(t)|+|y_2(t)|$ for the total integration time T and, consequently, the realization of the bifurcation diagram for (28); the outcoming bifurcation diagram is given in Fig. 8 which displays the value of $\log (R(T))$ as a function of $p_{\psi _0}$. Let us notice that stability is lost when $p_{\psi _0}$ tends to 0, as expected from our second-order analysis, $\delta$ depending on $p_{\psi _0}$ and $p_{\psi _0}=p_{\phi _0}$.

With the aim of studying the Levitron’s behavior when the dissipation due to air friction is taken into account, as in Ref. [11, 12], at least two positive constants are needed, namely $C_T$ and $C_R$ corresponding to both translation and rotation, i.e., the two different types of motion involved in the flight of the spinning top. Furthermore, two mechanical schemes which correspond to forcing the vertical location of the permanent magnetic base by small motions are proposed to inject energy into the system. Indeed, a parametric perturbation of the magnetic base can be introduced by forcing the equilibrium point of the system (19) to vary in the fashion

$$\begin{aligned} Z_s\longmapsto Z_s (1 + \beta \cos \omega t),\qquad \end{aligned}$$

(30)

whereas a hysteretic perturbation can be modeled just by changing the equilibrium point according to

$$\begin{aligned} Z_s&\longmapsto Z_s + \beta \cos \omega t .\quad \qquad \ \end{aligned}$$

(31)

On the other hand, the dissipative terms $-C_T p_X$, $-C_T p_Y$, and $-C_T p_Z$ are to be added to Eq. (9g–i) in ${\dot{p}}_X,{\dot{p}}_Y,{\dot{p}}_Z$, respectively. Besides, and since the rotational velocity is very high compared to the translational velocity, a quadratic term would be to model the concomitant friction, the dissipative terms added to the Eq. (9j–l) being $-C_R p_\theta |p_\theta |$, $-C_R p_\psi |p_\psi |$ and $-C_R p_\phi |p_\phi |$, respectively.

Let us then incorporate both parametric and hysteretic perturbations as well as the damping forces (see [12] for details) in our asymptotic scheme. The excitation forces should be introduced at order $\epsilon ^1$, by means of (31) or (30) being applied in the Z-equation in ref. (25), but with $\beta$ rescaled as $\epsilon \beta$, such that the former $\epsilon \beta$ coefficient is actually of order $\epsilon ^2$. In the same direction, the dissipation parameters are rescaled in the fashion $\epsilon ^2 C_T$ and $\epsilon ^2 C_R$. It is clear that these damping forces contribute to Eq. (28), causing the amplitude of R(T) to be reduced but leaving the bifurcation point unaltered. The hysteretic and parametric forces have a similar solution to that of the Mathieu equation, the $z_1$ coordinate being able to grow in case $\omega$ is resonant to (27). The coordinates $x_2$, $y_2$ and $\theta _2$, however, are not modified. We can thus conclude that the hysteretic and parametric forces cannot restore the energy loss in the rotational terms at least at order $\epsilon ^2$.

The stability of Eqs. (26), (27), and (28) requires that $p_{\psi _n}=p_{\phi _n}$, for $n=0,1,2,3$. This result agrees with that of the numerical integration of the original equations (9), the Levitron undergoing a stable levitation as long as the quotients in the right hand of (9e, f and j) remain bounded (i.e., for $|p_{\psi } - p_{\phi }|<< 1$ and $|\theta |<< 1$). Therefore, the spinning top preserves its stable flight, even though the rotation frequency reduces its value due to the energy losses of the system, but there exists a bifurcation point from which (24) is no longer fulfilled. Unfortunately, our asymptotic study does not manage to detect such bifurcation point when considering the asymptotic behavior up to order $\epsilon ^2$.

9 Conclusions

The present effort, which follows the guideline of the works of Dullin and Easton, and Gans, concerns the study of the dynamics of the Levitron. Not only has a local study been performed which disclose the dynamics on an invariant manifold in phase space, but a periodic solution for the complete system has been obtained as well. Moreover, we have extended the results of Gans, being able to determine further stable regions for the magnetic levitation of the Levitron. Symmetric and asymmetric trajectories close to an analytical solution have been numerically explored.

Furthermore, to elucidate the nonlinear behavior of the interacting translational and rotational modes, multiscale asymptotic computations have been carried out, which provide evidence of the nutation affecting the spinning body’s translation. Our main motivation in such a practice has been to distinguish how the varying difference between the rotational and precession momenta affects at different time scales.

Our asymptotic analysis allows us to conclude that neither parametric nor hysteretic perturbations (see [12]) can prevent the loss of energy of the Levitron, but, through the reduction of the flying body nutation, they delay the energy loss due to friction.