Numerical study of laser synapse connecting Hindmarsh–Rose neurons

Abstract

We study numerically the dynamics of a system composed of two artificial neurons connected via an erbium-doped fiber laser. In our system, the laser acts as an optical synapse whose dynamics is controlled with a signal generated by a presynaptic Hindmarsh–Rose neuron, while the laser output drives a postsynaptic Hindmarsh–Rose neuron. Depending on the laser parameter, the postsynaptic neuron can be turned to different dynamical regimes including silence, tonic spikes, bursts with different number of spikes, and chaos.

1 Introduction

The human brain consists of approximately 86 billion neurons interconnected in a complex way to perform computational, cognition, and memory tasks. Neurons usually interact via synapses, which allow information transmission from one neural cell to the other. Each neuron has an average of 7000 synapses, which being subserved by a complex molecular mechanism are capable of changing the efficiency of signal transmission between neurons by sensing their electrical activity and the concentration of chemical components. In many models, a synapse is usually characterized by the synaptic weight, strength, and efficacy. If the synaptic weight is constant, the amplitude of the response of a postsynaptic neuron j to the arrival of action potential from a presynaptic neuron i should always be the same. Electrophysiological experiments, however, show that the response amplitude is not fixed but can vary over time. The change in the synaptic strength is called synaptic plasticity [1].

In the formal theory of neural networks, it is assumed that the synaptic weight of the connection of neuron i with j is turned in such a way as to optimize the network performance for a given task. The process of synaptic adaptation is called learning and governed by learning rules. In a broad sense, learning implies synaptic changes during the reception, transmission, and processing of information necessary to perform a specific task, for example, memorizing received information or performing a movement. There are many learning rules, among which one should mention “unsupervised learning”, which has great biological significance, and “supervised learning”, which are an important issue in the fields of artificial neural networks and machine learning.

A number of experimental results on synaptic plasticity have been accumulated. Many of these experiments are inspirited by the Hebb’s postulates [2], which state how the connection from a presynaptic neuron to a postsynaptic neuron should be modified. It is believed that the flexibility of the synaptic connection with time dependence (e.g., synaptic plasticity) underlies the implementation of computational and cognitive tasks in brain networks. While in living cells, the synaptic plasticity is mediated by complex molecular transformation, in an artificial biosystem, the synaptic transmission can be regulated by adjusting the parameters of an artificial synapse.

Since the advent of artificial intelligence, great efforts have been invested in the creation of electronic networks capable of reproducing biological neural activity. Among the most promising areas of interdisciplinary research in neuroscience, we can consider neuroprosthetics, that aims to develop electronic devices implanted in the brain to repair missing or malfunctioning brain functions due to trauma or diseases [3]. Neuroprosthetics finds many biomedical applications [4,5,6], and has also been investigated as potential in neuromorphic engineering [7,8,9]. In addition, much attention was paid to the development of neuromorphic devices due their relevance not only for medical applications, but also for non-medical tasks, such as information processing, intellectual adaptive automatic control, biorobots, brain–computer interfaces, etc. [10,11,12].

On the other hand, significant advances have been made in neural modelling. Adequate neuron models have been developed to simulate biological neurons. In particular, a simplified modification of the detailed neurophysiological Hodgkin–Huxley model [13], the well-known Hindmarsh–Rose (HR) [14], has become the subject of intensive research in engineering sciences [15] due to its relative simplicity which allows analytical research, as well as electronic implementation capable to generate nonlinear effects leading to the emergence of complex dynamics simulating neural activity.

However, the electronic implementation of synaptic communication is a rather complex technical task, primarily due to synaptic plasticity. This is due to the fact that chemical and electrical synapses are extremely complex biomolecular devices which establish functional connections between neural cells or between neurons and other types of cells, controlling the transmission of neural information encoded as spike sequences [16]. For the development of efficient neuromorphic networks, it is important to have not only adequate models of neuronal cells, but also effective communication devices with a high level of flexibility and time-dependent spike transmission. A new approach to implement synaptic circuits was developed in [17, 18]. This way may be combined with nanotechnologies based on carbon nanostructures to miniaturize artificial synapses [19]. In addition, the information transmission from one artificial neuron to another was realized via an optical fiber [20]. Moreover, living neurons were stimulated by a signal generated by an artificial neuron and transmitted via an optical fiber [21]. Furthermore, Garasimova and colleagues [22,23,24] modelled and implemented a synapse based on a memristive device.

The first laser synapse was proposed in 2011 [25, 26]. It was based on an erbium-doped fiber laser (EDFL) which connected and synchronized two electronic FitzHugh–Nagumo neurons. In the other words, the laser transmitted a signal from a presynaptic neuron to a postsynaptic neuron. Due to relative simplicity, compatibility with modern fiber optic technology, and possibility to control the signal waveform, the implementation of such a synaptic device makes it very promising for biorobotic and bioengineering applications.

In this paper, we extend the application of the EDFL synapse to another neuron models, in particular, to the Hindmarsh–Rose model. The paper structure is organized as follows. In Sects. 2 and 3, we present the mathematical models of HR neurons and EDFL, respectively, used for numerical simulations. The dynamics of the presynaptic neuron, optical synapse, and postsynaptic neuron are analyzed in Sects. 4, 5, and 6, respectively. Finally, in Sect. 7 we present the suggested experimental setup and in Sect. 8 give the main conclusions.

2 Theoretical model

The Hindmarsh–Rose (HR) mathematical model is a simplified version of the Hodgkin–Huxley model of a neuron membrane. Two HR neurons unidirectionally coupled by laser power $P(x_{1})$ are modeled by the following equations [14, 27,28,29]

$$\begin{aligned} \dot{x}_1= & {} y_{1}-ax^{3}_{1}+bx^{2}_{1}-z_{1}+I_{\text {ext}}, \end{aligned}$$

(1)

$$\begin{aligned} \dot{y}_{1}= & {} c-dx^{2}_{1}-y_{1}, \end{aligned}$$

(2)

$$\begin{aligned} \dot{z}_{1}= & {} r(s(x_{1}-x_{0})-z_{1}), \end{aligned}$$

(3)

$$\begin{aligned} \dot{x}_{2}= & {} y_{2}-ax^{3}_{2}+bx^{2}_{2}-z_{2}+\sigma P(x_{1}), \end{aligned}$$

(4)

$$\begin{aligned} \dot{y}_{2}= & {} c-dx^{2}_{2}-y_{2}, \end{aligned}$$

(5)

$$\begin{aligned} \dot{z}_{2}= & {} r(s(x_{2}-x_{0})-z_{2}), \end{aligned}$$

(6)

where variables $x_{1,2}$ represent membrane potentials of two couple neurons, $x_{0}$ stands for the resting potential, $y_{1,2}$ represent fast Na$^{+}$ and K$^{+}$ currents, variables $z_{1,2}$ are slow Ca$^{2+}$ currents, $I_{\text {ext}}$ is the external current, a, b, c, d, r, s are constants, and $\sigma$ is the synaptic strength coupling. The laser power $P(x_{1})$ drives the membrane potential $x_{1}$ acting as an optical stimulus for the postsynaptic neuron.

Fig. 1

Bifurcation diagrams of a peak values of $x_{1}$ and b ISI of peak $x_{1}$ as a function of external current $I_{\text {ext}}$. The arrows show the parameter values for the time series presented in Fig. 2

3 Optical stimulation

The optical stimulation from the diode-pumped EDFL is described using a power-balance approach which takes into consideration the excited state absorption (ESA) in erbium at the 1.5-$\upmu$m wavelength and by averaging the population inversion along the pumped active fiber. Such a model addresses the evident factors (i.e., ESA at the laser wavelength and the depleting of the pump wave at propagation along the active fiber) leading to non-dumped natural oscillations in the laser, observed experimentally without external modulation [27,28,29]

The balance equations for the intracavity laser power P (i.e., a sum of the contra-propagating waves’ powers inside the cavity, in $s^{-1}$) and the averaged (over the active fiber length) population y of the upper (“2”) level (i.e., a dimensionless variable, $0\le y \le 1$) are derived as follows

$$\begin{aligned} \begin{aligned} \dot{P}&=\frac{2L}{T_{r}}P \lbrace r_{w}\alpha _{0}(y[\xi -\eta ]-1)-\alpha _{\text {th}} \rbrace +P_{\text {sp}}\\ \dot{y}&=-\frac{\sigma _{12}r_{w}P}{\pi r_{0}^{2}}(\xi y-1)-\frac{y}{\tau }+P_{\text {pump}}, \end{aligned} \end{aligned}$$

(7)

where $\sigma _{12}$ is the cross-section of the absorption transition from the ground state “1” to the upper state “2”. We suppose that the cross-section of the return stimulated transition $\sigma _{12}$ is practically the same in magnitude that gives $\xi =(\sigma _{12}+\sigma _{21})/\sigma _{12}=2$, $\eta = \sigma _{23}/\sigma _{12}$ being the coefficient that stands for the ratio between ESA $\sigma _{23}$ and ground-state absorption cross-sections at the laser wavelength. $T_{r}=2 n_{0}(L+l_{0})/c$ is the lifetime of a photon in the cavity ($l_{0}$ being the intra-cavity tails of FBG-couplers), $\alpha _{0}=N_{0}\sigma _{12}$ is the small-signal absorption of the erbium fiber at the laser wavelength $N_{0}=N_{1}+N_{2}$ is the total concentration of erbium ions in the active fiber), $\alpha _{\text {th}}=\gamma _{0}+nL(1/R)/(2L)$ is the intra-cavity losses on the threshold ($\gamma _{0}$ being the non-resonant fiber loss and R is the total reflection coefficient of the FBG-couplers), $\tau$ is the lifetime of erbium ions in the excited state“2”, $r_{0}$ is the fiber core radius, $w_{0}$ is the radius of the fundamental fiber mode and $r_{w}=1+\exp [2(r_{0}/w_{0})^{2}]$ is the factor addressing a match between the laser fundamental mode and erbium-doped core volumes inside the active fiber.

The population of the upper laser level “2” is given as

$$\begin{aligned} y=\frac{1}{n_{0} L}\int _{0}^{L}N_{2}(z){\text {d}}z, \end{aligned}$$

where $N_{2}$ is the population of the upper laser level“2”, $n_{0}$ is the refractive index of a “cold” erbium-doped fiber core, and L is the active fiber length),

$$\begin{aligned} P_{\text {sp}}=\frac{10^{-3}y}{\tau T_{r}}\frac{\lambda _{g}}{w_{0}}\frac{r^{2}_{0}\alpha _{0}L}{4\pi ^{2}\sigma _{12}}, \end{aligned}$$

is the spontaneous emission into the fundamental laser mode, and the pump power is

$$\begin{aligned} P_{\text {pump}}=P_{p}\frac{1-\exp [-\beta \alpha _{0}L(1-y)]}{n_{0} \pi r_{0}^{2}L}, \end{aligned}$$

where $P_{p}$ is the pump power at the fiber entrance and $\beta = \alpha _{p}/\alpha _{0}$ is the ratio of absorption coefficients of the erbium fiber at pump wavelength $\lambda _{p}$ and laser wavelength $\lambda _{g}$. We assume that the laser spectrum width is $10^{-3}$ of the erbium luminescence spectral bandwidth.

Fig. 2

Time series of membrane potential $x_{1}$ for external currents (i) $I_{\text {ext}}= 1.4052$ (regular spiking), (ii) $I_{\text {ext}}=1.7396$ (bursting with two spikes), (iii) $I_{\text {ext}}=2.4084$ (bursting with three spikes), (iv) $I_{\text {ext}}= 2.7884$ (bursting with four spikes), (v) $I_{\text {ext}}= 3.2064$ (chaotic bursting), and (vi) $I_{\text {ext}}= 4.0424$ (high-frequency tonic spiking)

Note that Eqs. (1)–(7) describe the laser dynamics without external modulation. The intracavity pump power at the active fiber facet reads

$$\begin{aligned} P_{p}^{m}=P_{p}(1+m_{0} x_{1}), \end{aligned}$$

(8)

where $m_{0}$ is the modulation depth.

The parameters used in our simulations correspond to the real EDFL with an active erbium-doped fiber of $L = 70$ cm. Other parameters are $n_{0} = 1.45$, $l_{0} = 20$ cm, $T_{r} = 8.7$ ns, $r_{0} = 1.5$ cm, and $w_{0} = 3.5\times 10^{-4}$ cm. The last value was measured experimentally and it was a bit higher than $2.5\times 10^{-4}$ cm given by the formula for a step-index single-mode fiber $w_{0}=r_{0}(0.65+1.619/V^{1.5}+2.879/V^{6})$, where the parameter V relates to numerical aperture NA and $r_{0}$ as $V=2\pi r_{0}NA/\lambda _{g}$, while the values $r_{0}$ and $w_{0}$ result in $r_{w} = 0.308$.

The coefficients characterizing resonant-absorption properties of the erbium-doped fiber at lasing and pumping wavelengths are $\alpha _{0} = 0.4$ cm$^{-1}$ and $\beta = 0.5$, respectively, and correspond to direct measurements for heavily doped fiber with erbium concentration of 2300 ppm, $\sigma _{12} = \sigma _{21}= 3\times 10^{-21}$ cm$^{2}$, $\sigma _{23} =0.6\times 10^{-21}$ cm$^{2}$, $\xi =2$, $\eta =0.2$, $\tau =10^{-2}$ s [27], $\gamma _{0}= 0.038$, and $R = 0.8$ that yields $\alpha _{\text {th}}=3.92\times 10^{-2}$. At last, the generation wavelength $\lambda _{g}= 1.56\times 10^{-4}$ cm ($h\nu =1.274\times 10^{-19}$ J) is measured experimentally, while the maximum reflection coefficients of both FBGs are centered on this wavelength. The pump parameters are the excess over the laser threshold $\varepsilon$ defined as $P_{p}=\varepsilon P_{\text {th}}$, where the threshold pump power

$$\begin{aligned} P_{\text {th}}=\frac{y_{\text {th}}}{\tau }\frac{n_{0}L\pi w_{p}^{2}}{1- \exp [-\alpha _{0} L \beta (1-y_{\text {th}}) ]} \end{aligned}$$

and the threshold population of the level“2”

$$\begin{aligned} y_{\text {th}}=\frac{1}{\xi } \left( 1+\frac{\alpha _{\text {th}}}{r_{w} \alpha _{0}} \right) \end{aligned}$$

with the pump beam radius taken, for simplicity, to be the same as that for generation ($\omega _{p} = \omega _{0}$).

4 Presynaptic Hindmarsh–Rose neuron

The dynamical behavior of the membrane potential $x_{1}$ of the presynaptic neuron is determined by changes in the external current $I_{\text {ext}}$, as seen from the bifurcation diagrams of peak $x_{1}$ and inter-spike intervals (ISI) presented in Fig. 1a, b, respectively, and the time series shown in Fig. 2. All values are given in arbitrary units. For small values of the external current ($1.4<I_{\text {ext}}< 2.9$), the dynamics of the membrane potential $x_{1}$ is regular, displaying tonic spikes at $I_{\text {ext}} =1.4052$ (Fig. 2(i)) and periodic bursts at $I_{\text {ext}} =1.7396$, 2.4084 and 2.7884 containing two, three, and four spikes, as shown in Fig. 2(ii), (iii), and (iv), respectively.

One can see that for the intermediate values of the external current ($2.9<I_{\text {ext}}<3.4$), the $x_{1}$ dynamics exhibits chaotic bursts (Fig. 2(v)), while for larger values of of the external current ($I_{\text {ext}}>3.4$) the membrane potential $x_{1}$ displays regular high-frequency spiking (Fig. 2(vi)). The $I_{\text {ext}}$ values corresponding to these time series are shown in Fig. 1b by blue arrows. It is worth noting that the depolarization values of the membrane potential $x_{1}$ (minima in the time series) for regular high-frequency spiking are above $-1$, while for regular spiking and bursting are under $-1.5$ and for chaotic bursting it is situated in between $-1.5<x_{1}<-1$. The depolarization value is minimum $x_{1}$ required for neuron activation to obtain either spiking or bursting regimes. The parameter used in Eqs. (1)–(7) are $a=1$, $b=3$, $c=1$, $d=5$, $r=0.006$, $s=4$, and $x_{0}=-1.6$.

Fig. 3

Bifurcation diagram of peak values of laser pulses versus external current $I_{\text {ext}}$ for $m_{0}=0.9$

5 Laser synaptic response

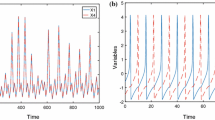
Figure 3 shows the laser response to the EDFL pump power modulation by the membrane potential $x_{1}$ of the presynaptic neuron, as a function of the external current $I_{\text {ext}}$. In Fig. 3a we plot the bifurcation diagram of the peak values of the laser pulses for $m_{0}=0.9$. In the diagram we can distinguish bistable regions shown by blue ellipses. These regions appear at the boundaries between different dynamical regimes, in particular, between tonic spikes and periodic bursting with two, three, and four spikes. The corresponding values of $I_{\text {ext}}$ are indicated by blue arrows in Fig. 1b and the laser time series are present in Fig. 4a–c. The time series show periodic train pulses of small and large amplitudes.

In addition, bistability also exists when the membrane potential changes its dynamics from chaotic bursting to regular high-frequency spiking. This value of $I_{\text {ext}}$ is indicated by the blue arrow (v) in Fig. 1b and the corresponding time series are shown in Fig. 4d. Besides, the laser synapse exhibits bistability for $I_{\text {ext}}>4.0424$ where it generates high-frequency periodic pulses of small and large amplitudes, as illustrated in Fig. 4e.

Fig. 4

Time series of laser synapse representing bistability for $m_{0}=0.9$, with a (i)–(ii) large and small amplitudes with $I_{\text {ext}}=1.6028$, b (iii)–(iv) large and small amplitudes with $I_{\text {ext}}=2.1880$, c (v)–(vi) large and small amplitudes with $I_{\text {ext}}=2.6212$, d (vii)–(viii) large and small amplitudes with $I_{\text {ext}}=3.4116$, and e (ix)–(x) large and small amplitudes with $I_{\text {ext}}=4.0424$

6 Postsynaptic neuron response to laser stimulation

In this section, the response of the postsynaptic HR neuron to the laser input is considered, i.e., the response to the signal from the presynaptic neuron transmitted through the optical synapse. The dynamics of the postsynaptic neuron can be controlled by manipulating two control parameters, modulation depth $m_{0}$ and synaptic strength coupling $\sigma$. As mentioned early, the parameter $\sigma$ acts as a coupling coefficient between the laser and the postsynaptic neuron.

Consider now the response of the postsynaptic HR neuron to the laser input with large values of the modulation depth $m_{0}=0.9$ for the synaptic coupling strength fixed at $\sigma = 0.9$. In this case, the membrane potential $x_{2}$ has a high frequency, as it can be seen in the Fig. 5 (time series and instantaneous frequency are shown in the left and right columns, respectively). For small values of external current $I_{\text {ext}}= 1.5876$ the $x_{2}$ present irregular burst behavior, see Fig. 5a, b, while with an increase in the external current at $I_{\text {ext}}=2.6212$ the membrane potential $x_{2}$ oscillate in regular burst behavior, see Fig. 5c, d. For large values of $I_{\text {ext}}=3.0164$ and $I_{\text {ext}}=3.3964$, $x_{2}$ (see Fig. 5e, f and g, h, respectively) are changed to chaotic spiking. The bifurcation diagram of local maxima of the time series and instantaneous frequency presented in Fig. 6a, b exhibit complex dynamics of the membrane potential $x_{2}$ as a function of the external current $I_{\text {ext}}$. In the case shown in Fig. 6b the membrane potential $x_{2}$ displays an average peak frequency close to 0.3820.

Fig. 5

Time series and instantaneous frequency of membrane potential $x_{2}$ are shown in the left and right columns, respectively, at $m_{0}=0.9$ and $\sigma = 0.9$. a, b $I_{\text {ext}}= 1.5876$, c, d $I_{\text {ext}}=2.6212$, e, f $I_{\text {ext}}=3.0164$, and g, h $I_{\text {ext}}=3.3964$

Fig. 6

Bifurcation diagrams of a local maxima and b instantaneous frequency of membrane potential $x_{2}$ respectively, with external current $I_{\text {ext}}$ as a control parameter for $m_{0}=0.9$ and $\sigma = 0.9$

Fig. 7

Bifurcation diagrams of a, c local maxima and b, d largest Lyapunov exponent $\lambda$ for membrane potential $x_{2}$ as a function of synaptic strength $\sigma$ at modulation depth $m_{0}=0.9$ and external currents a, b $I_{\text {ext}}= 2.7884$ and c, d $I_{\text {ext}}= 3.2064$

Figure 7a–d show the bifurcation diagrams of the local maxima of the time series and largest Lyapunov exponent $\lambda$ of the membrane potential $x_{2}$ [30] as a function of the synaptic strength $\sigma$ and modulation depth at $m_{0}=0.9$. For $I_{\text {ext}}= 2.7884$, Fig. 7a, b represent different dynamical regimes of the postsynaptic neuron, including periodic ($\lambda \approx 0$) and chaotic ($\lambda > 0$) bursting. By comparing the diagrams for small and large external currents, one can see that the postsynaptic neuron dynamics is more regular for a small current (Fig. 7a, b) than for a strong current (Fig. 7c, d).

Finally, in Fig. 8 we plot the time-averaged peak frequency of $x_{2}$ as a function of the synaptic strength $\sigma$, for different values of the modulation depth $m_{0}$. One can see that the average frequency grows as $\sigma$ is increased and saturates at a certain value which depends on $m_{0}$. Moreover, the average frequency is almost independent of $m_{0}$ when $m_{0}>0.8$ and reach the maximum value to be equal to 0.4 Hz. It is also seen that the threshold value of the coupling strength for the appearance of a periodic regime increases as the modulation depth $m_{0}$ is decreased.

7 Suggested experimental setup

The system described above can easily be implemented experimentally. The suggested experiment setup is present in Fig. 9. It consists of two electronic schemes based on the Hindmarsh–Rose model coupled by the EDFL. The EDFL is pumped by a laser diode (LD) through a wavelength-division multiplexing coupler (WDM) and a polarization controller (PC). The laser cavity is formed by an erbium-doped fiber (EDF) and two fiber Bragg gratings (BG1 and BG2).

The signal from the presynaptic HR neuron (Pre-N) is connected to the controller (D) which drives the current of the pump laser diode (LD). The EDFL output is recorded with a photo-detector (PD) connected to the postsynaptic HR neuron (Post-N) through a variable resistance (C) that acts as a coupling controller. The output signals from both HR circuits and from EDFL are visualized with an oscilloscope (OS).

Fig. 8

Average peak frequency of $x_{2}$ versus synaptic strength $\sigma$ for different values of modulation depth $m_{0}$ and $I_{\text {ext}}= 3.2064$

Fig. 9

Suggested experimental scheme of the system of two electronic HR neurons connected by the EDFL synapse. Pre-N and Post-N are the presynaptic and postsynaptic neurons, D is the laser diode current controller, LD is the laser pump diode, P is the polarizer, WDM is the wavelength division multiplexer, EDF is the erbium-doped fiber, BG1 and BG2 are the Bragg gratings, OI is the optical isolator, PD is the photodetector, C is the coupler, and OS is the oscilloscope

8 Conclusions

In summary, we have studied dynamics of a system of two Hindmarsh–Rose neurons with synaptic coupling by means of an erbium-doped fiber laser (EDFL). We have demonstrated that the signal from the presynaptic neuron transmitted via the laser synapse exhibits a complex dynamical behavior depending on the modulation depth $m_{0}$ and the external current $I_{\text {ext}}$. Very rich dynamics of the postsynaptic neuron, including spiking and bursting periodic and chaotic regimes controlled by the EDFL, has been obtained. The bifurcation analysis of action potential $x_{2}$ of the postsynaptic neuron as a function of $I_{\text {ext}}$ allowed understanding how the neuron dynamics depends on the modulation depth $m_{0}$ and synaptic strength $\sigma$. Note that $m_{0}$ and $\sigma$ provide additional flexibility for controlling the action potential $x_{2}$, i.e., changes in the instantaneous frequency of $x_{2}$ as the laser parameters are varied. Finally, we proposed the experimental setup for electronic implementation of the described laser synapse.