Collective effect of preformed plasma channel and plasma density ramp on second harmonic generation of Laguerre–Gaussian laser beam in plasma

Abstract

Present study demonstrates the relativistic optical guiding of Laguerre–Gaussian laser beam in preformed plasma channel with density ramp. Relativistic nonlinearity leads to electronic mass variation when the plasma electrons oscillate at high velocities close to the light’s velocity. Focusing is always contradicted by the diffractive nature of the laser beam. Preformed plasma channel and an exponential density ramp have been used to overcome natural diffraction of laser and thus lead to arrest power loss. Studies have also been done on the incident laser beam’s second harmonic generation. Laguerre–Gaussian profile of the laser beam is taken into account which is a non-uniform kind of irradiated intensity along the laser wavefront. Laser self-focusing has been detected from the differential equation which itself has been derived by the method of moments where different moments of the laser field signify different physical quantities. Numerical results have been obtained by Runge–Kutta 4th-order method. It has been determined that the density transition and the plasma channel both significantly increase the second harmonic yield of the incident laser beam. It is further observed that the different modes $(L_m^n)$ of the LG laser beam are more productive for harmonic generation than the Gaussian beam.

1 Introduction

Several nonlinear phenomena result from the laser interaction with plasma such as self-focusing [1], filamentation [2], higher harmonic production [3, 4], electron acceleration [5, 6], and terahertz radiations [7]. Scientists are continuously working in this field by taking any one or a pair of these processes to make them worthwhile in challenging and important applications like inertial confinement fusion [8,9,10]. For the above-stated application, it is always required to travel laser beam without losing its power. But phenomena like stimulated Raman scattering, stimulated Brillouin scattering, filamentation and the diffractive divergence of the laser beam always try to terminate the laser power. Due to the diffractive behavior of the laser with distance, the laser beam can merely travel up to a few Rayleigh lengths $(R_H)$ and lose its power. With an optical guiding mechanism, one can provide a preformed plasma channel to the incident laser beam, which helps the laser beam to travel up to many Rayleigh lengths $(R_H)$ without losing much of its intensity. Conventional optical fibers can work only up to $10^{12}\,{\rm Watt/cm}^2$ but the lasers included in these applications are having their intensities over $10^{18}\,{\rm Watt/cm}^2$. Therefore, some other techniques such as the two-pulse technique and capillary discharge technique are being used to guide the incident laser beam inside the plasma medium from $20R_H$ to $75R_H$ which has been also experimentally proved [11, 12]. In ICF, plasma expands outwards due to pressure exerted from the inside. Such an expansion of plasma will automatically generate a density gradient or density transition which along the plasma channel would help to focus the laser beam inside the plasma medium. The different kinds of density transitions such as exponential density transition, tangential density transition, and sinusoidal density transition have already been used by many authors [13,14,15] and have always been figured out that they enhance the laser self-focusing.

Self-focusing is a root phenomenon for second harmonic generation and affects it directly [16]. Self-focusing of non-Gaussian laser beam has been studied by many researchers [17,18,19,20,21,22]. The second-harmonic generation which is commonly known as the frequency doubling phenomenon will come into play due to any one of the known mechanisms such as resonant absorption [23], photon acceleration [24], electron plasma wave excitation [25], ionization fronts [26], density gradient with light filament [27] and many more. The electron plasma wave excitation is a commonly used mechanism. The field of the incoming beam disturbs the plasma in such a way that $e^{-}$ oscillates and then the movement of electrons starts in the form of a wave. Such $e^{-}$ wave often called as $e^{-}$ plasma wave when excited and interacted with the incident laser leads to the generation of 2nd harmonics of the incoming beam if couples in-phase with the incoming beam. Low-frequency radiation from SHG has been utilized as a diagnostic tool to learn more about the plasma’s characteristics, including electrical conductivity, local electron density, and many more [28]. One can also track the incident laser’s path in underdense plasmas with the help of second harmonic generation. It can also travel through the overdense region of the plasma and heat it, thus having an immense use in inertial confinement fusion. Researchers also studied the high harmonic generation of laser beam in their work [29,30,31].

Many scientists and researchers have already performed a lot of theoretical and experimental work in the field of optical guiding and harmonic generation [32,33,34]. Gupta and Singh [22] used the q-Gaussian laser beam profile along with a prepared plasma channel to recognize its harmonic generation. [35] studied the self-distortion of the laser pulse under the influence of a plasma channel. Salih et al. [36] used a magnetized plasma channel and Gaussian laser and discovered that the channel improved the harmonic production of the incident beam. Brandi et al [37] solved the 2nd-order inhomogeneous equation using perturbation theory and paraxial approach in cold underdense plasma, and observations show that the preformed plasma density affects the 2nd harmonics of the incoming intense lasers efficiently. Dua et al [38] show that the conversion efficiency of 2nd harmonics is good for ultra-fast lasers when propagating through plasma. Harmonic production of LG laser beam in relativistic plasma and collisionless plasma has been recently studied by Bhatia et al [39, 40] where they have taken exponential plasma density ramp which escalated the harmonic yield.

In the previous studies, it has been seen that most of the work on the harmonic production of the laser beam has been carried out for Gaussian and non-Gaussian beams with the help of paraxial theory. The paraxial theory approach [41, 42] takes into consideration only paraxial region of the beam, which in turn leads to large errors in the analysis for the non-Gaussian beams. In the paraxial theory, the nonlinear part of the dielectric constant is Taylor expanded up to second-order term, and higher-order terms are neglected. However, the moment theory approach [43, 44] which is based on the calculation of moments does not suffer from this defect. In the moment theory approach, the whole nonlinear part of the dielectric constant is considered in calculations [45,46,47]. The best about the theory is that it takes the whole laser intensity profile into consideration, whereas in the paraxial theory, only the axial intensity is taken into consideration. In the present investigation, Laguerre–Gaussian laser beam (non-Gaussian) has been used and the analysis has been carried out with the moment theory approach. This theory is important for the present analysis as the higher-order modes have maximum irradiance on the off-axial portion and hence play a key role in laser-induced fusion. In most of the earlier investigation, uniform plasmas were taken into consideration, which is not a real situation. In laser driven fusion, the heated plasma rapidly expands outwards due to its large pressure. So, the authors take a density transition due to the inner pressure of plasma into consideration. To the best of the authors knowledge, no one has investigated the combined effect of the preformed plasma channel and the plasma density transition on 2nd harmonic generation in relativistic plasma. So, in this paper, the authors make an effort to find the 2nd harmonics of the Laguerre–Gaussian laser beam by first guiding it through a preformed plasma channel and then taking into account the consequence of an exponential density transition due to the inner plasma pressure.

The paper has been categorized in the following manner:

Section 2 involves the distribution of laser intensity in the LG beam profile. Section 3 provides the modifications in the plasma dielectric function with laser. Section 4 expresses the brief moment theory for self-focusing of the laser in relativistic plasma. Sections 5 and 6 elaborate on the plasma wave excitation and the resultant harmonic yield, respectively. Section 7 includes the graphical results of the investigation and their detailed discussion. In the end, the conclusion is given in Sect. 8.

2 Intensity distribution in Laguerre–Gaussian beam profile

The LG laser’s wavefront intensity distribution at z = 0 is described by [48],

$$\begin{aligned} {E_0E_0^*}_{z=0}= E_{00}^2 \left( \frac{r^2}{r_0^2}\right) ^{m} e^{- \frac{r^2}{r_0^2}} \left[ L_n^m\left( \frac{r^2}{r_0^2}\right) \right] ^2 \end{aligned}$$

(1)

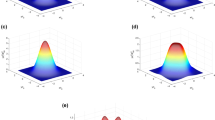
Here, $E_0$ represents the complex amplitude of the laser beam and the axial amplitude is given by $E_{00}$; $r,~r_0$ represent the instantaneous beam radius and the beam spot size, respectively, $L_n^m$ represents the Laguerre polynomial. Index m denotes the orbital angular momentum (OAM) associated with LG beams and n denotes the radial index which provides $(n+1)$ radial nodes in the laser mode profile. Figures 1, 2, 3 and 4 represent the intensity distribution of different LG modes with radial distance from the axis. Figure 1 represents a 3-dimensional intensity plot for $m=n=0$, i.e., $L_0^0$ mode which represents the Gaussian beam. Figures 1, 2, 3 and 4 represent the higher LG modes with radial index zero, which provide one radial node and with different OAM. A central dark region with intensity on the off-axial region is observed for OAM modes. For a high OAM index, the intensity shifts more from the center toward the edges due to the centrifugal force experienced by the photons.

The distribution of the laser intensity for $z>0$ can be written as,

$$\begin{aligned} {E_0E_0^*}_{z>0}= \frac{E_{00}^2}{f^2} \left( \frac{r^2}{r_0^2 f^2}\right) ^{m} e^{- \frac{r^2}{r_0^2 f^2}} \left[ L_n^m\left( \frac{r^2}{r_0^2 f^2}\right) \right] ^2 \end{aligned}$$

(2)

Fig. 1

3-dimensional dispersal of intensity for $LG_0^0$ mode

Fig. 2

3-dimensional dispersal of intensity for $LG_0^1$ mode

Fig. 3

3-dimensional dispersal of intensity for $LG_0^2$ mode

Fig. 4

3-dimensional dispersal of intensity for $LG_0^3$ mode

Here, $r_0f$ represents the modified radius of the beam where f is called the dimensionless parameter for the beam width which is accountable for the laser focusing or defocusing in the plasma medium.

3 Modifications in the plasma dielectric function with laser

Consider a laser beam having frequency $\omega$, wave vector $k_0$ propagating through the plasma medium along the z-direction with velocity v. The electric field vector for such a beam is,

$$\begin{aligned} E(r,z,t)= E_{0}(r,z) e^{\iota (\omega t -k_0z) } \end{aligned}$$

(3)

The plasma pressure exerted by the plasma electrons from the inner to the outer part of plasma forms a density transition in the plasma medium and thus modifies the electron density by,

$$\begin{aligned} n_{0}(z)= n_0 exp\left( \frac{z/k_0r_0^2}{d}\right) \end{aligned}$$

(4)

where $n_0, d, n_0(z)$ is the density of plasma at $z=0$, the slope of density ramp, and the density of plasma for $z > 0$, respectively. A subsequent laser beam (prepulse) further ionizes such plasma and thus creates a plasma channel, which is a function of r and is given by,

$$\begin{aligned} n_0(r)= n_0(0)+ \Delta n_0 \frac{ r^2}{r_{ch}^2} \end{aligned}$$

(5)

Here, the channel depth is given by $\Delta n_0=n_0({r_{ch}})-n_0(0)$, and the density of electrons along the channel axis is $n_0(0)$.

so, the overall modifications in the plasma density can be written as,

$$\begin{aligned} n_{0}(r,z)= \bigg (n_0(0)+ \Delta n_0 \frac{ r^2}{r_{ch}^2}\bigg ) exp\left( \frac{z/k_0r_0^2}{d}\right) \end{aligned}$$

(6)

The high electric field of intense lasers makes the plasma electrons quiver at a high velocity comparable to the light’s velocity, which raises the electronic mass to $m_0 \gamma$ and further modifies the transverse plasma density $n_e(r,z)$. Here $m_0$ represents the rest mass of $e^-$.

$$\begin{aligned} n_e(r,z)=n_0(r,z) \gamma \end{aligned}$$

(7)

where

$$\begin{aligned} \gamma =(1+\beta E E^*)^{\frac{1}{2}} \end{aligned}$$

(8)

and

$$\begin{aligned} \beta =\frac{e^2 }{m_0^2 \omega ^2 c^2} \end{aligned}$$

The dielectric function of such plasma is written as,

$$\begin{aligned} \epsilon =1- \frac{4\pi n_e(r,z) e^2}{m_0 \omega ^2} \end{aligned}$$

(9)

Using Eqs. 6 and 7 in Eq. 9, we get

$$\begin{aligned} \epsilon =1-\left[ \frac{\omega _{p0}^2}{ \omega ^2}+\frac{\omega _{pch}^2}{ \omega ^2} \frac{r^2}{r_{ch^2}} \right] exp\left( \frac{z/k_0r_0^2}{d}\right) (1+\beta E E^*)^{-\frac{1}{2}} \end{aligned}$$

(10)

The dielectric function $\epsilon$ can also be written as the sum of the linear term $\epsilon _0$ and the nonlinear term $\phi (E_0E_0^*)$. On comparing Eq. 10 with the general equation for dielectric function, we get an equation for the nonlinear term given by,

$$\begin{aligned} \begin{aligned}&\phi = exp\left( \frac{z/k_0r_0^2}{d}\right) \Big [ \frac{\omega _{p0}^2}{ \omega ^2}-\left( \frac{\omega _{p0}^2}{ \omega ^2}+ \frac{\omega _{pch}^2}{ \omega ^2}\frac{r^2}{r_{ch^2}}\right) \\&\Big (1+\frac{\beta E_{00}^2}{f^2} \left( \frac{r^2}{r_0^2 f}\right) ^{m} e^{- \frac{r^2}{r_0^2 f^2}} \left[ L_n^m\left( \frac{r^2}{r_0^2 f^2}\right) \right] ^2\Big )^{-\frac{1}{2}}\Big ] \end{aligned} \end{aligned}$$

(11)

4 Self-focusing of the laser beam

We find the following equation for an electromagnetic wave using Maxwell’s equations for non-conducting $(J=0)$, non-magnetic$(\mu = 1)$, and isotropic medium $(\rho =0)$,

$$\begin{aligned} \nabla ^2 E_0- \nabla (\nabla . E_0)+\epsilon (E_0E_0^*)E_0=0 \end{aligned}$$

(12)

The second term $\nabla (\nabla . E_0)$ can be neglected as its magnitude is very small and we will only be left with the following part,

$$\begin{aligned} \nabla ^2 E_0+\epsilon (E_0E_0^*)E_0=0 \end{aligned}$$

(13)

Using Eq. 3 in Eq. 13, we get a semi-optic equation

$$\begin{aligned} \iota \frac{dE_0}{dz}=\frac{1}{2k_0}\nabla _\perp ^2 E_0 +\chi (E_0 E_0^*)E_0 \end{aligned}$$

(14)

here, $\chi (E_0 E_0^*)=\frac{k_0}{2\epsilon _0} \phi (E_0E_0^*)$

Method of moments defines the laser intensity and mean square radius of the laser beam by the following equations,

$$\begin{aligned} I_0= & {} \int \int E_0 E_0^* d\tau \end{aligned}$$

(15)

$$\begin{aligned} <a>^2= & {} \frac{1}{I_0}\int \int r E_0 E_0^* d\tau \end{aligned}$$

(16)

where $d\tau = r~ dr ~d\theta$

By using the intensity distribution of the laser beam from 2, we get,

$$\begin{aligned} I_0= & {} \pi r_0^2 E_{00}^2 \frac{(n+m)!}{n!} \end{aligned}$$

(17)

$$\begin{aligned} <a>^2= & {} r_0^2 f^2 (2n+m+1) \end{aligned}$$

(18)

Using the procedure given by Lam [44], we get a 2nd-order differential equation,

$$\begin{aligned} \frac{ d<a>^2}{dz}=\frac{4I_2}{I_0}-\frac{4Q}{I_0} \end{aligned}$$

(19)

where,

$$\begin{aligned} I_2= & {} \int \int \frac{1}{2 k_0^2} (\nabla _\perp E_0^2 -F) d\tau \end{aligned}$$

(20)

$$\begin{aligned} F(E_0E_0^*)= & {} \frac{1}{2\epsilon _0} \int _0^{E_0E_0^*} \chi (E_0E_0^*) d(E_0E_0^*) \end{aligned}$$

(21)

and

$$\begin{aligned} Q=\int \int \Big (\frac{1}{2\epsilon _0}E_0E_0^* \chi (E_0E_0^*)-2F)\Big )d\tau \end{aligned}$$

(22)

Differentiating Eq. 18 twice w.r.t. z and following the procedure of moment theory, we get

$$\begin{aligned} \begin{aligned} \frac{d^2f}{d\xi ^2} + \frac{1}{f} \biggl (\frac{df}{d\xi }\biggr )^2= \frac{n!}{(m+n)!\,(2n+m+1)}\frac{1}{f^3} \biggl [\frac{(n+m)!}{n!}\\ (-2n-m+1)+ (2n+m)^2 J_1 +4(m+n)^2\\ J_2 -4(m+n)(m+2n) J_3+ \frac{ \beta E_{00}^2}{4} \exp (\xi /d) J_4\biggr ] \\ -\frac{n!}{(m+n)!\,(2n+m+1)} f^3 \Bigl (\frac{\omega _{p0} r_0}{c}\Bigr )^2 \Big (\frac{r_0^2}{r_{ch}^2}\Big ) \exp (\xi /d) J_5 \end{aligned} \end{aligned}$$

(23)

where

$$\begin{aligned} J_1&=\int _{0}^{\infty }x^{m-1} e^{-x} [L_n^m(x)]^2dx \\ J_2&=\int _{0}^{\infty }x^{m-1} e^{-x} [L_{n-1}^m(x)]^2dx\\ J_3&=\int _{0}^{\infty }x^{m-1} e^{-x} [L_n^m(x)][L_{n-1}^m(x)]dx\\ J_4&=\int _{0}^{\infty }x^{2m} e^{-2x} [L_n^m(x)]^3 \Big (1+\frac{\beta E_{00}^2}{f^2} \left( \frac{r^2}{r_0^2 f}\right) ^{m} e^{- \frac{r^2}{r_0^2 f^2}} \left[ L_n^m\left( \frac{r^2}{r_0^2 f^2}\right) \right] ^2\Big )^{-\frac{3}{2}} \\&\quad \Big [\Bigl (\frac{\omega _{p0} r_0}{c}\Bigr )^2 +\Bigl (\frac{\omega _{p0} r_0}{c}\Bigr )^2 \Big (\frac{r_0^2}{r_{ch}^2}\Big )x f^2\Big ]\Big [ (-2x+2(m+2n)L_n^m(x)-4(m+n)\\&\quad L_{n-1}^m(x))\Big ]dx \\ J_5&= \int _{0}^{\infty } x^{m+1} [L_n^m(x)]^2\Big (1+\frac{\beta E_{00}^2}{f^2} \left( \frac{r^2}{r_0^2 f}\right) ^{m} e^{- \frac{r^2}{r_0^2 f^2}} \left[ L_n^m\left( \frac{r^2}{r_0^2 f^2}\right) \right] dx ^2\Big )^{-\frac{1}{2}} \end{aligned}$$

and $x=\frac{r^2}{r_0^2f^2}$, dimensionless propagation distance $\xi =(\frac{z}{k_0r_0^2})$, and the boundary conditions $f=1$ and $\frac{df}{d\xi }=0$ at $\xi =0$.

5 Equation for the excited plasma wave

The oscillating plasma electrons create an electron plasma wave, which is influenced by the laser beam. The equation for the excitation of plasma wave can be derived by using the fluid equation of motion, equation of continuity, equation of state, and Poisson’s equation.

• Momentum balance equation or equation of motion,

  $$\begin{aligned} m_e\frac{\partial (v)}{\partial t} + (v.\nabla )v =-eE- \frac{\nabla P}{n_e(r,\xi )} \end{aligned}$$

• Continuity Equation

  $$\begin{aligned} \frac{\partial n_e(\xi )}{\partial t} + \nabla (n_e(r,\xi ) v) = 0 \end{aligned}$$

• Equation of state

  $$\begin{aligned} \frac{P}{n_e^3(r,\xi )}=constant \end{aligned}$$

• Poisson’s equation

  $$\begin{aligned} \nabla .E = -4\pi n(r,\xi )e \end{aligned}$$

Here, E consists of the pump field and the field of plasma wave, $n_e{(r,\xi )}$ consisting of unperturbed plasma density $n_0{(r,\xi )}$ and perturbed plasma density $n{(r,\xi )}$. A linear perturbation theory is applied to the above set of equations and all the terms containing higher powers of the perturbed quantities are neglected to get an equation given below,

$$\begin{aligned} \frac{\partial ^2 n(r,\xi )}{\partial t^2}- v_{th}^2\nabla ^2 n(r,\xi )+\omega _{po}^2(r,\xi ) \frac{n_{e}(r,\xi )}{n_0(r,\xi )}n(r,\xi ) = \frac{e n_0(r,\xi )}{m_e}\nabla .E \end{aligned}$$

(24)

where $v_{\rm th}=\sqrt{\frac{3 K_BT_0}{m_e}}$ is the $e^-$ thermal velocity. Since the oscillatory quantities behave sinusoidally, we have

$$\begin{aligned} n(r,\xi ) \propto e^{\iota (\omega t - k_0 z)} \end{aligned}$$

Using the above relation in 24, we get an equation for the perturbed electron density,

$$\begin{aligned} n(r,\xi )=-\frac{e n_0(r,\xi )}{m_e} \frac{\nabla .E}{\left( \omega ^2-k_0^2 v_{th}^2-\omega _{p0}^2(r,\xi ) \frac{n_e(r,\xi )}{n_0(r,\xi )}\right) } \end{aligned}$$

(25)

This perturbation in plasma density originates the plasma wave and this plasma wave is the basic source of the 2nd harmonic production of the incoming laser beam.

6 Equation for harmonic yield

Second harmonics are created when the electron plasma wave and incident laser beam are coupled in phase. One may easily construct the following expression for the second harmonic field $E_2$ from Maxwell’s equations.

$$\begin{aligned} \nabla ^2 E_2+ \frac{\epsilon _2(\omega _2)}{c^2}\omega _2^2 E_2=-\frac{4\pi }{c^2}\iota \omega _2 J_2 \end{aligned}$$

(26)

Here, $J_2=- \frac{n_e e^2 E_0}{\iota m_e \omega _2}$ is the second harmonic current density, $\epsilon _2$ is the dielectric function of the plasma in the presence of 2nd harmonic field and $\omega _2$ represents the frequency of second harmonics. On substituting the value of $J_2$, we get

$$\begin{aligned} \nabla ^2 E_2+ \frac{\epsilon _2(\omega _2)}{c^2}\omega _2^2 E_2=-\frac{\omega _{p0}^2(r,\xi )}{c^2}\frac{n{(r,\xi )}}{n_0{(r,\xi )}}E_0 \end{aligned}$$

(27)

On rearranging the above equation, we get an equation for the second harmonic field given by,

$$\begin{aligned} E_2=\frac{\omega _{p0}^2 (r,\xi )}{c^2} \frac{n{(r,\xi )}}{n_0{(r,\xi )}}\frac{E_0}{(k_2^2-4k_0^2)} \end{aligned}$$

(28)

where $k_2$ represents propagation constant of 2nd harmonics. Use the above equation in the expression for the power of the 2nd harmonic beam, which is defined as

$$\begin{aligned} P_2=\int \int E_2 E_2^* d\tau \end{aligned}$$

(29)

Now, one can easily determine the second harmonic yield by dividing the $2^{nd}$ harmonic power by the initial beam power.

$$\begin{aligned} \eta= & {} \frac{\int \int E_2 E_2^* d\tau }{\int \int E_0 E_0^* d\tau } \end{aligned}$$

(30)

$$\begin{aligned} \eta= & {} \frac{1}{9} \frac{\beta E_{00}^2}{f^4}\frac{n!}{(n+m)!} W J_6 \end{aligned}$$

(31)

$$\begin{aligned} J_6&=\int _{0}^{\infty } x^{2m+1} e^{-2x} [L_n^m(x)]^2 \Big [ L_n^m(x)\Big (-1+\frac{m+2n}{x}\Big )-\frac{2(m+n)}{x} \\&\quad L_{n-1}^m \Big ]^2 dx ~~/~~\Big [ W-\Big ( W-\Omega ~ exp\Big (\frac{\xi }{d}\Big )\Big ) \frac{v_{th}^2}{c^2}- \Bigl (\frac{\omega _{p0} r_0}{c}\Bigr )^2 \Big (\frac{r_0^2}{r_{ch}^2}\Big )\\&\quad ~x ~f^2 ~exp\Big (\frac{\xi }{d}\Big ) ~\Big (1+\frac{\beta E_{00}^2}{f^2} \left( \frac{r^2}{r_0^2 f}\right) ^{m} e^{- \frac{r^2}{r_0^2 f^2}} \left[ L_n^m\left( \frac{r^2}{r_0^2 f^2}\right) \right] ^2\Big )^{-\frac{1}{2}}\Big ]^2 \end{aligned}$$

where

$$\begin{aligned} W=\frac{\omega _{0}^2r_0^2}{c^2}~~~~~~\Omega =\frac{\omega _{p0}^2r_0^2}{c^2} \end{aligned}$$

7 Discussion of results

The above analysis provides the equations for laser self-focusing and the second harmonic generation of the Laguerre–Gaussian laser beam in plasma where relativistic nonlinearity is present. The first equation (i.e., eq. 23) has three different terms on RHS. The first term on RHS originates from $\nabla ^2$ has its physical meaning, i.e., diffractive behavior of laser, while the other two terms include the relativistic nonlinearity of the plasma medium and are thus responsible for the laser focusing. The dominating behavior of either of the term will decide whether the laser beam is going to focus or defocus in the plasma medium. To solve this nonlinear differential equation numerically, we have used the Runge–Kutta fourth-order method by taking the following set of laser and plasma parameters which are given below:

Laser frequency $\omega =1.78\times 10^{15}\, {\rm rad\,s}^{-1}$, laser spot size $r_0=15 \times 10^{-6}\,{\rm m}$, channel radius $r_{ch}=150\times 10^{-6}$, $\beta E_{00}^2=0.5$, $\frac{\omega _{p0}^2r_0^2}{c^2}=4.0$, $\Bigl (\frac{\omega _{p0} r_0}{c}\Bigr )^2 \Big (\frac{r_0^2}{r_{ch}^2}\Big )=0.8$, plasma temperature $T_0=10^6\,{\rm K}$.

Figure 5 shows the density transition (Eq. 4) for different values of slope parameter ’d.’ It has been found from the figure that for lower values of the slope parameter ’d,’ the exponential transition in density is more. This plot will be more helpful in the next discussion.

Fig. 5

Variation of ratio $n_e/n_0$ with $\xi$ for distinct value of slope parameter ’d’

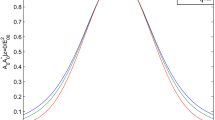
Figure 6 shows the variation of f with dimensionless distance $\xi$ for different modes of the Laguerre–Gaussian laser beam. The other parameters are fixed as mentioned earlier. The plot clearly shows that the laser is more focused for (0, 3) mode, i.e., $LG_0^3$. This is because as we increase the number of modes from (0, 0) to (0, 3), the contribution of the nonlinear part in Eq. 23 becomes considerably larger than the diffractive part which enhances the laser self-focusing in the plasma medium.

Fig. 6

Change of dimensionless parameter of beam width f with $\xi$ for distinct laser modes

Figure 7 provides the second harmonic yield for distinct laser modes. It has been seen from the figure that the harmonic production of the pump beam also increases with an increase in the modes from (0, 0) to (0, 3). This is due to the reason that second harmonic generation directly depends on the laser focusing. As the laser focusing increases with increasing laser modes so does the harmonic yield.

Fig. 7

Second harmonic yield $\eta$ for distinct laser modes

Figures 8 and 9 show self-focusing and harmonic yield $\eta$ of $LG_0^3$ mode of laser, respectively, at distinct values of normalized channel depth, i.e., $(\frac{\omega _{pch}r_0}{c})^2 (\frac{r_{ch}}{r_0})^2=0.0,~0.4,~0.8$. The other parameters are fixed as explained earlier. It has been seen from the Fig. 8 that the laser beam defocuses in the absence of any channel. But as we introduce the channel, the laser beam gets more self-focused in the plasma medium with the increasing value of the channel depth. This is because the inclusion of the plasma channel makes the nonlinear refraction term dominant over the laser diffraction term in Eq. 23.

Fig. 8

Variation of dimensionless parameter of beam width f with $\xi$ for distinct channel depth

Fig. 9

Second harmonic yield $\eta$ for distinct channel depth

Figure 9 displays the harmonic yield of $LG_0^3$ mode of laser for different channel depths. It has been found that harmonic yield increases with channel depth. The reason for the enhanced harmonic yield is the enhanced self-focusing of laser with the increase in plasma channel depth.

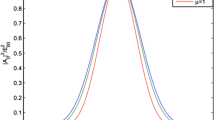
Figure 10 shows that on decreasing the value of slope parameter $'d'$, the beam gets more self-focused. For a better understanding, one can see plot 2. As it is clear from Fig. 2 that the density gradient in the plasma is more for the lower values of parameter $'d'$ so does the laser self-focusing. This density gradient modifies the plasma dielectric function which leads to the laser focusing in the plasma medium.

Fig. 10

Variation of dimensionless parameter of beam width f with $\xi$ for distinct values of parameter ’d’

Figure 11 shows that the harmonic yield of $LG_0^3$ mode of laser beam also increases with the decreasing value of $'d'$ or one can say with an increasing density gradient.

Fig. 11

Second harmonic yield $\eta$ for distinct values of parameter ’d’

Figure 12 shows the variation of f with $\xi$ for distinct combinations of $\Big (\frac{\omega _{p0}r_0}{c}\Big )^2\Big (\frac{r_0}{r_{ch}}\Big )^2$ and $'d'$. It has been seen from the plot that when there is no plasma channel, i.e., $\Big (\frac{\omega _{p0}r_0}{c}\Big )^2\Big (\frac{r_0}{r_{ch}}\Big )^2=0$ and no density gradient, i.e., $'d'=\infty$, then the laser beam defocuses. But on the inclusion of plasma channel, i.e., $\Big (\frac{\omega _{p0}r_0}{c}\Big )^2\Big (\frac{r_0}{r_{ch}}\Big )^2=0.8$, the laser beam start focusing in the plasma and on further inclusion of density gradient, i.e., $'d'=7$ the laser focusing becomes stronger from the previous focusing. This is because both the plasma channel and density ramp collectively support self-focusing by modifying the plasma dielectric function.

Fig. 12

Change of dimensionless parameter of beam width f with $\xi$ for distinct combinations of channel depth and slope parameter $'d'$

Figure 13 shows that the harmonic yield of the incoming laser increases under the collective effect of the plasma channel and density ramp. This is because of the enhanced focusing of the laser.

Fig. 13

Second harmonic yield $\eta$ for distinct combinations of channel depth and slope parameter $'d'$

8 Conclusion

From the main results, it is observed that the self-focusing and harmonic yield of the laser beam increase with an increase in channel depth, and also on decreasing the value of slope parameter $'d'$. It is further observed that the self-focusing and harmonic yield of the laser beam are higher for the $L_0^3$ mode as compared to the Gaussian mode $(L_0^0)$. The results of the current analysis have led to the conclusion that the self-focusing and harmonic yield of the laser beam can be enhanced by utilizing the collective effect of the preformed plasma channel and the plasma density ramp along with higher modes of the Laguerre–Gaussian laser beam. Self-focusing of the laser beam concentrates the laser energy on the target and thereby improves the efficiency of laser energy deposition into the fuel pellet. The enhanced intensity resulting from self-focusing helps in achieving better compression of the fuel, which further leads to the high temperature and pressure needed for inertial confinement fusion (ICF). Higher second harmonic yield further improves the optical conversion efficiency of the laser energy to the fuel pellet. In a nutshell above effects help to optimize the conditions for ICF and thereby improve the possibility of successful commissioning of ICF. So, the results of the present analysis will be useful for the researchers working in the field of ICF.