Interplay of steric factor and high zeta potential on entropy generation during nanofluid slip flow in a microfluidic tube

Abstract

Of concern in the paper is entropy generation during electrically modulated transport of a nanofluid in a hydrophobic cylindrical microtube. For thermodynamic analysis of the system under consideration, the combined effects of nonlinear thermal radiation, viscous dissipation and Joule heating have been considered. Global irreversibility of the system has been optimized by accounting for different thermo-physical parameters. An appropriate finite difference approach has been developed to solve the nonlinear coupled equations numerically. Numerical simulations have been conducted to investigate the nature of the velocity, temperature, and entropy distributions for different parametric variations, such as steric parameter, surface zeta potential, Grashof number, velocity slip, and the radiation parameter. The Nusselt number, local and global entropy generation, Bejan number are examined for the system studied here. The Nusselt number exhibits asymptotic behavior during heat generation through viscous dissipation. The global entropy of the system is found to be reduced under the influence of nonlinear thermal radiation, implying better working efficiency of the system.

1 Introduction

Electrically modulated transport is one of the most efficient mechanisms in microfluidic devices, because it has several advantages [1,2,3]. Electroosmotic flow is now widely regarded as an appropriate flow actuation mechanism in micro/nanofluidic channels, especially in microelectromechanical systems (MEMS). Electroosmosis is a significant electrokinetic phenomenon in surface physics that largely depends on the development of the electric double layer (EDL) and the application of an electric field. Electrostatic energy controls the movement of mobile ions within the EDL area. Owing to viscous drag, the bulk liquid moves. It is well known as the “electroosmotic flow” (EOF). The hydrodynamic and thermal transport processes in electroosmotically modulated flow in microchannels were studied by a number of researchers [4,5,6,7]. Horiuchi and Dutta [8] investigated the situation of thermally developed electroosmotic flows across microchannels and presented analytical estimates for the thermal distribution and Nusselt number. Meanwhile, Saravani and Kalteh [9] analyzed the combined influences of electroosmotic and pressure on nanofluid flow in a microchannel. Considering the effect of heterogeneous surface potential and boundary slip conditions, they concluded that the higher volume fraction of nanoparticles decreases the velocity while it ameliorates the thermal energy transmission through the solid surfaces of the microchannel. Recently, Mukherjee and Shit [10] used differential transform method to perform an analytical study on couple stress nanofluid flow in a microchannel embedded in porous medium. Considering electrothermal phenomenon, they reported that the thermal performance ameliorates as ion diffusion coefficient increases, which significantly enhances the nanofluidic temperature. Several authors [11, 12] investigated the physical evolution of velocity and heat transfer in fluids flowing in a microchannel driven by electrokinetic force. In the aforesaid EOF research, the scientists treated the ions as point charges and ignored their volumes. In reality, the specific size of ions has a significant impact on the EDL, EOF velocity and electrical potential distributions. This is applicable for suitably dilute solutions, but when estimating the electrical potential at larger zeta potentials, considerable inaccuracies might occur. The steric factor, which is the average volume of ions, is calculated as $\nu = a^3 n_0$ (a is the ionic length scale, $n_0$ the nominal ionic concentration at liquids), is generally used to measure the ionic size effect for electrokinetically driven flow.

With the increasing importance of studying the dynamics of nanofluids in microchannels/microtubes, there has been an increase in the study of nanofluid flow in microchannel/microtubes [13,14,15,16,17]. Barnoon [18] conducted a numerical investigation on electroosmotically regulated hybrid nanofluid flow in a microchannel integrated with a dual mixer. A new design was developed in this study by mounting four pairs of electrodes to boost the rate of mass diffusion by means of ion absorption into the electrodes and generating vortices. It has been concluded that the hybrid nanofluid model provides enhancing effect to heat transfer compared to pure fluid. Barnoon et al. [19] investigated the characteristics of heat transfer and entropy generation during two-phase nanofluid flow in a circular channel using the finite volume method (FEM). They investigated the dominance of thermal entropy generation over frictional entropy generation, which significantly impacts the distribution of Bejan number. Using Eulerian–Lagrangian method, Cai et al. [20] evaluated a numerical simulation on the thermofluidic characteristics and entropy generation analysis of nanofluid using Ferromagnetic nanoparticles. They demonstrated that nanoparticle migration increases the pressure drop, skin friction factor, heat transfer coefficient, cumulative thermal performance of nanofluid, and thermal as well as frictional entropy generation in a microchannel constructed by ribbed-blocks. Recently, a mathematical model has been proposed by Monfared et al. [21] to study the swirling nanofluid flow and associated problem of heat transfer in a tube containing helical ribs. Considering diverse geometric scenarios, they showed that the presence of helical ribs boosts the Nusselt number and friction factor for two phase flow of nanofluid. Also resistance against the flow rises with increase in the nanoparticle volume fraction which indicated that the nanoparticles aid to control the flow characteristics.

Several authors reported the consequences of thermal radiation on the thermodynamic behavior of various types of flows [22,23,24,25,26]. Most of the mathematical models used by them for the determination of the radiative heat transfer are linear. Mukhopadhyay [22] investigated the influences of thermal radiation on magnetohydrodynamic flow over a slip aided exponentially stretching sheet, neglecting viscous dissipation effects. Hayat and Sajid [23] took into account the viscous dissipation effect on the thermal energy balance equation for a problem similar to that considered by Mukhopadhyay [22]. More recently, some theoretical studies were performed by considering nonlinear thermal radiation and its impact on thermofluidic transport [24,25,26]. Cortell [27], as well as Pantokratoras and Fang [28] presented the results of their studies of a similar problem, considering nonlinear radiative heat transfer. A three dimensional study for Jeffrey nanofluid flow was carried out by Shehzad et al. [29], by the use of homotopy analysis method. Tripathi et al. [30] designed a mathematical model to estimate the thermal transport in peristaltic flow of micropolar nanofluid through an asymmetric microchannel, and their research took into account the impacts of thermal radiation. However, it should be kept in mind that specific system parameters need to be estimated along with the consideration of the reduction in energy loss within the microdevices/systems involving thermo-fluidic transport, that can escalate the thermodynamic efficiency [31,32,33].

It may, however, be mentioned that the minimization of entropy generation serves as an effective tool for the optimization of the thermo-physical and geometrical parameters of the system. Keeping this in view, an attempt has been made in this work to determine the combined effects of Joule heating and nonlinearity of thermal radiation in a situation where zeta potential is considerably high. It may be noted that the effect of steric factor on electroosmotic transport in microtubes has been seldom taken into account. So, consideration of the steric factor in the present study is a novel step toward studies pertaining to electroosmotic flow in the area of microfluidics. The present investigation takes care of the nonlinear thermoradiative effects while studying fluid flow through a microchannel. This effect allows the minimization of global entropy due to the significant reduction in thermofluidic temperature. These factors have rarely been investigated by previous researchers. While in most of the similar previous studies, the surface potential was considered to be small, the present study has relaxed the restriction of the surface potential and so is more general. Considering buoyancy parameter in the momentum equation, a detailed analysis has been performed to determine the effect of various parameters on flow velocity, temperature, entropy of the system. Numerical solutions have been obtained for determining the distributions of the electrokinetic potential, nanofluid velocity and temperature. Numerical estimates of the Nusselt number, and entropy generation have also been presented. Novelty of this investigation is the consideration of ion-size-dependent electrothermal flow and entropy generation for nanofluids, as well as the incorporation of the Joule and viscous heating with the consideration of nonlinear thermal radiation.

2 The physical model

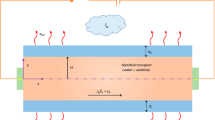
Capillary microfluidic devices constitute a class of microfluidic systems that are typically composed of the alignment of cylindrical glass tubes. The strong resistance of cylindrical microfluidic devices to chemicals and the ability to generate three-dimensional flows are two of the most significant benefits of these devices [34]. To this end, transportation of thermally developed nanofluids through a circular cylindrical microtube is the prime concern of this investigation. The nanofluid’s transport is thought to be influenced by a homogenized electroosmotic process and an axially induced pressure gradient. The diameter of the microtube is assumed to be $2R^*$ and the $z^*$-axis is expected to coincide with the centre-line of the tube (cf. Fig. 1). In order to produce an electric field of a certain strength within the microtube, an electrode has been installed at the entry and exit points of the microtube.

Fig. 1

Schematic representation of the present problem

The microtube’s diameter should be substantially smaller than its length, i.e., $2R^*\ll L$. Because of this, simulations can be carried out in a one-dimensional system. In this study, the development of the ionic structure on the electric double layer (EDL) is investigated while considering finite ionic size (steric) effect. The microtube’s surface is also subjected to a high zeta potential $(\zeta ^*)$. The application of an axial electric field generates electric charge that change their position at random in close proximity to the walls, and after a while, the movement becomes stationary. For heat transfer analysis, the effect of nonlinear thermal radiation on the energy equation is taken into account. The effect of buoyant force on the motion of nanofluid has also been considered.

3 Governing equations

3.1 Basic equations

The equations that determine the thermodynamic transport of an incompressible nanofluid flow (cf. [35, 36] ) are given by

$$\begin{aligned} \mathbf{\nabla }\cdot \mathbf{U}= & {} 0, \end{aligned}$$

(1)

$$\begin{aligned} \rho _{nf}\Bigg (\frac{\partial \mathbf{U}}{\partial t}+\mathbf{U}\cdot { \nabla }{} \mathbf{U}\Bigg )=\, & {} -{ \nabla }p^*+\mu _{nf}\nabla \cdot {\varvec{\tau }}+\mathbf{F}, \end{aligned}$$

(2)

$$\begin{aligned} (\rho c_p)_{nf}\Bigg (\frac{\partial T}{\partial t}+\mathbf{U}\cdot \mathbf{\nabla } T\Bigg )= {} k_{nf}\nabla ^2 T-\mathbf{\nabla }\cdot \mathbf{q}+\mu _{nf}(\tau \cdot \nabla \mathbf{U})+\ddot{\text{ Q }}, \end{aligned}$$

(3)

in which ${\varvec{\tau }}=\nabla \mathbf{U}+\nabla \mathbf{U}^T$ is the stress, $\mathbf{U}$ the velocity, $p^*$ the pressure and T the temperature of the fluid. Here $\rho _{nf},\mu _{nf}$, $(c_p)_{nf}$, $k_{nf},$ respectively, denotes the effective density, viscosity, specific heat capacity and conduction of heat in the nanofluid. The last term $\mathbf{F}$, which has appeared in the momentum Eq. (2) for interactions between applied electrical field and the buoyancy effect, reflects the net external body forces per unit volume which may be mathematically expressed as

$$\begin{aligned} \mathbf{F}=\rho _e\mathbf{E}\pm {\textbf {g}}(\rho \beta )_{nf} T, \end{aligned}$$

(4)

where $\rho _e$ is the net density of electric charge, $\mathbf{E}(\mathbf{E}=-\nabla \psi ^*, ~\psi ^*$ being the electrical potential) the electric field applied externally and $\mathbf{g}$ the gravitational force vector. It is noteworthy that ‘±’ sign in Eq. (4), respectively, corresponds to the assisting and opposing flow due to buoyancy effect. In view of the Rosseland approximation (c.f [37, 38]), the heat flux $\mathbf{q}$ in energy Eq. (3) can be taken as $\mathbf{q}=-4\sigma ^*\nabla T^{4}/3k^*$, in which $\sigma ^*$ is the Stefan–Boltzmann constant and $k^*$ is the absorption coefficient. Therefore, divergence of the radiative heat flux vector $\mathbf{q}$ becomes

$$\begin{aligned} \mathbf{\nabla } \cdot \mathbf{q}=-\frac{16\sigma ^\star }{3k^\star }\Big [ T^3\nabla ^2 T+3 T^2(\nabla T \cdot \nabla T) \Big ]. \end{aligned}$$

(5)

The last two terms of Eq. (3), respectively, represent the internal heat generation/absorption in the system due to viscous dissipation and exterior heat generation/absorption due to Joule heating effects. As a result of the Joule heating phenomenon, the rate at which the external volumetric heat is produced, being governed by the Ohm’s law [39], can be represented as

$$\begin{aligned} \ddot{\text{ Q }}=\frac{2n_0\sigma _{nf}}{n^++n^-}\mathbf{E}\cdot \mathbf{E}, \end{aligned}$$

(6)

where $\sigma _{nf}$ is the effective electrical conductivity of the nanofluid, $n^\pm$ the number densities of the positive and negative ions within the electric double layer (EDL) and $n_0$ the ionic concentration in the bulk. In the aforesaid equations, the thermo-physical expressions for nanofluid are listed in Table 1. Here, the quantities with subscript ‘nf’, ‘s’ and ‘f,’ respectively. stand for nanofluids, nanoparticles and base fluid properties.

Table 1 Thermo-physical expressions for nanofluid [40, 41]

3.2 Ion-size-dependent EDL

The concentrations of the ionic species follow a modified Boltzmann distribution which can be used to calculate local volumetric charge density. It is known that the electrical potential $\psi ^*$ in the electric double layer (EDL) satisfies the Poisson equation [42, 43] given by

$$\begin{aligned} \nabla ^2\psi ^*=-\rho _e/\varepsilon , \end{aligned}$$

(7)

in which $\varepsilon$ is the medium permittivity. For a symmetric electrolyte ($\varsigma : \varsigma$), the density of net ionic charge can be represented as $\rho _e=e\varsigma (n^+ - n^-)$. One may now write from the modified Boltzmann distribution while considering steric influence on ionic densities, as

$$\begin{aligned} n^\pm =\frac{n_0 \exp (\mp e\varsigma \psi ^*/k_bT_a)}{1+2\wp (\cosh (e\varsigma \psi ^*/k_bT_a)-1)}, \end{aligned}$$

(8)

$n_0$ being the bulk ionic concentration, e the charge of an electron, $\varsigma$ the ionic valency, $k_b$ the Boltzmann constant and $T_{a}$ the absolute temperature of the system. In cylindrical coordinate system, the term $\displaystyle \frac{1}{r^{*2}}\frac{\partial ^2\psi ^*}{\partial \varphi ^2}$ appearing in the expansion of the Laplacian of Eq.(7) can be neglected for angular symmetry. Using Eq.(8) in Eq.(7), the Poisson equation (7) for a long microtube, $(i.e., L\gg R^*)$, reduces to

$$\begin{aligned} \frac{1}{r}\frac{\partial }{\partial r}\Bigg (r\frac{\partial \psi }{\partial r}\Bigg )=\frac{\lambda ^2~\sinh (\psi )}{1+4\wp \sinh ^2(\psi /2)}, \end{aligned}$$

(9)

where $r=r^*/R^*$, $\psi =e\varsigma \psi ^*/k_bT_a$, $\lambda =R^*/\lambda _D$ in which $\lambda _D=(\varepsilon k_b T_a/2n_o e^2\varsigma ^2)^{1/2}$ denotes the Debye length. The zeta potential $(\zeta ^*)$ on the microtube’s surfaces is assumed to be uniform. Therefore, the corresponding boundary conditions for Eq.(9) can be put in a cylindrical coordinate system as

$$\begin{aligned} \frac{\partial \psi }{\partial r}=0~~~\text{ at }~~~r=0~~~\text{ and }~~~\psi =\zeta ~~~\text{ at }~~~r=1, \end{aligned}$$

(10)

$\zeta =e\varsigma \zeta ^*/k_bT_a$ being the non-dimensional zeta potential on the surface layer of the microtube. It’s worth noting that when the zeta potential on the surface of the microtube is sufficiently small, i.e., $|e\varsigma \psi ^*|<|k_bT_a|$, the steric impact may be ignored. In such a case, $\wp =0$ and one may utilize the highly celebrated Debye–Hückel approximation $(\sinh (\psi )\approx \psi )$ in Eq. (9). With these assumptions, electrical potential can be analytically estimated as $\psi =\zeta I_0(\lambda r)/I_0(\lambda )$, where $I_0$ is the zeroth-order modified Bessel function of the first kind. This finding is identical to Bhattacharjee and De’s [44] recent findings. However, to keep the scope of this study as broad as possible, an appropriate numerical approach has been utilized to derive a substantial solution of the boundary value problem given by Eqs. (9–10), that goes beyond such approximations and limits.

3.3 Characterization of flow and temperature

The microtube containing an incompressible and viscous electrolytic solution is assumed to be long enough so that it is sufficient to analyze the flow that is fully developed at the central portion of the microtube. For fully developed flow, the motion of fluid particles governed by the momentum Eq. (2) becomes steady at each section of the microtube and will not vary over time. For Reynolds number of small magnitude, the transport phenomena is supposed to take place unidirectionally with $u_z^*(r^*)$ representing the velocity along z-direction. As a result, for the sake of this analysis, the flow velocity along the radial and azimuthal directions can be neglected, i.e., $u_r^*\approx 0,u_\varphi ^*\approx 0$. From this point of view, the flow controlling Navier–Stokes equation (2) can be represented for a cylindrical coordinate system as (cf. [45])

$$\begin{aligned} -\frac{\partial p^*}{\partial z^*}+\frac{1}{r^*}\frac{\partial }{\partial r^*}\Bigg (\mu _{nf} r^*\frac{\partial u_z^*}{\partial r^*}\Bigg )=-\rho _e E_z \mp g(\rho \beta )_{nf} T. \end{aligned}$$

(11)

No-slip boundary conditions are known to be ineffective for physiological fluid flow in capillaries, arteries and heart valves, thin films and rarefied fluid motion. When a dilute concentration of particles passes through a capillary tube, it forms a thin film along the capillary’s surfaces as observed by Thompson and Troian [46]. In light of these factors, the velocity-slip conditions on the microtube’s surface, as well as the symmetric condition at the microtube’s central line, must be addressed in order to solve the current problem. Mathematically,

$$\begin{aligned} \frac{\partial u_z^*}{\partial r^*}=0 ~~\text{ at }~~r^*=0~~ \text{ and } ~~ u_z^*+l^*\frac{\partial u_z^*}{\partial r^*}=0~~~~\text{ at }~~~~r^*= R^*. \end{aligned}$$

(12)

This boundary condition is termed as the Navier slip boundary condition. In (12), $l^*$ represents the slip length. It’s worth noting that, for non-appearance of slip length, i.e., $l^*=0$, the Navier slip condition reduces to the well-known no-slip boundary condition, while for slip length values that are substantially bigger, i.e., $l^*\rightarrow \infty$, it yields the surface truncation boundary condition. Another important goal of this work is to investigate the heat transfer mechanism connected with electrohydrodynamic flow within the microtube. For this, Eq. (3) for thermal energy transmission may be reformulated for the cylindrical coordinate system using the aforementioned assumptions as (cf. [35])

$$\begin{aligned}&-\Bigg [\Bigg (k_{nf}+\frac{16 \sigma ^*}{3k^*}T^3\bigg )\frac{1}{r^*}\frac{\partial }{\partial r^*}\Bigg (r^*\frac{\partial T}{\partial r^*}\Bigg )+\frac{16\sigma ^*}{k^*}T^2\Bigg (\frac{\partial T}{\partial r^*}\Bigg )^2\Bigg ] \nonumber\\&\quad=\quad \frac{\sigma _{nf} E_z^2}{\cosh (\psi )}\Bigg [1+4\wp \sinh ^2\Bigg (\frac{\psi }{2}\Bigg )\Bigg ]+\mu _{nf}\Bigg (\frac{\partial u_z^*}{\partial r^*}\Bigg )^2. \end{aligned}$$

(13)

Appropriate boundary conditions need to be used for the energy equation since the heat transport takes place in presence of thermoradiative heat source. For this, the heat transmission mechanism has been investigated under the purview of convective-radiative boundary condition at the solid surface of the microtube, which goes beyond the typical constant wall temperature/thermal leap at solid surfaces. As a result, for Eq. (13), the relevant boundary conditions are

$$\begin{aligned} \frac{\partial T}{\partial r^*}=0~~\text{ at }~~r^*=0~~\text{ and }~~k_{nf}\frac{\partial T}{\partial r^*}=-(h_f T+\epsilon \sigma ^*T^4)~~\text{ at }~~r^*= R^*, \end{aligned}$$

(14)

where the convective heat transfer coefficient and microtube surface emissivities are represented by $h_f$ and $\epsilon$, respectively. Helmholtz–Smoluchowski velocity $u_s=-\varepsilon \zeta ^*E_z/\mu _f$ and classical non-dimensional temperature $\Theta =T/T_s$ are now being introduced in order to obtain the dimensionless representations of Eqs. (11) and (13) as

$$\begin{aligned}&\Gamma +\frac{\mu _{nf}}{\mu _f}\frac{1}{r}\frac{\partial }{\partial r}\Bigg (r\frac{\partial u_z}{\partial r}\Bigg )=-\frac{\lambda ^2}{\zeta }\frac{\sinh (\psi )}{1+4\wp \sinh ^2(\psi /2)} \mp \frac{(\rho \beta )_{nf}}{(\rho \beta )_{f}} Gr \Theta , \end{aligned}$$

(15)

$$\begin{aligned}& -\frac{k_{nf}}{k_f}\Bigg [(1+Rd\Theta ^3)\frac{1}{r}\frac{\partial }{\partial r}\Bigg (r\frac{\partial \Theta }{\partial r}\Bigg )+3Rd\Theta ^2\Bigg (\frac{\partial \Theta }{\partial r}\Bigg )^2\Bigg ]\nonumber \\&\quad =\frac{\sigma _{nf}}{\sigma _f}\frac{S}{\cosh (\psi )}\Bigg [1+4\wp \sinh ^2\Bigg (\frac{\psi }{2}\Bigg )\Bigg ]+\frac{\mu _{nf}}{\mu _f}Br\Bigg (\frac{\partial u}{\partial r}\Bigg )^2, \end{aligned}$$

(16)

while the respective boundary conditions (12) and (14) take the form

$$\begin{aligned}&\frac{\partial u_z}{\partial r}=0~~\text{ at }~~r=0~~\text{ and }~~u_z+l\frac{\partial u_z}{\partial r}=0~~\text{ at }~~r=1, \end{aligned}$$

(17)

$$\begin{aligned}&\quad \frac{\partial \Theta }{\partial r}=0~~\text{ at }~~r=0~~\text{ and }~~\frac{k_{nf}}{k_f}\frac{\partial \Theta }{\partial r}=-(Bi ~\Theta +Nr~\Theta ^4)~~\text{ at }~~r=1, \end{aligned}$$

(18)

where $\Gamma$ is the scale ratio of pressure-driven flow velocity and electrokinetic velocity within the microtube, Gr the Grashof number, Rd the thermal radiation parameter, S the Joule heating parameter, Br the Brinkman number, l the non-dimensional velocity slip parameter, Bi the Biot number and Nr the conduction-radiation parameter. All of the symbols stated above have unique mathematical form, which is listed below.

$$\begin{aligned}&u_z=\frac{u_z^*}{u_s},~~\Gamma =-\frac{\partial p}{\partial z}\frac{R^{*2}}{\mu _f u_s},~u_s=-\frac{\varepsilon \zeta ^*E_z}{\mu _f},~Gr=\frac{(\rho \beta )_f g T_s R^{*2}}{\mu _f u_s},~Rd=\frac{16\sigma ^*T_s^3}{3k^*k_f},\nonumber \\& ~S=\frac{\sigma _f E_z^2R^{*2}}{kT_s},~Br=\frac{\mu _f u_s^2}{k_f T_s},~Bi=\frac{h_f R^*}{k_f},~Nr=\frac{\epsilon \sigma ^*T_s^3R^*}{k_f}~\text{ and }~l=\frac{l^*}{R^*}. \end{aligned}$$

(19)

It is difficult to find a precise solution of Eqs. (9), (15), and (16) subject to respective boundary conditions since they are inextricably linked and nonlinear. Consequently, in the preceding section, an iterative numerical method was designed to evaluate a numerical solution of the dimensionless unidirectional velocity profile $(u_z)$ and temperature distribution $(\Theta )$.

3.4 Average velocity and skin friction coefficient

After obtaining the axial velocity distribution, the average velocity $u_ a$ normalized by $u_s$ [43] may be calculated by evaluating the integral provided by

$$\begin{aligned} u_a=\frac{\int\limits_0^{2\pi }\int\limits_0^{R^*} u_z^*r^*dr^*d\varphi ^*}{\pi R^{*2}}=2\int\limits_0^1u_z r dr. \end{aligned}$$

(20)

One of the main properties of fluid flow is the analysis of shear stress at the microtube’s surface. Owing to this, the dimensionless shear stress in terms of friction coefficient may be expressed as

$$\begin{aligned} C_f=\frac{R^*}{\mu _f u_s}\tau _{r^*z^*}\Bigg |_{r^*=R^*}=-\frac{\mu _{nf}}{\mu _f}\frac{\partial u_z}{\partial r}\Bigg |_{r=1}. \end{aligned}$$

(21)

3.5 Performance of heat transfer

Some certain physical values that are critical for heat transfer analysis, such as the Nusselt number and bulk mean temperature [47], are now being calculated. Nusselt number for heated surface of microfluidic tube may be written as

$$\begin{aligned} Nu=\frac{2R^*}{k_{nf}}\frac{q_w}{T|_{r^*=R^*}-T_m}, \end{aligned}$$

(22)

where $\displaystyle T_m=\int\limits_0^{2\pi }\int\limits_{0}^{R^*}u_z^*T r^*dr^*d\varphi ^*\Bigg /\int\limits_0^{2\pi }\int\limits_{0}^{R^*} u_z^*r^*dr^*d\varphi ^*$ represents the bulk mean temperature/average temperature of the nanofluid flowing in the microtube and $\displaystyle q_w=-\Big (k_{nf}+\frac{16\sigma ^\star T^3}{3k^\star }\Big )\frac{dT}{dr^*}\Big |_{r^*=R^*}$ the wall heat flux. Now, in terms of the above-mentioned dimensionless variables, the Nusselt number can be expressed as

$$\begin{aligned} Nu=-\frac{2}{k_{nf}/k_f}\frac{\frac{k_{nf}}{k_f}+Rd\Theta ^3\Bigg |_{r=1}}{\Theta |_{r=1}-\Theta _m}\frac{\partial \Theta }{\partial r}\Bigg |_{r=1}, \end{aligned}$$

(23)

in which $\displaystyle \Theta _m=T_m/T_s=\int\limits_{0}^{1}u_z \Theta r dr\bigg/\int\limits_{0}^1 u_z r dr$ is the non-dimensional bulk mean temperature.

3.6 Entropy generation analysis

Entropy generation study using the second law of thermodynamics is of another concern of this investigation, because it determines the efficiency of the thermodynamical system under consideration (for details cf. [32, 33, 48]). Such an analysis helps in determining the thermodynamic state of a system. With the help of entropy measurement, one can know whether the process is reversible, irriversible, or even possible in the first place. Analysis of entropy generation in thermodynamics, fluid mechanics, heat transfer, helps to establish the relationships between the physical configuration and the entropy generation [49]. Specifically, the ultimate goal is to minimize the entropy generation within a system in order to determine the optimal operating conditions of the system under consideration. The following equation may be used to calculate the volumetric rate of local entropy formation (cf.[50]):

$$\begin{aligned} \text{ S}_G^*=(k_{nf}{} \mathbf{\nabla }{T}-\mathbf{q})\cdot \frac{\nabla { T}}{ T^2}+\frac{2n_0\sigma _{nf}}{{T}}\frac{\mathbf{E}\cdot \mathbf{E}}{n^++n^-}+\frac{\mu _{nf}({\varvec{\tau }}\cdot \mathbf{\nabla U})}{{ T}}, \end{aligned}$$

(24)

where S$_{G}^{*}$ reflects the rate at which local volumetric entropy is generated per unit volume. Utilizing the aforementioned assumptions for unidirectional flow through long microtube, Eq. (24) may be represented as follows

$$\begin{aligned} \text{ S}_G^*=\text{ S}_T^*+\text{ S}_J^*+\text{ S}_F^*, \end{aligned}$$

(25)

where

$$\begin{aligned}&\text{ S}_T^*=\frac{1}{T^2}\Bigg [\Bigg (k_{nf}+\frac{16\sigma ^*T^3}{3k^*}\Bigg )\Bigg (\frac{\partial T}{\partial r^*}\Bigg )^2\Bigg ],~~~~~~\text{ S}_J^*=\frac{\sigma _{nf}}{T}\frac{E_{z}^2}{\cosh (\psi )}\Bigg [1+4\wp \sinh ^2\Bigg (\frac{\psi }{2}\Bigg )\Bigg ]\nonumber \\&\quad \text{ and }~~~~~~\text{ S}_F^*=\frac{\mu _{nf}}{T}\Bigg (\frac{\partial u_z^*}{\partial r^*}\Bigg )^2, \end{aligned}$$

in which S$_{T}^*$, S$_{J}^*$ and S$_{F}^*,$ respectively, denotes irreversibilities due to the heat transfer, Joule heating and the fluid flow. In non-dimensional form, Eq. (25) may be rewritten as

$$\begin{aligned}\text{ S}_G&=\frac{\text{ S}_G^*}{\text{ S}_G^o}=\frac{1}{ \Theta ^2}\Bigg [\Bigg (\frac{k_{nf}}{k_f}+Rd\Theta ^3\Bigg )\Bigg (\frac{\partial \Theta }{\partial r}\Bigg )^2\nonumber \\&\quad\quad+\frac{\sigma _{nf}}{\sigma _f}\frac{S}{\Theta ~ \cosh (\psi )}\Bigg [1+4\wp \sinh ^2\Bigg (\frac{\psi }{2}\Bigg )\Bigg ]+\frac{\mu _{nf}}{\mu _f}\frac{Br}{\Theta }\Bigg (\frac{\partial u_z}{\partial r}\Bigg )^2, \end{aligned}$$

(26)

where $S_G^*$ is normalized by entropy generation rate $S_G^0(=k_f/R^{*2})$. The average entropy generation $(S_G^m)$ can be obtained without sacrificing generality of the analysis by integrating Eq. (26) throughout the whole circumference of the circular cylindrical microtube, i.e.,

$$\begin{aligned} S_G^m=\frac{1}{\pi r^{*2}}\int\limits_0^{2\pi }\int\limits_0^{R^*} S_G^*r^*dr^*d\varphi ^*. \end{aligned}$$

(27)

The Bejan number is the ratio of heat transfer irreversibility to the total system irreversibility (cf.[51]), which can also be used to measure the thermal irreversibility of the system. Mathematically,

$$\begin{aligned} \text{ Be }=\frac{\text{ S}_T^*}{\text{ S}_G^*}=\frac{\text{ S}_G^{-1}}{\Theta ^2}\Bigg [\Bigg (\frac{k_{nf}}{k_f}+Rd~\Theta ^3\Bigg )\Bigg (\frac{\partial \Theta }{\partial r}\Bigg )^2\Bigg ]. \end{aligned}$$

(28)

Similarly, the average Bejan number (Be$_{m})$ over the microtube is

$$\begin{aligned} \text{ Be}_m=\frac{1}{\pi r^{*2}}\int\limits_0^{2\pi }\int\limits_0^{R^*} \text{ Be }~ r^*dr^*d\varphi ^*. \end{aligned}$$

(29)

The Bejan number, usually denoted by Be, for this problem might range from 0 to 1. Net irreversibility of the system is controlled by joint irreversibilities caused by the Joule heating and fluid friction when Be=0, whereas it is dominated solely by heat transmission irreversibility when Be=1. Also, Be=1/2 if the heat transfer contribution is equal to the composite contribution of Joule heating and fluid friction to the entropy production within the system. In conclusion,

$$\begin{aligned} \text{ Be } = {\left\{ \begin{array}{ll} 0 &{} \text {if }\text{ S}_J^*+ \text{ S}_F^*= \text{ S}_G^*\\ 1/2 &{} \text {if }\text{ S}_J^*+ \text{ S}_F^*= \text{ S}_T^*\\ 1 &{} \text {if }\text{ S}_J^*+ \text{ S}_F^*= 0. \end{array}\right. } \end{aligned}$$

4 Numerical approach to solve nonlinear coupled equations

A strongly coupled nonlinear system is represented by the multi-variable Eqs. (9), (15), and (16) subject to the respective boundary conditions. As a result, finding accurate solutions to these equations is difficult. In this section, an iterative numerical technique has been constructed in order to get considerable numerical solutions. To begin, Newton’s linearization technique has been utilized to linearize all of the dimensionless governing equations, and then solutions for the electrical potential $\psi$, axial velocity $u_z$, and temperature $\Theta$ are obtained numerically with the help of an iterative process involving finite difference method (FDM) followed by the tri-diagonal matrix algorithm (TDMA) (for detail c.f.[48, 52]). Eqs. (9), (15), and (16) can be rearranged in the following form using Newton’s linearization approach as

$$\begin{aligned} A_1^i\Bigg (\frac{\partial ^2 \psi }{\partial r^2}\Bigg )^{i+1}+A_2^i\Bigg (\frac{\partial \psi }{\partial r}\Bigg )^{i+1}+A_3^i \psi ^{i+1}&=A_4^i,\nonumber \\ B_1^i\Bigg (\frac{\partial ^2 u_z}{\partial r^2}\Bigg )^{i+1}+B_2^i\Bigg (\frac{\partial u_z}{\partial r}\Bigg )^{i+1}+B_3^i u_z^{i+1}&=B_4^i,\nonumber \\ C_1^i\Bigg (\frac{\partial ^2 \Theta }{\partial r^2}\Bigg )^{i+1}+C_2^i\Bigg (\frac{\partial \Theta }{\partial r}\Bigg )^{i+1}+C_3^i \Theta ^{i+1}&=C_4^i, \end{aligned}$$

(30)

subject to the boundary conditions

$$\begin{aligned}&\Bigg (\frac{\partial \psi }{\partial r}\Bigg )^{i+1}\Bigg |_{r=0}=0,~~(\psi )^{i+1}\Big |_{r=1}=\zeta ,\nonumber \\&\quad \Bigg (\frac{\partial u_z}{\partial r}\Bigg )^{i+1}\Bigg |_{r=0}=0,~~(u_z)^{i+1}+l\Bigg (\frac{\partial u_z}{\partial r}\Bigg )^{i+1}\Bigg |_{r=1}=0,\nonumber \\&\quad \Bigg (\frac{\partial \Theta }{\partial r}\Bigg )^{i+1}\Bigg |_{r=0}=0,~~D_1^i(\Theta )^{i+1}+\frac{k_{nf}}{k_f}\Bigg (\frac{\partial \Theta }{\partial r}\Bigg )^{i+1}\Bigg |_{r=1}=0. \end{aligned}$$

(31)

The terms involving the superscript $(i+1)$ in the above set of equations are determined during the current iteration by utilizing the known quantities associated with the superscript i that were evaluated in the previous iteration. Coefficients that appeared in the system of Eqs. (30) and (31) are listed below.

$$\begin{aligned}A_1^i&=1,~A_2^i=\frac{1}{r^i},~A_3^i=-\frac{\lambda ^2}{\zeta }\frac{ \sinh (\psi ^i)/\psi ^i}{[1+4\wp \sinh ^2(\psi ^i/2)]},~A_4^i=0,\\ B_1^i&=\frac{\mu _{nf}}{\mu _f},~B_2^i=\frac{\mu _{nf}/\mu _f}{r^i},~B_3^i=0,~B_4^i=-\Bigg (\Gamma +\frac{\lambda ^2}{\zeta }\frac{\sinh (\psi ^i)}{[1+4\wp \sinh ^2(\psi ^i/2)]}\pm \frac{(\rho \beta )_{nf}}{(\rho \beta )_{f}}Gr~\Theta ^i\Bigg ),\\ C_1^i&=-\frac{k_{nf}}{k_f}\Big (1+Rd[\Theta ^3]^i\Big ),~~~~C_2^i=-\frac{k_{nf}}{k_f}\Bigg (\frac{(1+Rd[\Theta ^3]^i)}{r^i}+3Rd[\Theta ^2]^i\Bigg [\frac{\partial \Theta }{\partial r}\Bigg ]^i\Bigg ),~~~~C_3^i=0,\\ C_4^i&=\frac{\sigma _{nf}}{\sigma _f}\frac{S}{\cosh (\psi ^i)}\Bigg [1+4\wp \sinh ^2\Bigg (\frac{\psi ^i}{2}\Bigg )\Bigg ]+ \frac{\mu _{nf}}{\mu _f}Br\Bigg [\Bigg (\frac{\partial u_z}{\partial r}\Bigg )^2\Bigg ]^i,~~~~D_1^i=\Big (Bi+Nr[\Theta ^3]^i\Big ). \end{aligned}$$

Using a second-order central finite difference approach, the system (30) was discretized for r-derivatives. Forward differences were used to discretize boundary conditions at the microtube’s central line (i.e., at $r=0$), whereas backward differences were used to discretize boundary conditions at the solid surface (i.e., at $r=1$). A consistent grid size of $\Delta r=1/(r_{\max }-1)$ has been utilized for repeated computations, where $r_{\max }$ is the number of grid points that are uniformly spaced along the coordinate axis. At each iterative step, the set of Eqs.(30) reduces to a set of linear algebraic equations whose coefficient matrix is of the tri-diagonal matrix form. The block matrices have now been solved using the tri-diagonal matrix method. In a nutshell, the basic framework of the whole numerical technique is as follows.

• Initial distributions have been assigned to all profiles under consideration at the computational domain’s inner grid points, as well as boundary points.

• In order to obtain an updated estimate of electrical potential $\psi (r)$, the first equation of the system (30) has been solved.

• A new estimate for $u_z(r)$ from the second equation of the system (30) has been derived considering $\psi$ to be known.

• Electrothermal solution for $\Theta (r)$ was evaluated using the known values of $\psi (r)$ and $u_z(r)$ from the rearmost equation of the system (30).

The estimating process is repeated until the amount of the related error between any two successive computations is less than $10^{-6}$. As a consequence, the following mathematical expression may be used to define the convergence requirement for the current numerical computation:

$$\begin{aligned} \max \Bigg \{\Big |\psi ^{i+1}(r)-\psi ^{i}(r)\Big |,\Big |u_z^{i+1}(r)-u_z^{i}(r)\Big |,\Big |\Theta ^{i+1}(r)-\Theta ^{i}(r)\Big |\Bigg \}\le 10^{-6}. \end{aligned}$$

(32)

After determining the requisite potential, velocity, and temperature distributions, the Nusselt number, local entropy, and Bejan number may be estimated adopting the mathematical expressions provided in Eqs. (23), (26), and (28), in that order. Using the Cavalieri–Simpson method for numerical integration, the average velocity, entropy, Bejan number, and bulk mean temperature were also analyzed.

5 Results and discussion

The preceding section dealt with the deduction of a mathematical expression for the axial velocity, temperature and entropy production in the system. Meticulously sought out findings of this investigation will now culminate with the study of the influences of different dimensionless parameters on the velocity, temperature and entropy for blood flow through microcirculatory systems.

5.1 Parameter estimation

Keeping focus on the numerical computation, values of various physical parameters which are ubiquitous in the present investigation, as presented in Table 2. Physical properties of the working fluid (Blood) are enlisted in Table 3.

Table 2 Typical values of physical parameters [1, 2, 53, 54]

Table 3 Properties of base fluid and nanoparticle [55, 56]

5.2 Validation of results

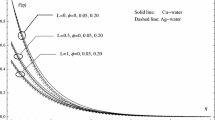
For the purpose of validation, the results of the present investigation have been compared with those of a study (Ref. [53]) reported earlier. Here, two extreme cases have been considered, viz. (i) the flow driven by the pressure assisting force and (ii) the flow subjected to pressure opposing force. Xie et al. [53] studied the flow of heat during electroosmotic flow in a cylindrical microchannel under the magnetic environment. Comparison of axial velocity for the current investigation with the results reported by [53] are performed for the limiting case $\wp =0,~ Gr=0,~Rd=0, ~l=0,~ \phi =0,~ Bi=0,~Nr=0$ and presented in Fig. 2 (smooth line). To bring both the studies into the same platform for better comparison, the values of zeta potential and electroosmotic parameter can be taken as $\zeta =1$ and $\lambda =10$. Further, the effect of external magnetic body force reported in [53] was neglected by putting $Ha\rightarrow 0$ and $S=0$. In light of all of the above, the analytical result of velocity profile reported by [53] has been graphically presented in Fig. 2 (dotted points). It is worth noting that the outcomes of both the study match to an agreeable extent which provides a satisfactory validation of the present numerical solution.

Fig. 2

Comparison of the current findings to those presented in [53], when $\zeta =1,~\lambda =10,~\wp =0,~ Gr=0, ~l=0,~ \phi =0,~Rd=0, Bi=0,~Nr=0.$

5.3 Velocity distribution

Figure 3 depicts the variation of normalized velocity profile $u_z$ with the dimensionless transversal coordinate r at different steric parameters $\wp =0,0.1,0.3$, keeping all others parameters fixed which is mentioned in the figure. The Debye–Hückel parameter $\lambda$ is fixed at 10 which confirms that the electric double layer (EDL) will be developed at the close vicinity of the channel walls and most of the portion of the microtube will remain outside the EDL region. The extreme case ($\wp =0$) which corresponds to the absence of the steric parameter has also been considered. Figure 3 also shows that the steric parameter greatly effects the normalized velocity profile. Figure 4 presents the change in the velocity distribution for various values of the Grashof number. Evidently, with an increase in the value of the Grashof number, velocity of the nanofluid rises. More precisely, the centre-line and boundary line velocities of fluid particles increase approximately by $3.6\%$ and $2.1\%,$ respectively, when the values of Grashof number shift from $-1$ to 1.

Fig. 3

Influence of steric factor on velocity

Fig. 4

Influence of Grashof number on velocity

Fig. 5

Influence of velocity slip parameter on velocity

Fig. 6

Influence of surface zeta potential on velocity

The velocity increases as the hydrophobicity of the microtube surface increases, as seen in Fig. 5. However, the velocity at the vicinity of the microtube axis largely remains unaffected by the velocity-slip. Further, the slip effect is large near the surface of the microtube. From the physical perspective, the fluid particles get detached due to the enhancement in the slip length thereby causing an increase in their kinetic energy which results in a significant rise in the nanofluid velocity. Figure 6 depicts the velocity distribution for different magnitudes of zeta potential $(\zeta )$. It has been revealed that when the surface potential is low $(\zeta =1)$, the velocity is maximum and thereafter, the velocity profile drastically falls with an increase in the strength of the applied surface zeta potential. Furthermore, it should be noted that the sharp decrease in the axial velocity occurs precisely when $\zeta$ lies in the range between 1 and 2. Also, the rate of decrease in the velocity gradually reduces with an increase in the magnitude of zeta potential. To be more specific, for example, when $\Gamma =1,\phi =0.01, \wp =0.3,\lambda =10,\nu =0.1,l=0.01, Br=0.01, S=0.5, Gr=1, Rd=1,Bi=0.01,Nr=1$, the velocity of the core region of the microtube decreases approximately by $47.35\%$ as $\zeta$ increases from 1 to 3. According to the electric double-layer principle, counter-ions in close proximity to the microtube would be attracted due to the presence of powerful electrostatic forces. Hence, higher surface potential will result in the absorption of the counter-ions by the hydrophobic surfaces of the microtube and the fluid movements are less impacted by the presence of static electric field. Consequently, the axial velocity is diminished for higher magnitude of surface potential.

5.4 Temperature distribution and heat transfer

The effects of Joule heating on temperature distribution on the passage of electric current through the mircotube whereby the electrical conductor gets affected as a whole are depicted in Fig. 7.

Fig. 7

Influence of Joule heating on temperature

Fig. 8

Influence of thermal radiation on temperature

The depiction shows a uniform rise in the fluid temperature with an increase in the Joule heating effect. It is also worth mentioning that the fluid temperature varies negatively during heat absorption $(S<0)$ and positively during the heat generation $(S>0)$ as well as in the absence of Joule heating. Specifically, when $\Gamma =1,\phi =0.01, \wp =0.3, \zeta =4, \lambda =10,\nu =0.1,l=0.05, Br=0.01, Gr=2, Rd=1,Bi=0.01,Nr=1$, the temperature distribution at the core of the microtube reduces approximately by $140\%$ while the system undergoes transition from heat generation $(S=0.5)$ to absorption $(S=-0.5)$ by the Joule heating.

Fig. 9

Influence of Biot number on temperature

Fig. 10

Influence of conduction-radiation parameter on temperature

The temperature profile is also found to be parabolic. The observations from Fig. 7 yield the fact that the temperature in the microfluidic tube is highly influenced by Joule heating. Figure 8 gives us some idea on the variation of thermal distribution occurring because of the thermal radiation parameter. It is also seen that the fluid temperature in the microtube reduces rapidly during heat generation, when the parameter associated with thermal radiation has been strengthened in presence of nonlinear thermal radiation. Figure 9 illustrates the change in temperature distribution with corresponding change in the Biot number. One may note here that the minor changes in the magnitude of Biot number lead to the higher reduction of the thermal distribution. It can be noticed from Fig. 10 that the presence of conduction-radiation parameter decreases the temperature of the nanofluid. This finding may be interpreted by an increase in the heat transfer rate through the microtube surfaces, which results in a substantial reduction in nanofluid temperature.

Fig. 11

Impact of thermal radiation and Joule heating on Nusselt number

Fig. 12

Impact of Grashof number and Brinkman number on Nusselt number

The transfer of heat through the solid surfaces of the microtube, characterized by the Nusselt number, has been depicted in Figs. 11, 12. In Fig. 11, it has been revealed that Nusselt number increases as heat generates due to Joule heating effect. Due to an adequate input of heat into the system for heat generation case defined by positive values of Joule heating parameter $(S>0)$, the Nusselt number grows when the Joule heating parameter is increased. However, Nusselt number Nu decreases as the thermal radiation parameter increases from $Rd=0$ to $Rd=3$. To be more specific, in particular, for $\Gamma =1,\phi =0.05, \wp =0.4, \zeta =4, \lambda =10,\nu =0.1,l=0.05, Br=0.01, Gr=1, Bi=0.01$ and $Nr=1$, the Nusselt number decreases approximately by $5.5\%$ and $52\%$ as Rd increases from $Rd=0$ to $Rd=3.0$ when $S=0$ and $S=1,$ respectively. Further, Nusselt number exhibits non-continuous behavior for various values of the Brinkman number. From Fig. 12, it is evident that the critical Brinkman numbers $(Br_{cr})$ appear during the heat generation through viscous dissipation process $(Br>0)$ within the system. The critical Brinkman numbers, according to thermodynamic theory, denote the point at which the internal heat created by viscous dissipation effects equalizes the heat flow passing through the surface of the microtube. In particular, at the critical Brinkman number, the mean temperature coincides with the surface temperature. It is also observed that the heat generated through the viscous dissipation causes the Nusselt number to reduce as the Brinkman number rises in the positive direction and thereafter tends to an asymptotic value. It is noteworthy that the critical Brinkman number $Br_{cr}$ gets inclined toward the direction of the positive Brinkman coordinate as the buoyancy effect in the proposed system (characterized by the Grashof number Gr) decreases. For the values of $Gr=-2,~0$ and 2, the critical Brinkman numbers are $Br_{cr}=0.22,~0.27$ and 0.38, respectively, as observed from Fig. 12.

5.5 Entropy generation and Bejan number

The formation of entropy occurs during the transmission of heat in the presence of frictional force, Joule heating, and thermal diffusion in the system under consideration. Because of this, it is necessary to investigate the effects of relevant physical parameters on the generation of entropy. The degree of influence exercised by the variation of Grashof number (Gr) and the thermal radiation parameter (Rd) is illustrated by Figs. 13 and 14. One may observe from Fig. 13 that local entropy generated in the system rises with Grashof number (Gr) in the region of EDL. However, a reverse trend is depicted near the vicinity of the core region of the microtube. It is worthy to emphasize that the critical value of local entropy is observed at $r=0.38$ due to the variation of the Grashof number (Gr). Local entropy generation is more rectilinear in the central portion of the microfluidic tube than near the tube’s surface, where it is more curvilinear in shape. From Fig. 14, it is seen that local entropy enhances uniformly in the presence of nonlinear thermal radiation. Entropy production is considerably larger near the microtube’s edge and grows as the absolute magnitude of the thermal radiation parameter (Rd) increases. This means that the thermal system will perform more efficiently when subjected to the nonlinear thermal radiation effect.

Fig. 13

Impact of Grashof number on local entropy

Fig. 14

Impact of thermal radiation on local entropy

Fig. 15

Impact of Joule heating on local Bejan number

Fig. 16

Impact of Grashof number on local Bejan number

From Figs. 15, 16, one can acquire some inkling of the variation in Bejan number as Joule heating and Grashof number increases. It is intriguing to make a note of the disappearing value of the Bejan number in the central area of the microtube. This observation is an implication to the fact that owing to the effects of electric field and friction between the fluid particles, the thermal irrversibility is inconsequential. Further, one can also notice from Fig. 15, that rise in the external Joule heating causes an enhancement in thermal irreversibility in the EDL region, whereas Fig. 16 shows a steady rate of decrease in Bejan number in the microtube for higher values of Grashof number. Additionally, it is noticed that the thermal irreversibility is at its peak at the electric double-layer region, and in the central region it is at its lowest.

Fig. 17

Impact of Joule heating and nanoparticle volume fraction on global entropy

Fig. 18

Impact of conduction-radiation parameter and thermal radiation on global Bejan number

Figure 17 reveals the effects of Joule heating and nanoparticle volume fraction on the average entropy production in the bulk fluid. Increase in nanoparticle volume fraction related to more heat transfer effect in the system under consideration results in reduction of the irreversibilities leading to decreasing entropy generation as observed in Fig. 17. Due to the reduction of irreversibilities, a thermal system with a higher nanoparticle volume fraction will function more effectively. Global entropy production drops significantly when it varies with the Joule heating parameter, and eventually reaches an asymptotic value. Thus, no contribution of both Joule heating and nanoparticle volume fraction effect is seen at initial stage and beyond $S\approx 0.4$. Individual contribution of thermal radiation and conduction-radiation parameter to the distribution of global Bejan number is revealed in Fig. 18. Obviously, as nonlinear thermoradiative effect increases, Bejan number reduces uniformly. In particular, for $\Gamma =1, \phi =0.05, \zeta =4, \wp =0.5, \lambda =10, \nu =0.1, l=0.05, S=0.5, Gr=1$ and $Bi=Br=0.001$, the global entropy Be$_{m}$ reduces approximately by $3.6\%$ when the thermal radiation parameter Rd increases from $Rd=0$ to $Rd=1$ in absence of conduction-radiation parameter Nr and the percentage of entropy minimization increases approximately by $2\%$ when $Nr=3$. However, the heat transfer between the wall and fluid by means of conduction-radiation effect increases the global Bejan number. Thus, the global irreversibility of the system alters under thermal radiation and conduction-radiation effects which helps to determine the optimal parametric values in order to maintain entropy minimization for better efficiency of the system.

6 Concluding remarks

The work examines the fully developed mixed convection nanofluid flow in a hydrophobic microtube under the combined impact of an electric field and nonlinear thermal radiation. The second law of thermodynamics was used to determine the efficacy of the designed thermal system. Going beyond the traditional Debye–Hückel approximation, steric effect has been considered for the electrical potential distribution. Present study was designed to explore the effect of nonlinear thermal radiation on heat transfer and entropy formation during electroosmotically modulated nanofluid flow. The nonlinear and coupled governing equations are put in its dimensionless form after introducing suitable non-dimensional variables and then solved numerically by developing an iterative numerical scheme. The observations so far made from the investigation has led us to the following conclusions.

• The steric effect suppresses velocity in the EDL, and a reversal of this tendency is observed in the microtube’s core region.

• Fluid flow in the microtube increases with the augmentation of buoyancy forces.

• Presence of nonlinear thermal radiation can reduce the fluid temperature.

• Characteristics of fluid temperature alters during heat generation/absorption by means of Joule heating effect. In particular, the temperature at the core region of the microtube decreases approximately by $140\%$ as S changes from 0.5 to $-0.5$.

• Nusselt number shows an asymptotic behavior due to internal heat generation by viscous dissipation.

• Quantum of entropy generation increases due to buoyancy effect in the EDL regions much more and a critical value is observed near the core region $(r=0.38)$ of the microtube.

• Combined influence of Joule heating and fluid friction on the irreversibility of the system coincides with the total irreversibility at the core region of the microtube.

• At a higher percentile of nanoparticle volume fraction, the system will function more effectively under thermal radiation effect. A unit magnitude increase in radiation parameter leads to approximately $3.6\%$ reduction in the global entropy of the system.