1 Introduction

The FCC-ee can produce the Higgs boson directly in the s-channel, e\(^+\)e\(^- \rightarrow H\), in a dedicated run at \(\sim \)125 GeV center-of-mass (c.m.) energy [1, 2]. A measurement of the electron Yukawa coupling is possible by reducing the center-of-mass energy spread, e.g., making it comparable to the width of the standard model Higgs boson itself, \(\Gamma _H \approx \) 4.2 MeV [3]. Since the Higgs resonance is narrow, the integrated luminosity required to generate a certain number of Higgs bosons varies roughly in proportion to the effective energy spread, which explains the interest in monochromatization.

The natural collision-energy spread at 125 GeV, due to synchrotron radiation, is about 50 MeV. In standard FCC-ee running conditions, it blows up further due to beamstrahlung by another factor of two, or so. The energy spread can be reduced, by up to an order of magnitude, by means of monochromatization [4,5,6,7,8,9,10,11,12,13,14,15,16,17], e.g., through introducing nonzero horizontal dispersion of opposite sign at the interaction point (IP), for the two colliding beams.

Such nonzero IP dispersion leads to a significant increase in the horizontal emittance due to beamstrahlung, i.e., synchrotron radiation emittance in the field of the opposing bunch during the collision. At the same time, thanks to the much increased horizontal beam size, the beam energy spread and bunch length return to their natural values attained without collision. This effect alone already decreases the collision energy spread. An additional reduction comes about from colliding particles with exactly opposite energy deviations, thanks to the opposite sign of IP dispersion. Self-consistent IP parameters need to be determined and optimized for maximum sensitivity to the Yukawa coupling. Modifications of the standard final-focus optics are required for generating the required IP dispersion and for the possible accommodation of crab cavities [13, 18]. A recently proposed approach is to introduce a correlation between the local collision energy and the transverse or longitudinal location inside the detector [A. Blondel, private communication, 2020]. This would profit from the anticipated superb detector resolution and allow for a continuous scanning of the Higgs resonance curve. Such a scenario can be realized simply by omitting (or turning off) the crab cavities, which corresponds to a monochromatization scenario already considered in Ref. [16].

2 FCC-ee monochromatization schemes

Introducing IP dispersion of opposite sign for the two colliding beams reduces the rms spread \(\sigma _{W}\) in the center-of-mass energy \(W=2 E_{\mathrm{b}}\) as \( \left( \sigma _{ w}/W \right) _{\mathrm{m.c.}} =\sigma _{\delta }/(\sqrt{2}\lambda ) \), by the monochromatization (m.c.) factor \( \lambda = \left( {D_{x}^{*}}^2 \sigma _{\delta }^{2}/(\varepsilon _{x}\beta _{x}^{*})+1\right) ^{1/2} \), where \(\sigma _{\delta }\equiv \sigma _{E_{\mathrm{b}}}/E_{\mathrm{b}}\) denotes the relative beam energy spread (which for ultra-relativistic beams is equal to the relative momentum spread), \(E_{\mathrm{b}}\) the beam energy, \(\beta _{x}^{*}\) the horizontal beta function at the IP, \(D_{x}^{*}\) the horizontal IP dispersion function, and \(\varepsilon _{x}\) the horizontal emittance.

In the definition of \(\lambda \), we may take \(\sigma _{E_{\mathrm{b}}}\) to mean the energy spread without collision so that \(\sigma _{\delta } = \sigma _{\delta ,\mathrm{SR}}\), where \(\sigma _{\delta ,\mathrm{SR}}\) denotes the natural relative momentum spread due to synchrotron radiation in the collider arcs. Alternatively, we may also wish to take into account the additional beneficial effect that monochromatization avoids the blow up of the relative rms beam energy spread to a larger value of \(\sigma _{\delta ,\mathrm{coll}}\) due to the additional contribution from beamstrahlung, which is significant in collisions with zero IP dispersion (subindex \(D^{*}=0\)). To this end, we introduce the effective monochromatization factor \(\lambda _\mathrm{eff}\), that compares the true collision energy spread without and with monochromatization (subindex m.c.) \( \lambda _{\mathrm{eff}} \equiv \sigma _{W,D^{*}=0}/\sigma _{W,\mathrm{m.c.}} = ( \sigma _{\delta ,\mathrm{coll}}/\sigma _{\delta ,\mathrm{SR}} ) \; ( {D_{x}^{*}}^2 \sigma _{\delta ,\mathrm{SR}}^{2}/(\varepsilon _{x}\beta _{x}^{*})+1 )^{1/2} \). For the examples we consider in this article, \(\lambda _{\mathrm{eff}}\) is more than two times larger than \(\lambda \).

Differently from classical proposals [4,5,6,7,8,9,10,11,12, 15], due to the strong impact of beamstrahlung at the higher beam energy of FCC-ee, it is convenient to introduce dispersion in the horizontal plane. A wide horizontal beam size reduces the beamstrahlung, while preserving a small vertical beam size, which is crucial for attaining a high luminosity. For FCC-ee the dispersion is also created more easily in the horizontal plane than in the vertical, since the beams are crossed and separated in this plane.

The baseline layout of FCC-ee was optimized for operation on the Z-pole resonance, for WW pair production, for ZH running and at the top quark threshold and features a large crossing angle of 30 mrad. A large crossing angle is also required in the possible additional run for s-channel Higgs production, to separate the two beams and feed them into their respective beam pipe, corresponding to the right aperture in the next arc, and to avoid any harmful effects of parasitic collisions.

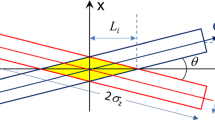
Figure 1 illustrates two monochromatization schemes compatible with the above assumptions. In the first approach, crab cavities are added for both beams on either side of each IP. With an average beta function at the crab cavity of about 2300 m for an IP beta function \(\beta ^{*}\) of 0.1 m, a crab rf frequency \(f_{\mathrm{rf}}\) of 400 MHz and at a full crossing angle \(\theta _c\) of 30 mrad, the crab-cavity voltage required is \(V_{\mathrm{crab}} = (\theta _c/2)(cE_{\mathrm{beam}}/e)/(2\pi f_\mathrm{rf})/\sqrt{\beta _x^{*}\beta _{\mathrm{crab}}} \approx 2\) MV per side of the IP and per beam, to be compared with an HL-LHC crab-cavity voltage of 6 MV. These crab cavities would render the collision effectively head-on, and yield the “optimum” monochromatization, i.e., the smallest possible collision energy spread, for a given value of IP dispersion. In the second approach, the crab cavities are omitted. The combination of large crossing angle and nonzero IP dispersion then leads to a correlation between collision energy and longitudinal position, as indicated in the bottom picture of Fig. 1.

Fig. 1
figure 1

FCC-ee monochromatization scheme featuring interaction-point dispersion of opposite sign for the two colliding beams, with (top), or without crab crossing and integrated resonance scan, as first sketched in Ref. [16] (bottom). Different colors schematically indicate bunch portions with slightly different energies

Full size image

3 Generating IP dispersion

The nonzero dispersion at the IP, \(D_{x}^{*}\), as required for monochromatization, can be generated by a set of (additional or stronger) dipole magnets in the final focus. The nominal final-focus optics was designed such that the critical energy of synchrotron-radiation photons emitted from the dipoles up to 500 m upstream of the IP was below 100 keV at the \(\mathrm{t}\bar{\mathrm{t}}\) running mode [19]. For the direct Higgs production mode, the beam energy is about 2.9 times lower, and the dipole fields can be 25 times stronger, while still complying with the same limit on the critical photon energy. For example, one could insert, or excite, a dipole at a horizontal betatron phase advance of about 90\(^{\circ }\) from the IP, and another dipole, with opposite sign, at 270\(^{\circ }\). This introduces a chicane-like structure, that might still fit inside the same tunnel as the baseline beam line. Generalizations to more than two dipoles are straightforward and provide more flexibility. Approximating the dipoles as thin lenses with integrated deflection angles \(\theta _{i}\), and using Transport notation [20] for the R and T matrix elements between dipole i and the IP, in case of \(N_{\mathrm{dip}}\) dipoles, the following conditions must be met:

$$\begin{aligned} \sum _{i=1}^{N_{\mathrm{dip}}} (T_{126,i} - R_{12,i})\theta _i = D_{x}^{*} \quad \mathrm{and } \quad \sum _{i=1}^{N_{\mathrm{dip}}} (T_{226,i} - R_{22,i})\theta _i = {D'}_{x}^{*} {\mathop {=}\limits ^{!}} 0 . \end{aligned}$$
(1)

With more than two dipoles (\(N_{\mathrm{dip}}>2\)), we could further add geometrical beam-line constraints.

4 Emittance

With zero IP dispersion, beamstrahlung increases energy spread and bunch length. Instead, for the case of monochromatization the horizontal emittance increases, roughly as

$$\begin{aligned} \varepsilon _{x,\mathrm{tot}} = \varepsilon _{x,\mathrm{SR}} + \Delta \varepsilon _{x,\mathrm{BS}} , \end{aligned}$$
(2)

while the energy spread returns to the natural value \(\sigma _{\delta ,\mathrm{SR}}\approx 0.0715\%\), as determined by synchrotron radiation in the arcs alone. The horizontal emittance growth due to beamstrahlung \(\Delta \varepsilon _{x,\mathrm{BS}}\) is proportional to \({D_{x}^{*}}^2/\beta _{x}^{*}\). From the simulation results of Ref. [21], we can infer the approximate relation \(\Delta \varepsilon _{x,\mathrm{BS}} \approx C {D_{x}^{*}}^2/\beta _{x}^{*} \) with \(C\approx 1.8\times 10^{-9}/0.11\), which yields the reported growth of \(\Delta \varepsilon _{x,\mathrm{BS}}\approx 1.8\) nm for \({D_{x}^{*}}^2/\beta _{x}^{*}=(0.1624^2/0.24)\;\mathrm{m}\approx 0.11\) m.

It is expected that the FCC-ee detector resolution in radial and longitudinal direction is of order \(\Delta \approx 3\) \(\upmu \)m. Choosing, for example, the betatron beam size equal to 5 times this resolution \(\sqrt{\beta _{x}^{*}\varepsilon _{x}}=5\Delta \approx 15\) \(\upmu \)m, we may require the natural dispersive beam size to be another factor of 3.5 larger again, so that \(\lambda \ge 3.5\), referring to the natural energy spread from arc synchrotron radiation, or \(\lambda _{\mathrm{eff}} \ge 9\) comparing with the collision energy spread including beamstrahlung at \(D_{x}^{*}=0\). This yields the minimum required IP dispersion as \(D_{x}\ge 0.105\) m, and the corresponding IP beta function as \(\beta _{x}^{*}=(25 \Delta ^{2} -\beta _{x}^{*} \Delta \varepsilon _{x,\mathrm{BS}})/\varepsilon _{x,\mathrm{SR}}=9\) cm.

If the above approximate relation were strictly true, the IP dispersion required to achieve a certain \(\lambda \) would be \(D_{x}^{*}=\lambda \sigma _{x}^{*}/(\sigma _{\delta }^2-\lambda ^2 C)^{1/2}\), and the maximum possible monochromatization parameter \(\lambda _{\mathrm{max}}\approx \sigma _{\delta }/C^{1/2} \approx \) 4—the reason why, for our example, we chose a value of 3.5, which is close to this limit. More detailed calculations of the emittance growth due to beamstrahlung [21, 22] show that a value of up to about \(\lambda \approx 8\) can be reached (see Fig. 2).

5 Performance optimization

Searching for an optimal point in parameter space, for \(\beta _{y}^{*}\) we adopt the design value of 1 mm [19]. Given \(\beta _{y}^{*}\), and choosing a desired value of \(\lambda \) for fixed values of horizontal emittance and momentum spread, we introduce two scan parameters S, related to the horizontal beam size, and T, connected to the bunch intensity. Namely, we transform \(\beta _{x}^{*}\) and \(D_{x}^{*}\) with parameter S [18], so as to keep \(\lambda \) without beamstrahlung fixed, namely \(D_x^{*} = S \times D_{x,0}^{*}\), starting from an initial value \(D_{x,0}^{*} = 0.22\) m, and \(\beta _x^{*} = S^2 \times \beta _{x,0}^{*}\), starting from \(\beta _{x,0}^{*} = 1.0\) m. The second scan parameter T [18] changes the number of bunches as \(n_b = n_{b,0} \times T\) and the bunch population as \(N_b = N_{b,0} / T\), where the values with subindex 0 denote the initial values for our optimization procedure. The transformation is defined such that, when varying T, the product \(n_{b} N_{b}\) is held constant, as the total beam current is limited by the arc synchrotron radiation. The second transformation would lead to a scaling of the luminosity L as \(L \propto T^{-1}\) in the absence of beamstrahlung and if the beam-beam tune shift could increase without any constraint.

The initial values are chosen so as to correspond to a certain value of \(\lambda \), where \(\lambda \) is computed without the effect of beamstrahlung [18]. Including the effects of beamstrahlung, the actual monochromatization factor is reduced and no longer constant in the (S, T) parameter space.

Figure 2 illustrates the maximum luminosity as a function of the monochromatization factor \(\lambda \), as obtained by our optimization, for the two scenarios. Each point corresponds to the result of one two-dimensional scan in the S–T plane for fixed initial values of \(\lambda \) and \(\varepsilon _{y}\). The two scenarios, with and without crab cavities, lead to nearly identical results. This is expected, as with the natural energy spread and blow up horizontal emittance the Piwinski angle \(\Phi \equiv \theta _{c}\sigma _{z}/(2\sigma _{x}^{*})\) is much smaller than one.

Different assumptions for the vertical emittance can be made, e.g., one could assume a constant emittance ratio \(\varepsilon _{y}/\varepsilon _{x}\), or one could consider that the limitation on the vertical emittance is set by the available diagnostics and tuning procedure, so that the vertical emittance is constant, equal to 1 pm, or a nearby value, independently of the horizontal emittance. In Fig. 2, we are making this latter assumption. The various colored markers or curves correspond to slightly different (constant) values of the vertical emittance, as indicated.

Fig. 2
figure 2

Optimal luminosity per IP as a function of \(\lambda \) for a constant vertical emittance between 1.6 and 2.4 pm (the five different curves), with crab cavities [21] (top) or without them (bottom), considering a total of two IPs

Full size image

Figure 3 (top picture) presents the FCC-ee design luminosity in standard operation mode as a function of center-of-mass energy \(E_{\mathrm{c.m.}}\), a fit to these working points revealing the dependence \(L\propto E^{-3.5}\), and the extrapolated performance at the Higgs-mass energy of 125 GeV—without monochromatization—of about \(7.6\times 10^{35}\) cm\(^{-2}\)s\(^{-1}\). This point serves as a reference. The bottom picture of Fig. 3 shows the luminosity at 125 GeV as a function of energy spread and compares the reference point with the values achieved by either of the two monochromatization approaches.

Fig. 3
figure 3

FCC-ee luminosity per interaction point as a function of c.m. energy at its four different baseline operating points [blue markers], fitted curve [blue line and legend], and extrapolated luminosity at 125 GeV [red-orange marker] (top) and luminosity as a function of c.m. energy spread for either monochromatization scheme (bottom). Without crab cavities, the c.m. energy spread refers to the effective energy spread at the center of the longitudinal distribution (see Fig. 4, bottom picture). For all cases two IPs are assumed

Full size image
Table 1 Example parameters for monochromatization with an overall c.m. energy spread of \(\sigma _{W}\approx 13\) MeV (with crab crossing) and \(\sim \)25 MeV (without crab cavities, but compare Fig. 4, bottom picture)
Full size table

Table 1 summarizes IP parameters and the expected effective energy spread and luminosity performance for a typical scenario. For the example of Table 1, Fig. 4 (top picture) compares the collision energy spread with and without crab crossing, as obtained from a simulation of a single collision with the code Guinea-Pig [23]. For the Guinea-Pig simulation we assumed the equilibrium beam parameters including the effect of beamstrahlung, which were obtained from the analytical description of [22] and the optimization procedure of Sect. 5. The correlation between collision energy and longitudinal position for the second scenario is evidenced in the bottom picture. The effective rms energy spread over 100 \(\upmu \)m around \(z\approx 0\) is the same as for the scenario with crab cavities.

Fig. 4
figure 4

Centre-of-mass energy distribution with and without crab cavities (top) and correlation between collision energy and longitudinal position (bottom), obtained from the simulation of a beam-beam collision using the code Guinea-Pig [23]

Full size image

Concerning integrated luminosity, following the assumptions laid out in the CDR [2] of 185 physics days per year, with a physics efficiency of 75%, an instantaneous luminosity of \(10^{35}\) cm\(^{-2}\)s\(^{-1}\) would result in 1.2 ab\(^{-1}\)/year/IP, while \(7.6 \times 10^{35}\) cm\(^{-2}\)s\(^{-1}\) would deliver 9.1 ab\(^{-1}\) per year per IP.

For completeness, we further note that a horizontal orbit offset of the two beams at the collision point together with nonzero IP dispersion in the same plane leads to a shift in the center-of-mass collision energy [24]. Considering the case of monochromatization with \(\lambda \gg 1\), the acceptable horizontal beam-beam offset \(\Delta x^{*}\) is limited to \(\Delta x^{*} \le D_x^{*} (\Delta W/W )\), where \((\Delta W/W )\) denotes the desired collision energy uncertainty. The larger the IP dispersion, the more relaxed is this tolerance. The same constraint also follows from Eq. (7.7) in Ref. [25]. As an example, with \((\Delta W/W )\le 10^{-6}\), and \(D_x^{*}\approx 30\) cm, the corresponding tolerance is \(\Delta x^{*}\approx 300\) nm, and, hence, much larger than the offset tolerance in the vertical plane, which is of order 10 nm.

6 Other options

Over the past half a century, several alternative monochromatization scenarios have been proposed, e.g., creating a large dispersion at deflecting-mode radiofrequency cavities located at a betatron phase of approximately \(\pi /2\) away from the IP [15], or generating a nonzero slope of IP dispersion along with a crossing angle [17]. Such alternative approaches along with their possible implementation methods, merits and drawbacks for FCC-ee could be explored in the future.

7 Conclusions

At FCC-ee the monochromatized s-channel Higgs production can be accomplished by operating at a beam energy of 62.5 GeV and introducing a nonzero horizontal dispersion at the collision point. A luminosity of about \(2.5\times 10^{35}\) cm\(^{-2}\)s\(^{-1}\) is expected for an effective center-of-mass energy spread \(\sigma _{W}\) of 13 MeV, compared with close to \(8\times 10^{35}\) cm\(^{-2}\)s\(^{-1}\) at \(\sigma _{W}\approx 115\) MeV without monochromatization. In view of the narrow width of the Higgs resonance, \(\Gamma _H\approx 4.2\) MeV, the former scenario, with monochromatization, will deliver a significantly enhanced rate of Higgs bosons, about 3 times higher, and with a similarly improved signal-to-background ratio. The monochromatized collision scheme works well both with and without crab cavities. In the latter case, the local rms energy spread at the center of the detector is the same, e.g., 13 MeV, but the total rms spread is higher and a resonance scan is automatically performed, since the average collision energy W varies with longitudinal position. Future work will include the optics design and a technical implementation of this collision scheme, compatible with the standard FCC-ee collider layout.