Semileptonic $B_c$ meson decays to S-wave charmonium states

Abstract

We study the semileptonic decays of $B_c$ meson to S-wave charmonium states in the framework of relativistic independent quark model based on an average flavor-independent confining potential U(r) in the scalar–vector harmonic form $U(r)=\frac{1}{2}(1+\gamma ^0)(ar^2+V_0)$, where (a, $V_0$) are the potential parameters. The form factors for $B_c^+\rightarrow \eta _c /\psi e^+\nu _e$ transitions are studied in the physical kinematic range. Our predicted branching ratios (BR) for transitions to ground-state charmonia are found comparatively large $\sim$ $10^{-2}$, compared to those for transitions to radially excited 2S and 3S states. Like all other model predictions, our predicted BR are obtained in the hierarchy: BR($B_c^+\rightarrow \eta _c /\psi (3S)$) < BR($B_c^+\rightarrow \eta _c/ \psi (2S)$) < BR($B_c^+\rightarrow \eta _c /\psi (1S)$). The longitudinal ($\varGamma _L$) and transverse ($\varGamma _T$) polarization for $B_c \rightarrow \psi (ns)$ decay modes is predicted in the small and large $q^2$-region as well as in the whole physical region. Our predicted polarization ratios: $\frac{\varGamma _L}{\varGamma _T} < 1$ for $B_c^+\rightarrow J/\psi e^+\nu _e$ and $B_c^+\rightarrow \psi (2S)e^+\nu _e$ which means these transitions take place predominantly in transverse mode, whereas for $B_c\rightarrow \psi (3S)e\nu _e$, $\varGamma _L$ is comparable with $\varGamma _T$ in the whole physical region. These theoretical predictions could be tested in the LHCb and the forthcoming Super-B experiments.

1 Introduction

Ever since the discovery of $B_c$ meson in the Fermilab by the collider detector (CDF) collaborations [1] in 1998, the experimental probe to detect its family members in their ground and excited states continues over the last two decades. With the observation of $B_c$ meson at the Tevatron [2, 3], a detailed study of $B_c$ family members is expected at the LHC, where the available energy is more and luminosity is much higher. The lifetime of $B_c$ has been measured [4,5,6,7] using decay channels: ${B_c}^{\pm } \rightarrow J/\psi e^{\pm } \nu _e$ and ${B_c}^{\pm } \rightarrow J/\psi \pi ^ {\pm }$. A more precise measurement of $B_c$-lifetime: $\tau _{B_c}=0.51^{+0.18}_{-0.16}(stat.)\pm 0.03(syst.)\;ps$ and its mass: $M =6.40\pm 0.39\pm 0.13\;GeV$ have been obtained [8] using the decay mode $B_c \rightarrow J/\psi \mu \nu _\mu X$, where X denotes any possible additional particle in the final state. The branching fraction for $B_c^+ \rightarrow J/\psi \pi ^+$ relative to that of $B_c^+ \rightarrow J/\psi \mu ^+ \nu _{\mu }$ has been measured by LHCb collaborations yielding [9]:

$$\begin{aligned} \frac{BR (B_c\rightarrow J/\psi \pi ^+)}{BR (B_c\rightarrow J/\psi \mu ^+ \nu _{\mu })} = 0.0469 \pm 0.0028(stat.)\pm 0.0046(syst.) \end{aligned}$$

Recently, ATLAS collaboration at LHC has detected excited $B_c$ state [10] through the channel $B_c^{\pm }(2S) \rightarrow B_c^{\pm }(1S)\pi ^+\pi ^-$ by using 4.9 $fb^{-1}$ of 7 TeV and 19.2 $fb^{-1}$ of 8 TeV pp collision data which yielded $B_c$(2S) meson mass $\sim$ $6842\pm 4\pm 5$ MeV. Although masses of the ground and first excited state of $B_c$ with $J^P = 0^-$ have been measured, it has not yet been possible to detect its higher excited states and even the ground state of $B_c^*$. Hopefully with the available energy and higher luminosity at LHC and at $Z_0$ factory, the event accumulation rate for these undetected states can be enhanced in near future providing scope for detailed studies of $B_c$ and $B_c^*$ counterpart. The recent observed data and possibility of high statistics $B_c$ events expected in upcoming experiments provide the necessary motivation to investigate the semileptonic $B_c$ meson decays to charmonium states which are easier to identify in the experiment.

The $B_c$ meson has aroused a great deal of theoretical interest due to its outstanding features. It is the lowest bound state of two heavy constituent quarks (charm and bottom) with an open (explicit) flavor, unlike the symmetric heavy quarkonium ($b{\bar{b}}, c{\bar{c}}$) states. The charmonium ($c{\bar{c}}$) and bottomonium ($b{\bar{b}}$) with hidden flavors decay via strong and electromagnetic interactions, whereas $B_c$ meson with open flavors decay only via the weak interaction since it lies below the B${\bar{D}}$ threshold. Therefore, it has a comparatively long lifetime and very rich weak decay channels with sizable branching ratios. Thus, $B_c$-meson provides a unique window into heavy quark dynamics and gives scope for an independent test of quantum chromodynamics. The study of semileptonic decays, in particular, is significant because it not only helps in extracting accurate values of the Cabbibo–Kobayashi–Masakawa (CKM) matrix element but also helps in separating the effect of strong interaction from that of weak interaction into a set of Lorentz-invariant form factors. The analysis of semileptonic decays is therefore reduced essentially to the calculation of relevant weak form factors.

Among a large number of theoretical studies on semileptonic $B_c$ decays, some noteworthy ones are: potential models [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], nonrelativistic qurak models [27, 28], relativistic quark models [29,30,31,32,33,34,35], instantaneous nonrelativistic approach to BS equation [36, 37], relativistic quark model on BS approach [38], nonrelativistic QCD [39,40,41,42,43], light-cone QCD sum rule [44,45,46], covariant light-front model [47], light-front quark model constrained by the variational principle for QCD motivated effective Hamiltonian [48], light-front quark model [49], QCD potential model [50,51,52], perturbative QCD approach [53,54,55,56,57], constituent quark model [58,59,60,61,62,63] and Isgur, Scora, Grinstein and Wise (ISGW) model [64]. One would also like to refer to the review paper [65] and references therein. In this paper, we would like to extend the applicability of the relativistic independent quark (RIQ) model [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89] which has already been tested in describing wide-ranging hadronic phenomena including the static properties of hadrons [66,67,68] and various decay processes such as the radiative, weak radiative, rare radiative [69,70,71,72,73,74]; leptonic, weak leptonic, radiative leptonic [75,76,77,78,79,80]; semileptonic [81,82,83] and nonleptonic [84,85,86,87] decays of hadrons in the light and heavy flavor sector. In our previous work on semileptonic $B_c$ meson decays, we consider the participating mesons in their respective ground state only. Given observed $B_c$(2S) states and possible detection of higher $B_c$(nS) states ($n>2$) as well as $B_c^*$ (1S) state at LHC and $Z_0$ factory in the near future, it is worthwhile to predict energetically allowed semileptonic $B_c$ decays to excited charmonium states too. Several theoretical approaches in this direction have appeared in the literature. Being inspired by our recent prediction of magnetic dipole [88] and electromagnetic [89] transitions of $B_c$ and $B_c^*$ mesons in their ground and possible excited states, we extend our previous work [83] to analyze $B_c^+(nS)\rightarrow \eta _c(nS)/\psi (nS) e^+\nu _e$ decays, where the radial quantum numbers $n=1,2,3$. We do not consider here the decay modes with higher 4S charmonia as their properties are not yet understood well.

Here we would like to note a few points that motivate us to undertake this exercise: (1) The relevant form factors representing the weak decay amplitudes are expected to have their $q^2$ dependence (where $q^2$ denotes the four-momentum transfer squared) over the allowed kinematic range. In some of the theoretical approaches cited above, the weak decay form factors and their $q^2$ dependence are determined first with an end point normalization at either $q^2 =0$ or $q^2 = q^2_{max}$ and then using some phenomenological monopole/dipole/Gaussian ansatz, they are extrapolated to the whole physical region. To avoid possible uncertainties in the calculation, we shall not resort to any such phenomenological ansatz and instead study the $q^2$ dependence of relevant form factors in the allowed kinematic range: $0\le \ q^2\le \ (M-m)^2$, where M and m refer to the mass of the parent and daughter meson, respectively. (2) In our previous analysis [81,82,83], two weak form factors $a_+$ and $a_-$ corresponding to $0^-\rightarrow 1^-$ semileptonic transition are found to be equal under a simplifying assumption. On closure scrutiny, it is realized that $a_+$ is not strictly equal to $a_-$. It is not necessary to invoke any kind of simplifying assumption but one can get model expressions for $a_+$ and $a_-$ separately. (3) In this work, we intend to predict the BR for decay channels involving the ground as well as excited charmonia in the final state and compare our results with other model predictions. (4) Finally, we shall update some input hadronic parameters according to the Particle Data Group (PDG) [90] in our calculation.

This paper is organized as follows: In Sect. 2, we provide the general formalism and kinematics of $B_c$ meson semileptonic decays. Section 3 briefly describes the framework of the RIQ model and extraction of model expression for the weak form factors. In Sect. 4, we provide our numerical results and discussion. Section 5 encompasses our summary and conclusion.

2 General formalism and kinematics

The invariant transition matrix element for exclusive semileptonic decays such as $B_c^+ \rightarrow X e^+\nu _e$ is written as [81,82,83, 91,92,93,94]

$$\begin{aligned} {{\mathscr {M}}}={{G_F}\over {\sqrt{2}}}V_{bc}l^{\mu }h_{\mu } \end{aligned}$$

(1)

where X denotes $\eta _c$ or $J/\psi$, $G_F$ is the effective Fermi coupling constant, $V_{bc}$ is the CKM parameter, $l^{\mu }$ and $h_{\mu }$, respectively, are the leptonic and hadronic amplitudes expressed as:

$$\begin{aligned} l^\mu= & {} {{\bar{u}}}_e(\mathbf {p}_1,\delta _1)\gamma ^{\mu }(1-\gamma _5)v_{\nu _e}(\mathbf {p}_2\;, \delta _2), \end{aligned}$$

(2)

$$\begin{aligned} h_{\mu }= & {} \;\langle X(\mathbf {k}, S_X)\mid J^h_{\mu }(0)\mid B_c(\mathbf {p}, S_{B_c})\rangle \end{aligned}$$

(3)

Here $J^h_{\mu }=V_{\mu }-A_{\mu }$ is the vector–axial vector current. We take here (M, m) to be the mass, (p, k) the four-momentum and ($S_{B_c}, S_{X}$) the spin projection of parent and daughter meson, respectively. $q=(p-k)=(p_1+p_2)$ is the four-momentum transfer where ($p_1, p_2$) are four momenta of the lepton pair.

Fig. 1

Coordinate system for the semileptonic decay of $B_c$-meson a decaying virtual W and b decaying final vector meson

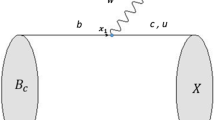
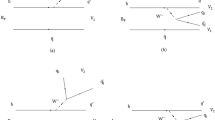
Here we consider two frames of reference: (i) the parent meson rest frame and (ii) the e$\nu _e$ center-of-mass frame. The coordinate system chosen here is such that the daughter meson momentum $\mathbf {k}$ is along the negative Z-axis with the charged lepton momentum $\mathbf {p}_1$ subtending an angle $\theta _e$ to Z-axis (Fig. 1a) in the e$\nu _e$ center-of-mass frame. The Y-axis is oriented perpendicular to the plane containing the final particles’ momenta.

We also introduce here a pair of dimensionless variables (y, x) scaled to the parent meson mass as $y=(q^2/{M}^2)$ and $x=(p_1.p_2/{M}^2)$. Since the Lorentz-invariant quantities like $q^2$ are frame independent, we calculate the minimum value of $q^2$ in the $e\nu _e$ center-of-mass frame and its maximum value in the parent meson rest frame for the sake of convenience. In doing so, the allowed kinematic range of the dimensionless variable y in the vanishing lepton mass limit is found to be:

$$\begin{aligned} 0\le y\le \left( 1-{m\over M}\right) ^2 \end{aligned}$$

(4)

The physical quantities of interest associated with the final state particles are their energy and momentum, which can be calculated in both the frames considered here.

In the e$\nu _e$ center-of-mass frame, they are

$$\begin{aligned} E_1= & {} E_2={M\over 2}{\sqrt{y}} \end{aligned}$$

(5)

$$\begin{aligned} E_X= & {} {M\over {2\sqrt{y}}}\left( 1-{{m^2}\over {M^2}}-y\right) \end{aligned}$$

(6)

$$\begin{aligned} \mid {\mathbf {k}}\mid= & {} K/{\sqrt{y}} \end{aligned}$$

(7)

$$\begin{aligned} K= & {} {M\over 2}\left[ \left( 1-{{m^2}\over {M^2}}-y\right) ^2- 4{{m^2}\over {M^2}}y\right] ^{1/2} \end{aligned}$$

(8)

In the parent meson rest frame, however, the quantities are

$$\begin{aligned} {{\tilde{E}}}_1= & {} Mx = {K\over 2}\cos \theta _e +{M\over 4}\left( 1-{{m^2}\over {M^2}}+y\right) . \end{aligned}$$

(9)

$$\begin{aligned} {{\tilde{E}}}_X= & {} {M\over 2}\left( 1+{{m^2}\over {M^2}}-y\right) \end{aligned}$$

(10)

$$\begin{aligned} \mid {\tilde{\mathbf {k}}}\mid= & {} K \end{aligned}$$

(11)

The hadronic amplitudes are covariantly expanded in terms of the Lorentz-invariant form factors. For a transition of type ($0^- \rightarrow 0^-$), the expansion is

$$\begin{aligned} \langle X(k)\mid V_{\mu }(0)\mid B_c(p)\rangle= & {} f_+(q^2)(p+k)_{\mu }\nonumber \\&+f_-(q^2)(p-k)_{\mu } \end{aligned}$$

(12)

For $(0^-\rightarrow 1^-)$-type transitions, they are

$$\begin{aligned}&\langle X(k,\epsilon ^*)\mid V_{\mu }(0)\mid B_c(p)\rangle = ig(q^2)\in _{\mu \nu \rho \sigma }\epsilon ^{*\nu } \times (p+k)^{\rho }(p-k)^{\sigma } \end{aligned}$$

(13)

$$\begin{aligned}&\langle X(k,\epsilon ^*)\mid A_{\mu }(0)\mid B_c(p)\rangle = f(q^2)\epsilon ^*_{\mu }\nonumber \\&\quad + a_+(q^2)(\epsilon ^*.p)(p+k)_{\mu }-a_-(q^2)(\epsilon ^*.p)(p-k)_{\mu } \end{aligned}$$

(14)

Here $\epsilon ^*\equiv (\epsilon ^*_0,\mathbf {\varvec{\epsilon }^*})$ with $\epsilon ^*.k=0$, represents the vector meson polarization.

The differential decay rate is written in the generic form

$$\begin{aligned} d\varGamma =\frac{1}{2E_{B_c}}\sum _{\delta _1,\delta _2,\lambda }|{{\mathscr {M}}}|^2d\varPi _3 \end{aligned}$$

(15)

where the three-body phase space factor is

$$\begin{aligned} d\varPi _3= & {} (2\pi )^4\delta ^{(4)}(p-p_1-p_2-k)\nonumber \\&\times \frac{d^3\mathbf {k}}{(2\pi )^32E_X} \frac{d^3\mathbf {p}_1}{(2\pi )^32E_1}\frac{d^3\mathbf {p}_2}{(2\pi )^32E_2} \end{aligned}$$

(16)

and the invariant transition amplitude squared is given by

$$\begin{aligned} \sum _{\delta _1, \delta _2, \lambda }|{{\mathscr {M}}}|^2=\frac{G_F^2}{2} |V_{bc}|^2l^{\mu \sigma }h_{\mu \sigma } \end{aligned}$$

(17)

We write $l^{\mu \sigma }=\sum _{\delta _1,\delta _2}(l^\mu {l^\sigma }^\dagger )$ with a sum over lepton spin indices ($\delta _1, \delta _2$) and also $h_{\mu \sigma }=\sum _{\lambda }(h_\mu h_\sigma ^\dagger )$ with a sum over daughter meson (vector) polarization index $\lambda$.

It is convenient to calculate the Lorentz-invariant leptonic piece $l^{\mu \sigma }$ obtained in the form:

$$\begin{aligned} l^{\mu \sigma }=8\Biggl [(p_1^\mu p_2^\sigma - p_1.p_2 g^{\mu \sigma }+ p_1^\sigma p_2^\mu )+i\epsilon ^{\mu \alpha \sigma \beta }p_1^{\alpha }p_2^{\beta }\Biggr ] \end{aligned}$$

(18)

in the e$\nu _e$ center-of-mass frame. Since its timelike component $l^{00}$ is zero in the vanishing lepton mass limit, the nonvanishing contribution to ${{\mathscr {M}}}$ comes from the product $l^{ij}h_{ij}$ only. Then, integration of $l^{ij}$ over the lepton phase space in the e$\nu _e$ center-of-mass frame yields:

$$\begin{aligned} \int \int \frac{d^3{\mathbf {p}}_1}{2E_1}\frac{d^3{\mathbf {p}}_2}{2E_2}\;l^{ij}\; \delta ^{(4)}(p-p_1-p_2-k)=\frac{4\pi }{3}\;q^2\;\delta ^{ij} \end{aligned}$$

(19)

Then, the expression of the differential decay rate in the e$\nu _e$ center-of-mass frame is reduced to:

$$\begin{aligned} d{{\bar{\varGamma }}}=\frac{1}{(2\pi )^5}\frac{1}{2E_{B_c}}\frac{G_F^2}{2} |V_{bc}|^2\frac{d^3\mathbf {k}}{2E_X}\frac{4\pi }{3}q^2\sum _\lambda h_{ii} \end{aligned}$$

(20)

It is worthwhile to note here that the hadronic amplitude ‘$h_i$’ can be expressed, in this frame, in a simple and convenient form as the terms involving the form factors $f_-(q^2)$ and $a_-(q^2)$ do not contribute to $\mathbf {h}$ on transitions of the type ($0^- \rightarrow 0^-$) and ($0^- \rightarrow 1^-$), respectively. For ($0^- \rightarrow 0^-$)-type transitions, one obtains $h_i$ (12) in terms of a single form factor $f_+(q^2)$ as

$$\begin{aligned} \mathbf {h} =(\mathbf {p}+\mathbf {k} )f_+(q^2) \end{aligned}$$

(21)

Similarly, for transitions of type $(0^-\rightarrow 1^-)$, we obtain $\mathbf {h}$ from Eqs. (13) and (14) as

$$\begin{aligned} \mathbf {h}=2i{\sqrt{y}}Mg(q^2)({\mathbf {\epsilon }}\;^*\times \mathbf {k})-f(q^2) {\mathbf {\epsilon }}\;^*-2(\epsilon ^*.p)a_+(q^2)\mathbf {k} \end{aligned}$$

(22)

To calculate the hadronic amplitude, it is more convenient to use helicity amplitudes, which are linearly related to the invariant form factors [81,82,83, 91,92,93,94]. We, therefore, expand $\mathbf {h}$ in terms of helicity basis (effectively of the virtual W) as

$$\begin{aligned} \mathbf {h}={{\mathscr {H}}}_+{{\hat{e}}}_++{{\mathscr {H}}}_-{{\hat{e}}}_-+{{\mathscr {H}}}_0{{\hat{e}}}_0 \end{aligned}$$

(23)

with

$$\begin{aligned} {{\hat{e}}}_{\pm }={1\over {\sqrt{2}}}(\mp {{\hat{x}}}-i{{\hat{y}}});\; {{\hat{e}}}_0={{\hat{z}}} \end{aligned}$$

(24)

The polarization vector ${\hat{\epsilon }}^*$ with the polar and azimuthal angle $(\theta ^*,\phi ^*)$ in the vector meson helicity frame (Fig. 1b) can be Lorentz-transformed to the (e$\nu _e$) center-of-mass frame to be obtained in the form:

$$\begin{aligned} {{\hat{\epsilon }}}^*={1\over {\sqrt{2}}}\sin \theta ^*e^{i\phi ^*}{{\hat{e}}}_+ -{1\over {\sqrt{2}}}\sin \theta ^*e^{-i\phi ^*}{{\hat{e}}}_- -{{E_X}\over {M_X}}\cos \theta ^*{{\hat{e}}}_0 \end{aligned}$$

(25)

Then expanding $h_i$ in terms of helicity basis (23, 24) and using the Lorentz-transformed form of ${\hat{\epsilon }}^{\star }$ (25), one can obtain the helicity amplitudes ${{\mathscr {H}}}_{\pm }$ and ${{\mathscr {H}}}_0$ from Eq. (22) as

$$\begin{aligned} {{\mathscr {H}}}_{\pm }= & {} \mp \frac{sin\theta ^*}{\sqrt{2}}e^{\pm i\phi ^*}{\bar{ H}}_{\pm } \end{aligned}$$

(26)

$$\begin{aligned} {{\mathscr {H}}}_0= & {} cos\theta ^*{\bar{H}}_0 \end{aligned}$$

(27)

where ${{\bar{H}}}_{\pm }$ and ${{\bar{H}}}_0$ are reduced helicity amplitudes. For ($0^- \rightarrow 1^-$)-type semileptonic transitions, these reduced helicity amplitudes are obtained in terms of invariant form factors f, g and $a_+$ as

$$\begin{aligned} {{\bar{H}}}_{\pm }= & {} [\; f(q^2)\mp 2MKg(q^2)\; ], \end{aligned}$$

(28)

$$\begin{aligned} {{\bar{H}}}_0= & {} {M\over {2m\sqrt{y}}}\left[ \left( 1-{{m^2}\over {M^2}}-y\right) f(q^2) +4K^2a_+(q^2)\right] . \end{aligned}$$

(29)

Now $h_{ii}=\sum _{\lambda }h_ih_i^\dagger$ in Eq. (20) can be expressed in terms of reduced helicity amplitudes (28, 29). Then, integration over the polar and azimuthal angles ($\theta ^*, \phi ^*$) and sum over the daughter meson (vector) polarization yield an invariant expression for the differential decay rate. Once obtained in an invariant form, it is then convenient to cast in any frame (here the parent meson rest-frame) to get the final expression of the differential decay rate as:

$$\begin{aligned} {{\mathrm{d}{{\tilde{\varGamma }}}}\over {\mathrm{d}y}}=\frac{1}{96\pi ^3}{G_F}^2\mid V_{bc}\mid ^2M^2Ky \;[\;\mid {{\bar{H}}}_+\mid ^2+\mid {{\bar{H}}}_-\mid ^2+\mid {{\bar{H}}}_0\mid ^2\;] \end{aligned}$$

(30)

Here the contribution of $\mid {{\bar{H}}}_0\mid ^2$ term to the differential decay rate (30) refers to the longitudinal mode and that of the combined term $[\;\mid {{\bar{H}}}_+\mid ^2+\mid {{\bar{H}}}_-\mid ^2\;]$ refers to the transverse polarization mode for the semileptonic transitions of the type ($0^- \rightarrow 1^-$). However, in the case of ($0^- \rightarrow 0^-$)-type transitions, one can realize corresponding expressions by appropriately identifying

$$\begin{aligned} {\bar{H}}_{\pm }=0;\;\;{\bar{H}}_0=-2{K\over {\sqrt{y}}}f_+(q^2) \end{aligned}$$

(31)

which leads to the differential decay rate in parent meson rest frame as

$$\begin{aligned} {{\mathrm{d}{{\tilde{\varGamma }}}}\over {\mathrm{d}y}}={{{G_F}^2\mid V_{bc}\mid ^2K^3M^2}\over {24\pi ^3}} \mid f_+(q^2)\mid ^2 \end{aligned}$$

(32)

3 Transition matrix element and weak form factors

The decay process physically occurs between the momentum eigenstates of participating mesons. Therefore, in a field theoretic description, the meson states are represented by their appropriate momentum wave packets reflecting the momentum and spin distribution between constituent quark and antiquark inside the meson core. In the RIQ model, the appropriate wave packet representing the meson state $|B_c(\mathbf {p},S_{B_c})\rangle$ is considered at definite momentum $\mathbf {p}$ and spin state $S_{B_c}$ as [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89]

$$\begin{aligned} |B_c(\mathbf {p}, S_{B_c})\rangle ={{\hat{\varLambda }}(\mathbf {p},S_{B_c})}|(\mathbf {p}_{b},\lambda _b);(\mathbf {p}_{c},\lambda _c) \rangle \end{aligned}$$

(33)

where $|(\mathbf {p}_{b},\lambda _b);(\mathbf {p}_{c},\lambda _c)\rangle = {\hat{b}}_{b}^\dagger (\mathbf {p}_{b},\lambda _b) {\hat{\tilde{b}}}_{c}^\dagger (\mathbf {p}_{c},\lambda _{c})|0 \rangle$ is a Fock space representation of the unbound quark and antiquark in a color-singlet configuration with their respective momentum and spin as $(\mathbf {p}_{b},\lambda _{b})$ and $(\mathbf {p}_{c},\lambda _{c})$. Here ${\hat{b}}_{b}^\dagger (\mathbf {p}_{b},\lambda _{b})$ and ${\hat{\tilde{b}}}_{c}^\dagger (\mathbf {p}_{c},\lambda _{c})$ are, respectively, the quark and antiquark creation operators. ${{\hat{\varLambda }}}(\mathbf {p},S_{B_c})$ represents an integral operator:

$$\begin{aligned} {{\hat{\varLambda }}}(\mathbf {p},S_{B_c})= & {} \frac{\sqrt{3}}{\sqrt{N(\mathbf {p})}}\; \sum _{{\delta _b},{\delta _{{\bar{c}}}}}\zeta _{bc}^{B_c}(\lambda _{b},\lambda _{c})\nonumber \\&\times \int d^3{\mathbf {p}}_{b}\;d^3{\mathbf {p}}_{c}\;\delta ^{(3)}(\mathbf {p}_{b}+\mathbf {p}_{c}-\mathbf {p}) {{\mathscr {G}}}_{B_c}(\mathbf {p}_{b},\mathbf {p}_{c}) \end{aligned}$$

(34)

Here $\sqrt{3}$ is the effective color factor, $\zeta ^{B_c}(\lambda _{b},\lambda _{c})$ stands for SU-(6) spin flavor coefficients for the $B_c$ meson. $N(\mathbf {p})$ is the meson-state normalization which is realized from $\langle {B_c}(\mathbf {p})\mid {B_c}({\mathbf {p}}\;^{\prime })\rangle =\delta ^{(3)}(\mathbf {p}-{\mathbf {p}}\;^{\prime })$ in an integral form

$$\begin{aligned} N(\mathbf {p})=\int d^3{\mathbf {p}}_{b}\;\mid {{\mathscr {G}}}_{B_c}({\mathbf {p}}_{b},\mathbf {p}-{\mathbf {p}}_{b})\mid ^{2} \end{aligned}$$

(35)

Finally, ${{\mathscr {G}}}_{B_c}({\mathbf {p}_{b}}, \mathbf {p} - \mathbf {p}_{b})$ is the effective momentum profile function for the quark-antiquark pair. In terms of individual momentum probability amplitudes ${G}_{b}(\mathbf {p}_{b})$ and ${G}_{c}(\mathbf {p}_{c})$ of the constituent quark b and c, respectively, ${{\mathscr {G}}}_{B_c}({\mathbf {p}_{b}}, \mathbf {p} - \mathbf {p}_{b})$ is taken in this model in the form:

$$\begin{aligned} {{\mathscr {G}}}_{B_c}({\mathbf {p}_{b}},{\mathbf {p}_{c}})=\sqrt{G_{b}(\mathbf {p}_{b}){{\tilde{G}}}_{c}(\mathbf {p}_{c})} \end{aligned}$$

(36)

in a straightforward extension of the ansatz of Margolis and Mendel in their bag model analysis [95]. A brief account of the model framework and quark orbitals derivable in the RIQ model along with those of the corresponding momentum probability amplitudes are given in “Appendix.” In the wave packet representation of meson bound state

$|B_c(\mathbf {p},S_{B_c})\rangle$, the bound-state character is embedded in the effective momentum distribution function ${{\mathscr {G}}}_{B_c}({\mathbf {p}_{b}}, \mathbf {p}_{c})$. Any residual internal dynamics responsible for decay process can therefore be described at the level of otherwise free quark and antiquark using appropriate Feynman diagram shown in Fig. 2. The total contribution from the Feynman diagram provides the constituent level S-matrix element $S_{fi}^{bc}$ which when operated by the baglike operator gives the meson level effective S-matrix element $S_{fi}^{B_c}$ as:

$$\begin{aligned} S_{fi}^{B_c} = {{\hat{\varLambda }}} S_{fi}^{bc} \end{aligned}$$

(37)

Fig. 2

Semileptonic decay of $B_c$ meson

3.1 Transition amplitude

The S-matrix element for the decay process $B_c^{+} \rightarrow X e^+\nu _e$ depicted in Fig. 2 can be written in the general form:

$$\begin{aligned} S^{B_c}_{fi}= & {} -i\frac{G_F V^*_{bc}}{\sqrt{2} (2\pi )^4}\int d^4{x_1}d^4{x_2}d^4 qe^{-iq(x_2 - x_1)}\nonumber \\&\times \langle e^+(\mathbf {p}_{1})\nu _e(\mathbf {p}_{2})X(\mathbf {k}, S_X)|J^{\mu }_l(x_2)J^{h}_\mu (x_1)|B_c(\mathbf {p}, S_{B_c})\rangle \end{aligned}$$

(38)

where the matrix element corresponding to leptonic weak current is found as

$$\begin{aligned}&\langle e^+(\mathbf {p}_{1})\nu _e(\mathbf {p}_{2})|j^{\mu }_l(x_2)|0 \rangle&= \frac{e^{i(\mathbf {p}_1 + \mathbf {p}_2)x_2}}{\sqrt{(2\pi )^3 2E_1(2\pi )^32E_{2}}} l^{\mu } \end{aligned}$$

(39)

with $l^{\mu }={{\bar{u}}}_e(\mathbf {p}_1, \delta _1)\gamma ^{\mu }(1-\gamma _5)v_{\nu _e} (\mathbf {p}_2, \delta _2)$

Using the appropriate wave packet representation (33) of the parent and daughter meson, the hadronic amplitude $h_\mu$ can be obtained in a straightforward manner. From the contribution of leptonic and hadronic amplitudes, the S-matrix element for the decay process is cast in the standard form:

$$\begin{aligned} S^{B_c}_{fi}= & {} (2\pi )^4\delta ^{(4)}(p-k-p_1-p_2)(-i{{\mathscr {M}}}_{fi})\nonumber \\&\times \frac{1}{\sqrt{{(2\pi )^3} 2E_{B_c}}}\prod _f\left( \frac{1}{\sqrt{2E_f {(2\pi )^3}}}\right) \end{aligned}$$

(40)

Here the hadronic part $h_\mu$ of the invariant transition amplitude ${{\mathscr {M}}}_{fi}$ is obtained in the parent meson rest frame in the form

$$\begin{aligned} {h_\mu }= & {} \frac{\sqrt{4ME_X}}{\sqrt{N_{B_c}(0)N_X(\mathbf {k})}} \times \int \frac{d^3\mathbf {p}_{b}}{\sqrt{2E_{\mathbf {p}_{b}}2E_{\mathbf {k}+\mathbf {p}_{b}}}}\nonumber \\&\times \,{{\mathscr {G}}}_{B_c}(\mathbf {p}_{b},-\mathbf {p}_{b}){{\mathscr {G}}}_X (\mathbf {k}+\mathbf {p}_{b}, -\mathbf {p}_{b}) \langle S_X|J^h_\mu (0)|S_{B_c} \rangle \end{aligned}$$

(41)

where $E_{\mathbf {p}_{b}}$ and $E_{\mathbf {p}_{b}+\mathbf {k}}$ stand for the energy of non-spectator quark of the parent and daughter meson, respectively, and $\langle S_X|{J_\mu }{^h}(0)|S_{B_c} \rangle$ represents symbolically the spin matrix elements of the vector–axial vector current.

3.2 Weak decay form factors

To extract model expression of weak decay form factors, the covariant expansion of the hadronic decay amplitudes [12,13,14,15,16,17,18,19,20,21] is compared with corresponding model expressions. For $0^-\rightarrow 0^-$ transitions, the axial vector current does not contribute. Simplifying the nonvanishing vector current parts, the spin matrix elements are obtained in the form:

$$\begin{aligned} \langle S_X(\mathbf {k})|V_0|S_{B_c}(0)\rangle= & {} \frac{(E_{\mathbf {p}_b+\mathbf {k}}+ m_c)(E_{\mathbf {p}_b}+m_b)+\mathbf {p}_b\;^2}{\sqrt{(E_{\mathbf {p}_b+\mathbf {k}}+m_c) (E_{\mathbf {p}_b}+m_b)}} \end{aligned}$$

(42)

$$\begin{aligned} \langle S_X(\mathbf {k})|V_i|S_{B_c}(0)\rangle= & {} \frac{(E_{\mathbf {p}_b}+m_b)k_i}{\sqrt{(E_{\mathbf {p}_b+\mathbf {k}}+m_c)(E_{\mathbf {p}_b}+m_b)}} \end{aligned}$$

(43)

The form factor $f_+(q^2)$ for $0^- \rightarrow 0^-$ type transitions is thus found in the form:

$$\begin{aligned} f_+=\frac{1}{2M}\int d\mathbf {p}_{b} {{\mathscr {C}}}(\mathbf {p}_{b})\left[ (E_{p_b}+m_b) (E_{\mathbf {p}_{b}+\mathbf {k}}+m_c+M-{E_X}) +\mathbf {p}_{b}^2\right] \end{aligned}$$

(44)

where

$$\begin{aligned} {{\mathscr {C}}}(\mathbf {p}_{b})= & {} \sqrt{\frac{M{E_X}}{N_{B_c}(0)N_X(\mathbf {k})}}\nonumber \\&\times \frac{{{\mathscr {G}}}_{B_c}(\mathbf {p}_{b}, -\mathbf {p}_{b}) {{\mathscr {G}}}_X(\mathbf {k}+\mathbf {p}_{b}, -\mathbf {p}_{b})}{\sqrt{E_{\mathbf {p}_{b}}E_{\mathbf {p}_{b}+\mathbf {k}}(E_{\mathbf {p}_{b}}+m_b)(E_{\mathbf {p}_{b}+\mathbf {k}}+m_c)}} \end{aligned}$$

(45)

However, for $(0^- \rightarrow 1^-)$ transitions, the spin matrix element for vector and axial vector current are obtained separately as:

$$\begin{aligned}&\langle S_X(\mathbf {k}, {{\hat{\epsilon }}^*})|V_0|S_{B_c}(0)\rangle =0 \end{aligned}$$

(46)

$$\begin{aligned}&\langle S_X(\mathbf {k},{{\hat{\epsilon }}^*})|V_i|S_{B_c}(0)\rangle =\frac{i(E_{\mathbf {p}_{b}}+m_b)({{\hat{\epsilon }}^*}\times \mathbf {k})_i}{\sqrt{(E_{\mathbf {p}_{b}}+m_b)(E_{\mathbf {p}_{b}+\mathbf {k}}+m_c)}} \end{aligned}$$

(47)

$$\begin{aligned}&\langle S_X(\mathbf {k}, {{\hat{\epsilon }}^*})|A_i|S_{B_c}(0)\rangle \nonumber \\&\quad =\frac{[(E_{\mathbf {p}_{b}}+m_b)(E_{\mathbf {p}_{b}+\mathbf {k}}+m_c)-\mathbf {p}_{b}\;^2/3]\epsilon ^*_i}{\sqrt{(E_{\mathbf {p}_{b}}+m_b)(E_{{p_b}+\mathbf {k}}+m_c)}} \end{aligned}$$

(48)

$$\begin{aligned}&\langle S_X(\mathbf {k},{{\hat{\epsilon }}^*})|A_0|S_{B_c}(0)\rangle = \frac{-(E_{\mathbf {p}_{b}+m_b})({{\hat{\epsilon }}^*}.\mathbf {k})}{\sqrt{(E_{\mathbf {p}_{b}}+m_b)(E_{\mathbf {p}_{b}+\mathbf {k}}+m_c)}} \end{aligned}$$

(49)

A term-by-term comparison of results in Eqs. (47) and (48) with corresponding expressions from Eqs. (13) and (14) yields the form factor $g(q^2)$ and $f(q^2)$ in the form:

$$\begin{aligned} g= & {} -\frac{1}{2M}\int d\mathbf {p}_{b}{{\mathscr {C}}} (\mathbf {p}_{b})(E_{\mathbf {p}_{b}}+m_b) \end{aligned}$$

(50)

$$\begin{aligned} f= & {} -\int d\mathbf {p}_{b}{{\mathscr {C}}}^0(\mathbf {p}_{b}) [(E_{\mathbf {p}_{b}}+m_b)(E^0_{p_b}+m_c) - \mathbf {p}_{b}^2/3] \end{aligned}$$

(51)

where

$$\begin{aligned} {{\mathscr {C}}}^0(\mathbf {p}_{b})= & {} \sqrt{\frac{Mm}{N_{B_c}(0)N_X(0)}}\nonumber \\&\times \frac{{{\mathscr {G}}}_{B_c}(\mathbf {p}_{b}, -\mathbf {p}_{b}) {{\mathscr {G}}}_X(\mathbf {p}_{b}, -\mathbf {p}_{b})}{\sqrt{E_{\mathbf {p}_{b}}E^{0}_{\mathbf {p}_{b}} (E_{\mathbf {p}_{b}}+m_b)(E^0_{\mathbf {p}_{b}}+m_c)}} \end{aligned}$$

(52)

with, $E^0_{p_b}=\sqrt{{|\mathbf {p}_b|^2}+m_c^2}$.

Now considering both the timelike and spacelike parts of axial vector current contribution and simplifying, we finally obtain the model expression for the weak form factor $a_+(q^2)$ in the form:

$$\begin{aligned} a_+=-\frac{1}{2M^2}\Big [(J - f)+\frac{(I-{f})E_X(M-{E_X})}{{E_X}^2-{m^2}}\Big ] \end{aligned}$$

(53)

where

$$\begin{aligned} J= & {} \sqrt{\frac{M{E_X}}{N_{B_c}(0)N_X(\mathbf {k})}}\nonumber \\&\times \int \frac{d\mathbf {p}_b{{\mathscr {G}}}_{B_c}(\mathbf {p}_{b}, -\mathbf {p}_{b}) {{\mathscr {G}}}_X(\mathbf {p}_{b}+\mathbf {k}, -\mathbf {p}_{b})(E_{\mathbf {p}_{b}} + m_{b})E_X}{\sqrt{E_{p_b}E_{\mathbf {p}_{b}+\mathbf {k}} (E_{\mathbf {p}_{b}}+m_b)(E_{\mathbf {p}_{b}+\mathbf {k}}+m_c)}} \end{aligned}$$

(54)

and

$$\begin{aligned} I= & {} \sqrt{\frac{M{E_X}}{N_{B_c}(0)N_X(\mathbf {k})}}\nonumber \\&\times \int \frac{d\mathbf {p}_b{{\mathscr {G}}}_{B_c}(\mathbf {p}_{b}, -\mathbf {p}_{b}) {{\mathscr {G}}}_X(\mathbf {p}_{b}+\mathbf {k}, -\mathbf {p}_{b})}{\sqrt{E_{p_b} E_{\mathbf {p}_{b}+\mathbf {k}} (E_{\mathbf {p}_{b}}+m_b) (E_{\mathbf {p}_{b}+\mathbf {k}}+m_c)}}\nonumber \\&\times [(E_{\mathbf {p}_{b}}+m_b)(E_{\mathbf {p}_{b}+\mathbf {k}}+m_c) - {\mathbf {p}}_{b}\;^2/3] \end{aligned}$$

(55)

Note that the spin quantization axis is taken here opposite to the boost direction. Therefore, the longitudinal spin polarization of the daughter meson is boosted yielding its timelike component ${\epsilon _0^{*(L)}} = {-\mathbf {k}\over m}$ whereas its corresponding transverse component ${\epsilon _0^{*(T)}} = 0$. We take into account ${\epsilon _0^{*(L)}}$ while calculating the contribution of the timelike part of the axial vector current.

The weak form factors $f_+(q^2)$, $g(q^2)$, $f(q^2)$ and $a_+(q^2)$ can be expressed in the dimensionless form, as often cited in the literature, as:

$$\begin{aligned} \begin{aligned} F_1(q^2)&=f_+(q^2)\\ V(q^2)&=(M_{B_c}+M_X)g(q^2)\\ A_1(q^2)&=(M_{B_c}+M_X)^{-1}f(q^2)\\ A_2(q^2)&=-(M_{B_c}+M_X)a_+(q^2) \end{aligned} \end{aligned}$$

(56)

The $q^2$-dependence of the weak form factors and branching ratios for semileptonic $B_c$-decays to S-wave charmonium states are obtained using relevant hadronic quantities and RIQ-model parameters in the next section.

4 Numerical results and discussion

For numerical calculation, we use the model parameters (a,$V_0$), quark masses $m_q$ and quark binding energies $E_q$ which have already been fixed from hadron spectroscopy by fitting the data of heavy flavored mesons as:

$$\begin{aligned} (a, V_0)\equiv & {} (0.017166\;{\mathrm{GeV}}^3, -0.1375\;\mathrm{GeV})\nonumber \\ (m_{b}, m_{c})\equiv & {} (4.77659, 1.49276)\;\mathrm{GeV}\\ (E_{b}, E_{c})\equiv & {} (4.76633, 1.57951)\;\mathrm{GeV}\nonumber \end{aligned}$$

(57)

With the same set of input parameters, wide-ranging hadronic phenomena involving hadrons in their ground states [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89] have been described in the framework of the RIQ model. However, for processes involving radially excited meson states where the constituent quarks are expected to have higher binding energies, we solved the cubic equation representing respective quark bound-state condition. Accordingly, the binding energies used here for the constituent quarks (b,c) inside radially excited 2S and 3S states of the $(c{\bar{b}})$ and $(c {\bar{c}})$ systems are taken, respectively, [88, 89] as:

$$\begin{aligned} \begin{aligned} ( E_{b} ; E_{c} )= & {} ( 5.05366 ; 1.97016 ) \mathrm{GeV} \\ ( E_{b} ; E_{c} )= & {} ( 5.21703 ; 2.22479 ) \mathrm{GeV} \end{aligned} \end{aligned}$$

(58)

The mass of participating mesons in their ground and radially excited 2S states are taken in GeV from the PDG [90] as: $M_{B_c}=6.2749$, $M_{\eta _c}=2.9839$, $M_{\eta _c(2S)}=3.6375$, $M_{J/\psi }=3.0969$, and $M_{\psi (2S)}=3.6861$. Since mass of 3S states of $(c {\bar{c}})$ system has not yet been observed, we take our model masses which have been obtained in the hyperfine splitting of heavy meson spectra [88, 89]. The difficulty encountered here was to make sure all the meson states to have their respective correct masses using same set of input parameters. This is indeed a problem common to all potential models, especially for the states above threshold. Therefore, we adjust the potential parameters $V_0$ to a new value $\sim -0.01545$ GeV and retain all other appropriate input parameters (a, $m_q$, $E_q$) [88, 89] in reproducing the mass splitting, following the technique used by T. Wang etal. in their analysis based on the instantaneous approximated Bethe–Salpeter approach [96]. In doing so, we obtain the mass of $\eta _c$(2S) and $\psi$(2S) close to their observed values [90] and those of their 3S state as $M_{\eta _c(3S)} = 3.8381$ GeV and $M_{\psi (3S)} = 4.1104$ GeV. For CKM parameter $V_{bc}$ and $B_c$ meson lifetime $\tau _{B_c}$, we use their central value from the PDG [90] as $V_{bc} = 0.0410$ and $\tau _{B_c} = 0.51$ps, respectively.

Fig. 3

Overlap of momentum distribution amplitudes of initial and final meson state

Before calculating the weak form factors and their $q^2$-dependence in the allowed kinematic range, it is interesting to study the behavior of radial quark momentum distribution amplitude function related to $B_c$ meson state together with those of the final S-wave charmonium states. The shape of the behavior of momentum distribution amplitude is shown in Fig. 3. One can see that the overlap region between the momentum distribution amplitude function of the initial $B_c$ meson state and final charmonium 1S state is maximum, whereas it is less for the decay mode to 2S and least for the decay to 3S charmonium state.

The Lorentz-invariant weak form factors representing the decay amplitudes are calculated from the overlapping integrals of participating hadron wave functions. It is evident therefore that the contribution of weak form factors to the decay width/branching fractions should be obtained in the decreasing order of magnitude as one considers various semileptonic $B_c$ decays to S-wave charmonium states from 1S to higher 2S and 3S states.

Our predicted $q^2$-dependence of weak form factors for the decay modes studied here in their physical kinematic range is shown in Figs. 4, 5, 6. We find that transitions $B_c^+ \rightarrow \eta _c,(J/\psi ) e^+ \nu _e$ have a relatively strong $q^2$-dependence as relevant form factors increase with increasing $q^2$. This behavior, however, is not universal. For example, in the transition: $B_c^+ \rightarrow \eta _c(2S), \psi (2S) e^+\nu _e$ and $B_c^+ \rightarrow \eta _c(3S), \psi (3S) e^+\nu _e$ some of the form factors decrease with increasing $q^2$. Similar predictions have been obtained in other model calculations based on the perturbative QCD approach [53], light-front quark model [49], and ISGW2 quark model [47]. This is attributed to the nodal structure in the momentum distribution amplitude functions corresponding to $B_c$ decay to different S-wave charmonium states and the momentum transfer involved in the decay process.

One may naively expect the weak form factors to satisfy the heavy quark symmetry (HQS) relations:

$$\begin{aligned} F_1(q^2)\simeq V(q^2)\simeq A_2(q^2)\simeq \tilde{A_1}(q^2) \end{aligned}$$

(59)

with

$$\begin{aligned} \tilde{A_1}(q^2)= [1-\frac{q^2}{(M+m)^2}]^{-1} A_1(q^2). \end{aligned}$$

as an outcome of heavy quark effective theory (HQET). From the predicted $q^2$-dependence (Fig. 4, 5, 6), it is evident that the weak form factors do not simultaneously satisfy HQS relation. This corroborates to the well-known fact that the HQS is not strictly applicable to the case of mesons with two heavy quarks [97]. Integrating the expression for partial decay width over the allowed kinematic range, one can calculate the decay width and hence BR for six decay modes considered in this work. Our predicted BR for all considered decays is shown in Table 1 in comparison with other model predictions.

Fig. 4

$q^2$-dependence of form factors for $B_c\rightarrow X(1S) e \nu _e$

Fig. 5

$q^2$-dependence of form factors for $B_c\rightarrow X(2S) e \nu _e$

Fig. 6

$q^2$-dependence of form factors for $B_c\rightarrow X(3S) e \nu _e$

Note that we have not shown any theoretical uncertainties in our predictions. This is because all the input parameters used here including the model parameters (a, $V_0$), quark masses $m_q$ and corresponding binding energies $E_q$ have already been fixed from hadron spectroscopy in the basic level application of this model in reproducing the hyperfine splitting of baryon and light as well as heavy meson spectra. We use the same set of fixed parameters to describe a wide-ranging hadronic phenomena as pointed out earlier. As such we have no free parameters at our disposal to show any kind of uncertainties here in our model prediction. The uncertainties that might creep into theoretical calculation are due to the uncertainty of the CKM matrix element which is very small and hence we neglect it.

We find, for $B_c \rightarrow \eta _c/(J/\psi ) e \nu _e$ decays, our predictions are in overall agreement with those of the nonrelativistic quark model [28], relativistic quark model [33,34,35], Bethe–Salpeter quark model [38], light-cone QCD sum rule [46] and QCD potential model [50]. For $B_c \rightarrow \eta _c(2S)/\psi (2S) e \nu _e$ decays, our results are found to have an order of magnitude agreement with the results of the perturbative QCD approach [53]. However, for $B_c \rightarrow \eta _c(3S)/\psi (3s) e\nu _e$ transitions analyzed by a few theoretical approaches [35, 42, 43, 53] the order of magnitude of predicted BR is found to vary widely from one model to another. While the relativistic quark model predictions [33, 34] are typically smaller, those of the light-front QCD sum rule [46] and perturbative QCD approach [53] are two orders of magnitude higher. Our predictions in this sector, although found overestimated, compared to that of [35] are in overall agreement with [53]. Since data in this sector are scant, the results of all these approaches can only be discriminated in future LHC experiments. As expected, our predicted BR are obtained in the following hierarchy: BR($B_c^+\rightarrow \eta _c\psi (3S)$) < BR($B_c^+\rightarrow \eta _c \psi (2S)$) < BR($B_c^+\rightarrow \eta _c, J/\psi (1S)$). This is due to the tighter phase space and weaker $q^2$-dependence of weak form factors contributing to decays to higher excited charmonium states.

It is also important to study the longitudinal ($\varGamma _L$) and transverse ($\varGamma _T$) polarization contribution to the BR of $B_c \rightarrow \psi (nS)e\nu _e$ decays in the lower, higher, and whole physical region. Our predicted polarization ratios and BR in the Region-I $0\le \ q^2\le \frac{(M-m)^2}{2}$, Region-II $\frac{(M-m)^2}{2}\le \ q^2\le \ (M-m)^2$ and in the whole physical region are given separately in Table 2.

Table 1 Predicted branching ratios $(\%)$ of $B_c^+\rightarrow X e^+\nu _e$ decay in comparison with other model predictions

Table 2 Partial branching ratios $(\%)$ and polarization ratio: $\frac{\varGamma _L}{\varGamma _T}$ of $B_c^+\rightarrow Xe^+ \nu _e$ decays in different $q^2$ regions

From Table 2, we find $\frac{\varGamma _L}{\varGamma _T} < 1$ in the Region-II for all decay modes considered here, which means that transitions occur dominantly in transverse mode in this region.

In the Region-I, it is found that $B_c^+\rightarrow J/\psi e^+\nu _e$ though remains dominantly in transverse mode, the contribution of $\varGamma _L$ relative to $\varGamma _T$ is found to increase for the decay to radially excited 2S and 3S charmonium states. Taking into account the contribution from both the regions, the decay to 2S charmonium states is still found moderately dominant in the transverse mode. On the other hand, the longitudinal mode moderately dominates for $B_c$ decays to 3S charmonium state in the whole physical region due to a large contribution coming from the low $q^2$-region. These results are attributed to the behavior of relevant form factors $V(q^2)$, $A_1(q^2)$, and $A_2(q^2)$ in different regions. In our model calculation, the form factor V$(q^2)$ increases throughout with increasing $q^2$ which enhances the transverse polarization contribution in large $q^2$ region. On the other hand, form factor $A_2{(q^2)}$ which provides dominant contribution to $\varGamma _L$ as compared to $A_1{(q^2)}$ is found suppressed mostly in large $q^2$ region giving minimal contribution to $\varGamma _L$. Our predicted polarization ratio in the whole physical region is in agreement with those of [53]. These results could be tested by LHCb and forthcoming Super-B experiments.

5 Summary and conclusion

In this paper, we analyze the semileptonic $B_c$ decays to S-wave charmonium states in the framework of relativistic independent quark model based on confining potential in equally mixed scalar–vector harmonic form. The weak form factors as overlap integrals of the participating mesons’ wave functions, derived from the RIQ model dynamics, are calculated explicitly in the allowed kinematic range. We predict the branching ratios (BR), longitudinal- to-transverse polarization ratios $\frac{\varGamma _L}{\varGamma _T}$ for these decays which are found to be in general agreement with predictions of other theoretical approaches. It is found that the predicted BR’s for $B_c$ decays to the ground-state charmonium is comparatively large $\sim$ $10^{-2}$ while those for decays to higher excited charmonium states are relatively small owing to the phase space suppression and weaker $q^2$ dependence of the form factors. The BR and polarization ratios for $B_c\rightarrow \psi (nS)e\nu _e$ decays are predicted separately in the low, high $q^2$ region as well as in the whole physical region. We find that $B_c\rightarrow J/\psi , \psi (2S)e\nu _e$, is dominated by transverse polarization mode, whereas $B_c\rightarrow \psi (3S)e\nu _e$ is dominated by longitudinal mode in the whole physical region. These theoretical predictions could be tested in LHCb and forthcoming Super-B experiments. With the possible data on $B_c$ decays expected in near future, one can extract the accurate value of CKM parameter which would provide an important consistency check for the standard model.

Appendix A: Constituent quark orbitals and momentum probability amplitudes

In the RIQ model, a meson is picturized as a color-singlet assembly of a quark and an antiquark independently confined by an effective and average flavor independent potential in the form: $U(r)=\frac{1}{2}(1+\gamma ^0)(ar^2+V_0)$ where (a, $V_0$) are the potential parameters. It is believed that the zeroth-order quark dynamics generated by the phenomenological confining potential U(r) taken in equally mixed scalar–vector harmonic form can provide an adequate tree-level description of the decay process being analyzed in this work. With the interaction potential U(r) put into the zeroth-order quark Lagrangian density, the ensuing Dirac equation admits static solution of positive and negative energy as:

$$\begin{aligned} \begin{aligned} \psi ^{(+)}_{\xi }(\mathbf {r})\;&=\;\left( \begin{array}{c} \frac{ig_{\xi }(r)}{r} \\ \frac{{\mathbf {\sigma }}.{{\hat{r}}}f_{\xi }(r)}{r} \end{array}\;\right) U_{\xi }({\hat{r}}) \\ \psi ^{(-)}_{\xi }(\mathbf {r})\;&=\;\left( \begin{array}{c} \frac{i({\mathbf {\sigma }}.{{\hat{r}}})f_{\xi }(r)}{r}\\ \frac{g_{\xi }(r)}{r} \end{array}\;\right) {{\tilde{U}}}_{\xi }({\hat{r}}) \end{aligned} \end{aligned}$$

(A.1)

where $\xi =(nlj)$ represents a set of Dirac quantum numbers specifying the eigenmodes; $U_{\xi }({\hat{r}})$ and ${{\tilde{U}}}_{\xi }({\hat{r}})$ are the spin angular parts given by,

$$\begin{aligned} \begin{aligned} U_{ljm}({\hat{r}})&=\sum _{m_l,m_s}\langle lm_l\;{1\over {2}}m_s| jm \rangle Y_l^{m_l}({\hat{r}})\chi ^{m_s}_{\frac{1}{2}}\\ {{\tilde{U}}}_{ljm}({\hat{r}})&=(-1)^{j+m-l}U_{lj-m}({\hat{r}}) \end{aligned} \end{aligned}$$

(A.2)

With the quark binding energy $E_q$ and quark mass $m_q$ written in the form $E_q^{\prime }=(E_q-V_0/2)$, $m_q^{\prime }=(m_q+V_0/2)$ and $\omega _q=E_q^{\prime }+m_q^{\prime }$, one can obtain solutions to the resulting radial equation for $g_{\xi }(r)$ and $f_{\xi }(r)$in the form:

$$\begin{aligned} g_{nl}= & {} N_{nl} \left( \frac{r}{r_{nl}}\right) ^{l+l}\exp (-r^2/2r^2_{nl}) L_{n-1}^{l+1/2}(r^2/r^2_{nl})\nonumber \\ f_{nl}= & {} N_{nl} \left( \frac{r}{r_{nl}}\right) ^{l}\exp (-r^2/2r^2_{nl})\nonumber \\\times & {} \left[ \left( n+l-\frac{1}{2}\right) L_{n-1}^{l-1/2}(r^2/r^2_{nl}) +nL_n^{l-1/2}(r^2/r^2_{nl})\right] \end{aligned}$$

(A.3)

where $r_{nl}= a\omega _{q}^{-1/4}$ is a state-independent length parameter, $N_{nl}$ is an overall normalization constant given by

$$\begin{aligned} N^2_{nl}=\frac{4\varGamma (n)}{\varGamma (n+l+1/2)}\frac{(\omega _{nl}/r_{nl})}{(3E_q^{\prime }+m_q^{\prime })} \end{aligned}$$

(A.4)

and $L_{n-1}^{l+1/2}(r^2/r_{nl}^2)$ are associated with Laguerre polynomials. The radial solutions yield an independent quark bound-state condition in the form of a cubic equation:

$$\begin{aligned} \sqrt{(\omega _q/a)} (E_q^{\prime }-m_q^{\prime })=(4n+2l-1) \end{aligned}$$

(A.5)

The solution of the cubic equation provides the zeroth-order binding energies of the confined quark and antiquark for all possible eigenmodes.

In the relativistic independent particle picture of this model, the constituent quark and antiquark are thought to move independently inside the $B_c$-meson bound state with momentum $\mathbf {p}_b$ and $\mathbf {p}_c$, respectively. Their individual momentum probability amplitudes are obtained in this model via momentum projection of respective quark orbitals (A1) in following forms:

For ground-state mesons:($n=1$, $l=0$)

$$\begin{aligned} G_b(\mathbf {p}_b)= & {} {{i\pi {{\mathscr {N}}}_b}\over {2\alpha _b\omega _b}} \sqrt{{(E_{p_b}+m_b)}\over {E_{p_b}}}(E_{p_b}+E_b)\nonumber \\&\times \exp {\left( -{ {\mathbf {p_b}}^2\over {4\alpha _b}}\right) }\nonumber \\ {{\tilde{G}}}_c(\mathbf {p}_c)= & {} -{{i\pi {{\mathscr {N}}}_c}\over {2\alpha _c\omega _c}} \sqrt{{(E_{p_c}+m_c)}\over {E_{p_c}}}(E_{p_c}+E_c)\nonumber \\&\times \exp {\left( -{ {\mathbf {p_c}}^2\over {4\alpha _c}}\right) } \end{aligned}$$

(A.6)

For the excited meson state: $(n=2, l=0$)

$$\begin{aligned} G_b(\mathbf {p}_b)= & {} {{i\pi {{\mathscr {N}}}_b}\over {2\alpha _b}} \sqrt{{(E_{p_b}+m_b)}\over {E_{p_b}}} {(E_{p_b}+E_b)\over {(E_b+m_b)}}\nonumber \\&\times \left( {\mathbf {p_b}^2\over {2\alpha _b}}-{3\over 2}\right) \exp {\left( -{{\mathbf {p}_b}^2\over {4\alpha _b}}\right) }\nonumber \\ {{\tilde{G}}}_c(\mathbf {p}_c)= & {} {{i\pi {{\mathscr {N}}}_c}\over {2\alpha _c}} \sqrt{{(E_{p_c}+m_c)}\over {E_{p_c}}} {(E_{p_c}+E_c)\over {(E_c+m_c)}}\nonumber \\&\times \left( {\mathbf {p_c}^2\over {2\alpha _c}}-{3\over 2}\right) \exp {\left( -{ {\mathbf {p}_c}^2\over {4\alpha _c}}\right) } \end{aligned}$$

(A.7)

For the excited meson state ($n=3, l=0$)

$$\begin{aligned} G_b(\mathbf {p}_b)= & {} {{i\pi {{\mathscr {N}}}_b}\over {2\alpha _b}} \sqrt{{(E_{p_b}+m_b)}\over {E_{p_b}}} {(E_{p_b}+E_b)\over {(E_b+m_b)}} \nonumber \\&\times \left( {\mathbf {p_b}^4\over {8 {\alpha _b}^2}}-{{5{\mathbf {p}_b}^2}\over {4\alpha _b}}+{{15\over 8}}\right) \exp {\left( -{{\mathbf {p}_b}^2\over {4\alpha _b}}\right) }\nonumber \\ {{\tilde{G}}}_c(\mathbf {p}_c)= & {} {{i\pi {{\mathscr {N}}}_c}\over {2\alpha _c}} \sqrt{{(E_{p_c}+m_c)}\over {E_{p_c}}} {(E_{p_c}+E_c)\over {(E_c+m_c)}} \nonumber \\&\times \left( {\mathbf {p_c}^4\over {8 {\alpha _c}^2}}-{{5{\mathbf {p}_c}^2}\over {4\alpha _c}}+{{15\over 8}}\right) \exp {\left( -{{\mathbf {p}_c}^2\over {4\alpha _c}}\right) } \end{aligned}$$

(A.8)

The binding energy of the constituent quark and antiquark for the ground state of $B_c$ meson as well as the ground and excited final meson states for $n=1,2,3$; $l=0$ can also be obtained by solving respective cubic equations representing appropriate bound-state conditions.