1 Introduction

Interaction of highly charged ions (HCI, charge \(q \gg 1\)) with solid surfaces has been intensively studied both experimentally and theoretically. Concerning the experimental researches, one type of the problem is the analysis of the radiation effects (X-ray emission) from the ions approaching the surface [1,2,3]. Another class of experiments is related to the surface modification. First experiments of that kind have been carried out with swift heavy ions (SHI). Later on, the modification has been achieved by the slow HCI: the nanostructures such as hillocks, craters, and rings have been obtained for the HCI impinging upon the conduction surfaces, insulators, etc. [4,5,6,7,8,9]. An advantage of using the HCI is in the fact that the nanosized structures can be obtained at lower energies in comparison to the SHI. Theoretical studies are mainly based on the molecular dynamics simulations [10, 11] and the inelastic thermal spike model [12, 13]. Recently, the problem of nanostructure formation on metal surface has been considered from the standpoint of the energy dissipation in the ion-surface system [14,15,16], but the problem of the influence of the ionic type on the structure shape and size remains open. The studies are based on the calculation of the population probabilities, neutralization distances, neutralization energy, kinetic energy loss, etc.

The aim of the present paper is to analyze the influence of the ionic type (Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions) on the total energy necessary for the nanostructure creation for low to moderate ionic velocities. For that purpose, we employ the quantum time-symmetrized two-state vector model (TVM) [17,18,19] and the micro-staircase model [20] in order to calculate the neutralization energy, as well as the charge dependent ion-target atom interaction potential model for the calculation of the nuclear stopping power [16]. The measure of the relative importance of these two energy dissipations is described by the critical velocities \(v_c\) [16], which we study from the standpoint of the ionic type. Namely, the ions of different type of the same charge q can have very different electronic core structures, i.e., different core polarizations, as well as different interaction potential inside the solid. Up to now [18, 21], the core polarization effect has been considered concerning the population probabilities and the corresponding neutralization distances for ionic velocities \(v=0.005\) a.u. and 0.01 a.u., respectively. Also, we analyzed [15] the influence of the core polarization of the Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions on the final ionic charges and the corresponding neutralization energies for metal–dielectric–vacuum system for arbitrary angle of incidence and different types of dielectric films covering the metal surface for the ionic velocity \(v=0.25\) a.u. The kinetic energy loss for these ions inside the C-foil has been calculated for the velocity \(v=0.3\) a.u. [22]. The velocity effect on the kinetic energy loss has been considered only for Xe\(^{q+}\) ion impinging upon gold and titanium targets [16].

Within the framework of the micro-staircase model (in which the fine structure of the neutralization cascade of the ions approaching the solid surface is taken into account) the initial ionic charge reduces in time: \(q\rightarrow q-1 \rightarrow ...\; Q(R) \rightarrow ... \rightarrow Q_{{fin}}^{(q)}\). In the treatment of the intermediate stages of the neutralization process (population of the ionic Rydberg states) the polarization of the electronic cloud of the ionic core we take into account via the Simons-Bloch interaction potential [18]. According to the present analysis, we obtain the same values of the final ionic charges for Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions in the considered velocity range. The ions enter the solid with charge \(Q_{fin}^{(q)}\) and collide with target atoms; the deposited kinetic energies inside the solid of these ions are different due to different nuclear charges.

This article is organized as follows. In Sect. 2 we elaborate the quasi-resonant TVM and the micro-staircase model for arbitrary velocity case for the Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions including the core polarization effect and calculate the final ionic charges and the corresponding neutralization energies. In Sect. 3 we analyze the process of the kinetic energy loss below the surface for different ionic types and calculate the deposited kinetic energy. In Sect. 4 we obtain the critical ionic velocities for the nanostructure creation on a metal surface by an impact of the considered ions and discuss the formation of a particular nanostructure type. The concluding remarks are given in Sect. 5.

Atomic units (\(e^{{ 2}} = \hbar = m_{{e}} = 1\)) will be used throughout the paper unless indicated otherwise.

2 Neutralization energy

We consider the slow highly charged ions (initial charge \(q \gg 1\)) moving at velocity v (\( v\le 0.4 \) a.u.) upon a metal surface in a normal direction (metal–vacuum, MV-system). During the ionic motion the cascade neutralization \(q\rightarrow q-1... \rightarrow Q(R) ... \rightarrow Q_{{fin}}^{(q)}\) process occurs [20]; the instant ion-surface distance R decreases in time according to the law \(dR=-vdt\). Intermediate stages of the process of the cascade neutralization (macro steps) are schematically presented in Fig. 1. In the course of the process \(q \rightarrow Q_{fin}^{(q)}\), the neutralization energy is deposited into the surface, which induces a first destabilization of the lattice structure and the corresponding surface modification. The ions of charge \(Q_{fin}^{(q)}\) penetrate the solid losing their kinetic energies via elastic and inelastic collisions with target atoms [16]. The deposition of the kinetic energy into the surface leads to an additional dislocation of the atoms. Both steps of the energy depositions contribute to the formation of the particular surface nanostructure (hillocks, craters, rings, etc.) [14,15,16].

The quantum mechanical aspects of the cascade neutralization we consider within the quasi-resonant TVM [19, 20]. The characteristic feature of the TVM is that the state of the active electron in the particular step of the neutralization process is described by the two wave functions \(\Psi _1(\vec {r},t)\) and \(\Psi _2(\vec {r},t)\), which simultaneously evolve in two opposite directions in time carrying the information about the initial condition (electron is in the metal) and the final condition (electron is bound to the ion), respectively. The state of the active electron at the intermediate time t (between the initial time \(t_{in}\) and the final time \(t_{fin}\)), is expressed by two intermediate eigenstates \(\mid \mu _M(R)\rangle \) and \(\mid \nu _A(R)\rangle \) of the in- and out- Hamiltonians \({\hat{H}}_1\) and \({\hat{H}}_2\) (\(\mu _M=(\gamma _M,n_{1M},m_M)\) and \(\nu _A=(n_A,l_A,m_A)\) are the metallic parabolic and atomic spherical quantum numbers, respectively). We point out that the use of two wave functions has the practical advantage: the influence of the polarized surface and the polarized ionic core can be treated independently.

Fig. 1
figure 1

Intermediate stages of the process of the cascade neutralization (macro steps) and deposition of the neutralization energy into the solid

Full size image

The expressions for the in- and out- Hamiltonians (\(i=1,2\), respectively) are given by:

$$\begin{aligned} \hat{H}_i(R)=-\frac{1}{2}\nabla ^2+{U}_{{MV}{i}}^{(Q)},\quad i=1,2. \end{aligned}$$
(1)

The \({U}_{{MV}{i}}^{(Q)}\) for \(i=1\) and \(i=2\) are the potential energies of the active electron from the standpoint of the in- and out-Hamiltonians, respectively.

In order to determine the explicit expressions for the in- and out- Hamiltonians we distinguish the region outside the solid (\(z>0\), where z is the axis along the ionic motion perpendicular to the metal with origin at the surface) and the region inside the solid (\(z<0\)). The quantity \({U}_{{MV}{i}}^{(Q)}\) for \(z>0\) consists of the effective potential energy \({U}_A^{(i)}\) of the active electron in the field of the polarized ionic core and the potential energy \({U}_S^{(i)}\) in the field of the polarized solid [18].

In the region inside the solid we have \({U}_{{MV}{1}}^{(Q)}=-U_0\), where \(U_0\) is the depth of the potential well in the Sommerfeld model of the solid; the model assumes that the quantity \({U}_{{MV}{2}}^{(Q)}\) is negligible.

The specific features of the TVM concerning the ionic type is expressed via Hamiltonian \({\hat{H}}_2\). The interaction \({U}_A^{(2)}\) of the active electron with the ionic core (for the electron in the ionic subregion) is described by Simons-Bloch potential \({U}_A^{(2)}=-{Q}/{r_A}+ \sum _ {l^{\prime }}^{\infty } {c_{l^{\prime }}}\hat{P}_{l^{\prime }}/{r_{A}^2}\), where \( \hat{P}_{l^{\prime }}\) is the projection operator onto the subspace of a given angular momentum \(l^{\prime }\), and \(r_A\) is the electron position in respect to the ionic core [18]. The effect of the polarization of the ionic core introduced by constants \(c_{l^{\prime }}\) leads to the modification of the eigenfunctions as well as the eigenenergies in comparison to expression for the same quantities for the point like core charges. Outside the solid, \({U}_S^{(2)} = -1/(4z) +Q/(z+R) \approx {(2Q-1)}/{4R}\). To summarize, for \(z>0\), the potential energy of the active electron in out-Hamiltonian is given by

$$\begin{aligned} \hat{U}_{{MV}{2}}^{(Q)}=-\frac{Q}{r_A}-\sum _ {l^{\prime }}^{\infty } \frac{c_{l^{\prime }}}{r_{A}^2}\hat{P}_{l^{\prime }}+\frac{2Q-1}{4R}. \end{aligned}$$
(2)

Within the framework of the TVM, we consider the electron capture from the metal into the high \(n_A\) (Rydberg) state by tunneling through the potential barrier formed between the solid and the ion. The electron transitions occur in the narrow cylindrical region along the ionic trajectory (low-\(l_A\) state, see Fig. 1). The interplay of the wave functions \(\Psi _1(\vec {r},t)\) and \(\Psi _2 (\vec {r},t)\) obtained by solving the time dependent Schrödinger equations with in- and out-Hamiltonians is expressed by the mixed flux \(I_{\mu _M,\nu _A}(R)\) [18]. The absolute square of the time integral of the mixed flux determines the neutralization probability \(T_{\mu _M,\nu _A}(R)\) per unit \(\gamma _M\); the intermediate population probability is given by \(P_{\nu _A}^{(Q)}(R)= \int \sum _{n_{1M}, m_M} T_{\mu _M,\nu _A}(R) d\gamma _M\) (see [18]).

Fig. 2
figure 2

Final ionic charges \(Q_{fin}^{(q)}\) via ionic velocity for Ar\(^{q+}\)(\(q = 15,18)\), Kr\(^{q+}\) (\(q = 15,18,...30)\), and Xe\(^{q+}\) (\(q = 15,18,...30)\) ions in the MV-system

Full size image

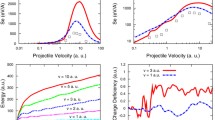
The cascade neutralization process we consider by the micro-staircase model [20], valid for moderate ionic velocities. At each micro-cascade, which constitutes the particular macro step, see Fig. 1, the intermediate ionic Rydberg states (\(\nu _A^{(Q)}\)) of the ion with core charge Q populate quasi-resonantly with probability \(P_{\nu _A}^{(Q)}(R)\), which exhibits maximal value at the neutralization distance \(R_c^N\). The macro step finishes when the total population probability \(P_{\nu _A}^{Q,tot} =1\); after that, the ionic charge reduces by 1 as \(Q\rightarrow Q-1\), and the next macro step begins, and so on. The final ionic charge \(Q_{fin}^{(q)}\) at a distance \(R_{min}\) from the surface is given by Eq. (20) in [20]. In Fig. 2, we present the final ionic charge \(Q_{fin}^{(q)}\) versus ionic velocity v for Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions in the MV-system. For the same initial charge q these ions are distinguished by different core polarization. The final ionic charges are nearly the same for all ions with the same value of q what is a direct consequence of the applied TVM. That is, the population processes of Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions are localized at nearly the same neutralization distances \(R_c^N\) with the probabilities of the same order of magnitude, even though different Rydberg states are populated in the particular micro cascade. The velocity effect on the final ionic charges is significant: \(Q_{{fin}}^{(q)}\) increases with increasing of the ionic velocity and becomes approximately equal to the initial ionic charge q for velocities larger than \( v = 0.35 \) a.u.

Fig. 3
figure 3

Neutralization energy via ionic velocity for Ar\(^{q+}\) (\(q = 15,18)\), Kr\(^{q+}\) (q = 15,18,...,30), and Xe\(^{q+}\) (q = 15,18, ...,45) ions in the MV-system

Full size image

The ions approaching the metal surface are partially neutralized by the multi-electron capture into the intermediate Rydberg states and arrive in the very vicinity of the solid surface at distance \(R_{min}\) with the final charge \(Q_{fin}^{(q)}\). Simultaneously by the rapid deexcitation proposed within the micro-staircase model [16, 20], the neutralization energy \(W^{(q,MV)}\) is deposited into the first nanometers of the surface very fast (few fs for metal targets ([6, 23]). The neutralization energy is determined by the difference between the potential energy \(W_{q,pot}\) (describes the state of the ion before the neutralization begins) and the potential energy in front of the solid surface \(W_{Q_{fin}^{(q)},pot}\) [14,15,16]:

$$\begin{aligned} W^{(q,MV)}=W_{q,pot}-W_{Q_{fin}^{(q)},pot}. \end{aligned}$$
(3)

In Fig. 3, we present the velocity dependence of the neutralization energy \(W^{(q,MV)}\) for Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions in the MV-system. The influence of the ionic type on the neutralization energy is noticeable. An increase in the core polarization (Ar \(\rightarrow \) Kr \( \rightarrow \) Xe) leads to decreasing of ionic neutralization energies.

3 Deposited kinetic energy

After the neutralization cascade finishes in front of the surface, the ions with charge \(Q=Q_{fin}^{(q)}\) penetrate the surface. The charge \(Q=Q_{fin}^{(q)}\) we consider as the initial ionic charge for the kinetic energy deposition below the surface. Inside the solid the elastic collisions between the ion and target atoms (nuclear stopping power - for velocities considering here the electronic stopping power is negligible [7, 16, 24, 25]) induce the collision cascade and the dissipation of the kinetic energy (see Fig. 4). The deposited kinetic energy \(E_{k,dep}\) contributes to the additional disordering of the target atoms from their lattice sites and to the modification of the surface.

Fig. 4
figure 4

Schematic description of the elastic collisions below the surface and deposition of the kinetic energy into the solid

Full size image

For the calculation of the deposited kinetic energy \(E_{k,dep}\) we employ the charge state dependent model of the ion-surface interaction [16]. We take into account the charge of the projectile \(Q=Q_{fin}^{(q)}(v)\) obtained in Sect. 2 to define the ion–atom interaction. The model potential energy at ion-target atom internuclear distance r [26] is

$$\begin{aligned} V_{int}(r)=\frac{(Z_1-Q)Z_2}{r}\phi \left( \frac{r}{a_u}\right) +\frac{Q Z_2}{r}\phi \left( \frac{r}{a_s}\right) , \end{aligned}$$
(4)

where \(Z_1\) and \(Z_2\) are the nuclear charges of the projectile and the target atom, respectively, and \(a_u=0.8853/\left( (Z_1-Q)^{0.23}+Z_2^{0.23})\right) \) and \(a_s=0.8853/Z_2^{1/3}\) are the screening lengths for the interaction of the atom of nuclear charge \(Z_1-Q\) with the target atom and the point charge Q with the target atom, respectively [26].

Fig. 5
figure 5

Nuclear stopping power via ionic velocity for Ar\(^{q+}\)(\(q = 15,18)\), Kr\(^{q+}\) \((q = 15,18,...,30)\), and Xe\(^{q+}\) \((q = 15,18,...,45)\) ions impinging upon gold target

Full size image

The energy transfer during the collision is determined by the scattering angle \(\theta (Q,\rho )\); according to the classical scattering theory, in the center of mass system (CMS)

$$\begin{aligned} \theta (Q,\rho )_{cms} = \pi - 2 \int _{r_{min}}^{\infty } dr \frac{\rho }{r^2 \sqrt{1-\frac{V_{int}(r)}{E_{cms}}-\frac{\rho ^2}{r^2}}} , \end{aligned}$$
(5)

where \(\rho \) is the impact parameter and \(r_{min}\) is the distance of the closest approach [26].

The kinetic energy transfer T is given by the well known relation \(T=T_{max}\sin ^2\left( {\theta (Q,\rho )_{cms}}/2\right) \), where \(T_{max}\) is the maximal value of T. The nuclear stopping power is expressed by \({dE}/{dx}=n S_n\), where n is the atomic density of the target and \(S_n\) is the nuclear stopping cross section \(S_n(Q,v)=2\pi \int _{0}^{\rho _{max}} \rho T d\rho \). The details of the calculation of the nuclear stopping power \(dE_n/dx\) are exposed in [16].

In Fig. 5, we present the nuclear stopping power for Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions interacting with gold target. For all considered ions, the quantity dE/dx increases with velocity in the velocity region from very low to moderate, which is a well known effect. For velocities larger than considered in Fig. 5, the nuclear stopping power decreases, mainly because the electronic stopping power becomes dominant [24]. Within the framework of our model, we get the q-dependent nuclear stopping power, which is in agreement with previous theoretical approaches elaborated in [26]. The effect of the core polarization on the nuclear stopping power is significant: the increasing of the core polarization leads to the increasing of the nuclear stopping power, which is a direct consequence of the different nuclear charges of these ions, see Eq. 4. The similar effect was obtained in [22] for Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions transmitted through carbon foil at velocity \(v=0.3\) a.u.

Deposited kinetic energy is given by

$$\begin{aligned} E_{k,dep}=(dE_n/dx )\Delta x , \end{aligned}$$
(6)

where \(dE_n/dx \) is the nuclear stopping power. We calculate the deposited kinetic energy for the interaction depth \(\Delta x\) relevant for the nanostructure formation (\(\Delta x = 38.5\) a.u. for gold target [16]).

4 Critical velocity

In order to discuss the shapes of the surface nanostructures we calculate the critical ionic velocity \(v_c\), defined by the relation [16]:

$$\begin{aligned} W^{(q,MV)}(v_c)=E_{k,dep}(v_c) , \end{aligned}$$
(7)

where \(W^{(q,MV)}\) is given by (3) and deposited kinetic energy by (6). The quantity \(v_c\) separates the velocity region into two subregions: for very low ionic velocities (\( v < v_c\)) the model predicts the hillocks as a dominant structures, while for the velocities larger than critical one (\( v> v_c \)), expected structures are craters. In the first case (hillock formation), the neutralization energy has a dominant influence in the surface modification, while the main contribution on the surface nanocraters formation is given by the deposited kinetic energy.

Fig. 6
figure 6

\(\{q,v\}\) diagram for Ar\(^{q+}\)(\(q = 15,18)\), Kr\(^{q+}\) \((q = 15,18,...,30)\), and Xe\(^{q+}\) \((q = 15,18,...,45)\) ions impinging upon gold target [27]

Full size image

In Fig. 6, we present the critical ionic velocity \(v_c\) for the Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions interacting with gold target [27]. The decreasing character for the critical ionic velocities with increasing of the core polarization (Ar\(^{q+}\) \(\rightarrow \) Kr\(^{q+}\) \(\rightarrow \) Xe\(^{q+}\)) for the same ionic charge is noticeable. For example, the Ar\(^{18+}\) ions in the interaction with gold target will form craters for velocities larger than \(v_c=0.34\) a.u., while Kr\(^{18+}\) and Xe\(^{18+}\) ions create the same structure for velocities larger than 0.09 a.u. and 0.02 a.u., respectively. From Fig. 6, we can predict the shape of the nanostructure for the discussed ions and gold target; for example, the Kr\(^{22+}\) ions for velocities \(v < 0.17\) a.u create the nanohillocks, and for larger one, the craters. The predicted types of the nanostructures are in accord with the experimental results for the interaction of the Xe\(^{q+}\) ions with gold targets [6,7,8]. The critical velocities for other ion-target combinations can be also obtained from our model. The agreement is also obtained for Xe\(^{q+}\) ions interacting with titanium targets [7, 16]. From the \(\{q,v\}\) diagram one can tune the velocity needed for the particular surface structure formation by an impact of the ion of a given charge q. The values of the critical velocities are given in Table 1.

Table 1 Critical velocities in a.u. for Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions impinging upon gold target
Full size table

5 Concluding remarks

In the present paper we analyzed the influence of the ionic type (Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\)) on the process of the particular surface nanostructure formation. For that purpose, we employed the TVM and micro-staircase model for the calculation of the neutralization energy and charge dependent ion-target atom potential for the calculation of the deposited kinetic energy, both relevant for the surface modification. Within the framework of the applied models these energies strongly depend on the ionic charge, velocity and the ionic type. We calculated the critical ionic velocities for Ar\(^{q+}\), Kr\(^{q+}\), and Xe\(^{q+}\) ions as a measure of the relative contribution of the neutralization energy and the deposited kinetic energy in the process of the nanosized surface structure creation. For velocities lower than critical (\( v < v_c\)), the predicted structures are hillocks, and the neutralization energy makes a main contribution on the surface modification; for velocities larger than the critical one (\( v> v_c \)), expected structures are craters, and the deposited kinetic energy plays a major role in their formation. The presented effect of the ionic type on the surface modification is noticeable: with increasing of the core polarization (Ar\(^{q+}\) \(\rightarrow \) Kr\(^{q+}\) \(\rightarrow \) Xe\(^{q+}\)) for the same ionic charge the critical ionic velocities decreasing. This means that krypton and xenon ions will create craters for lower velocities compared to the case of argon ions with the same charge q. For example, the Ar\(^{18+}\) ions in the interaction with gold target will form craters for velocities larger than \(v_c=0.34\) a.u., while Kr\(^{18+}\), and Xe\(^{18+}\) ions create the same structure for velocities larger than 0.09 a.u., and 0.02 a.u., respectively.

Few additional comments may be relevant for future research concerning the theoretical and experimental studies of the surface nanostructures creation and related phenomena.

First, the presented model can be applied to other ion-surface combination in order to analyze the influence of the target type on the surface modification. The new experiments, with new ionic types and metal targets, are necessary for the systematic analysis of the role of the system parameters, as well as the influence of the initial ionic charges and velocities. Second, the model of the intermediate Rydberg state population can be used for the analysis of the radiation effects (X-ray emission) from the ions approaching the surface.