1 Introduction

“There is no relativity of rotation”. This relatively famous quote by Feynman [1] may look as the final word on the discussion of rotation in the context of special relativity. Based on the fact that the presence of acceleration in a uniformly rotating frame, by the equivalence principle, takes us into the realm of general relativity may convince one not to bother with the formulation of rotation in the context of special relativity and look for the resolution of each rotation-based problem in general relativity and in the suitably chosen/constructed solutions of Einstein field equations (which are of course not usually available). Indeed the problem of the relativistic rigidly rotating disk and the spacetime metric in such a frame has been claimed to be the missing link that led Einstein to the introduction of the inevitable relation between curved spacetimes and gravitational fields in the years between 1912 to 1913 [2]. On the other hand rotation and rotating frames have always been a source of confusion while treated in the context of special relativity; the famous example is the Ehrenfest’s Paradox [3]. Indeed, looking at the literature [4], one finds how diverse are ideas on the relativistic physics in rotating frames and consequently how distant we are from establishing a general consensus even over the main concepts and notions in this subject.Footnote 1 So in practice one uses either the Galilean rotational transformation (GRT), which is only valid for centrally rotating observers, or consecutive Lorentz transformations between an inertial (laboratory) frame and comoving inertial frames which are momentarily at rest with respect to the non-inertial rotating observers (eccentric observers). The latter could be obtained either by employing the so-called hypothesis of locality along with the same procedure which led to the Fermi coordinates of an accelerated spinning observer [5, 6], or by reducing a general Lorentz transformation obtained for accelerated spinning frames [7, 8] to the case of rotating frames [9]. Another alternative is the introduction of a relativistic rotational transformation (RRT), which is the main subject of the present paper.

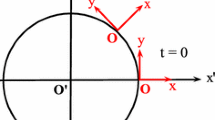
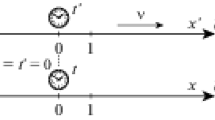
It seems that Ehrenfest’s Paradox is a good starting point to begin our discussion on rotation and RRTs. To explain the paradox we consider two frames/observers one at rest (the laboratory observer/frame) and the other one rotating counter-clockswise around it with constant angular velocity \(\Omega \) (the rotating observer/frame) measured by/in the inertial (non-rotating) observer/frame. At this point we use frames (set of clocks and extended fiduciary triad axes) and observers interchangeably but to be more precise one should differentiate between them, for a rotating frame is a non-inertial frame but not all observers in a rotating frame are non-inertial. In other words we should distinguish between a centrally rotating observer (i.e. at the center of the disk) which is an inertial observer and those at nonzero radii which are non-inertial. We will elaborate on this point later in this section. Using cylindrical coordinates we denote the spacetime points in the non-rotating frame with coordinates \((t, r, \phi , z)\) and in the one rotating around the \(z\)(\(z^\prime \)) axis with \((t^\prime , r^\prime , \phi ^\prime , z^\prime )\) where \(\phi ^\prime \) is measured from the \(x^\prime \) axis. These are related through the GRT as follows:

$$\begin{aligned} t^\prime = t, \;\;\; r^\prime = r, \;\;\; \phi ^\prime = \phi - \Omega t, \;\;\; z^\prime = z \end{aligned}$$
(1)

or in its differential form

$$\begin{aligned} dt^\prime = dt, \;\;\; d r^\prime = d r, \;\;\; d\phi ^\prime = d\phi - \Omega dt, \;\;\; dz^\prime = dz. \end{aligned}$$
(2)

It is noted that in both rotating and the non-rotating frames the radial distances are measured from the rotation axis. Through the above equation we would like to emphasize the meaning of the GRT. Interpreted kinematically, as in the cases of linear Galilean and Lorentz transformations, it introduces a prescription of how the spacetime coordinates of an event in the two frames are related to one another. This interpretation leads to the following relation between the angular velocities of a test particle observed in the two frames (Fig. 1):

$$\begin{aligned} \omega ^\prime = \omega - \Omega , \end{aligned}$$
(3)

which in turn leads to the well-known relation \(E^\prime = E - {{\mathbf {L}}} . {\varvec{\Omega }}\) between the energies of the particle in the two frames [10]. Usually the problem of rotation and rotating frames is discussed in the context of uniformly rotating rigid disks [11], in other words the rotating frame is a frame attached to a uniformly rotating incompressible disk whose constant angular velocity is measured in the non-rotating (inertial) frame. The above coordinate transformation could also be employed for a uniformly rotating disk and its points (at different times) taken as events whose spacetime coordinates are measured both in the laboratory frame and in the rotating frame attached to the disk. Obviously in this case it is expected that for any point on the disk \(\omega ^\prime = 0\) and \(\omega = \Omega \) (Fig. 2).

Fig. 1
figure 1

Two frames, one rotating (solid) around the other one (dashed) with uniform angular velocity \(\Omega \). Trajectory of a test particle and a point \(P\) on it as an event observed in the two frames, assigned with angular velocities \(\omega \) and \(\omega ^\prime \)

Full size image
Fig. 2
figure 2

A disk and its frame (solid) rotating around the laboratory frame (dashed) with uniform angular velocity \(\Omega \). Coordinates of a point \(P\) in the rim are given in the two frames with angular velocities \(\omega ^\prime = 0\) and \(\omega = \Omega \)

Full size image

1.1 Ehrenfest’s Paradox

Ehrenfest’s Paradox is the contradiction that an inertial (laboratory) observer faces in applying special relativistic length contraction to a rotating disk. From an inertial observer’s point of view the rim of a rotating disk undergoes a length contraction due to its transverse motion with velocity \(v=R\Omega \) and so the circumference of a rotating disk (\(P^\prime \)) is shorter than the one non-rotating (\(P\)), i.e. \(P^\prime < P \). On the other hand since the radius of the disk is perpendicular to the direction of the rotational motion of the rim, the same observer will not attribute a length contraction to it and so \(R^\prime = R\). Therefore the inertial (laboratory) observer, living in a flat spacetime and thereby using the Euclidean prescription for the circumference of a circle, finds the contradictory result \(P=2\pi R = 2\pi R^\prime = P^\prime \).

Perhaps it should be left for experiment to decide which relation holds between \(P\) and \(P^\prime \), but nevertheless many have tried hard to find either a theoretical resolution to this paradox or otherwise to invalidate it. An apparently favorite resolution in the literature is based on considering the situation from a rotating observer’s point of view and on the idea, introduced by Einstein [11–13], that the spatial geometry in such a frame is non-Euclidean.Footnote 2 But, as we will show below, that does not seem to be leading to any kind of resolution of the paradox but to a somewhat similar paradox from the rotating frame’s point of view.

As pointed out earlier, in the case of a rotating disk one should distinguish between the observer at the center of the disk (called the centrally rotating observer/frame) whose spatial coordinates, measured in the non-rotating (laboratory) frame, are fixed and those at different nonzero radii which are non-inertial due to the centrifugal force felt by them and called orbiting observers/frames. Einstein calls them eccentric observers “relative to whom a gravitational field prevails” [11]. In other words these observers, by the equivalence principle, find themselves and anything fixed with respect to the disk in a gravitational field. Later, elaborating on this matter, it will be shown that rotating observers at nonzero radii are of central importance in our discussion of RRTs but for the purpose of Ehrenfest’s Paradox we only deal with the rotating observer/frame at the center of the disk. From a rotating observer’s point of view the above-mentioned non-Euclidean character of the disk geometry could be obtained from considering the metric of flat spacetime in the rotating frame, as it is the spatial geometry (metric), defined through spacetime metric, which accounts for spatial distances including that of the disk circumference. Using the differential GRT (2), the flat spacetime metric in the non-rotating frame

$$\begin{aligned} ds^2 = c^2 dt^2 - dr^2 - r^2 d\phi ^2 - dz^2 \end{aligned}$$
(4)

transforms into [15, 16]

$$\begin{aligned} ds^2 \!=\! (c^2\!-\! \Omega ^2r^2) dt^2 \!-\! 2\Omega r^2 dt d{\phi ^\prime } \!-\!dr^2 \!-\! r^2 d{\phi ^\prime }^2 - dz^2\nonumber \\ \end{aligned}$$
(5)

in the rotating frame. It is seen that this metric is applicable for radii less than \(c/\Omega \), corresponding to the so-called light cylinder, beyond which \(g_{00}\) becomes negative (with the corresponding points having velocities greater than \(c\)) and hence from the physical point of view is not of interest [15, 16].

The famous result, based on special relativistic arguments made by Einstein, that a rotating clock at nonzero radius \(r = R\) runs slower than that sitting at the center of the disk (or very close to it) [11, 12] is clearly encoded in the above metric, from which we have \(d\tau = \sqrt{1- \frac{\Omega ^2 R^2}{c^2}} dt\) where \(dt\) is the world time recorded by the inertial/laboratory clocks as well as the one at the center of the disk. The above spacetime metric plays the same role for a centrally rotating observer as the Rindler spacetime metric

$$\begin{aligned} ds^2 = \eta _{ab} dx^a dx^b&= {(1 + a \bar{x}^{1})}^2 {(d\bar{x}^{0})}^2 \nonumber \\&-{(d\bar{x}^{1})}^2 - {(d\bar{x}^{2})}^2 - {(d\bar{x}^{3})}^2 \end{aligned}$$
(6)

with

$$\begin{aligned} \begin{aligned}&x^0 = (a^{-1} + \bar{x}^1)\sinh (a\bar{x}^0); \;\;\;\;\;\;\;\; x^2 = \bar{x}^2 \\&x^1 = (a^{-1} + \bar{x}^1)\cosh (a\bar{x}^0); \;\;\;\;\;\;\;\; x^3 = \bar{x}^3 \end{aligned} \end{aligned}$$
(7)

plays for a uniformly accelerating observer with 3-acceleration \({\mathbf {a}} = (a,0,0)\). In other words the Rindler metric in the limit \(\bar{x}^{1} \ll 1\) (i.e. for points infinitesimally close to the world line of the observer) is equivalent to the Fermi metric [17], at first order (i.e. \(\mathcal {O}( \bar{x}^{l})\) ), in the absence of rotation (i.e. \(\Omega = 0\)), while (5) in the limit \( r \ll 1\) (i.e. infinitesimally close to the centrally rotating observer) is equivalent to the Fermi metric, at the same order, in the absence of linear acceleration (i.e. \( a = 0 \)) [9]. It should be noted that the spacetime in a rotating observer’s frame (5), like Rindler spacetime, is the flat spacetime in a coordinate system which is not maximally extended due to the existence of a light cylinder in the former and the horizon in the latter. On the other hand, unlike Rindler spacetime, it is a stationary spacetime (reflected in the presence of its cross term \(dt d\phi \)) and so one needs to employ a spacetime decomposition formalism to define spatial distances and time intervals, and on their basis to prescribe suitable measurement procedures. In what follows we will employ the \(1+3\) or threading formulation of a spacetime decomposition [15] which is essentially based on sending and receiving light signals between nearby observers (refer to the appendix for a brief introduction). Although we are not going to discuss the spacetime measurement procedure here, the employment of the \(1+3\) formulation makes it clear that, in principle, we are using light signals to measure the relevant physical quantities, namely spatial distance and time intervals. Based on a \(1+3\) formulation, the spatial line element for the metric (5) is given by [15]

$$\begin{aligned} dl^2 = dr^2 + dz^2 + \frac{r^2 d{\phi ^\prime }^2}{1-\frac{\Omega ^2 r^2}{c^2}}. \end{aligned}$$
(8)

Now for a circle of radius \(r = r^\prime = R\) in the \(z=\)constant plane the circumference is given by

$$\begin{aligned} P^\prime = \int _0^{2\pi } dl = \frac{2\pi R}{\sqrt{1-\Omega ^2 {R}^2/c^2}} = \frac{P}{\sqrt{1-\Omega ^2 {R}^2/c^2}}, \end{aligned}$$
(9)

so that \(P^\prime > P\) with \(P\) the circumference of a non-rotating disk. Therefore from the rotating observer’s point of view \(P\) and \(P^\prime \) are also not equal, but the relation between the two quantities is just the opposite of that found by the inertial (laboratory) observer based on Lorentz contraction.

The interpretation of the above results goes as follows: Although the transformed spacetime is the flat spacetime in disguise, its spatial geometry now has nonzero Gaussian curvature, leading to the fact that the ratio of the circumference of a circle to its radius is larger than \(2 \pi \). We are not going to follow this disagreement on the relation between \(P\) and \(P^\prime \) from the two observers’ points of view nor discuss further the content of Ehrefest’s Paradox. But there remains a legitimate question that one might ask and that is: Are we allowed to use the GRT (1) in all the above considerations? Specially we note that the metric in the rotating frame can be employed out to a specific radius, given by \(c/\Omega \), which decreases as we increase the angular velocity. A negative answer to this question has led to the introduction of RRTs.

1.2 Relativistic rotational transformations

Our experience with Lorentz transformations intuitively leads to the expectation that GRT is an approximation valid for points near the axis of rotation having small linear (tangential) velocities. Hence for eccentric observers at large radii and/or with high angular velocities one needs to replace the GRT with a relativistic (Lorentz-type) rotational transformation to account for linear (tangential) velocities comparable to \(c\). Obviously if one could devise a proper RRT, it might be expected that either the transformation (based on its kinematical interpretation) or the spatial line element of the transformed flat spacetime metric leads to a contracted/dilated circumference for a rotating disk or any other circle of a given radius.

A comparison between the usual Lorentz transformation (LT), and GRT is useful at this point. In the case of LT the length contraction is built into the transformation itself and, since the flat spacetime line element is form invariant under the transformation, the length contraction is not expected to be tractable in the form of the corresponding spatial metric. On the other hand in the case of GRT as we noticed, the transformation (1) is devoid of any length contraction or dilation, while the transformed spatial metric (8) leads to the length dilation. An interesting RRT was introduced by Philip Franklin, a Princeton mathematician, in 1922 [18] and some 30 years later by Trocheris [19] and Takeno [20].Footnote 3 The Franklin transformation is not the only non-classical rotational transformation and there are a few other proposals such as those introduced in [21–25]. RRTs could be classified into two general categories: I—those which employ the same linear velocity distribution as in GRT [22, 23, 25] and II—those which introduce a nonlinear velocity distribution in their construction [18, 21, 24]. In the former cases the construction of the RRT is based, in one way or another, on the application of an instantaneous Lorentz transformation. For example Post uses the GRT but with a time dilation applying a \(\gamma \)-factor with a linear velocity distribution [22], while Strauss modifies the Franklin transformation by replacing its nonlinear velocity distribution by a linear one [23]. In [25] the authors introduce an RRT between inertial and non-inertial frames rotating at nonzero radii on circular orbits. Their transformation does not reduce to GRT when the orbit radius is set equal to zero. As an example of the second category, in [21], Hill introduces an RRT with a nonlinear velocity distribution in terms of Bessel functions, which reduces to the classical linear distribution near the rotation axis and approaches the upper limit of light velocity at infinity.

In the present article we will discuss the Franklin transformation and its characteristics including its advantages over the classical transformation and also its drawbacks specially with respect to the corresponding spacetime metric and show how a simple modified version of the transformation could lead to the resolution of some of these drawbacks. Obviously the main criterion for the preference of any non-classical rotational transformation over the classical one (i.e. GRT) should be the verification of its experimental consequences. For the sake of completeness we will give a brief derivation of Franklin transformation in the next section.

2 Franklin transformation

Taking two coordinate frames, \(S\) and \(S^\prime \), with \(S^\prime \) uniformly rotating about \(S\), Franklin requires the following plausible conditions and properties to be valid on the relation between the two frames [18]:

  1. 1.

    The velocity of a fixed point in \(S^\prime \) with respect to the point in \(S\) with which it momentarily coincides is independent of the time, and is the same for all points at a given distance from the axis of rotation.

  2. 2.

    For the two concentric circles \(r^\prime =r=\) Constant, the equations of the transformation are similar to those for a Lorentz boost (say along the x-direction) with \(r\phi \) the arclength replacing the linear distance (say x). These two properties lead to the following transformation law:

    $$\begin{aligned}&t^\prime = \gamma (r)\left( t - v(r) r\phi /c^2 \right) ; \;\;\; r^\prime = r\nonumber \\&r^\prime \phi ^\prime = \gamma (r) \left( r \phi - v(r) t \right) ; \;\;\; z^\prime = z, \end{aligned}$$
    (10)

    in which \(\gamma =\frac{1}{\sqrt{1-v(r)^2/c^2}}\) is the Lorentz-type factor with velocity \(v(r)\) to be determined through the last property which is as follows.

  3. 3.

    The velocity of a point at the distance \(r^\prime + \Delta r^\prime \) from the axis with respect to a point at the distance \(r^\prime \) from the axis (both in the system \(S^\prime \)) is given by \(\Omega \Delta r^\prime \). In other words two different points at two different radii with two different rotational velocities are taken as the analogs of two inertial frames moving uniformly with respect to one another.

In effect, the last property is a prescription for the velocity composition law, out of which the nontrivial form of the rotational velocity is obtained. For two points \(B\) and \(C\) at radii \(r_B = r \) and \(r_C = r + \Delta r \) with velocities \(v(r)\) and \(v(r + \Delta r)\) (with respect to the point \(A\) at the center of the disk), respectively, the composition law reads

$$\begin{aligned} v_{BC} = \frac{v_{AC} - v_{AB}}{1 - \frac{v_{AC}v_{AB}}{c^2}} \Rightarrow \Omega \Delta r = \frac{v(r + \Delta r) - v(r)}{1 - \frac{v(r + \Delta r) v(r)}{c^2}}. \end{aligned}$$
(11)

In the limit \(\Delta r \rightarrow 0\) this leads to the velocity relation

$$\begin{aligned} v(r) = c \tanh (\Omega r/c). \end{aligned}$$
(12)

Substituting (12) in (10), the explicit form of the Franklin transformation (FT) is given by

$$\begin{aligned} t^\prime&= \cosh (\Omega r/c)t - \frac{r}{c} \sinh (\Omega r/c) \phi ; \;\;\; r^\prime = r\nonumber \\ \phi ^\prime&= \cosh (\Omega r/c) \phi - \frac{c}{r} \sinh (\Omega r/c) t; \;\;\; z^\prime = z. \end{aligned}$$
(13)

For points close to the rotation axis i.e. when \(\frac{\Omega r}{c} \ll 1\) Footnote 4 this transformation reduces to the classical Galilean transformation by neglecting terms of order \(\frac{\Omega ^2 r^2}{c^2}\) and higher. These transformations form a group and the inverse transformation is given by changing \(\Omega \) to \(-\Omega \). One of the advantages of this transformation over the old Galilean one is in the definition of the velocity given in (12), which approaches \(c\) at \(r\rightarrow \infty \) (i.e. the light cylinder is not at a finite distance but is sent to infinity) and reduces to the Newtonian value \(v=\Omega r\) for points near the axis. A formal comparison with a pure Lorentz transformation as a hyperbolic rotation reveals that it is the linear velocity \(v=\Omega r\) in (12) which now plays the role of some kind of rapidity.

Another obvious difference between the Franklin transformation and the Lorentz transformation, when FT is rewritten in the following form:

$$\begin{aligned} \begin{aligned} ct^\prime&= \frac{1}{\sqrt{1-\frac{v(r)^2}{c^2}}}\left( ct - \frac{v(r)}{c} r\phi \right) ; \;\;\; r^\prime = r\\ r \phi ^\prime&= \frac{1}{\sqrt{1-\frac{v(r)^2}{c^2}}}\left( r\phi - \frac{v(r)}{c} ct\right) ; \;\;\; z^\prime = z, \end{aligned} \end{aligned}$$
(14)

is the fact that velocity entering the definition of FT unlike LT is not a constant but an \(r\)-dependent quantity. This will lead to undesirable results in the case of FT when we consider the transformed spacetime metric (i.e. in the rotating frame) and the corresponding spatial distances and time intervals. It will be shown that neither will reduce to their expected expressions at small rotational velocities (i.e. when \(\frac{\Omega r}{c} \ll 1\)). But before discussing these issues, it seems appropriate to discuss the interpretation of FT as compared to those of GRT and LT.

2.1 Interpretation of FT

An important issue about the Franklin transformation, which seems to be taken for granted in most of the previous studies, is its interpretation as the transformation of the spacetime coordinates of an event between two frames; a non-rotating (inertial) frame and another one rotating uniformly about their common axis. This is the same usual interpretation attributed to the GRT as illustrated in Fig. 1. But the characteristics of FT would prevent one to easily interpret this transformation as a kinematical one. The main characteristic acting so is the radial dependence of the velocity entering the transformation. This velocity distribution is attributed to the rigid arms of the rotating frame (or disk points if the frame is attached to a uniformly rotating rigid disk) and so, taking into account the fact that in FT the non-rotating and rotating frames share the rotation axis, the transformation of the arclengths in FT (which is given in terms of this velocity) is only valid for disk points. By the above reasoning, it seems more reasonable to look at FT as a transformation specially tailored for the problem of a rotating disk in which events are nothing but different points of a rotating disk at different times. In other words one should be cautious in interpreting FT as a kinematical transformation relating coordinates of an event in a rotating frame to that of an inertial non-rotating one. For example, based on a kinematical interpretation of FT, for events on the rotation axis i.e. for \(r = r^\prime = 0\) (where the cylindrical coordinate system is degenerate and \(v(0)= 0\)), FT reduces exactly to GRT and this has no clear interpretation. If FT is going to be elevated to a kinematical transformation one needs to modify and reinterpret it.

3 Spacetime Metric and Spatial Geometry in the Rotating Frame through a Franklin transformation

Using the inverse of the Franklin transformation in its differential form,

$$\begin{aligned} c dt \!&=\! \cosh (\Omega r/c) c dt^\prime \!+\! r \sinh (\Omega r/c) d\phi ^\prime \!+\! A_1 dr; \;\;\; dr \!=\! dr^\prime \nonumber \\ r d\phi \!&=\! \cosh (\Omega r/c) r d\phi ^\prime \!+\! \sinh (\Omega r/c) c dt^\prime \!+\! A_2 dr; \;\;\; dz \!=\! dz^\prime \nonumber \\ A_1&= \sinh (\Omega r/c) (\phi ^\prime + \Omega t^\prime ) + \cosh (\Omega r/c)\left( \frac{\Omega r}{c} \phi ^\prime \right) \nonumber \\ A_2&= \sinh (\Omega r/c) \left( \frac{\Omega r}{c} \phi ^\prime - c t^\prime /r\right) + \cosh (\Omega r/c)(\Omega t^\prime ), \end{aligned}$$
(15)

and substituting in (4) the spacetime metric in the rotating frame is given by

$$\begin{aligned} ds^2&= c^2 {dt^\prime } ^2 - (1 - A_1^2 + A_2^2 ) dr^2 - r^2 d{\phi ^\prime }^2 - dz^2 +\nonumber \\&2 c \left( A_1 \cosh (\Omega r/c)- A_2 \sinh (\Omega r/c)\right) dr dt^\prime \nonumber \\&+ 2 \left( A_1\sinh (\Omega r/c) - A_2 \cosh (\Omega r/c)\right) r dr d{\phi ^\prime }. \end{aligned}$$
(16)

Unlike the cross term in (5), which is the typical \(dt^\prime d{\phi ^\prime }\) term representing the rotational character of the metric, the cross terms in the above metric include \(dr dt^\prime \) and \(dr d{\phi ^\prime }\) terms and that is why the reduction of this metric form to (5) for \(\Omega r/c \ll 1\) is not expected. Also it should be noted that due to the explicit appearance of \(\phi ^\prime \) and \(t^\prime \) in (16) both the temporal and the angular isometries present in (5) are now lost.

3.1 Spatial distances and time intervals

From the above result on the spacetime metric it is obviously not expected that the spatial geometry corresponding to (16) is reducible to the one given by (8) in the limit \(\Omega r/c \ll 1\). Indeed using the \(1+3\) decomposition [Eq. (A2)] the spatial metric corresponding to (15) is given by

$$\begin{aligned} dl^2&= \{1 - A_1^2 + A_2^2 + 4c^2 [ A_1 \cosh (\Omega r/c)- A_2 \sinh (\Omega r/c)]^2\} dr^2 +\nonumber \\&-2 [ A_1\sinh (\Omega r/c) - A_2 \cosh (\Omega r/c)] r dr d{\phi ^\prime } + dz^2 + {r^2 d{\phi ^\prime }^2},\nonumber \\ \end{aligned}$$
(17)

through which the circumference of a disk with radius \(r=R\) in the \(z=constant\) plane is given by the Euclidean value \(2 \pi R\) compared to the non-Euclidean value (9) obtained through the Galilean transformed spatial metric (8). It should be noted that despite the above fact the Gaussian curvature of the spatial metric is not zero indicating the non-Euclidean nature of the spatial metric [18]. It should also be noted from (16) that the proper time interval in the rotating frame, for a clock fixed at \(r=R\), is given by

$$\begin{aligned} d\tau ^\prime = dt^{\prime } = \cosh ^{-1} (\Omega R/c) dt \end{aligned}$$
(18)

where use is made of (15). In the limit \(\frac{\Omega R}{c} \ll 1\) the above relation reduces to that obtained from the Galilean transformed metric for rotating clocks at nonzero radii i.e. \(d\tau ^\prime = \sqrt{1-\frac{\Omega ^2 R^2}{c^2}} dt\). On the other hand, as we discussed earlier, one could relate spatial distances and time intervals not only through the metric obtained from the Franklin transformation but also through the coordinate transformations themselves according to their kinematical interpretation. Obviously using the formal analogy between FT and LT one can obtain a relation between spatial distances (arclengths) and time intervals in the two coordinate systems as follows:

$$\begin{aligned} \Delta t&= \frac{1}{\sqrt{1- \frac{v^2}{c^2}}} \Delta t^\prime ,\end{aligned}$$
(19)
$$\begin{aligned} \Delta l&= R\Delta \phi = \sqrt{1- \frac{v^2}{c^2}} R\Delta \phi ^\prime = \sqrt{1- \frac{v^2}{c^2}} \Delta l^\prime , \end{aligned}$$
(20)

where in (19) we employed \(\Delta \phi ^\prime = 0\) (see Fig. 2) and in (20) we used the simultaneous measurements (\(\Delta t = 0\)) of both ends of the corresponding arclength. The above equations correspond to the time dilation and length contraction of clocks and rulers at rest in the rotating observer’s frame \(S^\prime \), respectively. With \(v=c\tanh (\frac{\Omega R}{c})\) at radius \(r=R\), the above results are consistent with what one expects from applying a special relativistic length contraction (based on LT) to a rotating disk for \(\frac{\Omega R}{c} \ll 1\). It seems that once again we are faced with Ehrenfest’s Paradox, in the sense that using the spatial geometry given by Eq. (17) implies that the circumference of a rotating disk is the same as the circumference of the non-rotating disk, whereas, employing the Franklin transformation, the circumference of a rotating disk is found to be shorter than the one non-rotating.

3.2 Angular velocity of a test particle/disk point in the two frames related by FT

Using the differential Franklin transformation (15) to calculate the rotational frequency in the inertial observer’s frame we find

$$\begin{aligned} \omega = \frac{d\phi }{dt} = \frac{ \cosh (\Omega r/c) d\phi ^\prime + \frac{c dt^\prime }{r}\sinh (\Omega r/c) + \frac{A_2}{r}dr^\prime }{ \cosh (\Omega r/c) dt^\prime + \frac{r}{c}\sinh (\Omega r/c) d\phi ^\prime + \frac{A_1}{c}dr^\prime }\nonumber \\ \end{aligned}$$
(21)

from which for the frequency in the rotating frame we have

$$\begin{aligned} \omega ^\prime \!=\! \frac{d\phi ^\prime }{dt^\prime } \!=\! \frac{\omega \cosh (\Omega r/c) \!-\! \frac{c}{r} \sinh (\Omega r/c) \!+\! \frac{dr}{dt^\prime }(\frac{A_1}{c} \omega \!-\! \frac{A_2}{r})}{\cosh (\Omega r/c) \!- \!\omega \frac{r}{c} \sinh (\Omega r/c)}.\nonumber \\ \end{aligned}$$
(22)

In the limit where \((\Omega r/c) \ll 1\), the above expression reduces to the classical relation (3)

$$\begin{aligned} \omega ^\prime \approx \omega - \Omega . \end{aligned}$$
(23)

4 Modified Franklin transformation: its interpretation and the spacetime metric in the rotating frame

As is obvious from its derivation, the Franklin transformation was obtained in close analogy with the usual Lorentz transformation for inertial frames moving with constant velocities relative to one another. Our starting point for the modification of the Franklin transformation is its main formal difference from the Lorentz transformation which is the dependence of relative velocity on the radial coordinate (i.e. \(v \equiv v(r)\)) in (12)). It is clear from Franklin’s derivation of (12) that this coordinate-dependent velocity is a direct consequence of applying the relativistic composition law to high rotational velocities. Indeed the nonlinear velocity relation (12) could also be obtained by the requirement that for any two infinitesimally close points (separated by a radial distance \(dr\)) on a uniformly rotating rigid rod (divided into \(n\) infinitesimal segments), the difference in their linear velocities is given by \(\Omega d r\) [26]. Then using the relativistic composition law iteratively to find the velocity at a finite distance along the rod, in the limit \(n\rightarrow \infty \), one ends up with the velocity distribution (12). Since the kinematical transformation is supposed to give the relation between coordinates assigned to events by two observers, an inertial non-rotating one (laboratory observer/frame) and a non-inertial rotating observer at a given radius \(R\), going back to the transformation law (by formal analogy with LT), it is the observer velocity at that radius (i.e. \(v = c \tanh (R\Omega /c)\)) which should enter the transformation law. Indeed it has already been pointed out in some literature [27, 28], without further clarification, that a Franklin transformation leads to inconsistencies if one neglects the fact that it is determined at \(r=\)constant as well as at \(z=\)constant. We have mentioned some of these inconsistencies in the previous sections, and so by the above argument we introduce the following modified Franklin transformation (MFT):

$$\begin{aligned} t^\prime&= \cosh (\Omega R/c)t - \frac{R}{c} \sinh (\Omega R/c)\phi ; \;\;\; r^\prime = r\nonumber \\ \phi ^\prime&= \cosh (\Omega R/c) \phi - \frac{c}{R} \sinh (\Omega R/c) t; \;\;\; z^\prime = z. \end{aligned}$$
(24)

This could be obtained by changing the second and third steps in the derivation of the Franklin transformation by assigning observers to the disk points at a given radius \(r=R\), for which the velocity with respect to the inertial observers, using the third step, is found to be \(v = c \tanh (R\Omega /c)\). In terms of this velocity the MFT could be written as follows:

$$\begin{aligned} \begin{aligned}&ct^\prime = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left( ct - \frac{v}{c} R\phi \right) ; \;\;\; r^\prime = r\\&R \phi ^\prime = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left( R\phi - \frac{v}{c} ct\right) ; \;\;\; z^\prime = z. \end{aligned} \end{aligned}$$
(25)

This is indeed a simple, physical modification with profound consequences. To see its effects, first of all we find the equivalent metric by finding the inverse differential transformation, which is

$$\begin{aligned} dt&= \cosh (\Omega R/c)dt^\prime + \frac{R}{c} \sinh (\Omega R/c)d\phi ^\prime ; \;\;\; dr = dr^\prime \nonumber \\ d\phi&= \cosh (\Omega R/c) d\phi ^\prime + \frac{c}{R} \sinh (\Omega R/c) dt^\prime ; \;\;\; dz = dz^\prime , \end{aligned}$$
(26)

and substituting them in the inertial frame’s flat spacetime metric (4) upon which we end up with (taking \(\beta = \frac{R \Omega }{c}\))

$$\begin{aligned} ds^2&= c^2\cosh ^2\beta \left( 1- \frac{{r}^2}{R^2}\tanh ^2\beta \right) {dt^\prime }^2 - {dr}^2\nonumber \\&\quad - {r}^2 \cosh ^2\beta \left( 1- \frac{R^2}{{r}^2}\tanh ^2\beta \right) d{\phi ^\prime }^2\nonumber \\&\quad + 2cR \sinh \beta \cosh \beta \left( 1- \frac{{r}^2}{R^2}\right) dt^\prime d\phi ^\prime - {dz}^2. \end{aligned}$$
(27)

Note that now there is a radial coordinate \(r\) as well as a constant radius \(R\) which specifies a class of observers fixed at that radius. This will allow a kinematical interpretation of the above MFT. In other words no matter what the constant radius in (24), this transformation gives a prescription of how the temporal (\(t \; and \; t^\prime \)) and angular (\(\phi \; and \; \phi ^\prime \)) coordinates of an event in the two frames are related. Indeed, it is now that one could justify the division of the originally introduced transformation of arclengths (\( r^\prime \phi ^\prime \; \& \; r\phi \) for an event at radial coordinate \(r=r^\prime \)) by the common radial coordinate leading to the transformation of angular coordinates \(\phi \; \mathrm{and} \; \phi ^\prime \). In other words the angular coordinates are defined using the arclengths at the radial position \(r=r^\prime = R\) of the eccentric observer. It should be noted that spatial coordinate measurements by the inertial as well as the eccentric (non-inertial) observers are made from the axis of rotation as a preferred direction and the eccentric observers carry their own clocks but use the triad axes of the centrally rotating observer to designate spatial coordinates to events. The presence of \(R\) as a constant in the transformed flat spacetime as given by (26) may look strange but obviously it is no stranger than the appearance of \(\Omega \) in (1) or in (13). Both \(\Omega \) and \(R\) are transformation parameters, one (\(\Omega \)) from an inertial observer’s frame to a centrally rotating frame and the other (\(R\)) from the centrally rotating observer’s frame to a set of equivalent rotating observers at radius \(R\) (non-inertial observers). Indeed they are now combined to form the new transformation parameter, which is the velocity \(v = c \tanh (R\Omega /c)\) (or \(R\Omega \) for that matter). Also compared to the case of the Rindler metric, in which the observer’s acceleration enters the spacetime metric (6), the appearance of the parameter \(R\) which determines an eccentric observer’s velocity and acceleration is expected on the same grounds. Further it should not be forgotten that the spacetime in the rotating coordinates is always flat, for a coordinate transformation never changes the nature of a spacetime whether it is the old Galilean transformation (5) or FT (both having the parameter \(\Omega \)) or MFT (with parameter \(R\Omega \)), and it is only the spatial metric in the rotating observer’s frame which loses its Euclidean character. Obviously the metric (27) is of interest for radial distances

$$\begin{aligned} r \leqslant \frac{\beta }{|\tanh \beta |}\left( \frac{c}{\Omega }\right) , \end{aligned}$$
(28)

and in the classical Galilean limit where \(\beta \ll 1\) (i.e. close to the rotation axis) it reduces to

$$\begin{aligned} ds^2&= c^2 \left( 1- \frac{r^2 \Omega ^2}{c^2}\right) {dt^\prime }^2 - {dr}^2 - r^2 \left( 1- \frac{R^2}{r^2}\beta ^2\right) d{\phi ^\prime }^2 \nonumber \\&\qquad + 2R^2 \Omega \left( 1- \frac{r^2}{R^2}\right) dt^\prime d\phi ^\prime - {dz}^2, \end{aligned}$$
(29)

which in turn reduces to the spacetime metric (5) under the extra condition that the radial coordinates of the events under consideration are larger than or equal to \(R\). In other words, for observers close to the axis the range \(R \leqslant r < \frac{c}{\Omega }\) replaces the range \(0 \leqslant r < \frac{c}{\Omega }\).Footnote 5 So, unlike the Franklin transformation, not only the transformation itself, but also the metric in the rotating frame reduces to the Galilean one in the limit \(\beta \ll 1\). It should be noted that for \(r = R\) in (27), i.e. at the radial position of the eccentric observer, the metric reduces to that of a spatially Euclidean flat spacetime (5) of an inertial observer, i.e. at \(r = R\) the form of the spacetime metric is invariant under MFT. This is a feature of (29) which is somewhat shared with the Fermi metric of an accelerated, spinning observer in a flat or curved background. Recall the feature of the Fermi metric that on the observer’s world line reduces to the Minkowski metric [17]. Now the reduction of MFT to exact GRT, by setting \(R=0\) in (24), while (27) reduces to (5), has a consistent interpretation (in contrast to setting \(r=0\) in FT which was shown to lead to inconsistencies with respect to its kinematical interpretation); it corresponds to the centrally rotating observer who is at rest with respect to the non-rotating inertial (laboratory) observer, and so their observations are naturally related through GRT. So in our setting of the problem of rotation and rotating frames, we have drastically changed the scenario by introducing non-inertial observers fixed at nonzero radii on the disk and also introducing the MFT as the kinematical transformation between the coordinates assigned to events by these observers and the inertial ones.

In the next two subsections we find how the spatial and time intervals in the rotating and inertial frames are related through MFT. We also discuss the energy and angular velocity of a test particle (disk point) in the two frames. It should be noted that the eccentric observers use a local Cartesian coordinate system attached to a rigidly rotating disk at their position such that its axes are always parallel to the axes of the Cartesian coordinate system used by the centrally rotating observer. In this way the radial coordinates assigned to events by all observers are measured from the rotation axis.

4.1 Spatial line element and spatial distances

Using the \(1+3\) approach (Appendix A), the metric (27) could be written in the following form:

$$\begin{aligned} ds^2 \!=\! c^2\cosh ^2\beta \left( 1\!-\! \frac{r^2}{R^2}\tanh ^2\beta \right) \left( {dt^\prime } \!-\! A_\alpha d{x^\prime }^\alpha \right) ^2 \!-\! dl^2,\nonumber \\ \end{aligned}$$
(30)

in which the spatial line element is given by

$$\begin{aligned} dl^2&= dr^2 + dz^2 + \left( r^2\cosh ^2\beta \left( 1-\frac{R^2}{r^2}\tanh ^2\beta \right) \right. \nonumber \\&\qquad \left. +\, R^2 \frac{\sinh ^2\beta (1-\frac{r^2}{R^2})^2}{(1-\frac{r^2}{R^2}\tanh ^2\beta )}\right) {d\phi ^\prime }^2, \end{aligned}$$
(31)

and the gravitomagnetic potential is

$$\begin{aligned} A_\alpha \equiv A_{\phi ^\prime } \delta ^{\phi ^\prime }_\alpha = \left( 0, 0, -R \frac{\tanh \beta (1-\frac{r^2}{R^2})}{(1-\frac{r^2}{R^2}\tanh ^2\beta )}\right) . \end{aligned}$$
(32)

Now one could find the circumference of a circle/disk of radius \(r\) in \(z= constant\) plane using the above line element as

$$\begin{aligned} L_{MFT} = \int dl&= \int _0^ {2 \pi } \left( r^2\cosh ^2\beta (1-\frac{R^2}{r^2}\tanh ^2\beta )\right. \nonumber \\&\quad +\left. R^2 {\frac{\sinh ^2\beta (1-\frac{r^2}{R^2})^2}{(1-\frac{r^2}{R^2}\tanh ^2\beta )}}\right) ^{1/2}{d\phi ^\prime }. \end{aligned}$$
(33)

It is an easy task to show that the above spatial line element (27) reduces to the classical spatial element (8) in the limit of \(\beta \ll 1\). Also it is noted that for an observer fixed at nonzero radius \(R\), a circle at that radius, i.e. \(r=R\), has the Euclidean circumference \(2\pi R\) as expected from the form invariance of the metric (27) at that radius. On the other hand using the MFT (26), one obtains the following relation between the differential arclengths (at radius \(R\)) as measured by the rotating and inertial observers:

$$\begin{aligned} R d\phi = \cosh (\Omega R/c) R d\phi ^\prime . \end{aligned}$$
(34)

In other words as in the case of FT, again we are faced with the Ehrenfest’s paradox in the sense that an arclength of a rotating disk, measured by the inertial observer, is the same as that of the non-rotating disk if the spacetime metric is employed but different if MFT is used. The relation between length measurements by the inertial and rotating observers, based on MFT and the hypothesis of locality [29], are discussed and compared in [30].

4.2 Time intervals and their relations

As in the case of FT one can obtain the relation between proper time intervals in the inertial observer’s frame and that of a rotating one at a nonzero radius \(R\) using the MFT. Using the MFT or its corresponding metric (27) in the rotating frame, we find that the proper time intervals at the rest frame of the clock at \(r=R\) and that at the center of the disk \(r = 0\) (measured by an inertial observer) are related by

$$\begin{aligned} {d\tau _0}= \cosh \beta {d\tau }, \end{aligned}$$
(35)

corresponding to time dilation of rotating clock readings as measured by an observer in the inertial frame. This is the same relation as obtained in the case of FT (see Eq. (18)). In the limit where \(\beta \ll 1\) the above relation for finite time intervals reduces to

$$\begin{aligned} {\Delta \tau _0} \approx \left( 1 + \frac{\Omega ^2}{2c^2}{R}^{2} + \frac{5}{24}\frac{\Omega ^4}{c^4}{R}^{4}\right) {\Delta \tau }, \end{aligned}$$
(36)

which up to the second order in \(\beta \) agrees with the relation based on applying instantaneous Lorentz transformation along with the linear velocity distribution employed in GRT [30]. An application of the instantaneous Lorentz transformation is experimentally verified in the measurements of circulating muons lifetime at CERN [31], but one should be cautious that in applying MFT the ticking clock is fixed at a nonzero radius on a rotating platform and not forced to move on a circular path by the application of electromagnetic fields. So if one is going to test the above theoretical prediction in an experimental setup, it should be a setup with an unstable particle fixed at a nonzero radius on a rotating platform. The same argument as above could be used to discuss the transverse Doppler effect as a rotational phenomenon in the context of MFT [30].

4.3 Energy of a test particle

The energy of a particle of mass \(m\) moving with 3-velocity \(v\) in a stationary field is shown in Appendix A to be given by

$$\begin{aligned} E = \frac{mc^2 \sqrt{g_{00}}}{\sqrt{1-\frac{v^2}{c^2}}}, \end{aligned}$$
(37)

which is a conserved quantity. For a particle fixed at a constant radius \(R\) on the rotating frame (e.g. on a rigidly rotating disk), in the comoving frame (i.e. \(v=0\)), which is the rotating frame of the eccentric observer at \(R\), the same energy is given by \(E^\prime =mc^2 \sqrt{g_{00}(r=R)}\) so that Eq. (37) could be rewritten as follows:

$$\begin{aligned} E = \frac{E^\prime }{\sqrt{1-\frac{v^2}{c^2}}}. \end{aligned}$$
(38)

Now using the fact that in MFT the 3-velocity at radius \(R\) is given by \(v=c\tanh (R\Omega /c)\), the above relation reduces to,

$$\begin{aligned} E \!=\! \cosh (R\Omega /c) {E^\prime } \approx \left( 1 \!+\! \frac{\Omega ^2}{2c^2}{R}^{2} \!+\! \frac{5}{24}\frac{\Omega ^4}{c^4}{R}^{4}\right) {E^\prime },\qquad \end{aligned}$$
(39)

which is again, up to the second order in \(\beta \), in agreement with the relation based on applying instantaneous Lorentz transformation along with the linear velocity distribution on a uniformly rotating disk. Obviously both the above result and the relation (36), are direct consequences of the nonlinear velocity distribution \(v = c\tanh (R\Omega /c)\) on the disk.

4.4 Angular velocity of a test particle/disk in MFT

In terms of the kinematical interpretation, the angular velocities of a test particle in the two frames related by the MFT are found by employing the inverse differential rotation (26) so that

$$\begin{aligned} \omega = \frac{d\phi }{dt} = \frac{ \cosh \beta d\phi ^\prime + \frac{c}{R}\sinh \beta dt^\prime }{\cosh \beta dt^\prime + \frac{R}{c}\sinh \beta d\phi ^\prime }, \end{aligned}$$
(40)

leading to

$$\begin{aligned} \omega ^\prime = \omega \left( 1 + \frac{R}{c}\tanh \beta \right) - \frac{c}{R}\tanh \beta , \end{aligned}$$
(41)

in which we used the fact that \(\omega ^\prime = \frac{d\phi ^\prime }{dt^\prime }\). As in the case of FT, it could easily be seen that in the limit of \(\beta \ll 1\) the above relation reduces to the classical relation (3), which was found through the Galilean transformation. On the other hand, from an inertial observer’s point of view, the angular velocity of the disk (or its points) is \(\frac{d\phi }{dt}=\Omega \), and so the above relation for the disk itself changes into

$$\begin{aligned} \omega ^\prime = \Omega \left( 1 + \frac{R}{c}\tanh \beta \right) - \frac{c}{R}\tanh \beta ; \end{aligned}$$
(42)

in other words, in MFT, for the eccentric observers, the angular velocity of the rotating disk depends on the radial position of the observer. But close to the centrally rotating observers, i.e. in the limit \(\beta \ll 1\), the expectation based on GRT is restored where \(\omega ^\prime \approx 0\).

5 Non-invariance of electromagnetism under (modified) Franklin transformation

In some of the studies in the literature discussing the Franklin transformation it is claimed that this transformation restores the full Lorentz (-type) covariance of electrodynamics [28, 32]. Here we show in detail that such a claim is not correct and the covariance mentioned in those studies only is satisfied by implicitly fixing the radial coordinate in the transformation (i.e. \(r=\)constant), in which case the transformed metric (16) retains its Euclidean form by setting \(dr=0\). But for a general transformation this is not true as shown below for the MFT, in which case again, the covariance is only restored at the position of the observer i.e. at \(r=R\) where the spacetime, as discussed and interpreted previously, is Euclidean form invariant.

To be specific, under a Lorentz transformation, the Maxwell equations are invariant in the sense that they retain the same three-dimensional vector form in the transformed coordinates, and consequently the electromagnetic wave equation which is obtained from these equations is also form invariant. In what follows we show that neither the Maxwell equations nor the wave equation are form invariant under Franklin transformation. To make life easier we show this in the absence of any EM sources and for the modified Franklin transformation, but the same result (non-invariance of electromagnetism) holds for the original Franklin transformation. From the modified Franklin transformation (24) we have the following relation between the partial derivatives:

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial t^\prime } = \cosh \beta \frac{\partial }{\partial t} + \frac{1}{R} \sinh \beta \frac{\partial }{\partial \phi }\\&\frac{\partial }{\partial \phi ^\prime } = R\sinh \beta \frac{\partial }{\partial t}+ \cosh \beta \frac{\partial }{\partial \phi }\\&\frac{\partial }{\partial r^\prime } = \frac{\partial }{\partial r}; \;\;\;\; \frac{\partial }{\partial z^\prime } = \frac{\partial }{\partial z}. \end{aligned} \end{aligned}$$
(43)

5.1 Non-invariance of wave equation under MFT

Using the above relations the wave equation in the unprimed coordinates (inertial frame),

$$\begin{aligned} \frac{\partial ^{2}\psi }{\partial {{t}^{2}}}-\frac{1}{r}\partial _{r}\left( r{\frac{\partial \psi }{\partial r}}\right) - \frac{1}{r^{2}}\frac{\partial ^{2}\psi }{\partial {{\phi }^{2}}}-\frac{\partial ^{2}\psi }{\partial {z^{2}}}=0, \end{aligned}$$
(44)

transforms into

$$\begin{aligned}&\left( \frac{r^{2}\cosh ^{2}\beta -R^2\sinh ^{2}\beta }{r^2}\right) \frac{\partial ^{2}\psi }{\partial {{t^\prime }^{2}}}\nonumber \\&\quad +2\left( \frac{(R^2-r^{2})\sinh \beta \cosh \beta }{Rr^2}\right) \frac{\partial ^{2}\psi }{\partial {t^\prime }\partial {\phi ^\prime }} -\frac{1}{r}\partial _{r}\left( r{\frac{\partial \psi }{\partial r}}\right) \nonumber \\&\quad + \left( \frac{r^{2}\sinh ^{2}\beta -R^2\cosh ^{2}\beta }{R^2r^2}\right) \frac{\partial ^{2}\psi }{\partial {{\phi ^\prime }^{2}}}-\frac{\partial ^{2}\psi }{\partial {z^{2}}}=0 \end{aligned}$$
(45)

under MFT, i.e. the wave equation is not form invariant under MFT. The same result could also be obtained by using the metric corresponding to MFT [Eq. (27)] and the following general form of the wave equation in a curved background with metric \(g_{ij}\):

$$\begin{aligned} {\Box }{\psi }=\frac{1}{\sqrt{g}}\frac{\partial }{\partial {q_i}}\left( g^{1/2}g^{ik}\frac{\partial \psi }{\partial {q_k}}\right) =0 \end{aligned}$$
(46)

where \(q_i=t^\prime ,r,\phi ^\prime ,z\).

5.2 Non-invariance of Maxwell equations under MFT

To obtain the (source-free) Maxwell equations for a rotating observer from those in the frame of an inertial observer related through MFT we use the field tensor in the spacetime of a rotating observer (MFT metric) given by

$$\begin{aligned} {F^\prime }_{ij}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} -\frac{A}{R}{E^\prime }_r &{} -{r}{E^\prime }_{\phi ^\prime } &{} -\frac{A}{R}{E^\prime }_z \\ \frac{A}{R}{E^\prime }_r &{} 0 &{} -\frac{\tilde{A}}{A}{E^\prime }_r+\frac{R{r}}{A}{B^\prime }_z &{} -{B^\prime }_{\phi ^\prime } \\ {r}{E^\prime }_{\phi ^\prime } &{} \frac{\tilde{A}}{A}{E^\prime }_r-\frac{R{r}}{A}{B^\prime }_z &{} 0 &{} \frac{\tilde{A}}{A}{E^\prime }_z+\frac{R{r}}{A}{B^\prime }_r \\ \frac{A}{R}{E^\prime }_z &{} {B^\prime }_\phi &{} -\frac{\tilde{A}}{A}{E^\prime }_z-\frac{R{r}}{A}{B^\prime }_r &{} 0 \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$
(47)

where

$$\begin{aligned}&A=\sqrt{R^2\cosh ^{2}\beta -r^{2}\sinh ^{2}\beta }\quad \mathrm{and}\nonumber \\&\tilde{A}=(-R^2+r^{2})\sinh \beta \cosh \beta , \end{aligned}$$
(48)

so that the inhomogeneous equations

$$\begin{aligned} \frac{1}{\sqrt{g}}\,\partial _{i}(\sqrt{g}{F^\prime }^{ij})= 0 \end{aligned}$$
(49)

are given by

$$\begin{aligned}&\partial _r\left[ r\left( \frac{R}{A}{E^\prime }_r-\frac{\tilde{A}}{r{A}}{B^\prime }_z\right) \right] +\partial _{\phi ^\prime }({E^\prime }_{\phi ^\prime })\nonumber \\&\quad +\partial _z\left[ r(\frac{R}{A}{E^\prime }_z+\frac{\tilde{A}}{A}{B^\prime }_r)\right] =0,\end{aligned}$$
(50)
$$\begin{aligned}&\frac{R}{A}\partial _{t^\prime } {E^\prime }_r-\frac{\tilde{A}}{r{A}}\partial _{t^\prime } {B^\prime }_z-\frac{A}{r{R}}\partial _{\phi ^\prime }{{B^\prime }_z}+\partial _z{{B^\prime }_{\phi ^\prime }}=0,\end{aligned}$$
(51)
$$\begin{aligned}&\partial _{t^\prime } {E^\prime }_{\phi ^\prime }+\partial _r\left( \frac{A}{R}{B^\prime }_z\right) -\partial _z\left( \frac{A}{R}{B^\prime }_r\right) =0,\end{aligned}$$
(52)
$$\begin{aligned}&\frac{r{R}}{A}\partial _{t^\prime } {E^\prime }_z+\frac{\tilde{A}}{A}\partial _{t^\prime } {B^\prime }_r-\partial _r\left( r{{B^\prime }_{\phi ^\prime }}\right) +\frac{A}{R}\partial _{\phi ^\prime }{{B^\prime }_r}=0, \end{aligned}$$
(53)

respectively, for \(j=0,1,2,3\). Also the homogeneous equations

$$\begin{aligned} \partial _{[i}{{F^\prime }_{jk]}}=0 \end{aligned}$$
(54)

give rise to

$$\begin{aligned}&\partial _r\left( \frac{\tilde{A}}{A}{E^\prime }_z+\frac{R{r}}{A}{B^\prime }_r\right) +\partial _{\phi ^\prime }{{B^\prime }_{\phi ^\prime }}+\partial _z(-\frac{\tilde{A}}{A}{E^\prime }_r+\frac{R{r}}{A}{B^\prime }_z)=0,\end{aligned}$$
(55)
$$\begin{aligned}&\partial _{t^\prime }\left( -\frac{\tilde{A}}{A}{E^\prime }_r+\frac{R{r}}{A}{B^\prime }_z\right) +\partial _r(r{{E^\prime }_{\phi ^\prime }})-\partial _{\phi ^\prime }\left( \frac{A}{R}{E^\prime }_r\right) =0,\end{aligned}$$
(56)
$$\begin{aligned}&\partial _{t^\prime } {B^\prime }_{\phi ^\prime } -\partial _r\left( \frac{A}{R}{E^\prime }_z)+\partial _z(\frac{A}{R}{E^\prime }_r\right) =0,\end{aligned}$$
(57)
$$\begin{aligned}&\frac{\tilde{A}}{A}\partial _{t^\prime } {E^\prime }_z+\frac{r{R}}{A}\partial _{t^\prime } {B^\prime }_r+\frac{A}{R}\partial _{\phi ^\prime }{{E^\prime }_z}-\partial _z\left( r{{E^\prime }_{\phi ^\prime }}\right) =0. \end{aligned}$$
(58)

These equations are different in form from those obtained in the non-rotating inertial frame which are given by the above equations with \(A=R\) and \(\tilde{A} = 0\). On the other hand in the limit \(\beta \ll 1\), where MFT reduces to GRT, from (48) we have \(A\approx R\) and \(\tilde{A} \approx 0\), i.e. the above homogeneous equations retain their inertial forms. In other words for points close to the rotation axis, where MFT reduces to GRT, the homogeneous Maxwell equations are form invariant under GRT, a result first shown by Schiff [33].

The same results as above could also be obtained by first writing the Maxwell equations in the non-rotating inertial frame using the field tensor in flat spacetime in cylindrical coordinates as follows:

$$\begin{aligned} {F}_{ij}=\left( \begin{array}{cccc} 0 &{} -{E}_r &{} -{r}{E}_\phi &{} -{E}_z \\ {E}_r &{} 0 &{} {r}{B}_z &{} -{B}_\phi \\ {r}{E}_\phi &{} -{r}{B}_z &{} 0 &{} {r}{B}_r \\ {E}_z &{} {B}_\phi &{} -{r}{B}_r &{} 0 \\ \end{array} \right) \end{aligned}$$
(59)

and then employ the general relation between the field tensors in the two frames,

$$\begin{aligned} {F}_{ij}=\frac{\partial {{x^\prime }^m}}{\partial {{x}}^i}\frac{\partial {{x^\prime }^n}}{\partial {{x}}^j}{F^\prime }_{mn} \end{aligned}$$
(60)

to relate the primed and unprimed electromagnetic fields using (47), and finally replace the unprimed quantities (including partial differentials using Eq. (43)) by the primed ones. So in general neither the wave equation nor the Maxwell equations are invariant under MFT.

6 Discussion and summary

The Galilean rotational transformation is only true for centrally rotating observers. To relate the observations of inertial observers to those of eccentric, non-inertial ones (at large radii leading to relativist rotational velocities) on a rigidly rotating disk, one should either apply instantaneous LTs, introduced by Mashhoon et al. [34] in the context of the hypothesis of locality, or alternatively look for consistent RRTs. In the present article, we have discussed the characteristics of a proposed RRT, dubbed as a Franklin transformation, which relates coordinates of an event in two frames, one an inertial non-rotating frame and the other one rotating around their common axis with constant angular velocity \(\Omega \) (measured by the inertial observers). The advantages and also drawbacks of this transformation specially with respect to the spacetime metric from the rotating observer’s point of view as well as of its kinematical interpretation are pointed out. By introducing non-inertial observers at nonzero radii we have modified FT and showed how the modified transformation gives rise to a more consistent spacetime metric for these observers. The resulting spacetime metric includes two parameters, \(\Omega \) and \(R\), corresponding to the rotational angular velocity and radial position of these observers. Though we have a flat spacetime, it has a non-Euclidean spatial line element (found through the \(1+3\) formulation of a spacetime decomposition) leading to a non-Euclidean value for the circumference of a rotating disk or any other circle of a given radius. In our setting of the problem of relativistic rotational transformations, there are three different kinds of observers: I inertial non-rotating (laboratory) observers; II centrally rotating (spinning) observer, and III non-inertial rotating observers at nonzero radii (eccentric observers) who are rotating analogs of Rindler observers. In brief, the following are the important features of the MFT:

  1. 1.

    Unlike FT it leads to a spacetime metric in the rotating frame which reduces to the spacetime metric obtained through GRT in the corresponding limit (i.e. close to the rotation axis).

  2. 2.

    Unlike in FT, the spacetime metric obtained via MFT preserves the temporal and angular isometries present in (5).

  3. 3.

    At \(R=0\) it reduces to the exact GRT as expected from its interpretation.

  4. 4.

    It gives a possible answer to the question: what is the spacetime metric for an eccentric observer on a rotating disk?

  5. 5.

    Related to the above point, at the position of an eccentric observer (i.e. at \(r=R\)), the spacetime metric is found to be form invariant (i.e. it reduces to the spatially Euclidean flat metric), a fact hinting toward a possible relation with Fermi metric and Fermi coordinates.

The last point above seems to be interesting evidence reinforcing our interpretation of the MFT and its corresponding metric. The fact that the MFT includes two parameters, \(\Omega \) and \(R\), does not change its group character inherited from FT. Indeed, comparing (14) and (25), the group parameter in MFT is \(v=c \tanh \beta \), whereas in FT it is \(\Omega \).Footnote 6 Indeed when it is compared to the coordinate transformation obtained in the approach based on the hypothesis of locality and Fermi metric (restricted to a uniformly rotating observer) the appearance of \(R\) is expected naturally as in that case the radial position of the eccentric observer enters the transformation both explicitly and also through the parameter \(\beta \) (refer to [34]). The above-mentioned relation could be further investigated by a comparative study between the approaches based on MFT and its corresponding metric (27) on the one hand, and the Fermi metric [17] attributed to a uniformly rotating observer [34] on the other hand. These features are discussed and analyzed in detail in [30].

It is also shown explicitly that, against the previous claims, neither the Maxwell equations are invariant under FT or MFT, nor is the wave equation.

From the experimental and observational points of view it is expected that the application of a relativistic rotational transformation to known physical effects related to the rotating systems and phenomena should lead to predictions different from those obtained through application of GRT or rotational transformations based on the hypothesis of locality. Some of the examples include the transverse Doppler effect, the Sagnac effect [35] and rotational properties of pulsars [28]. For a light source circling a receiver on a rotating disk, the transverse Doppler effect will be affected naturally by FT and MFT, due to the nonlinear velocity distribution (12) introduced in FT, and this could be the most feasible test of the validity of MFT. Also it is expected that employing a relativistic rotational transformation will lead to a relativistic Sagnac effect distinct from the one due to propagation of light in a non-vacuum medium where the relativistic velocity addition rule applies. Finally, the fastest rotating celestial objects (apart from the supermassive black holes) are pulsars and the fastest pulsar, named PSR J1748-2446ad, is located some 28,000 light-years from Earth in the constellation Sagittarius and is spinning at 716 Hertz. If its radius is taken to be 16 km it will have a Galilean linear velocity of 75,000 km/s, i.e. about \(25\,\%\) that of light speed, at the equator. It is expected that at this rotational velocity a relativistic rotational transformation is at work and observationally effective. To look for experimental signatures of departure from GRT or rotational transformations based on the hypothesis of locality, other physical effects (mainly electromagnetic in nature), which have already been studied in rotating frames [29, 36–38], should be reconsidered and interpreted in terms of MFT. In this regard, some of the rotational phenomena mentioned above are studied comparatively using both MFT and the formalism based on the hypothesis of locality in [30].

Another very interesting issue which needs a careful treatment is the Unruh effect for uniformly rotating eccentric observers, which is already expected to be a controversial issue. By the above discussions it seems inevitable that one should employ a relativistic rotational transformation, such as MFT, to see whether eccentric observers detect any particle in the vacuum state of an inertial observer. These matters will be discussed elsewhere [39].