1 INTRODUCTION

Currently the experimental thermonuclear reactor is being developed, based on the principle of heated plasma retention in the certain quite large volume with magnetic field (ITER project). Simultaneously fundamentally different thermonuclear energy direction is being developed – inertial confinement fusion (ICF) based on heating the dense fuel to thermonuclear temperatures such fast that the significant fusion energy could release before the fuel dissipates. The bombarded target diameter is near 1 mm [1, 2] or even less [3]. The research as per MagLIF program occupies intermediate position between magnetic retention of plasma and ICF both for fuel chamber size (liner) – 1 cm, and for fuel impact – with the help of a driver and magnetic field [1, 4].

The effectiveness of thermonuclear burning is expressed in Lawson criterion reflecting the balance between thermonuclear energy and energy supplied for heating the fuel. Initially the Lawson criterion was written for the rigs of plasma magnetic confinement as nτ > 1014 s/cm3 (for DT-reaction), where n is the number of nuclei in 1 cm3; τ is the time of confinement of heated plasma to thermonuclear temperature in seconds [1–3, 5, 6].

And for the ICF and MagLIF the Lawson criterion is expressed in the terms of parameter ρR: ρR > 1 g/cm2, where ρ is the density of the fuel in g/cm3; R is the initial radius in centimeters [1–3, 6]. Currently the problem of burning-out is being set up of up to 30% of the fuel. In this case the Lawson criterion may be written as follows: ρR ≥ 3 g/cm2 [1–3, 6]. For the target diameter near 1 mm and initial density of ρ = 0.21 g/cm3 the condition presumes the necessity of initial implosion of the fuel to very high densities [1–3].

In order to implement the ICF and MagLIF technologies it is considered necessary to use α-particles evolving in the course of the thermonuclear reaction. For that purpose the α-particles should remain during the reaction in the fuel volume. For the expected during practical implementation thermonuclear fusion temperatures of plasma 10–50 keV (more than 100–500 Kelvin) the complete deceleration of the α-particles inside plasma corresponds to the following range of the Lawson criterion: ρR ~ 0.3–3.5 g/cm2 [1, 6]. The higher temperatures lead to the higher values in the Lawson criterion.

The present work is devoted to the exploration of the possibility of energy extraction as a result of heating of low-scale thermonuclear target (without initial implosion) with its further expansion to the surrounding environment under the magnetic field. The peculiarity of the offered way of energy extraction is the deceleration by the external magnetic field of the dissipation of target substance in order to enlarge the percentage of the burned-out fuel.

The principal difference of the MagLIF and the way of extraction of thermonuclear energy offered in the paper is the fuel size (larger by an order) and the fact that the magnetic confinement in the MagLIF approach takes place only at a start phase – before liner explosion and destruction of wiring. The latter is connected with one of the severe difficulties of practical implementation of the MagLIF – each step requires fast change of wiring [4].

The aim of the work is to obtain the conditions under which the thermonuclear energy output compensates the initial thermal energy of the target. The minimum of that energy for various values of magnetic induction of the external magnetic field are compared to the known estimates obtained within the ICF.

To achieve the stated aim it is necessary to derive the equations for the expansion of a plasma ball of a mixture of deuterium and tritium in an external magnetic field and, calculating for various values of initial radius of the ball, various initial temperatures of target heating and values of magnetic induction of the external magnetic field the extracted thermonuclear energy, to find the conditions such that the energy is equal to the initial thermal energy that would be expended for target heating.

In the present work the initial optimal parameters of deuterium and tritium mixture (such that thermonuclear energy output is equal to the thermal energy spent for fuel heating) is defined not on the basis of the Lawson criterion, but on the basis of magnetohydrodynamic model of the process and through obtaining the numerical solution for some special plasma expansion modes . The obtained solutions show how parameters affect the output of thermonuclear energy.

2 THE DEVELOPMENT OF THE MATHEMATICAL MODEL OF EXPANSION OF A PLASMA BALL UNDER THE EXTERNAL MAGNETIC FIELD

The adiabatic behavior of the expansion is presumed. In the papers (for e.g. [1–6]) it is shown that for the small-scale plasma with characteristic dimension L, L < 1 cm, it is possible to neglect the deceleration emission and recombination influence at high temperatures of heating Т, Т > 108 K.

Also the fact of suppression of electronic thermal conduction by the strong magnetic field is used, as it is in paper [4]. For the conditions in the paper – density 0.21 g/cm3 and initial fuel radius under 1 cm – plasma is transparent both for neutrons and for α-particles [1, 6]. In the processes under consideration the expansion speed of plasma is several orders lower than the velocity of light. Therefore the system of electromagnetic equations for moving media obtained within classical mechanics [7, 8] is used for the description of the phenomena.

For the purpose of the description of plasma movement in the external magnetic field normally the model of conductive liquid is used, comprised by the mixture of two different liquids forming plasma – electronic and ionic components [9, 10]. These components will be considered in the present model as mixed in equal concentrations so that plasma is quasi-neutral on the whole.

The magnetic hydrodynamics methods are used for the analysis of plasma processes. The necessary condition of applicability of such methods is the fulfillment of relation [9, 10]

$$R \gg D,$$
(1)

where R is the radius of a plasma ball; D is the Debye radius.

To estimate the value of the Debye radius the following relation is used [9]:

$$D \approx 4.75 \times {{10}^{3}}\sqrt {{T \mathord{\left/ {\vphantom {T n}} \right. \kern-0em} n}} ,\,\,{\text{m}},$$
(2)

where Т is the temperature in Kelvin; n is the molecules number in 1 m3.

For the considered condition: Т > 108; n ~ 5 × 1028 we obtain from (2)

$$D \sim 2 \times {{10}^{{ - 7}}},\,\,{\text{m}}{\text{.}}$$
(3)

In order to apply the methods of magnetic hydrodynamics and utilize the adiabatic character of movement we will assume the radius of plasma ball equal to ~ 0.1–10 mm in the equations for plasma ball expansion into the external magnetic field.

The movement equations for both plasma components have form [9, 10]

$${{\rho }_{e}}\frac{{d{{{v}}_{e}}}}{{dt}} = - ne{{F}_{e}} - \nabla {{p}_{e}} - {{F}_{{ei}}},$$
(4)
$${{\rho }_{i}}\frac{{d{{{v}}_{i}}}}{{dt}} = ne{{F}_{i}} - \nabla {{p}_{i}} + {{F}_{{ei}}},$$
(5)

where \({{\rho }_{e}},{{\rho }_{i}}\); \({{{v}}_{e}}\), \({{{v}}_{i}}\); \({{p}_{e}},{{p}_{i}}\) are densities, velocity vectors and pressures for electronic and ionic components respectively;

\({{F}_{{ei}}}\) is the vector of tension force, applied to electrons in the unit volume from the side of ions;

\(n\) is the concentration of deuterium and tritium nuclei; e is an electronic charge;

\({{F}_{e}}\) and \({{F}_{i}}\) are vectors of electromagnetic forces, applied to electrons and ions respectively;

$${{F}_{e}} = ne{{E}_{e}},\,\,\,\,{{F}_{i}} = ne{{E}_{i}},$$
(6)

\({{E}_{e}}\), \({{E}_{i}}\) are the vectors of electric field strength, acting on electrons and ions respectively.

Using the results in [7, 8], we have the following:

$${{E}_{e}} = - \frac{{\partial A}}{{\partial t}} - \nabla \varphi - \alpha B \times {{{v}}_{e}},\,\,\,\,{{E}_{i}} = - \frac{{\partial A}}{{\partial t}} - \nabla \varphi - \alpha B \times {{{v}}_{i}}.$$
(7)

Here A, \(\varphi \) represent vector and scalar potentials respectively;

B is the magnetic induction vector; t is the time;

\(\alpha \) is the coefficient, \(\alpha = \frac{{\mu \varepsilon - {{\mu }_{0}}{{\varepsilon }_{0}}}}{{\mu \varepsilon }}\);

\({{\varepsilon }_{0}},\varepsilon \) represent dielectric constants of vacuum and medium respectively;

\({{\mu }_{0}},\mu \) represent magnetic permeability of vacuum and medium respectively.

The values in the right side of equations (4)–(5) represent forces acting on all the particles of the given type in the unit volume and caused by the presence of the electromagnetic field, pressure gradient and by the collisions with the other type of particles in plasma.

By summing (4) and (5), we obtain the model of homogenous conductive quasi-neutral liquid, further referred to as plasma dispersoid

$$\rho \frac{{d{v}}}{{dt}} = - \nabla p + \alpha B \times j,$$
(8)

where \(\rho ,{v},j\) are plasma density, velocity and the current density of the dispersoid, respectively;

\(p\) is the total pressure;

$$\rho = n{\kern 1pt} ({{m}_{e}} + {{m}_{i}}),$$
(9)
$${v} = \frac{1}{\rho }({{\rho }_{e}}{{{v}}_{e}} + {{\rho }_{i}}{{{v}}_{i}}),$$
(10)
$$j = ne({{{v}}_{i}} - {{{v}}_{e}}),$$
(11)
$$p = {{p}_{e}} + {{p}_{i}}.$$
(12)

The continuity equation within the dispersoid model has the following form [10]:

$$\frac{{\partial \rho }}{{\partial t}} + {\text{div}}\rho {v} = 0.$$
(13)

In [11, 12] the problem of interaction of the expanding plasma ball in spherical symmetry was observed with infinite conductivity under the external magnetic field. It was shown that the magnetic field is displaced from the volume occupied by plasma, and the expanding plasma cloud sustains the resistance and decelerates. There is only electric field component on the surface of the ball to be considered, caused by movement of the ball’s border in the magnetic field, which within the dispersoid model which may be expressed as follows with regard to (7)

$$E = - \alpha B \times {v}.$$
(14)

The material equation takes place

$$j = \sigma E.$$
(15)

Equation (8) with regard to relations (14), (15) will take the following form

$$\rho \frac{{d{v}}}{{dt}} = - \nabla p + {{\alpha }^{2}}\sigma B \times (B \times {v}),$$
(16)

Initially the spherical plasma cloud expanding under the external magnetic field decelerates non-uniformly, and its form is distorted with the time, elongating in the direction of the poles. However from the start phase of expansion with intense extraction of thermonuclear energy (twofold expansion) the behavior of the cloud in general falls on the estimates based on spherical symmetry of plasma cloud [11, 12].

To assume the spherical symmetry of the plasma cloud, taking into consideration the geometry of the magnetic field lines [11, 12], equations (13), (16) may be written as

$$\frac{{\partial \rho }}{{\partial t}} + {v}\frac{{\partial \rho }}{{\partial r}} + \rho \frac{{\partial {v}}}{{\partial r}} + \frac{{2\rho {v}}}{r} = 0,$$
(17)
$$\frac{{\partial {v}}}{{\partial t}} + {v}\frac{{\partial {v}}}{{\partial r}} + \frac{1}{\rho }\frac{{\partial p}}{{\partial r}} + {{\alpha }^{2}}\sigma {{B}^{2}}{v} = 0,$$
(18)

where r is a spatial coordinate.

Equations (17)–(18) describe the expansion of the plasma cloud in the surrounding homogenous magnetic field. It is necessary to supply the equations with thermodynamics relation, establishing the dependence between the pressure and density of plasma. Setting the temperature of ionic and electronic components equal to the same value T, we come to relation [9, 10]

$$p = 2nkT,$$
(19)

where k is the Boltzmann constant.

To assume (19), equation (18) will take form

$$\frac{{\partial {v}}}{{\partial t}} + {v}\frac{{\partial {v}}}{{\partial r}} + \frac{{2k}}{\rho }\frac{{\partial (nT)}}{{\partial r}} + {{\alpha }^{2}}\sigma {{B}^{2}}{v} = 0.$$
(20)

In order to perform approximate calculations, we use the class of the solutions leading to self-similar distribution of values [13]

$${v} = F(t){\kern 1pt} r,$$
(21)
$$\rho = {{\rho }_{0}}{{\left( {\frac{{{{R}_{0}}}}{R}} \right)}^{3}},$$
(22)
$$T = {{T}_{0}}{{\left( {\frac{{{{R}_{0}}}}{R}} \right)}^{2}}\left( {1 - \frac{{{{r}^{2}}}}{{{{R}^{2}}}}} \right),$$
(23)

where \({{R}_{0}},R\) are the initial and current (at time t) radii respectfully; \(F(t)\) is the function of the time; \({{\rho }_{0}},{{T}_{0}}\) are the initial density and temperature in the centre of the ball respectively. On substituting (21)–(22) into (17), the form of F(t) is obtained:

$$F(t) = \frac{{\dot {R}}}{R}.$$
(24)

In accordance with (22) we have

$$n = {{n}_{0}}{{\left( {\frac{{{{R}_{0}}}}{R}} \right)}^{3}},$$
(25)

where \({{n}_{0}}\) is the initial concentration.

Substituting (21)–(25) into (20), we obtain the equation describing the expansion of the plasma ball into the external homogenous magnetic field

$$\ddot {R} + \frac{{{{\alpha }^{2}}\sigma {{B}^{2}}}}{{{{\rho }_{0}}{{c}^{2}}R_{0}^{3}}}{{R}^{3}}\dot {R} = \frac{{8k{{T}_{0}}R_{0}^{2}}}{{5{{m}_{p}}}}\frac{1}{{{{R}^{3}}}}.$$
(26)

In the process of expansion as a result of thermonuclear fusion reaction the energy given out makes [10]

$${{E}_{c}} = \pi \varepsilon \int\limits_0^t {dt} \int\limits_0^{R(t)} {{{n}^{2}}{{\omega }_{{DT}}}(t,r){{r}^{2}}dr} ,\,\,{\text{eV}},$$
(27)

where \(\varepsilon \) is the energy of a thermonuclear neutron, \(\varepsilon = 14.06 \times {{10}^{6}}\) eV; \({{\omega }_{{DT}}}\) represents averaging of the fusion reactions cross-section with respects to Maxwell distribution (Maxwell distribution is quite admissible for dense plasma).

In the calculations the following relation is used in order to estimate \({{\omega }_{{DT}}}\) [10]

$${{\omega }_{{DT}}} = 1.6 \times {{10}^{{ - 7}}}\frac{1}{{{{T}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{e}^{{\frac{{ - 4.52 \times {{{10}}^{3}}}}{{{{T}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}}}},\,\,\frac{{{\text{c}}{{{\text{m}}}^{3}}}}{{\text{s}}}.$$
(28)

The initial concentration of DT-mixture is given as follows

$${{n}_{0}} = 5 \times {{10}^{{22}}},\,\,\,\,\frac{1}{{{\text{c}}{{{\text{m}}}^{3}}}}.$$
(29)

Initial thermal energy \({{E}_{0}}\) expended for heating of the plasma ball is evaluated using formula

$${{E}_{0}} = 4\pi \int\limits_0^{{{R}_{0}}} {3knT{{r}^{2}}dr = \frac{{24}}{{15}}k\pi {{n}_{0}}} {{T}_{0}}R_{0}^{3},\,\,{\text{erg}}.$$
(30)

3 EVALUATION OF THE PARAMETERS PROVIDING THE THERMONUCLEAR ENERGY OUTPUT COMPENSATION OF THE INITIAL THERMAL ENERGY OF THE TARGET

The expended thermal energy (30) is calculated as well as the output thermonuclear energy produced (27) for various values of \({{R}_{0}},{{T}_{0}},B,\) during the expansion of the plasma ball (26). As a rule, the computation terminated after the twofold expansion of the plasma ball in connection with abrupt decrease of the thermonuclear reactions intensity with further expansion. The conditions of the energies equality were obtained

$$\frac{{{{E}_{c}}}}{{{{E}_{0}}}} = 1.$$
(31)

For different values of magnetic induction \(B\) varying from 0 до 109 G, parameters \({{R}_{0}},{{T}_{0}}\) were obtained corresponding to minimum value of \({{E}_{0}}\) satisfying equation (31).

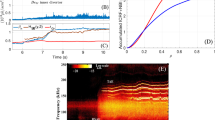
The results of computation are shown in Fig. 1. The data in Fig. 1 illustrate the influence of various factors on the values of optimal parameters providing the output thermonuclear energy equality to the thermal energy expended for heating.

Fig. 1.
figure 1

The conditions of equality of the integral fusion energy and the energy expended for the initial heating of the plasma for various values of magnetic induction of the external magnetic field: 0 Gs (upper curve), 107, 108, 5 × 108 and 109 G (lower curve). The monochrome temperature scale is shown on the right.

Full size image

The analysis of the results is listed in Table 1.

Table 1.   The conditions of minimum energy values E0 expended for the initial heating of the plasma at which the equality to the integral fusion energy is achieved for various values of \({{R}_{0}},{{T}_{0}},B\)
Full size table

The table reflects the influence of the three parameters – the induction of the external magnetic field, temperature and radius of the fuel on the necessary minimum thermal energy providing its equality to the output thermonuclear energy during the expansion of the heated deuterium and tritium mixture plasma.

It is interesting to compare the computation results in Table 1 of the necessary minimum thermal energy to the known estimates obtained for the ICF.

For the target sized nearly 1 mm in diameter (volume ≈ 0.5 mm3) the requirements on the initial thermal energy are close for both methods to Е ≈ 106 J ([1] and lines 2–3 of Table 1), and for the target sized ≈ 0.015 mm3 in volume the initial energy Е ≈ 1.6 × 105 J is required for the ICF [3], and the method offered herein requires Е ≈ 3 × 104 J (lines 1–2 of Table 1).

Thus the energy extraction as a result of heating of a small-scale thermonuclear target with its further expansion into the surrounding magnetic field at certain modes of expansion may require essentially lower energy input for the initial heating of the plasma in comparison with the ITF for the targets equally sized. However to judge on the advantages of this or that method of thermonuclear energy extraction will be possible only after technical fulfillment of all the necessary conditions for execution of the reactions.