Personalized Computational Evaluation of Physical Endurance in a Treadmill Test with Increasing Load

Abstract

In this work, we propose a model of the transport and balance of blood gases and lactate in the blood. The model includes regulation of the respiratory minute volume and cardiac output basing on the partial pressures of oxygen and carbon dioxide in the central and peripheral regulators. The model consists of lumped compartments, which represent the lungs and parts of the circulatory system. For each blood compartment, we solve the equations of haemoglobin oxygenation, acid-base balance, aerobic and anaerobic energy production and consumption, lactate production and utilisation. The treadmill test with increasing load gives input parameters to the model. The model allows simulations of metabolic parameters of athletes during prolonged moderate physical exercise and evaluates their physical endurance.

1 INTRODUCTION

Three key elements are responsible for energy production for physical work. They are muscle, respiratory and cardiovascular systems. These systems limit production of maximum power by an organism. Aerobic resynthesis of adenosine triphosphate (ATF) in muscles cells produces energy for mechanical work during low intensive exercise. It includes chemical reactions of oxidative phosphorylation, which involves oxygen, glucose, fatty acids and proteins to produce pyruvate. Mitochondria utilise the most amount of pyruvate and produce ATF. The amount of pyruvate, which transforms into lactate and goes to the blood, is not significant. Thus, the concentration of lactate in the blood remains low and constant. High intensive exercise requires more energy for the increase in mechanical work. In these conditions aerobic pathway rate unable producing sufficient amount of ATF and anaerobic pathway dominates. At the beginning of the high intensive exercise creatine phosphate breaks up and phosphorylates adenosine diphosphate to ATF. The metabolic processes during this short period produce no lactate, which is up to one minute. After that, anaerobic glycolysis produces the most amount of energy, which involves breaking up muscular glycogen and glucose and produces ATF and lactate. The lactate concentration in the blood increases with time and may cause a lactic acidosis accompanied by muscular weakness, elevated respiratory rate and even coma. The processes of lactate utilisation are highly individual. Thus, effectiveness and rate of lactate utilisation, as well as the non-metabolic production of $CO_{2}$ during high-intensity exercise are important factors for evaluation of physical endurance and training level of the sportsmen and other people.

Exercise stress test (EST) is a general method for evaluation of working capacity. Sports medicine uses this method as well. The tests with increasing load allow studying conditions with extremal fatiguing and maximum oxygen uptake. The non-invasive standard measurements during EST include oxygen ($O_{2}$) uptake rate, carbon dioxide ($CO_{2}$) excretion rate, lungs ventilation, heart rate. Invasive measurements include a concentration of the lactate in the blood. It exists no conventional procedure for measurements of the coefficients of the effectiveness and rate of lactate utilisation as well as the non-metabolic production of $CO_{2}$. In this work, we propose a mathematical model, which allows computing these parameters basing on standard measurements during EST.

The mathematical model should include functions of the closed-loop cardiovascular system and respiratory system as well as transport of blood gases ($O_{2}$ and $CO_{2}$) and lactate. It also should include feedback regulation of cradiovascular and respiratory functions basing on the concentration of the blood gases in the blood. Approaches to modeling respiratory function include 3D models of trachea region and main bronchi, which are constructed using CT data [1–3]; 1D and 0D models of segmental bronchi, bronchioles and alveolar volume [4–8]; multiscale models [1, 7, 9]. Closed loop cardiovascular models use 1D or lumped approaches [10–14]. The work [15] presents a model of binding of oxygen and carbon dioxide by haemoglobin. A model of buffer system of blood is proposed in [16]. Physical activity increases the respiratory minute volume (RMV) and cardiac output as a result of regulation, which is caused by changes in metabolism. Some feedback regulation processes are recently modelled in [17–21]. Currently, it exists no algorithm, which is suitable for computing lactate concentration in the blood. Lumped models of the lactate balance in the blood include biochemical features, which are not sufficiently studied [22–25]. A separate problem is modelling the closed-loop transport, which should consist of several subsystems and their connections. Such models have been recently published in [16, 28, 29]. Specific mathematical models for sport applications are developed in [24, 25].

In this work, we propose a model of the transport and balance of blood gases and lactate in the blood during prolonged moderate physical exercise. The model includes regulation of the RMV and cardiac output basing on the partial pressures of $O_{2}$ and $CO_{2}$ in the central and peripheral regulators. The model consists of lumped compartments, which correspond to the lungs and parts of the circulatory system. For each blood compartment, we solve the system of equations, which describes the interconnected biochemical process including haemoglobin oxygenation, acid-base balance, aerobic and anaerobic energy production and consumption, lactate production and utilisation. The parameters of the model were set according to the treadmill test with increasing load. The patient-specific parameters, which describe physical endurance, were computed using the algorithm of stochastic optimisation [39]. Actually, we extend our previous model of $O_{2}$ and $CO_{2}$ balance with respiratory regulation which was applied to the simulations of hypoxia and hypercapnia conditions [26]. Here we provide detailed compartment decomposition of the cardiovascular system, include control of cardiac output and the model of lactate balance. Due to the presence of lactate, we have to update the balance equations of $O_{2}$ and $CO_{2}$.

2 METHODOLOGY

2.1 Preliminary Remarks

The balance of $O_{2}$, $CO_{2}$ and lactate in the organism determines metabolic features and associated physical endurance. It is computed by the integrated model, including respiratory and cardiovascular systems. The model of regulated RMV uses single compartment lung’s model with feedback from cardiovascular system basing on the concentration of $O_{2}$ and $CO_{2}$ in the blood. There are two basic regulatory principles including the sensitivity of central regulator to the variations of the partial pressure of $CO_{2}$ in the cerebral arteries and cerebrospinal fluid and sensitivity of the peripheral regulator to the changes of the partial pressure of $O_{2}$ and $CO_{2}$ in the carotid sinus. The dashed lines in Figure 1 designate activity of the regulators.

Fig. 1

Compartment decomposition of the respiratory and cardiovascular systems.

The model of the cardiovascular system combines five lumped parts, which correspond to the brain arteries, the other systemic arteries and veins and pulmonary arteries and veins (see Fig. 1). At rest cardiac output $\left(Q\right)$ is constant. The minute flow is divided between the brain $\left(Q_{B}\right)$ and the other part of the body $\left(Q-Q_{B}\right)$. A set of metabolic processes producing power, which is needed for the physical exercise, changes $O_{2}$ and $CO_{2}$ concentrations in the blood and initiates feedback control by modifying cardiac output and ventilation parameters. These changes affect the transport of $O_{2}$ and $CO_{2}$ until a new equilibrium state is achieved. The ratio of $\frac{Q_{B}}{Q}$ is also modified. For this reason, we need a separate compartment for brain arteries.

2.2 The Model of Regulated Respiratory Minute Volume

For the lungs ventilation, we use the single compartment approach similar to [4, 5, 27]. The single compartment lumped model of the lungs ventilation in the linear approximation is stated as

$$R\frac{dV}{dt}+E\left(V-V_{0}\right)=P_{g}\sin{wt},$$

(1)

where $t$ is time, $V$ is the volume of the lungs $V_{0}$ is zero stress volume, $R$ is the resistance of the respiratory airways, $E$ is the elasticity of the lung’s tissue, $w$ is respiratory rate, $P_{g}$ is pleural pressure. We neglect here inertia term because we neglect a short-time dynamics. Also, the lung’s muscles spend the most work to the overcome elastic stress of the thorax and aerodynamic resistance of the airways [30]. Analytic solution of the (1) is

$$V\left(t\right)=V_{0}+\frac{P_{g}}{R\sqrt{\lambda^{2}+w^{2}}}\sin\left(wt-\arctan\frac{w}{\lambda}\right)+\frac{P_{g}w}{R\left(\lambda^{2}+w^{2}\right)}e^{-\lambda t},\quad\lambda=\frac{E}{R}.$$

(2)

From (2) it follows, that tidal volume $V_{T}$ in a steady state is

$$V_{T}=\frac{2P_{g}}{R\sqrt{\lambda^{2}+w^{2}}}.$$

We assume, that gas exchange between alveolar volume and capillary blood in pulmonary circulation is proportional to the gradient of partial pressure of $O_{2}$ and $CO_{2}$

$$\frac{d\left(C_{i}V\right)}{dt}=Q_{i}+D_{i}S\left(C_{i,pa}-C_{i}\right),$$

(3)

$$Q_{i}=\begin{cases}\displaystyle C_{i}^{air}\frac{dV}{dt},\quad\frac{dV}{dt}\geq 0,\\ \displaystyle C_{i}\frac{dV}{dt},\quad\frac{dV}{dt}<0,\end{cases}S=\sqrt[3]{36\pi V^{2}},$$

where $i$ is symbolic notation for $O_{2}$ or $CO_{2}$, $C_{i}$ is concentration of $i^{th}$ substance in lungs, $C_{i}^{air}$ is concentration of the $i^{th}$ substance in respiratory gas outside the body, $C_{i,pa}$ is concentration of $i^{th}$ substance in pulmonary arteries, $D_{i}$ is permeability coefficient for the $i^{th}$ substance, $S$ is the area of the contact surface between alveolar volume and capillaries.

There are two types of respiratory regulation basing on the concentration of $O_{2}$ and $CO_{2}$ in the blood. An elevation of $CO_{2}$ partial pressure in the cerebrospinal fluid and in the cerebral circulation activates central regulator. An elevation of $CO_{2}$ partial pressure and a reduction of $O_{2}$ partial pressure in the blood in the aortic arch and in the carotid sinus activates peripheral regulator [20]. Action of central and peripheral regulators is independent. Regulators modify the RMV as $V_{E}=V_{SS}+V_{C}+V_{P},$ where $V_{E}$ is respiratory minute ventilation, $V_{SS}$ is basal ventilation, $V_{C}$ is an additional RMV due to activity of central regulator, $V_{P}$ is an additional RMV due to activity of peripheral regulator.

The action of chemoreceptors of central regulator produces the following additional RMV [20] $V_{C}=K_{CO_{2}}\left(P_{CO_{2}}-T_{CO_{2}}\right),$ where $P_{CO_{2}}$ is the partial pressure of $CO_{2}$ in cerebral circulation, $T_{CO_{2}}$ is the reference partial pressure of $CO_{2}$ in central regulator, $K_{CO_{2}}$ is the constant coefficient. If $V_{C}<0$, then we set $V_{C}=0$.

The action of chemoreceptors of peripheral regulator is also linearly proportional to the elevation of $CO_{2}$ partial pressure (hypercapnia). It is also inversely proportional to the reduction of $O_{2}$ partial pressure (hypoxia). A response of peripheral regulator to a sharp decrease of $O_{2}$ partial pressure has two phases. First, it increases ventilation. Second, increased ventilation results in increased washing out of $CO_{2}$, which leads to a decrease of the activity of $CO_{2}$ sensitive chemoreceptors. The net effect is stated as [20]

$$V_{P}=K_{pCO_{2}}\left(P_{pCO_{2}}-T_{pCO_{2}}\right)+\left(\frac{p_{1}}{P_{pO_{2}}-p_{2}}-p_{3}\right)F(P_{pCO_{2}}),\quad V_{p}\geq 0,$$

$$F(P_{pCO_{2}})=\begin{cases}\left(5-4N_{pCO_{2}}^{4}\right)^{-1},&N_{pCO_{2}}\leq 1\\ N_{pCO_{2}}^{3},&N_{pCO_{2}}>1\end{cases},\quad N_{pCO_{2}}=\frac{P_{pCO_{2}}}{P_{pCO_{2}}^{0}},$$

where $T_{pCO_{2}}$ is the first reference partial pressure of $CO_{2}$ in peripheral regulator, $K_{pCO_{2}}$ is constant coefficient, $P_{pO_{2}},P_{pCO_{2}}$ are partial pressures of $O_{2}$ and $CO_{2}$ in the blood of systemic circulation, $P_{pCO_{2}}^{0}$ is the second reference partial pressure of $CO_{2}$ in peripheral regulator, $p_{1},p_{2},p_{3}$ are empirical constants. If $V_{P}<0$, then we set $V_{P}=0$.

RMV also can be defined as

$$V_{E}=\frac{30w}{\pi}V_{T}.$$

(4)

Empiric relationship gives

$$V_{T}=\alpha V_{E}^{\displaystyle\beta},$$

(5)

which allows computing regulated tidal volume and then respiratory rate by (4). The values of constant coefficients $\alpha$ and $\beta$ are set according to [20].

All constants of the regulated RVM model are defined in Table 1.

Table 1 Constants of the model of regulated respiratory minute volume

2.3 The Model of Oxygen and Carbon Dioxide Regulated Balance in the Blood Compartments

The blood carries $O_{2}$ in two forms: dissolved in plasma (up to 2$\%$) and reversibly bound to haemoglobin (up to 98$\%$). The haemoglobin molecule ($Hb$) can bind up to four $O_{2}$ molecules. The healthy blood contains at least six different types of $Hb$ with different oxygen-binding capability [31]. Oxyhaemoglobin is produced by the chemical reaction

$$Hb+mO_{2}\longleftrightarrow Hb\left(O_{2}\right)_{m},$$

(6)

where $1\leq m\leq 4$ is the coefficient of the $Hb$ oxygenation. In this work we use the empirically proven effective value [32] is $m=3.6$. The total concentration of the $O_{2}$ is

$$C_{O_{2}}=C_{O_{2},f}+mC_{Hb_{m}},$$

(7)

where $C_{O_{2,f}}$ is the molar concentration of the dissolved $O_{2}$, $C_{Hb_{m}}$ is the molar concentration of the bound haemoglobin (oxyhaemoglobin). The total concentration of the $Hb$ remains constant $T_{Hb}=C_{Hb}+C_{Hb_{m}},$ where $C_{Hb}$ is the molar concentration of the unbounded $Hb$. Assuming that the reaction (6) is fast enough and pseudo-steady state is achieved, one may derive

$$K_{O_{2}}C_{Hb_{m}}=\left(T_{Hb}-C_{Hb_{m}}\right)C_{O_{2,f}}^{m},\quad K_{O_{2}}=\frac{k_{O_{2}}^{-}}{k_{O_{2}}^{+}},$$

(8)

where $k_{O_{2}}^{+}$ is the rate of the forward reaction (6), $k_{O_{2}}^{-}$ is the rate of the reverse reaction (6).

Using the compartment decomposition (see Fig. 1) the balance of $O_{2}$ in the cardiovascular system is written as

$$\displaystyle\frac{d\mathbf{C}_{O_{2}}}{dt}=\mathbf{A}\mathbf{C}_{O_{2}}+\begin{pmatrix}\displaystyle\frac{D_{O_{2}}S}{V_{1}}\left(C_{O_{2},alv}-C_{O_{2},f,1}\right)\\ 0\\ 0\\ \displaystyle-\frac{\dot{V}_{O_{2},b}}{V_{4}}\\ \displaystyle-\frac{\dot{V}_{O_{2},t}}{V_{5}}\end{pmatrix},$$

(9)

$$\mathbf{A}=\begin{pmatrix}-\frac{Q}{V_{1}}&0&\frac{Q}{V_{1}}&0&0\\ \frac{Q}{V_{2}}&-\frac{Q}{V_{2}}&0&0&0\\ 0&0&-\frac{Q}{V_{3}}&\frac{Q_{B}}{V_{3}}&\frac{Q-Q_{B}}{V_{3}}\\ 0&\frac{Q_{B}}{V_{4}}&0&-\frac{Q_{B}}{V_{4}}&0\\ 0&\frac{Q_{-}Q_{B}}{V_{5}}&0&0&-\frac{Q-Q_{B}}{V_{5}}\\ \end{pmatrix},$$

(10)

where $\mathbf{C}_{O_{2}}=\{C_{O_{2},i}\}_{i\in[1,..,5]}$, $C_{O_{2},i}$ is concentration of $O_{2}$ in $i^{th}$ blood compartment (1—pulmonary arteries, 2—pulmonary veins, 3—sytemic veins, 4—brain arteries, 5—systemic arteries), $C_{O_{2},alv}$ is concentration of $O_{2}$ in alveolar compartment, $\dot{V}_{O_{2},b}$ is consumption rate of $O_{2}$ by brain, $\dot{V}_{O_{2},t}$ is consumption rate of $O_{2}$ by tissues, $V_{i}$ is the volume of $i^{th}$ blood compartment, $Q$ is cardiac output, $Q_{B}$ is minute blood flow through brain arteries. Substituting (7), (8) into (9) one may derive

$$\displaystyle\frac{d\mathbf{x}}{dt}=\mathbf{A}\mathbf{\xi}_{O_{2}}(\mathbf{x})+\mathbf{\chi}_{O_{2}}(\mathbf{x}),$$

(11)

$$\mathbf{\xi}_{O_{2}}(\mathbf{x})_{i}=\frac{\displaystyle x_{i}+\frac{mT_{Hb}x_{i}^{m}}{K_{O_{2}}+x_{i}^{m}}}{S_{O_{2}}(x_{i})},\quad S_{O_{2}}(x_{i})=1+\frac{m^{2}K_{O_{2}}T_{Hb}x_{i}^{m-1}}{\left(K_{O_{2}}+x_{i}^{m}\right)^{2}},$$

(12)

$$\mathbf{\chi}_{O_{2}}(\mathbf{x})=\begin{pmatrix}\displaystyle\frac{D_{O_{2}}S}{V_{1}S_{O_{2}}(x_{1})}\left(C_{O_{2},alv}-x_{1}\right)\\ 0\\ 0\\ \displaystyle-\frac{\dot{V}_{O_{2},b}}{V_{4}S_{O_{2}}(x_{4})}\\ \displaystyle-\frac{\dot{V}_{O_{2},t}}{V_{5}S_{O_{2}}(x_{5})}\end{pmatrix},$$

(13)

where $\mathbf{x}=\{C_{O_{2},f,i}\}_{i\in[1,..,5]},$ $\mathbf{x}$ is the vector, which is composed by the values of the $C_{O_{2},f}$ in the $i^{th}$ blood compartments (see Fig. 1).

The blood carries $CO_{2}$ in two forms: dissolved in plasma and reversibly bound. The value of $CO_{2}$ concentration affects the acid-base balance in blood. Chemical reaction of hydratation of $CO_{2}$ molecules with the production of carbonic acid and subsequent dissociation to ion of hydrocarbonate and ion of hydrogen is

$$CO_{2}+H_{2}\longleftrightarrow HCO_{3}^{-}+H^{+},$$

(14)

$$C_{CO_{2}}=C_{CO_{2,f}}+C_{HCO_{3}^{-}},$$

(15)

where $C_{CO_{2,f}}$ is the molar concentration of the $CO_{2}$, which is dissolved in the blood. Assuming that the reaction (14) is fast enough and pseudo-steady state is achieved, one may derive

$$C_{HCO_{3}^{-}}=K_{CO_{2}}\frac{C_{CO_{2,f}}}{C_{H^{+}}},\quad K_{CO_{2}}=\frac{k_{CO_{2}}^{-}}{k_{CO_{2}}^{+}},$$

(16)

where $k_{CO_{2}}^{+}$ is the rate of the forward reaction (14), $k_{CO_{2}}^{-}$ is the rate of the reverse reaction (14). For the ions $HCO_{3}^{-}$ and $H^{+}$ we have

$$\frac{dC_{HCO_{3}^{-}}}{dt}=k_{CO_{2}}^{+}C_{CO_{2,f}}-k_{CO_{2}}^{-}C_{H^{+}}C_{HCO_{3}^{-}}+Q_{HCO_{3}^{-}},$$

(17)

$$\frac{dC_{H^{+}}}{dt}=k_{CO_{2}}^{+}C_{CO_{2,f}}-k_{CO_{2}}^{-}C_{H^{+}}C_{HCO_{3}^{-}}+Q_{H^{+}},$$

(18)

where $Q_{HCO_{3}^{-}}$ and $Q_{H^{+}}$ are convective flows. Using new variable $Hc_{i}=C_{HCO_{3}^{-},i}-C_{H^{+},i}$ one may derive from (17), (18)

$$\frac{d\mathbf{Hc}}{dt}=\mathbf{A}\mathbf{Hc},$$

(19)

where $\mathbf{A}$ is defined by (10). Similar to (9) we have

$$\displaystyle\frac{d\mathbf{C}_{CO_{2}}}{dt}=\mathbf{A}\mathbf{C}_{CO_{2}}+\begin{pmatrix}\displaystyle\frac{D_{CO_{2}}S}{V_{1}}\left(C_{CO_{2},alv}-C_{CO_{2,f},1}\right)\\ 0\\ 0\\ \displaystyle\frac{\dot{V}_{CO_{2},b}}{V_{4}}\\ \displaystyle\frac{\dot{V}_{CO_{2},t}}{V_{5}}\end{pmatrix},$$

(20)

where $\mathbf{C}_{CO_{2}}=\{C_{CO_{2}},i\}_{i\in[1,..,5]}$, $C_{CO_{2},i}$ is concentration of $CO_{2}$ in $i^{th}$ blood compartment, $\dot{V}_{CO_{2},b}$ is excretion rate of $CO_{2}$ by brain, $\dot{V}_{CO_{2},t}$ is excretion rate of $CO_{2}$ by tissues.

Substituting (15), (16), (18), (19) into (20) one may derive

$$\displaystyle\frac{d\mathbf{y}}{dt}=\mathbf{A}\mathbf{\xi}_{CO_{2}}(\mathbf{y})+\mathbf{\chi}_{CO_{2}}(\mathbf{y}),$$

(21)

$$\mathbf{\xi}_{CO_{2}}(\mathbf{y})_{i}=\frac{y_{i}^{2}+(K_{CO_{2}}-h_{i})y_{i}}{K_{CO_{2}}-h_{i}+2y_{i}},\quad S_{CO_{2}}(y_{i})=\frac{K_{CO_{2}}-h_{i}+2y_{i}}{K_{CO_{2}}},$$

(22)

$$\mathbf{\chi}_{CO_{2}}(\mathbf{y})=\begin{pmatrix}\displaystyle\frac{D_{CO_{2}}S}{V_{1}S_{CO_{2}}(y_{1})}\left(C_{CO_{2},alv}-\frac{y_{1}^{2}-y_{1}h_{1}}{K_{CO_{2}}}\right)\\ 0\\ 0\\ \displaystyle\frac{\dot{V}_{CO_{2},b}}{V_{4}S_{CO_{2}}(y_{4})}\\ \displaystyle\frac{\dot{V}_{CO_{2},t}}{V_{5}S_{CO_{2}}(y_{5})}\end{pmatrix},$$

(23)

where $\mathbf{y}=\{C_{HCO_{3}^{-},i}\}_{i\in[1,..,5]},$ $\mathbf{y}$ is the vector, which is composed by the values of the $C_{HCO_{3}^{-}}$ concentration in the cardiovascular compartments (see Fig. 1).

Peripheral regulator affects heart rate and cardiac output. Variations of cardiac output are driven by changes both in concentration of $O_{2}$ and $CO_{2}$ [20]

$$Q=\left(q_{1}+\frac{q_{2}}{1+\left(\frac{P_{O_{2},5}}{q_{3}}\right)^{q_{4}}}\right)I(P_{CO_{2},5})Q_{MCO},$$

(24)

where

$$I(P_{CO_{2},5})=\begin{cases}1+q_{5}(P_{CO_{2},5}-P_{CO_{2},5,0}),\quad N_{pCO_{2}}\leq 1\\ 1-q_{6}(P_{CO_{2},5}-P_{CO_{2},5,0}),\quad N_{pCO_{2}}>1\end{cases},\quad N_{pCO_{2}}=\frac{P_{CO_{2},5}}{P_{CO_{2},5,0}}.$$

(25)

Variations of blood flow through the brain are driven by changes of concentration of $CO_{2}$ [20]

$$\displaystyle Q_{B}=\left(b_{1}+\frac{b_{2}}{1+\left(\frac{P_{CO_{2},5}}{b_{3}}\right)^{b_{4}}}\right)\left(b_{5}+\frac{b_{6}}{1+b_{7}e^{b_{8}log_{10}P_{CO_{2},5}}}\right)Q_{MCBF},$$

where $Q_{MCO}$ cardiac output at rest, $Q_{MCBF}$ minute blood flow through the brain at rest. All constants of the model of $O_{2}$ and $CO_{2}$ regulated balance in blood compartments are defined in Table 2.

Table 2 Blood gases balance parameters and initial values [15, 20, 32]

2.4 Muscle Metabolism and Mechanical Efficiency

Aerobic and anaerobic metabolic pathways produce energy in the body concurrently. One of them predominates depending on the type of physical activity. The aerobic pathway is driven by the $O_{2}$ consumption. It plays a major role during short and intense activities. The power, which is produced by the aerobic pathway ($W_{a}$), is

$$W_{a}=e_{a}\dot{V}_{O_{2},m},$$

(26)

where $e_{a}$ is the energy equivalent of the $O_{2}$, $\dot{V}_{O_{2},m}$ is the oxygen consumption rate, which is required by the muscles for physical activity. Anaerobic pathway produces lactate. It prevails during low-intensity activities over an extended period. The power, which is produced by the anaerobic pathway ($W_{an}$), is

$$W_{an}=e_{la}\dot{V}_{la},$$

(27)

where $e_{la}$ is the energy equivalent of the lactate, $\dot{V}_{la}$ is the rate of the lactate production.

The power, which is produced by an aerobic pathway with the release of 1 mole of the lactate, is equal to the power, which is produced by an anaerobic pathway with the consumption of 3 litres of the $O_{2}$ per 1 kilogram of the body weight [34, 35]. Thus, the values of $e_{a}$ and $e_{la}$ relate to each other as

$$e_{la}=\frac{3M}{V_{blood}}e_{a},$$

(28)

where $M$ is the weight of the body, $V_{blood}$ is the total blood volume.

At every moment the total power $W$ of a physical work is

$$W=W_{a}+W_{an}.$$

(29)

Lactate (anaerobic) threshold ($W_{LT}$) is a power of physical activity at which outputs of aerobic and anaerobic pathways are equal. The dimensionless function $\sigma\left(W\right)$ characterises it as

$$\sigma\left(W\right)=\frac{W_{a}}{W}=\frac{W_{LT}}{W+W_{LT}}.$$

(30)

The muscles and myocardium utilises up to 60$\%$ of the produced lactate, while liver and intestine utilises up to 20$\%$ of the lactate by the gluconeogenesis. We consider combined effect of these processes as some effective reaction of the first order, which gives

$$\dot{V}_{la,u}=\begin{cases}u_{la}\left(C_{la}-C_{la,0}\right),\quad C_{la}\geq C_{la,0},\\ 0,\quad C_{la}<C_{la,0},\end{cases}$$

(31)

where $u_{la}$ is the effective rate of the lactate utilisation by the muscles, myocardium, liver and intestine, $C_{la}$ is the lactate concentration, $C_{la,0}$ is the lactate concentration at rest. Bicarbonate buffer system of the blood partially neutralises the excessive lactate, which results in the non-metabolic $CO_{2}$ production

$$\dot{V}_{CO_{2}}=\begin{cases}\kappa_{CO_{2}}\left(C_{la}-C_{la,0}\right),\quad C_{la}\geq C_{la,0},\\ 0,\quad C_{la}<C_{la,0},\end{cases}$$

(32)

where $\kappa_{CO_{2}}$ is the coefficient of the non-metabolic $CO_{2}$ production.

Finally, the lactate balance in the blood compartments is written as

$$\frac{d\mathbf{z}}{dt}=\mathbf{A}\mathbf{z}+\mathbf{\chi}_{la}(\mathbf{z}),\quad\mathbf{\chi}_{la}(\mathbf{z})=\begin{pmatrix}0\\ 0\\ \displaystyle-u_{la}(z_{3}-C_{la,0})\\ 0\\ \displaystyle-u_{la}(z_{5}-C_{la,0})+\frac{\dot{V}_{la}}{V_{5}}\end{pmatrix},$$

(33)

where $\mathbf{z}$ is the vector, which is composed by the values of the lactate concentration in the blood compartments (see Fig. 1).

Accounting of the muscle metabolism (26)–(30), (13) modifies (23) as follows

$$\mathbf{\chi}_{O_{2}}(\mathbf{x})=\begin{pmatrix}\displaystyle\frac{D_{O_{2}}S}{V_{1}S_{O_{2}}(x_{1})}\left(C_{O_{2},alv}-x_{1}\right)\\ 0\\ 0\\ \displaystyle-\frac{\dot{V}_{O_{2},b}}{V_{4}S_{O_{2}}(x_{4})}\\ \displaystyle-\frac{\dot{V}_{O_{2},t}+\dot{V}_{O_{2},m}}{V_{5}S_{O_{2}}(x_{5})}\end{pmatrix},$$

$$\mathbf{\chi}_{CO_{2}}(\mathbf{y})=\begin{pmatrix}\displaystyle\frac{D_{CO_{2}}S}{V_{1}S_{CO_{2}}(y_{1})}\left(C_{CO_{2},alv}-\frac{y_{1}^{2}-h_{1}y_{1}}{K_{CO_{2}}}\right)\\ 0\\ \displaystyle\frac{\kappa_{CO_{2}}\left(z_{3}-C_{la,0}\right)}{S_{CO_{2}}(y_{3})}\\ \displaystyle\frac{\dot{V}_{CO_{2},b}}{V_{4}S_{CO_{2}}(y_{4})}\\ \displaystyle\frac{1}{S_{CO_{2}}(y_{5})}\left(\frac{\dot{V}_{CO_{2},t}+\dot{V}_{O_{2},m}RQ}{V_{5}}+\kappa_{CO_{2}}\left(z_{5}-C_{la,0}\right)\right)\end{pmatrix},$$

where $RQ=\frac{\dot{V}_{CO_{2},t}}{\dot{V}_{O_{2},t}}$ is the respiratory coefficient.

In this work we evaluate the mechanical efficiency as a ratio of the mechanical aerobic power to the chemical power, which is produced by the body

$$\eta=\frac{e_{a}}{e_{O_{2}}}.$$

(34)

Assume, that carbohydrates and fats are the only sources for aerobic energy production. Assume also, that carbohydrates and fats fractions are constant during considered physical activity. Carbohydrate metabolism is equivalent to the $RQ=1$ and fat metabolism is equivalent to the $RQ=0.7$ [30, 36]. Thus, the fraction of the substrates can be found from the set

$$\begin{cases}\gamma_{C}+0.7\gamma_{F}=RQ,\\ \gamma_{C}+\gamma_{F}=1,\end{cases}$$

(35)

where $\gamma_{C}$ is the fraction of carbohydrates, $\gamma_{C}$ is the fraction of fats. The power equivalence between carbohydrates, fats and oxygen [37] and (35) allow us to write

$$e_{O_{2}}=20.9\gamma_{C}+19.5\gamma_{F}\approx 4.7RQ+16.23.$$

(36)

Thus, substituting (28) and (36) to the (34) we derive

$$\eta=\frac{3Me_{la}}{V_{blood}\left(4.7RQ+16.23\right)}.$$

2.5 Experimental Data Acquisition

Anonymous data were collected from 10 middle distance athletes of the first category. The following individual data were measured at rest before the exersise: height $\left(H\right)$, weight $\left(M\right)$, respiratory coefficient $\left(RQ\right)$, oxygen consumption rate $\left(\dot{V}_{O_{2}}\right)$, lactate concentration in the blood $\left(C_{la,0}\right)$, anaerobic threshold $\left(W_{LT}\right)$, RMV $\left(V_{E}=V_{SS}\right)$, respiratory rate $\left(n_{0}\right)$ and duration of the test (see Table 3).

Table 3 Individual initial data at rest

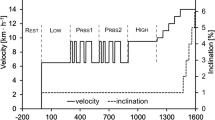
The gradually increased treadmill test was performed in each case. The treadmill incline angle was set to 5 deg. Initial treadmill velocity ($\vartheta$) was set to 7 km/h. It was increased by 0.1 km/h every 10 s. The test was terminated upon the athlete’s request. Expired tidal volume and composition of the exhaled gas ($O_{2}$ and $CO_{2}$ concentrations) were continuously monitored during the test by the device ‘‘METAMAX${}^{\textregistered}$ 3B’’ (Germany). Lactate concentration was observed from the blood samples, which were collected every 3 min. The experimental set up is shown at the Fig. 2.

Fig. 2

Experimental setup.

2.6 Parameters Identification and Computational Algorithms

Oxygen consumption by the tissues $\left(\dot{V}_{O_{2},t}=0.85\dot{V}_{O_{2}}\right)$ and by the brain $\left(\dot{V}_{O_{2},b}=0.15\dot{V}_{O_{2}}\right)$ was set according to [30]. The values of the lungs volume ($V$), total blood volume ($V_{blood}$) and blood distribution among the compartments ($V_{i}$) (see Fig. 1) were calculated as [30]

$$V=2.5H,\quad V_{blood}=77\times 10^{-3}M,\quad V_{i}=\xi_{i}V_{blood},\quad i=1,\dots,5.$$

Initial respiratory rate was computed as $w_{0}={\pi}n_{0}/30.$ The values of the blood fraction $\xi_{i}$ are shown in the Table 4.

Table 4 The blood fraction in the blood compartments [30] (see Fig. 1)

The values of the minute cardiac output ($Q_{MCO}$) and the minute cerebral blood flow ($Q_{MCBF}$) at rest were evaluated as [30, 38] $Q_{MCO}=0.187M^{0.81}$, $Q_{MCBF}=0.13Q_{MCO}.$ The required power of the treadmill test was evaluated as $W=9.8M\vartheta\sin 5^{\circ}.$ The other constants and initial concentrations of blood gases were set according to the Tables 1, 2.

Parameters of the muscle metabolism $e_{a}$, $u_{la}$ and $\kappa_{CO_{2}}$ were computed by fitting measured and computed time series of lungs ventilation, concentrations of the $O_{2}$ and $CO_{2}$ in the exhaled gas and lactate concentration in the blood. The fitting procedure uses the minimisation of the functionals $\Phi_{I}\left(e_{a},u_{la},\kappa_{CO_{2}}\right)$

$$\Phi_{I}\left(e_{a},u_{la},\kappa_{CO_{2}}\right)=\sum\limits_{I\in\{O_{2},CO_{2},V_{E},LA\}}\left(\frac{1}{N_{I}}\sum_{i=1}^{N_{I}}\text{huber}\left(\Delta_{I,i}\right)\right),$$

(37)

where

$$\text{huber}(\Delta)=\begin{cases}\frac{1}{2}\Delta^{2},\quad|\Delta|\leq\delta,\\ \delta(|\Delta|-\frac{1}{2}\delta),\quad|\Delta|>\delta,\end{cases}\quad\Delta_{I,i}=\frac{a_{I,i}^{exp}-a_{I,i}^{num}}{a_{I,i}^{exp}},\quad\delta_{I}=1.5\sqrt{\frac{1}{N_{I}}\sum_{i=1}^{N_{I}}\Delta_{I,i}^{2}},$$

$I$ is symbolic parameter index ($O_{2}$, $CO_{2}$, $V_{E}$, $LA$), $N_{I}$ is the number of the measurements, $a_{I,i}^{exp}$ is $i^{th}$ is measured value of the parameter $I$, $a_{I,i}^{num}$ $i^{th}$ is computed value of the parameter $I$,

$$a_{0_{2},i}^{num}=\dot{V}_{O_{2},t,i}+\dot{V}_{O_{2},m,i},\quad a_{V_{E},i}^{num}=V_{E,i},\quad a_{LA,i}^{num}=C_{la,5,i},$$

$$a_{CO_{2},i}^{num}=\dot{V}_{CO_{2},t,i}+\dot{V}_{O_{2},m,i}\cdot RQ+V_{5}\cdot\kappa_{CO_{2}}\left(C_{la,5,i}-C_{la,0}\right)+V_{3}\cdot\kappa_{CO_{2}}\left(C_{la,3,i}-C_{la,0}\right).$$

The functionals (37) were minimised simultaneously by the method of differential evolution [39]. In this algorithm initial generation of the parameter’s vectors is produced stochastically. The new generation of the parameter’s vectors is produced stochastically by the linear combinations of the vectors from the previous generation. This procedure repeats until convergence condition is achieved. We use scipy.optimize implementation of this algorithm with the default settings [40]. The number of the functionals computations in every case was less, than 1500. The parameters were taken from the physiologically acceptable limits: $0.1\cdot e_{O_{2}}\leqslant e_{a}\leqslant 0.4\cdot e_{O_{2}}$, $10^{-4}\leqslant u_{la}\leqslant 10^{-2}$, $0.1\leqslant\kappa_{CO_{2}}\leqslant 10$.

For the given values of $e_{a}$, $u_{la}$, $\kappa_{CO_{2}}$ the following iterative algorithm computes new time series of the parameters $C_{O_{2}}$, $C_{CO_{2}}$, $V_{E}$, $C_{LA}$.

• 1. Muscle metabolism

  • (a) The fraction of the aerobic power $\sigma$ is computed by (30).

  • (b) The value of $\dot{V}_{O_{2},m}$ is computed by (26).

  • (c) The rate of the lactate production by anaerobic pathway $\dot{V}_{la}$ is computed by (27).

• 2. Systemic parameters

  • (a) Tidal volume $V_{T}$ and respiratory rate $n$ are computed by (5).

  • (b) Cardiac output $Q$ and minute blood flow through the brain arteries $Q_{B}$ are computed by (24), (25).

  • (c) The lung’s volume $V$ is computed by (2). Concentrations of $O_{2}$ and $CO_{2}$ in the alceolar volume are computed by (3).

• 3. Concentrations of $O_{2},CO_{2}$ and lactate in the blood compartments

  • (a) Lactate production and utilisation are computed by (33).

  • (b) $O_{2}$ balance is computed by (11)–(13).

  • (c) The difference between hydrocarbonate and hydrogen $C_{HCO_{3}^{-}}-C_{H^{+}}$ is computed by (19).

  • (d) The hydrocarbonate $HCO_{3}^{-}$ is computed by (21)–(23).

  • (e) $CO_{2}$ balance is computed by (15), (16).

The calculated values of $C_{O_{2}}$, $C_{CO_{2}}$, $V_{E}$, $C_{LA}$ are used for comparison with experimental data in the algorithm of the minimisation of functionals (37) and update the values $e_{a}$, $u_{la}$, $\kappa_{CO_{2}}$. The procedure repeats until achieving the convergence.

It should be mentioned, that the systems of equations (11)–(13) and (21)–(23) are stiff. The stiffness coefficient of the system (11)–(13) is by the order of $10^{4}$. The stifness coefficient of the system (21)–(23) is by the order of $10^{5}$. The stiffness coefficients of the systems (33) and (19) are by the order of $10$. All these systems of ordinary differential equations were solved by the implicit single step A and L stable method of the $3^{rd}$ order Obreshlov’s pairs method [41–43] with the time step $\tau=10^{-2}$ s.

Confidential intervals were calculated using the moving block bootstrap method [44]. It allows analysis of the effect of outliers and noise on optimisation results.

3 RESULTS

The results of the simulations are shown in Tables 5–7 and in Figure 3. Figure 3 shows the average error of the fitting computed and measured time series of lungs ventilation, concentrations of the $O_{2}$ and $CO_{2}$ in the exhaled gas and lactate concentration in the blood by minimisation of the functionals (37). The average values are computed after nondimensionalisation of the time scale as the duration of the tests was different in every case (see Table 3). From Fig. 3, we observe substantial error during the initial stage of the exercise, which is approximately 5–10$\%$ of the total time. It conforms with the expectations, as far as our model does not include short-time metabolic and regulatory processes, which are not important for prolonged physical activity.

Table 5 Relative standard deviations for time series fitting (the data for the first 60 seconds were excluded)

Table 6 Identified parameters (the data for the first 60 seconds were excluded)

Table 7 Relative standard deviations for identified parameters (the data for the first 60 seconds were excluded)

Fig. 3

The average error curves of the fitting of the experimental time series with 95$\%$ confidence intervals.

The maximum and the average relative standard deviations (RSD) are shown in Table 5. We remove the measured and calculated data corresponding to the first 60 seconds of the physical exercise. From the Table 5 we observe, that the maximum RSD is about 10$\%$ and the average RSD is approximately 5$\%$ for all four parameters, which were both measured and simulated. Thus, we conclude that our model provides reasonable accuracy for prolonged and moderate physical exercise.

The values of the identified parameters are shown in Table 6. The RSDs for these parameters are shown in Table 7. The maximum and the average RSDs for $e_{a}$ and $\eta$ are less than 2$\%$. The maximum RSD is almost 20$\%$ for the $u_{la}$ and almost 30$\%$ for the $\kappa_{CO_{2}}$. Thus the model allows achieving only qualitative agreement for these values. The absence of the details may be a reason for the high values of RSD for $u_{la}$ and $\kappa_{CO_{2}}$. We consider lactate utilisation and production as well as the bicarbonate buffer system of the blood as some effective reactions of the first order (see (31) and (32)). The more detailed approach will increase the accuracy of the method. We mention, that removing two peak values decreases the maximum and the average values of RSD for $u_{la}$ to $11.3$ and $7.8\%$ and for $\kappa_{CO_{2}}$ to $16$ and $9.4\%$. These values are close to the RSDs for the time series fitting (see Table 5). We also mention that personal features may cause an increase of RSD for $u_{la}$ and $\kappa_{CO_{2}}$. Thus, more cases should be considered for the rigorous verification of the model.

The identified parameters $e_{a}$, $u_{la}$, $\kappa_{CO_{2}}$, $\eta$ (see Table 6) help to evaluate physical endurance of a sportsman. Mechanical effectiveness $\eta$ and, obviously related parameter $e_{a}$ (see (34)), characterise the percentage of the energy, which is spent to the exercise. Of course, higher values are preferable. The other two parameters $u_{la}$ and $\kappa_{CO_{2}}$ characterise the ability of lactate utilisation and, thus, reveal the actual level of training, the ability to perform a prolonged physical exercise with moderate power and, thus, endurance. From Table 6 we conclude, that $u_{la}$ and $\kappa_{CO_{2}}$ not necessary correlate with $e_{a}$ and $u_{la}$. An organism with higher values of these parameters performs work at more safe conditions with possibly less concentration of the lactate in the blood. Parameters $u_{la}$ and $\kappa_{CO_{2}}$ may be additional and even more critical markers of the level of training.

Direct comparison of the identified parameters $e_{a}$, $u_{la}$, $\kappa_{CO_{2}}$, $\eta$ with some known values is difficult because they are not used in sports medicine and other related fields due to the difficulties of their measurements. We mention, that the values of the rate of lactate utilisation $u_{la}$ conform to the experimental data, which state, that lactate concentration reaches the initial value in 60–90 minutes after the finish of the exercise [45]. The values of mechanical effectiveness $\eta$ correlate with the other works [46–48]. It ranges from $18$ to $27\%$ and depends on the power and duration of the exercise and the type of sport. The most experimental works evaluate mechanical effectiveness below the anaerobic threshold. It raises additional difficulties in the direct comparison.

4 DISCUSSION

There are some assumptions, which limits the accuracy of the model. We do not include creatine phosphate degradation as it acts as a source of power during a short period (up to one minute) at the beginning of the intensive exercise and does not produce lactate. It provides substantial error up to 50$\%$ at the beginning of the activity, but it causes no significant effect in the evaluation of the endurance in prolonged exercise up to 20 minutes. There are several sources of error in the estimation of lactate concentration. We are not considering specific processes of lactate utilisation in the muscles, myocardium, liver and intestine due to the glucogenesis as well as individual features of the buffer systems of blood. The correct approach should consider the metabolism of the heart, lungs and muscles separately.

The history of previous physical activity may cause-effect to the specific oxygen uptake and production and consumption of the lactate. Thus, the results of the additional treadmill tests over a long time may increase the accuracy of the model. We do not consider Bohr and Haldane effects in the dissociation of $O_{2}$ and $CO_{2}$ in the blood. It may cause an impact on the accuracy of computation of the partial pressures and to the simulation of the regulatory feedback. The effect of the absence of Cori cycle, Krebs (TCA) cycle and lactate shuttle is not clear.

5 CONCLUSION

Anaerobic glycolysis is the primary source of energy during high-intensity exercise. The accessory substance of this process is lactate. The elevation of the concentration of lactate in the blood may cause side effects, which decrease mechanical effectiveness and physical endurance of the organism. Thus, the processes of lactate utilisation are essential. In this work, we propose a model for personalised computational evaluation of the parameters, which characterise the lactate production and utilisation during prolonged physical exercise with a moderate load. It includes the combined model of the cardiovascular and respiratory system with regulatory feedback. The personally identified parameters include energy equivalent of $O_{2}$, which is proportional to the energy equivalent of lactate, effective rate of the lactate utilisation by an organism and coefficient of the non-metabolic production of $CO_{2}$, which characterises lactate utilisation by the bicarbonate buffer system of the blood. We evaluate mechanical efficiency as a ratio of the aerobic power to the power of the degradation of carbohydrates and fats. Standard treadmill test with increasing load provides sufficient input parameters for the realistic personalised simulations. The parameters are evaluated without biomedical tests, myography and other complex and costly procedures. The change of these parameters in time will help a sports coach to evaluate the physical endurance of a sportsman. Our model also will help to develop a training schedule using TRIMP model [33] for different exercises. Thus, the model provides additional information, which is not available in the standard protocol. In the future the model can be enhanced either by a more detailed description of the functioning of cardiovascular and respiratory systems under intense physical load [7, 49, 50] and by introducing more details on metabolic processes in the human body.