Base Fluids, Its Temperature and Heat Source on MHD Couette–Poiseuille Nanofluid Flow through Slippy Porous Microchannel with Convective-Radiative Condition: Entropy Analysis

Abstract

The intention behind this research work is to analyze the flow, heat transfer and entropy generation in a vertical channel filled with a nanofluid. The vertical microchannel is made of two parallel porous and slippy plates. The hot fluid is injected from the left side and succeeded from the right side. Fluid flow within the channel is induced due to an applied favorable/adverse pressure gradient (due to Couette–Poiseuille flow), right plate movement, buoyancy force due to the temperature difference of the channel plates in the presence of heat generation/absorption inside the channel and subjected to a constant applied transverse magnetic field. The resulting governing equations are solved numerically by the shooting method. The conventional fluids are chosen as water, and ethylene glycol-water mixture. The nanoparticles are selected as Al₂O₃ and CuO. Nanofluids modeling, which takes care of base fluid temperature, Brownian motion, diameter and concentration of nano particles, and base fluid physical properties are considered here. Roles of pressure gradient P (at the inlet), temperature of base fluids, heat generation/absorption, the density of the nanoparticle volume fraction on flow and heat transfer characteristics (velocity and temperature distribution, Nusselt number (Nu) distribution, entropy generation and Bejan Number) are investigated here. How the sequence of appearance of curves of flow and heat transfer characteristics (due to variation of aforesaid parameters) are disturbed by the presence of injection/suction, radiation and convective boundary condition is discussed here. A critical analysis is conducted on the individual contribution of irreversibilities due to heat flow, fluid friction and Joule heating to the total entropy generation. At last, we try to find an optimum condition at which local and global entropy generation are minimally generated in the channel.

1. INTRODUCTION

Water, engine oil, and ethylene glycol are basically used as traditional heat transfer fluids. These conventional fluids have low heat transfer and heat exchanger capacity. Nevertheless, there exist many techniques which can improve the heat transfer performance of these fluids. One such technique is that improving the thermal conductivity of these fluids. As the solid particles have a more significant thermal conductivity than base fluid, suspending metallic solid fine particles into the base fluid is expected to improve the fluid’s thermal conductivity. It has been well known for more than 100 years [1] that the conventional fluid heat transfer can be improved by adding millimeter- or micrometer-sized solid particles with the base fluid. However, the problems like fouling, sedimentation, erosion, and increased pressure drop of the flow channel had no practical interest. The modern advance in materials technology has made it believable to produce nanometer-sized particles that can beat these problems. Heat transfer fluids suspended with nanometer-sized solid particles are called ‘nanofluids.’

In recent years, this technique was applied by Wang and Majumdar [2]. This innovative method was first introduced by Choi [3] by using the fusion of nanoparticles and base fluids to enhance the heat transfer of nanofluids. After that, Buongiorno [4] clarified the reasons for the improvement of nanofluids’ enhancement and concluded that the effect of Brownian and thermophoresis diffusion is mainly responsible for heat transfer improvement. Based on this idea, Kuznetsov and Nield [5] have developed the natural convective double-diffusive boundary layer flow of nanofluids passes through a flat plate. The effective thermal diffusivity and the thermal conductivity of nanofluids are generally a function of volume fraction/nanoparticle concentration or nanoparticle size. Makinde and Aziz [6] have examined the convective boundary layer flow, and the heat transfer of nanofluids passes through a linearly stretching sheet with the effects of Brownian and thermophoresis motion. The convective heat transfer on Cu-water nanofluids and Ag-water, together with the nanoparticle volume fraction, was studied by Vajravelu et al. [7]. They have also investigated the thermal buoyancy effects in the appearance of internal heat generation or absorption. Chen et al. [8] solved Al₂O₃-water magnetohydrodynamics nanofluid flow through a vertical asymmetrically heated parallel plates with mixed convection. Also, average entropy generation number and Nusselt number are reduced for applying the magnetic field. Noreen et al. [9] have examined the entropy generation of an asymmetric porous microchannel filled with water-based nanofluids. Xu and Cui [10] have investigated the fully developed nano-fluid of nanoparticles and microorganisms flow through a mixed convection upper plate moving channel. Xu and Pop [11] have examined the fully developed flow, heat, and mass transfer of a porous upper plate moving horizontal channel saturated with a nanofluid in the suspension of nanoparticles and microorganisms by considering the Brownian and Thermophoretic diffusion. Xu and Cui [10] have introduced the pressure effect and slip boundary condition on the above problem. Ataei et al. [12] examined the flow and heat transfer quality of hybrid nanofluid through a microchannel with heat absorption and pressure drop. Their results showed that hybrid nanofluid has better heat transfer quality than pure base fluid. Al-shyyab et al. [13] analytically studied the effect of Knudsen number (Kn), Biot number (Bi) on the flow and heat transfer of a parallel plate. According to them Nu increases with Kn but decreases with Bi. Maiti and Mandal [14] analytically studied the impact of ramped plate temperature, radiation, slip, and buoyancy effects on an infinite vertical plate. They reported that a forceful flow near to the plate is generated by buoyancy and radiation, and accelerated by the slip effect.

Bachok et al. [15] studied the flow and heat transfer characteristics of steady two-dimensional boundary layer flow past a moving flat plate in a nanofluid with injection/suction. Rana et al. [16] examined the effect of Hartmann number, Reynolds number, and injection/suction parameter on velocity components and skin friction of an MHD Couette flow with injection/suction. The case of steady laminar flow of an incompressible electrically conducting viscous fluid due to natural convection through a vertical channel in the presence of uniform suction/injection through the walls, constant axial pressure gradient, and transversely imposed magnetic field was investigated by Makinde and Chinyoka [17]. Effect of thermal diffusion, chemical reacting MHD with injection/suction of a moving vertical plate on flow, heat and mass transfer is numerically studied by Olanrewaju and Makinde [18], and reported that the heat transfer rate at the plate surface is an increasing function of buoyancy force. Makinde and Chinyoka [19] examined the effects of suction/injection on unsteady reactive variable viscosity with convective boundary conditions flow in a channel fluid in a thin stationary slit wall. Chamkha et al. [20] numerically examined the effect of a uniform magnetic field, suction (injection), buoyancy forces, and free convective flow of an electrically conducting fluid along a vertical plate with localized heating/cooling on flow, heat and mass transfer. According to them suction reduces both the momentum and thermal boundary layer thicknesses.

Hashemabadi et al. [21] analytically studied the fully-developed heat transfer of a Couette–Poiseuille flow between parallel plates. Davaa et al. [22] numerically studied the heat transfer of a Couette–Poiseuille flow between parallel plates with viscous dissipation and pressure drop has been studied. They observed that with an increase of Br, Nu increase at the moving wall. Kyritsi-Yiallourou and Georgiou [23] have examined the heat transfer of Couette flow through a duct filled with Newtonian fluid. Mokarizadeh et al. [24] studied the heat transfer of a fully developed heat transfer of a Couette–Poiseuille flow with viscous dissipation. Francisca et al. [25] analytically presented the heat transfer of a fully developed laminar Couette–Poiseuille flow in the presence of viscous dissipation with constant but distinct heat fluxes at the walls. Tlili et al. [26] investigated the combined effect of MHD on Couette–Poiseuille flow of water-based nanofluid, hall current and radiation on thermodynamics. Also, the work of Bruin [27] presents the collection of references of early works, and Coelho and Poole [28] gives the collection of reference of the recent works on Couette–Poiseuille flow.

Kar et al. [29] investigated the combined effect of chemical reaction, hall current effect, and internal heat generation/absorption of an MHD flow passes through an accelerated porous flat plate, and reported that the injection coupled with heat generation results in a backflow rise. Ibrahim et al. [30] examined the effects of a heat source and Joule heating on radiative MHD flow over a porous channel with injection/suction. Valitabar et al. [31] have experimentally examined the forced convective heat transfer quality of the ferrofluid between two aluminum parallel plates with heat source, different flow rates and different magnetic field. The convective heat transfer quality of Al₂O₃-water nanofluid of a horizontal channel with two heat sources was studied by Ghaneifar et al. [32]. The result shows that, the impact of nanofluid concentration on Reynolds number was found more than Nusselt number. The effect of natural convection, internal heat generation of a moving vertical plate with convective boundary condition, is studied by Makinde [33]. Makinde reported that velocity and thermal boundary layer thickness increases with the increase of the heat generation parameter, while the opposite behavior is observed for Prandtl number. The effect of slip, forced convection on flow and heat transfer of Al₂O₃-water nanofluid in a parallel-plate microchannel in the presence of heat source/sink is theoretically investigated by Malvandi et al. [34]. They asserted that the system’s performance is increased in the presence of heat absorption since it enhances the heat transfer rate with no significant change in the pressure drop. Adesanya and Makinde [35] studied the effect of viscous dissipation, internal heat generation on flow, heat transfer, Bejan number, and entropy generation of a third-grade fluid passes through a vertical channel. Effect of fully developed, natural convection, internal heat generation/absorption and uniform transverse magnetic field on flow and heat transfer of a viscous incompressible fluid flow between two vertical isothermal walls in the presence of homogeneous porous medium is studied by Singh et al. [36], and reported that the temperature increases for heat source parameter while decreases with the heat sink parameter. Upriti et al. [37] studied the impact of suction/injection, heat generation/absorption of an MHD Ag-water nanofluid passes through a flat porous plate. They reported that the momentum boundary layer thickness decreases by increasing the values of volume fraction of silver solid particles, but the opposite behavior is observed for the thermal boundary layer. Also many more researchers work on heat generation/absorption on various situation.

Ranjit and Shit [38] have examined the entropy generation of a porous asymmetric microchannel under the effect of Joule heating. They have found that the Joule heating effects increase the production of the entropy in the channel. Monaledi and Makinde [39] studied the entropy generation of a Poiseuille flow of a microchannel filled with nanofluid and variable viscosity. According to them, nanofluid generates more entropy as compared to the base fluid. Ibáñez et al. [40] numerically studied the flow, heat transfer and entropy generation of a porous microchannel filled with Al₂O₃-water nanofluid with the combined effect of nonlinear radiative heat flux, slip and convective-radiative boundary conditions. They reported that the optimum values of slip length and nanoparticle volume fraction could minimize the global entropy generation. Srinivasacharya and Bindu [41] studied the entropy generation in a micropolar fluid flow through an inclined channel with slip and convective boundary conditions. They reported that the irreversibility due to heat transfer dominates at the center of the channel. Ibáñez [42] studied the same problem with additional hydrodynamic slip and convective boundary conditions. The result shows that entropy generation can be minimized by taking optimum values of the Biot number ($Bi$), Hartmann number ($Ha$) and Prandtl number ($Pr$). Ibáñez et al. [43] have extended the above work by adding radiation effect and considering the water Al₂O₃ nanofluid. They found that the optimum values of nanoparticle volume fraction ($\phi$) and magnetic field strength can maximize the heat transfer rate, while optimum values of the Radiation parameter and $\phi$ minimize the global entropy generation. Finally, López et al. [44] introduce a nonlinear radiative heat flux and buoyancy term in the above work. They reported optimum values of slip at which the entropy generation is minimum. Global entropy generation decreases with $\phi$ and suction/injection based Reynolds number. Makinde et al. [45] added the time-dependent velocity and temperature, and heat generation/absorption effect on the above problem with water as fluid.

Being inspired by the above-mentioned fruitful investigations, we aim to unfold the characteristics of unsteady nanofluid flow over a porous nano-channel considering the convective boundary condition and the Navier’s velocity slip. The problem becomes more interesting and complicated if additional mechanism, like Couette–Poiseuille flow, magnetic field, injection-suction, radiation, internal heat generation, temperature of base fluid, nano-fluid parameters (base fluid: Water and EG:Water), nanoparticle, concentration of nanoparticle, are applied to the said problem. A rigorous review of previously published research articles reveals that no such attempt has been made earlier. In our previous study [46] (accepted for publication), we investigated the effects of favorable/adverse pressure gradient, forward/backward movement of one plate, magnetic field, rate of injection/suction and radiation on the flow, heat transfer, and entropy generation inside the porous channel. However, we missed to take care of remaining parameters (like, internal heat absorption/generation, temperature of base fluid and nanofluid parameters). As a sequel to the previous study, the present work continues for the following objectives:

• To calculate the thermophysical properties of the nanofluid systematically at different fluid temperatures, leading to some typical values of parameters due to geometry and physical property of a fluid.

• To delineate the effect of pressure gradient, temperature of the base fluid, internal heat generation/absorption, kind of base fluid, nano particles, concentration of nano particle on flow, heat transfer, local and global entropy generation.

• To analyze the production of local and global entropy in the microchannel by scrutinizing the individual contribution of irreversibility of heat transfer, viscous dissipation, and Joule heating. Bejan number is also calculated here. At last, we tried to report an optimum situation for minimum local and global entropy generation inside the channel.

2. FORMULATION OF THE PROBLEM AND ITS SOLUTION

2.1. Problem Formulation

Fig. 1

A physical sketch of the problem.

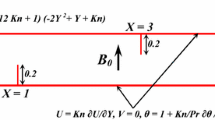
Consider a fully developed mixed convection flow of nanofluids (water and ethylene glycol-water mixture (EG:W, 60:40 by weight) as a base fluid, and CuO and Al₂O₃ as nanoparticle) between two infinite parallel vertical plates separated by a distance a, whose left plate is fixed at $y=0$ and the right plate, situated at $y=a$, is moving upward with a constant velocity $u_0$. As shown in Fig. 1, the Cartesian coordinate system is chosen with the $y'$-axis being along the channel walls and the $x'$-axis being perpendicular to the channel walls. The hot fluid is injected from the left porous wall into the channel with temperature $T_2$ at velocity $v_0$ and succeeding from the right porous wall of the channel with temperature $T_1$ and same velocity $v_0$. The reference temperature of the base fluid $T_0$ is independent of $T_1$ and $T_2$. Flow is subjected to a constant applied transverse magnetic field $B_0$ perpendicular to the plates. A favorable/adverse pressure gradient is applied to the channel. Also, the heat generation/absorption effect is also considered here.

2.2. Governing Equations with Boundary Conditions

Owing to the above assumptions, the momentum equation with Boussinesq approximation [44, 45] becomes,

$$\rho_{nf} v_0\frac{du'}{dy'} = -\frac{dp'}{dx'}+g(\beta\rho)_{nf}(T-T_0)+\eta_{nf} \frac{d^2u'}{dy'^2}-\sigma_{nf} B_0^2u', $$

(1)

where $u'$ is the velocity along $x'$ direction, $p'$ is the pressure, $g$ is the gravitational acceleration, $T$ is the temperature of the fluid. $\beta$, $\rho$, $\eta$, and $\sigma$ denotes thermal expansion coefficient, density, dynamic viscosity and electrical conductivity, respectively. The subscript ‘$f$’ and ‘$nf$’ denote for base fluid and nanofluid, respectively. With the above considerations, the energy balance equation reduces to

$$(\rho C)_{nf} v_0\frac{dT}{dy'}=\kappa_{nf}\frac{d^2T}{dy'^2}+\eta_{nf} (\frac{du'}{dy'})^2+\sigma_{nf} B_0^2u'^2-\frac{dq_r}{dy'}+Q_0(T-T_0), $$

(2)

where $C$ and $\kappa$ are heat capacitance and thermal conductivity, respectively, while $q_r$ is the thermal radiation flux, and $Q_0$ is the heat generation/absorption parameter. Boundary conditions are written as per the dependent variable.

I. Velocity boundary conditions:

For a unidirectional flow past a solid plate, Navier [47] proposed the following velocity slip condition

$$u' = \alpha'\frac{du'}{dy'}, $$

(3)

where $u'$ is the slip velocity at the fluid-plate interface and $\alpha'$ is the partial slip ($0<\alpha<\infty$). However, due to the consideration of upward plate movement and favorable/adverse pressure gradient, the slip velocity at the plates is seen to be dependent on P or/and $Re_u$.

a. Left stationary plate($y'=0$):

Fig. 2

(a) Velocity profile for classical Couette–Poiseuille flow (without slip) for favorable/adverse pressure gradient $P=(- \frac{du'}{dx'})$, and forward movement of the right plate. Sold lines: $P=1$, dashed lines: $P=-1$ and (b) variation of $\frac{du'}{dy'}$ with $P.Re_u$.

As seen in the velocity profile of classical Couette–Poiseuille flow without slip, presented in Fig. 2a, the forward/backward flow takes place inside the channel depending on the positive/negative value of P or/and $Re_u$. In order to clear the conundrum, the variation of $\frac{du'}{dy'}$ at both plates with $PRe_u$ is presented in Fig. 2b. As seen from the variation in the left plate:

$$\frac{du'}{dy'} = \begin{cases} >0 & \text{for $-2<PRe_u<\infty$, leading to a forward flow, and} \\<0 & \text{for $-\infty<PRe_u\leq -2$, leading to a backward flow.} \end{cases}$$

Therefore, when $Re_u>0$, the slip velocity at the left plate with slip length $\alpha_2'$ can be expressed as:

$$u' = \begin{cases} \alpha'_2 |\frac{du'}{dy'}| & \text{for P$\geq 0$}, \\ -\alpha'_2 |\frac{du'}{dy'}| & \text{for P$< 0$}, \\ \end{cases}$$

while for $Re_u<0$:

$$u' = \begin{cases} \alpha'_2 |\frac{du'}{dy'}| & \text{for P$>0$}, \\ -\alpha'_2 |\frac{du'}{dy'}| & \text{for P$\leq 0$}. \\ \end{cases}$$

Where $\alpha_2'$ is the slip length at the left plate. These expressions for the slip velocity are consistent with what is expected in the velocity profile presented in Figs. 2a, 2b for all negative and positive values of P and $Re_u$.

b. Right moving plate($y'=a$):

With the similar argument made for the left plate, one can write the following expressions by considering the velocity profile and its gradient at the right plate presented in Fig. 2:

when $Re_u>0$:

$$u' = \begin{cases} u'_0 + \alpha'_1|\frac{du'}{dy'}| & \text{for P$>0$}, \\ u'_0 - \alpha'_1|\frac{du'}{dy'}| & \text{for P$\leq 0$}, \\ \end{cases}$$

and when $Re_u<0$:

$$u' = \begin{cases} -u'_0 + \alpha'_1|\frac{du'}{dy'}| & \text{for P$\geq0$}, \\ -u'_0 - \alpha'_1|\frac{du'}{dy'}| & \text{for P$< 0$}. \\ \end{cases}$$

Where $\alpha_1'$ is the slip length at the right plate.

II. Thermal boundary conditions:

Lin et. al. [48] recommended to use the convective thermal boundary conditions for problems when the viscous dissipation effect is considered. Therefore, because of the model equation (2), the convective boundary condition is considered here.

a. At the left plate:

$$\kappa_{nf} \frac{dT}{dy'}-h_2(T-T_2)-\epsilon_2 \sigma^* (T^4-T_2^4)=0; ~~{\rm for~~all}~~ P~~{\rm and}~~ Re_u. $$

(4)

b. At the right plate:

$$\kappa_{nf} \frac{dT}{dy'}+h_1(T-T_1)+\epsilon_1\sigma^*(T^4-T_1^4)=0; ~~{\rm for}~~ {\rm all}~~ P~~ {\rm and}~~ Re_u, $$

(5)

where $\epsilon_1$ and $\epsilon_2$ are emissivity of right and left plate respectively, $\sigma^*$ is Stefan Boltzmann constant, $h_1$ and $h_2$ denote the convective heat transfer coefficient for right and left plates, respectively, are defined as:

$$h_1=\frac{\kappa_f}{(T_1-T_0)}\frac{dT}{dy'}|_{y'=a}, $$

(6)

$$h_2=\frac{\kappa_f}{(T_2-T_0)}\frac{dT}{dy'}|_{ y'=0}. $$

(7)

Now the thermal radiation flux $q_r$ is approximated using Rossland diffusion approximation as:

$$q_r=-\frac{4\sigma^*}{3\kappa^*}\frac{dT^4}{dy'}=-\frac{16\sigma^*}{3\kappa^*}T^3\frac{dT}{dy'}, $$

(8)

where $\kappa^*$ is the mean absorption coefficient.

Introducing the following dimensionless variables

$$u=u'/u_0 ,~~ x=x'/a,~~ y=y'/a,~~ \theta=(T-T_0)/(T_2-T_0),~~ {\rm and}~~ p=p'/(\rho u_0^2),$$

the above governing equations (1), (2) along with the corresponding boundary conditions are reducing sequentially as:

$$\frac{\rho_{nf}}{\rho_f} Re_u Re_v\frac{du}{dy}=\frac{\rho_{nf}}{\rho_f} Re_u^2 P+\frac{(\rho \beta)_{nf}}{(\rho \beta)_f}Gr \theta+\frac{\eta_{nf}}{\eta_f}Re_u \frac{d^2u}{dy^2}-\frac{\sigma_{nf}}{\sigma_f}Re_u Ha^2 u, $$

(9)

$$\frac{(\rho C)_{nf}}{(\rho C)_f}Pr Re_v \frac{d \theta}{dy} =\frac{\kappa_{nf}}{\kappa_f}\frac{d^2 \theta}{dy^2}+3 Rd (\theta_h-1)[\theta (\theta_h-1) +1]^2 \left(\frac{d\theta}{dy}\right)^2$$

$$+Rd[\theta(\theta_h-1)+1]^3 \left(\frac{d^2 \theta}{dy^2}\right) + Br[\frac{\eta_{nf}}{\eta_f} \left(\frac{du}{dy}\right)^2+\frac{\sigma_{nf}}{\sigma_f} {Ha}^2 u^2]+Q\theta . $$

(10)

I. Velocity boundary conditions:

a. Left stationary plate:

when $Re_u>0$:

$$u = \begin{cases} \alpha_2 |\frac{du}{dy}| & \text{for P$\geq0$}, \\ -\alpha_2 |\frac{du}{dy}| & \text{for P$< 0$}, \\ \end{cases}$$

while for $Re_u<0$:

$$u = \begin{cases} \alpha_2 |\frac{du}{dy}| & \text{for P$>0$},\\ -\alpha_2 |\frac{du}{dy}| & \text{for P$\leq 0$}.\\ \end{cases}$$

b. Right moving plate:

when $Re_u>0$:

$$u = \begin{cases} 1 + \alpha_1|\frac{du}{dy}| & \text{for P$>0$}, \\ 1 - \alpha_1|\frac{du}{dy}| & \text{for P$\leq 0$},\\ \end{cases}$$

while $Re_u<0$:

$$u = \begin{cases} -1 + \alpha_1|\frac{du}{dy}| & \text{for P$\geq0$}, \\ -1 - \alpha_1|\frac{du}{dy}| & \text{for P$< 0$}.\\ \end{cases}$$

II. Thermal boundary conditions:

a. Left plate:

$$\frac{\kappa_{nf}}{\kappa_f} \frac{d\theta}{dy}+(\theta - 1)\frac{d\theta}{dy} - \frac{Nr_2}{(\theta_h-1)}[(\theta(\theta_h-1)+1)^4-\theta_h^4]=0 ~~ {\rm for} ~~ {\rm all} ~~ P~~ {\rm and} ~~ Re_u. $$

(11)

b. Right plate:

$$\frac{\kappa_{nf}}{\kappa_f} \frac{d\theta}{dy}-(\theta \theta_1 +1)\frac{d\theta}{dy} + \frac{Nr_1}{(\theta_h-1)}[( \theta(\theta_h-1)+1)^4-\theta_2^4]=0 ~~ {\rm for} ~~ {\rm all} ~~ P~~ {\rm and} ~~ Re_u. $$

(12)

Here the operational dimensionless parameters are defined as $(i)$ $Re_u=u_0a\rho_f /\eta_f$: the Reynolds number due to plate movement, $(ii)$ $Re_v=v_0a\rho_f / \eta_f$: the Reynolds number due to injection and suction, $(iii)$ $P=-dp'/dx'$: the pressure gradient, $(iv)$ $Pr=\eta_f C /\kappa_f$: the Prandtl number, $(v)$ $Br=\eta_f u_0^2 / (\kappa_f (T_2-T_1))$: the Brinkman number, $(vi)$ $Gr=g(\rho_f \beta_f) a^3(T_2-T_0)/(\rho_f \nu_f^2)$: the Grashof number, $(vii)$ $Rd=16\sigma^* T_1^3/(3 \kappa^* \kappa_f)$: the radiation parameter, $(viii)$ $Ha=B_0 a \sqrt(\sigma/\eta_f)$: the Hartman number, $(ix)$ $Nr=a\epsilon\sigma^*T_1^3/\kappa_f$: the conduction-radiation parameter, $(x)$ $Q=Q_0a^2/\kappa_f$: the heat generation/absorption parameter, $(xi)$ $\theta_h=T_2/T_0$, $(xii)$ $\theta_1=\frac{(T_2-T_0)}{(T_0-T_1)}$, and $(xiii)$ $\theta_2=T_1/T_0$.

2.3. Nanofluid Modeling

Water and EG:W are considered as the base fluid whereas nanoparticles are Al₂O₃ and CuO. Also considered that the nanoparticles are uniform shape and size, and homogeneously distributed in the base fluid. The thermophysical properties of the nanofluids are assumed constant. Thermophysical properties are calculated as follows:

• Density: From the proposed equation of Pak and Cho [49], the density of nanofluids are calculated.

• Specific heat: By using the equation given by Xuan and Roetzel [50], the specific heat of nanofluids is determined.

• Thermal conductivity: Vajjha and Das [51] modified the proposed relation by Koo and Kleinstreuer [52] for thermal conductivity as a two terms function (Which takes into account the effect of nanoparticles diameter $d_{np}$ and volume fraction $\phi$ , temperature T and the properties of the base fluid) is considered here. Kim et al. [53] experimentally, and Ebrahimnia Bajestan et al. [54] numerically, confirmed that this model predicts the thermal conductivity and hence the heat transfer coefficient of nanofluids more accurately as compared to the models based on the pure static conditions of the nanofluids.

• Viscosity: Considering the effects of Brownian motion, temperature of the base fluid, $d_{np}$, $\phi$, nanoparticle density and base fluid physical properties, the theoretical model for the prediction of the effective viscosity of nanofluids is developed by Masoumi et al. [55].

  The model is as follows:

  $$\mu_{nf}=\mu_f+\frac{\rho_s V_b d_s^2}{72 C \delta}, $$

  (13)

  where $V_b$=$\frac{1}{d_{np}}\sqrt{\frac{18\kappa T}{\pi \rho_{np} d_{np}}}$ is the Brownian velocity, $C$ is the correlation factor defined by $C={\mu_{bf}}^{-1}[a\phi+b]$ with $a=-1.33\times 10^{-6}\times d_{np}\times 10^9-2.771 \times \times 10^{-6}$ and $b=90\times 10{-8}\times d_{np}\times 10^9-3.93 \times 10^{-7}$ and $\delta=\sqrt[3]{\frac{\pi}{6 \phi}} d_{np}$ is the distance between the centers of particles. Also, we have to multiply $10^9$ with $d_{np}$ to convert it in meter.

• Thermophysical properties of Water and EG:W ($\rho_{np}$, $C_{p,bf}$, $\kappa_{bf}$), and the physical properties of nanoparticles ($\rho_{np}$, $C_{p,np}$, $\kappa_{np}$) are calculated by using the relations given by Etminan-Farooji et al. [56].

2.4. Numerical Method

This system of ordinary differential equations is solved together with the boundary conditions using MATLAB’s routine bvp4c, which is based on the Runge–Kutta–Fehlberg method along with shooting technique. The governing equations are reduced into a set of first-order initial value problem by introducing the new variables $y_1$, $y_2$, $y_3$, and $y_4$ as $y_1=u$, $y_2=y_1'$, $y_3=\theta$, and $y_4=y_3'$, and the equations reduce to:

$$y_2=y_1'=du/dy, $$

(14)

$$y_2'=\frac{ \left(\frac{(\rho C)_{nf}}{(\rho C)_f}Re_uRe_vy_2-\frac{(\rho \beta)_{nf}} {(\rho \beta)_f}Gry_3-\frac{\sigma_{nf}}{\sigma_f}Re_uHa^2y_1 \right)}{\frac{\eta_{nf}}{\eta_f}Re_u}, $$

(15)

$$y_4=y_3', $$

(16)

$$y_4'=\frac{\frac{(\rho C)_{nf}}{(\rho C)_f}PrRe_vy_2-3Rd(\theta_h-1)[y_3(\theta_h-1)+1]^2y_4^2- Br[\frac{\eta_{nf}}{\eta_f}y_2^2+\frac{\sigma_{nf}}{\sigma_f}Ha^2y_1^2]-Qy_3}{\frac{\kappa_{nf}}{\kappa_f}+Rd[y_3(\theta_h-1)+1]^3}, $$

(17)

with the following boundary conditions:

$$y_1(0)=\xi, $$

(18)

when $Re_u>0$:

$$\xi-\alpha_2\vert {y_2(0)}\vert =0 ~~ {\rm for}~~ P\geq 0, $$

(19a)

$$\xi+\alpha_2\vert {y_2(0)}\vert =0 ~~ {\rm for}~~ P< 0; $$

(19b)

when $Re_u<0$:

$$\xi-\alpha_2\vert {y_2(0)}\vert =0 ~~ {\rm for}~~ P> 0, $$

(20a)

$$\xi+\alpha_2\vert {y_2(0)}\vert =0 ~~ {\rm for}~~ P\leq 0; $$

(20b)

$$y_3(0)=\delta, $$

(21)

$$\frac{\kappa_{nf}}{\kappa_f}y_4(0)+8(\delta - 1)y_4(0) - \frac{Nr_2}{(\theta_h-1)}[(\delta(\theta_h-1)+1)^4-\theta_h^4]=0;$$

$${\rm for} ~~ {\rm all} ~~ P~~ {\rm and} ~~ Re_u, $$

(22)

where the unknowns $\xi$ and $\delta$ are determined in such a way that the following conditions are satisfied:

when $Re_u>0$:

$$y_1(1)-1-\alpha_1\vert {y_2(1)}\vert =0 ~~ {\rm for}~~ P> 0, $$

(23a)

$$y_1(1)-1+\alpha_1\vert {y_2(1)}\vert =0 ~~ {\rm for}~~ P\leq 0; $$

(23b)

when $Re_u<0$:

$$y_1(1)+1-\alpha_1\vert {y_2(1)}\vert =0 ~~ {\rm for}~~ P\geq 0, $$

(24a)

$$y_1(1)+1+\alpha_1\vert {y_2(1)}\vert =0 ~~ {\rm for}~~ P< 0; $$

(24b)

$$\frac{\kappa_{nf}}{\kappa_f} y_4(1)- (\theta_1y_3 (1) +1) y_4(1) + \frac{Nr_1} {(\theta_h-1)} [(y_3(1)(\theta_h-1)+1)^4-\theta_2^4]=0;$$

$${\rm for} ~~ {\rm all} ~~ P~~ {\rm and} ~~ Re_u. $$

(25)

2.5. Parameters Value

Table 1. Values of Grashof number and Prandtl number at different temperatures for water and EG:W

Width of the microchannel is typically taken as $a=0.5mm.$ The thermophysical properties ($\rho$, $C_p$, $\kappa$, and $\eta$) of nanofluid with base fluid water and EG:W and nanoparticle Al₂O₃ and CuO are calculated from the temperature-dependent relations at various temperature, available in Etminan-Farooji et al. [56] paper. Here, the reference temperature $T_0$ is chosen randomly between $T_1$ and $T_2$. We consider three temperature values and the values of all thermophysical properties are calculated at every different temperature for both base fluid, accordingly the value of parameters $Gr$ and $Pr$ are computes (ref. Table 1). The effects of $Re_u$ (and $Re_v$) have been studied in our previous study by varying $u=0.0025$ m/s to 0.01 $m/s$ (and 0.0025 m/s to $0.0075$ m/s). Therefore the values Ha, Rd, Br, Nr, Q, $\alpha$, $Re_u$, and $Re_v$ for water is considered as fixed, and the corresponding values for EG:W is converted by the respective factors. The default values are chosen for these parameters for water as $Ha=Rd=Nr=Q=1$, $Br=0.1$, and $Re_u=3$ ($u_0$ is approximate $0.006$ m/s), $Re_v=1$ ($v_0$ is approximate $0.0025$ m/s) and $\alpha_1=\alpha_2=\alpha=0.1$ for water, while $Ha=0.414$, $Rd=Nr=1.695$, $Q=1.695$, $Br=0.795$, $Re_u=0.6084$, and $Re_v=0.2028$ for EG:W. Moreover, values of $T_2$, $T_1$, $T_0$, P, and $\phi$ are generally taken here as $T_2=320$ K, $T_0=310$ K, $T_1=300$ K, 1 and $\phi=0.04$ respectively for both base fluids, until otherwise specified particularly. The value of P is set as $\pm1$. Therefore, the governing parameters for this study becomes; (i) base fluid (water (W) and EG:W), (ii) type of nano particles (CuO and Al₂O₃), (iii) nanoparticle volume fraction $\phi$, (iv) ambient walls temperature ($T_2$ and $T_1$) (v) fluid temperature entering the channel ($T_0$) and (vi) heat source/absorption parameter Q $(=-3,-1,0,2)$.

3. RESULTS AND DISCUSSION

3.1. Velocity Distribution

Fig. 3

Velocity profile for different values of $\phi$ and both base fluids at $P=\pm1$. Solid line: CuO and dashed line: Al₂O₃.

Fig. 4

Velocity profile for different values of Q at $P=\pm1$. Solid line: W–CuO and dashed line: EG:W–CuO.

This segment displays the physics involved in the flow regime. Figure 3 presents the impact of nanofluids (W–CuO, W–Al₂O₃, EG:W–CuO and EG:W–Al₂O₃), nano particle concentration ($\phi$) and pressure gradients ($P=\pm1$) on the fluid velocity across the channel. The forward flow is found for $P=1$ throughout the channel, while the backward flow is found at some specific value of $y$ for $P=-1$. The existence of denser nanoparticles in the flow region reduces the intensity of velocity of the nanofluids since the viscosity of the nanofluid increases with $\phi$. The velocity of the Water nanofluids is more than that of EG:W nanofluids. Physically, this is possible because EG:W has greater viscosity, which makes the fluid thick. The effect of pressure gradient and plate movement on EG:W is less than that on Water. Major differences between base fluid role on the velocity is observed for $P=-1$ case. While comparing the role of nano particles (CuO and Al₂O₃), the velocity profile of CuO is found to be slidely more. Therefore we use CuO throughout the section. Similar exercise was made for the downward movement of the plate ($Re_u=-3$), not presented here, and eventually similar effects of the considered parameters on the velocity are observed.

Fig. 5

Velocity profile for different values of $T_0$ for two sets of $T_2$ and $T_1$: (a) $T_2=320$ K, $T_1=300$ K and (b) $T_2=340$ K, $T_1=320$ K. Solid line: W–CuO and dashed line: EG:W–CuO.

Figure 4 depicts the curves for velocity profiles due to variations in heat generation/absorption parameter Q. The pressure gradient force and heat generation (absorption) are less effective to EG:W compared to Water. The backward flow is limited to the left plate premises only for W at $P=-1$. Velocity in the channel marginally increases with heat generation for both base fluids and P, while with the increase of heat absorption the velocity marginally decreases for forward flow but it becomes more negative for backward flow. Physically, due to increases in Q, internal energy of the fluid increases, as a result velocity of the molecules increases.

The effect of base fluid temperature on velocity are visible in Fig. 5 for two sets of $T_2$ and $T_1$. We observe that the velocity of the fluid reduces with more temperature $T_0$ for fixed $T_2$ and $T_1$ for forward flow, while it becomes more negative for backward flow. This is due to the fact that as $T_0$ increases, ($T_2-T_0$) decreases for fixed $T_2$, and as a result buoyancy force decreases. In comparison to the effect of $\phi$ and $\theta$, the base fluid temperature has major role in influencing the velocity inside the channel.

3.2. Temperature Profile

Fig. 6

Dimensional temperature profile for different values of $\phi$. Solid line: W–CuO and dashed line: EG:W–CuO. Inset figure shows the temperature profile for different values of $\phi$ without radiation and, radiative-convective boundary condition. For inset figure, thermal boundary condition of first kind ($T=T_2$ at left plate and $T=T_1$ at right plate) is applied.

Fig. 7

Dimensional temperature profile for different values of Q. Solid line: W–CuO and dashed line: EG:W–CuO.

Fig. 8

Dimensional temperature profile for different values of $T_0$.

This portion shows the material science engaged with the temperature profile. The influence of nanofluids, and nanoparticles concentration $\phi$ on temperature profile is shown in Fig. 6. Here the temperature reduces nominally for the increasing values of $\phi$ at the left side of the channel for both W–CuO and EG:W–CuO. But, in the next half of the channel, the opposite behavior is found, which is due to the effect of radiation, and convective and radiative thermal boundary condition (ref. inset figure in Fig. 6). The thermal conductivity of EgW–CuO is higher than W–CuO. Also, when $\phi$ increases, the thermal conductivity of the fluid increases. So the temperature for EgW–CuO is more than W–CuO. It may be noted here that due to injection of hot fluid from left plate, right plate temperature is increased, which depends on the injection rate (previous study). The temperature profile of CuO and Al₂O₃ for water and EG:W is approximately the same, not presented here.

Figure 7 demonstrates the effect of heat generation/absorption parameter Q on the temperature of nanofluids. Eventually, the temperature inside the channel increases with increment in heat generation and decreases with the increase of heat absorption. Physically, the heat source adds more heat to the system boundary, while reverse effect for heat absorption. Effect of heat source/absorption term on the temperature of different base fluids is almost insensitive.

Figure 8 displays the reference temperature’s impact on the temperature profile. In both cases, we found that as we increase the fluid’s reference temperature, the fluid temperature for the fully developed stage gets low in the channel, except close to the cold plate where reverse phenomena are observed. This is physically possible, as the $T_0$ increases, the fluid gets lighter and $Pr$ gets low. As a result the temperature of the fluid gets low. Apparently, temperature throughout the channel can be increased by increasing the temperature of injected hot fluid at a fixed temperature of right side. The effect is almost similar for EG:W base fluid. The reverse trend in the temperature profile at the right plate (in comparison to the left plate) reported in Fig. 8.

3.3. Heat Transfer Analysis

From Fourier’s law of heat conduction and Newton’s law for convective heat flow between a solid surface and fluid, the convective heat transfer coefficient h is defined as $h=-\frac{\kappa_{nf}}{\Delta T}(\frac{\partial T}{\partial y})_w$, where $\kappa$ is the thermal conductivity of the fluid and $\Delta T=T_w-T_b$. Here ‘$w$’ denotes plates (hot plate: $y=0$ and cold plate $y=1$) and $T_b=I'/K'$ is the cross-sectional average temperature where

$$I'=\int\limits_{0}^{a}u'Tdy' ~~ {\rm and} ~~ K'=\int\limits_{0}^{a}u'dy'. $$

(26)

The non-dimensional form of $h$, called the Nusselt number $Nu$, is given by

$$Nu=\frac{ah}{2 \kappa}=- \left(\frac{\kappa_{nf}}{\kappa_f} \right)\frac{1}{2 (\theta_w-I/K)} \left(\frac{d \theta}{d y}\right)_w $$

(27)

with

$$I=\int\limits_{0}^{1}u\theta dy ~~ {\rm and} ~~ K=\int\limits_{0}^{1}udy. $$

(28)

Fig. 9

Nusselt number as a function of $\phi$ with different values of Q. Inset figure of Fig. 9b shows the Nu for the same condition with no injection/suction ($Re_v=0$).

Fig. 10

Nusselt number as a function of $\phi$ with different values of Q, in the absence of radiation and convective boundary condition. Here thermal boundary condition of first kind ($T=T_2$ at left plate and $T=T_1$ at right plate) is applied.

Figure 9 illustrates the variation of Nu for both base fluids and different values of $\phi$, and Q. Figure 9 shows that the Nu increases with the increasing values $\phi$. The increment rate and value of heat transfer are more at the suction side in comparison to the injection side. This is because the nanoparticles in the fluid rise the thermal conductivity of the fluid. While looking at the effect of Q on Nu, it is seen at the injection side that the heat transfer increases with heat absorption increases, but it is decreases with increase of heat source. With the increase of heat absorption, temperature difference between the heated wall and flowing fluid increases, leading to increase heat transfer from the wall. An opposite behavior of Nu is observed for heat source case. Physically heat source add more heat to the boundary layer region and increase the thickness of thermal boundary layer, and hence reduce the rate of heat transfer from the boundary to the fluid. The sequence of appearance of Nu curve with Q as reported at the left plate (Fig. 9a), is not maintain at the right plate (Fig. 9b). Also the order at which Nu curve with Q variation appears at the right plate for water base fluid is not the same for EG:W fluid. It is observed that presence of suction disturbs these sequences (inset figure of Fig. 9b). Despite having more thermal conductivity for EG:W, than water, Nu is marginally higher for EG:W because of presence of radiation and convective boundary condition (Figs. 10a and 10b) in the considered physical problem. When Rd = 0 is considered then the thermal boundary condition for left plate $T=T_2$ and at right plate $T=T_1$ is considered, instead of convection-radiation thermal boundary condition. Therefore, one can see the use of radiation and convective boundary condition in the present flow configuration.

Fig. 11

Nusselt number as a function of $T_0$ with different values of Q.

Fig. 12

Nusselt number as a function of $T_0$ with different values of Q, in the absence of radiation and convective boundary condition. Here thermal boundary condition of first kind ($T=T_2$ at left plate and $T=T_1$ at right plate) is applied.

Fig. 13

Nusselt number as a function of $T_0$ with different values of $\phi$.

The influence of reference temperature ($T_0$) on the heat transfer at both plates is examined based on Figs. 11–13. Here we have not used any inlet boundary condition. Temperature inside the channel is controlled by plates thermal condition. It is plausible that for the case of without radiation and convective boundary condition with the increase of $T_0$ the considered fluid becomes lighter, having lower $Pr$, resulting to lower the heat transfer. This situation is presented in Fig. 12, where it is seen that the absolute value of Nu decreases with the increase of $T_0$. Apparently for the case of heat source, heat transfer take place from fluid to left plate. In other words, here, $Pr$ and $Re_v$ in the energy equation are mechanically similar. In our previous study, it was observed that heat transfer from the hot wall increases with $Re_v$. In presence of radiation and convective boundary condition, as seen in Fig. 11a, with the increase of $T_0$, Nu is also decreases for the case of heat absorption, while it increases for hat source case. Opposite situation is observed in Fig. 11b, that is, Nu increases for heat absorption and decrease for heat source case with increase of $T_0$. Here also, from Figs. 12a, 12b it is observed that with the absence of Radiation and convective boundary condition, Nu for EG:W is more than water.

A similar effort is made for different values of $\phi$ and presented in Fig. 13. It is seen that all curves are qualitatively similar to each other, and Nu is increasing function of $T_0$ for all $\phi$ at left plate, while it is a decreasing function of $T_0$ at right plate. This is consistent with previous figure Fig. 11 since the value of $\phi$ is taken as $Q=1$.

3.4. Entropy (Local and Global) Generation

The study of entropy generation is quite imperative to have an idea about the irreversibility of a particular system’s thermal energy. In most industrial and engineering processes, entropy production leads to destroying the system’s available energy. Thus entropy generation performs a vital job in determining thermal machines’ performance, such as heat pumps, heat engines, power plants, air conditioners, and refrigerators. Due to this immense importance, it is essential to find the rate of entropy generated for a system to optimize the energy system for efficient operation. Now, from the second law of thermodynamics, the expression for the entropy generation of the system is given by

$$S'=\frac{1}{T^2} \left(\kappa_{nf}+\frac{16\sigma^* T^3}{3\kappa^*}\right) \left(\frac{\partial T}{\partial y'}\right)^2 +\frac{\eta_{nf}}{T}\left(\frac{du'}{dy'}\right)^2+\frac{\sigma_{nf} B_0^2}{T}u'^2, $$

(29)

and its non-dimensional form is as follows (normalizing by $\frac{\kappa_f}{a^2}$):

$$S=S_H+S_F+S_J, $$

(30)

where

$$S_H=\frac{(\theta_h-1)^2}{[\theta(\theta_h-1)+1]^2} \left[\frac{\kappa_{nf}}{\kappa_f}+Rd(\theta(\theta_h-1) +1)^3\right]\left(\frac{d\theta}{dy}\right)^2,$$

$$S_F=\frac{\eta_{nf}}{\eta_f}Br\frac{(\theta_h-1)}{[\theta(\theta_h-1)+1]} \left(\frac{du}{dy}\right)^2,~~ {\rm and}$$

$$S_J=\frac{\sigma_{nf}}{\sigma_f}Br\frac{(\theta_h-1)}{[\theta(\theta_h-1)+1]}Ha^2u^2.$$

Here $S_H$ is the entropy generation due to heat transfer irreversibility, $S_F$ is due to viscous dissipation or fluid friction and $S_J$ is the Joule heating or Ohmic heating, which is due to the magnetic field. Bejan number, Be, of a system is the ratio of entropy generation due to heat transfer with total entropy generation, i.e., $Be=S_H/S$. Physically, the Bejan number is used to measure the irreversibility of thermal energy to the total system irreversibility. Also the relative irreversibility due to fluid friction and Joule heating is defined by $F=S_F/S$ and $J=S_J/S$ respectively. Again integrating S between 0 to 1, we find the global entropy generation $\langle S\rangle$. Here we define $\langle S\rangle _H$, $\langle S\rangle _F$ and $\langle S\rangle _J$ as follows:

 $\langle S\rangle _H$ = (Total entropy generation due to Heat transfer)/$\langle S\rangle =\langle S_H\rangle /\langle S\rangle$,

 $\langle S\rangle _F$ = (Total entropy generation due to Viscous Dissipation)/$\langle S\rangle =\langle S_F\rangle /\langle S\rangle$, and

 $\langle S\rangle _J$ = (Total entropy generation due to Joule Heating)/$\langle S\rangle =\langle S_J\rangle /\langle S\rangle$.

Fig. 14

Local Entropy generation for different values of $\phi$. Solid line: W–CuO(w), and dashed line: EG:W–CuO. Inset figure shows the individual contribution of each part of the local entropy generation (due to heat transfer irreversibility—Be, due to viscous dissipation—F, due to Joule heating—J).

Figure 14 portrays the impacts of $\phi$ and, EG:W–CuO and W–CuO on local entropy generation (S). The change in particle concentration ($\phi$) on S is visible only for EG:W base fluid. For both nanofluids, the system irreversibility is found maximum at the wall sides, while minimum at the interior of the channel. The ascending values of $\phi$ caused an ascendance in $S$. As can be seen in inset figure, fluid friction part dominates at the left wall. Apparently, frictional part becomes more for EG:W due to more viscosity. As we increase $\phi$, viscosity becomes more, resulting to increase the system irreversibility. While looking into the thermal part, it is seen that Bejan number (Be) increases with $y$, indicating that thermal irreversibility is minimum at the injection side, while maximum at the suction side. As reported in Figs. 6–8, temperature variations were minimum at the injection, while maximum at the suction, because on the left side hot fluid is directly injected. While temperature on the suction side depends on the physical properties of fluid and wall, flow activities, and others. Because of higher thermal conductivity of EG:W base fluid, heat transfer at the suction side takes place easily, compared to water, and hence thermal irreversibility is found less for EG:W base fluid in comparison to water. With the similar argument (here left plate fixed and right plate moving) one can understand why the frictional irreversibility is maximum on the left plate and minimum at the right plate. Joule heating part moderately contribute to the total entropy generation only at the channel center.

Fig. 15

Local Entropy generation for different values of Q. Solid line: W–CuO, and dashed line: EG:W–CuO. Inset figure shows the individual contribution (water) of each part of the local entropy generation (due to heat transfer irreversibility—Be, due to viscous dissipation—F, due to Joule heating—J).

Fig. 16

(a) Local Entropy Generation for different values of $T_0$ with $T_2=320$ K, $T_1=300$ K and, $\phi=0.04$. Solid line: Water–CuO, and dashed line: EG:W–CuO. Individual contribution for (b) water and (c) EG:W. Entropy generation, due to heat transfer irreversibility—Be, due to viscous dissipation—F, due to Joule heating—J.

Fig. 17

Local Entropy generation for different values of $T_0$ with $T_2=340$ K, $T_1=320$ K. Solid line: Water-CuO, and dashed line: EG:W–CuO.

The effect of Q on S is exhibited in Fig. 15. It is seen that system irreversibility is sensitive to Q at the right wall for both the fluids, but at the left wall only for EG:W. The ascending values of Q (from $-3$ to 2) results to increasing the entropy generation at the wall premises. The pattern of curves inside the inset figure (as the individual contribution for Water and EG:W are similar, so only the individual contribution of water is presented in the inset figure) is analogous to three respective curves presented the inset figure of Fig. 14. Now with the increase of Q, velocity changes more at the left wall and gradient also increases. As reported in Fig. 7, fluid temperature increases with Q, as a result temperature gradient is found to be minimum at the left plate, while maximum at the right plate, which directly increase/decrease the entropy generation.

The effect of $T_0$ for fixed $T_1$ and $T_2$ is presented in Figs. 16 and 17 for two sets of $T_2$ and $T_1$. In both cases the individual contributions are similar, therefore, individual contribution of first one only presented in Figs. 16b, 16c. The maximum entropy generation is found for EG:W–CuO. At $y=0$, S is dependent on fluid friction effect, and at $y=1$ it is dependent on heat transfer irreversibility. Moreover, right sides figures depicts that $T_0$ has a tendency to enhance the heat transfer irreversibility for water and decreased for EG:W, while it reduces the fluid friction and joule heating irreversibility. Though both the cases (Figs. 16 and 17) the temperature differences between the plate are same, the system irreversibility is found more for the case of higher $T_2$ and $T_1$.

Fig. 18

(a) Global entropy generation as a function of $\phi$ for different values of Q. Individual contribution (heat transfer irreversibility-$\langle S\rangle _H$, fluid friction-$\langle S\rangle _F$, and Joule heating-$\langle S\rangle_J$) for (b) water and (c) EG:W.

Fig. 19

(a) Global entropy generation as a function of $T_0$ for different values of Q. Individual contribution (heat transfer irreversibility-$\langle S\rangle _H$, fluid friction-$\langle S\rangle _F$, and Joule heating-$\langle S\rangle_J$) for (b) water and (c) EG:W.

With a view to describe the variation of the global entropy generation graphically against some of the parameters, Figs. 18, 19 have been plotted. It is clear from Fig. 18 that with an intensification in the heat generation parameter or/and nanofluid concentration, there is an increment in the global entropy generation. When looking at the relative contribution of heat transfer, fluid friction and heating from Joule effect, it is observed for water base fluid that heat transfer irreversibility is the major contributing part than fluid friction contributes (ref. Fig. 18b). It may be noted that difference between the heat transfer and fluid friction irreversibilities increases with heat generation (ref. Fig. 18b, 18c). On the other hand, for EG:W base fluid, fluid friction part takes major role to the total entropy, even for the case of maximum heat absorption considered here (ref. Fig. 18c).

The influence of $T_0$ on global entropy generation is shown in Fig. 19. One can perceive that with the higher values of $T_0$, the global entropy generation for both W–CuO and EG:W–CuO starts to exhibit a declining property. From Figs. 19b, 19c, it is clear that frictional part inversely proportional to $T_0$ because as $T_0$increases fluid become lighter, resulting to reduce the fluid friction. On the other hand thermal part increases with $T_0$. It may be noted that at comparatively lower $T_0$, where $\langle S\rangle$ is maximum, $\langle S\rangle _F$ and $\langle S\rangle _H$ contribute almost equally to $\langle S\rangle$ for water, while $\langle S\rangle _F$ contributes more than $70\%$ to $\langle S\rangle$ for EG:W.

From Figs. 18, 19 it can be conclude that for EG:W base fluid, due to more thermal conductivity and viscosity compare to water, fluid friction is the major contributing part than heat transfer irreversibility for global entropy generation. The opposite behavior is found for water base fluid.

4. CONCLUSIONS

Flow, heat transfer and entropy generation in a microchannel consisting of two parallel slip plates (one plate kept at rest while other plate moving upward/downward at a constant velocity) are investigated under the combined actions of bouncy force and transverse magnetic field. The hot fluid is injected from the left side and succeeded from the right side. The magnitude and direction of the pressure gradient due to Couette–Poiseuille flow is varied. Heat exchange between plate and ambient fluid is due to the conjugate convective-non-linear-radiative thermal conditions at boundaries. The primary observation of the present study can be highlighted as follows:

• The existence of denser nanoparticles in the flow region reduces the intensity of velocity of the nanofluids since the viscosity of the nanofluid increases with $\phi$. Apparently, the velocity of the water based nanofluids is more than that EG:W based nanofluids. Velocity in the channel increases with heat generation for both base fluids, while reduces with the increase in base fluid temperature $T_0$. Among all parameters, $T_0$ is found major influencing parameter to the velocity.

• The temperature inside the channel increases with increment in heat generation and decreases with the increase of heat absorption parameter. Increase the base fluid’s temperature, the fluid temperature gets low in the channel, except close to the cold plate where reverse phenomena are observed due to consideration of injection/suction.

• Heat transfer value (Nu) as well as its increment rate, due to the presence of nanoparticle in the fluid, are reported more at the suction side in comparison to the injection side. At the injection side, Nu increases with heat absorption ($-$Q) increases, but decreases with increase of heat source (Q) and $T_0$. However, presence of suction disturbs these sequences at the suction side. Beyond a certain value of Q, heat transfer takes place from fluid to heated wall. Despite having more thermal conductivity for EG:W, than water, Nu is found marginally higher for EG:W because of the consideration of radiation and convective boundary conditions.

• System irreversibility is maximum at plates side (on which frictional part dominates on the left while thermal part on the right side and Joule heating part marginally at channel center), and minimum at the interior of the channel. An intensification in the heat generation parameter or/and nanofluid concentration results to increment in the global entropy generation, whereas it is a decreasing function of $T_0$. Heat transfer irreversibility is leading the global entropy generation for water, while for EG:W fluid friction irreversibility is the major (around 70%) contributing part of the global entropy. Apparently, EG:W is harmful than water base fluid in terms of total system irreversibility.