Formation of Multiple Vortices in a Confined Two-Fluid Swirling Flow

Abstract

This numerical study explains the formation of multiple circulation cells in a confined swirling two-fluid flow. Providing fine and nonintrusive mixing of ingredients, multiple vortices are beneficial for the growth of tissue culture in aerial bioreactors. A convenient model of bioreactor is a sealed vertical cylindrical container filled with air and liquid. Rotation of the bottom disk drives the circulation of both fluids. Our study reveals that as the rotation intensifies, at least ten circulation cells develop: six in the lower fluid and four in the upper fluid. This steady axisymmetric multi-cell flow exists in some range of the rotation speed. There arises shear-layer instability as the rotation speed significantly exceeds this range. Therefore, such multi-cell flow might have applications in bioreactors where the rotation speed must be moderate for avoidance of destruction of tissue.

1. INTRODUCTION

A practically important and intriguing fluid-mechanics phenomenon is the emergence of a circulation cell in a swirling flow, often referred to as vortex breakdown (VB). The VB is dangerous for delta-wing aircraft, causing abrupt change in the lift and drag forces. The VB is beneficial for burners because it stabilizes the flame and reduces the harmful emissions. The VB, enhancing mixing of ingredients, is also beneficial for biological and chemical reactors [1].

Following Vogel [2] and Escudier [3], many researchers have performed fundamental studies of the VB in a sealed cylindrical container. Its simple geometry, absence of ambient disturbances, and convenient means of flow control ease experimental and numerical investigations, which helps understand the mechanism of cell formation and disappearance.

Two-fluid swirling flows attracted the attention of researchers due to applications in aerial vortex bioreactors [4]. The air flow transports oxygen (O$_2$), required for tissue growth, to the interface. O$_2$ diffuses through the interface and dissolves in the water. The meridional circulation of the water helps mix the dissolved O$_2$ and other ingredients. Thus, an aerial vortex bioreactor provides nonintrusive and fine mixing, required for efficient growth of tissue cultures. Multiple flow cells can significantly intensify the mixing. The growth of tissue culture is a time-consuming process and large stresses can be harmful for a culture. Therefore, the Reynolds number Re must be small or modest. An appropriate model of aerial vortex bioreactor is a sealed vertical cylindrical container, one end disk of which rotates, thus driving a flow of two immiscible fluids filling the container.

Carrión et al. [5] revealed steady axisymmetric multi-cellular patterns of air-water flow driven by a rotating bottom disk. Among other striking features, they found that the flow can have at least seven cells at Re of around 1300: three cells in the water and four cells in the air. Unfortunately, the new water cells are small compared with the entire water domain, and therefore we do not expect the cell contribution to the mixing to be significant. The current work is a significant advance of that study. Compared with the results of Carrión et al. [5], the advance is that in our case (a) the new cells are large and extend from the interface down to the bottom, (b) this multi-cell flow is quite stable since it occurs at Re of around 2500, while the critical Re is around 3300, and (c) six cells develop in the lower fluid.

Our study was inspired by the recent paper of Yang et al. [6]. Their numerical simulations revealed a curious three-cell flow pattern in the lower fluid at Re = 3304. We explored how this pattern evolves from rest as the rotation intensifies and found that the six-cell flow of the lower fluid develops at Re = 2500. Such a pattern seems to be beneficiary for chemical and biological reactors, where circulation eddies enhance the mixing and transfer of mass, momentum, and energy.

In addition, the topological analysis performed so far does not cover the development of multi-cell patterns similar to those shown in Figs. 1(v) and 1(w) of the paper by Brøns et al. [7]. The formation of a complicated well-organized multi-cell flow from a simple one as the rotation speeds up is of the fundamental interest as an instructive manifestation of the topological fluid mechanics. The current study hopefully helps understand the mechanism of evolution of such multi-cell patterns.

In the rest of this paper, we formulate the problem and describe our numerical technique in Section 2, the pattern of creeping flow in Section 3, the first change of the flow topology in Section 4, the mechanism of multiple cells in Section 5, the reduction of cells in Section 6, and the flow instability in Section 7, and summarize the results in Section 8.

2. PROBLEM FORMULATION

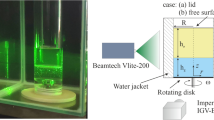
2.1. Flow Geometry and Parameter Values

Figure 1 presents the schematic of the problem. We consider a sealed vertical cylindrical container of the radius $R$ and height $h$ and use the cylindrical coordinates ($r,\phi,z$). With no motion, the lower part of the container ($0<z<h_{g}$) is filled with a glycerol (80%)-water (20%) solution (hereafter referred to as glycerol for brevity). The upper part ($h_{g}<z<h$) is filled with air. The air-glycerol interface is flat ($z=z_{i}=h_{g}$), as the thin horizontal line depicts in Fig. 1; $g$ is the gravity acceleration. If the bottom disk at $z=0$ rotates with the angular velocity $\omega$, while the other walls are still, the interface deforms downward near the axis and upward near the sidewall, as the curve schematically depicts in Fig. 1. Such deformation of interface is typical of whirlpools.

Fig. 1

Schematic of problem.

One control parameter is the aspect ratio $H=h/R$. $R$ serves as the length scale and $\omega R$ is the velocity scale here. Since in bioreactor applications, typically, $h$ and $R$ are close, we use $H= 0.5$. The dimensionless height of the glycerol at rest is $H_{g}=h_{g}/R$; we use $H_{g}=0.25$ here. Other control parameters are the Reynolds number $\mathrm{ Re}=\omega R^{2}/\nu_{g}$, characterizing the swirl strength; the Froude number $Fr=\omega^{2}R/g$, which is the centrifugal-to-gravity acceleration ratio; the Weber number $We=\rho g\omega^{2}R^{3}/\sigma$, characterizing the effect of surface tension $\sigma$ at the interface. The flow is isothermal at a temperature of 20°C, at which the kinematic viscosity of glycerol $\nu_{g}= 61$ mm²/s, the glycerol density $\rho_{g}= 1240$ kg/m³, $\sigma= 0.0315$ kg/s², and $g= 9.81$ m²/s. We assume that the pressure on the interface at rest has its atmospheric value, the air density is $\rho_{a}=1.22$ kg/m³, and the air kinematic viscosity is $\nu_{a}= 14$ mm²/s.

To explore the scenario of the formation of multiple flow cells, we perform simulations using the numerical technique described in detail by Carrión et al. [5]. An important difference is that they used $R$ = 1 mm, while here we use $R$ = 140 mm to compare our results with further experiments and with the results obtained by Yang et al. [6]. The only difference in the problem formulation is that Yang et al. use a free-slip condition, while we apply a no-slip condition at $z$ = 0.5. This choice is relevant for bioreactor applications.

To explore how multiple flow cells emerge starting with a small Re, we use the relations $Fr=a\mathrm{ Re}^{2}$ and $We=b\mathrm{ Re}^{2}$, where $a=\nu_{l}^{2}/(gR^{3})$ and $b=\rho_{l}\nu_{l}^{2}/(\sigma R)$. For the above values of the parameters, $a=8.06\times 10^{-8}$ and $b=2.89\times 10^{-4}$. We fix these values of $a$ and $b$ and gradually increase the rotation speed, starting with Re = 0.5, in order to disclose topological transformations of the flow pattern.

2.2. Governing Equations

Using $R$, $1/\omega$, $\omega R$, and $\rho_{w}\omega^{2}R^{2}$ as scales for the length, time, velocity, and pressure, respectively, renders all variables dimensionless. We consider flows of two viscous incompressible immiscible fluids governed by the Navier–Stokes equations

$$\frac{1}{r}\frac{\partial(ru)}{\partial r}+\frac{1}{r}\frac{\partial v}{\partial\phi}+\frac{\partial w}{\partial z}=0, $$

(1)

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}+\frac{v}{r}\frac{\partial u}{\partial\phi}+w\frac{\partial u}{\partial z}-\frac{v^{2}}{r}=-\rho_{n}\frac{\partial p}{\partial r}+\frac{\nu_{n}}{\mathrm{ Re}}\left(\nabla^{2}u-\frac{u}{r^{2}}-\frac{2}{r^{2}}\frac{\partial v}{\partial\phi}\right), $$

(2)

$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial r}+\frac{v}{r}\frac{\partial v}{\partial\phi}+w\frac{\partial v}{\partial z}+\frac{uv}{r}=-\frac{\rho_{n}}{r}\frac{\partial p}{\partial\phi}+\frac{\nu_{n}}{\mathrm{ Re}}\left(\nabla^{2}v-\frac{v}{r^{2}}+\frac{2}{r^{2}}\frac{\partial u}{\partial\phi}\right), $$

(3)

$$\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial r}+\frac{v}{r}\frac{\partial w}{\partial\phi}+w\frac{\partial w}{\partial z}=-\rho_{n}\frac{\partial p}{\partial z}+\frac{\nu_{n}}{\mathrm{ Re}}\nabla^{2}w, $$

(4)

where $\nabla^{2}=\frac{1}{r}\frac{\partial}{\partial}\left(r \frac{\partial}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial\phi^{2}}+\frac{\partial^{2}}{\partial z^{2}}$ is the Laplace operator for a scalar field, $(u,v,w)$ are the velocity components in the cylindrical coordinates $(r,\phi,z)$, $t$ is the time, and $p$ is the reduced pressure. The coefficients $\rho_{n}$ and $\nu_{n}$ are both equal to 1 at $n=1$ (for the lower flow), while $\rho_{n}=\rho_{g}/\rho_{a}$ and $\nu_{n}=\nu_{a}/\nu_{g}$ at $n =2$ (for the air flow).

We denote the list $(u,v,w,p)$ as $V$ and look for a solution of system (1)–(4) in the form

$$V=V_{b}\left(r,z\right)+\varepsilon V_{d}\left(r,z\right)e^{(im\phi-i\Omega t)}+c.c., $$

(5)

where the subscripts $b$ and $d$ denote the base flow and disturbance, respectively; $c.c.$ denotes the complex conjugate of the preceding term; $\varepsilon\ll 1$ is the amplitude; the integer $m$ is the azimuthal wave number; $\Omega=\Omega_{r}+i\Omega_{i}$ is the complex number to be found, with the frequency $\Omega_{r}$ and the disturbance growth rate $\Omega_{i}$. For a decaying (growing) disturbance, $\Omega_{i}$ is negative (positive). Disturbances with $\Omega_{i}=0$ are neutral. We are looking for the minimum Re at $\Omega_{i}=0$. The equations governing the base flow result from substitution of (5) in system (1)–(4) and setting $\varepsilon=0$. The terms of order $O(\varepsilon)$ constitute equations governing infinitesimal disturbances.

2.3. Boundary Conditions

Equations (1)–(4) are solved under the following boundary conditions:

(i) Regularity at the axis, $0<z<H$, $r=0$:

(a) $u=v=0$, $\partial w/\partial r=0$ (basic flow and $m=0$ disturbances).

(b) $w_{d}=0$, $u_{d}+mv_{d}=0$, $\partial u_{d}/\partial r=0$ ($m = 1$ disturbances).

(c) $w_{d}=u_{d}=v_{d}=0$ ($m>1$ disturbances).

(ii) No-slip at the walls: $u=v=w=0$ at the still disk, $0<r<1$, $z=H$, and at the sidewall, $0<z<H$, $r=1$; $u=w=0$, $v=r$ at the rotating disk, $0<r<1$, $z=0$.

(iii) Continuity of all the velocity and tangential stress components at the interface, $z=F(r,\phi,t)$. The balance for the normal stresses yields that

$$p_{w}-p_{a}=\frac{1}{We}\nabla.\mathbf{n}-\frac{1}{\mathrm{ Re}}{\mathbf n}.\left(\tau_{w}-\mu_{r} \tau_{a}\right).{\mathbf n}-\frac{1}{Fr} \left(1-\rho_{r}\right)z, $$

(6)

where $\mathrm{ n}$ is the unit vector normal to the interface, $\tau_{w}$ and $\tau_{a}$ is the tensor of the viscous stresses in the heavy and light fluids, respectively, and $\mu_{r}$ and $\rho_{r}$ is the light-to-heavy fluid ratio of the dynamic viscosities and densities, respectively.

(iv) The kinematic equation for the interface shape $z=F(r,\phi,t)$ is

$$\frac{\partial F}{\partial t}-w+u\frac{\partial F}{\partial r}+\frac{v}{r}\frac{\partial F}{\partial\phi}=0, $$

(7)

which provides the water and air mass conservation. We look for a solution of Eq. (7) in the form

$$z=F_{b}(r,z)+\varepsilon F_{d}(r,z)e^{(im\phi-i\Omega t)}+c.c. $$

(8)

In our stability studies, all the boundary conditions including Eqs. (6) and (7) are also linearized with the use of Eqs. (5) and (8) and extraction of terms of the order $O(\varepsilon)$ in the system governing infinitesimal disturbances.

2.4. Numerical Technique

To simulate the nonlinear problem for the basic flow and the generalized eigenvalue problem for disturbances, we use a numerical technique, which is a variation of that described in detail by Herrada and Montanero [8]. First, the heavy fluid (glycerol) and light fluid (air) regions are mapped onto the standard square domain $0\le\eta_{(w,a)}\le1$, $0\le\xi\le1$, by means of the coordinate transformations (a) $\eta_{w}=z/F$ and $\xi=r$ and (b) $\eta_{a}=(z-F)/(H-F)$ and $\xi=r$ for the glycerol and air, respectively. Then each variable (the velocities, pressure, and interface shape) and all its spatial and temporal derivatives that appear in the transformed equations are composed as a single symbolic vector. For example, for the axial velocity in the glycerol flow $w_{w}$, we create a vector having 11 components: $x_{w} = [w_{w}$, $\partial w_{w}/\partial\eta$, $\partial w_{w}/\partial\xi$, $\partial^{2}w_{w}/\partial\eta^{2}$, $\partial^{2}w_{w}/\partial\xi^{2}$, $\partial^{2}w_{w}/\partial\xi\partial\eta$, $\partial w_{w}/\partial\phi$, $\partial^{2}w_{w}/\partial\phi^{2}$, $\partial^{2}w_{w}/\partial\phi\partial\xi$, $\partial^{2}w_{w}/\partial\phi\partial\eta$, $\partial w_{w}/\partial t]$. The next step is to use a symbolic toolbox to calculate the analytical Jacobians of all the equations with respect to all the symbolic vectors. Using these analytical Jacobians, we generate functions, which are then evaluated point by point in the square domain. In this procedure, we used the MATLAB tool matlabFunction to convert the symbolic Jacobians into MATLAB functions.

Then we carry out the spatial and temporal discretization of the problem. The water and air domains are discretized using a set of $n_{w}$ and $n_{a}$ Chebyshev spectral collocation points in the axial direction (along the $\eta_{w}$ and $\eta_{a}$ axes, respectively). Next, the glycerol and air domains are discretized using a set of $n_{\xi}$ Chebyshev spectral collocation points in the radial direction. The second-order backward finite differences are used for computation of the time derivatives for the basic flow. Since the basic flow is axisymmetric, all the azimuthal derivatives are set equal to zero. For disturbances, we obtain the temporal and azimuthal derivatives using Eqs. (5) and (8).

The final step is to set up the numerical matrices allowing us to solve the problem by using the Newton procedure for the basic steady flow and by solving the generalized eigenvalue problem for the disturbances. To summarize, the numeric procedure includes mapping of the glycerol and air regions, the proper spatial and temporal discretization creating a discrete Jacobian matrix for the Newton procedure for the basic flow and two more matrices for the generalized eigenvalue problem for the disturbances. For the basic flow, we get the final steady solution through using an unsteady scheme. Starting from the rest and selecting a time step, we advance the solution in the time until a steady state is reached. Since the nonlinear procedure used for the computation of the basic flow is fully implicit, the time step can be taken sufficiently large for the steady solution to be reached quickly. Once the base flow is computed, given the azimuthal wavenumber $m$, we use the MATLAB subroutine eigs to calculate the eigenvalues $\omega$ of the system of discrete linear equations.

Most of the simulations presented here are done with $n_{w}= 120$, $n_{a}=70$, and $n_{\xi}=70$ (standard grid), but some runs for flows having small circulation regions are performed with finer grids. For $\mathrm{ Re}> 1000$, we use $n_{\eta w}=180$, $n_{\eta a} = 100$, and $n_{\xi} = 100$ (fine grid). Since the Chebyshev grid points concentrate near the interface from both sides, the approach is adequate for resolving small circulation layers located near the interface, even at moderate values of $n_{w}$, $n_{a}$, and $n_{\xi}$. More information on the checkup of the numerical accuracy is in the paper by Carrión et al. [5].

3. PATTERN OF CREEPING FLOW

Figure 2 depicts our numerical results, describing some features of the creeping flow at Re = 0.5. Although the meridional motion is very slow compared with the rotation, as Figs. 2b and 2c indicate, there are two cells in the air flow, as Fig. 2a reveals. The physical reasoning for these two cells, C2 and C3, is the following. Near the rotating bottom, the centrifugal force pushes the lower fluid from the axis to the sidewall [9], generating the centrifugal circulation marked as C1 in Fig. 2a. Near the interface, the lower fluid converges from the periphery toward the axis, as Fig. 2b indicates, where the radial velocity is negative. This convergence drives the anti-centrifugal circulation of the air, shown by the light-blue contours and marked as C2 in Fig. 2a. Oppositely, the rotation drives the centrifugal circulation of the air, marked as C3 in Fig. 2a. As the curve Re = 0.5 in Fig. 3 shows, the maximum swirl velocity at the interface is around 0.5R even if the motion is creeping.

Fig. 2

Creeping flow at Re = 0.5. (a) Streamline pattern. Profiles of (b) radial velocity at interface and (c) velocity distribution at axis in lower (solid curve) and upper (dashed curve) fluids.

Fig. 3

Distribution of swirl velocity at interface and bottom.

Fig. 4

Streamline patterns at (a) Re = 1000 and (b) Re =1500; (c) meridional tangential velocity at interface and (d) axis.

Therefore, as $z$ increases from the bottom to the interface, the decay of swirl does not significantly weakens the mechanism driving the centrifugal circulation of the air. First, the interface serves for the air as the rotating liquid bottom providing the Kármán pumping. Second, as the rotating air approaches the top wall, the radial gradient of the pressure pushes the air from the periphery to the axis. This effect (Bödewadt [10]) enhances the centrifugal circulation of the air. This double (Kármán and Bödewadt) driving and the difference in the kinematic viscosities ($\nu_{g}= 61$ mm²/s and $\nu_{a}= 14$ mm²/s) explain why the maximum magnitude of the velocity at the axis in the air is significantly larger than that in the lower fluid, as Fig. 2c shows. Thus, the competition of the convergence and rotation of the lower fluid generates the two bulk cells of the air motion, C2 and C3. As $r$ decreases, the $z$-size of C2 also decreases, but it vanishes only at the axis, $r= 0$, where C1 and C3 meet in Fig. 2a.

4. FIRST TOPOLOGICAL CHANGE

Figure 3 depicts how the azimuthal velocity is redistributed at the interface as Re increases. The $r$-profile of $V$ remains close to that for the creeping motion even at Re = 100, i.e., the impact of the meridional advection of the angular momentum remains small compared with that of the diffusion. This impact becomes significant for $\mathrm{ Re}\geq 1000$: the converging flow transports the angular momentum toward the axis, which shifts the right-hand part of the $V_{\theta}$ profile to the left and then increases the maximum value of $V_{\theta}$, resulting in an overshoot, which was first observed in the numerical simulations by Yang et al. [6]; see the $r$-ranges where the curves are above the line $V_{\theta}=r$ in Fig. 3. The overshoot emerges at Re of around 1500.

At $\mathrm{ Re}>1000$, topological changes in the flow pattern start to occur. Figure 4 shows the first topological change: the formation of an anti-centrifugal circulation cell (say, C4) in the lower fluid. The bends of the streamlines in Fig. 4a near $r=0.4$ below the interface are a precursor of the appearance of C4, depicted by light-blue contours below the interface in Fig. 4b. Figure 4c shows the $r$-profile of the meridional velocity $V_{t}$, which is tangential to the interface. Hereafter we use $V_{t}^{1/3}$ and $V_{z}^{1/3}$ in order to conveniently observe small and large velocity values in one plot.

The dashed curve in Fig. 4c has a local maximum near $r=0.4$, which is negative at Re = 1000. The maximum becomes positive at Re = 1500, as the solid curve in Fig. 4c reveals. Therefore, the meridional tangential velocity reverses, becoming positive in a small $r$-range near $r$ = 0.4. In addition to generating C4 (which is an off-axis vortex breakdown bubble), this reversal cuts C2 into two separated parts: (i) the near-sidewall part (which remains denoted as C2), shown by the light-blue contours above the interface in Fig. 4b, and (ii) the near-axis part (say, C5), which is too thin to be visible in Fig. 4b, but it is revealed by the near-axis portion of the solid curve in Fig. 4c where $V_{t}< 0$.

It seems that this $V_{t}$ reversal occurs due to the air wind. Figure 4d shows the $z$-profile of the velocity at the axis $V_{z}$ and reveals that $V_{z}$ in the air is significantly (by two orders of magnitude!) larger than that in the lower fluid (glycerol). The air moves downward near the axis, turns radially outward near the interface, and forms a strong jet, observed as the thin layer of packed streamlines located above the interface and above C2 in Fig. 4a. This jet forms due to the Kármán pumping. The radial velocity of the jet reaches its maximum near $r= 0.4$. Namely there, the jet cuts C2 and generates C4. This mechanism of topology change is similar to that described in Section 6.3 of the paper by Carrión et al. [5]. However, the following development of multiple cells is different.

5. MECHANISM GENERATING MULTIPLE CELLS

Fig. 5

Streamline patterns at (a) Re = 2000 and (b) Re = 2500; meridional tangential velocity at (c) interface and (d) axis.

Fig. 6

Streamline pattern at Re = 3302 shows reduction of cells.

Figure 5 discloses a few further topological changes as Re increases. The intensifying air wind expands the cell C4 downward. C4 touches the bottom and thus cuts the cell C1 into two separated parts: (i) the near-sidewall part (which remains denoted as C1) and (ii) the near-axis part (say, C6), shown by the deep-blue contours in the left lower corner of Fig. 5a.

Then, this process, generating new cells, repeats: the air wind cuts the cell C5 into two separated parts: (i) the right-hand part (which remains denoted as C5) and (ii) the near-axis part (say, C7). The local maximum of the solid curve near $r = 0.2$ in Fig. 4c is a precursor of this second reversal of $V_{t}$, depicted near $r = 0.2$ in Fig. 5c. The air wind also generates the cell C8 in the lower fluid, shown by the light-blue contours and separated from the bottom in the left lower corner of Fig. 5a.

Next, C8 expands downward and touches the bottom, as Fig. 5b shows. This touching cuts C6 into two separated parts: (i) the right-hand part (which remains denoted as C6) and (ii) the near-axis part (say, C9), represented by the small deep-blue contour in Fig. 5b.

Accordingly, the sign (i.e., direction) of $V_{t}$ alternates as Fig. 5c depicts. The cell C9 corresponds to the closest-to-axis $r$-range, where $V_{t}<0$, in Fig. 5c. Since the dashed curve near the axis corresponds to the positive $V_{t}$ in Fig. 5c, at least one more cell (say, C10) must exist at Re = 2500, although it is invisible in Fig. 5b.

Based on the pattern shown in Fig. 5b and the fact that the dashed curve in Fig. 5c has three $r$-ranges of positive $V_{t}$ and three $r$-ranges of negative $V_{t}$, we conclude that the lower fluid flow has at least six circulation cells and the air flow has at least four circulation cells at Re = 2500. All these ten cells are attached to the interface.

6. REDUCTION OF CELLS

As Re further increases, the size and number of the cells are reducing because the near-axis part of the interface becomes very close to the bottom. Since $V_{r}$ and $V_{z}$ are zero at the bottom, the bottom serves as a brake: the meridional velocity of the lower fluid becomes very small, as Fig. 5d illustrates. The proximity of the interface and the bottom suppresses the lower fluid cells, as comparison of Figs. 5b and 6 demonstrates. There are only six cells at Re = 3302. Five of them are observed in Fig. 6. The cell C5 of the anti-centrifugal circulation of the air, located between the cells C3 and C4, is too thin to be observed in Fig. 6. Figure 6 is very similar to Fig. 7b in the paper by Yang et al. [6]. This similarity is an additional verification of our numerical technique. Thus, the whirlpool flow has the largest number of cells at a Re value of around 2500.

7. INSTABILITY

To explore the stability of multi-cell flow, we apply the approach and technique elaborated by Herrada and Montanero [8]. Table 1 summarizes our results concerning the instability. It shows parameter values corresponding to the marginal Re (minimum Re at a fixed $m$ and $\omega_{i}= 0$) and the critical Re (minimum among the marginal Re). The critical Re corresponds to double-helix disturbances, i.e., $m= 2$. No instability was found for $m= 0$. Disturbances with other $m$ are less dangerous than those presented in Table 1. Figure 6 depicts the streamline pattern at critical Re.

Fig. 7

(a) Contours of critical-disturbance energy $E_{d}$. (b) $r$-profiles of $E_{d}$ (solid), $V_\theta$ (dashed), $V_r$ (dotted), and $V_{z}$ (dash-dotted) at $z = 0.1708$. (c) $z$-profiles of $E_{d}$ (solid), $V_\theta$ (dashed), and $V_r$ (dotted) at $r = 0.429$.

Table 1. Marginal and critical (bold) stability parameters

Figure 7a depicts the contours of the critical-disturbance kinetic energy $E_{d}$ = constant; $E_{d}$ is averaged with respect to the time and azimuthal angle and normalized by its maximum value. The $E_{d}$ peak is located in the lower fluid at $r=0.429$ and $z = 0.1708$, i.e., very close to the interface, where $V_{t}$ changes its sign (see Fig. 6). $E_{d}$ is localized near the peak: the outmost $E_{d}$ contour corresponds to 0.1, which is also a step between the $E_{d}$ contours in Fig. 7a. Figure 7b reveals that $E_{d}$ peak is very thin in the $r$-direction compared with $E_{d}$ peak in the $z$-direction shown in Fig. 7c. The $E_{d}$ peak is located near the inflection point of $V_{z}(r)$, as Fig. 7b shows. This indicates that the instability is of the shear-layer type. The $V_{\theta}$ maximum and $V_{r}$ minimum near $z=0.5$ in Fig. 7c are due to the Bödewadt boundary layer. Based on these stability results and the fact that the critical Re is 3302, we conclude that the steady axisymmetric multi-cell flow is quite stable at Re of around 2500 and therefore can be utilized for technologies.

8. CONCLUSION

This numerical study reveals and explains the formation of ten circulation cells in a confined two-fluid swirling flow. The rotating bottom disk drives the glycerol-water solution and air in a sealed vertical cylindrical container where the sidewall and the top wall are stationary. At rest, both fluids have equal volume and height (0.25 of the container radius $R$). We found that even in creeping motion, the competition of the lower fluid rotation and convergence near the interface generates two bulk circulation cells in the air flow. As the rotation intensifies, the air wind generates a new cell in the lower fluid flow near the interface at a distance from the axis of around $0.4R$. This cell expands downward and reaches the bottom. The process of cell formation repeats until the lower fluid flow has at least six circulation cells and the air flow has at least four circulation cells at a Reynolds number Re of around 2500. All these ten cells are attached to the interface. As the interface approaches the bottom, the number and size of the cells reduce. The flow becomes unstable at Re = 3302. Therefore, the pattern with the maximum number of cells corresponds to a stable steady axisymmetric flow. This multi-cell flow can be utilized in vortex devices where circulation eddies typically enhance the transfer of the mass, momentum, and energy.

FUNDING

The research was supported by the Russian Science Foundation (project no. 19-19-00083) and by Ministerio de Economı́a y Competitividad and Junta de Andalucı́a (Spain grants no. PID2019-108278-RB-C31 and PAIDI: P18-FR-3623, respectively).