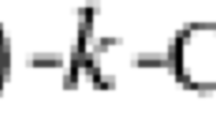This paper deals with an important version of Borsuk’s classical problem of partitioning sets into parts of smaller diameter (see [1]).

Let \(b \in (0,\;1]\) and \(n \in \mathbb{N}\). Define \(\chi (n,b)\) as the minimum number of subsets of diameter strictly smaller than b into which an arbitrary set of diameter 1 can be partitioned in \({{\mathbb{R}}^{n}}\). For b = 1, we obtain exactly the classical Borsuk number, about which we know that \(\chi (1,\;1) = 2\), \(\chi (2,\;1) = 3\), \(\chi (3,\;1) = 4\), and

$$\mathop {\left( {\mathop {\left( {\frac{2}{{\sqrt 3 }}} \right)}\nolimits^{\sqrt 2 } + o(1)} \right)}\nolimits^{\sqrt n } \leqslant \chi (n,1{\text{)}} \leqslant \mathop {\left( {\sqrt {\frac{3}{2}} + o(1)} \right)}\nolimits^n $$
(1)

(see [1, 2]). For small n and various b, a variety of results and references can be found in [1, 3].

We are interested in the case when \(n \to \infty \) and \(b = b(n)\). In this case, all known upper bounds are exponential in n. For example, Rogers’s work concerning packings of spherical caps on the sphere (see [4]) implies the inequality

$$\chi (n,b) \leqslant \mathop {\left( {\frac{{\sqrt 2 }}{b} + o(1)} \right)}\nolimits^n .$$

Here, \(\tfrac{{\sqrt 2 }}{b}\) can be reduced by applying the technique of [5].

The lower bounds are much subtler. Roughly speaking, below we will show that, if \(b(n) \leqslant c < 1\) for all \(n\), then these bounds are also exponential. If \(b(n) \to 1\) as \(n \to \infty \), then the bounds become subexponential, gradually decreasing (as the rate of convergence of b to unity increases) to the form given by the left-hand side of bound (1), i.e., to an asymptotic constant raised to power \(\sqrt n \). Rigorous formulations of the corresponding new results are given in the rest of this paper.

Theorem 1. Let \(k = k(n)\) be an arbitrary function with values in the set \(\left\{ {1, \ldots ,\tfrac{n}{2}} \right\}\). For every n, consider the maximum integer \(a = a(n)\) for which \(\sqrt {1 - \tfrac{{a(n)}}{{k(n)}}} \geqslant b(n)\). Let \(m(n,r,s)\) be the maximum cardinality of the collection of r-element subsets of the set \({{\mathcal{R}}_{n}} = {\text{\{ }}1,\; \ldots ,\;n{\text{\} }}\) such that each two subsets share at least s elements. Then

$$\chi (n,b(n)) \geqslant \frac{{C_{n}^{{k(n)}}}}{{m(n,k(n),a(n) + 1)}}.$$

The value of \(m(n,r,s)\) has been found for all \(n\), r, and s. For completeness’ sake, we state the corresponding result (see [6]).

Theorem 2 (P. Frankl, R.M. Wilson, R. Ahlswede, L. Khachatrian). Suppose that \(2r - n < s\) and \(1 \leqslant s \leqslant r \leqslant n\). For \(0 \leqslant i \leqslant \tfrac{{n - s}}{2}\) and \(i \leqslant r - s\), define the collection

$$\begin{gathered} {{\mathcal{M}}_{i}}(n,r,s) \\ = \left\{ {M \subseteq {{\mathcal{R}}_{n}}{\text{:}}\;\left| M \right| = r,\;\left| {M \cap {\text{\{ }}1, \ldots ,s + 2i{\text{\} }}} \right| \geqslant s + i} \right\}, \\ \end{gathered} $$

i.e., \({{\mathcal{M}}_{i}}(n,r,s)\) is the collection of all possible r-element subsets of the set \({{\mathcal{R}}_{n}}\) with at least s + i elements taken from \({\text{\{ }}1,\; \ldots ,\;s + 2i{\text{\} }} \subseteq {{\mathcal{R}}_{n}}\). If for some \(l \in \mathbb{N} \cup {\text{\{ }}0{\text{\} }}\)

$$(r - s + 1)\left( {2 + \frac{{s - 1}}{{l + 1}}} \right) \leqslant n < (r - s + 1)\left( {2 + \frac{{s - 1}}{l}} \right),$$

then \(m(n,r,s) = \left| {{{\mathcal{M}}_{l}}(n,r,s)} \right|\) (we assume that \(\tfrac{{s - 1}}{l} = \infty \) whenever l = 0).

Theorem 1 can be refined as follows.

Theorem 3. Suppose that \({{k}_{{ - 1}}} = {{k}_{{ - 1}}}(n)\), \({{k}_{0}} = {{k}_{0}}(n)\), and \({{k}_{1}} = {{k}_{1}}(n)\) are arbitrary functions with values in \({{\mathcal{R}}_{n}}\) that satisfy the relations

$$\begin{gathered} {{k}_{{ - 1}}}(n) + {{k}_{0}}(n) + {{k}_{1}}(n) = n, \\ {{k}_{{ - 1}}}(n) + {{k}_{1}}(n) \leqslant \frac{n}{2},\quad {{k}_{{ - 1}}}(n) \leqslant {{k}_{1}}(n). \\ \end{gathered} $$

For each \(n\), consider the maximum integer \(a = a(n)\) for which

$$\sqrt {\frac{{{{k}_{1}}(n) + {{k}_{{ - 1}}}(n) - a(n)}}{{{{k}_{1}}(n) + 3{{k}_{{ - 1}}}(n)}}} \geqslant b(n).$$

Let \(f(n,{{k}_{{ - 1}}},{{k}_{0}},{{k}_{1}},s)\) be the maximum cardinality of a set of \(( - {\kern 1pt} 1,\;0,\;1)\)-vectors in \({{\mathbb{R}}^{n}}\) such that each vector has exactly ki coordinates equal to \(i\), \(i \in {\text{\{ }}{\kern 1pt} - {\kern 1pt} 1,0,1{\text{\} }}\), and the scalar product of any two vectors is at least s. Then

$$\chi (n,b(n)) \geqslant \frac{{C_{n}^{{{{k}_{1}}(n)}}C_{{n - {{k}_{1}}(n)}}^{{{{k}_{{ - 1}}}(n)}}}}{{f(n,{{k}_{{ - 1}}}(n),{{k}_{0}}(n),{{k}_{1}}(n),a(n) + 1)}}.$$

The idea of this refinement is that, for \({{k}_{{ - 1}}}(n)\) vanishing identically, we obtain exactly Theorem 1: when the vectors have only zero and unit coordinates, their scalar product is equal to the cardinality of the intersection of the sets of their unit coordinates. Of course, it would be possible to produce even bulkier generalizations by gradually adding new coordinate values. However, the matter is that even \(f(n,{{k}_{{ - 1}}},{{k}_{0}},{{k}_{1}},s)\) can hardly be estimated in the general case. Nevertheless, some bounds for it are available, and they can be used to refine Theorem 1 in a number of situations. For other similar quantities, the results are scarce, and it is no use considering them in the current context.

Concerning bounds for \(f(n,{{k}_{{ - 1}}},{{k}_{0}},{{k}_{1}},s)\), a conjecture about its exact value can be found in [7]. Additionally, there are more recent results of Frankl and Kupavskii (see [8]) and related results of other authors (see [9–15]). However, the linear-algebraic method remains one of the most effective tools in this case (see [1, 2, 12–15]). Specifically, the following theorem can be proved with the help of this method.

Theorem 4. Given all the parameters of Theorem 3, suppose that \(q = q(n)\) is the minimum number equal to a prime power such that \({{k}_{{ - 1}}}(n) + {{k}_{1}}(n) - q(n) \leqslant a(n)\). Then

$$f(n,{{k}_{{ - 1}}}(n),{{k}_{0}}(n),{{k}_{1}}(n),a(n) + 1) \leqslant \sum\limits_{(i,j) \in \mathcal{A}} {C_{n}^{i}} C_{{n - i}}^{j},$$

where

$$\mathcal{A} = {\text{\{ }}(i,j){\text{:}}\;i + 2j \in {\text{\{ }}q(n) - 2,q(n) - 1{\text{\} \} }}.$$

A fairly standard asymptotic analysis can be applied to the bounds from Theorems 1 and 3. Accurate optimization is difficult, including because the bound in Theorem 4 depends on the prime number distribution. Nevertheless, it is relatively easy to see that, if \(b(n) \leqslant c < 1\), where c is a constant, then both theorems give bounds of the form \({{(C + o(1))}^{n}}\), where C > 1. On the contrary, both bounds become subexponential when \(b(n) \to 1\) as \(n \to \infty \). If \(b(n) = 1\), then both bounds, in fact, degenerate, becoming equal in order to n. However, inequality (1) suggests that Theorems 1 and 3 do not cover the situation entirely. Below, we present two new theorems that work in the case when b(n) tends rather rapidly to unity.

Theorem 5. Suppose that \(d = d(n)\) and \(a = a(n)\) are such that \(d = 4q\), where \(q = q(n)\) is a prime power and

$$n \geqslant C_{{d(n) - \left\lceil {a(n)/2} \right\rceil }}^{2},\quad \sqrt {1 - \frac{{{{a}^{2}}(n)}}{{{{d}^{2}}(n)}}} \geqslant b(n).$$

Then

$$\chi (n,b(n)) \geqslant \frac{{{{2}^{{d(n) - \left\lceil {a(n)/2} \right\rceil - 2}}}}}{{\sum\limits_{i = 0}^{q(n) - a(n) - 1} {C_{{d(n) - \left\lceil {a(n)/2} \right\rceil - 1}}^{i}} }}.$$

For example, if \(b(n) = 1 - \tfrac{1}{{\sqrt n }}\), then \(d(n) = \Theta (\sqrt n )\), \(a(n) = \Theta (\sqrt[4]{n})\), and the bound in Theorem 5 resembles the lower bound in (1). The closer the b(n) to the identical unity, the closer the a(n) to zero. For a(n) = 0, the bound in Theorem 5 coarsened in the style of inequality (1) taking into account the Stirling formula and the prime number density turns into the inequality

$$\begin{gathered} \chi (n,1) \geqslant \mathop {\left( {2\mathop {\left( {\frac{1}{4}} \right)}\nolimits^{1/4} \mathop {\left( {\frac{3}{4}} \right)}\nolimits^{3/4} + o(1)} \right)}\nolimits^n \\ = \;\mathop {\left( {\mathop {\left( {2\mathop {\left( {\frac{1}{4}} \right)}\nolimits^{1/4} \mathop {\left( {\frac{3}{4}} \right)}\nolimits^{3/4} } \right)}\nolimits^{\sqrt 2 } + o(1)} \right)}\nolimits^{\sqrt d } . \\ \end{gathered} $$

The constant under the subexponential sign is smaller than the constant in the lower bound in (1). An improvement leading to the same constant is given in the last theorem.

Theorem 6. Suppose that \(d = d(n)\), \(q = q(n)\), and \(a = a(n)\) are such that q is a prime power, \(q(n) \leqslant \tfrac{{d(n)}}{2}\), and

$$n \geqslant C_{{d(n) + 1}}^{2},\quad \sqrt {1 - \frac{{{{a}^{2}}(n)}}{{{{q}^{2}}(n)}}} \geqslant b(n).$$

Then

$$\chi (n,b(n)) \geqslant \frac{{{{2}^{{q(n) - a(n) - 1}}}C_{{d(n)}}^{{q(n)}}}}{{\sum\limits_{(i,j) \in \mathcal{A}} {C_{{d(n)}}^{i}} C_{{d(n) - i}}^{j}}},$$

where

$$\mathcal{A} = {\text{\{ }}(i,j){\text{:}}\;i + 2j \in {\text{\{ }}q(n) - a(n) - 2,q(n) - a(n) - 1{\text{\} \} }}.$$