1 INTRODUCTION

The question considered in this study belongs to the scope of the general relativity theory and is associated with the search for the proof of frequently formulated statement concerning the possibility or impossibility of artificially created weightlessness of material bodies on the surface of the Earth (or some other planet).

It may appear that since a phenomenon such as Mohammed’s coffin, which is associated with floating of a superconducting metal in a magnetic field, is possible, the levitation effect can also exist.

We will consider this question in detail and substantiate strictly analytically the possibility of observation of the effect of a body “floating” in the gravity field. Running ahead, we note that the main factor required for implementing this effect must be only the large surface density \(\sigma = {{E}_{n}}\) of electric charges (of any polarity), where En is the normal component of the electric field strength. This will be rigorously proved below.

To solve this problem, we consider the fundamentals of the general relativity theory (GRT), the main idea of which is based on the assumption that the spatiotemporal metric varies in the gravity field. Therefore, the energy–momentum tensor of matter, which is formally introduced (based on this assumption) into the right-hand side of the basic GRT equation, leads to the classical law of gravitation in the nonrelativistic approximation. This factor is considered as an indisputable proof of the correctness of the resulting equations along with the predicted possibility of the existence of gravity waves as well as the “red shift” effect.

The space–time distortion itself can be determined by specifying the right-hand side of the basic GRT equation (i.e., the energy–momentum tensor). Further, the values of metric tensor components \({{g}_{{ik}}}\) of interest (in particular, the Schwarzschild solution, the Kerr–Newman metric, and the Friedman metric) can also be determined by solving the nonlinear differential equation.

If, however, we also formally introduce the energy–momentum tensor of the electromagnetic (EM) field along with the energy–momentum tensor of matter (which actually does not contradict the theory), we arrive at the equation that determines the distortion of the spatiotemporal continuum with account for the possible effect of electromagnetic fields on it.

This means that a new paradox appears: namely, the spatiotemporal continuum can be distorted by not only the gravity field, but also by an electromagnetic field. A dubious proof of this effect was obtained in 1943 in Philadelphia experiment with Eldridge destroyer.

From the standpoint of physics, it can obviously be proposed that the origins of gravitational and electromagnetic fields must be interrelated; i.e., for large values of wavelengths (at low frequencies) on the electromagnetic scale, the EM spectrum must be continuously transformed into the gravitational spectrum. In other words, at large wavelengths, their physical origins somehow intersect.

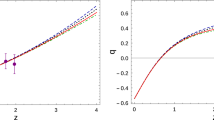
The following fact appears as curious. Using experimental data from the table of baryons (see [1–3]) and evaluating the ratio of the natural logarithms of their masses and lifetimes (i.e., find number

$$\gamma = \frac{{\ln m}}{{\ln \tau }},$$
(1)

where m is the mass in electronvolts and τ is the lifetime), we arrive at the fractal dependence shown in Fig. 1. This dependence holds to within the second decimal place. Such a fact cannot be treated as a random coincidence. The calculation based on expression (1) gives

$$\gamma \approx - 0.3.$$
(2)
Fig. 1.
figure 1

Fractal dependence of the mass of baryon on their lifetime.

Full size image

2 BASIC GRT EQUATION AND ITS ANALYSIS WITH ACCOUNT FOR THE EM FIELD

It is well known (see [4]) that the Einstein equation has form

$${{R}_{{ik}}} - \frac{1}{2}R{{\delta }_{{ik}}} = \frac{{8\pi G}}{{{{c}^{4}}}}{{T}_{{ik}}},$$
(3)

where Rik is the Ricci tensor or just a convolution of Riemann tensor \(R_{{klm}}^{i}\) in indices \(i,m\); δik is the Kronecker delta; c is the velocity of light, G is the gravitational constant, and Tik is the energy–momentum tensor of the gravity field. Some aspects of the possible linearization of Eq. (3) are described, for example, in [5] (see also [6]). This tensor is given by

$${{T}_{{ik}}} = \rho {{c}^{2}}{{u}_{i}}{{u}_{k}},$$
(4)

where ρ is the density of the body, and ui is the four-velocity defined as [4]

$${{u}^{i}} = \frac{{{{{v}}^{i}}}}{{c\sqrt {1 - \frac{{{{{v}}^{2}}}}{{{{c}^{2}}}}} }},$$
(5)
$${{{v}}^{i}} = \left( {c,{\mathbf{v}}} \right).$$

The modification of Eq. (3) to the case when the EM field is taken into account makes it possible to write it in form

$${{R}_{{ik}}} - \frac{1}{2}R{{\delta }_{{ik}}} = \frac{{8\pi G}}{{{{c}^{4}}}}\left( {{{T}_{{ik}}} + {{A}_{{ik}}}} \right),$$
(6)

where the energy–momentum tensor \({{A}_{{ik}}}\) of the EM field is defined as

$${{A}_{{ik}}} = \left( {\frac{{\partial {{A}_{i}}}}{{\partial {{x}^{s}}}} - \frac{{\partial {{A}_{s}}}}{{\partial {{x}^{i}}}}} \right)\left( {\frac{{\partial {{A}_{s}}}}{{\partial {{x}^{k}}}} - \frac{{\partial {{A}_{k}}}}{{\partial {{x}^{s}}}}} \right);$$
(7)

here, the contravariant vector is \({{A}^{i}} = \left( {\psi ,{\mathbf{A}}} \right)\), ψ is the scalar potential of the electric field, and A is the vector potential (H = curl A).

In the nonrelativistic limit, we obtain the following expression for the zeroth component from Eq. (6) with account for (7):

$${{R}_{{00}}} - \frac{1}{2}R = \frac{{8\pi G}}{{{{c}^{4}}}}\left( {{{T}_{{00}}} + {{A}_{{00}}}} \right).$$
(8)

Since (see [4])

$${{R}_{{00}}} - \frac{1}{2}R = - \Delta {{h}_{{00}}},$$
(9)

where Δ is the Laplace operator, and the temporal component of the metric tensor in the nonrelativistic limit can be represented by

$${{g}_{{00}}} = 1 + {{h}_{{00}}},$$
(10)

where

$${{h}_{{00}}} = \frac{{2\varphi }}{{{{c}^{2}}}},$$
(11)

and φ is the gravitational field potential, we obtain from Eq. (8) combined with (9) and (11)

$$\Delta \varphi = - \frac{{4\pi \rho G}}{{{{c}^{2}}}}\left( {1 + \frac{{{{A}_{{00}}}}}{{\rho {{c}^{2}}}}} \right).$$
(12)

According to definition (7), zeroth component \({{A}_{{00}}}\) can be calculated as follows:

$$\begin{gathered} {{A}_{{00}}} = - {{\left( {\frac{{\partial {{A}_{0}}}}{{\partial {{x}^{s}}}} - \frac{{\partial {{A}_{s}}}}{{\partial {{x}^{0}}}}} \right)}^{2}} \\ = - \left[ {{{{\left( {\nabla {{A}_{0}}} \right)}}^{2}} + 2\nabla {{A}_{0}} \cdot \frac{{\partial {\mathbf{A}}}}{{\partial {{x}^{0}}}} + {{{\left( {\frac{{\partial {\mathbf{A}}}}{{\partial {{x}^{0}}}}} \right)}}^{2}}} \right]. \\ \end{gathered} $$
(13)

Using the standard definition of electric field,

$${\mathbf{E}} = - \frac{{\partial {\mathbf{A}}}}{{\partial {{x}^{0}}}} - \nabla \varphi ,$$
(14)

where \({{x}^{0}} = ct\), we obtain from relation (13)

$${{A}_{{00}}} = - {{{\mathbf{E}}}^{2}}.$$
(15)

Therefore, Eq. (12) can be transformed to

$$\Delta \varphi = - \frac{{4\pi \rho G}}{{{{c}^{2}}}}\left( {1 - \frac{{{{{\mathbf{E}}}^{2}}}}{{\rho {{c}^{2}}}}} \right).$$
(16)

If we assume that E = const, the solution to Eq. (16) can be written in form

$$\varphi = \frac{{GM}}{r} - \frac{{2GV{{E}^{2}}}}{{{{c}^{2}}r}}\left[ {{{{\left( {\frac{r}{R}} \right)}}^{3}} - 1} \right].$$
(17)

This means that the potential energy of the interaction with a body of mass m is given by

$$U = - \frac{{Gm}}{r}\left\{ {M - \frac{{2V{{E}^{2}}}}{{{{c}^{2}}}}\left[ {{{{\left( {\frac{r}{R}} \right)}}^{3}} - 1} \right]} \right\}.$$
(18)

Differentiating this expression with respect to r and then assuming that \(r = R\), where R is the radius of the spherical object in question, we obtain

$$\begin{gathered} {\mathbf{F}} = {{\left. { - \nabla U} \right|}_{{r = R}}} \\ = {{\left. { - \frac{{Gm{\mathbf{r}}}}{{{{r}^{3}}}}\left\{ {M - \frac{{2V{{E}^{2}}}}{{{{c}^{2}}}}\left[ {2{{{\left( {\frac{r}{R}} \right)}}^{3}} + 1} \right]} \right\}} \right|}_{{r = R}}}, \\ \end{gathered} $$
(19)

whence

$$F = \frac{{\partial U}}{{\partial R}} = \frac{{GmM}}{{{{R}^{2}}}}\left( {1 - \frac{{2{{E}^{2}}}}{{\rho {{c}^{2}}}}} \right).$$
(20)

Setting \(F = 0\), we arrive at the “levitation” condition

$$E = c\sqrt {\frac{\rho }{2}} .$$
(21)

If a body resting on the planet surface is charged with surface density \(\sigma \), i.e., \(\sigma = {{E}_{n}}\), we obtain the following expression for the critical “floating” density:

$$\sigma = c\sqrt {\frac{\rho }{2}} .$$
(22)

It should be noted that a large number of publications are devoted to levitation (see, in particular, [7–10]).

3 CONCLUSIONS

Summarizing the results of this study, it should be noted that the floating of a body above the Earth surface is quite possible theoretically if the body possesses a surface charge density obeying relation (22).