1 INTRODUCTION

Observations indicate the existence of a larger content of mass-energy than predicted [1–6]. The mass-energy of the universe is dominated by non-baryonic and non-relativistic particles, indicated as “cold dark matter” [3], and a second component, dubbed “dark energy” (DE), a fluid with exotic properties, like that of having negative pressure, and giving rise to the accelerated expansion of the universe. In its simplest form, and in the \(\Lambda \)CDM model, DE is represented by the cosmological constant \(\Lambda \).

Despite the success of the \(\Lambda \)CDM model [1, 7, 8], precise data are revealing drawbacks, and tensions both at large scales [9], and at small ones [3, 10–18].

Despite a large number of indirect evidences from small to large scales [19–24], and a large campaign of direct and indirect searches [3, 20, 25–28], the particles that should constitute the DM have never been observed [25].

The so called “small scale problems” of the \(\Lambda \)CDM [18, 29–31, 134–136] are plaguing the model, apart from the issues related to the DM component of the \(\Lambda \)CDM model, the cosmological constant \(\Lambda \) suffers from the “cosmological constant fine tuning problem”, and the “cosmic coincidence problem” [32–35].

One of the way to determine the dark matter content of a structure is to calculate its the mass-to-light ratio.

Calculation of the mass-to-light (\(M{\text{/}}L\)) ratios of group of galaxies in the past [36] is in disagreement with newer measurements based on the virial theorem [37]. The new measurements give smaller (\(M{\text{/}}L\)) ratios. This means that the local matter density should be a fraction of the global one. It is well known that the virial theorem gives reliable results if the system is in dynamical equilibrium. This condition is often assumed if the crossing time is less than the Hubble time. This assumption has been shown to be often not correct by [38]. Lynden-Bell [39], Sandage [40] proposed an alternative approach to the virial theorem based on the Lemaitre-Tolman (LT) model [41, 42] giving a good description of a gravitationally bound central core located inside an homogeneous region whose density decreases till reaching the background value. The model describes the evolution of the system in a similar way to that done by the spherical collapse model. Considering a shell of given radius containing a mass M, it initially expands following the Hubble flow. When the density overcomes a critical value the shell reaches a maximum radius, known as a turn-around radius, \({{R}_{0}}\), characterized by zero velocity, and then collapses. In the LT model there is a central region in equilibrium, surrounded by a region which reaches its maximum expansion and collapses, and a zero totally energy region constituted by shells still bound to the structure and unbound ones [137]. The LT model was applied to the local group [40] and to the Virgo cluster [43–45]. The model was modified taking into account the cosmological constant by [46, 47] applying it to the Virgo cluster, the pair M31-MW, M81, the Centaurus A-M83 group, the IC342/Maffei-I group, and the NGC 253 group. As shown in [46, 47] the introduction of the cosmological constant modifies the mass, M, and turn-around radius, \({{R}_{0}}\), relation. As a consequence for a given \({{R}_{0}}\), the value of the mass of the system is \( \simeq {\kern 1pt} 30{\kern 1pt} \% \) larger with respect to the LT model [46, 47], while the Hubble constant of the modified model is smaller than in the standard LT.

However, Peirani and de Freitas Pacheco [46, 47], differently from Sandage [40], did not use the standard LT (SLT) \(M{\kern 1pt} - {\kern 1pt} {{R}_{0}}\) relation, or its extension to the case the cosmological constant (modified LT model) (MLT). They build up a velocity-distance relationship, \({v}{\kern 1pt} - {\kern 1pt} R\), describing the kinematic status of the systems studied. Knowing the values of \({v}\), and \(R\) for the members of the groups studied, the mass of the group, M, and the Hubble parameter can be obtained by means of a non-linear fit of the \({v}{\kern 1pt} - {\kern 1pt} R\) relation to the data.

Recently, the turnaround radius (TAR) has been proposed as a promising way to test cosmological models [48], dark energy, and disentangle between \(\Lambda \)CDM model, dark energy, and modified gravity models [35, 48–53]. According to some authors (e.g., [49]), the TAR is a well-defined, and unambiguous boundary of a structure, in the spherical collapse model (SCM), simulations, analytic calculations, and is clean from baryons physics. Concerning the last point, contrarily to [49], we already showed in [2, 54–59] that the non-linear equation driving the evolution of the overdensity contrast depends on shear, and vorticity [55, 59–66], which conversely depends from the mass of the forming structure, and the way it forms.

The effects of shear and rotation (slowing down the collapse [63, 64, 67, 68], changing turnaround epoch and collapse time) were investigate in [54, 55, 69–72] for smooth DE models, [73] in clustering DE cosmologies, and [74] in Chaplygin cosmologies.

As we have already shown, shear, vorticity, and dynamical friction [24, 28, 60, 75, 76] change the typical parameters of the SCM [2], the mass function [2, 54, 56, 57], the two-point correlation function [61], and the weak lensing peaks [59].

In the following, we will show that the TAR also depends from dynamical friction.

To this aim, we will further extend the MLT model to take account of the effect of angular momentum (JLT model) and dynamical friction (J\(\eta \)LT model). The effect of these two quantities on the spherical collapse model and its effect on the clusters of galaxies structure and evolution, the turn-around, the threshold of collapse, their mass function are studied (see also [1, 23, 24, 28, 60–62, 77–83]).

Similarly to [46, 47], we will solve the equation of the spherical collapse model, using [84] and find a relation between the mass, M, and turn-around radius, \({{R}_{0}}\), showing going from the SLT to the \(J\eta LT\) model. Then we show how angular momentum and dynamical friction change the threshold collapse, the virial overdensity, and the mass function, in different dark energy models.

The paper is organized as follows. In Section 2, we introduce the model, and solve it. In Section 3, we find the \(M{\kern 1pt} - {\kern 1pt} {{R}_{0}}\) relation. In Section 4, we show how dynamical friction and angular momentum changes the collapse threshold, the virial overdensity, and the mass function coming from the spherical collapse model. Section 5 is devoted to conclusions.

2 MODEL

The simplest form of the spherical collapse model (SCM) was introduced by Gunn and Gott [85]. It is a simple and popular method to study the analytically the non-linear evolution of perturbations of dark matter (DM) and dark energy (DE). As previously described, the model describes the evolution of a spherical symmetric over density which initially expands with the Hubble flow, then detaches from it, when the density overcomes a critical value, reaches a maximum radius, dubbed turn-around radius, and finally collapse and virialize. SCM [85] is a very simple model assuming that matter moves in a radial fashion. Tidal angular momentum [86, 87], random angular momentum [88–90], dynamical friction [76, 91], etc., are not taken into account. SCM [85] was improved in several papers [88, 90, 92–96], adding the cosmological constant [97], and tidal and random angular momentum [88, 90, 96, 98–105].Footnote 1 Dynamical friction was studied in [76, 91], while [106–108] discussed the role of shear in the gravitational collapse.

The SCM with negligible DE perturbations was extensively investigated in literature (see, e.g., [109–115]), while DE fluid perturbation were taken into account in articles [116–124].

Using the non-linear differential equations for the evolution of the matter density contrast derived from Newtonian hydrodynamics in [114], Del Popolo, Pace, and Lima [55] showed that the parameters of the spherical collapse model become mass dependent.

Del Popolo, Pace, and Lima [54, 55] studied the effects of shear and rotation in smooth DE models. The effects of shear and rotation were investigated in [54, 55] for smooth dark energy models, [73] in clustering DE cosmologies, and [74] in Chaplygin cosmologies.

In this paper, we show how angular momentum, and dynamical friction change several predictions of the SCM. To start with, we consider some gravitationally growing mass concentration collecting into a potential well. Let \(dP = f(L,r,{{{v}}_{r}},t)dLd{{{v}}_{r}}dr\) be the probability that a particle, having angular momentum \(L = r{{{v}}_{\theta }}\), is located at \([r,r + dr]\), with velocity (\({{{v}}_{r}} = \dot {r}\)) \([{{{v}}_{r}},{{{v}}_{r}} + d{{{v}}_{r}}]\), and angular momentum \([L,L + dL]\). The term \(L\) takes into account ordered angular momentum generated by tidal torques and random angular momentum (see [76, Appendix C.2]). The radial acceleration of the particle [60, 61, 97, 125, 126] is:

$$\frac{{d{{{v}}_{R}}}}{{dt}} = - \frac{{GM}}{{{{R}^{2}}}} + \frac{{{{L}^{2}}(R)}}{{{{M}^{2}}{{R}^{3}}}} + \frac{\Lambda }{3}R - \eta \frac{{{\text{d}}R}}{{{\text{d}}t}},$$
(1)

with \(\Lambda \) being the cosmological constant and \(\eta \) the dynamical friction coefficient. The previous equation can be obtained via Liouville’s theorem [61]. The last term, the dynamical friction force per unit mass, is more explicitly given in [76, Appendix D, Eq. (D.5)]. A similar equation (excluding the dynamical friction term) was obtained by several authors, e.g., [55, 127, 128] and generalized to smooth dark energy models in [59].

In terms of the specific angular momentum \(J = \tfrac{L}{M}\), and the \({{\Omega }_{\Lambda }} = \tfrac{{{{\rho }_{\Lambda }}}}{{{{\rho }_{{{\text{cr}}}}}}}\), where \({{\rho }_{{{\text{cr}}}}}\) is the critical density, Eq. (1) can be written as

$$\begin{gathered} \frac{{d{{{v}}_{R}}}}{{dt}} = - \frac{{GM}}{{{{R}^{2}}}} + \frac{{{{J}^{2}}}}{{{{R}^{3}}}} \\ \; - \frac{{1 + 3w}}{2}{{\Omega }_{\Lambda }}H_{0}^{2}\mathop {\left( {\frac{{{{a}_{0}}}}{a}} \right)}\nolimits^{3(1 + w)} R - \eta \frac{{dR}}{{dt}}, \\ \end{gathered} $$
(2)

where \(\eta \tfrac{{dr}}{{dt}}\) is given in [76, Appendix D, Eq. (D.5)], and [24, Eq. (5)]; \(w\) is the DE equation of state (EoS) parameter. DE is modeled by a fluid with an EoS \(P = w\rho \), where \(\rho \) is the energy density; \(a\) is the expansion parameter. Eq. (2) satisfies equation

$$H = \frac{{\dot {a}}}{a} = {{H}_{0}}\sqrt {{{\Omega }_{{\text{m}}}}\mathop {\left( {\frac{{{{a}_{0}}}}{a}} \right)}\nolimits^3 + {{\Omega }_{\Lambda }}\mathop {\left( {\frac{{{{a}_{0}}}}{a}} \right)}\nolimits^{3(1 + w)} .} $$
(3)

Assuming that \(J = k{{R}^{\alpha }}\), with \(\alpha = 1\), in agreement with [129],Footnote 2 and \(k\) constant. In terms of the variables \(y = R{\text{/}}{{R}_{0}}\), \(t = x{\text{/}}{{H}_{0}}\), Eqs. (2), and (3) can be written as

$$\frac{{{{d}^{2}}y}}{{d{{x}^{2}}}} = - \frac{A}{{2{{y}^{2}}}} - \frac{{1 + 3w}}{2}{{\Omega }_{\Lambda }}y{{\xi }^{{ - 3(1 + w)}}} + \frac{{{{K}_{j}}}}{y} - \frac{\eta }{{{{H}_{0}}}}\frac{{dy}}{{dx}},$$
(4)

where \({{K}_{j}} = \tfrac{k}{{{{{({{H}_{0}}{{R}_{0}})}}^{2}}}}\), \(A = \tfrac{{2GM}}{{H_{0}^{2}R_{0}^{3}}}\), and

$$\frac{{d\xi }}{{dx}} = \sqrt {\frac{{{{\Omega }_{m}}}}{\xi } + \frac{{{{\Omega }_{\Lambda }}}}{{{{\xi }^{{(1 + 3w)}}}}}} .$$
(5)

Equation (4) has a first integral, given by

$$\begin{gathered} {{u}^{2}} = \mathop {\left( {\frac{{dy}}{{dx}}} \right)}\nolimits^2 = \frac{A}{y} - \frac{{1 + 3w}}{2}{{\Omega }_{\Lambda }}{{y}^{2}}{{\xi }^{{ - 3(1 + w)}}} \\ + \;2{K}_{j}\log y - 2\frac{\eta }{{{{H}_{0}}}}\int {\mathop {\left( {\frac{{dy}}{{dx}}} \right)}\nolimits^2 dx} + K, \\ \end{gathered} $$
(6)

where \(K = \tfrac{{2E}}{{{{{({{H}_{0}}{{R}_{0}})}}^{2}}}}\), and \(E\) is the energy per unit mass of a shell. At the turn-around epoch, when \(R = {{R}_{0}}\) or \(y = 1\), Eq. (6) gives the condition

$$0 = A + (1 + 3w){{\Omega }_{\Lambda }}{{\xi }^{{ - 3(1 + w)}}} + K,$$
(7)

which implies \(K = - A - (1 + 3w){{\Omega }_{\Lambda }}{{\xi }^{{ - 3(1 + w)}}}\). Equations (3) and (4) where solved as described in [46, 47]. Fixing a redshift, the initial value of the scale parameter and the corresponding time are obtained from Eq. (3). At high redshift, the gravitational term dominates and through a Taylor expansion of the standard Lemaitre-Tolman solution one can get the initial c-onditions (initial values of \(y\) and \(\tfrac{{dy}}{{dx}}\)). For a given value of \(w\), the parameter \(A\) is varied until the condition defining the zero-velocity surface, \(\tfrac{{dy}}{{dx}} = 0\), at \(y = 1\) is satisfied.

As an example of the solution, let’s show how \(A\) is obtained in the case \(w = - 1\), and angular momentum are present (JLT case)

$$\frac{{{{d}^{2}}y}}{{d{{x}^{2}}}} = - \frac{A}{{2{{y}^{2}}}} + {{\Omega }_{\Lambda }}y + \frac{{{{K}_{j}}}}{y}.$$
(8)

At high redshifts (\(z = 1000\)), or \(y \ll 1\), as wrote the gravitational term dominates, and by a Taylor expansion one gets the relation \(y \simeq \mathop {\left( {\tfrac{{9A}}{4}} \right)}\nolimits^{1/3} {{x}^{{2/3}}}\). Assuming a initial value of \(y\), \({{y}_{i}} = 0.001\), corresponding approximately to 1 kpc, the initial time \({{x}_{i}}\) can be obtained. The initial value of the velocity \({{u}_{i}}\) can be obtained through Eq. (6). The value of \(A\) is obtained as follows. Equation (8) can be written as

$$x = \int\limits_{{{y}_{i}}}^1 \frac{{dy}}{{\sqrt {\tfrac{A}{y} + {{\Omega }_{\Lambda }}{{y}^{2}} + \tfrac{{{{K}_{j}}}}{y} - A - {{\Omega }_{\Lambda }}} }}.$$
(9)

Equation (5), recalling that \(\tfrac{{{{a}_{0}}}}{a} = 1 + z\), can be written as

$$x(y = 1) = \int\limits_0^\infty \frac{{dz}}{{(1 + z)\sqrt {{{\Omega }_{\Lambda }} + {{\Omega }_{{\text{m}}}}{{{(1 + z)}}^{3}}} }} = 0.964.$$
(10)

For \({{\Omega }_{\Lambda }} = 0.7\), \({{\Omega }_{{\text{m}}}} = 0.3\), \({{K}_{j}} = 0.78\), \(x = 0.964\), Eq. (9) can be solved to get \(A = 5.037\).Footnote 3

Equation (8) can be solved with the conditions \({{y}_{i}} = 0.001\), and

$$\begin{gathered} u(0) = \sqrt {\frac{{5.037}}{{{{y}_{i}}}} + 0.7y_{i}^{2} + 2{{K}_{J}}\log{{y}_{i}} - 6.07} \\ = 70.833943. \\ \end{gathered} $$
(11)

In Fig. 1, we plot the result of the solution. The red line correspond to the case \(K = - A - {{\Omega }_{\Lambda }} = - 5.737\), being \(A = 5.037\). This solution is the one that has just reached the maximum expansion, or turn-around, and the collapse happens in \( \simeq {\kern 1pt} 13.8\) Gyr. The cyan line is characterized by \(K = - 6.2\). It reached the turn-around in the past. Turn-around will happen only for \(K < - 5.56812\), for larger values the collapse will never occur, as the case of the green line characterized by \(K = - 5.1\).

Fig. 1.
figure 1

Evolution of shell radius for different values of \(K\). The red, cyan, and green lines correspond to \(K = - 5.737\), \(K = - 6.2\), and \(K = - 5.1\), respectively.

Full size image

Concerning the general case, also taking into account dynamical friction, Eq. (6) at turn-around, \(R = {{R}_{0}}\), namely \(y = 1\), gives K = –A – (1 + 3w) × \({{\Omega }_{\Lambda }}{{\xi }^{{ - 3(1 + w)}}}\). The same equation gives (for example in the case \(w = - 1\)) the value of \(A = 6.05\) following the method described for the other cases. Equation (4) can be solved with the condition \({{y}_{i}} = 0.001\), and the velocity \({{u}_{i}}\) obtained from Eq. (6).

3 THE MASS, M, AND \({{R}_{0}}\) RELATIONS FOR THE MODELS MLT, JLT, \({\text{J}}\eta \)LT

The mass predicted by the LT model is given by

$$M = \frac{{{{\pi }^{2}}R_{0}^{3}}}{{8GT_{0}^{2}}} = 3.06 \times {{10}^{{12}}}{{h}^{2}}R_{0}^{3}{{M}_{ \odot }}.$$
(12)

For the MLT, the value of \(A\) can be obtained combining Eqs. (9), and (10), and one gets \(A = 3.6575\). By the definition of \(A = \tfrac{{2GM}}{{H_{0}^{2}R_{0}^{3}}}\), and recalling that in the \(\Lambda \)CDM model \({{H}_{0}} = f(\Omega ){\text{/}}{{T}_{0}}\), where

$$f(\Omega ) = \int\limits_0^\infty \frac{{dz}}{{(1 + z)\sqrt {{{\Omega }_{\Lambda }} + {{\Omega }_{{\text{m}}}}{{{(1 + z)}}^{3}}} }},$$
(13)

we obtain, for \({{\Omega }_{\Lambda }} = 0.7\)

$$M = 4.22 \times {{10}^{{12}}}{{h}^{2}}R_{0}^{3}{{M}_{ \odot }}.$$
(14)

Comparing Eqs. (12), and (14), we get a difference of 38%.

In the case JLT, with \({{k}_{j}} = 0.78\), the value of \(A\) is 5.037, then

$$\begin{gathered} M = \frac{{2.5185H_{0}^{2}R_{0}^{3}}}{G} = \frac{{2.3404R_{0}^{3}}}{{GT_{0}^{2}}} \\ = 5.8148 \times {{10}^{{12}}}{{h}^{2}}R_{0}^{3}{{M}_{ \odot }} \\ \end{gathered} $$
(15)

and then the difference with the case LT is 89%. Finally, in the case J\(\eta \)LT, \(A = 6.05\)

$$\begin{gathered} M = \frac{{3.025H_{0}^{2}R_{0}^{3}}}{G} = \frac{{2.8111R_{0}^{3}}}{{GT_{0}^{2}}} \\ = 6.9843 \times {{10}^{{12}}}{{h}^{2}}R_{0}^{3}{{M}_{ \odot }}, \\ \end{gathered} $$
(16)

which means that the mass in this case is more than double of the case LT. The difference in mass between the previous cases is due to the modification of the perturbation evolution due to the effect of angular momentum, and dynamical friction as also shown in several papers [23, 24, 60–62, 77, 82].

The previous different \(M{\kern 1pt} - {\kern 1pt} {{R}_{0}}\) relations are plotted in Fig. 2, showing an increase of the acquired mass moving from the LT to the \({\text{J}}\eta \)LT model.

Fig. 2.
figure 2

\(M{\kern 1pt} - {\kern 1pt} {{R}_{0}}\) relationship for the LT model (black curve), MLT model (blue curve), JLT (green curve), and J\(\eta \)LT (red curve).

Full size image

4 TRESHOLD OF COLLAPSE AND THE VIRIAL OVERDENSITY

In this section we present results for the two main quantities derived in the framework of the SCM, in particular the linear overdensity parameter \({{\delta }_{{\text{c}}}}\) and the virial overdensity \({{\Delta }_{{\text{V}}}}\). We assume as reference model the \(\Lambda \)CDM model, with the following cosmological parameters: \({{\Omega }_{{\text{m}}}} = 0.274\), \({{\Omega }_{{{\text{de}}}}} = 0.726\), and \(h = 0.7\).

In Fig. 3, we plot the threshold of collapse in terms of mass \({{\delta }_{{\text{c}}}}\) as a function of the peak height \(\nu \). The red solid line shows the result in [130], the green short-dashed line the results of [60], taking into account the effect of the tidal field, the orange long-dashed the result of [77] taking into account the effect of the tidal field and the cosmological constant, while the blue dot-dashed line takes into account the effect of the tidal field, the cosmological constant and the DF. As the plot shows, adding the cosmological constant, angular momentum, and dynamical friction, change the behavior of \({{\delta }_{{\text{c}}}}\) which is no longer constant but depend on mass. The mass dependence is more already evident when the cosmological constant is taken into account, and becomes even more evident when angular momentum, and dynamical friction are present. The change in the behavior of the threshold is due to the modification of the turn-around time, and slowing down of the collapse.

Fig. 3.
figure 3

The collapse threshold \({{\delta }_{{\text{c}}}}\) as a function of the peak height \(\nu \). The red solid line shows the result in [130], the green short-dashed line the results of [60], taking into account the effect of the tidal field, the orange long-dashed the result of [77] taking into account the effect of the tidal field and the cosmological constant, while the blue dot-dashed line takes into account the effect of the tidal field, the cosmological constant and the DF.

Full size image

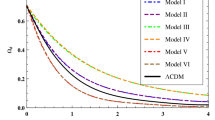
In Fig. 4, we show the dependence of the collapse threshold with redshift, \(z\).

Fig. 4.
figure 4

The left panels show the time evolution of the linear overdensity \({{\delta }_{{\text{c}}}}(z)\), the right panels the time evolution for the virial overdensity \({{\Delta }_{{\text{V}}}}(z)\) for the different classes of models. In all panels, the \(\Lambda \)CDM solution (black solid curve) is the reference model. All the curves assume a galactic mass for the collapsing sphere. The panels present the quintessence models: the INV1 (INV2) model is shown with the light-green dashed (dark-green short-dashed) curve, the 2EXP model with the blue dotted curve, the AS model with the cyan dot-dashed curve, the CPL (CNR) model with the red dot-dotted (orange dot-short-dashed) curve and finally the SUGRA model with the violet dot-dot-dashed curve. Right panel: same as the left panel but for the virial overdensity.

Full size image

An important result that it is worth to notice, is the time behavior of \({{\delta }_{{\text{c}}}}\). We observe that the contribution of the cosmological constant, angular momentum, dynamical friction is maximum at \(z = 0\) and it decreases with increasing redshift till \({{\delta }_{{\text{c}}}}\) reaches an approximately constant value, generally higher or equal to the value for the standard SCM, according to the mass range considered.

This is expected when we compare the nonlinear term (term with angular momentum, and dynamical friction) with the gravitational term. This can be interpreted as an additional term counteracting the collapse even at high redshifts, making therefore \({{\delta }_{{\text{c}}}}\) higher than the standard value.

In Fig. 4 we also present results for the different dark energy models considered in this work: INV1, INV2, 2EXP, AS, CNR, CPL, and SUGRA. All these models can be described by the following equation-of-state parameter, valid after matter-radiation equality,

$$\begin{gathered} w(a) = {{w}_{0}} + ({{w}_{{\text{m}}}} - {{w}_{0}})\frac{{1 + \exp({{a}_{{\text{m}}}}{\text{/}}{{\Delta }_{{\text{m}}}})}}{{1 + \exp(({{a}_{{\text{m}}}} - a){\text{/}}{{\Delta }_{{\text{m}}}})}} \\ \times \;\frac{{1 - \exp((1 - a){\text{/}}{{\Delta }_{{\text{m}}}})}}{{1 - \exp(1{\text{/}}{{\Delta }_{{\text{m}}}})}}. \\ \end{gathered} $$
(17)

In Table 1, we list the values of the parameters \({{a}_{{\text{m}}}}\), \({{\Delta }_{{\text{m}}}}\), \({{w}_{{\text{m}}}}\), and \({{w}_{0}}\) characterizing the models discussed above.

Table 1.   Parameter values for the quintessence models
Full size table

On the left panel we show results for the linear overdensity parameter \({{\delta }_{{\text{c}}}}\) while on the right panel we show the expected values for the virial overdensity \({{\Delta }_{{\text{V}}}}\). We will consider as reference the standard \(\Lambda \)CDM model and to maximize the effect of the non linear term, all the figures show results for galactic masses (\(M \approx {{10}^{{11}}}{{M}_{ \odot }}{\text{/}}h\)).

For the models INV1, INV2, 2EXP, AS, CNR, CPL, SUGRA, we see that the models are in general very similar to each other and they slightly differ from each other, with differences at most of the order of 4.5% for the AS model. The INV1, CNR, and 2EXP models are basically indistinguishable from the \(\Lambda \)CDM model. We interpret this result as due to the equation of state of the models considered. As shown in [114], the INV1 model has an equation of state basically constant over the whole cosmic history, but its present value is quite different from all the other models, being \({{w}_{0}} \approx - 0.4\), while for all the other models is \( - 1 \leqslant {{w}_{0}} \leqslant - 0.8\). Comparing our present results with the ones of the upper left panel of [114, Fig. 4], we see that the behavior of the models is very similar. The inclusion of the non-linear term just changes the values of the linear overdensity parameter, but not the respective ratios with the \(\Lambda \)CDM model.

All the models studied with a time-varying dark energy equation-of-state parameter show that the collapse, even if retarded by the inclusion of angular momentum, and dynamical friction is easier as compared with the \(\Lambda \)CDM model. In this case, with easier we mean that the values for the extended \({{\delta }_{{\text{c}}}}(z)\) are smaller than for the reference model. With extended we mean the model taking into account cosmological constant, angular momentum, and dynamical friction. This is expected and it has the same explanation as for the usual case. Since at early times the amount of dark energy is higher, we need structures to grow faster in order to observe cosmic structures today. This is plausible, since the linear overdensity parameter represents the time evolution of the initial overdensity, whose evolution is dictated by the growth rate that is described by the same differential equation. In other words, since at early times the amount of dark energy is higher, we need lower values of \({{\delta }_{{\text{c}}}}\) to have objects collapsing. This is analogous to the case of the linear growth factor, since the equation to be solved is the same.

On the right panels, we show results for the quantity \({{\Delta }_{{\text{V}}}}\). Also in this case we limit ourselves to galactic masses. We notice that for the quintessence models in general the virial overdensity shows higher values than for the extended \(\Lambda \)CDM model, except for the INV2 model. This is opposite to what found for the standard case, where all the models had smaller values than the \(\Lambda \)CDM model. Also in this case none of the models approximates the extended \(\Lambda \)CDM model at high redshifts. This is not the result of the additional non-linear term only, but also of the influence of the dark energy equation of state, consistently with results from [114].

Differences in the linear overdensity parameter reflect in the differential mass function. In this work we decide to use the parametric form by [130–132] (ST).

We consider three different redshifts, namely \(z = 0\), 0.5, 1.

At this point, it is worth noticing that in the first paper of [131] the mass function was calculated as a fit to numerical simulations. Later on, [130, 132] showed that the effects of non-sphericity (shear and tides) introduce a mass dependence in the collapse threshold (see [130, Eq. (4)] and following discussion). By using this threshold as the barrier in the excursion set approach one gets a mass function in good agreement with simulations (see Eq. (5) and the discussion in the last part of Section 2.2 of [130] and moreover [132]).

For the \(\Lambda \)CDM model we choose as power spectrum normalization the value \({{\sigma }_{8}} = 0.776\). Since we want that perturbations at the CMB epoch are the same for all the models, we normalize the dark energy model according to the formula

$${{\sigma }_{{8,{\text{DE}}}}} = {{\sigma }_{{8,\Lambda {\text{CDM}}}}}\frac{{{{D}_{{ + ,\Lambda {\text{CDM}}}}}({{a}_{{{\text{CMB}}}}})}}{{{{D}_{{ + ,{\text{DE}}}}}({{a}_{{{\text{CMB}}}}})}},$$
(18)

where \({{D}_{ + }}({{a}_{{{\text{CMB}}}}})\) is the growth factor at the CMB epoch.

In Table 2, we display the different normalizations used for the models considered in this work (\(K\) is the curvature parameter).

Table 2.   Table with the power spectrum normalization for the different dark energy models
Full size table

In Fig. 5 we compare the differential mass function for the \(\Lambda \)CDM model in the standard and in the extended SCM. Analyzing the three curves, we can appreciate the effect of the term non-linear term on the mass function. On small masses, the mass function is largely independent of the cosmological model, but it depends strongly on \({{\delta }_{{\text{c}}}}\). Since in the extended SCM this is higher, we observe an increase in the number of objects at galactic scale at \(z = 0\), to decrease at higher redshifts where the contribution of the non-linear term decreases. We observe a general decrement in the number of objects at high masses (up to \(M \approx {{10}^{{14}}}{{M}_{ \odot }}{\text{/}}h\)) to increase again to unity for masses of the order of \({{10}^{{15}}}{{M}_{ \odot }}{\text{/}}h\). This is explained by the fact that at such masses, the linear overdensity parameter are practically the same, therefore the mass function must not change.

Fig. 5.
figure 5

Ratio between the differential mass function of the extended and standard \(\Lambda \)CDM model. The curves represent three different redshifts: \(z = 0\) (dotted red curve), \(z = 0.5\) (short-dashed blue curve), \(z = 1\) (dashed green curve).

Full size image

In this concern, it should be recalled that angular momentum, and dynamical friction have the maximum effect on \({{\delta }_{{\text{c}}}}\), at galactic scale (see Fig. 3). However, in the calculation of the ratio between the differential mass functions (Fig. 5), beside \({{\delta }_{{\text{c}}}}\) we need to take into account the factor \(\sigma (M)\), the r.m.s. of mass overdensity. Now, recalling the Sheth and Tormen [131, 132] multiplicity function

$${{f}_{{{\text{ST}}}}}\, = \,A\sqrt {\frac{{2a}}{\pi }} \left[ {1\, + \,\mathop {\left( {\frac{{{{\sigma }^{2}}(M)}}{{\delta _{{\text{c}}}^{2}a}}} \right)}\nolimits^p } \right]\frac{{{{\delta }_{{\text{c}}}}}}{{\sigma (M)}}\exp\left( { - \frac{{a\delta _{{\text{c}}}^{2}}}{{2{{\sigma }^{2}}(M)}}} \right),$$
(19)

with A = 0.3222, a = 0.707, and p = 0.3, we have that at galactic scale the dominant term in Eq. (19) is the term \({{\delta }_{{\text{c}}}}{\text{/}}\sigma \), consequently the ratio \({{f}_{{{\text{ST}},{\text{extended}}}}}{\text{/}}{{f}_{{{\text{ST}},\Lambda {\text{CDM}}}}} \simeq \) \({{\delta }_{{{\text{c}},{\text{extended}}}}}{\text{/}}{{\delta }_{{{\text{c}},\Lambda {\text{CDM}}}}}\). At larger masses, the effect of rotation and shear diminishes with the consequence that \({{\delta }_{{{\text{c}},{\text{extended}}}}} \simeq {{\delta }_{{{\text{c}},\Lambda {\text{CDM}}}}}\) and that the \(\sigma (M)\) term is fixing the value of the \({{f}_{{{\text{ST}},{\text{extended}}}}}{\text{/}}{{f}_{{{\text{ST}},\Lambda {\text{CDM}}}}}\) ratio.

At this point it is necessary a deeper discussion of the results shown in Fig. 5. The ST mass function generalises the Press and Schechter (PS) [133] mass function to include the effects of shear and tidal forces with respect to the simpler spherical collapse model. In doing so it is necessary to consider the ellipsoidal collapse model and the corresponding linear overdensity parameter \({{\delta }_{{{\text{ec}}}}}\). Differently from the spherical collapse model, now \({{\delta }_{{{\text{ec}}}}}\) is not only a function of time, but of mass too and the relation between \({{\delta }_{{{\text{ec}}}}}\) and \({{\delta }_{{\text{c}}}}\) (\({{\delta }_{{{\text{sc}}}}}\) in [130]) is given in [130, Eq. (4)]. The moving barrier for the random walk is now set equal to \({{\delta }_{{{\text{ec}}}}}(M,z)\) and a good approximation to it is then given by their Eq. (5). The ST mass function fits quite well the results of N‑body simulations, but as shown in Fig. 5, for masses \(M \approx {{10}^{{14}}}{{M}_{ \odot }}{\text{/}}h\) our predictions, including rotation on top of the ellipsoidal collapse, predict approximately 40% less objects at \(z = 1\) than the standard \(\Lambda \)CDM model. This would be easily checked with a big enough spanned volume. Moreover one could identify ellipticity and rotation if halos acquire angular momentum by misalignment with the surrounding tidal field. Following this line of thought one could further use the \({{\delta }_{{\text{c}}}}(M,z)\) predicted by the extended spherical collapse model as the correct moving barrier. Therefore by direct comparison of expressions (2), (4), and (5) in [130] we substitute \({{\delta }_{{\text{c}}}}\), of our model, directly into their expression (2) (equivalent to the Press-Schechter multiplicity function). Results are shown in Fig. 5 for the three redshifts.

5 CONCLUSIONS

In this paper, we extended the modified LT (MLT) model [46, 47] to take account the effect of angular momentum and dynamical friction. The inclusion of these two quantities in the equation of motion modifies the evolution of perturbations as described by the MLT model. The collapse of shells inside the zero-velocity surface collapse earlier when adding the angular momentum, and dynamical friction term. After solving the equation of motion, we got the relationships between mass, M, and the turn-around radius \({{R}_{0}}\), similar to those obtained for the SLT model by [40], and for the MLT model by [46, 47]. The relationships show, for a given \({{R}_{0}}\), a larger mass of the perturbation when angular momentum, and dynamical friction are taken into account. If one can obtain by some method the value of the turn-around, these relations show that the perturbation mass is 71% (JLT model), and two times larger (J\(\eta \)LT model) with respect to the SLT model. We see that moving from the simple spherical collapse to that accounting angular momentum and dynamical friction the acquired mass increases. Then, we showed how angular momentum, and dynamical friction changes the threshold of collapse with mass, and also with redshift for different dark energy models. We repeated the calculation for the virial overdensity, and the mass function, founding noteworthy differences with the case of the simple spherical collapse.