INTRODUCTION

The excitation of small magnetic particles by an external alternating field is a highly sensitive method for both the micro- or nanorheological analysis [1–4] and the remote monitoring of the displacement/distribution of such particles in drug therapy [5–7] or magnetic resonance tomography. In both above-mentioned cases, the external action (field amplitude) is maintained at a low level to avoid the influence of the arising energy dissipation on the properties of both the particles and an ambient medium. In this connection, the considered situations differ from the case of magnetic hyperthermia, in which the generation of excess heat is the key factor.

The simplest method for monitoring the response of particles to an imposed field is the measurement of the linear magnetic susceptibility; however, this approach is neither the only nor the optimal one from the viewpoint of accuracy. The use of the nonlinear magnetic response, even a relatively weak one, has a number of important advantages and does not create substantial technical difficulties. For example, the measurements of the nonlinear susceptibility make it possible to find and visualize the distribution of nanoparticles in a living tissue [8–10]. In numerous cases, when a medium, the microrheology of which is measured, is rather transparent, these properties of the medium may be determined by recording the dynamic birefringence induced by the forced rotation of anisometric probe particles. The efficiency of this method for fluids with a simple (Newtonian) rheology has been convincingly proven previously [11–13].

Magnetic response of an ensemble of identical single-domain particles suspended in a liquid medium is generated under the joint action of two factors: (1) imposed field H, which orients magnetic particle moments along its direction and (2) the Brownian rotational diffusion of the particles, which hinders this orientation. Under these conditions and provided that the interparticle interaction may be ignored, equilibrium magnetization curve M(H) of a system is described by the Langevin law irrespective of the medium rheology. However, the viscoelasticity of a medium manifests itself upon dynamic probing, when the angle of particle rotation under the action of an alternating field is governed by the joint action of the instantaneous elasticity and viscous retardation. It is this situation that is considered in this work.

MODEL

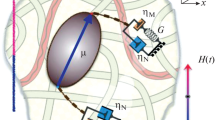
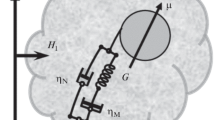
The orientational motion of a nanoparticle immersed in a viscoelastic medium is theoretically described on the basis of Jeffry’s model [14, 15]. This choice is predetermined by the simplicity and reliability of the aforementioned rheological scheme: it enables one to adequately pass from the macroscopic to the stochastic (Brownian) dynamics of a particle without encountering artifacts inherent in the Maxwell viscoelastic model [16, 17]. In Jeffry’s model (see Fig. 1), a viscoelastic medium is represented by a “hybrid” of two fluids, i.e., Newtonian and Maxwellian ones; therefore three phenomenological parameters, which characterize the medium, have clear qualitative meanings.

Fig. 1.
figure 1

Schematic representation of mechanical interaction between a particle and a viscoelastic matrix according to Jeffry’s model.

Full size image

Viscosity coefficient \({{{{\eta }}}_{{\text{N}}}}\) is commonly related to the low-molecular-weight (Newtonian) component of a Jeffry’s fluid, while coefficient \({{{{\eta }}}_{{\text{M}}}}\) is attributed to its high-molecular-weight (Maxwellian) component. It follows from natural condition \({{{{\eta }}}_{{\text{N}}}} \ll {{{{\eta }}}_{{\text{M}}}}\) that the response of a particle to an external action is a combination of the fast and slow components with greatly different response times. Elasticity modulus \(G\) (see Fig. 1) characterizes the elasticity of a polymer network of entanglements, while coefficient \({{{{\eta }}}_{{\text{M}}}}\) reflects the irreversible deformation of the network.

LANGEVIN AND FOKKER–PLANCK EQUATIONS

The set of equations describing the orientational motion of a Brownian particle in a Jeffry’s fluid with no account of inertia has the following form [17, 18]:

$$\begin{gathered} {\mathbf{\dot {e}}} = \left( {{\mathbf{\Omega }} \times {\mathbf{e}}} \right), \\ {\mathbf{\Omega }} = \frac{1}{{{{\zeta }_{N}}}}\left[ { - {\mathbf{\hat {L}}}E + {\mathbf{Q}} + {{{\mathbf{y}}}_{{\text{N}}}}\left( t \right)} \right],\,\,\,\,{\mathbf{\hat {L}}} = \left( {{\mathbf{e}} \times \frac{\partial }{{\partial e}}} \right), \\ \left( {1 + {{\tau }_{{\text{M}}}}\frac{\partial }{{\partial t}}} \right)Q = - {{\zeta }_{{\text{M}}}}{\mathbf{\Omega }} + {{{\mathbf{y}}}_{{\text{N}}}}\left( t \right),\,\,\,\,{{\tau }_{{\text{M}}}} = {{{{\zeta }_{{\text{M}}}}} \mathord{\left/ {\vphantom {{{{\zeta }_{{\text{M}}}}} K}} \right. \kern-0em} K}. \\ \end{gathered} $$
(1)

Here, \({\mathbf{e}}\) is the unit vector of particle orientation, Ω is the angular velocity, \(E\) is the energy of particle interaction with a field, \({\mathbf{\hat {L}}}\) is the operator of an infinitely small rotation, and the standard denotation is used for the vector products. Medium response coefficients are preset by expressions that are standard for microrheology [19]:

$${{\zeta }_{\alpha }} = 6{{\eta }_{\alpha }}V,\,\,\,\,K = 6GV,\,\,\,\,\alpha = {\text{N}},{\text{M}},$$

where \(G\) is the dynamic elasticity modulus, \({{\eta }_{\alpha }}\) is the Newtonian \(\left( {\alpha = {\text{N}}} \right)\) or Maxwellian \(\left( {\alpha = {\text{M}}} \right)\) viscosity, and \(V\) is the hydrodynamic particle volume. According to the fluctuation-dissipative theorem, random forces that simulate the thermal noise in a system are determined by the following correlation relations [17, 18]:

$$\left\langle {{{y}_{{i\alpha }}}\left( t \right){{y}_{{j\beta }}}\left( {t + \tau } \right)} \right\rangle = 2T{{\zeta }_{\alpha }}{{\delta }_{{\alpha \beta }}}{{\delta }_{{ij}}}\delta \left( \tau \right),$$
(2)

here and below, temperature \(T\) is measured in the energy units \(\left( {{{k}_{{\text{B}}}} = 1} \right).\)

In set of equations (1), the \({\mathbf{Q}}\) value has the meaning of the moment of forces applied to a particle from the side of a dynamic quasi-network, in which \({{\tau }_{{\text{M}}}}\) is the average lifetime of a node (entanglement). Thus, phase variable \({\mathbf{Q}}\) simulates the retarded response of the medium.

In the considered model, which is schematically represented in Fig. 1, the mechanisms of the retarded and ordinary viscous friction, which results from the dissipative interaction of the particle with the low-molecular-weight component of the medium, act in parallel. Therefore, the gel (equilibrium network in a good solvent) may be considered as the limiting case of Jeffry’s model at \({{\tau }_{{\text{M}}}} \to \infty .\) In the aforementioned limiting case, the equation for the retarded moment of friction forces is reduced to \({\mathbf{\dot {Q}}} = - K{\mathbf{\Omega }},\) i.e., the response of the high-molecular-weight component of the medium becomes purely elastic. In the case of the planar rotation of a particle, Eqs. (1) for this reduced system are simplified and yield the unidimensional Kelvin model. The Brownian motion of a particle in this situation has been considered in [20].

Set of stochastic equations (1) is consistent with the Fokker–Planck kinetic equation (FPE) for orientational distribution function \(W\left( {{\mathbf{e}},{\mathbf{Q}},t} \right),\) which is derived by the standard procedure (see, e.g., [18, 21]):

$$\begin{gathered} \frac{\partial }{{\partial t}}W = \left[ {\frac{1}{{{{\zeta }_{{\text{N}}}}}}\left( {{\mathbf{\hat {L}}} - \frac{\partial }{{\partial {\mathbf{Q}}}}} \right)W\left( {{\mathbf{\hat {L}}} - \frac{\partial }{{\partial {\mathbf{Q}}}}} \right) + \frac{1}{{{{\zeta }_{{\text{M}}}}}}\frac{\partial }{{\partial {\mathbf{Q}}}}W\frac{\partial }{{\partial {\mathbf{Q}}}}} \right] \\ \times \,\,\left[ {E\left( {\mathbf{e}} \right) + \frac{1}{2}K{{Q}^{2}} + T{\text{ln}}W} \right]. \\ \end{gathered} $$

Here and below, we use phase variable \({\mathbf{Q}}\) in the dimensionless form; i.e., we perform the \({\mathbf{Q}} \to K{\mathbf{Q}}\) replacement in initial set of equations (1). It follows from the structure of FPE that its stationary (equilibrium) solution is the generalized Boltzmann distribution:

$${{W}_{0}}\left( {{\mathbf{e}},{\mathbf{Q}}} \right)\sim {\text{exp}}\left[ { - \frac{1}{T}\left( {E\left( {\mathbf{e}} \right) + \frac{1}{2}K{{Q}^{2}}} \right)} \right].$$
(3)

Expression (3) shows that, in the absence of a field \(\left( {E = 0} \right)\), the equilibrium state of the system is isotropic, while, in a constant external field \(\left( {E \ne 0} \right)\), phase variables \({\mathbf{e}}\) and \({\mathbf{Q}}\) are statistically independent.

We assume that a model nanoparticle of a ferromagnetic has a rather high magnetic rigidity, so that its magnetic dipole moment \({\mathbf{\mu }}\) is immobilized (frozen-in) in the particle bulk; therefore, the energy of its interaction with the field has the standard form of the Zeeman orientational potential:

$$E\left( {{\mathbf{e}},{\mathbf{h}}} \right) = - {\mathbf{\mu H}} = - \mu H\left( {{\mathbf{eh}}} \right),\,\,\,\,{\mathbf{h}} = \left( {0,0,1} \right).$$
(4)

To calculate the system response to probe field \(H\left( t \right)\), we average stochastic Eqs. (1) over a statistical ensemble. After the substitution of the explicit form of the potential of particle interaction with the field, set (1) is transformed as follows:

$$\begin{gathered} {\mathbf{\dot {e}}} = {{\gamma }_{{\text{H}}}}\left( {{\mathbf{e}} \times \left( {{\mathbf{h}} \times {\mathbf{e}}} \right)} \right) + {{\gamma }_{{\text{N}}}}\left( {{\mathbf{Q}} \times {\mathbf{e}}} \right) + \left( {{\mathbf{u}} \times {\mathbf{e}}} \right), \\ {\mathbf{u}} = {{{{{\mathbf{y}}}_{{\text{N}}}}\left( t \right)} \mathord{\left/ {\vphantom {{{{{\mathbf{y}}}_{{\text{N}}}}\left( t \right)} {{{\zeta }_{{\text{N}}}}}}} \right. \kern-0em} {{{\zeta }_{{\text{N}}}}}},\,\,\,\,{\mathbf{\dot {Q}}} + {{\tilde {\gamma }}}{\mathbf{Q}} = - {{\gamma }_{{\text{H}}}}\left( {{\mathbf{e}} \times {\mathbf{h}}} \right) + {\mathbf{\tilde {u}}}, \\ {\mathbf{\tilde {u}}} = {{{{{\mathbf{y}}}_{{\text{M}}}}\left( t \right)} \mathord{\left/ {\vphantom {{{{{\mathbf{y}}}_{{\text{M}}}}\left( t \right)} {{{\zeta }_{{\text{M}}}}}}} \right. \kern-0em} {{{\zeta }_{{\text{M}}}}}} - {\mathbf{u}},\,\,\,\,{{\gamma }_{{\text{H}}}} = {{\mu H} \mathord{\left/ {\vphantom {{\mu H} {{{\zeta }_{{\text{N}}}}}}} \right. \kern-0em} {{{\zeta }_{{\text{N}}}}}}, \\ {{\gamma }_{\alpha }} = {K \mathord{\left/ {\vphantom {K {{{\zeta }_{\alpha }}}}} \right. \kern-0em} {{{\zeta }_{\alpha }}}},\,\,\,\,\tilde {\gamma } = {{\gamma }_{{\text{N}}}} + {{\gamma }_{{\text{M}}}} = {{\gamma }_{{\text{N}}}}\left( {1 + {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0em} q}} \right), \\ q = {{{{\eta }_{{\text{M}}}}} \mathord{\left/ {\vphantom {{{{\eta }_{{\text{M}}}}} {{{\eta }_{{\text{N}}}}}}} \right. \kern-0em} {{{\eta }_{{\text{N}}}}}}. \\ \end{gathered} $$
(5)

The correlation functions of the random forces involved in this system are determined by relation (2).

EQUILIBRIUM STATE

After the substitution of the Zeeman potential, equilibrium distribution function (3) acquires the following form:

$$\begin{gathered} {{W}_{0}}\left( {{\mathbf{e}},{\mathbf{Q}}} \right) = \frac{1}{Z}\left[ {\xi \left( {{\mathbf{eh}}} \right) - \frac{{{{Q}^{2}}}}{{2\tilde {T}}}} \right],\,\,\,\,Z = {{Z}_{\xi }}{{Z}_{Q}}, \\ {{Z}_{\xi }} = 2\pi \int\limits_{ - 1}^1 {dx~{\text{exp}}\left( {\xi x} \right)} = 4\pi {\text{sinh}}\xi {{\;}}, \\ {{Z}_{Q}} = \int {d{\mathbf{Q}}{\text{exp}}\left( {{{ - {{Q}^{2}}} \mathord{\left/ {\vphantom {{ - {{Q}^{2}}} {2\tilde {T}}}} \right. \kern-0em} {2\tilde {T}}}} \right)} = {{\left( {2\pi \tilde {T}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $$
(6)

where the last integral is calculated over all absolute values and directions of vector \({\mathbf{Q}}.\) In Eqs. (6), denotations \(\xi = {{\mu H} \mathord{\left/ {\vphantom {{\mu H} T}} \right. \kern-0em} T}\) and \(\tilde {T} = {T \mathord{\left/ {\vphantom {T K}} \right. \kern-0em} K}\) have been used for the dimensionless field strength and dimensionless temperature, respectively. In a weak field \(\left( {\xi \ll 1} \right)\) the equilibrium statistical moments of the orientational distribution function are expressed by the following relations:

$$\begin{gathered} {{\left\langle {{{{\left( {{\mathbf{eh}}} \right)}}^{{\left( n \right)}}}} \right\rangle }_{0}} \equiv {{\left\langle {e_{z}^{{\left( n \right)}}} \right\rangle }_{0}} \\ \cong \left\{ \begin{gathered} \frac{\xi }{{2k + 3}}\left[ {1 - \frac{{{{\xi }^{2}}}}{{3\left( {2k + 5} \right)}}} \right],\,\,\,\,~n = 2k + 1 \hfill \\ \frac{1}{{2k + 1}}\left[ {1 + \frac{{2{{\xi }^{2}}}}{{3\left( {2k + 3} \right)}}} \right],\,\,\,\,n = 2k.~ \hfill \\ \end{gathered} \right. \\ \end{gathered} $$
(7)

The pattern of functions (3) and (6) shows that the distribution of phase variable \({\mathbf{Q}}\) remains to be isotropic even in a constant field; therefore, all odd equilibrium statistical moments of this value vanish, while the even moments may be represented as

$$\begin{gathered} {{\left\langle {{{Q}^{{2n}}}} \right\rangle }_{0}} = Z_{Q}^{{ - 1}}\int {{{d}^{3}}{\mathbf{Q}}{{\;}}{{Q}^{{2n}}}} {\text{exp}}\left( {{{ - {{Q}^{2}}} \mathord{\left/ {\vphantom {{ - {{Q}^{2}}} {2\tilde {T}}}} \right. \kern-0em} {2\tilde {T}}}} \right) \\ = {{\left( {\tilde {T}} \right)}^{n}}\left( {2n + 1} \right)!!,\,\,\,\,{{\left\langle {Q_{x}^{{2n}}} \right\rangle }_{0}} = {{\left\langle {Q_{y}^{{2n}}} \right\rangle }_{0}} \\ = {{\left\langle {Q_{z}^{{2n}}} \right\rangle }_{0}} = {{\left( {\tilde {T}} \right)}^{n}}\left( {2n - 1} \right)!!. \\ \end{gathered} $$

In an ensemble of identical nanoparticles that do not interact with each other, magnetization is determined by their number concentration \({{\nu }}\) and the value of the projection of the total magnetic moment of unit volume onto the direction of the imposed field. In this work, we consider the system response to a weak probe field \(\left( {\xi \ll 1} \right)\) and take into account only main nonlinear contribution

$$M = \nu \left\langle {{\mathbf{\mu h}}} \right\rangle = \nu \mu \left\langle {{{e}_{z}}} \right\rangle = {{\chi }^{{(1)}}}H + {{\chi }^{{(3)}}}{{H}^{3}}.$$
(8)

Here, \({{\chi }^{{(1)}}}\) and \({{\chi }^{{(3)}}}~\) are the linear and cubic susceptibilities of the ferrocolloid, respectively. Their static values are found with the help of distribution (6):

$$\chi _{0}^{{(1)}} = \frac{{\nu {{\mu }^{2}}}}{{3T}},\,\,\,\,\chi _{0}^{{(3)}} = - \frac{{\nu {{\mu }^{4}}}}{{45{{T}^{3}}}}.$$
(9)

When nanoparticles have an anisotropic shape, their orientation by a field provides a colloid with an optical anisotropy. This effect is caused by different dielectric permittivities of the particles and the medium [22]. The optical anisotropy of the system manifests itself as the birefringence and is characterized by difference \({{\Delta }}n = {{n}_{{\text{e}}}} - {{n}_{{\text{o}}}}\) between the refractive indices of the extraordinary and ordinary rays, i.e., optical waves polarized in parallel and perpendicularly to direction \({\mathbf{h}}\) of an imposed field, respectively. Under the small perturbation approximation, the \({{\Delta }}n\) value of the considered system is proportional to the quadrupole parameter of the orientational order of particles. For the static case, expression (3) yields

$${{\Delta }}n \propto {{\left\langle {e_{z}^{2}} \right\rangle }_{0}} - \frac{1}{3} = \frac{2}{{45}}{{\xi }^{2}} = \frac{2}{{45}}\frac{{{{\mu }^{2}}}}{{{{T}^{2}}}}{{H}^{2}}.$$
(10)

NONEQUILIBRIUM DISTRIBUTION UNDER THE MEAN FIELD APPROXIMATION

Equations for the dynamics of the observed values are derived via the standard procedure [21] by averaging set of Langevin’s equations (1) with the nonequilibrium \(W\left( {{\mathbf{e}},{\mathbf{Q}},t} \right)\) distribution function. It is easily seen that this derivation yields an infinite chain of equations, which relates the statistical moments of increasing orders to each other. In [23, 24], the total functional basis was found for the W istribution function. This finding made it possible to formulate a convenient algorithm for the exact calculation of the statistical moments. Thus, the infinite chain of equations was solved, and linear dynamic susceptibility \({{\chi }^{{(1)}}}\left( \omega \right)\) was completely determined.

Unfortunately, the functional basis found in [23, 24] can be used for calculating the orientational averages of only the first order with respect to the amplitude of an imposed field; however, the \(\left\langle {e_{z}^{2}} \right\rangle \left( t \right)\) and \(\left\langle {e_{z}^{3}} \right\rangle \left( t \right)\) functions cannot be analytically calculated. In this work, the aforementioned values are calculated using a simplified approach, namely, the so-called effective field approximation [25, 26], which makes rather easy to close the set of equations for the moments of the nonequilibrium \(W\left( {{\mathbf{e}},{\mathbf{Q}},t} \right)\) distribution function. On the basis of our experience in comparing between the exact and approximate calculations of the linear dynamic susceptibility [23, 24], we assume that the approximations obtained for the nonlinear susceptibilities by the effective field method will not differ too greatly from the exact characteristics of the studied system.

The procedure of the effective field method implies the expansion of the nonequilibrium distribution function in terms of the minimum sufficient number of basis functions, which we shall represent in a coordinate system where the Oz axis is parallel to the direction of the imposed field (see Eq. (4)). It follows from the analysis of Eqs. (1) that, to take into account the viscoelasticity, along with phase variables \({{e}_{z}}\) and \(e_{z}^{2},\) functions of the first order with respect to the moment of retarded friction forces \({{P}_{z}} = {{\left( {{\mathbf{Q}} \times {\mathbf{e}}} \right)}_{z}}\) and \({{e}_{z}}{{P}_{z}}\) must be introduced into such functional basis.

Using the aforementioned set of the functions, the approximate solution of FPE (5) is represented in the following form:

$$\begin{gathered} W\left( {{\mathbf{e}},{\mathbf{Q}},t} \right) = {{W}_{0}}\left( {{\mathbf{e}},{\mathbf{Q}}} \right) \\ \times \,\,\left[ {1 + a(t){{e}_{z}} + b(t){{P}_{z}} + c(t)\left( {e_{z}^{2} - \frac{1}{3}} \right) + f(t){\kern 1pt} {{e}_{z}}{{P}_{z}}} \right]. \\ \end{gathered} $$
(11)

The basis functions used here satisfy normalization condition \(\left\langle 1 \right\rangle = {{\left\langle 1 \right\rangle }_{0}}\) and are mutually orthogonal: \(\left\langle {{{e}_{z}}\left( {e_{z}^{2} - \frac{1}{3}} \right)} \right\rangle = \left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle = 0.\) The relation between time-dependent coefficients \(a,\) \(b,\) \(c,\) and \(f\) and nonequilibrium average values of the basis functions is found by averaging the latter with distribution (11). This leads to the following relations:

$$\begin{gathered} \left\langle {{{e}_{z}}} \right\rangle = a{{\left\langle {e_{z}^{2}} \right\rangle }_{0}} = \frac{1}{3}a,\,\,\,\,\left\langle {{{P}_{z}}} \right\rangle = b{{\left\langle {P_{z}^{2}} \right\rangle }_{0}} = \frac{2}{3}b\tilde {T}, \\ \left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle = c{{\left\langle {{{{\left( {e_{z}^{2} - \frac{1}{3}} \right)}}^{2}}} \right\rangle }_{0}} = \frac{4}{{45}}c, \\ ~\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle = f{{\left\langle {{{{\left( {{{e}_{z}}{{P}_{z}}} \right)}}^{2}}} \right\rangle }_{0}} = \frac{2}{{15}}f\tilde {T}. \\ \end{gathered} $$
(12)

SET OF MOMENT EQUATIONS

Let us first consider the equation for the average (observed) magnetic moment vector. The formal averaging of the first equation in set (5) yields

$$\frac{\partial }{{\partial t}}\left\langle {\mathbf{e}} \right\rangle = {{\gamma }_{{\text{H}}}}\left\langle {\left( {{\mathbf{e}} \times \left( {{\mathbf{h}} \times {\mathbf{e}}} \right)} \right)} \right\rangle + {{\gamma }_{{\text{N}}}}\left\langle {\left( {{\mathbf{Q}} \times {\mathbf{e}}} \right)} \right\rangle + \left\langle {\left( {{\mathbf{u}} \times {\mathbf{e}}} \right)} \right\rangle .$$

The last term in the right-hand side determines the contribution of the rotational diffusion and is calculated by the following method [17, 21, 27]. Since the sought expression comprises a random function, the result is determined only by the singular (proportional to the random force) part of the solution of Eq. (5):

$$\delta {\mathbf{e}}(t) = \hat {I}\left( {{\mathbf{u}}{\kern 1pt} '\, \times {\mathbf{e}}{\kern 1pt} '} \right) \equiv \mathop {\lim }\limits_{\varepsilon \to 0} \int\limits_{t - \varepsilon }^t {dt{\kern 1pt} '\left( {{\mathbf{u}}\left( {t{\kern 1pt} '} \right) \times {\mathbf{e}}\left( {t{\kern 1pt} '} \right)} \right){\kern 1pt} } .$$
(13)

This relation expresses the causality principle, according to which, the current state of a physical system depends only on previous actions. After the term comprising the random force is averaged with the help of definition (13) and correlation expressions (2) are used, the motion equation for the projection of vector \(\left\langle {\mathbf{e}} \right\rangle \) acquires the form of

$$\begin{gathered} \left( {\frac{\partial }{{\partial t}} + {{\gamma }_{{\text{D}}}}} \right)\left\langle {{{e}_{z}}} \right\rangle = {{\gamma }_{{\text{H}}}}\left[ {\frac{2}{3} - \left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle } \right] + {{\gamma }_{{\text{N}}}}\left\langle {{{P}_{z}}} \right\rangle , \\ {{\gamma }_{{\text{D}}}} = \frac{1}{{{{\tau }_{{\text{D}}}}}}, \\ \end{gathered} $$
(14)

where the second basis function, i.e., the orientational order parameter, has appeared in the right-hand side. Here, \({{\tau }_{{\text{D}}}} = {{{{\zeta }_{{\text{N}}}}} \mathord{\left/ {\vphantom {{{{\zeta }_{{\text{N}}}}} {2T}}} \right. \kern-0em} {2T}}\) is the known Debye time of the Brownian rotational diffusion for a spherical particle in a Newtonian fluid with viscosity \({{\eta }_{{\text{N}}}}.\)

The equation derived for statistical moment \(\left\langle {{{P}_{z}}} \right\rangle ,\) from set (5) acquires the following form:

$$\begin{gathered} \frac{\partial }{{\partial t}}\left\langle {{{P}_{z}}} \right\rangle = \left\langle {{{{\left( {{\mathbf{\dot {Q}}} \times {\mathbf{e}}} \right)}}_{z}} + {{{\left( {{\mathbf{Q}} \times {\mathbf{\dot {e}}}} \right)}}_{z}}} \right\rangle \\ = {{\gamma }_{{\text{H}}}}\left[ {\left\langle {{{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{e}} \times \left( {{\mathbf{h}} \times {\mathbf{e}}} \right)} \right)} \right)}}_{z}}} \right\rangle - \left\langle {{{{\left( {{\mathbf{e}} \times \left( {{\mathbf{h}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle } \right] \\ + \,\,~{{\gamma }_{{\text{N}}}}\left\langle {{{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{Q}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle + \left\langle {{{{\left( {{\mathbf{\tilde {u}}} \times {\mathbf{e}}} \right)}}_{z}}} \right\rangle + \left\langle {{{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{u}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle . \\ \end{gathered} $$
(15)

Let us initially find its diffusion component, which is governed by the action of random forces:

$$\begin{gathered} \left\langle {{{{\left( {{\mathbf{\tilde {u}}} \times {\mathbf{e}}} \right)}}_{z}} + {{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{u}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle \\ = \hat {I}\left\langle {2{{{\left[ {{\mathbf{u}}{\kern 1pt} '\left( {{\mathbf{\tilde {u}e}}{\kern 1pt} '} \right) - {\mathbf{e}}{\kern 1pt} '\left( {{\mathbf{\tilde {u}u}}} \right)} \right]}}_{z}}} \right. \\ \left. { + \,\,{{{\left( {{\mathbf{Q}} \times \left[ {{\mathbf{u}}{\kern 1pt} '\left( {{\mathbf{ue}}{\kern 1pt} '} \right) - {\mathbf{e}}{\kern 1pt} '\left( {{\mathbf{uu}}{\kern 1pt} '} \right)} \right]} \right)}}_{z}}} \right\rangle = {{\gamma }_{{\text{D}}}}\left[ {2\left\langle {{{e}_{z}}} \right\rangle - \left\langle {{{P}_{z}}} \right\rangle } \right]. \\ \end{gathered} $$

Here procedure (12) has been used for calculating the singular part of the values averaged together with the random force, and relation \(\hat {\delta }Q\left( t \right) = \hat {I}\left( {{\mathbf{\tilde {u}}}{\kern 1pt} '} \right)\) = \(\mathop {\lim }\limits_{\varepsilon \to 0} \int_{t - \varepsilon }^t {dt{\kern 1pt} '{\mathbf{\tilde {u}}}\left( {t{\kern 1pt} '} \right)} .\) Has been taken into account.

The calculation of the moment that is quadratic with respect to \({\mathbf{Q}}\) and has distribution (11) gives

$$\begin{gathered} \left\langle {{{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{Q}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle = a{{\left\langle {{{e}_{z}}\left[ {{{Q}_{z}}\left( {{\mathbf{eQ}}} \right) - {{e}_{z}}{{{\mathbf{Q}}}^{2}}} \right]} \right\rangle }_{0}} \\ = a{{\left\langle {e_{z}^{2}\left( {Q_{z}^{2} - {{Q}^{2}}} \right)} \right\rangle }_{0}} = - \frac{2}{3}a\tilde {T} = - 2\tilde {T}\left\langle {{{e}_{z}}} \right\rangle , \\ \end{gathered} $$
(16)

and this result makes it possible to close the set of the moment equations with respect to variable \({\mathbf{Q}}.\) Indeed, taking into account relation (16), Eq. (14) is transformed into the form that contains only averages of the basis functions of effective field approximation (11):

$$\begin{gathered} \left( {\frac{\partial }{{\partial t}} + {{\gamma }_{{\text{D}}}} + \tilde {\gamma }} \right)\left\langle {{{P}_{z}}} \right\rangle \\ = {{\gamma }_{{\text{H}}}}\left( { - \frac{2}{3} + \left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle - \left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle } \right) + {{\gamma }_{{\text{D}}}}\left\langle {{{e}_{z}}} \right\rangle . \\ \end{gathered} $$
(17)

Dynamic equations for moments \(\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle \) and \(\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle \) are obtained in a similar way.

As a result, the total closed set of the moment equations has the following form:

$$\begin{gathered} \left( {1 + \frac{\partial }{{\partial t}}} \right)\left\langle {{{e}_{z}}} \right\rangle = \frac{1}{3}\xi \left( t \right)\left[ {1 - \frac{3}{2}\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle } \right] + \beta \left\langle {{{P}_{z}}} \right\rangle , \\ \left( {1 + \tilde {\beta } + \frac{\partial }{{\partial t}}} \right)\left\langle {{{P}_{z}}} \right\rangle = - \frac{1}{3}\xi \left( t \right) \\ \times \,\,\left[ {1 - \frac{3}{2}\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle + \frac{3}{2}\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle } \right] + \left\langle {{{e}_{z}}} \right\rangle ,\,\,\,\,\left( {3 + \frac{\partial }{{\partial t}}} \right)\left\langle {e_{z}^{2}} \right. \\ \left. { - \,\,\frac{1}{3}} \right\rangle = \frac{2}{5}\xi \left( t \right)\left\langle {{{e}_{z}}} \right\rangle + 2\beta \left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle ,\,\,\,\,\left( {3 + \tilde {\beta } + \frac{\partial }{{\partial t}}} \right)\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle \\ = \frac{1}{5}\xi \left( t \right)\left[ { - \left\langle {{{e}_{z}}} \right\rangle + \frac{3}{2}\left\langle {{{P}_{z}}} \right\rangle } \right] + \frac{3}{2}\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle , \\ \beta = {K \mathord{\left/ {\vphantom {K {2T}}} \right. \kern-0em} {2T}},\,\,\,\,\tilde {\beta } = \beta \left( {{{1 + 1} \mathord{\left/ {\vphantom {{1 + 1} q}} \right. \kern-0em} q}} \right). \\ \end{gathered} $$
(18)

Here, dimensionless time measured in the units of Debye time \({{\tau }_{{\text{D}}}}\) has been introduced. The solution of set (18) in the static limiting case (\({\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}} = 0\)) is specified by Eqs. (9) and (10).

DYNAMIC SUSCEPTIBILITIES

Let us find the first three harmonics of the system response to the probe field:

$$\xi \left( t \right) = {{\xi }_{0}}\cos \omega t = \frac{1}{2}{{\xi }_{0}}\left[ {{\text{exp}}\left( { - i\omega t} \right) + {\text{c}}.{\text{c}}.} \right].$$

The desired functions will be searched for as expansions in terms of the small parameter, which is, in this case, amplitude \({{\xi }_{0}}\) of the alternating field. For example, the averaged projection of the magnetic moment is represented as

$$\begin{gathered} \left\langle {{{e}_{z}}} \right\rangle = \frac{1}{2}{{\xi }_{0}}\left[ {A_{\omega }^{{\left( 1 \right)}}{\text{exp}}\left( { - i\omega t} \right) + {\text{c}}.{\text{c}}.} \right] \\ + \,\,\frac{1}{8}\xi _{0}^{3}\left[ {A_{{3\omega }}^{{\left( 3 \right)}}{\text{exp}}\left( { - 3i\omega t} \right) + {\text{c}}.{\text{c}}.} \right], \\ \end{gathered} $$
(19)

moment \(\left\langle {{{P}_{z}}} \right\rangle \) will also have a similar form. It follows from set (18) that orientational parameter \(\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle \) and moment \(\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle \) appear in the second order with respect to \(\xi .\) Thus, these values will contain a constant component and harmonic \(2\omega .\) The substitution of such expressions into set of differential equations (18) reduces it to an algebraic problem, the solution of which in the first order of smallness with respect to the expansion parameter leads to the result reported in [24]:

$$\begin{gathered} \tilde {\chi }_{\omega }^{{(1)}}\left( \omega \right) = \frac{{\chi _{\omega }^{{(1)}}}}{{\chi _{0}^{{(1)}}}} = \frac{1}{{1 - ix\left( {1{{\;}} + {{\;}}\frac{\beta }{{{{1 + \beta } \mathord{\left/ {\vphantom {{1 + \beta } {q - ix}}} \right. \kern-0em} {q - ix}}}}} \right)}}, \\ x \equiv \omega {{\tau }_{{\text{D}}}}, \\ \end{gathered} $$
(20)

here the static susceptibility is specified by relation (9), and the time dimensionality has been restored.

Using expression (19) and an analogous first approximation for moment \(\left\langle {{{P}_{z}}} \right\rangle ,\) we, from set (18), obtain an algebraic set for determining the complex amplitudes of the second harmonics of the orientational order parameter and moment \(\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle .\) The solution of this problem is as follows:

$$\begin{gathered} \tilde {\chi }_{{2\omega }}^{{(2)}} \equiv \frac{{\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle _{{2\omega }}^{{(2)}}}}{{\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle _{0}^{{(2)}}}} \\ = \tilde {\chi }_{\omega }^{{(1)}}\frac{{1 + \frac{{i\beta x}}{{2\left( {1 + \frac{\beta }{q} - ix} \right)\left( {1 + \frac{\beta }{{3q}} - {{2ix} \mathord{\left/ {\vphantom {{2ix} 3}} \right. \kern-0em} 3}} \right)}}}}{{1 - \frac{{2ix}}{3}\left( {1 + \frac{{{\beta \mathord{\left/ {\vphantom {\beta 3}} \right. \kern-0em} 3}}}{{1 + {{\;}}\frac{\beta }{{3q}} - {{~2ix} \mathord{\left/ {\vphantom {{~2ix} 3}} \right. \kern-0em} 3}}}} \right)}}{\kern 1pt} , \\ \tilde {s}_{{2\omega }}^{{(2)}} \equiv \frac{{\left\langle {P_{z}^{2}} \right\rangle _{{2\omega }}^{{(2)}}}}{{\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle _{0}^{{(2)}}}} = ix\tilde {\chi }_{\omega }^{{(1)}}\frac{{\frac{1}{{3 - 2ix~}} + \frac{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}{{1 + {\beta \mathord{\left/ {\vphantom {\beta {q - ix}}} \right. \kern-0em} {q - ix}}}}}}{{1 + \frac{\beta }{{3q}} - \frac{{2ix}}{3}\left( {1 + {{\;}}\frac{{{\beta \mathord{\left/ {\vphantom {\beta 3}} \right. \kern-0em} 3}}}{{{{1 - 2ix} \mathord{\left/ {\vphantom {{1 - 2ix} 3}} \right. \kern-0em} 3}}}} \right)}}. \\ \end{gathered} $$
(21)

Note that, in the second order, the dynamic magnetic susceptibility vanishes for the reasons of symmetry (see Eq. (19)).

Using Eqs. (21), we, from Eqs. (18), obtain an algebraic set for calculating the amplitude of the dynamic magnetic susceptibility at frequency \(3\omega .\) Solving this set, we, after standard calculations, obtain

$$\tilde {\chi }_{{3\omega }}^{{(3)}} \equiv \frac{{\left\langle {{{e}_{z}}} \right\rangle _{{3\omega }}^{{(3)}}}}{{\left\langle {{{e}_{z}}} \right\rangle _{0}^{{(3)}}}} = \frac{{\tilde {\chi }_{{2\omega }}^{{(2)}} + ~\frac{{\beta \tilde {s}_{{2\omega }}^{{(2)}}}}{{{{1 + \beta } \mathord{\left/ {\vphantom {{1 + \beta } q}} \right. \kern-0em} q} - 3ix}}}}{{1 - 3ix\left( {1 + \frac{\beta }{{{{1 + \beta } \mathord{\left/ {\vphantom {{1 + \beta } q}} \right. \kern-0em} q} - 3ix}}} \right)}}.$$
(22)

Relations (20)–(22) allow us to analyze the frequency dependence of the magnetic susceptibility at the initial frequency of the signal and the threefold increased frequency, as well as the dependence of the birefringence signal at the doubled frequency. As might be expected, in the general case of a simple viscous fluid (\(\beta \to 0\)), i.e., in the absence of viscoelasticity, these equations are reduced to the corresponding expressions obtained previously (see, e.g., [26]).

The studied model is distinguished by the appearance of a low-frequency relaxation mode in the spectra of colloids having developed elasticity (\(q \gg \beta \gg 1\)). In this case, we may represent linear dynamic susceptibility (20) as the sum of two main relaxation modes, i.e., the “slow” and “fast” ones,

$$\begin{gathered} \tilde {\chi }_{\omega }^{{(1)}} \cong \frac{1}{{1 - i\beta \omega {{\tau }_{{\text{D}}}}}} + \frac{1}{\beta }\frac{1}{{1 - {{i\omega {{\tau }_{{\text{D}}}}} \mathord{\left/ {\vphantom {{i\omega {{\tau }_{{\text{D}}}}} \beta }} \right. \kern-0em} \beta }}} \\ = \frac{1}{{1 - i\omega {{\tau }_{{\text{s}}}}}} + \frac{1}{\beta }\frac{1}{{1 - i\omega {{\tau }_{{\text{f}}}}}}, \\ \end{gathered} $$
(23)

and, thereby, introduce two characteristic times:

$${{\tau }_{{\text{s}}}} = \beta {{\tau }_{{\text{D}}}} = \frac{{{{\zeta }_{{\text{N}}}}K}}{{4{{T}^{2}}}} = {{\left( {\frac{{3V}}{T}} \right)}^{2}}{{\eta }_{{\text{N}}}}G,\,\,\,\,{{\tau }_{{\text{f}}}} = \frac{{{{\tau }_{{\text{D}}}}}}{\beta } = \frac{{{{\eta }_{{\text{N}}}}}}{G}.$$
(24)

It is seen that, in the considered limiting case, the Maxwellian viscosity is absent in the expressions for the relaxation times. It should also be noted that, at any values of Jeffry’s model parameters, the root-mean-square values of times (24) are always equal to the Debye time: \(\sqrt {{{\tau }_{{\text{s}}}}{{\tau }_{{\text{f}}}}} = {{\tau }_{{\text{D}}}}.\)

Expression (23) describes the linear susceptibility in the range of elasticity parameter values \(q \gg \beta \gg 1,\) where the system passes from the regime of the fast nanoparticle diffusion, which is governed by viscosity \({{\eta }_{{\text{N}}}}\) of the low-molecular-weight solvent, to the regime of the slow diffusion determined by the viscoelasticity of the high-molecular-weight component. In the dimensional form, condition \(q \gg \beta \) acquires the form of \({{\tau }_{{\text{M}}}} \gg {{\tau }_{{\text{D}}}},\) which is always fulfilled for submicron particles in viscoelastic systems. It has been shown in [23] that, in spite of the small amplitude of the high-frequency component of the susceptibility, it makes the greatest contribution to the power of the electromagnetic radiation absorbed by the system. In our opinion, the applicability of the studied model may be reliably verified by an experimental confirmation of this fact. From the theoretical point of view, the argument for the existence of the high-frequency component of the susceptibility is quite obvious, because, in the athermic limiting case (\(T \to 0\)), such a mode is always present in the spectrum of an elastic system characterized by friction.

It is of interest that the characteristic relaxation times depend on the probe size. For example, Eq. (24) shows that slow relaxation time \({{\tau }_{{\text{s}}}}\) is proportional to the squared volume of a probe particle, while fast relaxation time \({{\tau }_{{\text{f}}}}\) is entirely determined by the rheological parameters of a medium.

In the regime of developed elasticity (\(q \gg \beta \gg 1\)) the expression for the complex amplitude of the second harmonic of the response is reduced to the following form:

$$\begin{gathered} \tilde {\chi }_{{2\omega }}^{{(2)}} \cong \frac{{{{1 + i\omega {{\tau }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{1 + i\omega {{\tau }_{{\text{s}}}}} 2}} \right. \kern-0em} 2}}}{{\left( {1 - i\omega {{\tau }_{{\text{s}}}}} \right)\left( {{{1 - 2i\omega {{\tau }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{1 - 2i\omega {{\tau }_{{\text{s}}}}} 9}} \right. \kern-0em} 9}} \right)}} \\ + \,\,\frac{3}{{{{\beta }^{2}}}}\frac{{{{1 + 3} \mathord{\left/ {\vphantom {{1 + 3} {i\omega {{\tau }_{{\text{f}}}}}}} \right. \kern-0em} {i\omega {{\tau }_{{\text{f}}}}}}}}{{\left( {1 - i\omega {{\tau }_{{\text{f}}}}} \right)\left( {1 - 2i\omega {{\tau }_{{\text{f}}}}} \right)}}. \\ \end{gathered} $$
(25)

This asymptotic expression distinctly attests to a low-frequency shift of the birefringence frequency spectrum with an increase in the system elasticity. It should also be noted that the high-frequency component of this response decreases with a growth of the elasticity parameter in accordance with the square law.

The aforementioned features are also observed in the spectrum of the cubic susceptibility, for which, the approximation equation in the limiting case of \(q \gg \beta \gg 1\) is as follows:

$$\begin{gathered} \tilde {\chi }_{{3\omega }}^{{(3)}} \cong \frac{{1 + \left( {{{19} \mathord{\left/ {\vphantom {{19} {12}}} \right. \kern-0em} {12}}} \right)i\omega {{\tau }_{{\text{s}}}}}}{{\left( {1 - i\omega {{\tau }_{{\text{s}}}}} \right)\left( {1 - 3i\omega {{\tau }_{{\text{s}}}}} \right)\left( {{{1 - 2i\omega {{\tau }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{1 - 2i\omega {{\tau }_{{\text{s}}}}} 9}} \right. \kern-0em} 9}} \right)}} \\ + \,\,\frac{3}{{{{\beta }^{3}}}}\frac{{1 + {7 \mathord{\left/ {\vphantom {7 6}} \right. \kern-0em} 6}i\omega {{\tau }_{{\text{f}}}}}}{{\left( {1 - i\omega {{\tau }_{{\text{f}}}}} \right)\left( {1 - 3i\omega {{\tau }_{{\text{f}}}}} \right)\left( {1 - 2i\omega {{\tau }_{{\text{f}}}}} \right)}}. \\ \end{gathered} $$
(26)

Figures 2a–2c show the plots of the real (dashed lines) and imaginary (solid lines) components of the linear, quadratic, and cubic susceptibilities, with all of them being normalized with respect to corresponding static values. The calculation was performed by Eqs. (20)–(22), while the numerical values of the parameters were calculatied according to the following scheme:

$$\begin{gathered} \beta = {{\beta }_{0}}w,\,\,\,\,{{\beta }_{0}} = 1,\,\,\,\,q = {{q}_{0}}{{w}^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}},\,\,\,\,{{q}_{0}} = 1000, \\ w = \left( {{\phi \mathord{\left/ {\vphantom {\phi {{{\phi }_{0}}}}} \right. \kern-0em} {{{\phi }_{0}}}}} \right) = 0.1,{{\;}}1,{{\;}}4,{{\;}}16. \\ \end{gathered} $$
(27)
Fig. 2.
figure 2

Frequency dependences of the imaginary (solid lines) and real (dashed lines) components of (a) linear, (b) quadratic, and (c) cubic dynamic magnetic susceptibilities for Jeffry’s ferrocolloid: elasticity parameter \(\beta \) is equal to (1) 0.1, (2) 1, (3) 4, and (4) 16 at \({{q}_{0}} = {{10}^{3}}\) (see Eqs. (27)).

Full size image

Here, \(\phi \) is the volume fraction of a polymer in a solution and \({{\phi }_{0}}\) is some value used to normalize the former. The aforementioned dependences of parameters \(\beta \) and \(q\) on \(\phi \) are clarified below in Eqs. (33).

DYNAMIC BIREFRINGENCE

Although the dynamic orientational effect (quadratic susceptibility \(\chi _{{2\omega }}^{{(2)}}\)) in a ferrocolloid is due to the response of a nanoparticle to an imposed field, it cannot be detected by magnetic measurements, because it has a quadrupole rather than dipole character. However, this effect can be directly observed in polarization-optical measurements, provided that a ferrocolloid contains anisometric particles. Indeed, \(\chi _{{2\omega }}^{{(2)}}\) is, in this situation, the only source of optical anisotropy, because the ferrocolloid is optically isotropic in the absence of an external field.

Let us consider the appearance of optical anisotropy in such a ferrocolloid, assuming that nanoparticles suspended in a Jeffry’s medium are somewhat anisotropic, e.g., their shape resembles oblong ellipsoids of revolution (spheroids). This assumption is often realized in practice and commonly attributed to the fact that dispersions of magnetic nanoparticles contain their aggregates represented by short (2–3 particles) chains. Since the dielectric permittivities of the particles and the liquid medium are different, the field-forced orientation of the particles leads to the induced birefringence. The orientational tensor of a particle ensemble is the dynamic variable responsible for this phenomenon. Since magnetic moments \({\mathbf{\mu }}\) are, in this model, assumed to be “frozen-in,” we take that vector \({\mathbf{\mu }}\) of each anisotropic particle is directed along the major axis of the spheroid due to the magnetostatic anisotropy of its shape. In this case, the degree of the orientational order in a particle ensemble may be conveniently characterized by parameter

$${{S}_{{ik}}} = \frac{3}{2}\left( {\left\langle {{{e}_{i}}{{e}_{k}}} \right\rangle - \frac{1}{3}{{\delta }_{{ik}}}} \right).$$
(28)

In an isotropic system, all diagonal components of this traceless tensor are vanished, while, in the case of the complete particle orientation, its diagonal component in the direction of the field is equal to unity.

Induced optical anisotropy, i.e., the refractive index difference between extraordinary and ordinary rays, in a particle ensemble is expressed by the following equation, provided that the particle volume concentration is not too high, and the characteristic particle size is smaller than incident light wavelength \(\lambda \):

$$\Delta n = {{n}_{{\text{e}}}} - {{n}_{{\text{o}}}} = {{n}_{0}}A{{\phi }_{{\text{p}}}}{{S}_{{ik}}}{{h}_{i}}{{h}_{k}},$$
(29)

where \({{n}_{0}}\) is the refractive index of the medium in the isotropic state (at \(H = 0\)), \(A\) is a coefficient that depends on the shape and relative dielectric conductivity of a particle at the incident light frequency, \({{\phi }_{{\text{p}}}}\) is the particle volume concentration in the colloid (it is assumed to be low), and \({\mathbf{h}} = \left( {0,0,1} \right)\) is the unit vector of the imposed magnetic field.

Using the second-order solution of set of Eqs. (18) in field \(\xi \left( t \right) = \xi \cos \omega t\), we obtain the following relation for determining the main component of orientational tensor (28):

$$\begin{gathered} {{S}_{{ik}}}{{h}_{i}}{{h}_{k}} = {{S}_{{zz}}}\left( t \right) = \frac{1}{{30}}\xi _{0}^{2} \\ \times \,\,\left[ {P\left( \omega \right) + {\text{Re}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)\cos 2\omega t + {\text{Im}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right){\text{sin}}2\omega t} \right] \\ = \frac{1}{{30}}\xi _{0}^{2}\left[ {P\left( \omega \right) + \left| {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right|{\text{cos}}\left( {2\omega t - \delta } \right)} \right], \\ \end{gathered} $$
(30)

where

$$\begin{gathered} \left| {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right| = \sqrt {{{{\left[ {{\text{Re}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)} \right]}}^{2}} + {{{\left[ {{\text{Im}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)} \right]}}^{2}}} , \\ \delta = {\text{arctan}}\left[ {{{{\text{Im}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)} \mathord{\left/ {\vphantom {{{\text{Im}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)} {{\text{Re}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)}}} \right. \kern-0em} {{\text{Re}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)}}} \right]. \\ \end{gathered} $$

In the static case (\(\omega = 0\)), the value of \({{S}_{{zz}}}\) is specified by relation (10).

As it must be, the orientational response comprises two contributions, i.e., the time-independent \(P\left( \omega \right)\) function and the second harmonic of the main frequency. The constant component of the orientational order parameter is found from the same set of equations as are dependences (21). This component has the following form:

$$\begin{gathered} P\left( x \right) = \frac{{{{{\left( {1{{\;}} + {\beta \mathord{\left/ {\vphantom {\beta q}} \right. \kern-0em} q}} \right)}}^{2}} + {{x}^{2}}\left[ {1 - \frac{{{{\beta }^{2}}\left( {{{1 + 1} \mathord{\left/ {\vphantom {{1 + 1} {3q}}} \right. \kern-0em} {3q}}} \right)}}{{2\left( {{{1 + \beta } \mathord{\left/ {\vphantom {{1 + \beta } {3q}}} \right. \kern-0em} {3q}}} \right)}}} \right]}}{{{{{\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta q}} \right. \kern-0em} q} - {{x}^{2}}} \right)}}^{2}} + {{x}^{2}}{{{\left( {2 + \tilde {\beta }} \right)}}^{2}}}}, \\ x \equiv \omega {{\tau }_{{\text{D}}}}. \\ \end{gathered} $$
(31)

The substitution of Eq. (30) into expression (29) leads to the following relation, which describes the optical anisotropy of a viscoelastic ferrocolloid under the used approximation:

$$\begin{gathered} \Delta n = \frac{1}{{30}}{{n}_{0}}A{{\phi }_{{\text{p}}}}\xi _{0}^{2} \\ \times \,\,\left[ {P\left( {\omega {{\tau }_{{\text{D}}}}} \right) + \left| {\tilde {\chi }_{{2\omega }}^{{(2)}}\left( {\omega {{\tau }_{{\text{D}}}}} \right)} \right|{\text{cos}}\left( {2\omega t - \delta } \right)} \right], \\ \end{gathered} $$
(32)

where the frequency-dependent coefficients are specified by expressions (21) and (31).

Figure 3 shows the frequency dependences of these functions for the same sets of viscoelasticity parameters \(\beta \) and \(q,\) as in Fig. 2.

Fig. 3.
figure 3

Frequency dependences of the static (dashed lines) and dynamic (solid lines) components of optical anisotropy (32) for Jeffry’s ferrocolloid: elasticity parameter \(\beta \) is equal to (1) 0.1, (2) 1, (3) 4, and (4) 16 at \({{q}_{0}} = {{10}^{3}}\) (see Eqs. (27)). Each dashed line always lies to the left of the solid one corresponding to the same \(\beta \) value.

Full size image

RESULTS AND DISCUSSION

It follows from the performed analysis that, in the studied model, the frequency spectra of all dynamic responses are mainly governed by the value of dimensionless elasticity parameter \(\beta = {K \mathord{\left/ {\vphantom {K {2T}}} \right. \kern-0em} {2T}}.\) Systems with a weakly pronounced elasticity are similar to ordinary Newtonian fluids. As the elasticity increases, the spectra of the responses substantially alter: their main component shifts toward lower frequencies, while the high-frequency “wing” shifts to the right along the frequency scale and rapidly decreases.

Relation between the Jeffry’s Model and Polymer Properties

Let us consider a semidiluted solution of a linear polymer in a good solvent as an example of a carrier medium. The scaling theory of polymer solutions [28] relates the rheological parameters of a studied model to the main physical characteristics of such a medium, i.e., polymer volume fraction \(\phi \) and number N of units in a macromolecule. According to this theory, each macromolecule in a solution is represented by a chain of blobs, i.e., segments consisting of \(g\) units (monomers having size \(a\)), which interact only with each other. Blob size \(\rho \sim a{{g}^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0em} 5}}}}\sim a{{\phi }^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 4}} \right. \kern-0em} 4}}}}\) determines the approximate average distance between macromolecule fragments in a solution.

In a semidiluted solution, macromolecule conformation weakly depends on solvent concentration. Under these conditions, number \({{N}_{{\text{a}}}}\sim g{{N}_{{\text{e}}}}\) of units between entanglements must be independent of the polymer volume concentration [28]. Since the elasticity of such a solution is determined by the network of instantaneous entanglements between the network-forming Gaussian chains containing number \({{N}_{{\text{e}}}}\) of blobs, the entropy-related elasticity modulus of the system is approximately equal to

$$G\sim \frac{T}{{{{\rho }^{3}}{{N}_{{\text{e}}}}}}\sim \frac{{gT}}{{{{\rho }^{3}}{{N}_{{\text{a}}}}}}\sim \frac{\phi }{{{{a}^{3}}{{N}_{{\text{a}}}}}}T.$$

The thermal motion of a macromolecule in a semidiluted solution is described as a unidimensional diffusion of a chain of blobs in a tube of entanglements, with the tube diameter and length being equal to \(d~\sim \rho N_{{\text{e}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\) and \(L~\sim \left( {{N \mathord{\left/ {\vphantom {N {g{{N}_{{\text{e}}}}}}} \right. \kern-0em} {g{{N}_{{\text{e}}}}}}} \right)d,\) respectively. The diffusion coefficient is determined by the Einstein equation, in which the friction coefficient is proportional to the number of blobs in a chain and solvent viscosity \({{\eta }_{{\text{S}}}}\):

$${{D}_{{\text{t}}}}\sim \frac{T}{{\rho {{\eta }_{{\text{S}}}}\left( {{N \mathord{\left/ {\vphantom {N g}} \right. \kern-0em} g}} \right)}}\sim \frac{T}{{a{{\eta }_{{\text{S}}}}N}}{{\phi }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$$

The time of macromolecule creeping out of a tube of entanglements, or, in other words, the lifetime of quasi-network nodes, is determined as

$$\tau \sim \frac{{{{L}^{2}}}}{{{{D}_{{\text{t}}}}}}\sim \frac{{{{\eta }_{{\text{S}}}}}}{{T{{N}_{{\text{e}}}}}}{{\left( {\frac{{\rho N}}{g}} \right)}^{3}}\sim \left( {\frac{{{{a}^{3}}{{\eta }_{{\text{S}}}}}}{T}} \right)\frac{{{{N}^{3}}}}{{{{N}_{{\text{a}}}}}}{{\phi }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$$

while the viscosity caused by this retardation mechanism is

$${{\eta }_{{\text{M}}}}\sim \tau G\sim {{\eta }_{{\text{S}}}}\frac{{{{N}^{3}}}}{{{{g}^{3}}N_{{\text{e}}}^{2}}}\sim {{\eta }_{{\text{S}}}}\frac{{{{N}^{3}}}}{{N_{{\text{a}}}^{2}}}{{\phi }^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}}.$$

Using the aforementioned relations, the dimensionless rheological parameters of a Jeffry’s medium, which simulates a semidiluted polymer solution, may be represented as

$$\begin{gathered} \beta = \frac{K}{{2T}} = \frac{{3GV}}{T}\sim \left( {\frac{V}{{{{a}^{3}}{{N}_{{\text{a}}}}}}} \right)\phi ,\,\,\,\,q = \frac{{{{{{\eta }}}_{{\text{M}}}}}}{{{{{{\eta }}}_{{\text{N}}}}}}\sim \frac{{{{N}^{3}}}}{{N_{{\text{a}}}^{2}}}{{\phi }^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}}, \\ \frac{\beta }{q} = \frac{{{{\tau }_{{\text{D}}}}}}{{{{\tau }_{{\text{M}}}}}}\sim \frac{V}{{{{a}^{3}}}}\left( {\frac{{{{N}_{{\text{a}}}}}}{{{{N}^{3}}}}} \right){{\phi }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 4}} \right. \kern-0em} 4}}}} \ll 1, \\ \end{gathered} $$
(33)

where \(V\) is the volume of a magnetic nanoparticle.

These relations show that Jeffry’s model parameters \(\beta \) and \(q\) increase with polymer volume fraction, while relation \({\beta \mathord{\left/ {\vphantom {\beta q}} \right. \kern-0em} q} \ll 1\) is always fulfilled. It should also be noted that, while Maxwellian viscosity \({{\eta }_{{\text{M}}}}\) rap-idly increases with macromolecule length, the elasticity parameter is almost insensitive to this characteristic.

Substituting parameter \(\beta \) from relations (33) into expressions (24) for the “slow” and “fast” relaxation times, we obtain

$$\begin{gathered} {{\tau }_{{\text{s}}}}\sim \frac{V}{{{{a}^{3}}{{N}_{{\text{a}}}}}}\phi {{\tau }_{{\text{D}}}}\sim \frac{{3{{\eta }_{{\text{N}}}}{{V}^{2}}}}{{{{a}^{3}}{{N}_{{\text{a}}}}T}}\phi ,\,\,\,\,{{\tau }_{{\text{f}}}}\sim \frac{{{{a}^{3}}{{N}_{{\text{a}}}}}}{{\phi V}} \sim {{\tau }_{{\text{D}}}} \\ \sim \frac{{3{{{{\eta }}}_{{\text{N}}}}{{a}^{3}}{{N}_{{\text{a}}}}}}{{\phi T}}, \\ \end{gathered} $$
(34)

Estimates (34) indicate that both effective times are of diffusion origin and strongly depend on the polymer concentration in a solution. Slow relaxation time \({{\tau }_{{\text{s}}}}\) increases with \(\phi \) and quadratically grows with the size of a probe particle. It is obvious that the larger the particle the greater the hindrance to its rotational diffusion, which must overcome the drag of the quasi-network.

A decrease in fast relaxation time \({{\tau }_{{\text{f}}}}\) with an increase in the polymer concentration is, most probably, due to the fact that, as the system density rises, the amplitude of particle rotations that do not deform the quasi-network diminishes. Indeed, as \(\phi \) grows, the angular displacements, upon which the particle interacts only with the solvent, i.e., a Newtonian fluid having viscosity \({{\eta }_{{\text{N}}}},\) become increasingly limited.

These conclusions are illustrated by Fig. 2a, which shows the frequency spectra of the real and imaginary components of linear susceptibility \(\tilde {\chi }_{\omega }^{{(1)}}\) for several values of polymer volume fraction characterized by parameter w (see Eqs. (27). It is seen that, the role of the frequency dispersion relevant to slow effective relaxation time \({{\tau }_{{\text{s}}}}\) increases with the system density (elasticity parameter \(\beta \)). This frequency dispersion predetermines the main peak in absorption spectrum \({\text{Im}}\tilde {\chi }_{\omega }^{{(1)}}\), and this peak shifts toward lower frequencies, as is seen in Fig. 4. In addition, Fig. 4 presents the main maxima of the higher harmonics of susceptibility (see curves in Figs. 2b, 2c) as depending on the \(\beta \) value. It is seen that, in the normalized form, all curves appear to be rather close to each other. However, the question of whether this closeness will remain preserved in the exact solution remains open. Remember that here we use a simplified model, i.e., the effective field method. Nevertheless, we can say with certainty that, at the qualitative level, a decrease in the frequency of the absorption maximum is a proven fact.

Fig. 4.
figure 4

Frequencies of the main maxima of imaginary components of dynamic susceptibilities (see Fig. 2) as functions of elasticity parameter.

Full size image

Ferrocolloids with developed elasticity (\(\beta \gg 1\)) exhibit a local maximum relevant to fast relaxation with time \({{\tau }_{{\text{f}}}}\) in the right-hand wing of the \({\text{Im}}\tilde {\chi }_{\omega }^{{(1)}}\) absorption curve. However, the height of this maximum decreases with an increase in the system elasticity (the series of curves 1–4 in Fig. 2a). The second term in the right-hand side of expression (20) shows that the decrease obeys the \( \propto {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }\) law. In addition, the effect of the high-frequency mode of relaxation decreases with an increase in the order of the harmonic under consideration. Indeed, according to asymptotic relations (22) and (23), the high-frequency contributions to the higher-order susceptibilities decrease according to \( \propto {1 \mathord{\left/ {\vphantom {1 {{{\beta }^{2}}}}} \right. \kern-0em} {{{\beta }^{2}}}}\) and \( \propto {1 \mathord{\left/ {\vphantom {1 {{{\beta }^{3}}}}} \right. \kern-0em} {{{\beta }^{3}}}}\) laws for \({\text{Im}}\tilde {\chi }_{{2\omega }}^{{(2)}}\) and \({\text{Im}}\tilde {\chi }_{{3\omega }}^{{(3)}}\), respectively.

Comparison with Experimental Data

The reveal of the effects of viscoelasticity requires rather accurate and laborious measurements. However, the analysis of the published data has led to arguments for some of the aforementioned predictions. For example, in experimental works [3, 4], magnetically rigid nanoprobes were used to study the rheological properties of aqueous poly(ethylene glycol) and gelatin solutions. The linear susceptibility spectra were obtained in a wide frequency range from a few hertzes to several hundred hertzes. A rapid low-frequency shift of the spectra was observed with an increase in the concentration and length of macromolecules [3], as well as the crosslinking density [4].

The analysis of the plots presented in Fig. 2 indicates one more general tendency: the heights of the main maxima of the imaginary components of all susceptibilities, \({\text{Im}}{{\chi }_{\omega }},\) \({\text{Im}}{{\chi }_{{2\omega }}},\) and \({\text{Im}}{{\chi }_{{3\omega }}}\), behave nonmonotonically with an increase in \(\beta \): they initially decrease and then increase. An analogous behavior is also inherent in the real components of susceptibilities \({\text{Re}}{{\chi }_{{2\omega }}}\) and \({\text{Re}}{{\chi }_{{3\omega }}}\) (see Figs. 2b, 2c). These functions are characterized by a nonmonotonic dependence of the depth of the minimum located in the negative region on \(\beta \). This property is not observed only for \({\text{Re}}{{\chi }_{\omega }},\) because this function is nonnegative.

Namely such behavior was revealed in [29] for the imaginary component of the linear dynamic magnetic susceptibility (the real component was not presented). The \({\text{Im}}{{\chi }_{\omega }}\left( \omega \right)\) function was measured for nanosuspensions of CoFe2O4 (magnetically rigid ferrite), the particles of which were coated with poly(ethylene glycol). The viscoelastic medium, which surrounded the particles, was created by adding bovine serum albumin (BSA) to the solution. Poly(ethylene glycol) bound BSA molecules, thereby forming a biopolymer “corona” on a particle. Thus, a cobalt ferrite particle, which was subjected to rotational oscillations induced by a magnetic probe field, moved inside the viscoelastic corona, whose size and density increased with BSA concentration.

CONCLUSIONS

The response of a viscoelastic ferrocolloid to a weak alternating (probe) magnetic field has been considered. The ferrocolloid has been simulated as an ensemble of noninteracting magnetically rigid nanoparticles suspended in a non-Newtonian fluid that has the rheological characteristics of a Jeffry’s medium. The Langevin equations, which describe the rotational Brownian motion of a nanoparticle, have been used to derive a set of moment equations, which determine the average (observed) system characteristics: dynamic magnetization and orientation kinetics. The set of the moment equations has been solved under the effective field approximation. The frequency spectra of all studied responses—from the linear to the cubic one—have been presented in an analytical form. It has been shown that the effects of mechanical retardation (stress relaxation), which result from the viscoelasticity of the carrier medium of the colloidal particles, give rise to the appearance of specific features in the spectra of all orders. In particular, an increase in the medium elasticity leads to a low-frequency shift of the main maximum and to nonmonotonic variations in the height of this peak. Under the assumption that the Jeffry’s fluid is represented by a semidiluted solution of a flexible-chain polymer, the rheological parameters of this phenomenological model have been related to the structural characteristics of the solution, namely, the number of monomer units in a macromolecule, the blob size, and the number of entanglements in a physical network.