The development and study of modern mechanical engineering products in many matters are closely related to the fundamental problems of creating mathematical models that are as close as possible to the original. In particular, models of the interaction of structural elements with a layer of liquid or gas are necessary in the development and study of gas and hydraulic supports [1], sensitive elements of pressure sensors, and gas and hydraulic damping of vibrations in devices [2]. For example, a plane model of a thrust bearing with an absolutely rigid guide and a slider with an adapted profile was developed in [3], considering the supporting lubricating layer as a viscous incompressible fluid with allowance for the pressure and temperature dependence of its viscosity. A simplified approach for estimating the elastic deformation of the surface of an infinitely extended bearing under the effect of pressure in the lubricating gas layer was proposed in [4]. The essence of this approach is to consider the annular lubricating layer “unfolded” onto a plane, i.e., a transition to the plane problem, and adding to its thickness a linear term proportional to the gas pressure with a proportionality coefficient associated with the elastic modulus of the deformable bearing surface. A rigorous approach requires the formulation and solution of related problems of hydro- and aeroelasticity [5, 6]. Here is a brief overview of these studies. The interaction of a stamp on a linear elastic suspension, which is a part of the bottom of an infinitely long channel, with a layer of ideal incompressible fluid with a free surface located in it was studied in [7]. Standing waves, along with traveling ones, were established to appear in the liquid near the stamp, and the possibility of reducing the amplitudes of the latter to zero by varying the vibration frequency of the stamp was shown. The interaction of an ideal fluid located in a rigid pipe with the sensitive element of a pressure sensor installed at its end is considered in [8]. An integro-differential equation for the dynamics of the sensitive element of the sensor that relates its deformation to the pressure and temperature of the medium at the entrance to the pipeline was obtained and studied numerically. The eigenoscillations and stability of a rectangular plate interacting with a layer of ideal compressible fluid were studied numerically in [9] using the finite element method. The effect of the layer thickness on the eigenfrequencies of oscillation of the plate and the critical velocities, at which loss of stability occurs, is estimated. Steady-state oscillations of the walls of an infinitely long channel formed by two parallel plates resting on an elastic Winkler base and interacting with a pulsating layer of viscous fluid between them were studied in [10]. A similar problem for the more general case of a channel with a finite length was previously solved in [11]. Numerical modeling of the interaction of a compressible gas with and with no allowance for its viscosity with a rigid disk on a linear elastic suspension was carried out in [12, 13], as a part of the study of the actuation process of a safety valve. A model of the interaction between the layer of viscous incompressible fluid located in a narrow channel with parallel walls and its end wall on a nonlinear elastic suspension was proposed in [14]. The application of the model to study the hydroelastic response of a bellows-type damper is considered. A model of a plane gas damper in the framework of the interaction of a viscous gas filling the gap between two parallel rigid walls and a rigid plate located inside the gap and moving at a constant velocity in the direction normal to its walls was proposed in [17].

However, the above studies do not consider aeroelastic oscillations of a disk on a nonlinear elastic suspension during its interaction with a pulsating layer of viscous gas. Therefore, the proposed study is aimed at setting and solving this problem.

FORMULATION OF THE AEROELASTICITY PROBLEM: BASIC PRINCIPLES AND ASSUMPTIONS

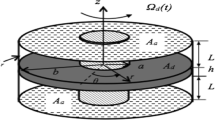
We consider a narrow channel with parallel walls that is schematically shown in Fig. 1. The walls of the channel are formed by two rigid disks of identical radii R, the symmetry axes of which coincide with the symmetry axis of the channel. The lower disk is fixed and considered motionless. The upper disk has a nonlinear elastic suspension, allowing it to oscillate in the vertical direction. We consider the suspension as a nonlinearly strengthening spring, the restoring force of which has linear and nonlinear components. The first is proportional to the movement of the disk, and the second is proportional to the cube of its movement; i.e., we consider the case of hardening cubic nonlinearity of the suspension [16, 17]. The channel is filled with a viscous gas, and on the contour, it is adjacent to the end cavity filled with the same gas. We assume that, in the unperturbed state in the gas located in the channel and the end cavity, there is constant pressure p0, which we take as the pressure reference point. In the unperturbed state, the distance between the disks is h0 and, due to the narrowness of the channel, h0 \( \ll \) R. In the end cavity, i.e., in the end section of the channel, pressure pulsation p1 is excited according to a harmonic law and superimposed on constant pressure level p0. Due to this pulsation, the upper disk performs nonlinear oscillations with the amplitude of zm \( \ll \) h0. The effect of gravity is neglected due to the low density of the gas. We introduce into consideration cylindrical coordinate system rφz, the z axis of which coincides with the axis of symmetry of the disks, while its center is located at the geometric center of the channel. Due to the axial symmetry of the channel, we consider an axisymmetric formulation. Next, we study the steady-state nonlinear oscillations [16, 17] of the disk interacting with a layer of viscous gas, assuming, similarly to the hydrodynamic theory of lubrication, that the state of the gas and the channel walls is isothermal [1, 18]. This assumption makes it possible to accept the dynamic viscosity of the gas as constant and to consider the law of change in its density to be barotropic.

Fig. 1.
figure 1

Diagram of a narrow channel formed by two parallel coaxial disks: (1) upper rigid disk having suspension 4 with hardening cubic nonlinearity, (2) lower absolutely rigid fixed disk, and (3) viscous gas located in the channel and end cavity.

Full size image

The harmonic law of gas pressure pulsation at the end along the contour of the channel (in the end cavity) is considered specified in the form

$${{p}_{1}} = {{p}_{{\text{m}}}}{{\sin\omega }}t,$$
(1)

where pm is the amplitude of pressure pulsation, ω is the specified pulsation frequency, and t is time.

We write the equation of motion of the upper disk as the mass on a nonlinear spring as follows:

$$m\frac{{{{d}^{2}}z}}{{d{{t}^{2}}}} + {{F}_{{\text{r}}}} = {{F}_{{\text{d}}}},$$
(2)

where z is the law of disk motion, m is the disk mass, t is the time, Fr is the restoring force of the nonlinear elastic suspension, and Fd is the disturbing force acting from the pulsating viscous gas in the channel.

Taking into account the anharmonicity of the oscillations of the upper disk, we present the law of its motion as z = zm  f(θt). Here, θ = 1/T is the characteristic frequency of nonlinear oscillations of the upper disk and T is the characteristic period of its nonlinear oscillations.

We write the restoring force of the nonlinear elastic suspension as a spring with hardening cubic nonlinearity according to [17] as follows:

$${{F}_{{\text{r}}}} = {{n}_{1}}z + {{n}_{3}}{{z}^{3}}.$$
(3)

Here, n1 is the linear stiffness coefficient of the suspension and n3 is the stiffness coefficient of the cubic component of the restoring force of the suspension. Since the suspension is nonlinearly hardening, the restoring force increases nonlinearly with increasing displacement of the disk; i.e., there is the hardening cubic nonlinearity and it is assumed that n3 > 0 [16, 17].

The Fd disturbing force is determined by the qzz normal stress of the viscous gas at the boundary of its contact with the disk surface. In general, this stress can be represented as follows [18]:

$${{q}_{{zz}}} = - p + 2{{\mu }}\frac{{\partial {{V}_{z}}}}{{\partial z}} - \left( {\frac{2}{3}{{\mu }} - {{\mu '}}} \right)\left( {\frac{1}{r}\frac{{\partial (r{{V}_{r}})}}{{\partial r}} + \frac{{\partial {{V}_{z}}}}{{\partial z}}} \right)\;{\text{at}}\;z = \frac{{{{h}_{0}}}}{2} + {{z}_{{\text{m}}}}f.$$
(4)

Here, p is the gas pressure (directed inside the gas volume), Vz is the projection of the gas velocity onto the z axis, Vr is the projection of the gas velocity onto the r axis, μ is the coefficient of dynamic viscosity of the gas, and \(\mu '\) is the second or volumetric viscosity.

Taking into account the above, we write the expression for Fd in the form

$${{F}_{{\text{d}}}} = - \int\limits_0^{2\pi } {\int\limits_0^R {{{{\left. {{{q}_{{zz}}}} \right|}}_{{z = \frac{{{{h}_{0}}}}{2} + {{z}_{{\text{m}}}}f}}}rdrd\varphi } } = - 2{{\pi }}\int\limits_0^R {{{{\left. {{{q}_{{zz}}}} \right|}}_{{z = \frac{{{{h}_{0}}}}{2} + {{z}_{{\text{m}}}}f}}}rdr.} $$
(5)

Together with the equation of motion of the disk (2), it is necessary to consider the motion equations of a viscous gas in a narrow channel. We take into account that, in the proposed formulation, the movement of the gas can be taken as creeping [1, 18]. Then, the equations of its motion are the Navier–Stokes equations for a compressible fluid, from which local and convective accelerations are excluded:

$$\begin{gathered} \frac{{\partial p}}{{\partial r}} = {{\mu }}\left( {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{V}_{r}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{V}_{r}}}}{{\partial {{z}^{2}}}} - \frac{{{{V}_{r}}}}{{{{r}^{2}}}}} \right) + \left( {{{\mu '}} + \frac{1}{3}{{\mu }}} \right)\frac{\partial }{{\partial r}}\left( {\frac{1}{r}\frac{\partial }{{\partial r}}(r{{V}_{r}}) + \frac{{\partial {{V}_{z}}}}{{\partial z}}} \right), \\ \frac{{\partial p}}{{\partial z}} = {{\mu }}\left( {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{V}_{z}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{V}_{z}}}}{{\partial {{z}^{2}}}}} \right) + \left( {{{\mu '}} + \frac{1}{3}{{\mu }}} \right)\frac{\partial }{{\partial z}}\left( {\frac{1}{r}\frac{\partial }{{\partial r}}(r{{V}_{r}}) + \frac{{\partial {{V}_{z}}}}{{\partial z}}} \right). \\ \end{gathered} $$
(6)

Equations (6) are closed by the continuity equation for a compressible medium:

$$\frac{{\partial {{\rho }}}}{{\partial t}} + \frac{1}{r}\frac{\partial }{{\partial r}}(r{{\rho }}{{V}_{r}}) + \frac{\partial }{{\partial z}}({{\rho }}{{V}_{z}}) = 0,$$
(7)

and the barotropic law of changes in the density of a viscous gas:

$$\frac{p}{{{\rho }}} = {{c}^{2}}.$$
(8)

Here, ρ is the gas density and с is the isothermal speed of sound in gas (under normal conditions).

We supplement equations (6)–(8) with conditions at the boundaries of contact of the viscous gas with the channel walls. As conditions, we choose the no-slip conditions for a viscous gas at the walls of the channel [18]

$$\begin{gathered} {{V}_{r}} = 0\quad {\text{and}}\quad {{V}_{z}} = \frac{{dz}}{{dt}}\quad {\text{at}}\quad z = \frac{{{{h}_{0}}}}{2} + {{z}_{{\text{m}}}}f({{\theta }}t)\quad {\text{and}}\quad {{V}_{r}} = 0 \\ {\text{and}}\quad {{V}_{z}} = 0\quad {\text{at}}\quad z = - \frac{{{{h}_{0}}}}{2}. \\ \end{gathered} $$
(9)

Furthermore, we write the conditions for the pressure at the end of the channel and at the axis of symmetry. These conditions represent the condition for the pressure at the end section of the channel to coincide with the pressure in the end cavity and the condition for the limited pressure on the axis of symmetry, which we write in the form

$$p = {{p}_{1}}({{\omega }}t)\quad {\text{at}}\quad r = R\quad {\text{and}}\quad r\frac{{\partial p}}{{\partial r}} = 0\quad {\text{at}}\quad r = 0.$$
(10)

Here, it is taken into account that constant pressure level p0 corresponding to the unperturbed state is taken as the starting point for the pressure in the channel and the end cavity. In addition, we keep in mind that, according to [18], in an isothermal process, as well as for the cases of monatomic gases, the second viscosity \(\mu '\) can be set equal to zero. Therefore, we further assume \(\mu '\) = 0 in (4) and (6).

ASYMPTOTIC ANALYSIS OF THE FORMULATED AEROELASTICITY PROBLEM

To study the aeroelastic oscillations of the disk-channel wall, we move on to consider the dimensionless problem by introducing the following characteristic small parameters and dimensionless variables:

$$\begin{gathered} \psi = \frac{{{{h}_{0}}}}{R} \ll 1,\quad {{\lambda }} = \frac{{{{z}_{{\text{m}}}}}}{{{{h}_{0}}}} \ll 1,\quad {{\tau }} = {{\theta }}t,\quad \xi = \frac{r}{R},\quad \zeta = \frac{{z + {{h}_{0}}{\text{/}}2}}{{{{h}_{0}}}},\quad {{V}_{z}} = {{z}_{{\text{m}}}}{{\theta }}{{U}_{\zeta }}, \\ {{V}_{r}} = \frac{{{{z}_{{\text{m}}}}{{\theta }}}}{\psi }{{U}_{\xi }},\quad p = P\frac{{{{\mu }}{{z}_{{\text{m}}}}{{\theta }}}}{{{{h}_{0}}{{\psi }^{2}}}}. \\ \end{gathered} $$
(11)

We represent the gas density as ρ = ρ0 + ρ*, where ρ0 is the gas density in an unperturbed state and ρ* is the gas density in a perturbed state, which varies according to the barotropic law: p/ρ = с2 (hereinafter in the equations, the superscript * denotes the disturbed state of the gas that we omit and take into account that \({{p}_{1}}({{\omega }}t)\) = \({{\mu }}{{z}_{{\text{m}}}}{{\theta }}{{({{\delta }}{{\psi }^{2}})}^{{ - 1}}}{{P}_{1}}({{\tau \omega /\theta }})\)). Then, substituting (11) into (6)–(10), we obtain the following dimensionless equations for the dynamics of a viscous gas in a narrow channel:

$$\begin{gathered} \frac{{\partial P}}{{\partial \xi }} = \frac{{{{\partial }^{2}}{{U}_{\xi }}}}{{\partial {{\zeta }^{2}}}} + {{\psi }^{2}}\left( {\frac{4}{3}\frac{{{{\partial }^{2}}{{U}_{\xi }}}}{{\partial {{\xi }^{2}}}} + \frac{4}{3}\frac{1}{\xi }\frac{{\partial {{U}_{\xi }}}}{{\partial \xi }} - \frac{4}{3}\frac{{{{U}_{\xi }}}}{{{{\xi }^{2}}}} + \frac{1}{3}\frac{{{{\partial }^{2}}{{U}_{\zeta }}}}{{\partial \xi \partial \zeta }}} \right), \\ \frac{{\partial P}}{{\partial \zeta }} = {{\psi }^{2}}\left[ {{{\psi }^{2}}\left( {\frac{{{{\partial }^{2}}{{U}_{\zeta }}}}{{\partial {{\xi }^{2}}}} + \frac{1}{\xi }\frac{{\partial {{U}_{\zeta }}}}{{\partial \xi }}} \right) + \frac{1}{3}\left( {\frac{{{{\partial }^{2}}{{U}_{\xi }}}}{{\partial \xi \partial \zeta }} + \frac{1}{\xi }\frac{{\partial {{U}_{\xi }}}}{{\partial \zeta }}} \right) + \frac{4}{3}\frac{{{{\partial }^{2}}{{U}_{\zeta }}}}{{\partial {{\zeta }^{2}}}}} \right], \\ \frac{{{{\theta }^{2}}{{\ell }^{2}}}}{{{{c}^{2}}}}\frac{{\partial P}}{{\partial \tau }} + \lambda \frac{{{{\theta }^{2}}{{\ell }^{2}}}}{{{{c}^{2}}}}\left( {{{U}_{\xi }}\frac{{\partial P}}{{\partial \xi }} + {{U}_{\zeta }}\frac{{\partial P}}{{\partial \zeta }}} \right) + \left( {\frac{{{{\delta }^{2}}\theta }}{{\mu {\text{/}}\rho _{0}^{{}}}} + \lambda \frac{{{{\theta }^{2}}{{\ell }^{2}}}}{{{{c}^{2}}}}P} \right)\left( {\frac{{\partial {{U}_{\xi }}}}{{\partial \xi }} + \frac{1}{\xi }{{U}_{\xi }} + \frac{{\partial {{U}_{\zeta }}}}{{\partial \zeta }}} \right) = 0, \\ \end{gathered} $$
(12)

and their complementary boundary conditions:

$$\begin{gathered} {{U}_{\xi }} = 0,\;\;{{U}_{\zeta }} = \frac{{df(\tau )}}{{d\tau }},\;\;{\text{at}}\;\;\zeta = 1 + \lambda f(\tau ),\;\;{{U}_{\xi }} = 0,\;\;{{U}_{\zeta }} = 0,\;\;{\text{at}}\;\;\zeta = 0, \\ P = {{P}_{1}}({{\tau \omega /\theta }}),\;\;{\text{at}}\;\;\,\xi = 1,\;\;{\text{and}}\;\;\xi \frac{{\partial P}}{{\partial \xi }} = 0\;\;{\text{at}}\;\;\xi = 0. \\ \end{gathered} $$
(13)

As is customary in the hydrodynamic theory of lubrication [18], we proceed to consideration of a thin layer of gas, excluding terms of ~ψ2 from consideration in (12). Then, we apply the perturbation method [19] to the simplified thin layer equations and boundary conditions (13), considering the asymptotic expansions in small parameter λ of the desired hydrodynamic parameters. As a result, we obtain a dimensionless hydromechanics problem for a thin layer of viscous gas:

$$\frac{{\partial P}}{{\partial \xi }} = \frac{{{{\partial }^{2}}{{U}_{\xi }}}}{{\partial {{\zeta }^{2}}}},\quad \frac{{\partial P}}{{\partial \zeta }} = 0,\quad \frac{{{{\theta }^{2}}{{\ell }^{2}}}}{{{{c}^{2}}}}\frac{{\mu {\text{/}}{{\rho }_{0}}}}{{h_{0}^{2}\theta }}\frac{{\partial P}}{{\partial \tau }} + \frac{{\partial {{U}_{\xi }}}}{{\partial \xi }} + \frac{1}{\xi }{{U}_{\xi }} + \frac{{\partial {{U}_{\zeta }}}}{{\partial \zeta }} = 0,$$
(14)

with boundary conditions

$$\begin{gathered} {{U}_{\xi }} = 0,\quad {{U}_{\zeta }} = \frac{{df(\tau )}}{{d\tau }}\quad {\text{at}}\quad \zeta = 1,\quad {{U}_{\xi }} = 0,\quad {{U}_{\zeta }} = 0\quad {\text{at}}\quad \zeta = 0, \\ P = {{P}_{1}}({{\tau \omega /\theta }})\quad {\text{at}}\quad \xi = 1\quad {\text{and}}\quad \xi \frac{{\partial P}}{{\partial \xi }} = 0\quad {\text{at}}\quad \xi = 0. \\ \end{gathered} $$
(15)

Substituting (11) into the normal stress (4) and excluding terms of ~ψ2 from it and also taking into account that, according to second equation (14), P does not depend on ζ, we write the expression for disturbing force (5) as follows:

$${{F}_{{\text{d}}}} = 2\pi {{R}^{2}}\frac{{\mu {{z}_{{\text{m}}}}\theta }}{{{{h}_{0}}{{\psi }^{2}}}}\int\limits_0^1 {P\xi d\xi } .$$
(16)

We use the iteration method [15] to solve (14) with boundary conditions (15). In the first iteration, we assume that the gas is incompressible; i.e., we assume that c2 → ∞, which makes it possible to exclude from consideration the first term, which takes into account the compressibility of the gas, in last equation (14). In the second iteration, we take into account the compressibility of the gas; i.e., we take into account the excluded term by substituting into it the pressure found at the first iteration step. Then, in the first iteration, we find that

$${{U}_{\xi }} = \frac{{{{\zeta }^{2}} - \zeta }}{2}\frac{{\partial P}}{{\partial \xi }},\quad {{U}_{\zeta }} = \frac{{3{{\zeta }^{2}} - 2{{\zeta }^{3}}}}{{12}}\left( {\frac{1}{\xi }\frac{{\partial P}}{{\partial \xi }} + \frac{{{{\partial }^{2}}P}}{{\partial {{\xi }^{2}}}}} \right),\quad P = {{P}_{1}}({{\tau \omega /\theta }}) + 3({{\xi }^{2}} - 1)\frac{{df(\tau )}}{{d\tau }}.$$
(17)

Carrying out the second iteration, we substitute pressure (17) into the third equation of system (14), and then solving it with conditions (15), we found the law of pressure change in the channel in the form

$$P = {{P}_{1}} + 3({{\xi }^{2}} - 1)\frac{{df}}{{d\tau }} + 3({{\xi }^{2}} - 1)\frac{{{{\theta }^{2}}{{\ell }^{2}}}}{{{{c}^{2}}}}\frac{{\mu {\text{/}}{{\rho }_{0}}}}{{h_{0}^{2}\theta }}\frac{{d{{P}_{1}}}}{{d\tau }} + \frac{9}{{14}}({{\xi }^{4}} - 4{{\xi }^{2}} + 3)\frac{{{{\theta }^{2}}{{\ell }^{2}}}}{{{{c}^{2}}}}\frac{{\mu {\text{/}}{{\rho }_{0}}}}{{h_{0}^{2}\theta }}\frac{{{{d}^{2}}f}}{{d{{\tau }^{2}}}}.$$
(18)

By substituting (18) into (16) and carrying out integration and then moving on to dimensional variables, we determine the disturbing force:

$${{F}_{{\text{d}}}} = \pi {{R}^{2}}{{p}_{1}} - \pi {{R}^{2}}{{T}_{{\text{g}}}}\frac{{d{{p}_{1}}}}{{dt}} - {{K}_{{\text{g}}}}\frac{{dz}}{{dt}} + {{M}_{{\text{g}}}}\frac{{{{d}^{2}}z}}{{d{{t}^{2}}}},$$
(19)

where \({{K}_{{\text{g}}}} = \frac{{3\pi }}{2}\frac{{{{R}^{4}}\mu }}{{h_{0}^{3}}}\), \({{T}_{{\text{g}}}} = \frac{3}{2}\frac{{\mu {{R}^{2}}}}{{{{c}^{2}}{{\rho }_{0}}h_{0}^{2}}}\), and \({{M}_{{\text{g}}}} = \frac{{15\pi }}{8}\frac{{{{\mu }^{2}}{{R}^{6}}}}{{{{c}^{2}}{{\rho }_{0}}h_{0}^{5}}}\).

Taking into account (1), (3), and (19), we write the equation of motion of disk (2) in the form

$$(m - {{M}_{{\text{g}}}})\frac{{{{d}^{2}}z}}{{d{{t}^{2}}}} + {{K}_{{\text{g}}}}\frac{{dz}}{{dt}} + {{n}_{1}}z + {{n}_{3}}{{z}^{3}} = \pi {{R}^{2}}\left( {{{p}_{1}} - {{T}_{{\text{g}}}}\frac{{d{{p}_{1}}}}{{dt}}} \right) = \pi {{R}^{2}}{{p}_{{\text{m}}}}A(\omega ){\text{sin}}(\omega t - \gamma (\omega )).$$
(20)

Here, \(A(\omega ) = \sqrt {{\text{1}} + {{{{\text{(}}{{T}_{{\text{g}}}}\omega {\text{)}}}}^{{\text{2}}}}} \), and \({\text{tan}}\gamma (\omega ) = {{T}_{{\text{g}}}}\omega \).

Equation (20) is a generalization of the Duffing oscillator equation. It makes it possible to study special cases: a viscous incompressible fluid at c2 → ∞ (Mg = 0 and Tg = 0) and a linear elastic suspension of a disk if we assume n3 = 0. Note that, on the right side of (20), in the general case, there are two components: the first is determined by the law of pressure pulsation in the end cavity, the second is determined by the time derivative of this law. From (20), it follows that gas compressibility leads to the appearance of additional phase shift γ, as well as to a decrease in the inertial properties of the oscillatory system compared to the case of an incompressible liquid (Tg = 0 and Mg = 0). The viscosity of the gas and the geometric dimensions of the channel determine the damping properties of the oscillatory system (coefficient Kg).

PRIMARY AEROELASTIC RESPONSE OF THE DISK AND ITS PHASE SHIFT

To solve (20), we use the harmonic balance method [17, 20]. We take into account that when studying oscillations of mechanical systems, primary attention is paid to the main oscillations at the frequency of the driving force [17]. Therefore, when carrying out the method, we consider the frequency of disk oscillations to be close to the frequency of pressure pulsation in the end cavity of θ ≈ ω and look for a solution in the form z = zmsin(ωt – γ) (i.e., using this method, we consider a one-term expansion in the Fourier series at the fundamental frequency). The right side of (20) is represented as πR2pmA(ω)sin(ωt – γ + ϕ) with allowance for phase shift ϕ due to the forces of viscous friction of the gas [17]. As a result, we obtain the following algebraic system:

$$\left[ {{{n}_{1}} + \frac{3}{4}{{n}_{3}}z_{{\text{m}}}^{2} - (m - {{M}_{{\text{g}}}}){{\omega }^{2}}} \right]{{z}_{{\text{m}}}} = \pi {{R}^{2}}{{p}_{{\text{m}}}}A(\omega ){\text{cos}}\phi ,\quad {{K}_{{\text{g}}}}\omega {{z}_{{\text{m}}}} = \pi {{R}^{2}}{{p}_{{\text{m}}}}A(\omega ){\text{sin}}\phi .$$
(21)

Resolving (21), we find the main nonlinear aeroelastic response of the disk

$${{z}_{{\text{m}}}} = \frac{{\pi {{R}^{2}}{{p}_{{\text{m}}}}\sqrt {{\text{1}} + {{{{\text{(}}{{T}_{{\text{g}}}}\omega {\text{)}}}}^{{\text{2}}}}} {\text{/}}(m - {{M}_{{\text{g}}}})}}{{\sqrt {{{{(\omega _{*}^{2} - {{\omega }^{2}})}}^{2}} + {{{({{K}_{{\text{g}}}}\omega {\text{/}}(m - {{M}_{{\text{g}}}}))}}^{2}}} }}$$
(22)

and its phase shift:

$${\text{tan}}\phi = \frac{{{{K}_{{\text{g}}}}\omega {\text{/}}(m - {{M}_{{\text{g}}}})}}{{\omega _{*}^{2} - {{\omega }^{2}}}}.$$
(23)

Here, \(\omega _{*}^{2} = ({{n}_{1}} + (3{\text{/}}4){{n}_{3}}z_{{\text{m}}}^{2}){\text{/}}(m - {{M}_{{\text{g}}}})\) is the backbone curve that determines the change in the eigenfrequency of the conservative nonlinear system corresponding to the one we are considering at Kg = 0, i.e., with the exception of the gas viscosity.

Note that, at n3 = 0, the backbone characteristic coincides with the eigenfrequency of the linear conservative oscillator. Moving on to the dimensionless frequency of η = \(\sqrt {{{\omega }^{2}}(m - {{M}_{{\text{g}}}}){\text{/}}{{n}_{1}}} \), we write (22) and (23) in the form

$${{z}_{{\text{m}}}} = \frac{{\pi {{R}^{2}}{{p}_{{\text{m}}}}\sqrt {{\text{1}} + {{{{\text{(}}{{T}_{{\text{g}}}}\eta {\text{)}}}}^{{\text{2}}}}{{n}_{1}}{\text{/}}(m - {{M}_{{\text{g}}}})} {\text{/}}{{n}_{1}}}}{{\sqrt {{{{(\eta _{*}^{2} - {{\eta }^{2}})}}^{2}} + {{S}^{2}}{{\eta }^{2}}} }},$$
(24)
$${\text{tan}}\phi = \frac{{S\eta }}{{\eta _{*}^{2} - {{\eta }^{2}}}},$$
(25)

where \(\eta _{*}^{2} = 1 + (3{\text{/}}4){{n}_{3}}z_{{\text{m}}}^{2}{\text{/}}{{n}_{1}}\) is the dimensionless backbone characteristic, \({{S}^{2}} = K_{{\text{g}}}^{2}{\text{/}}((m - {{M}_{{\text{g}}}}){{n}_{1}})\).

The found primary aeroelastic response and phase shift (22)–(25) at n3 ≠ 0 are implicit functions; however, they can be studied numerically. We give an example of such a study for the following initial data: R = 0.2 m, h0 = 5 × 10–4 m, ρ0 = 1.2 kg/m3, μ = 18.1 × 10–6 kg/(m s), c = 290 m/s, n1 = 6 × 108 N/m, n3 = 2 × 1016 N/m3, m = 3 kg, and pm = 104 Pa.

Figures 2–4 show the results of calculations of nonlinear and linear (n3 = 0) aeroelastic responses of the disk and the corresponding phase shifts according to (24) and (25) for pressure pulsation amplitudes in the end cavity of pm = 104 and 2 × 104 Pa. The graphs in Fig. 2 correspond to the case of a viscous compressible gas, and graphs in Fig. 3 correspond to the case of a viscous incompressible gas (liquid, i.e., at Mg = 0 and Tg = 0). Figure 4 shows graphs for viscous compressible gas with a reduced gap between the disks of h0 = 3.5 × 10–4 m.

Fig. 2.
figure 2

(a) Aeroelastic response and (b) phase shift of the disk with allowance for the compressibility of the gas (h0 = 5 × 10–4 m, η = 1 corresponds to ω = 14235.35 rad/s): (1) nonlinear elastic suspension of the disk pm = 104 Pa, (2) nonlinear elastic suspension of the disk pm = 2 × 104 Pa, (3) linear elastic suspension of the disk pm = 104 Pa, (4) linear elastic suspension of the disk is pm = 2 × 104 Pa, and (5) backbone curve η*.

Full size image
Fig. 3.
figure 3

(a) Aeroelastic response and (b) phase shift of the disk without taking into account gas compressibility (h0 = 5 × 10–4 m, η = 1 corresponds to ω = 14142.13 rad/s): (1) nonlinear elastic suspension of the disk pm = 104 Pa, (2) nonlinear elastic suspension of the disk pm = 2 × 104 Pa, (3) linear elastic suspension of the disk pm = 104 Pa, (4) linear elastic suspension of the disk pm = 2 × 104 Pa, and (5) backbone curve η*.

Full size image
Fig. 4.
figure 4

(a) Aeroelastic response and (b) phase shift of the disk taking into account the compressibility of the gas (h0 = 3.5 × 10–4 m, η = 1 corresponds to ω = 14725.56 rad/s): (1) nonlinear elastic suspension of the disk pm = 104 Pa, (2) nonlinear elastic suspension of the disk pm = 2 × 104 Pa, (3) linear elastic suspension of the disk pm = 104 Pa, (4) linear elastic suspension of the disk pm = 2 × 104 Pa, and (5) backbone curve η*.

Full size image

CONCLUSIONS

This study made it possible to establish that a change in gas density in the channel leads to an additional phase shift in the pressure pulsation law specified at the ends. A numerical study of the nonlinear and linear aeroelastic response of the disk and its phase shift showed that, in comparison with the incompressible case, the compressibility of the gas leads to an increase in the amplitudes of the disk oscillations and a slight decrease in the inertial properties of the oscillatory system considered, which is manifested in a slight increase in the values of the resonant frequencies of the disk. The rigid cubic nonlinearity of the suspension leads to a bend of the characteristics to the right and an increase in the values of the resonant frequencies with increasing amplitudes of pressure pulsation in the end cavity in comparison with the linear case. As is known [16, 17], bending of aeroelastic response curves can lead to unstable oscillations of the disk with abrupt changes in amplitudes in the frequency range of a given bend. The calculations presented in Figs. 2 and 3 showed the possibility of these oscillations. On the other hand, reducing the gap between the disks is shown to lead to suppression of the oscillation amplitudes and the intensity of the bending characteristics (Fig. 4), and, as a consequence, to the suppression of the possibility of unstable oscillations. In the case of a linearly elastic suspension of the disk, there is no bending of the aeroelastic response curves and no phase shift to the right; i.e., the resonant frequency does not depend on the amplitude of the pressure pulsation in the end cavity and there is no zone of unstable oscillations. In this case, the phase shift curves for different pressure pulsation amplitudes coincide (Figs. 2–4, phase shift curves 3 and 4).

The model of nonlinear aeroelastic oscillations of the disk that is proposed here and the aeroelastic response and phase shift obtained on its basis, as well as the results of studying these characteristics, can be used to study the dynamics of gas and liquid dampers and supports with nonlinear and linear elastic connections, as well as for elastic sensitive sensor elements having a nonlinear elastic suspension.