1. INTRODUCTION

The phenomenon of seismic (acoustic) emission has long been known. For example, in [1], it was explained by the rearrangement of the sand microstructure. Kilohertz frequencies were detected in this work. The authors pointed out the necessity of constructing a mathematical model for he adequate description of these effects. According to [2, 3], changes in the parameters of acoustic pulses were governed by the evolution of the state of a thin geomaterial layer between continuous blocks. Seismic emission is usually described within a continuum model [4]. Thus, the pore structure, which is used to explain new phenomena (multiple frequencies, discreteness of individual events, emission amplification and attenuation due to external sources [4]), was taken into account neither in equilibrium equations nor in equations of motion. The continuum model was also unable to explain the experimentally found quantization (discrete energy levels) of emission events [5, 6]. In addition, the time range of external loading of a granular medium is very wide: it can be seconds, minutes, and even hours [7]. This suggests that dynamic phenomena are accompanied by processes of quasi-static equilibrium. However, a continuous medium cannot satisfy both the equations of motion and equilibrium. This raises the problem of constructing a more complex continuum than the classical Cauchy–Poisson continuum.

The problem of constructing a structured continuum arose after the appearance of the works by M.A. Sadovsky [8], introducing a certain hierarchy of rock structures. Sadovsky’s ideas led to the development of discrete models of dynamic deformation of metals and rocks [9]. However, the presence of characteristic sizes of heterogeneities is not always an obstacle to the description of substructures by continuum mechanics methods. If the medium consists of similar materials, whose physical and mechanical parameters differ by several times rather than by many orders, then the solid model can serve as a fairly good first approximation. If the medium consists of materials whose elastic moduli (or at least one of them) differ by many orders (for example, a solid matrix and pores filled with liquid or gas), then the continuum approximation ceases to be adequate. Continuum mechanics assumes that the proximity of points leads the closeness of all medium properties (stresses, strains, electrical conductivity, temperatures, etc.). Otherwise, the medium ceases to be continuous, and the derivatives of any field lose their meaning at the matrix-fluid interface. A continuum model based on averaging procedures adequately describes deformation processes only when averaging of direct and inverse parameters (for example, elastic moduli and compliances) gives comparable results. Contrast microheterogeneous media containing fluids do not possess this property. Abandonment of the continuum model requires the description of structures by methods of integral geometry, which operates only with collective rock properties, such as porosity, specific surface area, average and Gaussian curvature of the pore space. In this case, the real medium is not thought to be continuous; its continuous analogue is constructed by the method of field transfer to all points of the pore space. The main concepts of this approach to the medium description were briefly presented in [10].

The main aim of the present work is to construct a seismic (acoustic) emission model that takes into account geometric parameters of the pore space and allows describing the transition from quasi-static loading to dynamic deformation (wave emission).

2. CONTINUUM OPERATORS AND EQUATIONS OF MOTION

The main idea underlying modeling is not to represent the real medium as a continuous model, but to construct a continuous pattern of the real rock containing microstructures of finite sizes. It is known from integral geometry that the specific surface area of pores or cracks σ0 is related to the average crack/pore spacing l0 by the equality [10]

$${\sigma _0}{l_0} = 4(1 - f),$$
((1))

where f is the specimen porosity. The one-dimensional operator of field transfer from point x to point x ± l0 is given by the well-known symbolic expression [11]

$$u(x \pm {l_0}) = u(x){e^{ \pm {l_0}{D_x}}},$$
((2))
$${D_x} = {\partial \over {\partial x}},\;P({D_x};\;{l_0}) = {e^{ \pm {l_0}{D_x}}}.$$

In (2), P(Dx; l0) is the one-dimensional field transfer operator. The formal Taylor series expansion of the exponential involves the use of derivatives of all orders to implement the transfer operation. If derivatives of all orders exist at point x, then the field can be transferred to any point of the solid, including pores and cracks. The use of such operators allows constructing an analogue of a continuum with a field at each point of the matrix and pore space (Fig. 1). The right scheme in Fig. 1 shows a section of the matrix containing fluid (closed lines). The average distance between two nearest centers of gravity l0 is related to the specific surface area σ0 by the formula of integral geometry (1).

Fig. 1.
figure 1

Unit block of a granular and fractured solid. l0 is the average pore/crack spacing (color online).

Full size image

Figure 1 (left) clearly shows the problem of equilibrium for a representative volume of the medium (surface C) and the lack of equilibrium for an unrepresentative volume (surface D, where the presence of forces on one side coexists with the absence of similar forces on the other side). Therefore, the averaging procedure is applied to a certain minimum representative volume rather than to each point.

In the three-dimensional case, after averaging over spherical angles θ and φ, the field transfer operator has the form [12]

$$P({D_x},\;{D_y},\;{D_z};\;{l_0}) = {1 \over {4\pi }}\int\limits_0^{2\pi } {\int\limits_0^\pi {\exp [{l_0}({D_x}\sin \theta \cos \varphi } } + {D_y}\sin \theta \sin \varphi + {D_z}\cos \theta )]\sin \theta \;{\rm{d}}\theta \;{\rm{d}}\varphi $$
$$ = {{{\rm{sinh}}({l_0}\sqrt \Delta )} \over {{l_0}\sqrt \Delta }} = E + {{l_0^2} \over {3!}}\Delta + {{l_0^4} \over {5!}}\Delta \Delta + ...,$$
((3))

where E is the unity operator, and Δ is the Laplace operator. The Cauchy–Poisson hypothesis has a simple mathematical expression P = E, i.e. a representative volume of the medium is a point. In the case of finite microstructures, the equation of motion contain not real rapidly changing forces, but their continuous pattern, which is supplemented by the continuum operator P(Dx, Dy, Dz; l0):

$${\partial \over {\partial {x_k}}}[P({\sigma _{ik}})] = \rho {\ddot u_i} = {\partial \over {\partial {x_k}}}\left[ {\left( {E + {{l_0^2\Delta } \over {3!}} + {{l_0^4\Delta \Delta } \over {5!}} + ...} \right)({\sigma _{ik}})} \right].$$
((4))

For one-dimensional stationary vibrations, Eq. (4) is written in displacements as follows:

$${u_{xx}}\left( {E + {{l_0^2\Delta } \over {3!}} + {{l_0^4\Delta \Delta } \over {5!}} + ...} \right) + k_{\rm{s}}^2u = 0,$$
((5))

where ks2 is the square of the usual wave number for longitudinal or transverse waves, and searching for a solution in the form u = Aexp(ikx) gives the following dispersion equation for the unknown wave number k:

$${{\sin (k{l_0})} \over {k{l_0}}} = {{k_{\rm{s}}^2} \over {{k^2}}}.$$
((6))

It is obvious that, as l0 → 0, k → ks, which points to usual (characteristic of a classical continuum) velocities of longitudinal or transverse waves at the fixed frequency. If l0 is finite, the wave velocities decrease without limit, while, at kl0 > π, the roots of Eq. (6) are complex, which corresponds to unstable solutions [11]. Calculation of real roots of (6) shows that the velocities of longitudinal waves decrease with growing microstructures, so do the velocities of transverse waves, but much less. Thus, as microstructures grow in size, the ratio between the velocities of transverse and longitudinal waves increases, i.e. Poisson’s ratio drops to negative values. It is possible that negative Poisson’s ratios determined from the ratio of wave velocities for oil and gas reservoirs present a dispersion effect [12].

The number of complex roots dependent on the specific surface area of pores or cracks corresponds to the energy distribution of the number of earthquakes (Gutenberg–Richter law) because the specific surface area of cracks is proportional to the deficit of potential energy of the medium, which, by the law of conservation of energy, was converted into the kinetic energy of waves. The slopes of these curves almost coincide [13].

3. EQUILIBRIUM EQUATION FOR MICROHETEROGENEOUS MEDIA AND INTERNAL FRICTION

The equilibrium equation differs from the equation of motion (7) in the lack of the term for inertial forces, and therefore it is written in the form

$$P\left[ {{{\partial {\sigma _{ik}}} \over {\partial {x_k}}}} \right] = 0,$$
((7))
$${{\partial {\sigma _{ik}}} \over {\partial {x_k}}} = {P^{ - 1}}.$$
((8))

The inverse operator P–1, along with the trivial solution typical of the classical equation of equilibrium of a continuum, has other solutions corresponding to dispersion Eq. (5) with zero frequency (zero wave number on the right-hand side of (5)):

$${u_{xx}}\left( {E + {{l_0^2\Delta } \over {3!}} + {{l_0^4\Delta \Delta } \over {5!}} + ...} \right) = 0.$$
((9))

In this case, from (9) follows

$${k^2}{{\sin (k{l_0})} \over {k{l_0}}}u = 0.$$
((10))

Thus, the equation of equilibrium of a microheterogeneous medium admits not only the classical solution k2 = 0, but also the nontrivial one:

$$\sin (k{l_0}) = 0.$$
((11))

Nontrivial solutions contain a set of values kl0 = mπ, where m is an integer, and satisfy the equilibrium equation of a microheterogeneous medium. Pure statics is supplemented by periodic vibrations dependent on the specific surface area of the microstructure. Under dry friction, it should be taken into account that the volumetric friction force Ffr is the product of pressure by the friction coefficient p and by the specific contact area of particles σ00:

$${F_{{\rm{fr}}}} = (\lambda + 2\mu )u'p{\sigma _{00}}.$$
((12))

Therefore, taking into account (12), the dispersion equation of motion in a medium with friction has the form

$${{\sin (k{l_0})} \over {k{l_0}}}\left( {1 + {{ip{\sigma _{00}}} \over k}} \right) = {{k_s^2} \over {{k^2}}}.$$
((13))

In a granular medium with small contact zones, their area differs little from the corresponding area on the spherical surface, and therefore

$${4 \over 3}{r_0}{\sigma _0} = 4(1 - f)$$

and

$${3 \over {{r_0}}} = 3{{\pi n{\rho ^2}} \over {4\pi r_0^3}} + {\sigma _0} = 3{{\pi n{\rho ^2}} \over {4\pi r_0^3}} + {{3(1 - f)} \over {{r_0}}}.$$
((14))

Here, 3πnρ2/(4πr03) is the specific contact area, n is the average number of contact zones, ρ is the contact radius, r0 is the grain radius, and σ0 is the specific matrix-fluid contact area.

Hence follows

$${\sigma _{00}} = 3{{\pi n{\rho ^2}} \over {4\pi r_0^3}} = f{\sigma _0},$$
((15))

where f is the porosity. The value of σ0 is measured either by mercury porosimetry or by the gas sorption method.

4. FREQUENCIES UNDER STATIC LOAD

Taking into account relations (14) and (15), Eq. (13) can be rewritten as

$$k{l_0}\sin (k{l_0})\left( {1 + ip{{4f} \over {k{l_0}}}} \right) = {({k_s}{l_0})^2}.$$
((16))

Under static load, this equation is equivalent to

$$k{l_0}\sin (k{l_0})\left( {1 + ip{{4f} \over {k{l_0}}}} \right) = 0.$$
((17))

Equation (17) has a set of real roots k = 0 (conventional statics) and k = πm/l0 (emission in a microheterogeneous medium). In addition, setting the parenthesis to zero gives the complex root k = –ip(4f/l0). This solution increases or decreases without limit, i.e. unstable processes also occur.

If we assume that the crack spacing is a random variable and can be represented in the form l = l0ξ, where ξ is the random variable with gamma distribution, then a different dispersion equation is valid. For gamma distribution, the probability density function is given by the following formula:

$$f = {{{\beta ^\alpha }} \over {\Gamma (\alpha )}}{x^{\alpha - 1}}{e^{ - \beta x}},$$
((18))

which is plotted in Figs. 2 and 3 at different distribution parameters.

Fig. 2.
figure 2

Deterministic type of the gamma distribution.

Full size image
Fig. 3.
figure 3

Turning of the gamma distribution to a normal one at high α.

Full size image

The requirement for a unit expected value entails the equality α = β. In this case, the dispersion σ is expressed by the single parameter α = 1/σ2.

Figure 2 shows the distribution density corresponding to distribution function (18). A special role is played by the parameter α = 1, at which the gamma distribution turns into an exponential distribution. The exponential distribution points to the importance of extra small particles with a very large specific surface area in the rock volume.

In this case, the continuum operator has a kernel containing gamma distribution, 0 < ξ < ∞, and takes the form

$$P({D_x},\;{D_y},\;{D_z};\;\alpha ,\;{l_0}\xi ) = {1 \over {4\pi }}\int\!\!\!\int {{\rm{d}}\omega } \int\limits_0^\infty {[{\xi ^{\alpha - 1}}\exp ( - \alpha \xi ){\rm{d}}\xi ]\exp [{l_0}\xi ({D_i}{n_i}){\rm{d}}\xi ,} $$
((19))

where α = 1/σ2 is the inverse dispersion of the random crack spacing. With Poisson’s formula (3), this integral can be calculated exactly:

$$P({D_x},\;{D_y},\;{D_z};\;\alpha ,\;{l_0}) = {\alpha \over {\alpha - 1}}{{{{(1 - \sqrt \Delta {{{l_0}} \mathord{\left/ {\vphantom {{{l_0}} \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}^{1 - \alpha }} - {{(1 + \sqrt \Delta {{{l_0}} \mathord{\left/ {\vphantom {{{l_0}} \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}^{1 - \alpha }}} \over {2{l_0}\sqrt \Delta }}.$$
((20))

As α → ∞, formula (20) takes the form (3). As α → 1, the averaging operator is simplified:

$$P({D_x},\;{D_y},\;{D_z};\;\alpha ,\;{l_0}) \to {{{\rm{arctan}}({l_0}\sqrt \Delta )} \over {{l_0}\sqrt \Delta }} = E - {{l_0^2\Delta } \over 3} + {{l_0^4\Delta \Delta } \over 5} - ...,\;{l_0}\sqrt \Delta < \alpha .$$
((21))

The roots of the corresponding dispersion equation are real, so that no catastrophes are possible in this case.

5. INTERMEDIATE STATES BETWEEN STATICS AND DYNAMICS

The difference in the operators P – E is zero for a continuum, while it is the sum of successively applied Laplace operators for microheterogeneous media. Thus, the equilibrium equation for large scales may be invalid for small scales. The simplest equation reflecting this phenomenon has the form

$$P\left( {{{\partial {\sigma _{ik}}} \over {\partial {x_k}}}} \right) = (P - E)\rho {\ddot u_i}.$$
((22))

The dispersion equation can be derived by substituting Δ1/2 → ikl0. In the frequency domain, operator (20) is represented as

$$P({D_x},\;{D_y},\;{D_z};\;\alpha ,\;{l_0}) = {{\exp [ik{l_0}(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })] - \exp [ - ik{l_0}(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })]} \over {2i(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}} = {{\sin k{l_0}(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })} \over {k{l_0}(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}}.$$
((23))

The dispersion equation corresponding to (16), accurate to the order 1/α2, is written in the form

$${{\sin k{l_0}(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })} \over {k{l_0}(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}} = {\left( {{{{k_s}{l_0}} \over {k{l_0}}}} \right)^2}\left( {{{\sin k{l_0}(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })} \over {k{l_0}(1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}} - 1} \right).$$
((24))

It can also be rewritten in the form

$${\left( {{z \over {\varepsilon (1 - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}}} \right)^2} = {{{{\sin z} \mathord{\left/ {\vphantom {{\sin z} z}} \right. \kern-\nulldelimiterspace} z} - 1} \over {{{\sin z} \mathord{\left/ {\vphantom {{\sin z} z}} \right. \kern-\nulldelimiterspace} z}}},$$
((25))

if we put z = kl0 = x + iy, ε = ksl0.

In Eq. (25), for real z, the left-hand side is always positive, and the right-hand side changes sign. Therefore, there are no real or complex roots for low z. This is an equilibrium state. However, in the general case, at given ε, there is a countable set of roots, both real and complex. The presence of real roots means the generation of waves that should not exist in a continuum. Complex roots mean unstable solutions (catastrophes or quiescence), where the real part determines the velocity of propagation of catastrophes at a given frequency, and the imaginary part indicates the degree of growth or decay of solutions. By the catastrophe velocity is meant the velocity of transition from one state to another. In the absence of dispersion (α → ∞), the first roots (the lowest in absolute value) of Eq. (25) were found as follows: formal expression of ε2 by (25) gives two surfaces (real and imaginary parts) dependent on x and y. Figure 4 shows the dependence of the real part of ε2 on the real (horizontal axis) and imaginary (vertical axis) parts of the variable z. The roots of Eq. (25) are points of intersection of the ε isolines with the curve Im(ε2) = 0 (pink line) corresponding to positive ε. Blue regions in Fig. 4 correspond to negative values of ε2, i.e. there are no roots. The domains of existence of possible roots of Eq. (25) are shown in yellow, red, and green. Points of intersection of the ε isolines (black lines) with the horizontal axis are the real roots of (25). It can be seen that, at ε < π, there are no real or complex roots on the horizontal axis, i.e. the equilibrium equation holds in this region. At ε ≥ π, real roots appear, which means that wave phenomena occur. Real roots close to the isolines ε ≈ 0 correspond to the velocities of usual seismic waves, and ε values about several units correspond to waves of anomalously low velocities (tens of centimeters per second). As for complex roots, the case is more complex. In the neighborhood of the coordinates x = 4.6, y = 2.8, there is the first complex root. The rest are repeated with a period approximately equal to 2π. The pink lines that intersect the ε isolines in the figure are the locus of possible complex roots, and the points of intersection of these lines with the ε isolines are the desired complex roots. In this case, the positions of the intersection points correspond to very high values ε = 5 or more. For river sand with the particle sizes 1–2 mm, this corresponds to frequencies of the order of several megahertz. In addition, poles arise in the vicinity of complex roots, where the ε isoline values vary from 10 to infinity. This means that catastrophes are possible at frequencies of the order of several megahertz and are not registered in the kilohertz frequency range. Experimental detection of such short waves is very difficult on account of their rapid attenuation. In this work, megahertz frequencies were not registered, but their existence (and quick attenuation) can be suggested by the appearance of crushed particles (8 vol %) and dusty submicroparticles. The catastrophe velocities vary in a wide range and are determined by a rapid change in the parameter ε in the vicinity of the poles. Low values (several units) of this quantity give very low catastrophe velocities (of the order of centimeters per second), and very high values (in the vicinity of the poles) give velocities of the order close to that of the velocity of transverse waves. These velocities decrease at high dispersion α → 1 and disappear completely at α = 1. A discrete set of roots (real and complex) means that the wave field in porous and fractured media has a quantized pattern, so that the transition from one state to another (each root corresponds to a certain state) requires some portion of energy.

Fig. 4.
figure 4

Dependence of the real part of ε2 from Eq. (25) on the real and imaginary parts of the complex variable z. Roots of Eq. (25) are the points of intersection of the ε isolines with the curve Im(ε2) = 0 (pink line) corresponding to positive ε (color online).

Full size image

6. INTEGRABLE SINGULARITIES IN THE GAMMA DISTRIBUTION. BELL SANDS

In the case α < 1, the gamma distribution has an integrable singularity. For very high dispersions, for which the following inequality holds:

$$({1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha } - 1)k{l_0} > > 1,$$

the continuum operator turns out to be different:

$$P({D_x},\;{D_y},\;{D_z};\;\alpha ,\;{l_0}) = - \left( {{{{{( - 1)}^{1 - \alpha }}{{({{ik{l_0}} \mathord{\left/ {\vphantom {{ik{l_0}} \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}^{1 - \alpha }}} \over {2{{ik{l_0}} \mathord{\left/ {\vphantom {{ik{l_0}} \alpha }} \right. \kern-\nulldelimiterspace} \alpha }}} - {{{{({{ik{l_0}} \mathord{\left/ {\vphantom {{ik{l_0}} \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}^{1 - \alpha }}{{({{ik{l_0}} \mathord{\left/ {\vphantom {{ik{l_0}} \alpha }} \right. \kern-\nulldelimiterspace} \alpha })}^{1 - \alpha }}} \over {2{{ik{l_0}} \mathord{\left/ {\vphantom {{ik{l_0}} \alpha }} \right. \kern-\nulldelimiterspace} \alpha }}}} \right).$$
((26))

Taking into account that (kl0/α)–α → 1 at α → 0, we obtain an approximate representation with an accuracy of the order α2:

$$P({D_x},\;{D_y},\;{D_z};\;\alpha ,\;{l_0}) \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}[\exp (2m\pi i\alpha ) + \exp (4m\pi i\alpha )].$$
((27))

Formally, at α → 0, we have a unity operator. However, m can be an arbitrary high integer. If α is a rational integer, then the number of complex roots corresponding to operator (27) is finite; otherwise it is infinite. Thus, the dispersion equation for very high dispersions of microstructural parameters takes the form of an attractor:

$${k^2} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}[\exp (2m\pi i\alpha ) + \exp (4m\pi i\alpha )]k_p^2.$$
((28))

As α → 0, one of the solutions to (25) (k = 0) is the usual equilibrium state. However, for an arbitrary low α, there exist complex roots (a finite or infinite set) corresponding to one or another local catastrophe. This scheme describes a variety of unstable states, which cause dynamic phenomena in the large-scale equilibrium state. At α → 0, the solution to the dispersion equation (k = 0) is the usual equilibrium state, while, for arbitrary low α, there is a very large or even infinite number of complex solutions that correspond to catastrophes of different scales. The related vibration frequencies have no upper limits, although the characteristic frequencies due to the finite time of the experiment, corresponding to the inverse loading time, are approximately 0.1 Hz.

7. EXPERIMENTAL RESULTS

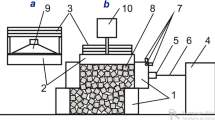
The specimen was coarse sand with the grain sizes 2–3 mm, which was placed in a section of the steel pipe with a diameter of 40 mm and a height of 80 mm [14]. An SV-20 seismic receiver was attached to the outer wall of the pipe. The specimen was loaded using a vertical press through the upper and lower holes of the tube section. The general view of the model is shown in Fig. 5.

Fig. 5.
figure 5

Schematic of pressure loading of sand.

Full size image

The experiment was carried out as follows. Once the recording system was on, pressure was applied to the specimen through the upper piston. Pressure was registered by a pressure gauge, and the displacement of the piston was measured by a mechanical sensor. The pressure was increased to 6 MPa within 10 s and kept at this level for another 10 s. Acoustic emission began from almost “zero” pressure and continued after the pressure pump stopped operating.

Acoustic emission in compressed sand begins at pressures significantly lower than the rock pressure, which is caused by “internal” stresses in sand particles and their complex surface. Spontaneous changes are observed in the intensity of acoustic emission. Figure 6 shows a general view of the vibration records. Along with the vibration receiver, a microphone was used in the experimental scheme, so that the frequency range and overtones were also monitored by ear.

Fig. 6.
figure 6

General view of microseismic vibrations.

Full size image

The frequencies associated with destruction of individual particles are about several megahertz and were experimentally undetected. This means that collective processes are registered. For low dispersions of particle sizes, from 0.00 to 0.05, the catastrophe velocity should be of the order of the Rayleigh velocity. However, according to the calculation data in Fig. 4, for high dispersions of particle sizes σ2 = 1/α in the range from 1.0 to 0.2, the catastrophe velocity should change from 0.0 to 0.1 of these velocities. Short pulses (1000 Hz) were also recorded, following each other at one second interval. These short pulses can be interpreted as disturbances corresponding to the first real roots of the dispersion equation and anomalously low velocities from 10 cm/s to 2 m/s. The repetition frequency of these short pulses is approximately 1 Hz. Vibration recording is performed at frequencies from 30 to 1000 Hz (Figs. 7, 8). However, it is possible that megahertz frequencies appear but quickly attenuate, which is evident from the presence of many crushed particles (8 vol %) of submicron size.

Fig. 7.
figure 7

Dependence of the number of events on their frequency. No events occur in the low-frequency region with the characteristic loading time 10 s and characteristic frequency 0.1 Hz as well as in the frequency region above 1000 Hz.

Full size image
Fig. 8.
figure 8

Distribution of events versus the time of static loading. Short millisecond pulses are relatively uniformly distributed in the time interval from 2 to 17 s.

Full size image

High dispersion, i.e. low values of α, is confirmed by a large number of wave events after loading (10). In addition, the presence of dusty particles appears to have a significant effect on the gamma distribution. Indeed, setting α = β, neglecting the exponent, and integrating over a small interval from 0 to α in distribution (18) give the approximate formula

$$F(\alpha ) = {{{\alpha ^\alpha }} \over {\Gamma (\alpha )}}\int\limits_0^\alpha {{z^{\alpha - 1}}{\rm{d}}z = } {{{\alpha ^{2\alpha }}} \over {\Gamma (\alpha + 1)}} \approx 1.$$
((29))

Thus, very small particles compared to the average size l0 have a decisive influence on the distribution function. 125 events were experimentally recorded, which can be considered a fairly large number compared to unity. This means that the number of catastrophic solutions implemented in the experiment is quite large.

Despite the fact that about 8% of the grains were destroyed during quasi-static loading, the parameters of the emitted waves were approximately the same throughout the experiment. For this reason, medium restructuring should be considered an unlikely cause of emission. The real reason is evidently the significant difference in the stress state in the vicinity of a medium microvolume, i.e. instability of the equilibrium state.

8. CONCLUSIONS

Microheterogeneous media contain a large (theoretically infinite) number of degrees of freedom. Therefore, both the state of equilibrium and of motion are described by infinite-order partial differential equations.

Equilibrium or motion does not have an absolute meaning for microheterogeneous media in that equilibrium can exist on large scales and be absent on small scales. Thus, intermediate states arise between statics and dynamics, which do not occur in a continuum. These phenomena appear to underlie seismic emission.

The emission frequencies are related neither to the characteristic time of static loading of the specimen, nor to the characteristic time of destruction of individual particles, but are the reaction of a certain set of particles to slow deformation. The lack of dispersion (periodic structures) also leads to a set of unstable states. Low dispersions stabilize the medium (reduce the number of unstable solutions until they disappear), while high dispersions destabilize it again.

High dispersions of particle sizes cause a set (theoretically unlimited) of elementary catastrophic events. 125 such events were experimentally recorded within 9 s, which can be considered a fairly large number compared to 1.