Equation of State of the H₂O–CO₂–CaCl₂ Fluid System and Properties of Fluid Phases at Р-Т Parameters of the Middle and Lower Crust

Abstract

A numerical thermodynamic model is proposed for one of the most important geological fluid system, ternary H₂O–CO₂–CaCl₂ system, at P-T conditions of the middle and lower crust and crust–mantle boundary. The model is based on the previously proposed equation for concentration dependence of the excess Gibbs free energy and on the first obtained P-T dependencies of the coefficients of the equation of state (EOS) expressed via molar volumes of the components. The EOS allows to predict the properties of the fluid participating in the majority of deep petrogenetic processes: its phase state (homogeneous or multi-phase), densities of fluid phases, concentrations of components in the co-existing phases, and the chemical activities of the components. The model precisely reproduces all available experimental data on the phase state of the ternary H₂O–CO₂–CaCl₂ fluid system in the ranges of temperatures 773.15–1073.15 K and pressures 0.1–0.9 GPa and also allows the correct application of the EOS beyond the experimentally studied range of temperatures and pressures up to P = 2 GPa and T = 1673.15 K. The possibility of the correct extrapolation of our EOS is ensured by using the parametrization of P-T dependencies via the molar volume of water. The latter remains in the experimental domain of values or falls slightly beyond its boundaries, when increasing temperatures and pressures.

INTRODUCTION

Deep fluids play an important role in the crustal petrogenesis and in the transportation of deep-seated matter to the upper crust. With ascent to the surface, the temperature (T) and pressure (P) of the deep fluids significantly change, which is accompanied by a change of the chemical activities of fluid components, the degree of dissociation of dissolved electrolytes, and fluid acidity. All these facts make relevant the theoretical study of the thermodynamics of natural fluids. Aqueous fluids usually contains chlorides of alkali and alkali-earth metals and non-polar gases, in particular, CO₂. Fluids of such composition play significant role in the formation of metamorphic mineral assemblages (e.g., Trommsdorff et al., 1985; Markl and Bucher, 1998; Heinrich et al., 2004; Manning and Aranovich, 2014). Together with the widest spread NaCl, the CaCl₂ is also an important component of natural aqueous–salt fluids. The CaCl₂-rich fluids, including those containing CO₂, significantly contribute to the metamorphic and metasomatic processes and the transportation of ore matter towards the upper crust (Bischoff et al., 1996; Aranovich, 2017).

In recent years, the great interest is focused on the phenomena related to the possible heterogenization of complex fluids at high Р and Т. Thermodynamic models available for the H₂O–CO₂–NaCl ternary system make it possible to describe its phase state and to obtain important thermodynamic characteristics at high temperature and pressure. Modern models are available for upper crustal P-T conditions (Sun and Dubessy, 2012; Dubacq et al., 2013). Models for the highest P-T conditions were developed in (Duan et al., 1995; Aranovich et al., 2010). At the same time, models for another important fluid system, the ternary H₂O–CO₂–CaCl₂ system, are absent. The aim of this work is to construct the thermodynamic model of the H₂O–CO₂–CaCl₂, system for the middle–lower crustal P-T conditions.

THEORETICAL METHOD

Gibbs Free Energy

A thermodynamic model of the H₂O–CO₂–CaCl₂ system for high pressures and temperatures was developed in this work on the basis of the equation for the excess Gibbs free energy. The form of concentration dependence of the Gibbs free mixing energy ${{G}^{{{\text{mix}}}}}$ (J/mol) coincides with that proposed for the H₂O–CO₂–NaCl ternary system in (Aranovich et al., 2010). The cited work also reports the corresponding formulas for the calculation of the activities of components of the ternary system. In our case, the Gibbs free energy for temperature (T, K), pressure $P$, and molar fractions of components ${{x}_{1}} = {{x}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$, ${{x}_{2}} = {{x}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$, ${{x}_{3}} = {{x}_{{{\text{CaC}}{{{\text{l}}}_{{\text{2}}}}}}}$ ($\sum {{{x}_{i}}} = 1$) can be written as follows:

$${{G}^{{{\text{mix}}}}} = {{G}^{{{\text{id}}}}} + {{G}_{{\alpha }}} + {{G}^{{{\text{ex}}}}},$$

((1))

$${{G}^{{{\text{id}}}}} = RT({{x}_{1}}\ln {{x}_{1}} + {{x}_{2}}\ln {{x}_{2}} + {{x}_{3}}\ln {{x}_{3}}),$$

((2))

$$\begin{gathered} {{G}_{\alpha }} = - {{x}_{1}}RT\ln \left[ {{{1 + \alpha {{x}_{3}}} \mathord{\left/ {\vphantom {{1 + \alpha {{x}_{3}}} {({{x}_{1}} + {{x}_{3}})}}} \right. \kern-0em} {({{x}_{1}} + {{x}_{3}})}}} \right] \\ + \,\,{{x}_{3}}\left\{ {(1 + \alpha )RT\ln (1 + \alpha ) + \alpha RT\ln \left[ {{{{{x}_{3}}} \mathord{\left/ {\vphantom {{{{x}_{3}}} {({{x}_{1}} + {{x}_{3}})}}} \right. \kern-0em} {({{x}_{1}} + {{x}_{3}})}}} \right]} \right. \\ \left. { - \,\,(1 + \alpha )RT\ln \left[ {1 + {{\alpha {{x}_{3}}} \mathord{\left/ {\vphantom {{\alpha {{x}_{3}}} {({{x}_{1}} + {{x}_{3}})}}} \right. \kern-0em} {({{x}_{1}} + {{x}_{3}})}}} \right]} \right\}, \\ \end{gathered} $$

((3))

$$\begin{gathered} {{G}^{{{\text{ex}}}}} = {{x}_{1}}{{x}_{2}}{{W}_{1}}(P,T){{\rho }_{{12}}}({{x}_{1}},{{x}_{2}}) + {{x}_{1}}{{x}_{3}}{{W}_{2}}(P,T) \\ {{ + \,\,{{x}_{2}}{{x}_{3}}[{{x}_{2}}{{W}_{3}}(P,T) + {{x}_{3}}{{W}_{4}}(P,T)]} \mathord{\left/ {\vphantom {{ + \,\,{{x}_{2}}{{x}_{3}}[{{x}_{2}}{{W}_{3}}(P,T) + {{x}_{3}}{{W}_{4}}(P,T)]} {({{x}_{2}} + {{x}_{3}})}}} \right. \kern-0em} {({{x}_{2}} + {{x}_{3}})}} \\ + \,\,{{x}_{1}}{{x}_{2}}{{x}_{3}}{{W}_{5}}(P,T). \\ \end{gathered} $$

((4))

The term ${{G}^{{{\text{id}}}}}$ is a contribution of the ideal entropy of mixing of three components of the system to the Gibbs free energy. The term ${{G}_{{\alpha }}}$ provides an additional entropic contribution of CaCl₂ dissociation to the free energy (Aranovich and Newton, 1996, 1997). $\alpha$ is the “efficient” degree of dissociation (average additional number of particles produced by the dissociation of a CaCl₂ molecule). At complete dissociation, $\alpha = {{\alpha }_{0}} = 2$. In the equation for the excess Gibbs free energy, ${{G}^{{{\text{ex}}}}}$ the term with coefficient ${{W}_{1}}$ describes the interaction between water and CO₂ molecules. This term coincides with that from (Aranovich et al., 2010; Aranovich, 2013).

$$\begin{gathered} {{W}_{1}} = 0.202046\,\,{{{{{\text{m}}}^{3}}} \mathord{\left/ {\vphantom {{{{{\text{m}}}^{3}}} {{\text{mol}}}}} \right. \kern-0em} {{\text{mol}}}}, \\ {{\rho }_{{12}}}({{x}_{1}},{{x}_{2}}) = {{({{x}_{1}} + {{x}_{2}})} \mathord{\left/ {\vphantom {{({{x}_{1}} + {{x}_{2}})} {({{V}_{1}}{{x}_{1}} + {{V}_{2}}{{x}_{2}})}}} \right. \kern-0em} {({{V}_{1}}{{x}_{1}} + {{V}_{2}}{{x}_{2}})}}, \\ \end{gathered} $$

((5))

where ${{V}_{1}} = {{V}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ and ${{V}_{2}} = {{V}_{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}}$ are the molar volumes of pure water and CO₂ at given temperature and pressure. These two values are precisely described by empirical formulas within sufficiently wide ranges of temperatures and pressures. Water properties are described by IAPWS-95 thermodynamic model (Wagner and Pruß, 2002), which with high accuracy reproduces numerous experimental results and is applied within the entire H₂O stability field. Similar thermodynamic model was obtained for CO₂ (Span and Wagner, 1996) on the basis of high-precision experimental data for pressure up to 800 MPa and temperature up to 1100 K. The results obtained using equation (Span and Wagner, 1996) showed an excellent agreement with experimental data for temperatures up to 1600 K and pressures up to 3600 MPa (Span and Wagner, 1996). This proves that the thermodynamic description of CO₂ can be applied for the entire CO₂ stability field (Span and Wagner, 1996). For this reason, we preferred in this work the model (Span and Wagner, 1996) to the model (Zhang and Duan, 2009). Thus, the description of pressure and temperature dependence of interaction of H₂O and CO₂ molecules in our model coincides with model (Aranovich et al., 2010). Corresponding dependences for $\alpha ,\;{{W}_{2}}, \ldots ,{{W}_{5}}$ values differ sharply from those in (Aranovich et al., 2010) and will be considered below in relation with experimental data.

Derivative Thermodynamic Values

As mentioned above, our model of the Gibbs free energy provides the calculation of activities of the components of the system using formulas from (Aranovich et al., 2010). In systems consisting of three- and more components, the state of the pure component is taken as a standard state.

Another important entity obtained from our model is the density of three-component fluid. Fluid density can be obtained from its molar volume given by the following equation:

$$V = {{\left( {\frac{{\partial G}}{{\partial P}}} \right)}_{{T,{{x}_{i}}}}} = {{V}^{{{\text{mix}}}}} + {{x}_{1}}{{V}_{1}} + {{x}_{2}}{{V}_{2}} + {{x}_{3}}{{V}_{3}},$$

where

$${{V}^{{{\text{mix}}}}} = {{\left( {\frac{{\partial {{G}^{{{\text{mix}}}}}}}{{\partial P}}} \right)}_{{T,{{x}_{i}}}}}.$$

The calculation of molar volumes of H₂O and CO₂ at given temperature and pressure was described above. The molar volume of molten CaCl₂ at high pressure was obtained using an equation for molar volume of salt melts from (Driesner, 2007):

$${{V}_{3}} = ({{{{M}_{3}}} \mathord{\left/ {\vphantom {{{{M}_{3}}} {{{\rho }_{{{\text{0}}{\text{,CaC}}{{{\text{l}}}_{{\text{2}}}}}}}}}} \right. \kern-0em} {{{\rho }_{{{\text{0}}{\text{,CaC}}{{{\text{l}}}_{{\text{2}}}}}}}}})[1 - 0.1\ln (1 + {{10}^{{ - 4}}}P{{\kappa }_{{\text{T}}}})],$$

where ${{M}_{3}} = {\text{110}}{\text{.984}}$ is the molecular mass of CaCl₂, ${{\kappa }_{{\text{T}}}}$ is its isothermal compressibility, and ${{\rho }_{{{\text{0}}{\text{,CaC}}{{{\text{l}}}_{{\text{2}}}}}}}$ is its density at atmospheric pressure. According to (Janz, 1988), the density of molten CaCl₂ at atmospheric pressure linearly depends on the temperature:

$${{\rho }_{{{\text{0}}{\text{,CaC}}{{{\text{l}}}_{{\text{2}}}}}}} = 2.5261 - 4.225 \times {{10}^{{ - 4}}}T,\,\,{{\text{g}} \mathord{\left/ {\vphantom {{\text{g}} {{\text{c}}{{{\text{m}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{c}}{{{\text{m}}}^{{\text{3}}}}}}{\text{.}}$$

In (Bockris et al., 1962), the linear temperature dependence was experimentally obtained for the adiabatic compressibility ${{\kappa }_{{\text{S}}}}$ of molten CaCl₂. This work also reports experimental values for the isobaric to isochoric heat capacities ratio for the CaCl₂ melt $\gamma = {{{{C}_{{\text{P}}}}} \mathord{\left/ {\vphantom {{{{C}_{{\text{P}}}}} {{{C}_{{\text{V}}}}}}} \right. \kern-0em} {{{C}_{{\text{V}}}}}}$ for temperatures 800, 900, and 1000°C. The use of relationships between ${{\kappa }_{{\text{S}}}}$, ${{\kappa }_{{\text{T}}}}$, and $\gamma$ from equations (1) and (5) of (Bockris and Richards, 1957) allows calculation of ${{\kappa }_{{\text{T}}}}$ in this three temperature points. These values were used for obtaining the linear approximation of temperature dependence ${{\kappa }_{{\text{T}}}}$, having the following form:

$${{\kappa }_{{\text{T}}}} = 1.6264 \times {{10}^{{ - 13}}}T - 3.6753 \times {{10}^{{ - 11}}},\,\,{\text{P}}{{{\text{a}}}^{{ - 1}}}$$

A combination of presented formulas defines the temperature and pressure dependence of V₃.

Reference Experimental Data

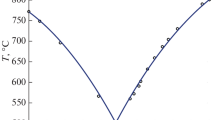
The main array of experimental data suitable for the calibration of the equation state of the ternary H₂O–CO₂–CaCl₂ system above the critical point of water is formed by experimental results on the phase state of this system (Zhang and Frantz, 1989; Shmulovich and Graham, 2004). These experiments are limited by the temperature range from 773.15 K to 1073.15 K and pressures from 100 MPa to 900 MPa. Results of these experiments are shown in Fig. 1. The numerical values of parameters, which determine the temperature and pressure dependences of values $\alpha$ and ${{W}_{2}}, \ldots ,{{W}_{5}}$, should be selected in such a way, that the boundaries between the fields of homogenous and two-phase fluids (solvus or binodal) (Diamond, 2003; Heinrich, 2007), given by our EOS, correspond to the experimental data.

Fig. 1.

Experimental and model data on the phase state of the H₂O–CO₂–CaCl₂ system. Open circles are two-phase fluid; filled circles mark homogenous fluid; solid lines show the boundary of the homogenous region (solvus) according to our model. Experimental data: (a)–(c), (e)–(g) from (Zhang and Frantz, 1989); (g)–(h) from (Shmulovich and Graham, 2004).

Approximation of P-T Dependences and Numerical Fitting

Fitting the values of $\alpha$ and ${{W}_{2}}, \ldots ,{{W}_{5}}$ for any separate pressure–temperature combination in formulas (1)–(4) could provide the model solvus completely corresponding to experimental data (Zhang and Frantz, 1989; Shmulovich and Graham, 2004). Our purpose is building a thermodynamic model suitable both for obtaining the phase state of the fluid and for the calculation of a wider range of thermodynamic parameters beyond the studied P and T combinations. The crucial point for this program is finding the forms of dependencies of parameters $\alpha ,\;{{W}_{2}}, \ldots ,{{W}_{5}}$ on the temperature and pressure, which reproduce experimental data in a maximal wide range of P and T values using a minimal possible number of empirical coefficients.

We begin to consider the temperature and pressure dependences of the model from value $\alpha$. The degree of dissociation of CaCl₂ molecules in a fluid should depend on all parameters determining the system. An accurate form of this dependence is unknown and cannot be obtained in the framework of this work. However, the aim of this work is to obtain the thermodynamic description for the H₂O–CO₂–CaCl₂ system, which is consistent with experimental data. This can be approached by reasonable approximation of the temperature and pressure dependence for $\alpha$ value.

The degree of dissociation of CaCl₂ molecules depends on the water density. On the one hand, if temperature is insufficiently high to cause dissociation in a gaseous phase, the degree of dissociation tends to zero as the water density approaches zero. On the other hand, the degree of dissociation of a strong electrolyte CaCl₂ at high water density is expected to be close to maximum $\alpha = {{\alpha }_{0}} = 2$. These conditions can be satisfied by the formula:

$$\alpha ({{V}_{1}}) = \frac{{{{\alpha }_{0}}}}{{1 + {{a}^{2}}\left[ {\sqrt {{{{({{V}_{{\text{1}}}} - {{V}_{0}})}}^{2}} + {{q}^{2}}} + {{V}_{{\text{1}}}} - {{V}_{0}}} \right]}}$$

((6))

with parameters a, ${{V}_{0}}$ and q providing a smooth transition from $\alpha ({{V}_{1}}) \approx {{\alpha }_{0}}$ at ${{V}_{1}} < {{V}_{0}} - q$ to $\alpha ({{V}_{1}}) \approx {{{{\alpha }_{0}}} \mathord{\left/ {\vphantom {{{{\alpha }_{0}}} {[1 + 2{{a}^{2}}({{V}_{1}} - {{V}_{0}})]}}} \right. \kern-0em} {[1 + 2{{a}^{2}}({{V}_{1}} - {{V}_{0}})]}}$ at ${{V}_{1}} > {{V}_{0}} + q$ with a transitional area 2q wide in the vicinity ${{V}_{1}} = {{V}_{0}}$. A formula similar to the denominator in equation (6) was used in (Ivanov, 2001) to provide a smooth transformation of real coordinates to the complex rotation coordinates in the Schrödinger equation. Since an accurate form of the dependence of dissociation is unknown, we applied formula (6) with parameters a, ${{V}_{0}}$, and q determined on the basis of the experiments. Such an approach is sufficient to describe the available experimental material.

To determine the temperature and pressure dependences of ${{W}_{2}}, \ldots ,{{W}_{5}}$ coefficients corresponding to experimental data, a numerical fitting of ${{W}_{2}}, \ldots ,{{W}_{5}}$ values was performed for each P-T combination experimentally studied in (Zhang and Frantz, 1989; Shmulovich and Graham, 2004).

As well as in the case of the complete set of experimental data (see below), the numerical values of the parameters were calculated by minimization of function that depends on the distance from phase boundary (determinable by model parameters) to experimetal points appearing at given parameters in the “incorrect” fields. This function can be either a sum of squares of these distances or a sum of these distances raised to a power less than two, that provides a greater robustness of the minimization algorithm. In the presented calculation, the minimization was carried out for the sum of distances to the power of 1.25, which ensures the lesser influence of scattered experimemntal points on the result. Details of calculation technique will be published in a separate work.

The Gibbs free energy calculated using ${{W}_{2}}, \ldots ,{{W}_{5}}$ values obtained for separate P-T combinations determines the boundary between the homogenous fluid and two-phase fluid (solvus) consistent with experimental data. Since experimental data are sufficiently far apart from each other and do not form continuous fields, such determination of ${{W}_{2}}, \ldots ,{{W}_{5}}$ values is ambiguous and serves only as a tool for identifying their P-T dependences. Analysis of the obtained data showed that the available set of experimental data could be described by the linear dependence of ${{W}_{2}}, \ldots ,{{W}_{5}}$ on the molar volume of water

$${{W}_{i}}(P,T) = {{u}_{{i0}}} + {{u}_{{i{\text{1}}}}}{{V}_{{\text{1}}}}(P,T),\,\,\,\,i = 2, \ldots ,5.$$

((7))

Analysis of pressure dependences of properties of deep-seated fluids containing water (Manning, 2018) shows a more smooth change of their physicochemical parameters with increasing pressure in the pressure region more than 0.5 GPa (middle and lower crustal conditions) than at relatively low pressures. The same behavior is typical of the molar volume of water (Fig. 2), which causes the corresponding behavior of ${{W}_{2}}, \ldots ,{{W}_{5}}$. From the physical point of view, it is also more reasonable to describe the interaction of water molecules with molecules of dissolved matter through the molar volume of water rather than through pressure. Pressure is an external factor determining the molar volume of water. The complex pressure dependence of this value (Wagner and Pruß, 2002) is based on experimental data, the number and accuracy of which are orders of magnitude higher than the data on the water interaction with dissolved matters. The physical interaction of molecules of water and dissolved matter described by values ${{W}_{2}}, \ldots ,{{W}_{5}}$ first of all depends on the intermolecular distances determined by molar volume.

Fig. 2.

Pressure dependencies of the molar volume of water at several temperature values.

Solid and Molten Phases of CaCl₂

At some proportions of components in the H₂O–CO₂–CaCl₂ system, fluid phase could coexist with solid or molten CaCl₂ phases. Unlike fluid phases, experimental data on thermodynamics of solid CaCl₂ at pressures above atmospheric one, including its melting temperature, are absent. At the same time, a number of experimental data is available on the pressure dependence of the melting temperatures of Na halides (Pistorius, 1966). For these compounds, the experimental pressure dependences of the melting temperature T_m(P) are precisely approximated by the Simon equation (Simon and Glatzel, 1929; Pistorius, 1966):

$${{T}_{{\text{m}}}}(P) = {{T}_{0}}{{\left[ {{{(P - {{P}_{0}})} \mathord{\left/ {\vphantom {{(P - {{P}_{0}})} {A + 1}}} \right. \kern-0em} {A + 1}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 c}} \right. \kern-0em} c}}}},$$

where P₀ could be taken to be zero, while T₀ is the melting temperature at the atmospheric pressure. Experimentally established values of A and c parameters for NaCl are 15 kbar and 2.969, respectively. The value Ac determines the initial slope of melting curve:

$${{\left( {{{d{{T}_{{\text{m}}}}} \mathord{\left/ {\vphantom {{d{{T}_{{\text{m}}}}} {dP}}} \right. \kern-0em} {dP}}} \right)}_{{P = 0}}} = {{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} {(Ac)}}} \right. \kern-0em} {(Ac)}}.$$

At the same time, the value of Ac can be determined from equation:

$${{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} {(Ac)}}} \right. \kern-0em} {(Ac)}} = {{\left( {{{\Delta {{V}_{{\text{f}}}}} \mathord{\left/ {\vphantom {{\Delta {{V}_{{\text{f}}}}} {\Delta {{S}_{{\text{f}}}}}}} \right. \kern-0em} {\Delta {{S}_{{\text{f}}}}}}} \right)}_{{P = 0}}}$$

(Pistorius, 1966), where $\Delta {{V}_{{\text{f}}}}$ is a change of the molar volume during melting, and $\Delta {{S}_{{\text{f}}}}$ is the corresponding change of the entropy. The difference between values of $\Delta {{S}_{{\text{f}}}}$ for NaCl and CaCl₂ is relatively small: they are 26.223 and 27.314 J/K/mol, correspondingly (Chase, 1988). However, the values of $\Delta {{V}_{{\text{f}}}}$ for these two compounds are sharply different and are 7.55 cm³/mol for NaCl vs. 0.49 cm³/mol for CaCl₂ (Schinke and Sauerwald, 1952). This implies that T_m of CaCl₂ shows the slower increase with pressure than that of NaCl. For complete melting curve, c was taken to be 2.969, which yields T_m = 1084 K at 2 GPa against T₀ = 1045 K, whereas for NaCl T₀ = 1074 K and T_m = 1357 K at 2 GPа.

For CaCl₂ as well as for other easily soluble salts, a complete miscibility with water is supposed at temperatures above the melting point (Shmulovich and Graham, 2004; Sterner et al., 1992; Chou I-Ming, 1987). Below the melting point, the presence or absence of crystalline CaCl₂ in equilibrium with its aqueous solution is determined by a change of CaCl₂ chemical potential $\Delta \mu (T)$ while passing from solid to liquid phase. For atmospheric pressure, this value as a function of temperature could be obtained from thermodynamic tables (Chase, 1988). For higher pressures, we applied the same function with a modified temperature $\Delta \mu (T - {{T}_{{\text{m}}}} + {{T}_{0}})$.

RESULTS

Correspondence between Model Results and Experimental Data

Correspondence of thermodynamic model (1)–(7) to experimental results was confirmed by the joint fit of parameters ${{u}_{{i0}}},\,{{u}_{{i{\text{1}}}}},\,a,\,{{V}_{0}},\,q$. Obtained numerical values of parameterts of the model are given in Table 1, while solvuses obtained using these parameters are shown as solid lines in Fig. 1. It is seen that that experiemtal data are well consistent with theoretical predictions of our model. Along with (Zhang and Frantz, 1989; Shmulovich and Graham, 2004), experimental data on the considered system were obtained by Shmulovich and Plyasunova (1993). Later, these data were critically revised in (Shmulovich and Graham, 2004, 1999). According to the explanations in these works, results obtained by Shmulovich and Plyasunova (1993) contain a systematic error, which decreases with increasing temperature. Thus, the results of this work for T = 773.15 K are unsuitable for application. However, there is a shortage in experimental data for pressures above 0.3 GPa. Therefore, data by (Shmulovich and Plyasunova, 1993) for P = 0.5 GPa and T = 973.15 K were used in addition to data by (Zhang and Frantz, 1989; Shmulovich and Graham, 2004), but with much lower statistical weight.

Table 1.   Numerical parameters of the model according to equations (1)–(7)

Phase Relations at Different Temperatures and Pressures

Examples of phase diagrams for the H₂O–CO₂–CaCl₂ system at different T and P both below and above the melting point are given at Figs. 3–8. Figure 3 demonstrates the general shape of the phase diagram of the system H₂O–CO₂–CaCl₂ at T < T_m. The diagram comprises five fields, which differ in number of fluid phases and in the presence or absence of solid CaCl₂. At relatively low concentrations of CO₂ and CaCl₂, the system exists as a homogenous fluid. An increase of concentrations of these components at moderate fraction of CO₂ leads to fluid splitting into two phases: CO₂-dominated low-CaCl₂ phase and low-CO₂ high-CaCl₂ phase. An increase of the CaCl₂ content both in homogenous and two-phase fluid regions leads to the appearance of solid CaCl₂ in association with a fluid. At extremely high fraction of CO₂, the system consists of solid CaCl₂ coexisting with CO₂–dominated fluid with some amount of water and negligibly low fraction of CaCl₂.

Fig. 3.

A general form of phase diagram for the H₂O–CO₂–CaCl₂ system at temperatures below the melting point of CaCl₂ (T = 773.15 K, P = 1.2 GPa). Bold lines are the boundaries of the two-fluid field. Thin line shows the boundaries of the stability field of the solid CaCl₂.

Fig. 4.

Phase diagram for the H₂O–CO₂–CaCl₂ system at T = 773.15 K and P = 0.2 GPa.

Fig. 5.

Phase diagram for the H₂O–CO₂–CaCl₂ system at T = 973.15 K and P = 0.5 GPa.

Fig. 6.

Phase diagram for the H₂O–CO₂–CaCl₂ system at temperature above the CaCl₂ melting point (T = 1123.15 K and P = 0.5 GPa).

Fig. 7.

Phase diagram for the H₂O–CO₂–CaCl₂ system at T = 1123.15 K and P = 0.9 GPa.

Fig. 8.

Phase diagram for the H₂O–CO₂–CaCl₂ system at T = 1073.15 K and P = 0.5 GPa.

Phase diagram in Fig. 3 is constructed for T = 773.15 K and P = 1.2 GPa. At these parameters, all fields of possible phase states of the system are well seen. The molar volume of water V₁ = 17.2 cm³/mol at these parameters is lower than its minimum values in the experimental region (V₁ = 23.3 cm³/mol at T = 773.15 K, P = 0.3 GPa; V₁ = 21.1 cm³/mol at T = 1073.15 K, P = 0.9 GPa). Similar phase diagrams for the experimental ranges of parameters are given in Figs. 4 and 5. For these parameters, the coexistence field of saturated brine and crystalline chloride lies closely to the H₂O–CaCl₂ axis, which implies practically zero CO₂ solubility in CaCl₂-saturated solutions.

Phase diagrams of the system at T > T_m are shown in Figs. 6–8. They have simpler form than at T < T_m. In addition to the fields of homogenous fluid and two coexisting fluid phases, these diagrams could contain the coexistence field of molten CaCl₂ and CO₂-dominated fluid with some amount of water and negligible amount of CaCl₂. With growing pressure, this field becomes more narrow and, finally, disappears (Figs. 6 and 7). An increase of temperature leads to some widening of this field (Figs. 8 and 6).

Activities of Components

Our thermodynamic model includes a complete description of the Gibbs free energy, which makes it possible to calculate the activities of the system components. In particular, the calculation of water activities in the solvus (boundary between homogenous and two-phase fluids) provides the determination of compositions of coexisting fluid phases in the two-phase field.

Curves of water and CaCl₂ activities along the solvus are shown in Fig. 9. In the extreme right and left points of the figure, the water activity has equal values of 0.4. These points correspond to two coexisting fluid phases, whose compositions correspond to ends of a tie line in Fig. 10. The upper horizontal line in Fig. 9 corresponds to the water activity of 0.5, which is shown as the shorter tie line in Fig. 10. This figure also shows the lines of equal water activities in the field of a homogenous fluid. The maximum value of water activity in Fig. 9 corresponds to the critical point at given P-T parameters. In contrast, the CaCl₂ activity is minimum in the critical point and increases with distance from it. Isolines of CaCl₂ activities and tie lines linking the points corresponding to the compositions of coexisting phases are shown in Fig. 11. It is obvious that CaCl₂ activity increases with increase of its molar fraction. However, for coexisting fluid phases, activities are equal for each of the three components. The compositions of coexisting phases corresponding to the tie lines with CaCl₂ activity of 0.2 or 0.3 are largely different. The upper ends of these tie lines correspond to the concentrated water–salt solutions with the extremely low CO₂ content. In contrast, the low end of the tie lines corresponds to water–CO₂ fluids with low salt content. Nevertheless, the activity of CaCl₂ in these fluids is similarly high to that of concentrated water–salt solutions.

Fig. 9.

Activities of water and CaCl₂ along solvus at Т = 1123.15 К and Р = 0.9 GPa.

Fig. 10.

Activity of water depending on the composition of a homogenous fluid H₂O–CO₂–CaCl₂ at Т = 1123 K and Р = 0.9 GPa. Bold solid line (solvus) separates the regions of homogenous and two-phase fluid, dashed lines are tie lines linking the coexisting fluid phases, thin solid lines are the isolines of ${{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$—the chemical activity of water.

Fig. 11.

Activity of CaCl₂ depending on the composition of a homogenous fluid H₂O–CO₂–CaCl₂ at Т = 1123 К and Р = 0.9 GPa. Bold solid line (solvus) separates the regions of homogenous and two-phase fluid, dashed lines are tie lines linking the coexisting fluid phases, thin solid lines are the isolines of ${{a}_{{{\text{CaC}}{{{\text{l}}}_{{\text{2}}}}}}}$—the chemical activity of CaCl₂.

Density of Fluids

The transport and physicochemical properties of a fluid are mainly determined by its density (Driesner, 2007; Mao et al., 2015; Manning, 2018). Figure 12 exemplifies the calculation of density of three-component fluid according to our model. At T = 850°C and P = 900 MPa, the densities of pure phases are 0.835, 1.132, and 2.239 g/cm³ for H₂O, CO₂, and CaCl₂, correspondingly. Presented set of isolines of density $\rho$ makes it possible to trace its increase with a change from the least dense H₂O to denser CO₂ and CaCl₂ fluids. Figure 13 shows the density of fluid in solvus depending on the water activity. Each curve in this figure consists of two branches converging at water activity corresponding to the critical point. The upper branch of the curve shows the density of fluid phase with the higher CaCl₂ content, while the lower branch corresponds to the fluid phase mainly of water–CO₂ composition with the low CaCl₂ content. Any imaginary drawn vertical line in this figure, which intersects curve $\rho ({{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})$ in two points, corresponds to a tie line, while the intersection points define the density of coexisting fluid phases. For two $\rho ({{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}})$ dependences (corresponding to two combinations of P and T), the densities of high-CaCl₂ phases are relatively close. In contrast, the density of the water–CO₂ fluid strongly depends on pressure and decreases with its decrease. Finally, at sufficiently low pressures, this leads to fluid splitting into nominally gas phase (water and CO₂) and denser brine practically free of CO₂.

Fig. 12.

Density $\rho$ (g/cm³) of a homogenous fluid H₂O–CO₂–CaCl₂ depending on the concentrations of its components at Т = 1123 K and Р = 0.9 GPa.

Fig. 13.

Density of fluid on solvus depending on the water activity. Points in the upper and lower branches of the curves with the same water activity correspond to the densities of coexisting fluid phases. The upper branch of each curve is the density of high-CaCl₂ fluid, while the lower branch corresponds mainly to water–CO₂ fluid with low CaCl₂ content.

Comparison with H₂O–CO₂–NaCl System

Of significant interest is the comparison of the behavior of aqueous fluids with CO₂ and different salts. In Fig. 14, we compare the solvus and tie lines corresponding to some values of water activity for the H₂O–CO₂–NaCl and H₂O–CO₂–CaCl₂ systems. Data on the H₂O–CO₂–CaCl₂ system are obtained using our model, while data on the H₂O–CO₂–NaCl system, using the model (Aranovich et al., 2010). The CO₂ solubility in the H₂O–CaCl₂ brine is much lower than in the H₂O–NaCl one. Therefore, the field of two-phase fluid in the phase diagram for the H₂O–CO₂–CaCl₂ system is wider than in the phase diagram for the H₂O–CO₂–NaCl system. Tie lines corresponding to the water activity of 0.4 are similar for both the systems in position and slope. For the higher water activity of 0.5, the mutual position of the tie lines remains sufficiently close, however, the slope of the tie lines of the H₂O–CO₂–CaCl₂ system relative to horizontal line is lower. With further increase of the water activity, the tie lines approach the critical points, while the difference in their slopes for the H₂O–CO₂–NaCl and H₂O–CO₂–CaCl₂ systems increases. Maximally possible values of water activity in the field of coexisting fluid phases distinctly differ for the H₂O–CO₂–CaCl₂ and H₂O–CO₂–NaCl systems. In the example with T = 1073.15 K and P = 0.9 GPa (Fig. 14), these values are 0.572 for the H₂O–CO₂–CaCl₂ and 0.547 for the H₂O–CO₂–NaCl systems.

Fig. 14.

Solvus and tie lines of the coexisting fluid phases for the H₂O–CO₂–CaCl₂ (1, this work) and H₂O–CO₂–NaCl (2, Aranovich et al., 2010) systems at T = 1073.15 K and P = 0.9 GPa. Open circles show critical points.

Possibilities of Extrapolation to the Higher P-T Parameters

Thermodynamic model (1)–(7) with parameters presented in Table 1 reproduces available experimental data within 773.15–1073.15 K and 0.1–0.9 GPa. Our parametrization of P-T dependences of the Gibbs free energy through natural and well known values of the molar volumes of water and CO₂ permits the application of our model beyond the experimental P-T ranges. Such an extrapolation is facilitated by the fact that the water and CO₂ density, together with the corresponding molar volumes, weakly changes near the upper boundary of the experimental P-T range. From a practical aspect, of most interest is the possibility of application of the model at high and extremely high pressures (Fig. 2). The range of experimental pressure values used in developing our model varies from 0.1 to 0.9 GPa. The water molar volume completely defining the behavior of our model in this pressure range shows approximately a three-fold change. At the same time, an increase of pressure from 0.9 to 2 GPa provides only 20% decrease of this value, which offers an opportunity of even a greater extrapolation than in the example presented below. Thereby, an increase of the temperature above 1173.15 K could lead to the increase of water molar volume for pressure of 0.9–2 GPa up to its values in the experimental region.

Verification of our model at temperatures and pressures falling beyond the experimentally studied area showed that it can be used at least up to pressures 2 GPa and temperatures up to 1673.15 K. The example of application of our equation of state for high P-T parameters is given in Fig. 15, where solvuses for T = 1173.15 K are shown for the pressure range from 0.4 to 2 GPa. The pressure increase is accompanied by the growth of CO₂ solubility in the H₂O–CaCl₂ brine and, respectively, a decrease of multiphase field with possible coexistence of two fluid phases.

Fig. 15.

Phase diagrams for series of pressure values at temperature of 1173.15 K. Bold curves are solvuses separating the regions of homogenous fluid (to the left and below the line) and two coexisting fluid phases (to the right and upper). Open circles show critical points, in which the chemical activity of water reaches maximum value for the given solvus and for the corresponding two-phase fluid region. For P = 0.4 GPa, phase diagram contains the field of coexisting molten CaCl₂ and CO₂-rich fluid (to the right of the thin line). For higher pressures, the phase diagrams contain only regions of fluid phases.

An important petrological characteristics is the maximum water activity, which is reached in critical points and is possible in the two-fluid field. In Fig. 15, the critical points are shown with circles. The values of the water activity in the critical points depending on pressure are shown in Fig. 16 for two temperature values. With pressure increase from 0.1 to 2 GPa, these values decrease by more than two times. It is pertinent to mention that the pressure growth causes a significant increase of CO₂ concentration in the critical points, which is accompanied by an insignificant change of CaCl₂ content.

Fig. 16.

Maximum water activities in two-phase field for the H₂O–CO₂–CaCl₂ system.

Fluids in a Natural Geological System

The above mentioned difference in physicochemical properties, for instance, in extreme values of water activity for two-phase immiscible fluids in the H₂O–CO₂–NaCl and H₂O–CO₂–CaCl₂ systems, is of a great significance for the interpretation and analysis of data on fluid systems in natural geological processes. This can be exemplified by the results of study of fluid phase of НР granulites and syngranulite НР metasomatites in the Lapland granulite belt of the Fennoscandian shield (Bushmin et al., 2017, 2018, 2019), with special focus on the Н₂О activity. The values of the water activity near ${{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = 0.51$ calculated from mineral equilibria at 10–11 kbar and 900°С lie within the field of a homogenous H₂O–CO₂–NaCl fluid. The same values of water activity fall in the range suggesting the existence of two immiscible phases in the H₂O–CO₂–CaCl₂ system. The study of fluid inclusions in the minerals of the same samples showed that a fluid phase, in addition to dissolved NaCl, contains predominant CaCl₂. This, in addition to other results, allowed us to conclude that the P–T range of the studied НР granulites (10–11 kbar and 900°С) comprises a wide composition field of Н₂О-fluids with variable contents of СО₂ and Na and Са chlorides, in which a homogenous fluid is immiscibly split into chemically and physically contrasting fluid phases: a brine and Н₂О–СО₂ fluid. This filed becomes much wider in the presence of CaCl₂.

CONCLUSIONS

Obtained equation of state (1)–(7) for three-component fluid H₂O–CO₂–CaCl₂ with parameters presented in Table 1 reproduces all presently available experimental data on phase composition (homogenous or two-phase) of the ternary fluid H₂O–CO₂–CaCl₂ system (Zhang and Frantz, 1989; Shmulovich and Graham, 2004). Experimental data span a temperature range of 773.15–1073.15 K and a pressure range of 0.1–0.9 GPa. Parametrization of the P-T dependences of coefficients of the Gibbs free energy through natural and well known value of the molar volume of water provides application of our model beyond the experimental P-T range. Examples of the application of our model within pressure range of 0.1–2 GPa are provided. Thus, using the important CaCl₂–bearing fluid system as an example, we demonstrate that the existence of immiscible fluids with contrasting physicochemical properties (brines and СО₂-rich fluids) is possible not only under upper and middle crustal P-T conditions, but also at lower crustal–upper mantle parameters. The proposed model makes it possible obtaining quantitative characteristics of these coexisting fluid phases, the most important of which are compositions, density and activities of Н₂О and dissolved salts and non-polar gases. These characteristics define, first of all, the solubility of rock-forming minerals and ascent of dissolved deep-seated matter (e.g., Newton and Manning, 2010; Manning, 2018).

The possible further development and specification of the proposed thermodynamic description of the three-component H₂O–CO₂–CaCl₂ system is primarily related to the need for obtaining additional experimental data on this ternary system and its binary subsystems. The availability of such experimental data would allow one, in particular, to apply an advanced and more accurate thermodynamic model of the H₂O–CaCl₂ system (Ivanov et al., 2018a, 2018b), which however contains the greater number of parameters, in the high temperature and pressure region.