INTRODUCTION

Processes of chemical electrothermy, such as the production of silicon carbide, phosphorus, etc., are reduction reactions, and a number of dissolution reactions proceed with the release of products in the gas phase. In electrothermal ore-reduction reactors for the production of phosphorus, dust is a contaminant of the product—phosphorus; in open-hearth furnaces, in the production of calcium carbide, the formation of dust is undesirable from an environmental point of view/ In evaporative, bubbling, contact heat exchangers, moisture carryover is a loss of a clean coolant.

One of the main reasons for the formation of dust during the operation of industrial heterogeneous reactors (phosphoric, open-hearth, carbide and other furnaces) is the entrainment of melt droplets by bubbling gases and their solidification, along with chemical reactions in the gas phase with the formation of solid particles and the processes of evaporation and condensation of fumes. More people support the hydrodynamic approach [1–3] with a hypothetical view of the problem than support the evaporation mechanism [4–6] or those who propose to take into account both mechanisms [7–9]. It is clear that if there is a theory that adequately describes the experimental research, we can talk about the share of each component. The main argument in favor of hydromechanics is the absence of dust above the molten metal mirror, where there are no gas flows, and, quite obviously, splashing and droplet entrainment in bubbling heat exchangers, where there are no fumes.

Furnace gases of the ore-reduction phosphoric furnace contain up to 200 g/m3 solid dust particles. This unwanted component is a source of sludge formation in the phosphorus condensers and reduces the quality of the product. The most likely mechanism for the formation of dust is the formation of melt droplets when the gas leaves the reaction zone of the furnace. This mechanism is supported by the results of the analysis of the chemical composition of the dust, which is characteristic of the melt in the melting zone, when the reduction process has not yet proceeded. High K2O content (up to 20%) in furnace dust samples can be attributed to the processes of sublimation and subsequent coagulation on dust particles [6]. In addition, the operating mode of the furnace, i.e., its capacity, has a significant effect on dustiness Z [6]. An absurd dependency was empirically obtained in which the dependence of the electrical resistance on power through temperature clearly follows, which is unacceptable in the regression equations:

$$Z = {\text{ }}125\varphi q_{{\text{v}}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}\rho _{{el}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}-62.5,$$
(1)

where ρel is the specific electrical resistance of the melt, φ is the constant characterizing the geometric similarity of the conductors, and qv is the volumetric capacity of the furnace.

The chemical composition of the charge also affects the dust content by changing the electrical resistivity and the coefficient of surface tension of the melt, which additively depends on the content and properties of individual components [6].

The mechanism of dust formation can be interpreted on the basis that gas bubbles, as a result of their rupture, form the smallest droplets. Therefore, with an increase in gas consumption, dust formation increases sharply.

In experiments [1], it was found that the process of bubble bursting is an integral part of the mechanism of dust formation, and the formation of dust was always preceded by the appearance of metal splashes. In cases where no splashing was observed, there was no formation of smoke.

According to concepts, the transporting entrainment of liquid is caused by the “jet” and “shell” mechanism of droplet formation, when gases leave the liquid phase [10].

According to [1], the bulk of the splashes is formed due to the rupture of a small part of the thin surface film protruding above the melt. At the moment of its rupture, the smallest splashes rush upward, and the liquid surrounding the bubble tends to fill the void that has arisen, at the same time causing an annular wave on the surface of the melt. The so-called collapse of the surface bubble occurs. Closing, it creates a cumulative jet (Rayleigh jet), throwing up a column of water, from the foot of which a wave propagates. The ejection of the melt is also accompanied by the formation of splashes; large droplets return back to the bath and small droplets are removed into the gas phase.

According to [1], 60% of all dust that is generated is small drops of a melt film that explode when a gas bubble floats up. Vapors and oxides account for about 27% of the dust mass [1].

HYDRODYNAMIC APPROACH TO THE THEORY OF DUST FORMATION AND DEVELOPMENT OF A MATHEMATICAL MODEL

Let us consider the formation of drops above the liquid surface, assuming that the gas carries the energy concentrated in the bubbles due to the lifting forces of the liquid. This energy is transformed into the energy of the surface tension of droplets formed upon the rupture of the liquid film [11].

The energy balance in this case can be written as

$$\frac{{{{G}_{{\text{g}}}}}}{{{{\rho }_{{\text{g}}}}}}\Delta \rho gl = \frac{{dn}}{{d\tau }}\pi d_{{\text{k}}}^{2}\sigma ,$$
(2)

where \(\frac{{dn}}{{d\tau }}\) is the rate of droplet formation; l is the characteristic size of the system, Gg is the mass flow rate of gas, ρg is gas density, ρl is the density of the liquid, dto is the droplet diameter, σ is the coefficient of the surface tension of the liquid phase, g is the acceleration of gravity, and Δρ = ρl – ρg.

Let us transform this expression:

$$\frac{{{{G}_{{\text{g}}}}}}{{{{\rho }_{{\text{g}}}}}}\Delta \rho gl = \frac{{dn}}{{d\tau }}\frac{{\pi d_{{\text{k}}}^{3}{{\rho }_{{\text{l}}}}6}}{{6{{d}_{{\text{k}}}}{{\rho }_{{\text{l}}}}}}\sigma = {{G}_{{{\text{lk}}}}}\frac{{6\sigma l}}{{{{d}_{{\text{k}}}}{{\rho }_{{\text{l}}}}l}}.$$

We obtain

$${{g}_{{{{t}_{0}}}}} = \frac{{{{G}_{{{\text{lk}}}}}}}{{{{G}_{{\text{g}}}}}} \sim \frac{{{{\rho }_{{\text{l}}}}}}{{6{{\rho }_{{\text{g}}}}}}\frac{{{{d}_{{\text{k}}}}}}{l}\frac{{\Delta \rho g{{l}^{2}}}}{\sigma } \sim \frac{{{{\rho }_{{\text{l}}}}}}{{6{{\rho }_{{\text{g}}}}}}\frac{{{{d}_{k}}}}{l}{\text{B}}{{{\text{o}}}_{l}},$$
(3)

where \({{g}_{{{{t}_{0}}}}}\) is the mass of droplets per unit mass of gas above the liquid, Glk is the mass of liquid droplets formed per unit time, and \({\text{B}}{{{\text{o}}}_{l}} = \frac{{\Delta \rho g{{l}^{2}}}}{\sigma }\) is the Bond number for the parameter l.

Estimates according to (3) give the value of the entrainment fraction of the order of 10, which practically coincides with experimental values \({{g}_{{{{t}_{0}}}}}\) ≈ 4 for an air–water system.

The experimental results on the entrainment of the liquid phase in metallurgical systems with gas blowing of the melt are given in Table 1, which shows a linear dependence of the ablation at the surface on the ratio of the liquid density to the gas density [12]. The same proportion is characteristic of relation (3).

Table 1.   Dependence of the entrainment of melt droplets during blowing
Full size table

When dispersed, droplets are distributed in size. The most characteristic is the dependence experimentally found in the form of the Rosin–Rammler distribution. The integral function of the particle-size distribution of dust particles for phosphoric furnaces has the values [6] presented in Table 2.

Table 2.   Dust particle-size distribution function on the top of a phosphoric furnace
Full size table

The fraction of droplets with diameters less than the characteristic one can be expressed by integrating the distribution density function within the appropriate limits. In addition, in this case, the simplified relation is valid after expansion into a series for small dt:

$${{g}_{{\text{t}}}} = {{g}_{{{{{\text{t}}}_{{\text{o}}}}}}}\left[ {1 - \exp {{{\left( { - \frac{{{{d}_{{\text{t}}}}}}{{{{d}_{{{\text{dis}}}}}}}} \right)}}^{n}}} \right] \approx {{g}_{{{{{\text{t}}}_{{\text{o}}}}}}}{{\left( {\frac{{{{d}_{{\text{t}}}}}}{{{{d}_{{{\text{dis}}}}}}}} \right)}^{n}},$$
(4)

where dt and ddis are the diameter of the soaring and the average diameter of the drops after dispersion.

Exponent n = 2/s, where s is the variance of the log-normal distribution (s ~ 1).

The diameter of the soaring is determined from the balance of resistance forces and the weight of the bodies:

$$\Delta \rho g\left( {\frac{{\pi d_{{\text{t}}}^{3}}}{6}} \right) = \left( {\frac{{\pi d_{{\text{t}}}^{2}}}{4}} \right)\xi \frac{{{{\rho }_{{\text{g}}}}\upsilon _{{\text{g}}}^{2}}}{2} \simeq 3\pi {{d}_{{\text{t}}}}{{\rho }_{{\text{g}}}}{{\nu }_{{\text{g}}}}{{\upsilon }_{{\text{g}}}}.$$
(5)

Hence, for low gas velocities,

$$\frac{{d_{{\text{t}}}^{2}}}{{{{\delta }^{2}}}} = 18{{\left( {\frac{{{{{{\rho }}}_{{\text{g}}}}\upsilon _{{\text{g}}}^{{\text{2}}}{{\delta }}}}{{{\sigma }}}} \right)}^{{0.5}}}\left( {\frac{\sigma }{{\Delta \rho g{{\delta }^{2}}}}} \right)\left( {\frac{{{{\nu }_{{\text{g}}}}\rho _{{\text{g}}}^{{0.5}}}}{{{{\sigma }^{{0.5}}}{{\delta }^{{0.5}}}}}} \right),$$

or

$$\frac{{{{d}_{{\text{t}}}}}}{\delta } = \sqrt {18} {\text{W}}{{{\text{e}}}^{{0.25}}}{\text{B}}{{{\text{o}}}^{{ - 0.5}}}{\text{Lp}}_{{{\delta }}}^{{ - 0.25}},$$
(6)

where \({\text{We}} = \frac{{{{{{\rho }}}_{{\text{g}}}}\upsilon _{{\text{g}}}^{{\text{2}}}{{\delta }}}}{{{\sigma }}}\) is the Weber number, \({\text{Bo}} = \frac{{\Delta \rho g{{\delta }^{2}}}}{\sigma }\) is the Bond number, and \({\text{L}}{{{\text{p}}}_{{{\delta }}}} = \frac{{\sigma \delta }}{{\nu _{{\text{g}}}^{2}{{\rho }_{{\text{g}}}}}}\) is the equivalent Laplace number.

If we assume that, as a result of the emergence of bubbles on the surface, cylindrical hollow films are formed which are flown around by accelerated gas flows from the bubbles, then random perturbations of the friction forces cause transverse and longitudinal vibrations of the films. Due to the development of these vibrations, the “jet” mechanism of dispersion is carried out. Many works are devoted to the problems of jet decay and dispersion [13–17]. The relationship between the average diameter during droplet generation and the characteristic size of the system is inversely proportional to the Weber number. This dependence can be approximately estimated from the relation

$$\frac{{{{\rho }_{{\text{g}}}}\upsilon _{{\text{g}}}^{2}}}{2} \sim 4\frac{\sigma }{{{{d}_{{{\text{dis}}}}}}},\,\,\,\,\frac{{{{d}_{{{\text{dis}}}}}}}{\delta } = 8\chi {\text{We}}_{{{\delta }}}^{{ - 1}},$$
(7)

where δ is the characteristic size of the system; χ is the coefficient of proportionality.

For gas flow around a liquid jet, the following relation holds:

$${{{{d}_{{{\text{dis}}}}}} \mathord{\left/ {\vphantom {{{{d}_{{{\text{dis}}}}}} \delta }} \right. \kern-0em} \delta }\sim We_{{{\delta }}}^{{ - 0.5}}.$$

More reasonably, the droplet diameter is obtained from considering the instability of a liquid jet experiencing radial perturbations; assuming that the jet breaks up into droplets, the volume of each is equal to the volume of rotation of the sinusoid of the wave around the axis passing through its minimum [16]:

$${{d}_{{{\text{dis}}}}} = {{\left( {\frac{{9{{\delta }^{2}}}}{4}{{\lambda }_{0}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$$

Relationship between the Weber number and wave number k0 in this case:

$${\text{W}}{{{\text{e}}}_{{{\delta }}}} = 1.5{{k}_{0}}\delta = \frac{{3\pi \delta }}{{{{\lambda }_{0}}}},$$

where \({{\lambda }_{0}} = \frac{{3\pi \delta }}{{{\text{W}}{{{\text{e}}}_{{{\delta }}}}}}\) is the wavelength of the fastest growing disturbance.

Then,

$$\frac{{{{d}_{{{\text{dis}}}}}}}{\delta } = \sqrt[3]{{\frac{{27\pi }}{4}}}{\text{We}}_{{_{l}}}^{{ - 0.33}}.$$
(8)

Thus, depending on the droplet-generation mode, there is a range of exponents for the gas velocity.

Then, taking the process of splitting the jets on the basis of strict stability provisions, we obtain

$${{g}_{{\text{t}}}} = c\frac{{{{\rho }_{l}}}}{{{{\rho }_{{\text{g}}}}}}{\text{B}}{{{\text{o}}}_{l}}{\text{We}}_{{{\delta }}}^{{0.83}}{\text{Bo}}_{{{\delta }}}^{{ - 1}}{\text{Lp}}_{{{\delta }}}^{{ - 0,5}}.$$
(9)

The dimensionless form of the equation allows it to be applied to systems with different properties.

Checking the adequacy of the model of dust and droplet entrainment. Figure 1 shows a comparison of the experimental data [18–24, 31, 32] and the values for the entrainment of dust in phosphoric and open-hearth furnaces, as well as the entrainment of water droplets in contact heat exchangers. Coefficient c is determined by selection. For the characteristic size in gas-liquid systems, the Laplace constant is usually assumed:

$${{l}_{{{\sigma }}}} = \sqrt {\frac{\sigma }{{\Delta \rho g}}} ,$$
(10)

where lσ is the Laplace constant (capillary).

Fig. 1.
figure 1

Dependence complex \({{{\text{g}}}_{{\text{t}}}}1\) from the Weber number: (a) experiment [16–19] (phosphoric stoves), (b) experiment [22] (contact heat exchanger), (c) experiment [20, 21] (open-hearth furnaces), and (d) theory.

Full size image

For a more visual graphical presentation of the results, relation (9) is transformed to the form

$${{{\text{g}}}_{{\text{t}}}}\frac{{{{{{\rho }}}_{{\text{g}}}}}}{{{{{{\rho }}}_{{\text{l}}}}}}{\text{Lp}}_{{{\delta }}}^{{0,5}} = {\text{cW}}{{{\text{e}}}^{{0.83}}}.$$
(11)

Coefficient c = 100. We denote \({{{\text{g}}}_{{\text{t}}}}1 = {{{\text{g}}}_{{\text{t}}}}\frac{{{{{{\rho }}}_{{\text{g}}}}}}{{{{{{\rho }}}_{{\text{l}}}}}}{\text{Lp}}_{{{\delta }}}^{{0.5}},\) and then \({{{\text{g}}}_{{\text{t}}}}1 = {\text{cW}}{{{\text{e}}}^{{0.83}}}.\)

The lower series of points is for dust entrainment in open-hearth furnaces, the middle one is for phosphoric ones, and the upper one is for bubbling heat exchangers.

Thus, there is a satisfactory agreement between the experimental data and the theoretical curve in a wide range of parameters in the generalized presentation for different aggregates.

ANALYSIS OF THE INFLUENCE OF OPERATING MODES OF A PROCESS REACTOR ON DUST FORMATION

Let us consider the problem using the example of a phosphoric furnace, the model of which, taking into account the complete interrelation of all parameters characterizing the modes of operation, is analyzed in [25].

The description of stationary states of a phosphorus electrothermal ore reduction furnace in the approximation of lumped parameters for the reaction zone in accordance with the phase composition and the mechanism of physicochemical transformations is based on the representation of the object in a zonal form, when the reactor bath for phosphorus reduction is conventionally divided into the following zones: charge, melting, carbonaceous, slag, and ferroalloy.

The processes of heat and mass transfer have a significant effect on the quality of the product (the gas temperature at the outlet of the furnace should not be lower than the condensation temperature of phosphorus, the removal of solid particles by the gas should be minimal to prevent the formation of sludge, etc.) and on the reliability of the reactor (roof temperature, the presence of a layer of the skull, etc.). Taking into account the energy interaction of different zones of the reactor makes it possible to reflect a feature like self-regulation.

Indicators of efficiency, the reliability of operation of furnace elements, and quality indicators are obtained from the description of processes in conjunction for all zones.

The description uses the stoichiometry of the phosphorus reduction reaction:

$${{{\text{P}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}} + 5{\text{C}} \to 5{\text{CO}} + {{{\text{P}}}_{2}}.$$
(12)

The analysis of stationary states of an electrothermal reactor for phosphorus reduction in the lumped-parameter approximation is based on the equations of conservation of mass and energy.

The general mass balance and component-wise mass balances for phosphorus pentoxide and for coke are as follows:

$${{G}_{{\text{s}}}} - {{G}_{{\text{g}}}} = {{G}_{{\text{l}}}},$$
(13)
$${{{{G}_{{\text{f}}}}C_{{\text{f}}}^{{{\text{p2o5}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{f}}}}C_{{\text{f}}}^{{{\text{p2o5}}}}} {{{\rho }_{{\text{f}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{f}}}}}} - {{\omega }_{{\text{R}}}} = {{{{G}_{{\text{l}}}}C_{{\text{l}}}^{{{\text{p2o5}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{l}}}}C_{{\text{l}}}^{{{\text{p2o5}}}}} {{{\rho }_{{\text{l}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{l}}}}}},$$
(14)
$${{G}_{{\text{c}}}} - {{g}_{{\text{c}}}}{{\omega }_{{\text{R}}}} = 0.$$
(15)

Furnace energy balance:

$$\begin{gathered} {{G}_{{\text{s}}}}{{c}_{{{\text{ps}}}}}t_{{\text{s}}}^{'} + {{\xi }_{e}}{{P}_{{{\text{el}}}}} = {{G}_{{\text{l}}}}{{c}_{{{\text{pl}}}}}{{t}_{{\text{R}}}} + {{G}_{{\text{g}}}}{{c}_{{{\text{pg}}}}}t_{{\text{g}}}^{*} + {{\omega }_{{\text{R}}}}{{Q}_{{\text{R}}}} \\ + \,\,\left( {{{G}_{{\text{s}}}} - {{G}_{{\text{c}}}}} \right){{Q}_{{\text{L}}}}. \\ \end{gathered} $$
(16)

Energy balance at the phase transition boundary:

$$\begin{gathered} {{2{{S}_{{\text{f}}}}{{\lambda }_{{\text{t}}}}\left( {{{t}_{{\text{R}}}} - {{t}_{{\text{L}}}}} \right)} \mathord{\left/ {\vphantom {{2{{S}_{{\text{f}}}}{{\lambda }_{{\text{t}}}}\left( {{{t}_{{\text{R}}}} - {{t}_{{\text{L}}}}} \right)} {{{h}_{{{\text{cz}}}}}}}} \right. \kern-0em} {{{h}_{{{\text{cz}}}}}}} - {{G}_{{\text{g}}}}{{c}_{{{\text{pg}}}}}{{t}_{{\text{g}}}} + {{G}_{{\text{s}}}}{{c}_{{{\text{ps}}}}}t_{{\text{s}}}^{{"}} \\ - \,\,\left( {{{G}_{{\text{s}}}} - {{G}_{{\text{c}}}}} \right){{Q}_{{\text{L}}}} = 0. \\ \end{gathered} $$
(17)

Electric power consumed by the reactor:

$${{P}_{{{\text{el}}}}} = {{U_{{{\text{el}}}}^{2}} \mathord{\left/ {\vphantom {{U_{{{\text{el}}}}^{2}} {({{\xi }_{{{\text{e1}}}}}{{h}_{{{\text{cz}}}}})}}} \right. \kern-0em} {({{\xi }_{{{\text{e1}}}}}{{h}_{{{\text{cz}}}}})}},$$
(18)

where ξe1 = ρel/Sf.

The rate of the chemical reduction reaction in the macro representation has the form

$${{\omega }_{{\text{R}}}}~ = {{k}_{0}}{{S}_{{\text{c}}}}{{\left( {1 + {{M}_{{\text{k}}}}} \right)}^{m}}C_{{\text{l}}}^{{{\text{p2o5}}}}{\text{exp}}\left( {{{ - E} \mathord{\left/ {\vphantom {{ - E} {R{{T}_{{\text{R}}}}}}} \right. \kern-0em} {R{{T}_{{\text{R}}}}}}} \right),$$
(19)

where \(C_{{\text{f}}}^{{{\text{p2o5}}}}\) is the content of phosphorus pentoxide in the ore; \(C_{{\text{l}}}^{{{\text{p2o5}}}}\) is the concentration of phosphorus pentoxide in the melt; Gs, Gl, Gg are the consumption of charge, slag, and gas; ρf is the density of the charge material; ρl is the density of the liquid melt; cps, cpl, cpg are the heat capacity of charge, slag, and gas; tL and tR are the melting and melting temperature; ωR and QR are the speed and thermal effect of the reduction reaction; Pel and ξe are the furnace power and its share used for the reaction zone; \({{U}_{{{\text{el}}}}}\) is the voltage on the electrodes; QL is the heat of fusion; \(t_{{\text{s}}}^{{{'}}}\) is the temperature of the charge at the entrance to the furnace; \(t_{{\text{g}}}^{{\text{*}}}\) is the temperature of furnace gases in the underroof space, Sf is the surface area of the phase transition, Sc = Mcz(6 (1 – εc) /dc)/ρc is the surface area of coke particles; E is activation energy; k0 is the preexponential factor; and \(t_{{\text{s}}}^{{{" }}}\) is the temperature of the charge at the entrance to the reaction zone.

The energy balance in the charge zone and the conditions at the phase transition boundary are presented in the distributed parameter approximation in a one-dimensional formulation. From the system of equations, which is significantly nonlinear, with linearization of the Arenius dependence, it is possible to obtain the basic relations for the analysis of the parameters of the reactor from the control parameters: the dosage of coke and the voltage on the electrodes.

Gas consumption is determined by the conditions of the phosphorus reduction reaction:

$$\begin{gathered} {{G}_{{\text{g}}}} = {{\gamma }_{{\text{g}}}}{{k}_{0}}\left[ {{{{{M}_{{{\text{cz}}}}}(1 - {{\varepsilon }_{c}})6} \mathord{\left/ {\vphantom {{{{M}_{{{\text{cz}}}}}(1 - {{\varepsilon }_{c}})6} {({{\rho }_{c}}{{d}_{c}}}}} \right. \kern-0em} {({{\rho }_{c}}{{d}_{c}}}}} \right]C_{1}^{{{{{\text{P}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}}}}\exp \left[ {{{ - E} \mathord{\left/ {\vphantom {{ - E} {R{{T}_{{\text{R}}}}}}} \right. \kern-0em} {R{{T}_{{\text{R}}}}}}} \right] \\ \times \,\,{{(1 - {{M}_{{\text{K}}}})}^{m}}. \\ \end{gathered} $$
(20)

Specific power consumption

$$\begin{gathered} {{b}_{{{\text{el}}}}} = {{{{\zeta }_{{\text{e}}}}{{P}_{{{\text{el}}}}}} \mathord{\left/ {\vphantom {{{{\zeta }_{{\text{e}}}}{{P}_{{{\text{el}}}}}} {{{G}_{{\text{g}}}}}}} \right. \kern-0em} {{{G}_{{\text{g}}}}}} = \left( {{{{{G}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{s}}}}} {{{G}_{{\text{g}}}}}}} \right. \kern-0em} {{{G}_{{\text{g}}}}}}-1} \right){{c}_{{{\text{pl}}}}}{{t}_{{\text{R}}}} + {{g}_{{\text{g}}}}{{Q}_{{\text{R}}}} \\ + \,{{{{G}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{s}}}}} {{{G}_{{\text{g}}}}}}} \right. \kern-0em} {{{G}_{{\text{g}}}}}}\left( {1{\text{ }}-{{g}_{{\text{c}}}}} \right){{Q}_{{\text{L}}}} + {{c}_{{{\text{pg}}}}}t_{g}^{*} - ({{{{G}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{s}}}}} {{{G}_{{\text{g}}}}}}} \right. \kern-0em} {{{G}_{{\text{g}}}}}}){{c}_{{{\text{pg}}}}}t_{g}^{{''}}, \\ \end{gathered} $$
(21)

where \({{g}_{{\text{i}}}}\) is the mass fractions of charge components, \({{G}_{{\text{g}}}} = {{g}_{{\text{g}}}}{{G}_{{\text{s}}}}\) is gas consumption, \({{G}_{{\text{f}}}} = {{g}_{{\text{f}}}}{{G}_{{\text{s}}}}\) is phosphorite consumption, \({{G}_{{{\text{si}}}}} = {{g}_{{{\text{si}}}}}{{G}_{{\text{s}}}}\) is quartzite consumption, and \({{G}_{{\text{c}}}} = {{g}_{{\text{c}}}}{{G}_{{\text{s}}}}\) is coke consumption.

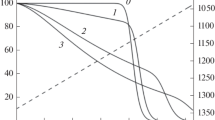
An analysis of the dependence of the temperature in the reaction zone on the voltage on the electrodes and the dosage of coke (Fig. 2) makes it possible to draw a conclusion about the concentration of the reaction product at the outlet of the reactor, the specific consumption of electricity, and other technological parameters. It is obvious that the operating mode of the reactor can be controlled by influencing the coke dosage and the voltage across the electrodes.

Fig. 2.
figure 2

Dependence of the temperature of the reaction zone (K) on the voltage on electrodes (V) and the dosage of coke (mass fraction).

Full size image

The state of the reduction zone determines the operating mode of the reactor as a whole. The main amount of heat is released there, and the formation of reaction products occurs there during the reduction of the initial substances.

The height of the coke bed is determined by the rate at which it is fed into the reactor and the rate at which it is consumed as a result of a chemical reaction. The reaction rate, in turn, is determined by the temperature of the reaction zone, the surface area of the reaction, and the concentration of the starting material. The rate of coke consumption is determined by the temperature in the reaction zone, which depends on the thermal power; therefore, the height of the coke zone decreases with an increase in the furnace power, which is determined by the voltage on the electrodes (Fig. 3). When the main contribution to the resistance of the reaction zone is made by the coke layer, the electrical resistance of the reactor is determined by the height of the coke layer.

Fig. 3.
figure 3

Dependence of the height of the reducing agent layer (m) on the voltage on the electrodes (V) and the dosage of coke (mass fraction).

Full size image

With an increase in the dosage of the reducing agent, layer thickness hcz increases; therefore, the resistance of the reaction zone increases, which leads to a decrease in the released power and, as a consequence, a decrease in the temperature of the reaction zone. The temperature of the gaseous reaction products also decreases in this case.

The considered model is evaluative. For more complex multidimensional representations of processes in this type of aggregates, a two-dimensional model was used, implemented by the finite element method [26–30]. Figure 4 shows the isolines of costs depending on the control variables. From relations (20) and (9), it is possible to obtain the values of dust content and the level of costs for cleaning out sludge. Unfortunately, the costs of cleaning out sludge do not have an extremum and one can be content only with limiting values, similar to how the limits of temperature change are shown in Fig. 4.

Fig. 4.
figure 4

Dependence of the cost of phosphorus production on the voltage on the electrodes and the dosage of coke.

Full size image

The analysis of the ratios makes it possible to almost completely describe the thermal operation of the furnace. The specific energy consumption depends on the control parameters—the voltage on the electrodes and the dosage of coke—by influencing intermediate technological parameters, such as the temperature in the reaction zone, the height of the coke zone, gas consumption, and charge consumption. With an increase in the voltage on the electrodes, the specific energy consumption decreases; the same effect is exerted by a decrease in the dosage of coke.

Thus, there are alternative ways to influence controls: an increase in voltage, leading to a decrease in specific energy consumption; an increase in productivity; and an increase in the degree of useful use of raw materials and an increase in undesirable indicators, such as the temperature of furnace gases, dust content, and an increase in the dosage of coke, which makes it possible to reduce the temperature of gases under the roof, dustiness, and the content of phosphorus pentoxide in the slag, while the productivity decreases and the specific power consumption in the furnace increases. All dependencies are essentially nonlinear. Particular attention should be paid to the relationship between voltage and power, which is determined by the height of the coke zone and, therefore, depends on the operating mode of the furnace. The size of the coke zone characterizes the resistance of the reaction zone and, therefore, a very complex mechanism for the formation of the electric mode of the furnace becomes clear. Describing the furnace operation under stationary conditions makes it possible to obtain an analytically complete relationship of control and technological parameters. From the results of the analysis of the main dependencies, areas of economical, reliable, and resource-saving modes of operation of the furnace are determined. On the basis of a comprehensive description of transport processes in heterogeneous chemically reacting systems based on the interaction of all phases, a theory of ore-reduction aggregates has been developed which includes the entire spectrum of phenomena inherent in devices of this type. An analysis of the dependences of the temperature in the reaction zone on the voltage at the electrodes and the dosage of coke makes it possible to draw a conclusion about the concentration of phosphorus at the outlet from the furnace, the temperature of gases in the underroof space, the specific consumption of electricity, and other technological parameters.

In principle, the optimal conditions can be found by minimizing the specific flow rate function and taking into account the restrictions on all indicators, for example, by the method of penalty functions.

Particular attention should be paid to the relationship between voltage and power, which is determined by the height of the coke zone and, therefore, depends on the operating mode of the furnace. The size of the coke zone characterizes the resistance of the reaction zone and, therefore, a very complex mechanism for the formation of the electric mode of the furnace becomes clear.

CONCLUSIONS

The expression for the formation of dust generalizes the dependence of the entrainment of droplets on the Weber number as a mode parameter for various types of technological reactors. From dependence (9) it follows that the chemical reaction regime has a significant effect on the transport of the liquid phase from the reaction zone due to an increase in the gas velocity. The composition of the liquid phase, determining the coefficient of surface tension, affects the proportion of the transported liquid [11]. The amount of the gas phase or the gas content depends on the operating mode of the reaction zone; i.e., the released power and temperature, and intensifies the process of droplet formation.

Dust particles are condensation centers for fumes, so the chemical composition of dust can change along the gas path.

In addition, the geometry of the layer of coke particles in the reaction zone forms the conditions for the growth of gas bubbles and, therefore, determines the mode of entrainment of melt droplets. The amount of the gas phase or the gas content depends on the operating mode of the reaction zone, i.e., the released power and temperature, and intensifies the process of droplet formation.

Using the obtained dependence, it is possible to predict the formation of sludge in the condensers of phosphoric furnaces and determine the operating conditions of the furnace with the maximum product quality.

From the above it is clear that the appearance of sludge can be influenced by regime measures, and the maps of regimes should include isolines of the dependence of flows in order to take into account the decrease in the quality of the product with the intensive formation of dust.

NOTATION

\(C_{{\text{f}}}^{{{{{\text{P}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}}}}\)

phosphorus pentoxide content in ore, kg/m3

\(C_{{\text{l}}}^{{{{{\text{P}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}}}}\)

concentration of phosphorus pentoxide in the melt, kg/m3

E

activation energy, J/mol

G c

coke consumption, kg/s

G f

phosphorite consumption, kg/s

G g

gas consumption, kg/s

G l

slag consumption, kg/s

G s

charge consumption, kg/s

G si

quartzite consumption, kg/s

G lk

mass of liquid droplets formed per unit time, kg/s

M cz

coke zone weight, kg

M k

acidity modulus

P el

furnace power, W

Q L

heat of fusion, kJ/kg

Q R

thermal effect of the reduction reaction, kJ/kg

R

gas constant, J/(mol K)

T R

melt temperature, K

S c

surface of coconut particles, m2

S f

charge particle surface, m2

Z

dust content, kg/m3

b el

specific power consumption, W/kg

c pg

heat capacity of gas, kJ/(kg K)

c pl

slag heat capacity, kJ/(kg K)

c ps

heat capacity of the charge, kJ/(kg K)

\(\frac{{dn}}{{d\tau }}\)

droplet formation rate, 1/s

d c

diameter of coke particles, m

d dis

average droplet diameter after dispersion, m

d t

soaring diameter, m

d to

drop diameter, m

g

free fall acceleration, m/s2

g i

mass fractions of charge components

g t0

mass of droplets per unit mass of gas

g t

carried away mass of droplets per unit mass of gas

h cz

reducing agent layer height, m

k 0

preexponential factor, s-one

\({{l}_{{{\sigma }}}}\)

Laplace constant (capillary)

l

characteristic size of the system, m

q v

volumetric power of the furnace, W/m3

s

variance of a lognormal distribution

\(t_{{\text{g}}}^{*}\)

temperature of furnace gases in the underroof space, K

t L

melting point, K

t R

melt temperature, K

\(t_{{\text{s}}}^{{\textquotedblleft}}\)

charge temperature at the entrance to the reaction zone, K

\(t_{{\text{s}}}^{'}\)

temperature of the charge at the entrance to the furnace, K

\({{\gamma }_{{\text{g}}}}\)

stoichiometric coefficient

ν

kinematic viscosity, m2/s

δ

characteristic size of the system, m

ξe

share of power used in the reaction zone

\({{\lambda }_{0}}\)

wavelength of the fastest growing disturbance, m

ρel

specific electrical resistance of the melt, Ohm m

ρf

batch material density

ρg

gas density, kg/m3

ρl

fluid density, kg/m3

σ

coefficient of surface tension of the liquid phase, N/m

φ

constant characterizing the geometric similarity of the conductors

χ

aspect ratio

ωR

reduction reaction rate, kg/s

\({{U}_{{{\text{el}}}}}\)

voltage on electrodes, V

Bo

Bond number

Bol

Bond number for the parameter l

\({\text{L}}{{{\text{p}}}_{{{\delta }}}}\)

equivalent Laplace number

We

Weber number

SUBSCRIPTS AND SUPERSCRIPTS

0

elementary

L

melting

R

reaction

c

coke

cz

coke zone

dis

dispersing

el

electric

f

phosphorus

g

gas

i

number

k

drop

l

liquid

p

constant pressure

g

gas

s

charge

si

quarzite

t

hovering

t0

initial moment of time

v

volume

δ

characteristic size

σ

surface tension