Spin Fluctuations and Negative Heat Capacity (Brief Review)

The problem of negative heat capacity, discussed in a number of theoretical and experimental works dealing with weak itinerant magnets, is studied. A detailed analysis of the heat capacity of helicoidal itinerant magnet MnSi apparently demonstrates that the negative heat capacity in this case is a false effect because the interaction of the spin subsystem with other degrees of freedom is ignored in the analysis of the partial contributions to the heat capacity of the system. The negative heat capacity obtained by subtracting the electron and phonon components from the total heat capacity of the system is obviously an effective magnetic contribution, including the effects of spin–phonon coupling.

In 1972, Murata and Doniach [1] formulated a theory describing the thermodynamic properties and phase transition in weak ferromagnets within the classical approach using the Ginzburg–Landau type Hamiltonian. According to [1], the phase transition in these systems is determined by the anharmonic term in the Hamiltonian, which corresponds to the interaction of excitation modes (mode–mode coupling). Just this mechanism underlies the emergence of giant fluctuations of the magnetization.

The authors of [1] concluded that the main physical consequence of the theory of fluctuating modes as applied to the spin subsystem is a negative contribution to the heat capacity at temperatures above the phase transition point. This negative contribution is due to an increase in the stiffening of fluctuating modes with a temperature-induced increase in the rms fluctuation of the order parameter (magnetization). The calculations within the high-temperature virial expansion in [2] also predicted this effect. By identifying the constants in the Hamiltonian with the parameters of the interacting electron gas, the authors calculated the heat capacity curve near the magnetic phase transition within their model and compared it with the experimental data for the Sc₃In compound using only one fitting parameter (Fig. 1).

Fig. 1.

(Solid line) Magnetic anomaly in the heat capacity predicted by the Murata–Doniach theory for the case of a weak itinerant ferromagnet as compared to (circles) the experimental data for Sc₃In with the subtracted nonmagnetic contribution plotted using data from [1].

In the subsequent work, Murata [3] substantiated the validity of the Murata–Doniach model [1]. Analyzing the effect of spin fluctuations on the heat capacity of weak itinerant ferromagnets using the theory of Moriya and Kawabata [6] self-consistently including the interaction of fluctuating spin modes, Makoshi and Moriya [4] (see also [5]) confirmed the existence of a negative contribution to the heat capacity caused by spin fluctuations (Fig. 2).

Fig. 2.

Heat capacity of weak ferromagnetic metals according to Makoshi and Moriya plotted using data reported in [4].

Mohn and Hilscher [7] (see also [8]), using the modified Landau expansion [9], also revealed the negative contribution to the heat capacity and entropy in the spin system caused by spin fluctuations at temperatures above the phase transition point. Finally, Takahashi and Nakano [10] (see also [11]) concluded that the negative contribution to the heat capacity and entropy found in a number of works on fluctuating spin systems is due to numerous simplifications.

However, the negative contribution to the heat capacity and entropy found for part of a certain system does not necessarily mean the general instability of the system and may well be observed.

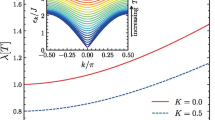
In this connection, the results of the classical Monte Carlo calculations including the simulation of longitudinal spin fluctuations performed in [12] for a system of interacting spins, which perfectly reproduce the characteristic features of the phase transition in MnSi and are shown in Fig. 3, are of interest. It follows from Fig. 3 that the negative heat capacity is not observed when simulating purely spin systems without other degrees of freedom, which always exist in real systems.

Fig. 3.

(Color online) (Left panel) Empirical spin dependences of the energy of longitudinal spin fluctuations, where the spin is treated as an independent fluctuating variable, and (right panel) the corresponding temperature dependence of the heat capacity plotted using data from [12].

Let us then address the experimental data. In Fig. 1, we demonstrate the behavior of the magnetic component of the specific heat of Sc₃In near the magnetic phase transition. The negative values of the heat capacity at temperatures above T_c are quite clearly seen, which seems to confirm the theoretical predictions in [1]. However, the main problem here is the adequacy of the procedure for subtracting the nonmagnetic contribution. It is obvious that incorrect identification and characterization of the corresponding nonmagnetic terms can lead to erroneous conclusions.

Another interesting example is related to the study of the heat capacity of the helicoidal itinerant magnet MnSi [13]. In Fig. 4, we show the measured temperature dependence of the heat capacity of MnSi in magnetic fields of 0 and 4 T. In addition, we present the results of calculations including the sum of the phonon heat capacity of the lattice and the linear electronic contribution $\gamma T$. The phonon heat capacity of MnSi was determined using a procedure including calculations of the total energy within the spin-polarized version of the density functional theory, the dispersion curves using the Quantum Espresso code, and the phonon density of states in the quasiharmonic approximation (see details in [13]¹). Taking into account a high Debye temperature for MnSi (660 K) [13], we can say that the quasiharmonic approximation is quite adequate within the temperature range considered in this work.

Fig. 4.

(Color online) Heat capacity of MnSi measured in a magnetic field of (red circles 1) 0 and (blue circles 2) 4 T. The solid line is the nonmagnetic contribution calculated as the sum of the phonon contribution and the linear electron term [13]. The inset demonstrates the phase transition region at an enlarged scale.

In Fig. 4, we can see that a magnetic field of 4 T suppresses the magnetic phase transition and accompanying spin-fluctuation phenomena, including an additional peak on the measured heat capacity curve. The ${{C}_{p}}(T)$ curve in the field of 4 T nearly coincides with the measured curve in the low- and high-temperature limits. At the same time, it crosses the latter in the range of the high-temperature slope of the fluctuation-induced peak. The calculated curve, merging with both sets of experimental data in the low-temperature limit, crosses the measured ${{C}_{p}}(T)$ curve at $H = 0$ at the base of the fluctuation-induced peak and progressively deviates from the measured curves toward higher heat capacity values with increasing temperature. Note that the suppression of helicoidal spin fluctuations by the magnetic field leads to an increase in the specific heat at T > T_c, as follows from Fig. 4. This behavior means that a certain mechanism allows specific spin fluctuations to affect the heat capacity of the system.

In Fig. 5, we can see that curve 2, which characterizes the behavior of the heat capacity of the electron and magnetic subsystems of MnSi in zero magnetic field at T > T_c, exhibits a very weak temperature dependence, whereas straight line 3 corresponding to the heat capacity of the electronic subsystem treated as a degenerate electron gas is above curve 2. The latter suggests that the heat capacity of MnSi at T > T_c should include a term that compensates the linear increase in the heat capacity of the electron gas. This term is apparently due to spin-fluctuation phenomena. At the same time, the linear approximation for the specific heat of electrons is valid at least at T < T_c, as follows from the behavior of the zero-phonon heat capacity of MnSi in high magnetic fields (Fig. 6).

Fig. 5.

(Color online) Temperature dependences of the (red circles 1) heat capacity ${{C}_{p}}$ and (blue circles 2) zero-phonon heat capacity of MnSi compared to (dashed line 3) the heat capacity of the electron gas $\gamma T$, where $\gamma =$ 0.036 J/(mol K²) [14].

Fig. 6.

(Color online) Temperature dependences of the (red circles 1) heat capacity ${{C}_{p}}$ and (blue circles 2) zero-phonon heat capacity ${{C}_{p}} - {{C}_{{ph}}}$ of MnSi in a magnetic field of 4 T. The inset shows the magnetic phase diagram of MnSi with (I) the paramagnetic region, (II, III) the helicoidal phases, and (IV) the spin-polarized ferromagnetic phase. The quasilinear form of dependence 2 below T ~ 40 K indicates the dominant role of the zero-phonon heat capacity in a magnetic field of 4 T within this temperature range.

Should we expect that the interaction of developed spin fluctuations with the electronic subsystem at T > T_c suppresses the electronic heat capacity? In this regard, we can address Fig. 7, which clearly demonstrates that the extrapolation of the high-temperature branch of the ratio ΔC_p/T to zero gives a value of 0.036 J/(mol K²), which is fully consistent with the coefficient γ in the electronic heat capacity obtained in [14]. Hence, the temperature dependence of the electronic specific heat at T > T_c hardly changes significantly (the Fermi energy in MnSi is on the order of 10⁵ K). The behavior of C_p − C_ph at T > T_c is apparently due to the specificity of the interaction of spin fluctuations with the phonon subsystem. This relation means that the theoretical phonon spectrum incompletely reflects the actual situation. Unfortunately, experimental studies of phonons in MnSi do not yet provide clear indications on this matter [15, 16]. Further, subtracting the heat capacity of the electron gas (line 3 in Fig. 5) from the zero-phonon heat capacity (blue circles 2 in Fig. 5), we obtain a contribution to the heat capacity of the system from the interaction between the spin and phonon subsystems (see Fig. 8).

Fig. 7.

(Color online) Temperature dependence of the ratio $\Delta {{C}_{p}}{\text{/}}T$, where $\Delta {{C}_{p}} = {{C}_{p}} - {{C}_{{ph}}}$ is the zero-phonon heat capacity of MnSi according to (empty blue circles 1) [15], (red filled circles 2) [13], and (dashed line 3) the extrapolation of the high-temperature branch of the dependence to $T = 0$.

Fig. 8.

(Color online) Temperature dependences of the magnetic contributions to the (red circles 1) heat capacity and (blue solid line 2) entropy of MnSi determined as the difference between the measured values of the corresponding characteristics and the calculated phonon and electron contributions [13].

In Fig. 8, we demonstrate the contributions to the heat capacity and entropy of MnSi from the interaction between the spin and phonon subsystems obtained by subtracting nonmagnetic contributions from experimental data at zero magnetic field (see the text above). Obviously, the negative partial heat capacity and entropy at temperatures above T_c are obviously not surprising since they are due to ignoring the contribution of spin–phonon coupling to the nonmagnetic component of the heat capacity. We conclude that the negative heat capacity and entropy can be considered as a false effect in strongly fluctuating spin systems. We expect that developed spin fluctuations at T > T_c arising in MnSi suppress the heat capacity of the system as a whole, apparently, owing to spin–phonon coupling. As a result, the attempts to separate the (spin) magnetic component of the heat capacity and entropy by subtracting the phonon and electron contributions that do not contain interaction terms are misleading. Thus, the negative effective magnetic heat capacity of the system also includes the effects of spin–phonon coupling. Finally, we note that these conclusions are valid in the case of a linear or quasilinear behavior of the electronic heat capacity of MnSi at T > T_c.