Abstract—The ERDA and IGRF-12 geomagnetic field models are used to study the behavior of Earth’s large-scale magnetic field. The unusualness of the modern field’s behavior is studied from the viewpoint of the appearance of a new reversal. Estimates are given for the change in energy of the potential magnetic field on the Earth’s surface and of the liquid core, as well as Joule dissipation in the liquid core over 12 000 years. Both values increase sharply for the modern field, which is associated with an increase in the resolution of observations. Various methods for describing geomagnetic field reversals are considered. It is shown that the estimate for the duration of the reversal may depend on the method. It is demonstrated how erroneous reversal predictions may be, based on short time series, in particular, over the last century.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 INTRODUCTION
A geomagnetic field is generated by dynamo processes in the Earth’s liquid core. Its spatiotemporal spectrum is extremely wide (Valet, 2003). The degree to which the field has been studied varies significantly in the transition from the modern field to more ancient times: measurement accuracy decreases accordingly. The latter causes difficulties when comparing models encompassing different time intervals, as well as when trying to extrapolate the behavior of the geomagnetic field to the future. A particular dilemma arises: which is better—a prediction based on a short but accurate series, e.g., with the IGRF-12 model (Thébault et al., 2015), which covers over a duration of about 0.01 of the characteristic time of geomagnetic dipole variations, including reversals (104 years) (Gubbins and Herrero-Bervera, 2007), or an attempt to find field characteristics that are known for longer times? Despite the apparent obviousness of the answer, that the characteristic prediction time should be at least somewhat commensurate with the duration of the used time series of observations, the number of studies on the onset of the geomagnetic field reversal based on modern field data increases every day; for more detail, see (Gubbins et al., 2006; Constable and Korte, 2006; Laj and Kissel, 2015; Poletti et al, 2018). To answer this question, let us consider a number of geomagnetic field models that describe its evolution and spatial structure.
Let us recall some of the provisions of the geodynamo that determine the features of geomagnetic field models. The sources that generate the field are separated from an observer on the Earth’s surface by the weakly conducting layer of the mantle. This allows us to consider the magnetic field B within the mantle at times greater than 10 years the potential field B = –∇U, where U is the scalar potential satisfying the Laplace equation ΔU = 0. The solution to the Laplace equation in a spherical coordinate system can be represented as a power series in spherical functions and powers of the radial coordinate. Power-series expansion was the basis for the spectral description of the geomagnetic field based on paleomagnetic (Kono and Tanaka, 1995; Shao et al. 1999) and archeomagnetic (Korte et al., 2011) data, as well as observatory and satellite observations (Thébault et al., 2015). The spectral method is convenient for analyzing the field. Depending on the age of the observations used, the spatial resolution of the models varies from l = 13 (the order of spherical harmonic) for the modern field in IGRF-12 models, which completely cover a significant part of the magnetic field penetrating from the Earth’s core to the surface, to models with l = 1–2 for paleomagnetic data.
Below, we consider the IGRF-12 and ERDA models, which cover the last 12 000 years and can be used to assess how atypical the the geomagnetic field behavior is for the last century. The ERDA archeomagnetic model (cals10k1b) (Korte et al., 2011), well known among paleomagnetologists, is the spline approximation of time of the Gaussian coefficients in the expansion in spherical functions; it is extremely convenient both for describing the geomagnetic field behavior and for comparison with geodynamic models based, as a rule, on expansion in spherical functions. The modern field data is taken from the IGRF-12 model, which is also based on the splines of Gaussian coefficients. The ERDA and IGRF-12 models can bring some clarity to studying a problem that has attracted much attention recently: the rapid decrease in the geomagnetic dipole and the possible onset of geomagnetic reversal, i.e., polarity reversal of the dipole (Gubbins et al., 2006). The paper shows how reversal predictions depend on the methods used, and how predictions in the past differ from present day.
2 EVOLUTION OF THE FIELD
For synthesize the geomagnetic field over the past 12 000 years, the ERDA model (cals10k1b) was used from 10 000 BCE to 1910, and the IGRF-12 model, from 1915 to 2015. The last point in time for 2018 was taken from the World Magnetic Model (WMM) (Chulliat et al., 2015). These models contain a tabulated set of Gaussian coefficients \(\left( {g_{l}^{m}{\text{,}}h_{l}^{m}} \right)\) with time steps of 40 and 5 years, respectively. The Gaussian coefficients determine the scalar potential (Parkinson, 1986):
where \({\text{(}}r{\text{,}}\theta ,\varphi )\) are spherical coordinates, \(P_{l}^{m}\) are associated Legendre polynomials, the Gaussian coefficients \(\left( {g_{l}^{m}{\text{,}}h_{l}^{m}} \right)\) are calculated on the Earth’s surface r = a, a = 6381 km, and \({{l}_{0}}\) is the maximum number of the harmonic. The potential U uniquely gives the magnetic field vector B. The use of the bispline approximation of time (De Bor, 1985) makes it possible to calculate the magnetic field at an arbitrary time instant.
The most reliable information about the geomagnetic field pertains to the behavior of the magnetic dipole. The dipole strength is proportional to \({{F}_{d}} = \sqrt {{{{\left( {g_{1}^{0}} \right)}}^{2}}{\text{ + }}{{{\left( {g_{1}^{1}} \right)}}^{2}}{\text{ + }}{{{\left( {h_{{{\kern 1pt} 1}}^{1}} \right)}}^{2}}} .\) Over the considered time interval, the dipole intensity varied more than two times (Fig. 1a). At present, a decrease in the dipole intensity is observed, comparable in rate to that observed 11 000 years ago. Variations in the dipole with a period of ~10 000 years are sometimes called the fundamental period of the geodynamo. The concept of period is very arbitrary: its varies from 8 to 11 000 years and is not the most energy-intensive compared to other oscillations (Ziegler and Constable, 2015).
A quadrupole \({{F}_{q}}\) = \(\sqrt {{{{\left( {g_{2}^{0}} \right)}}^{2}}{\text{ + }}{{{\left( {g_{2}^{1}} \right)}}^{2}}{\text{ + }}{{{\left( {h_{2}^{1}} \right)}}^{2}} + {{{\left( {g_{2}^{2}} \right)}}^{2}}{\text{ + }}{{{\left( {h_{2}^{2}} \right)}}^{2}}} \) has a shorter characteristic time (Fig. 1b). According to the estimates in (Christensen and Tilgner, 2004) based on the gufm model (1840–1990), the characteristic time of the variation in a quadrupole l = 2 is τl ~ 535l = 270 years. Extension of the time series taking into account the ERDA model results in variation with a large characteristic period (Fig. 1b), comparable to a period of Fd.
The horizontal dipole component \(F_{d}^{ \bot }\) = \(\sqrt {{{{\left( {g_{1}^{1}} \right)}}^{2}}{\text{ + }}{{{\left( {h_{1}^{1}} \right)}}^{2}}} \) (Fig. 1b) has a characteristic time scale close to \({{\tau }_{2}}\) without an appreciable long-term component, like for \({{F}_{q}}.\) The spatial scale of the field depends only on subscript l in \(\left( {g_{l}^{m}{\text{,}}h_{l}^{m}} \right);\) therefore, a decrease in the characteristic time for \(F_{d}^{ \bot }\) cannot be related to an increase in m. This is well known in geomagnetism: the characteristic time of western drift (103 k) (Gubbins and Herrero-Bervera, 2007), related to the drift of a nonaxisymmetric magnetic field, is an order of magnitude less than the oscillation period of an axisymmetric dipole, 104 years. Both quantities Fq and \(F_{d}^{ \bot },\) are now increasing. In the considered time interval, their current values are comparable with values in the past.
An interesting feature of the geodynamo is the excess, by three orders of magnitude, of magnetic field energy over the kinetic motion energy in the core in a rotating reference frame with respect to the mantle (Reshetnyak and Sokolov, 2003). In contrast to slowly rotating objects, such as our Galaxy or the Sun, in which a regime of equidistribution between the magnetic and kinetic energies has been established (Weinstein et al. 1980), in the planetary dynamo, where the Rossby number is much less than unity, magnetic energy accumulates, which exceeds the kinetic energy by several orders of magnitude. This, in turn, imposes restrictions on the law of conservation of total energy, including kinetic and thermal energy. For the Earth’s dynamo, oscillations of an axisymmetric dipole \(g_{1}^{0},\) significantly exceeding the values of the remaining harmonics, cause large fluctuations in magnetic energy.
To fulfill the general law of conservation of energy, the fluctuation \(g_{1}^{0}\) must be compensated by something. This can be done in two ways: redistribute the magnetic energy over the spectrum, i.e., transfer it to higher harmonics; the second is to perform the work of the Lorentz force. The latter cannot be done on a large scale, since, as mentioned above, the magnetic energy is much greater than kinetic energy, and we have no evidence that this property was violated. In other words, we dispense with catastrophic development scenarios and exclude from consideration the possibility of sharp jumps in kinetic energy by several orders of magnitude. It should also be noted that the impossibility of direct conversion of magnetic energy into motion energy is related to the forceless structure of the magnetic field, when a large-amplitude magnetic field is collinear to the electric current flowing in a fluid, as a result of which the Lorentz force remains relatively small. Taking into account the above, we conclude that fluctuations \(g_{1}^{0}\) are compensated both by the energy redistribution over the spectrum (on large scales) and the work of the Lorentz force (mainly on small scales). Since the local Rossby number increases with decreasing scale, the magnetic field and electric current cease to be collinear and, accordingly, the role of the Lorentz force in energy transfer from the magnetic field to the fluid flow increases.
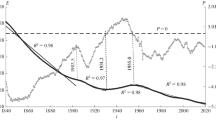
The motion of the dipole in the equatorial plane is described by the \(\left( {g_{l}^{m}{\text{,}}h_{l}^{m}} \right)\) diagram (Fig. 2). The amplitude of the equatorial dipole today is greater than its typical value in the past. Around the year 1330, an reversal of the equatorial dipole was observed: both components \(g_{1}^{1},\)\(h_{1}^{1}\) changed their sign (the event is marked with a triangle in the diagram). The axisymmetric dipole \(g_{1}^{0}\) at this moment reached its maximum: its value, accurate to a few percent, was maximum for the entire considered time interval. Reversals of the equatorial dipole occurred earlier, but after the reversal, the amplitude of the equatorial dipole was significantly less than in the last few hundred years.
Traditionally, magnetic field reversal is understood as a sign change \(g_{1}^{0}.\) However, there are indications that it is not limited to this: a change in sign and equatorial dipole can occur (Clement and Kent, 1985; Shao et al., 1999). Since the Lorentz force is quadratic in the magnetic field, this means that the system tends to return to a state with the same Lorentz force as before the reversal. The current observation accuracy is insufficient to state with certainty which dipole reversal occurs earlier: axisymmetric or equatorial. The presence of a large number of equatorial dipole reversals without \(g_{1}^{0}\) reversal does not contradict the viewpoint that for a complete reversal, all three dipole components should change sign.
For a number of reasons, in paleomagnetology, reversals are sometimes described not by \(g_{1}^{0},\) but by the angle of deviation \(\theta \) of the dipole from the axis of rotation. One reason for this preference is the large error in the absolute magnetic field strength (or sometimes even the complete absence of information thereof). In this case, it is extremely helpful to use the angular characteristics of the field operating at some relative strength (i.e., field values normalized to some value). As before, reversal is determined by a change in sign \(g_{1}^{0},\) but the dynamics of the process in terms of the angle of deviation of the magnetic dipole with respect to the vertical axis \(\theta = \frac{{180^\circ }}{\pi }\arccos \left( {\frac{{g_{1}^{0}}}{{{{F}_{d}}}}} \right)\) may already be very different from the behavior \(g_{1}^{0}\) in time. For example, if all three dipole components the have the same time dependence, then \(\theta \) will not depend on time until the change in sign \(g_{1}^{0}.\) More complex scenarios are also observed when Figs. 1 and 3 are compared, the latter of which shows the evolution of \(\theta .\) Whereas the decrease in the dipole amplitude over the past century is sometimes interpreted as an impending reversal, the behavior of \(\theta \) after 2000 demonstrates movement of the magnetic dipole toward the geographic pole, i.e., the reversal process. Clearly, a reliable conclusion about impending reversal requires information on \(g_{1}^{0}.\) If there is none, one should at least define what is meant by reversal in terms of \(\theta \), e.g., deviation beyond \(\theta > 20 - 30^\circ .\)
Description of reversals in various terms may cause wide scatter in estimates for the duration of magnetic field reversals, ranging from several thousand to one hundred years (Jacobs, 1994; Sagnotti et al., 2014). Whereas the first estimate is comparable in order of magnitude to the characteristic times of evolution of the large-scale magnetic field in the Earth’s liquid core and the decay time of the magnetic field in the solid core, the second estimate, as a rule, raises great doubts among dynamo theory specialists. When the duration of an reversal is estimated by \(\theta ,\) and the time dependences of all three magnetic dipole components are close, the duration of the reversal may be significantly reduced. In fact, its duration will be determined by that of the time interval during which the dipole amplitude will remain comparable to the amplitude of the nondipole field. In this time interval, for the current observation accuracy, the behavior of the dipole cannot be reproduced in detail. The dipole components cease to correlate with each other due to increased measurement error, and \(\theta \) begins to change rapidly over time.
It cannot be ruled out that unreliable estimates for the strength of the magnetic dipole during reversals are the reason for the different reversal scenarios (Petrova et al., 1992). According to one scenario, reversals occur with a successive decrease in amplitude \(g_{1}^{0},\) a change in its sign, and further recovery of the amplitude. According to another, during an reversal, the dipole flips under relatively constant strength. This, in turn, means that when \(\left| {g_{1}^{0}} \right|\) there is an increase \(F_{d}^{ \bot }.\) If we take into account the fact that the equatorial dipole has a shorter characteristic time, then the second scenario gives a shorter reversal duration. Such considerations should, of course, be approached with caution, since the relative accuracy in measuring the equatorial dipole in the past is much less than for an axisymmetric dipole. The latter follows from the fact that \({{F}_{d}} \gg F_{d}^{ \bot }.\)
The definition of reversal is not limited to the two ways considered above, namely, the evolution of \(g_{1}^{0}\) and \(\theta .\) From the vantage point of an observer with no knowledge about the multipole expansion of the magnetic field, it is possible to describe the reversal by monitoring the movement of the magnetic poles, i.e., points at which the tangential magnetic field is zero, but in practice it is equal to the minimum value in the hemisphere. Generally speaking, such a description can be obtained from more than one magnetic pole in the hemisphere, especially during an reversal, when the field ceases to be a dipole. Conversely, the method itself is much simpler; in fact, only information on the trajectory of the minima of the absolute values of the tangential magnetic field in each hemisphere is required. The accuracy of the method may be quite satisfactory as long as the poles are at high latitudes. In such an analysis, the position of the south and north magnetic poles need not be symmetrical with respect to the center of the Earth, as was the case with expansion in multipoles.
Figure 4 depicts the evolution of the latitudes \(\vartheta = 90 - \theta \) of the magnetic poles. Two features are noteworthy. First, movement of the magnetic poles over the past hundred years differs little from their movement in the past. Second, the south and north magnetic poles behave differently: fluctuations in the latitude of the north magnetic pole are less than those for the south over the entire time. It should be borne in mind that during calculation, the sphere was divided into latitudinal zones with a step of 5° and \(\vartheta ,\) was found for which the tangential field is minimal. Therefore, the coincidence of the magnetic and geographical poles observed for the Northern Hemisphere, with the exception of small spikes, reflects the accuracy of the data used. To answer whether the second feature is statistically significant, let us examine what other magnetic field characteristics related to location of the magnetic poles have broken symmetry with respect to the equator. Analysis shows that over the entire time interval, the maximum values of the magnetic field strength in the hemispheres (~6 × 104 nT) coincide to within 30%. The minimum strength values (2.5 × 104 nT) show even greater agreement. The maximum values of the tangential magnetic field (3 × 104 nT) are also close. However, the minimum values of the tangential field, which in fact also determine the movement of the poles, differ significantly from each other. For the Northern Hemisphere, this value is less than 100 nT, and for the Southern Hemisphere, about 500 nT. The resolution of fields with such amplitude is equivalent to a relative accuracy of ~1% or less, which is not comparable with the accuracy of archeomagnetic data. In summary, this method of determining the magnetic pole trajectories, which requires a large number of measurements, is inferior in accuracy to the other two described above.
3 SPECTRAL PROPERTIES
The Gaussian coefficients determine the so-called Mauersberger spectrum (Mauersberger, 1956). We write it in dimensional form so that the spectral coefficients are in J/m (magnetic energy density):
where \({{\mu }_{{\text{o}}}}\) = 1.25663706 N/A–2 is the magnetic constant and (g, h) is measured in B, T. On the l = lo (lo = 13) boundary, the spectrum has a kink (Lowes, 1974). Mode with l < lo pertain to sources at the core–mantle boundary. The high-frequency part of the spectrum is attributed to magnetized rocks in the crust. Spectrum (2) can be extrapolated to the core–mantle boundary r = rc, rc = 3480 km, where the field energy increases by two orders of magnitude, mainly due to high modes. On the surface of a liquid core, the magnetic energy density for the modern field has the dependence (Lowes, 1974)
The spectrum Sl between reversals has a maximum at l = 1 (dipole configuration of the geomagnetic field).
The energy density of the potential field E is equal to the sum Sl over all l. The behavior of energy E s (Fig. 5a) on the surface of the Earth will be determined by the magnetic dipole (Fig. 1), demonstrating an increase in the time interval (–10, 0) of a thousand years and a slight decrease over the last two millennia. The field energy on the surface of the liquid core E c indicates a similar increase for the first time interval, stabilization for the second interval, and a sharp increase in energy over the past century (Fig. 5b). The last increase in energy was accompanied by high-frequency oscillations. This behavior is associated with a change in observation accuracy, which which both spatially and temporally become less smoothed with decreasing age.
The magnetic field symmetry with respect to the equator is determined by parity of the value l – m. For antisymmetric (a) modes – l – m is odd, and for symmetric (s) modes, even. Using this terminology, we expand \({{E}^{c}}\) into two components: \({{E}^{c}} = E_{a}^{c} + E_{s}^{c},\) having excluded from consideration the dipole l = 1, which significantly exceeds other modes in amplitude, and we introduce the spatial parity parameter:
For predominance of the symmetric component,  tends to +1; for predominance of the antisymmetric component, to −1. The behavior of
tends to +1; for predominance of the antisymmetric component, to −1. The behavior of  is shown in Fig. 5b. For the first 11 000 years,
is shown in Fig. 5b. For the first 11 000 years,  was positive. Then, a short-term change in sign was observed
was positive. Then, a short-term change in sign was observed  The current value of
The current value of  is close to zero. It is possible that this phenomenon is associated with an increase in the accuracy of the observational data and reflects that for the high modes resolved in IGRF-12, the \(E_{a}^{c}\) and \(E_{s}^{c}\) values are close to each other. More details on the problems of magnetic field symmetry can be found in (Coe and Glatzmaier, 2006; Hulot and Bouligand, 2005).
is close to zero. It is possible that this phenomenon is associated with an increase in the accuracy of the observational data and reflects that for the high modes resolved in IGRF-12, the \(E_{a}^{c}\) and \(E_{s}^{c}\) values are close to each other. More details on the problems of magnetic field symmetry can be found in (Coe and Glatzmaier, 2006; Hulot and Bouligand, 2005).
It is interesting to compare the magnetic energy density with the kinetic energy density of flows in the core. The estimate for the western drift velocity on the surface of the core Vwd = 0.2 °/g. = 4 × 10–4 m/s gives a kinetic energy density of \({{E}_{k}} = {{\rho {{V}^{2}}} \mathord{\left/ {\vphantom {{\rho {{V}^{2}}} 2}} \right. \kern-0em} 2} = 7 \times {{10}^{{ - 4}}}\) J/m3, the value of the magnetic energy density of the dipole for the modern field \({{S}_{1}} = 2.6 \times {{10}^{{ - 2}}}\) J/m3 is 35 times greater. The excess of magnetic energy density over the kinetic energy density in the reference frame with respect to the Earth’s surface is associated with fast diurnal rotation. Below we will see that this ratio can be even larger. Also note that on the surface of the core, the dipole’s contribution to the total energy is small: \({{S}_{1}} \sim 0.44{{E}^{c}}.\) Because the magnetic Reynolds number \({{R}_{m}} = {{10}^{3}}\) in the liquid core is large and, therefore, the number of excited modes exceeds the number of observations \({{l}_{o}} = 13,\) the relative contribution of the dipole to \(E_{a}^{c}\) should be even smaller.
There are more fundamental reasons for the change in \(E_{a}^{c}\) when switching from the ERDA to the IGRF-12 model. To calculate the Gaussian coefficients in the ERDA model, the hypothesis of minimal Joule dissipation at the core–mantle boundary is used (Gubbins, 1975). For the IGRF-12 model, where the accuracy of the data is higher, this hypothesis is not used. Taking into account a priori information about the magnetic field on the surface of the liquid core makes it possible to suppress the increase in errors in the high-frequency part of the spectrum when calculating the Gaussian coefficients based on observations. Gubbins idea was that the minimal dissipation mode occurs when the solution is representable as the superposition of free damping modes. This hypothesis is based on the closeness of the period of magnetic dipole variation to the characteristic decay time of the magnetic field in the Earth’s liquid core, 10 000 years. This viewpoint, however, is quite controversial, because the magnetic Reynolds number in the liquid core is large, but at the same time, this approximation is seen in low-mode geodynamo models (Sobko et al., 2012), which reflect some features of the geomagnetic field. The amplitudes of the attenuation modes in the ERDA model are calculated from the condition of continuity of the magnetic field on the surface of the core. Calculating the current squared gives the required estimate for the minimum dissipation energy, which is used in the penalty function to minimize the functional. In sewing together the potential field and the solution in the liquid core at the core–mantle boundary, the ERDA model uses ordinal estimates based on the asymptotic behavior of the spherical Bessel functions that occur in free damping modes (Gubbins, 1975). As a result, the following expression is obtained for the ohmic dissipation spectrum:
where η is the magnetic diffusion coefficient. A more sequential analysis (Roberts et al., 2003), taking into account the exact shape of the free modes for the poloidal field (Moffat, 1980), leads to
where \({{\alpha }_{l}}\) is the minimum positive root of the spherical Bessel function \({{j}_{l}}(\alpha ).\) It is this estimate that we will use below. The total ohmic dissipation \(J = \sum\nolimits_{l = 1}^{{{l}_{o}}} {{{q}_{{\text{l}}}}} ,\) calculated by formula (6) exceeds estimate (5) by 50 times. The shapes of the evolutionary curves are similar. Since estimates (5) and (6) differ only by the numerical factor and their ratio does not depend on time, we can use estimate (6) below, although estimate (5) was used to construct the ERDA model itself.
Figure 5c shows the evolution of J using formula (6). If we exclude small variations J, then for the ERDA model, ohmic dissipation increases five times over 12 000 years. The increase in J may reflect both an objective change in the magnetic field generation regime in the Earth’s liquid core and be associated with an increase in the accuracy of data and their quantity, i.e., the resolution of the model. Most likely, an increase in the number of spherical functions lo used in (1)–(2) and in the IGRF-12 model leads to a sharp jump in J.
The maximum values of J ∼ 1 MW for the modern field is attributed to a poloidal magnetic field penetrating the Earth’s surface and contributing to the Gaussian coefficients. This estimate may be significantly increased due to three factors. First, modern dynamo models record a slight decrease in the spectrum of the magnetic field and kinetic energy in the liquid core (Christensen et al., 1999; Roberts et al., 2003). In other words, the length of magnetic energy spectrum can significantly exceed lo, the choice of which is determined by both the amount of observational data and the distribution of magnetic field sources in the crust. Second, taking into account the contribution of a poloidal magnetic field that does not penetrate the surface will also increase J. As shown by three-dimensional calculations, part of the poloidal magnetic field has closed field lines inside the liquid core and does not penetrate the surface. Lastly, this is a toroidal magnetic field, which is completely invisible to the observer. As a result, estimates of ohmic dissipation can reach 1–2 TW (Roberts et al., 2003). In summary, estimate (6) gives only a very approximate idea of the evolution of the magnetic field in the core.
Whereas in early works on archeo- and paleomagnetism (Petrova et al. 1992) and the linearized geodynamo theory (Braginsky 1967), emphasis was placed on substantiating periodic variations in the magnetic field, later, with the increase in observations and advent of new spectral methods (see, e.g., the wavelet analysis results in (Burakov et al., 1998)), quasiperiodic variations began to be favored. In fact, the longer the time series became, the more indications there were that the variations were of a relaxation nature and their characteristic time (quasiperiod) were on the same order with the duration of the variations: what was previously considered a variation period came to be regarded as the correlation time of the process. A similar viewpoint, supported by the large number of observed geomagnetic field quasiperiods (Petrova et al., 1992), raises no objections among dynamo experts, who clearly observe a continuous spectrum of kinetic and magnetic energies (Christensen et al., 1999). As expected from the idea of the turbulent nature of convection in the Earth’s liquid core, variations at different scales are statistically independent processes (Christensen and Tilgner, 2004; Hulot and Le Mouël, 1994). New statistical methods played an important role in this direction, making it possible to synthesize observations (Khokhlov, 2012).
Considerations about the random nature of geomagnetic field variations apply equally to the behavior of the dipole at large times, in particular, to the distribution of geomagnetic field reversals (Jacobs, 1994; Valet, 2003). If the spatial spectrum of the magnetic field were “purely” turbulent, i.e. self-similar, with a power-law dependence, the magnetic dipole would change sign in time according to a random law, one of the parameters of which would be the correlation time, in order of magnitude equal to the time of revolution of the convective vortex on a scale of l = 1. However, this viewpoint contradicts the observations. First, as follows from Fig. 1, the amplitude of the dipole on the Earth’s surface exceeds the amplitude of the quadrupole by seven to ten times. On the surface of the core, this corresponds to a ratio of 4–5, while according to (3), starting from l = 2, the decrease for the magnetic field is 5% with an increase in l by unity. This means that the dipole does not fit the typical idea of turbulence. It is more logical to compare it with the mean field, described by mean-field theory (Krause and Radler, 1984). Moreover, the exponential dependence (3) for 1 < l < lo is more reminiscent of damped turbulence near the solid core–mantle boundary than that developed in the bulk of the liquid core, where power-law dependences should be observed (Frick, 2010). Most likely, small-scale fields are a trigger that takes the dipole from an equilibrium position near the geographic poles (Reshetnyak and Hejda, 2013). The relaxation time of such a fluctuation, i.e., the duration of the reversal, is much less than time between the reversals themselves.
In addition to energy exchange between modes, when describing reversals, it is necessary to take into account the effect of rotation. Rotation can be considered an external field that leads to the appearance of attractors for magnetic poles, the position of which coincides with that of the geographical poles (Reshetnyak and Hejda, 2013). The higher the speed of diurnal rotation, the less often reversals occur, but rotation does not affect the random nature of reversals. All that rotation can do is to stop reversals or make them more frequent, i.e., change the statistical distribution law and increase the correlation time between adjacent reversals. One of the simplest laws of the time distribution of reversals is fractal (Anufriev and Sokoloff, 1994). The fact that rotation is also a necessary condition for the existence of a dipole field makes the geodynamo problem even more interesting. Therefore, obviously, it is impossible to predict reversals over time. The appearance of a new reversal in the near future is certainly possible, especially since the last reversal was 780 000 years ago (Gradstein et al., 2012), which in order of magnitude coincides with the time interval between the last reversals. However, the significance of such a prediction will be low. We show this by the example of the data considered above.
Let us ask ourselves what linear extrapolation will make it possible to predict a reversal. We estimate the time \({{\tau }_{1}},\) through which the sign of the modulo decreasing function f must change as – \({f \mathord{\left/ {\vphantom {f {f{\kern 1pt} '}}} \right. \kern-0em} {f{\kern 1pt} '}},\) where \(f{\kern 1pt} '\) is the time derivative. Knowing the function f, let us calculate the total duration of time intervals \({{\tau }_{2}},\) during which the reversal must occur no later than after time \({{\tau }_{1}}.\) For function \(g_{1}^{0}\) (or, which is almost the same, for Fd), the following approximation takes place in the interval \(1.1 \times {{10}^{3}} < {{\tau }_{1}} < {{10}^{4}}{\text{:}}\)\({{\tau }_{2}} = - 2.97 \times {{10}^{{ - 5}}}\tau _{1}^{2}\) + \(0.69{{\tau }_{1}} - 603,\) where \({{\tau }_{1}}\) and \({{\tau }_{2}}\) are measured in years. Using this formula, we calculate \({{\tau }_{2}},\) for which linear extrapolation predicts a reversal no later than the half-period of the dipole variation, taking \({{\tau }_{1}} = 4500\) years. The estimate gives \({{\tau }_{2}} = 2500\) years, i.e., more than half the time during which the field decreased (more than a quarter of the period). Since previously we indicated that the rate of modern field attenuation was observed 11 000 years ago, let us estimate \({{\tau }_{2}}\) for \({{\tau }_{1}} = 5500\) years: 3200 years. In other words, in the past 12 000 years, over the course of 3200 years, linear extrapolation predicts the appearance of a reversal no later than after 5500 years. Note that the contribution to \({{\tau }_{2}}\) does not correspond to any particular time period, e.g., the recent millennia, but consists of different time intervals. However, the fact that \({{\tau }_{2}}\) is comparable to one quarter of the period of the main cycle already indicates that the modern change in the magnetic dipole strength is not unusual in the history of the geomagnetic field.
Consider the probability of a reversal at short times. There are no indications that a reversal may occur earlier than after \({{\tau }_{1}} = 1100\) in the considered interval: \({{\tau }_{2}} = 0.\) For \({{\tau }_{1}} = 1100\) years, this was observed in 1925–1930. For \({{\tau }_{1}} = 1500\) years, we have \({{\tau }_{2}} = 120\) years. Two time periods contributed equally to this estimate: from (−8675, −8610) and from the 20th century For \({{\tau }_{1}} = 2000\) years, \({{\tau }_{2}} = 620\) years. The contribution comes from (−8750, −8360), (−5540, −5525) and for some periods, starting from 1785. Given the duration of these three time intervals, we conclude that the probability of a reversal over the course of 2000 years has now lessened. This simple analysis demonstrates how precarious it is to use linear extrapolation to predict reversals based on short time series, in particular, over the last century.
4 DISCUSSION AND CONCLUSIONS
The use of long series of geomagnetic field variations has been very instructive for assessing the uniqueness of the behavior of the modern field. On the one hand, we saw that there is nothing extraordinary in the behavior of the modern magnetic dipole. On the other hand, the number of energy characteristics associated with small-scale magnetic fields changes significantly as observation accuracy increases with time; in particular, this pertains to the magnetic energy density at the core–mantle boundary. Meanwhile, the change in symmetry of the magnetic field (parity  ) with respect to the equatorial plane depends weakly on the length of the series lo and may be a more significant evolutionary characteristic. The change in
) with respect to the equatorial plane depends weakly on the length of the series lo and may be a more significant evolutionary characteristic. The change in  indicates strengthening of modes asymmetric with respect to the equatorial plane over the past millennium.
indicates strengthening of modes asymmetric with respect to the equatorial plane over the past millennium.
Note that when calculating  , large-amplitude dipoles are excluded. The use of various methods for describing the evolution of the geomagnetic field indicates that estimates for the duration of the reversal can differ significantly using the same data. A evolutionary scenario is possible when a magnetic dipole decreasing in amplitude approaches the geographic pole, which is currently being observed. This behavior of the magnetic dipole corresponds to the reversal scenario when the dipole decreases in amplitude without reversal. However, as shown in this paper, over the past 12 000 years, such magnetic dipole behavior is not unique. With varying degrees of probability, there were predictions of an imminent new reversal during the entire time interval, which makes us very cautious about such predictions. However, the starkest of such predictions date back to 10 500 years ago. The behavior of the field at that time was reminiscent of the modern one.
, large-amplitude dipoles are excluded. The use of various methods for describing the evolution of the geomagnetic field indicates that estimates for the duration of the reversal can differ significantly using the same data. A evolutionary scenario is possible when a magnetic dipole decreasing in amplitude approaches the geographic pole, which is currently being observed. This behavior of the magnetic dipole corresponds to the reversal scenario when the dipole decreases in amplitude without reversal. However, as shown in this paper, over the past 12 000 years, such magnetic dipole behavior is not unique. With varying degrees of probability, there were predictions of an imminent new reversal during the entire time interval, which makes us very cautious about such predictions. However, the starkest of such predictions date back to 10 500 years ago. The behavior of the field at that time was reminiscent of the modern one.
This may mean that the currently observed decrease in magnetic field strength, taken as the beginning of a reversal, is nothing but a manifestation of the 10 000th variation cycle.
REFERENCES
Anufriev, A. and Sokoloff, D., Fractal properties of geodynamo models, Geophys. Astrophys. Fluid Dyn., 1994, vol. 74, pp. 207–218.
de Boor, C., A Practical Guide to Splines, New York: Springer, 1978; Moscow: Radio i svyaz', 1985.
Braginskii, S.I., Magnetic waves in the Earth’s core, Geomagn. Aeron., 1967, vol. 7, pp. 1050–1062.
Burakov, K.S., Galyagin, D.K., Nachasova, I.E., Reshetnyak, M.Yu., Sokolov, D.D., and Frick, P.G., Wavelet analysis of geomagnetic field intensity for the past 4000 years, Izv.,Phys. Solid Earth, 1998, vol. 34, no. 9, pp. 773–778.
Christensen, U.R. and Tilgner, A., Power requirement of the geodynamo from ohmic losses in numerical and laboratory dynamos, Nature, 2004, vol. 429, pp. 169–171.
Christensen, U., Olson, P., and Glatzmaier, G.A., Numerical modelling of the geodynamo: A systematic parameter study, Geophys. J. Int., 1999, vol. 138, pp. 393–409.
Chulliat, A., Macmillan, S., Alken, P., Beggan, C., Nair, M., Hamilton, B., Woods, A., Ridley, V., Maus, S., and Thomson, A., The US/UK World Magnetic Model for 2015–2020, NOAA National Geophysical Data Center Tech. Rep., 2015.
Clement, B.M. and Kent, D.V., A comparison of two sequential geomagnetic polarity transitions (upper Olduvai and lower Jaramillo) from the Southern Hemisphere, Phys. Earth Planet. Int., 1985, vol. 39, pp. 301–313.
Coe, R.S. and Glatzmaier, G.A., Symmetry and stability of the geomagnetic field, Geophys. Res. Lett., 2006, vol. 33, no. 21, L21311-1-5.
Constable, C. and Korte, M., Is Earth’s magnetic field reversing?, Earth Planet. Sci. Lett., 2006, vol. 246, pp. 1–16.
Frick, P.G., Turbulentnost’: modeli i podkhody (Turbulence: Approaches and Models), Moscow–Izhevsk: RKhD, 2010.
Gradstein, F.M., Ogg, J.G., Schmitz, M., and Ogg, G., The Geologic Time Scale 2012, Boston: Elsevier, 2012.
Gubbins, D., Can the Earth’s magnetic field be sustained by core oscillations?, Geophys. Res. Lett., 1975, vol. 2, pp. 409–412.
Gubbins, D. and Herrero-Bervera, E., Encyclopedia of Geomagnetism and Paleomagnetism, Dordrecht: Springer, 2007.
Gubbins, D., Jones, A.L., and Finlay, C.C., Fall in Earth’s magnetic field is erratic, Science, 2006, vol. 312, pp. 900–902.
Hulot, G. and Bouligand, C., Statistical palaeomagnetic field modelling and symmetry considerations, Geophys. J. Int., 2005, vol. 161, pp. 591–602.
Hulot, G. and Le Mouël, J.L., A statistical approach to the Earth’s main magnetic field, Phys. Earth Planet. Int., 1994, vol. 82, pp. 167–183.
Jacobs, J.A., Reversals of the Earth’s Magnetic Field, Cambridge: Cambridge University Press, 1994.
Khokhlov, A.V., Simulation of secular geomagnetic variations. Principles and implementation, Geofiz. Issled., 2012, vol. 13, pp. 50–61.
Kono, M. and Tanaka, H., Mapping the Gauss coefficients to the pole and the models of paleosecular variation, J. Geomagn. Geoelectr., 1995, vol. 47, pp. 115–130.
Korte, M., Constable, C., Donadini, F., and Holme, R., Reconstructing the Holocene geomagnetic field, Earth Planet. Sci. Lett., 2011, vol. 312, pp. 497–505.
Krause, F. and Rädler, K.-H., Mean-Field Magnetohydrodynamics and Dynamo Theory, Oxford: Pergamon, 1980; Moscow: Mir, 1984.
Laj, C. and Kissel, C., An impending geomagnetic transition? Hints from the path, Front. Earth Sci., 2015, vol. 3, pp. 1–10.
Lowes, F.J., Spatial power spectrum of the main geomagnetic field, Geophys. J. R. Astron. Soc., 1974, vol. 36, pp. 717–725.
Mauersberger, P., Das Mittel der Energiedichte des geomagnetischen Hauptfeldes an der Erdoberflache und seine säkulare Änderung, Gerlands Beitr. Geophys., 1956, vol. 65, pp. 207–215.
Moffatt, H.K., Magnetic Field Generation in Electrically Conducting Fluids, Cambridge: Cambridge Univ. Press, 1978; Moscow: Mir, 1980.
Parkinson, W.D., Introduction to Geomagnetism, Elsevier, 1983; Moscow: Mir, 1986.
Petrova, G.N., Nechaeva, T.B., and Pospelova, G.A., Kharakternye izmeneniya geomagnitnogo polya v proshlom (Characteristic Changes in the Geomagnetic Field in the Past), Moscow: Nauka, 1992.
Poletti, W., Biggin, A.J., Trindade, R.I., Hartmann, G.A., and Terra-Nova, F., Continuous millennial decrease of the Earth’s magnetic axial dipole, Phys. Earth Planet. Int., 2018, vol. 274, pp. 72–86.
Reshetnyak, M.Yu. and Hejda, P., Heat flux modulation in Domino dynamo model, Open J. Geol., 2013, vol. 3, pp. 55–59.
Reshetnyak, M.Yu. and Sokolov, D.D., Geomagnetic field intensity and suppression of helicity in the geodynamo, Izv.,Phys. Solid Earth, 2003, vol. 39, no. 9, pp. 774–777.
Roberts, P.H., Jones, C.A., and Calderwood, A.R., Energy fluxes and ohmic dissipation in the Earth’s core, Earth’s Core and Lower Mantle, Jones, C.A., Soward, A.M., and Zhang, K., Eds., Taylor & Francis, 2003, pp. 100–129.
Sagnotti, L., Scardia, G., Giaccio, B., Liddicoat, J.C., Nomade, S., Renne, P.R., and Sprain, C.J., Extremely rapid directional change during Matuyama–Brunhes geomagnetic polarity reversal, Geophys. J. Int., 2014, vol. 199, pp. 1110–1124.
Shao, J.-C., Fuller, M., Tanimoto, T., Dunn, J.R., and Stone, D.B., Spherical harmonic analyses of paleomagnetic data: The time-averaged geomagnetic field for the past 5 Myr and the Brunhes–Matuyama reversal, J. Geophys. Res.: Solid Earth, 1999, vol. 104, pp. 5015–5030.
Sobko, G.S., Zadkov, V.N., Sokolov, D.D., and Trukhin, V.I., Geomagnetic reversals in a simple geodynamo model, Geomagn. Aeron. (Engl. Transl.), 2012, vol. 52, no. 2, pp. 254–260.
Thébault, E., Finlay, C.C., Beggan, C.D., Alken, P., Aubert, J., Barrois, O., Bertrand, F., Bondar, T., Boness, A., Brocco, L., et al., International geomagnetic reference field: the 12th generation, Earth Planets Space, 2015, vol. 67, id 79.
Vainshtein, S.I., Zel’dovich, Ya.B., and Ruzmaikin, A.A., Turbulentnoe dinamo v astrofizike (Turbulent Dynamo Astrophysics), Moscow: Nauka, 1980.
Valet, J.-P., Time variations in geomagnetic intensity, Rev. Geophys., 2003, vol. 41, no. 1, id 1004, pp. 4-1–4-44.
Ziegler, L.B. and Constable, C.G., Testing the geocentric axial dipole hypothesis using regional paleomagnetic intensity records from 0 to 300 ka, Earth Planet. Sci. Lett., 2015, vol. 423, pp. 48–56.
ACKNOWLEDGMENTS
The author thanks V.E. Pavlov for his attention to the work.
Funding
The study was supported by the Russian Science Foundation (grant no. 19-47-04110).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Reshetnyak, M.Y. Evolution of the Large-Scale Geomagnetic Field over the Last 12 000 Years. Geomagn. Aeron. 60, 121–130 (2020). https://doi.org/10.1134/S0016793220010119
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0016793220010119


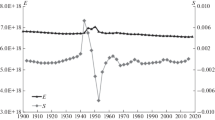






 , dotted line, (b); evolution of minimum joule dissipation energy J (c).
, dotted line, (b); evolution of minimum joule dissipation energy J (c).