Introduction

Airline routes and their fares in the United States were controlled by the Civil Aeronautics Board (CAB) prior to the deregulation of the airline industry. The Airline Deregulation Act of 1978 gave rise to the entry of Low-Cost Carriers (LCCs) into the market. Full-Service Carriers (FSCs) faced stiff competition from LCCs as the latter offered lower fares. Facing the threat of being wiped out from the market, American Airlines invented Dynamic Inventory Allocation and Maintenance Optimizer (DINAMO), and the practice of revenue management (RM) was born. With the help of DINAMO, American Airlines managed to recapture the market through effective segmentation of their business and leisure travelers and drove the newly entered LCCs out of business.

Even though RM techniques have been in practice for more than four decades, the International Air Transport Association’s 2019 End-year report on the Economic Performance of the Airline Industry shows that the net global profit per passenger is only around $6 (IATA 2019). Fiig et al. (2010) state that proper RM techniques can contribute to 5–8% increase in revenues. Further, Barnhart et al. (2003) assert that it is the frequent re-optimization of booking limits that contribute to a sizable portion of the revenue gained from practicing RM. Given that the optimization module lies at the core of all revenue management systems (RMS), the need to improve it is thus motivated.

The two key aspects of optimization in airline RM are the pricing and allocation decisions. To the best of our knowledge, little work on the simultaneous determination of fares and seat allocation under customer-choice behavior exist. A mathematical model that jointly optimizes product prices and their allocation quantities with choice-based demand is developed in this context. This paper addresses this problem with the following contributions:

  1. 1.

    Development of a mathematical programming model that jointly optimizes product fares and seat allocation, and uses a joint forecasting model as its input.

  2. 2.

    Development of a solution methodology that is easier to re-optimize as compared to existing methods.

  3. 3.

    Proposal of a heuristic-based solution for pricing that considers price elasticities of demand and capacitated substitutable products.

Literature review

Quantity-based RM

Single-leg RM

The single-leg RM problem is to compute the optimal protection levels on a single flight leg. Littlewood pioneered the work on single-leg RM in 1972 by developing a rule to determine the number of seats to protect for the higher fare class when there are only two fare classes in a flight. He states that a booking from the lower fare class should be accepted if and only if its revenue exceeds the expected revenue from reserving the xth unit for the higher fare class. This is referred to as Littlewood’s Rule (1972). Belobaba (1987a, b, 1989) extends Littlewood’s Rule to multiple fare classes with his Expected Marginal Seat Revenue (EMSR) heuristic. Two variants of the EMSR heuristic, namely EMSR-a and EMSR-b, exist in practice. EMSR-a calculates individual protection levels and aggregates them while EMSR-b aggregates the demand in order to calculate protection levels. Till date, EMSR remains the backbone of most RMS.

In spite of its significance, EMSR faces a major shortcoming—the heuristic assumes that demand arrives in the order of increasing fare classes, i.e. low to high. Lee and Hersh (1993) and subsequently Lautenbacher and Stidham Jr (1999) obviate this issue with the introduction of dynamic programming (DP). DP models account for interspersed arrival of demand by modeling it as a Poisson process. Even though DP models give optimal solutions, they suffer from what is known as the curse of dimensionality due to large number of state spaces that increase exponentially with the amount of resources.

Network RM

Single-leg RM expanded to network RM, or Origin-Destination (O-D) control, to accommodate connecting flights. Leg-based solution techniques yield only sub-optimal results in the network setting as they fail to consider a passenger’s contribution to the entire network. The notion of a fare class is replaced with Origin Destination Fare (ODF) since the fares in a network are related to the O-D information as well. Smith and Penn (1988) calculate the down-line displacement costs using Displacement-Adjusted Virtual Nesting (DAVN). The value of each leg is computed as the difference between the total O-D fare and the sum of all the displaced down-line costs. The limitation imposed by the deterministic nature of DAVN is overcome by Bratu (1998) through his Probabilistic Bid-Price Control (ProBP) mechanism. Leg-based bid-price is calculated using stochastic demand, and the bid-price of an O-D is the aggregation of the bid-prices across all the legs in the itinerary.

Mathematical programming model based network RM was first developed by Williamson (1992). The solution of these models is the set of partitioned seat allocations that maximize the total network revenue. In practice, the bid-prices obtained from the solution are utilized. Among the models, Deterministic Linear Program (DLP) and Probabilistic Non-Linear Program (PNLP) are the two most prevalent ones used in airline RM. The objective of both optimization models is to maximize the revenue subject to a set of linear constraints. The difference between the two lies in the nature of the demand being considered.

Choice-based RM

The single-leg and network RM models assume that the demand is independent, i.e., if a customer is unable to purchase a ticket for a particular ODF, the customer exits the system instead of evaluating the other alternatives. However, with increasing transparency of fares, customers have the ability to compare all the options available to them and choose the one that is most suited to their needs. This can potentially give rise to a buy-down behavior, wherein customers purchase tickets at a price lower than what they were willing to pay for. Further, attributes other than price can also play a role in a customer’s purchase decisions. This nullified the independence of demand assumption and paved way to choice-based RM.

The earliest work done to incorporate customer-choice behavior is done by Talluri and Van Ryzin (2004a). For a single-leg, they determine the set of fare classes to offer in each time period given that the probability of purchase of a fare class is dependent on the other available fare classes. The idea is extended to the network setting by Liu and Van Ryzin (2008). Another notable work done in the area of modeling customer-choice behavior is by Zhang and Cooper (2005). In the presence of several flights operating in an O-D pair, they calculate the protection levels in an environment where customers have to choose between the same fare class among multiple flights. The airline industry predominantly uses discrete-choice models to capture dependent demand in the airline industry (Phillips 2005; Garrow 2016; Balaiyan et al. 2019). These models determine the probability of selection of an ODF given the attributes of the other alternatives that are present.

Price-based RM

The section on Quantity-based RM outlined common RM methods in which revenue maximization is done by controlling the availability of the inventory of perishable goods. This is known as seat inventory control. Quantity and price-based RM are considered to be synonymous because closing a fare class is equivalent to raising its price (Talluri and Van Ryzin 2004b). However, in spite of the equivalence, RM literature has largely focused on seat inventory control. The ODF fares are exogenously determined and the quantity-based RM models only compute the protection levels. On the other hand, price-based RM dynamically vary the fares in order to maximize revenues. One of the first works which attempts to employ price-based RM with customer-choice behavior is by Zhang and Cooper (2009), whose setting is similar to that of Zhang and Cooper (2005), but in the presence of dynamic pricing. Zhang and Lu (2013) also develop a dynamic pricing model in the presence of customer-choice behavior and demonstrate that their model yields higher revenues than those that employ static prices, with or without choice-based RM.

Joint optimization of pricing and allocation

Although customer-choice behavior is considered in quantity and price-based RM, the pricing and optimization decisions themselves are taken separately. There is scant literature that consider quantity-based and price-based RM concurrently. The first to address this problem are Cizaire and Belobaba (2013). They consider the joint optimization of two products’ prices and allocation in a two-period setting. However, their results are limited to this setting and cannot be extended. A detailed overview of airline RM can be found in Talluri and Van Ryzin (2004b), Barnhart and Smith (2012) and Belobaba et al. (2015).

Joint forecasting model

Forecasting models also play an important role in the performance of an RMS’ optimization module since they provide information on the expected demand. Accurate forecasting leads to better pricing and capacity decisions; hence, the choice of input of the forecasting model is critical.

Fig. 1
figure 1

Booking curve

Full size image

A comparison between the desired and the actual booking curve is given in Fig. 1.

Although robust RMS are available in the industry, most of them assume that the booking curve is smooth in nature. However, in practice, the booking curve can undergo fluctuations and deviate from the optimal booking curve, as represented by the dotted lines. Traditional RM forecasting models have forecasted the volume of demand and customer-choice behavior separately. Balaiyan et al. (2019) propose three forecasting models that incorporate both demand volume and customer-choice behavior, where the latter is modeled in terms of choice probabilities. These models give the estimated demand for each product in an O-D market between two reading days (RD), or days to departure. A product is referred to as a specific fare class in a flight. A snapshot of a sample boarding pass is shown in Fig. 2 to help illustrate the same.

Fig. 2
figure 2

Definition of a product

Full size image

The motivation behind the development of the model by Balaiyan et al. (2019) is outlined below. The volume of the demand component is captured using three factors:

  1. 1.

    Mean level market demand (\(D_{M}\)): The average demand level in the O-D market.

  2. 2.

    Booking curve (\(e^{-\gamma R_{2}} - e^{-\gamma R_{1}}\)): The cumulative build-up of bookings between two reading days, \(R_{2}\) and \(R_{1}\).

  3. 3.

    Seasonality (\(\theta\)): The seasonal variations captured by the week-of-year and the day-of-week variations.

Similarly, customer-choice behavior is captured using the following concepts:

  1. 1.

    Willingness-to-Pay (WTP)

  2. 2.

    Discrete-Choice Model (DCM)

The concept of WTP and DCM is explained with the help of an O-D market Delhi (DEL) and London Heathrow (LHR). It is assumed that there are two flights operating in the market. The first flight is a direct flight that flies as DEL-LHR. The second flight has a stop in Frankfurt (FRA) and therefore takes the route DEL-FRA-LHR.

Table 1 Consideration sets of passengers
Full size table

The DEL-LHR ticket is priced at $1200 and the DEL-FRA-LHR ticket is priced at $1000. The market comprises of 4 types of passengers, each with a maximum willingness to pay (MWTP) of $1500, $1300, $1000 and $800. The passengers with MWTP of $1500, $1300 and $1000 will opt to fly because their valuation is higher than either of the ticket fares. However, the passenger with MWTP of $800 will not fly because his/her willingness to pay is lower than all the ticket fares available in the market.

The above example is extended to explain choice-modeling. The passengers with MWTP of $1500, $1300 and $1000 face the decision of choosing between the DEL-LHR and DEL-FRA-LHR flights. Each passenger’s consideration set comprises of all the options which is priced lesser than and equal to their MWTP. The passenger with MWTP of $1500 and $1300 both have {DEL-LHR, DEL-FRA-LHR} in their consideration sets. The passenger with MWTP of $1000 has a consideration set of only {DEL-FRA-LHR}. This is represented in Table 1.

The flight attributes are modeled as a Multinomial Logit Model (MNL). The attributes considered to capture customer-choice behavior are as follows:

  1. 1.

    Difference in fare Difference between the product fare and the mean fare in the market

  2. 2.

    Departure slot Time of departure of the flight

  3. 3.

    Elapsed time Duration of the flight

Willingness-to-pay and Discrete-choice model are combined and formulated into a mixed logit model. For each element in the consideration set, the passenger considers these attributes and picks the alternative that maximizes their utility.

Joint forecasting model with price attribute (JFM-PA)

There exists three variants to the joint forecasting models by Balaiyan et al. (2019). Although the volume of demand component is modeled identically, the representation of customer-choice behavior differs between them. Among the three variants, Joint forecasting model with price attribute (JFM-PA) incorporates price as a choice attribute in capturing customer-choice behavior and is selected to be used as the input to the optimization model developed in this paper. JFM-PA is superior because unlike the other two models, it includes price as an attribute in the choice model and decouples WTP from choice utilities, thereby enabling passenger segmentation and the determination of their corresponding consideration sets. Table 2 lists all notations used in JFM-PA.

Table 2 Notations used in JFM-PA
Full size table
$$Bkg_{k\Delta R}=D_{M} \times \big [e^{-\gamma R_{2}}-e^{-\gamma R_{1}}\big ] \times \theta \times \sum \limits _{C_{j}\in C_{kM}}\left[ \big (e^{-\alpha (p_{j}-p_{0})}-e^{-\alpha (p_{j+1}-p_{0})}\big ) \frac{e^{\sum \nolimits _{a_{k}\in A^{\prime}} \beta _{a}a_{k}}}{\sum \nolimits _{l\in C_{j}} e^{\sum \nolimits _{a_{l}\in A^{\prime}} \beta _{a}a_{l}}}\right]$$
(1)

\(Bkg_{k \Delta R}\) is the output of the model and it gives the incremental booking for product k between two reading days. The probability of product k being selected is the aggregation of each customer’s choice set across all \(C_{j} \in C_{kM}\). The volume of demand component is captured by the first three terms of Eq. (1) while the customer-choice behavior is accounted for by the remaining terms of the equation.

Joint optimization model (JOM)

An optimization model is developed using JFM-PA as its input. The model performs joint optimization of product prices and their respective allocation quantities. The Joint Optimization Model (JOM) is developed for an O-D market in which only parallel flights operate. The choice attributes in the MNL of JFM-PA thereby reduce to departure slots and difference in fares. All fare classes are assumed to be open on all flights throughout the booking horizon. Additionally, overbooking, cancellations and group bookings are not considered.

Table 3 Notations used in JOM
Full size table
$$\begin{aligned} \max \quad \sum \limits _{k=1}^{N} \ [p_{k} \times min\{D_{k}(p_{k}),q_{ik}\}] \end{aligned}$$
(2a)
$$\begin{aligned} \text {s.t.} \quad \sum \limits _{k=1}^{N} q_{ik}&\le S_{it}&\forall i \end{aligned}$$
(2b)
$$\begin{aligned} p_{l} \le p_{k}&\le p_{u}&\forall k \end{aligned}$$
(2c)
$$\begin{aligned} q_{ik}&\ge 0&\forall k \end{aligned}$$
(2d)
$$\text {where}~ D_{k}(p_{k}) = \sum \limits _{t}^{T} D_{M} \times \big [e^{-\gamma R_{2}}-e^{-\gamma R_{1}}\big ] \times \theta \times \sum \limits _{C_{j}\in C_{kM}}\left[ \big (e^{-\alpha (p_{j}-p_{0})}-e^{-\alpha (p_{j+1}-p_{0})}\big ) \frac{e^{\sum \nolimits _{a_{k}\in A^{\prime}} \beta _{a}a_{k}}}{\sum \nolimits _{l\in C_{j}} e^{\sum \nolimits _{a_{l}\in A^{\prime}} \beta _{a}a_{l}}}\right]$$
(3)

Consistent with the description in JFM-PA, a product is defined as the combination of flight and fare class. The joint forecasting model given by Eq. (1) is given in Eq. (3). The decision variables for JOM are \(p_{k}\) and \(q_{ik}\), the price for product k and its quantity allotted in flight i, respectively. In this context, the output of Eq. (3) gives the aggregated demand for product k from time t until the date of departure T, considering the WTP for each product and their respective consideration sets.

JOM is a variant of the probabilistic non-linear program (PNLP) proposed by Williamson (1992) with a relaxation of the integer constraint on allocation quantity \(q_{ik}\). However, unlike classical PNLP, product prices along with their respective allocation quantities are decision variables in JOM. The objective of this model is therefore to determine (i) the number of seats to be allotted for each product and (ii) the price at which each product should be offered such that the total revenue until the departure date is maximized.

The objective, given by Eq. (2a), is to maximize the total expected revenue. If demand \(D_{k}\) is high then only a portion of that demand, \(q_{ik}\), can be allocated as the capacity \(S_{it}\) will be exceeded otherwise. The revenue for each product will thus be \(p_{k} \times q_{ik}\). On the other hand, if demand \(D_{k}\) is low, there will be leftover capacity \(S_{it}\). Even if the entire capacity \(S_{it}\) is allocated, since \(D_{k} < q_{ik}\), the revenue for each product will only amount to \(p_{k} \times D_{k}\). This dynamics is captured by modeling the objective function as the product of \(p_{k}\) and the minimum of \(D_{k}\) and \(q_{ik}\). The forecasted demand is aggregated in the objective function to make the problem computationally tractable. The capacity constraint denoted by Eq. (2b) ensures that the allocation made on each flight is not in excess of its capacity. The price bounds for each product is set by the constraint given in Eq. (2c). Equation (2d) is the non-negativity constraint. The quantity of each product allotted is exogenous to the demand. The problem is a non-linear program due to the presence of the min function in the objective function.

Data description

All data used for development and testing purposes in this paper is simulated by Airline Planning and Operations Simulator (APOS), which is the platform used for simulation by Sabre GLBL Inc. APOS uses historical airline data to create virtual demand data. The input to APOS comprises of historical demand as well as information on fares, network and capacity. Using this real airline data, randomized future booking requests, demand volume and arrival patterns are generated. The dataset utilized in this paper comprises of an airline network with 260 flights operating in 276 O-D markets. The booking data for these flights on a particular date are detailed in the dataset. Seasonality is not captured because the data is for a single departure date. This is outlined in Table 4.

Table 4 Overview of data
Full size table

Model results

JOM is tested at a small-scale level to ensure that its performance is consistent with expectations. A single market in which two flights with different departure slots operate is considered. A total of six products are offered, among which three are from each flight. The products are indexed \(P_{1}\), \(P_{2}\),..., \(P_{6}\). Products \(P_{1}\), \(P_{3}\), and \(P_{5}\) belong to the first flight and products \(P_{2}\), \(P_{4}\), and \(P_{6}\) belong to the second flight. The products in each flight are arranged in the order of decreasing fares. Optimization is first done on reading day (RD) 14. Sales are observed for each RD until departure and re-optimization of the model is performed on RD 10, 5, 2 and 1. This experiment is replicated on various combinations of products on other demand streams as well. The results for one demand stream are shown in Tables 5 and 6.

Table 5 Allocation for Products 1, 3 and 5 on Flight No. 1
Full size table
Table 6 Allocation for Products 2, 4 and 6 on Flight No. 2
Full size table

The prices for products \(P_{1}\), \(P_{2}\), \(P_{3}\) and \(P_{4}\) are observed to take the upper bound \(p_{u}\) for all products. These are are higher than the fares simulated by APOS. However, the prices for products \(P_{5}\) and \(P_{6}\) are slightly lower than the fares proposed by APOS. This observation holds true across all the demand streams for which this experiment is replicated.

The allocations made for each product are also consistent with model expectations. Spoilage costs incurred in flying empty by protecting too many seats for high-value customers must be balanced with spillage costs endured by protecting too few seats for the same high-value customers to prevent revenue dilution. The results in Table 6 show that when the capacity is high and demand is low, product prices are lower and sales take place in the lower fare classes. Conversely, when the capacity is low and demand is high, product prices are higher and seats are allotted only to the highest fare class. These observations are indicated in bold in Table 6.

Solution methodology

Few literature have attempted to solve the probabilistic non-linear program (PNLP). The first is by Ciancimino et al. (1999), who implement PNLP for RM in the railway industry. They show that the objective function of PNLP is concave when the demand is a continuous random variable. Jiang (2008) propose a Lagrangian Relaxation approach to solve PNLP. He demonstrates that the objective function is convex and solves the Lagrangian Dual, which is equivalent to solving the PNLP, with a subgradient method. Chen and Homem-de Mello (2010) consider customer-choice behavior while determining seat allocations. Their choice model is based on customer preference orders. They solve PNLP by replacing the stochastic demand with its expected value, thereby transforming the model into a Deterministic Linear Program (DLP).

Sequential optimization

JOM cannot be converted into DLP as doing so will result in the loss of independence between the demand of the product \(D_{k}\) and the quantity allocated \(p_{k}\). Unlike traditional PNLP, where the decision variables are restricted to \(q_{k}\), it becomes intractable to prove the concavity of the objective function since \(p_{k}\) are also decision variables. The interaction between the variables \(p_{k}\) and \(D_{k}\) also prevent the simultaneous determination of both decision variables, i.e. it is not possible to determine the consideration set \(C_{j}\) of each passenger without establishing the price of each product \(p_{k}\) apriori.

Hence the solution methodology proposed to solve JOM is sequential optimization, wherein the problem is divided into a (i) master problem and a (ii) sub-problem. Product price changes are made in the master problem and optimization is performed in the sub-problem, where product allocation quantities are determined. This circumvents the issues raised by attempting joint optimization of prices and allocation quantities since prices are fixed in the sub-problem. The methodology is detailed in the subsequent sections.

Sub-problem

The prices of products are fixed in the sub-problem and it takes the following form:

$$\begin{aligned} \max \quad \sum \limits _{k=1}^{N} \ \big [p_{k} \times \text {min}\{D_{k},q_{ik}\}\big ] \end{aligned}$$
(4a)
$$\begin{aligned} \text {s.t.} \quad \sum \limits _{k=1}^{N} q_{ik}&\le S_{it}&\forall i \end{aligned}$$
(4b)
$$\begin{aligned} q_{ik}&\ge 0&\forall k \end{aligned}$$
(4c)

The notations are consistent with those given in Table 3. The price bounds are removed as a constraint. The number of decision variables have halved and the model given above becomes more computationally tractable to solve than JOM.

The objective function given by Eq. (4a) is referred to as the maximin objective function. The optimization problem is to maximize a function subject to a set of linear constraints. The maximin objective function problem is first solved by Kaplan (1974), who transforms the non-linear program (NLP) into a linear program (LP). Jiang and Pang (2011) are the first to employ this technique in the context of airline RM. They extend the basic DLP and PNLP models from a monopolistic to an oligopolistic setting by considering competition in the network setting. In order to solve the PNLP, they convert their model into an LP by introducing a new variable into the objective function, thereby obviating the min function.

The optimization model above is transformed to a linear model in this fashion. A new variable \(\lambda _{k}\) is introduced such that:

$$\begin{aligned} \max \quad \sum \limits _{k=1}^{N} \ [p_{k} \times \lambda _{k}] \end{aligned}$$
(5a)
$$\begin{aligned} \text {s.t.} \quad \sum \limits _{k=1}^{N} q_{ik}&\le S_{it}&\forall i \end{aligned}$$
(5b)
$$\begin{aligned} \lambda _{k}&\le q_{ik}&\forall k \end{aligned}$$
(5c)
$$\begin{aligned} \lambda _{k}&\le D_{k}&\forall k \end{aligned}$$
(5d)
$$\begin{aligned} q_{ik}, \lambda _{k}&\ge 0&\forall k \end{aligned}$$
(5e)

The new optimization model, thereafter referred to as L-JOM for linearized JOM, is now an LP. Two additional constraints, denoted by Eqs. (5c) and (5d) have been incorporated as the upper bounds for variable \(\lambda _{k}\). The objective function is to determine the values \(\lambda _{k}\) that maximize the total revenue. Along with these values of \(\lambda _{k}\), \(q_{ik}\) is also a solution to this LP model. Thereby the number of seats to allocate for each product can be determined.

L-JOM is tested on the market referred to in Sect. 4.2. The model is also extended for the entire network using the data described in Sect. 4.1. It is recorded to be computationally faster than the non-linear JOM model. Owing to the computational tractability of L-JOM, the sub-problem can be frequently re-optimized until the day of departure.

Master problem

Li and Huh (2011), Gallego and Wang (2014), Rayfield et al. (2015) and Du et al. (2016) address optimal pricing in the presence of an MNL model. Their research uses the model’s structural properties to derive the optimal pricing of substitutable products for a profit maximization problem in the retail setting. Wang (2013) considers the same problem in the presence of a capacity constraint. Unlike in the literature, there exists a WTP component that interacts with the MNL in the demand function given by Eq. (1). As both of them are functions of price, it is impossible to determine the structure of Eq. (1). Additionally, the complexity of the demand function makes it intractable to solve the model to optimality. Therefore a heuristic approach is recommended to solve the model efficiently.

Elasticity measures the responsiveness of demand with respect to a change in price. This concept is employed to determine the direction of price changes. Jacobs et al. (2010) and So (2017) consider elasticity in the context of the airline industry. Jacobs et al. (2010) develop a Price Balance Statistic (PBS) to measure the change in revenue from a unit change in fare price. So (2017) compute the elasticities of demand represented by commonly used functions and prescribe appropriate pricing policies. An elasticity-based heuristic is employed to solve the master problem.

Elasticity-integrated pricing and allocation heuristic (EPAH)

Using the concept of elasticity, a heuristic is proposed. For each product, its own price elasticity of demand with respect to its price and cross price elasticities of demand with respect to the prices of all the other available substitute products are computed. Multiplying the own price elasticity of demand with a percentage increase in price \(\rho\) results in the percentage change in demand for that product. Similarly, multiplying the cross price elasticity of demand with \(\rho\) gives the percentage change in demand of a product with respect to the change in price of another product. Aggregating the responsiveness in demand across all the products for the change in price of one product determines the cumulative change in demand in the market. This concept is explained with the help of a two-product example.

Table 7 Elasticity table for two products
Full size table

Table 7 is an example of an elasticity table for two products. The elasticity is denoted as \(\epsilon _{ij}\), where i is the product for which the change in price is made and j is the product which responds to the change in price of product i. For own price elasticity of demand, \(i = j\). This elasticity table is used as the basis for developing the heuristic.

The initialization is made by setting all product prices to their lower price bounds, \(p_{LB}\), and the corresponding revenue is calculated. Every \(\epsilon _{ij}\) is multiplied by \(\rho\) to determine the percentage change in demand of that product when the prices increase by \(\rho \%\). For each product, the cumulative percentage change in demand is defined as the linear combination of that product’s own price elasticity (\(\epsilon _{ii}\)) and cross price elasticity (\(\epsilon _{ij}\)) multiplied with \(\rho\). The tabular form of representation of this concept is shown in Table 8.

Table 8 Price responsiveness for two products
Full size table

The total percentage change in demand in the two-product case is \(d_{1}\) and \(d_{2}\). The product with lesser elasticity, i.e. the product that is less responsive to price, is denoted by the minimum of \(d_{1}\) and \(d_{2}\). Therefore \(\min \{d_{1}, d_{2}\}\) is selected and its corresponding fare is increased by \(\rho\). The revenue is computed with prices \(p_{k}+(p_{k} \times \rho )\) and compared with the old revenue. The algorithm terminates when the revenue obtained from the current iteration is lesser than the revenue obtained from the previous iteration. The pseudo-code of this Elasticity-integrated Pricing and Allocation Heuristic (EPAH) is as follows:

Algorithm 1
figure a

Elasticity-integrated pricing and allocation heuristic (EPAH)

Full size image

EPAH in a two-product setting

EPAH is tested on a two-product problem on a single flight and optimization is done on RD 10 with a capacity of 10. The percentage increase in fare \(\rho\) for each iteration is taken as 10%. Table 9 illustrates the performance of EPAH in the two-product setting.

Table 9 Illustration of performance of EPAH in a two-product setting
Full size table

Each cell in the table represents the revenue achieved from the particular product and price combination. The emboldened cells correspond to the the revenue obtained from EPAH in each iteration, with the best solution obtained from the heuristic method indicated in italics. The product and price combination which yields the highest revenue from solving L-JOM is underlined. It is observed that EPAH moves in the direction of the optimal solution.

Comparison of EPAH with JOM

The comparison of EPAH and JOM is extended up to a five product setting. EPAH is tested for two values of \(\rho\), namely \(\rho = 1\%\) and \(\rho = 0.5\%\). The results are provided in Table 10. The revenues obtained from JOM, which denote the optimal achievable revenues, are indicated on the rightmost side of Table 10. Similarly, the revenues obtained from EPAH are given under the columns ‘Heuristic Revenue’ of Table 10. The optimal revenue for each setting was computed in Microsoft Excel using the GRG Non-linear solver engine with Multistart setting. By enabling the Multistart option, repeated runs of the GRG Non-linear algorithm with different initial values of the decision variables is performed, thereby most likely converging to the optimal solution. The comparison is restricted to a small network owing to the computational limitation in determining the optimal revenues beyond a five product setting.

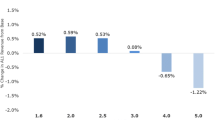
Table 10 Comparison of results of EPAH with JOM for a small network
Full size table

It can be observed from comparing these revenues that EPAH, although marginally lower, gives revenues that are close to the optimal revenues. The product prices and their corresponding demand and allocation quantities computed by the heuristic are also comparable with their respective optimal quantities. This is observed across all product settings. It is evident from the table that with a decrease in the value of \(\rho\), which is the step size in this search algorithm, the revenue increases.

Performance of EPAH in the network setting

EPAH has been extended from its small-scale setting and implemented for the entire network. The network considered in this paper comprises of five flights that operate in parallel in an O-D pair, with each flight having 11 fare classes. This constitutes of a total of 55 products (\(11 \times 5\)) in the market. Optimization has been performed on RD 27, RD 14, and RD 7 under constrained capacity. The lower bound for each product’s price is taken as the APOS fare of the preceding product. The revenue obtained from EPAH is compared with the revenue obtained from APOS fares. The APOS fares-based revenue is the revenue that would be obtained if the existing APOS fares are used in L-JOM. This experiment is repeated for two values of \(\rho\), namely \(\rho = 1\%\) and \(\rho = 0.5\%\), to observe the effects of increasing the fares by \(1\%\) in each iteration to just \(0.5\%\) in each step. The results are presented in Table 11.

Table 11 Results in network setting with existing lower bounds for price
Full size table

It can be observed that EPAH consistently gives higher revenues than the revenues generated from APOS. This is the case when the cumulative demand for each flight is lesser than or equal to the available capacity. In the case where the demand is significantly high with respect to the capacity, EPAH outperforms APOS fares-based L-JOM because the heuristic has the ability to better match the capacity with the demand by dynamically adjusting the prices. These results hold true for both values of \(\rho\).

Even though EPAH yields higher revenues, it has been observed that the product prices take the lower bounds for higher fare products. This indicates that the prices of the higher fare products are higher than their ideal values. The above experiment has therefore been repeated with a common lower bound for all products and the results are displayed in Table 12.

Table 12 Results in network setting with modified lower bounds for price
Full size table

It is observed that the modification in the lower bounds of product prices also yields in revenues that are higher than APOS revenues. These new revenues are also marginally higher than the revenues obtained in Table 11. However, in this case, the fares are less dispersed and have a lower range. Offer set optimization determines the subset of products to be made available on each RD. Since this practice is employed in APOS data, all 55 products are not open on all RD and this leads to a larger difference in fares among the products.

Conclusion

The evolution of choice-based revenue management brought forth by increased fare transparency force airlines to develop better passenger segmentation techniques. Even though the optimization module forms an integral part of any revenue management system, literature shows that pricing and allocation decisions continue to be taken independently. To overcome this gap, a model that jointly optimizes products fares and seat allocation under dependent demand is developed. JFM-PA forecasting model is used as the input to the optimization model as it is the first of its kind to consider demand volume and customer-choice behavior together.

A joint optimization model (JOM) is first developed and tested on a small-scale network to ensure that its performance is consistent with expectations, following which a solution approach to the model is proposed. Sequential optimization is identified as an appropriate solution methodology to the problem type. The model is divided into a master problem and a sub-problem. The sub-problem is solved by converting the NLP into an LP. A heuristic based on the own price and cross price elasticities of the products is developed to determine the direction of price changes in the master problem. The Elasticity-integrated Pricing and Allocation Heuristic (EPAH) is implemented on the entire network and is observed to consistently produce an increase in existing revenues. In addition to developing a joint optimization model for pricing and seat allocation, this paper also contributes to a solution methodology that takes into consideration the own price and cross price elasticities of substitutable products under a capacity constraint. This adds a variation to the modeling consideration and the solution methodology for choice-based modeling.

The optimization model is restricted to an O-D market which comprises of only parallel flights and can be extended to the network setting by considering layovers in the market. Further, it is assumed that all fare classes are open on all reading days. Offer set optimization can be performed in order to determine the sets of products to be offered at each time period. Additionally, an inherent assumption of the EPAH heuristic is that the net price elasticity of demand is an unweighted linear combination of the own price and cross price elasticities of demand. The effect of different weighted linear and non-linear functions on the solution can be discerned. Lastly, given the complexity of the problem, we have adopted a heuristic-based approach which, though does not guarantee global optima, has performed well on our data set. The structure of the model can be determined so that optimal pricing policies can be implemented. These are possible future directions in which the work can be taken forward.