An encryption algorithm for color images based on an improved dual-chaotic system combined with DNA encoding

Abstract

This study improves the Logistic chaotic system and combines it with the hyperchaotic Chen system to create a dual chaotic system. The algorithm encrypts images in three stages. In the first stage, a plaintext-related key generation scheme is designed to generate the parameters and initial values of the dual chaotic system. In the second stage, the chaotic sequences generated by the dual chaotic system are used for dynamic DNA encoding and computation. In the third stage, the chaotic sequences generated by the improved Logistic chaotic system are used to perform row-column permutations, completing the scrambling. The security analysis of the encrypted images shows that the algorithm described in this paper is robust and secure, capable of resisting most known attacks. The algorithm is fast in encryption, provides high-quality image reconstruction, and is suitable for scenarios with high comprehensive performance and image quality requirements.

Introduction

In today’s era of rapid technological advancement, the swift dissemination of information has become the norm. As of June last year, the number of internet users in China had reached 1.079 billion, reflecting an increasingly digital trend in society. Consequently, the world has become more diverse and enriched, with advertisements, images, and videos omnipresent in daily life. However, the rapid spread of various types of information has also raised concerns about its security. Information security involves critical issues such as corporate secrets, personal privacy, and national security, all of which require high levels of attention and ongoing development. The occurrence of information leaks can not only threaten personal privacy but also potentially harm commercial interests and even jeopardize national security¹. Several excellent cryptographic systems have been developed. Kanwal and colleagues proposed a novel public-key cryptosystem using non-commutative groups as the platform group. The underlying challenge of this cryptosystem is the combination of the discrete logarithm problem and the conjugacy search problem². Inam and colleagues developed an algebraic public-key cryptosystem based on general non-commutative rings. They defined polynomials over non-commutative rings and used them as the foundational structure, employing high-order matrices and larger modulus classes to resist known brute-force and other attacks³. Inam and colleagues also introduced various public-key encryption schemes based on general linear groups. These schemes utilized different techniques, including automorphisms related to the conjugacy search problem and its generalizations⁴. Ali and colleagues examined the security of the multivariate polynomial trapdoor public-key cryptosystem proposed by Markovski, Mileva, and Dimitrova (2014). Despite the fact that the number of polynomials in the public key is less than the number of variables, resulting in numerous solutions for the polynomial system, the cryptosystem still appears to be insecure⁵. Most of the aforementioned encryption schemes are suited for text encryption but are not applicable to image encryption. Due to their intuitive design, ease of understanding, and rich information content, digital images have become one of the most important sources of information among multimedia data. However, digital image data is vulnerable to malicious attacks during transmission, which can lead to information leaks, seriously threatening national defense security and exposing personal assets and corporate secrets. As a result, researchers have begun to explore new image encryption methods. Chaotic systems, similar to classical cryptography, possess unpredictable motion and irregular trajectories, and are characterized by destructive and diffusion rules. Consequently, various applications of chaotic systems exist in cryptography, data security, and secure communications. Image encryption methods based on chaotic theory are faster, more sensitive, and more efficient than traditional techniques, and offer higher levels of security. Therefore, chaotic-based image encryption technology holds great research potential. Pareek and colleagues proposed a novel encryption algorithm that uses the initial conditions of a chaotic system generated by a Logistic map-based external key for image encryption, continuously updating the key during the encryption process to enhance security⁶. Meanwhile, Patidar and colleagues introduced a lossless stackable color image encryption algorithm based on the Logistic map. This algorithm utilizes the initial conditions, parameters of the chaotic system, and iteration counts as part of the encryption key, incorporating two rounds of permutation and two rounds of diffusion in the encryption process⁷. Wang and his team proposed a new color image encryption algorithm based on a one-dimensional Logistic map to generate the key⁸. While these low-dimensional chaotic systems offer advantages such as simplicity, ease of implementation, and understandability, they have limitations in generating random sequences, which may lead to lower randomness and susceptibility to statistical analysis attacks.

As knowledge of chaotic systems continues to grow, researchers have begun focusing on higher-dimensional chaotic systems, moving beyond traditional three-dimensional systems. This trend has attracted considerable attention. In their research, Cang and colleagues constructed a four-dimensional autonomous hyperbolic fixed-point chaotic system and conducted a detailed analysis of its dynamic behavior, revealing a four-wing transient chaotic phenomenon⁹. At the same time, Ruan Wenjing and others, building on the work of Sprott A, introduced a novel four-dimensional hyperchaotic system by incorporating a linear feedback controller and sine functions. They rigorously proved the existence of a Hopf bifurcation and conducted an in-depth study of the system's dynamic characteristics¹⁰. Additionally, Wen and colleagues proposed a new five-dimensional chaotic system, which exhibits features such as chaotic degradation, multi-wing chaotic attractors, and coexisting attractors¹¹.

Gabr and colleagues introduced an innovative image encryption algorithm that combines unique image transformation techniques with principles from chaotic and hyperchaotic systems. By utilizing the unpredictable behavior of the Chua system and the hyperchaotic properties of the Chen system, the algorithm performs rescaling, rotation, and randomization of the target image. The inherent unpredictability and sensitivity to initial conditions of these chaotic systems result in a significantly expanded key space. This feature not only enhances resistance to brute-force attacks but also improves overall security¹².Higher-dimensional chaotic systems offer a larger key space, increasing the difficulty of decryption and thus enhancing encryption security. As the dimensionality increases, the system's dynamic behavior becomes more complex, further strengthening the encryption effect. Compared to low-dimensional systems, high-dimensional chaotic systems are better suited for scenarios requiring high security due to their rich dynamic characteristics, which make it more challenging for attackers to predict system states. However, high-dimensional chaotic systems involve complex parameter tuning and optimization processes. Finding the appropriate parameter combinations to ensure system stability and excellent encryption performance typically requires significant time and computational resources. Additionally, high-dimensional chaotic systems have higher hardware resource demands, which may limit their application on resource-constrained devices. Therefore, in practical applications, it is essential to balance these challenges and find a compromise between encryption security, computational efficiency, and hardware resource requirements.

Recent advancements in image cryptography based on chaos theory and DNA encoding have been significant. Alexan and colleagues extended the four-dimensional hyperchaotic Chen system to the fractional-order domain, implementing image encryption in three stages. In the first stage, they performed a discrete Fourier transform (DFT) on the fractional-order Chen system's numerical solutions, quantized the results, and used them for DNA encoding. In the second stage, they constructed a robust S-box from the DFT quantized solutions of the Chen system and applied it. In the third stage, the Mersenne Twister encryption key was converted to base φ and modular arithmetic was applied¹³. The proposed algorithm is efficient, secure, and robust. Gabr and colleagues introduced a three-stage image encryption system. In the first stage, a variant of the tangent function in logic mapping was used for DNA encoding. The second stage involved combining the numerical solutions of the Lorenz differential equations with a linear descent algorithm to construct a powerful S-box. In the third stage, the original form of the logic map was used¹⁴. This algorithm is also efficient, secure, and robust. Alexan and colleagues utilized the four-dimensional (4D) fractional-order hyperchaotic Chen map, combining it with sine chaotic mapping and a novel hybrid DNA encoding algorithm. They conducted comprehensive numerical analyses, demonstrating that the proposed color image encryption system exhibits strong security performance and high efficiency¹⁵. Zhang and colleagues integrated these methods to encrypt images, though while the method ensures the security of encrypted images, it still faces limitations in noise resistance, shear resistance, and overall robustness against external attacks¹⁶.Xu Changbiao and colleagues developed a two-dimensional discrete chaotic system with constant Lyapunov exponents using Arnold transformations, combined with DNA encoding techniques, to design a new chaotic image encryption algorithm. They also introduced a new nonlinear chaotic system with hyperchaotic properties¹⁷. Liu Congcong and colleagues addressed the inadequacies of existing DNA encryption algorithms by proposing a new information encryption scheme that integrates Henon chaotic mapping with DNA chain permutation reactions. This scheme demonstrated good encryption performance and security¹⁸. Jiang Gang and colleagues proposed a new image cryptographic method based on hash functions, combining chaos and DNA operations. This method effectively resists statistical and differential attacks but has limitations in countering noise attacks¹⁹. Additionally, Sun and colleagues introduced a new image encryption method involving further image scrambling and decomposition operations, combined with DNA encoding. However, this method has a small key space and struggles to effectively counter various attacks, necessitating improvements in security²⁰. Single chaotic systems often face issues with security and attack resistance in image encryption; therefore, combining DNA encoding techniques can enhance the complexity and security of encryption.

The main contributions of this paper are as follows:

• 1. Development of an enhanced logistic chaotic system: We propose an improved Logistic chaotic system that allows the mapping range, initial values, and parameters to be any real number. We analyze the Lyapunov exponents of the new Logistic chaotic system and present the results of NIST tests. The system exhibits high Lyapunov exponents, and the generated chaotic sequences demonstrate increased complexity and randomness, thereby enhancing the security of the image encryption scheme.

• 2. Integration of chaotic systems: We combine the new Logistic chaotic system with the hyperchaotic Chen system to create a dual-chaotic system. This dual-chaotic system offers greater complexity and randomness compared to single chaotic systems and low-dimensional chaotic systems, improving the security of the image encryption scheme.

• 3. Introduction of key schemes and encryption algorithm: We propose plaintext-associated key schemes and scrambling techniques, integrating the dual-chaotic system with dynamic DNA encoding operations to design an image encryption scheme. This scheme features fast encryption speed, high image reconstruction quality, and meets robustness and security requirements, effectively resisting most known attacks.

The remainder of the paper is organized as follows: "Theoretical Foundation": This section introduces the concepts of chaotic systems and dynamic DNA encoding operations. "Chaotic Systems": This section provides a detailed description of the proposed new chaotic system and analyzes its key performance indicators. "Image Encryption Scheme": This section outlines the detailed steps and processes of the image encryption scheme. "Simulation and Experimental Results": This section presents the experimental results and various security analyses. "Conclusion": This section summarizes the findings of the paper.

Methods

Chaotic systems

In 1963, Lorenz and colleagues first introduced the concept of "chaos"²¹, defining it as pseudo-random, unordered, and aperiodic behavior. While the concept of chaos is somewhat abstract and lacks a precise definition, it is understood in various ways. Among the definitions in the field of chaos theory, those by Li-Yorke and Devaney are widely accepted. The following provides an overview of these two definitions:

According to the Li-Yorke theorem, a continuous self-map f(x) on a closed interval I is considered chaotic if it satisfies the following conditions²²:

• 1. Unbounded Periodicity: There is no upper bound on the periods of f(x).

• 2. Existence of Uncountable Subset: There exists an uncountable subset S within I such that:

  • (a) $\forall x,y\in S,\text{where }x\ne y \, , \underset{n\to \infty }{lim} sup|{f}^{n}(x)-{f}^{n}(y)|>0$,

  • (b) $\forall x,y\in S,\underset{n\to \infty }{lim} inf\left|{f}^{n}\left(x\right)-{f}^{n}\left(y\right)\right|=0; \, \underset{n\to \infty }{lim} sup\left|{f}^{n}\left(x\right)-{f}^{n}\left(y\right)\right|<0$,

  • (c) $\forall x\in S\text{ and any periodic point} \, y to f\text{,}\underset{n\to \infty }{lim} sup\left|{f}^{n}(x)-{f}^{n}(y)\right|>0$.

According to Devaney’s definition of chaos, a mapping $f:U\to U$ on a metric space U is considered chaotic if it satisfies the following conditions²³:

• (1) There exists a $\delta >0,$ for all $\varepsilon >0$ and $x\in U$, In the $\varepsilon$ -neighborhood of $x$, there exist y and an integer n. such that $d({f}^{n}(x),{f}^{n}(y))>0$.

• (2) The periodic points of $f$ are dense in $U$.

• (3) For any open set Q in $U$ and any point $Y\in U$, there exists a $k>0$, such that ${f}^{k}(Z)\cap Y \ne {\varnothing }$.

The Eq. (1) of hyperchaotic Chen system is:

$$\left\{\begin{array}{c}\dot{{x}_{1}} = a \cdot ({x}_{2} - {x}_{1} )\\ \dot{{x}_{2}} = - {x}_{1}\cdot {x}_{3}+d \cdot {x}_{1} + c \cdot {x}_{2}\\ \dot{{x}_{3}} = {x}_{1} \cdot {x}_{2} - b \cdot {x}_{3} \\ \dot{{x}_{4}} ={x}_{2} \cdot {x}_{3} + e \cdot {x}_{4}\end{array}\right.$$

(1)

In the above description, $\dot{{x}_{1}}$ = ${x}_{i}$/dt denotes the derivative of the system state variable ${x}_{i}$ (where i = 1, 2, 3, 4) with respect to time t. When a = 35, b = 3, c = 12, d = 7, e = 0.55, the system represented by Eq. (1) is in hyperchaotic state. At this time, the system has two positive Lyapunov exponents for a long time, and has more significant chaotic behavior, The chaotic attractor of the hyperchaotic Chen system is shown in the Fig. 1.

Figure1

Partial chaotic attractor of the hyperchaotic Chen system (a) Partial Chaotic attractor of the hyperchaotic Chen system on the plane. (b) Partial Chaotic attractor of the hyperchaotic Chen system in space.

DNA technology

In DNA sequences, there are four types of nucleotides: A (adenine), C (cytosine), G (guanine), and T (thymine), where A pairs with T and C pairs with G. Similarly, in binary numbers, 00 and 11 are complementary, as are 01 and 10. Since nucleotides and binary numbers can be interchanged, there are a total of 24 possible encoding rules. However, only 8 of these rules satisfy the complementary condition, as shown in Table 1.

Table 1 DNA encoding rules.

For example, consider a grayscale image pixel with a value of 199. If we replace this value with the binary sequence “11000111” and encode it using the encoding rule number 2 from Table 1, the result is “TACT.” By applying the same encoding rule for decoding, the original pixel value can be accurately restored. Similarly, when applying encoding rule number 5, the pixel value 199 is encoded as “CGTC,” and the original value can still be restored using the same rule. However, using encoding rule number 7 results in the binary sequence “10010010,” which bears no relation to the original value. This demonstrates that encoding and decoding a single pixel with different rules can yield different results. Therefore, for successful DNA-based encryption and decryption of images, it is crucial to use the same encoding and operational rules consistently. This characteristic of DNA encoding provides more options and enhances the security of encrypted images. DNA can be manipulated using operations such as addition, subtraction, XOR (exclusive OR), and XNOR (exclusive NOR). For a given pixel, there are eight different encoding outcomes, each corresponding to a distinct encoding standard. For example, using encoding rule number 3 from Table 1 to process DNA results in the following outcomes, as shown in Tables 2, 3, 4 and 5:

Table 2 DNA addition operations.

Table 3 DNA subtraction operations.

Table 4 DNA XOR operations.

Table 5 DNA XNOR operations.

Improving the logistic chaos map

The Eq. (2) for the Logistic chaotic mapping is:

$${x}_{n+1}= \mu {x}_{n}(1 - {x}_{n})$$

(2)

where µ is the control parameter, with a range of (0,4], and the range of ${x}_{n}$ is [0,1]. However, the Logistic mapping has limitations such as a small parameter range and uneven point distribution, resulting in a small key space and less-than-ideal encryption effectiveness²⁴.

The Eq. (3) for the improved Logistic chaotic mapping is:

$${x}_{n+2}=mod( \mu {x}_{n+1}\left(1 - {x}_{n+1}\right)+(4-\mu ){x}_{n}\left(1 - {x}_{n}\right),1)$$

(3)

By introducing modular arithmetic, the parameters and initial values of this chaotic mapping can break through the value restrictions, allowing parameters and initial values to take any real number range, thereby expanding the key space of the encryption system. When µ = 0 or µ = 4, the mapping transforms into a Logistic surjection. The so-called attractor means that during the iteration process, the iterated values gradually converge to a certain point. Attractors include fixed points, limit cycles, tori, etc. Continuous fixed points are referred to as stable windows. To further intuitively compare the chaotic attractor states between the traditional Logistic mapping and the proposed improved mapping in this paper, we conducted Matlab simulation comparative experiments. In the simulation process, we selected initial values ${x}_{0}$ = 7.2001 and ${x}_{1}$ = 0.8001, set the parameter µ of the improved mapping in this paper to 0.01, and the sequence length N to 50,000. The simulation results are shown below: Fig. 2a displays the attractor trajectory of the Logistic mapping, while Fig. 2b shows the three-dimensional plot of the attractor in our proposed method. Through the simulation results, it can be observed that in the iteration process of the improved mapping proposed in this paper, there is a significant difference between the values of two consecutive iterations, and there is no apparent regularity. This effectively avoids the problem of iteration converging to the same value.

Fig. 2

Comparison chart of attractors before and after improvement: (a) Logistic mapping chaotic attractor. (b) Improved Logistic Mapping Chaotic Attractor.

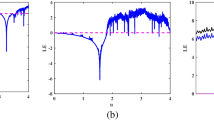
Utilizing the Lyapunov exponent as a criterion for determining the chaotic state of a system is a robust method. In the simulation process, we selected initial values ${x}_{0}$ = 7.2001 and ${x}_{1}$ = 0.8001. The parameter µ of the enhanced mapping in this paper was set to 0.01, and the sequence length N was set to 2000. The simulation results are depicted in Fig. 3. Observing the simulation outcomes in Fig. 3, it can be inferred that the proposed improvement in this paper significantly expands the parameter µ compared to the original mapping. Further analysis of the simulation experimental results reveals that, except for individual points not in a chaotic state, the majority of points in the system exhibit an evident chaotic state. An analysis of the Lyapunov exponent indicates that within the chosen parameter range, the proposed enhancement in this paper exhibits substantial improvement over the original Logistic mapping. Therefore, the improvement introduced in this paper broadens the range of available options for chaotic sequences and enhances the difficulty of decryption.

Fig. 3

Comparison chart of Lyapunov index before and after improvement: (a) Lyapunov exponent of logistic chaotic systems. (b) Improved Logistic Chaos System Lyapunov Exponent.

NIST tests

The randomness of the sequences can be quantitatively assessed using the NIST randomness tests²⁵. In this experiment, both the Logistic map and the improved Logistic map were subjected to NIST testing. Before testing, these sequences were converted to binary sequences. A p-value greater than 0.01 indicates that the sequence has sufficient randomness to pass the NIST test. Table 6 presents the test results, showing that the Logistic map failed some tests, while the improved Logistic map passed all tests, confirming the randomness of the chaotic sequences and ensuring the security of the encryption.

Table 6 NIST tests.

Algorithm introduction

The encryption algorithm is based on an improved double chaotic system combined with DNA encoding. The structure of the encryption algorithm is shown in Fig. 4. This paper improves upon the Logistic chaos map, addressing issues such as limited parameter ranges and uneven point distribution, which result in a small key space and suboptimal encryption effects. The improvements include the introduction of plaintext-related key generation for the initial values and parameters of the Logistic chaos map. Additionally, a new method for generating initial values for the Chen chaotic system is used, along with a newly designed permutation scheme.

Fig. 4

Encryption flow chart.

Encryption algorithm

The encryption algorithm, based on an enhanced dual-chaotic system combined with DNA encoding, is illustrated in Fig. 4.

Step 1: Read the plaintext color digital image of size M × N denoted as I, and partition I into three 2D matrices, R, G, B, as per Eq. (4).

$$\left\{\begin{array}{c}{I}_{1}=(:,:,1)\\ {I}_{2}=(:,:,2)\\ {I}_{3}=(:,:,3)\end{array}\right.$$

(4)

Step 2: Fill the data values with 0, padding the three 2D matrices to satisfy the size conditions as in Eq. (5).

$$\left\{\begin{array}{c}mod\left(N,t\right)=0\\ mod\left(M,t\right)=0\end{array}\right.$$

(5)

where t is the block size. Reassign the size of the zero-padded image to M and N.

Step 3: Obtain chaotic sequences: Given initial values ${m}_{a}$ and ${n}_{a}$, both initial values range from (0,1). Use ([${m}_{a}$ M], [${n}_{a}$ N]) as the dividing point, divide matrices ${I}_{1}$,${I}_{2},{I}_{3}$. into four parts each, and select the first part of ${I}_{1}$,${I}_{2},{I}_{3}$. Obtain the hash values ${\text{Hm}}_{1}$,${\text{Hm}}_{2}$,${\text{Hm}}_{3}$ of the three subregions through SHA-256. The Eq. (6) for the initial values ${x}_{0}$,${x}_{1}$, and parameter μ are:

$$\left\{\begin{array}{c}{x}_{0}=hex2dec\left({\text{Hm}}_{1}\left(1:8\right)\right)\times {10}^{10}+hex2dec\left({\text{Hm}}_{1}\left(9:16\right)\right)\times {10}^{15}\\ {x}_{1}=hex2dec\left({\text{Hm}}_{2}\left(1:8\right)\right)\times {10}^{10}+hex2dec\left({\text{Hm}}_{1}\left(9:16\right)\right)\times {10}^{15}\\ \mu =mod(hex2dec\left({\text{Hm}}_{3}\left(1:8\right)\right)\times {10}^{10}+hex2dec\left({\text{Hm}}_{2}\left(9:16\right)\right)\times {10}^{15},1)\end{array}\right.$$

(6)

Obtain the sequence {${k}_{i}$} using initial values ${x}_{0}$,${x}_{1}$, and parameter μ. Set the length of the obtained sequence to 1000 + MN + M + N, and discard the first 1000 values. Convert the 1001st to 1001 + MN terms of the sequence {${k}_{i}$} into a matrix R of size M × N. Use modulo operation to transform the values of the matrix into the range of 0 to 255, for DNA operations with ${I}_{i}$(i = 1,2,3).

Step 4: XOR the three hash values ${\text{Hm}}_{1}$,${\text{Hm}}_{2}$,${\text{Hm}}_{3}$ bit by bit to obtain the combined hash value H. Divide H into equally sized ${H}_{1}$,${H}_{2}$,${H}_{3}$,${H}_{4}$. The initial values of the hyper-chaotic Chen system are given by Eq. (7):

$$\left\{\begin{array}{c}{x}_{0}=hex2dec\left({H}_{1}\left(1:8\right)\right)\times {10}^{10}+hex2dec\left({H}_{1}\left(9:16\right)\right)\times {10}^{15}\\ {y}_{0}=hex2dec\left({H}_{2}\left(1:8\right)\right)\times {10}^{10}+hex2dec\left({H}_{2}\left(9:16\right)\right)\times {10}^{15}\\ {z}_{0}=hex2dec\left({H}_{3}\left(1:8\right)\right)\times {10}^{10}+hex2dec\left({H}_{3}\left(9:16\right)\right)\times {10}^{15}\\ {q}_{0}=hex2dec\left({H}_{4}\left(1:8\right)\right)\times {10}^{10}+hex2dec\left({H}_{4}\left(9:16\right)\right)\times {10}^{15}\end{array}\right.$$

(7)

After setting the initial values and parameters, calculate the Chen hyper-chaotic system to obtain four sequences {Xi},{Yi},{Zi},{Qi} each with a length of 3000 + (M × N)⁄ ${t }^{2}$, and discard the first 3000 terms.

Step 5: The sub-blocks at the same position of ${I}_{i}$(i = 1,2,3) use the same DNA coding method, uniformly determined by {Xi}; {Yi} dictates the DNA coding method of each sub-block within matrix R. Transform the sequences {Xi } and {Yi } as per Eq. (8):

$$\left\{\begin{array}{c}X=mod\left(round\left(X\times {10}^{4}\right),8\right)+1\\ Y=mod\left(round\left(Y\times {10}^{4}\right),8\right)+1\end{array}\right.$$

(8)

The DNA coding method of the i-th sub-block in ${I}_{i}$(i = 1,2,3) is Xi, and the DNA coding method of the i-th sub-block in the chaotic matrix R is Yi. The corresponding blocks of P1,P2,P3, and R use the same rule generated by the Chen hyper-chaotic system sequence {Zi}, and transform the sequence {Zi} as following Eq. (9):

$$Z=mod\left(round\left(Z\times {10}^{4}\right),4\right)+1$$

(9)

Zi = 0,1,2,3 are employed for addition, subtraction, XOR, and XNOR operations, respectively. To enhance diffusion, barring the initial sub-block, the encrypted outcome of the current sub-block undergoes DNA operation with the preceding sub-block. The operation rule is dictated by the sequence {Zi}. Subsequent to DNA operation, the matrix is decoded in blocks, wherein the sequence {Qi} serves as the DNA decoding rule for the manipulated sub-block. DNA decoding constitutes the inverse process of DNA encoding, offering eight decoding methods. The {Qi} sequence undergoes transformation as per the subsequent Eq. (10):

$$X=mod\left(round\left(X\times {10}^{4}\right),8\right)+1$$

(10)

The DNA decoding method for the i-th sub-block of ${I}_{i}$(i = 1,2,3) is the same as Qi.

Step 6: Let {${k}_{m}$} and {${k}_{n}$} be the sequences corresponding to the (1001 + MN)-th to (1001 + MN + M)-th item and (1001 + MN + M)-th to (1001 + MN + M + N)-th item in the sequence {${k}_{i}$}, respectively. Arrange {km} and {kn} in descending order and obtain increment sequences M and N at corresponding positions. As shown in Eq. (11).

$$\left\{ {\begin{array}{*{20}{c}} {[\sim,M] = sort(kx^{\prime}, descend^{\prime} ) + 1}\\ {[\sim,N] = sort(ky^{\prime}, descend^{\prime} ) + 1} \end{array}} \right.$$

(11)

Swap the matrices of the three channels decoded from DNA, using the M sequence values as row coordinates and the N sequence values as column coordinates. Perform both row and column permutations on the matrix. Obtain encrypted images ${I}_{e1}$, ${I}_{e2}$, ${I}_{e3}$. Combine ${I}_{e1}$, ${I}_{e2}$, ${I}_{e3}$ layers to get the final ciphertext image.

Decryption algorithm

The decryption process is the reverse of the encryption process. By using the same key as in encryption, the decrypted image can be obtained. Here is a brief description of the decryption steps for an image I with dimensions M × N:

• 1. Partition the image: According to formula (4), divide I into three 2D matrices R, G, and B, which are denoted as ${I}_{1}$, ${I}_{2}, {I}_{3}$, respectively.

• 2. Generate chaotic sequence: Obtain the improved Logistic chaotic sequence {${k}_{i}$} with the key consisting of the initial values ${x}_{0}$, ${x}_{1}$, and the parameter μ. The key used in decryption must be consistent with that used in encryption.

• 3. Matrix permutation: Perform column-row permutations on the matrices R, G, and B. The permutation should be the reverse of the encryption process: perform column permutation from the last column to the first column and row permutation from the last row to the first row.

• 4. Convert sequence to matrix: Convert the sequence {${k}_{i}$} from the 1001st term to the 1001 + MNth term into a binary matrix R of size M × N.

• 5. Generate chaotic system initial values: Using the plaintext-related key H, determine the initial values for the hyperchaotic Chen system. Calculate four sequences {Xi}, {Yi}, {Zi}, {Qi}, each with length $3000+\left(M\times N\right)/{t }^{2}$, and discard the first 3000 terms.

• 6. DNA encoding of matrix: Encode the matrix to be decrypted using DNA encoding. During encryption, the image used the sequence {Qi} for DNA encoding. In decryption, use the same sequence for the DNA encoding of the ciphertext image.

• 7. DNA inverse operations: Perform inverse DNA operations on blocks. The chaotic sequence {Zi} determines the algorithm. Unlike encryption, use subtraction instead of addition, and vice versa.

• 8. Break block connections: Each block's processing requires the previous block. Use the DNA operation rules from the previous block to determine the decryption process, paying attention to the interchange between addition and subtraction.

• 9. DNA decoding: Decode the DNA-encoded matrices for each color channel using {Xi} to determine the DNA decoding rules.

• 10. Remove added zero pixels: During decryption, remove any zero pixels added to improve algorithm universality.

• 11. Reconstruct the image: After removing zero pixels, reconstruct the decrypted color digital image by merging the three matrices into a single three-dimensional matrix.

Results and safety analysis

Experiments were conducted on a PC equipped with an Intel^® Core™ i7-12650H CPU operating at 2.30 GHz, 16 GB of memory, and a 64-bit Windows 11 operating system. The encryption algorithm described above was implemented using MATLAB R2018b.

Experimental results

In the simulation experiment, Baboon and Peppers color images were chosen, each with pixels arranged in a 512 × 512 grid. Figure 5 displays the original image, ciphertext image, and decrypted image. (The image source of Baboon and Peppers is https://sipi.usc.edu/database/).

Fig. 5

Simulation result diagrams. (a) Peppers plaintext image. (b) Encrypted image of peppers. (c) Decrypted image of peppers. (d) Baboon plaintext image. (e) Encrypted image of baboon. (c) Decrypted image of baboon.

Information entropy

Information entropy is a mathematical tool employed to quantify the uncertainty and disorder of information. In the realms of image processing and computer vision, information entropy evaluates the randomness of pixel values in images. The definition of information entropy is represented by Eq. (12):

$$H(x) = - \sum p(x)\log_{2}{p(x)}$$

(12)

In this expression, X represents a random variable, p(x) represents the probability of X taking the value x, and N is the grayscale level of the image, denoting the size of the set {x}. According to formula (12), the information entropy of a 256-level image can be calculated as 8. To compare with the encryption results presented in this paper, the information entropy of the encrypted image is calculated separately. Simultaneously, a comparison is made with the information entropy of the secret images in some references. Upon comparison, it is observed that under the encryption algorithm proposed in this paper, the information entropy of Lena's ciphertext image is closer to the ideal value of 8. Therefore, this algorithm demonstrates a more ideal resistance to statistical analysis, as shown in Table 7.

Table 7 Comparison table of information entropy of cryptographic images.

Key space analysis

To thwart brute force attacks effectively, it is crucial for the key range in image encryption algorithms to be expansive. When the key range exceeds 2 to the power of 100, the success rate of brute force attacks can be significantly reduced. In this paper, we propose a method that leverages chaos theory to generate initial values, aiming to produce three 256-bit hash values as keys. Our key range can reach 2 to the power of 768, surpassing 2 to the power of 100 by a significant margin. Consequently, this algorithm boasts a sufficiently large key range, providing robust resistance against brute force attacks.

Histogram analysis

The histogram depicts the frequency of each grayscale value, effectively illustrating the pixel distribution pattern of an image. In an excellently encrypted image, the histogram should display a horizontal distribution, as shown in Fig. 6, depicting the histograms of Lena's R,G,B channels before and after encryption.

Fig. 6

Simulation result diagrams. (a) The histogram of Lena's R channel before encryption. (b) The histogram of Lena's G channel before encryption. (c) The histogram of Lena's B channel before encryption. (d) The histogram of Lena's R channel after encryption. (e) The histogram of Lena's R channel after encryption. (c) The histogram of Lena's R channel after encryption.

Correlation analysis

To evaluate the correlation of the ciphertext image, we randomly selected 5000 pairs of adjacent pixel values in each direction of the ciphertext image and calculated their correlation coefficients using Eqs. (13), (14), and (15). The correlation coefficients of adjacent pixels can be computed accordingly. By calculating the correlation coefficients for both plaintext and ciphertext images, the comparison chart of adjacent element correlations is presented in Fig. 7, and the calculation results are listed in Tables 8 and 9.Upon observation, it was noted that the three channels of the original plaintext image exhibited a very strong correlation between pixels in the horizontal, vertical, and diagonal directions, with correlation coefficients very close to 1. However, after encryption, the correlation coefficients in these three directions of the ciphertext image approached zero. This indicates that the encryption system has successfully eliminated the correlation between adjacent pixels, achieving the desired encryption effect.

$${\gamma }_{xy} = \frac{cov (x,y)}{\sqrt{D(x)^{\prime} D(y)}}$$

(13)

where x and y are pixel values.

Fig. 7

Comparison chart of correlation analysis between adjacent elements before and after encryption. (a1) (b1) (c1) are the correlation coefficient maps of the R channel of Lena before encryption in the horizontal, vertical, and diagonal directions, respectively. (a2) (b2) (c2) are the correlation coefficient maps of the G channel of Lena before encryption in the horizontal, vertical, and diagonal directions, respectively. (a3) (b3) (c3) are the correlation coefficient maps of the B channel of Lena before encryption in the horizontal, vertical, and diagonal directions, respectively. (a4) (b4) (c4) are the correlation coefficient maps of the R channel of Lena after encryption in the horizontal, vertical, and diagonal directions, respectively. (a5) (b5) (c5) are the correlation coefficient maps of the G channel of Lena after encryption in the horizontal, vertical, and diagonal directions, respectively. (a6) (b6) (c6) are the correlation coefficient maps of the B channel of Lena after encryption in the horizontal, vertical, and diagonal directions, respectively.

Table 8 Table of correlation coefficients for the plaintext image.

Table 9 Table of correlation coefficients for the ciphertext image.

$$cov (x,y) = \frac{1}{N} \sum_{1}^{N}({x}_{i} - E(x))({y}_{i} - E( y))$$

(14)

$$E\left(x\right)= \frac{1}{N} \sum_{1}^{N}\left({x}_{i} \right), D(x) = \frac{1}{N} \sum_{1}^{N}({(xi - E(x))}^{2})$$

(15)

Differential attack analysis

A differential attack is fundamentally a chosen plaintext attack, wherein the assailant endeavors to infer the encryption key of the algorithm through scrutinizing the disparities between plaintext and ciphertext images, with the objective of revealing the corresponding relationship. In the context of resisting differential attack analysis, two frequently employed metrics are the Number of Pixel Changes Rate (NPCR) and the Unified Average Changing Intensity (UACI), serving as benchmarks for evaluating the algorithm's efficacy. The formula for calculating NPCR is:

$$NPCR = \frac{\sum_{i=1}^{M}\sum_{j=1}^{N}D(i,j)}{MN}\times 100\%$$

(16)

where M and N denote the width and height of two arbitrary images, respectively, and D(i, j) is defined as the percentage of pixels with distinct values to the total number of pixels in the entire image.

$$UACI = \frac{\sum_{i=1}^{M}\sum_{j=1}^{N}\frac{{C}_{1}\left(i,j\right)-{C}_{2}\left(i,j\right)}{255}}{MN}\times 100\%$$

(17)

where N signifies the total number of pixels in the image, and C₁(i, j), C₂(i, j) denote the pixel values of the original image and the compressed image at position (i, j), respectively. In the ideal state, the optimal values for NPCR and UACI are 99.6094% and 33.4635%, as depicted in Table 10. The performance of each algorithm is deemed satisfactory.

Table 10 Table comparing NPCR and UACI values for different algorithms.

Time complexity

The total time consumed by the protocol is referred to as computation time. Key attributes of computation costs include: to improve efficiency and reduce costs, we aim to minimize the total number of arithmetic operations performed by the algorithm. As the number of operations increases, the algorithm’s energy consumption and runtime may be affected. The comparison with other algorithms at a resolution of 512 × 512 pixels is shown in Table 11.

Table 11 Time complexity comparison chart.

Key sensitivity analysis

If a minor alteration in the key results in a substantial change in the ciphertext, the key is considered highly sensitive. Incorrect keys are unable to correctly decrypt the ciphertext image. Decrypting the ciphertext images with any one hash value incremented by 1 bit is illustrated in Fig. 8. The figure demonstrates that even a slight modification in the initial value or any one hash value of the key cannot lead to a correct decryption, indicating the algorithm's robust key sensitivity.

Fig. 8

Comparison chart of decryption with small changes in the key. (a) Decryption chart with the correct key. (b–d) Decryption Figure with hash value increased by 1 bit.

Anti-cropping performance

When ciphertext images are subjected to cropping attacks, it is crucial to preserve as much detail as possible, especially for images containing text. This helps minimize the overall impact of cropping on the image. For this purpose, we select an image with a significant amount of text for encryption. We then perform a cropping attack on the ciphertext image and decrypt the cropped image. Figure 9 shows the results after cropping the ciphertext image and adding zero pixels to the affected areas. This image will be used for decryption and image restoration.

Fig. 9

Cropping encrypted images.

Figure 10 shows the result obtained by decrypting the cropped and damaged ciphertext image. As observed, although the ciphertext image was partially cropped and damaged, the algorithm disperses the impact of the cropped areas across the entire image, thereby minimizing the local effects of cropping. This result indicates that the algorithm has strong resistance to cropping attacks, making it suitable for encrypting images containing detailed information.

Fig. 10

Decrypted image after cropping encrypted image.

Noise resistance performance

During image transmission, channel noise often affects and degrades the image. To test the noise resistance performance of this algorithm, different levels of salt-and-pepper noise were added to the ciphertext images to simulate transmission noise. Figure 11a–d show the images obtained after adding salt-and-pepper noise with mean square deviations of 0.05, 0.1, 0.15, and 0.2 to the three channels of the ciphertext image, followed by decryption. As seen in Fig. 11, as the mean square deviation of the added salt-and-pepper noise increases, the image quality deteriorates. However, from a visual standpoint, the main information of the original image can still be distinguished, indicating that this encryption algorithm has strong resistance to Gaussian noise.

Fig. 11

Decrypted image after cropping encrypted image. (a) Salt-and-pepper noise with 0.05. (b) Salt-and-pepper noise with 0.1. (c) Salt-and-pepper noise with 0.15. (d) Salt-and-pepper noise with 0.2.

Image quality assessment

In the field of image processing, the quality of reconstructed images can be evaluated using the peak signal-to-noise ratio (PSNR). A higher PSNR indicates better quality of the reconstructed image. For an original image I (with dimensions M × N) and a reconstructed image R, the mean squared error (MSE) is defined as follows (Eq. 18):

$$MSE=\frac{1}{m\times n}\sum_{i=1}^{m} \sum_{j=1}^{n} {\left[R(i,j)-I(i,j)\right]}^{2}$$

(18)

The equation for calculating PSNR is given as Eq. 19, as follows:

$$PSNR=10{\text{lg}}\left(\frac{{\left(256-1\right)}^{2}}{MSE}\right)$$

(19)

The MSE value is inversely proportional to image quality, while the PSNR value is directly proportional to image quality. In other words, a smaller MSE value results in a larger PSNR value, indicating a lower deviation between the reference image and the evaluated image, and thus a higher image quality. Salt-and-pepper noise ranging from 0 to 1, in intervals of 0.05, was added to the ciphertext images to obtain the corresponding decrypted images. Using the decrypted images as the evaluated images and the original image as the reference image, Eq. (19) was used to calculate the corresponding PSNR values. A curve of salt-and-pepper noise versus PSNR for the three channels was plotted, as shown in Fig. 12. Figure 12a–c show the salt-and-pepper noise versus PSNR curves for the R, G, and B channels, respectively. The simulation results show that as the salt-and-pepper noise increases from 0 to 0.4, the PSNR value rapidly decreases, indicating a rapid increase in the difference between the decrypted image and the original image. When the salt-and-pepper noise exceeds 0.4, the PSNR value changes very slowly as the noise continues to increase, indicating that the difference between the decrypted image and the original image has reached its limit and remains largely unchanged. At this point, it is also difficult to distinguish the original image from the decrypted image.

Fig. 12

PSNR curves for R, G, and B channels with added salt-and-pepper noise. (a) PSNR curve for the R Channel. (b) PSNR curve for the G channel. (c) PSNR Curve for the B channel.

During transmission, this encryption algorithm can withstand noise attacks when the Gaussian noise mean square deviation is relatively low to moderate. However, in environments with high levels of noise, it becomes difficult for the encryption algorithm to prevent noise from affecting the image data.

Conclusion

This paper presents an innovative color image encryption algorithm that harnesses the strengths of a dual chaotic system and an improved logistic mapping. The algorithm utilizes the hash value of the plaintext image to generate keys and incorporates DNA encoding technology to bolster resistance against chosen-plaintext attacks and differential attacks. Through simulation experiments and performance analysis, the algorithm showcased high reconstruction quality, effective resilience against various attacks, and commendable encryption performance. Comparative evaluations with other algorithms reveal that this algorithm excels in overall performance.