Polarized phonons carry angular momentum in ultrafast demagnetization

Abstract

Magnetic phenomena are ubiquitous in nature and indispensable for modern science and technology, but it is notoriously difficult to change the magnetic order of a material in a rapid way. However, if a thin nickel film is subjected to ultrashort laser pulses, it loses its magnetic order almost completely within femtosecond timescales¹. This phenomenon is widespread^2,3,4,5,6,7 and offers opportunities for rapid information processing^8,9,10,11 or ultrafast spintronics at frequencies approaching those of light^8,9,12. Consequently, the physics of ultrafast demagnetization is central to modern materials research^{1,2,3,4,5,6,7,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28}, but a crucial question has remained elusive: if a material loses its magnetization within mere femtoseconds, where is the missing angular momentum in such a short time? Here we use ultrafast electron diffraction to reveal in nickel an almost instantaneous, long-lasting, non-equilibrium population of anisotropic high-frequency phonons that appear within 150–750 fs. The anisotropy plane is perpendicular to the direction of the initial magnetization and the atomic oscillation amplitude is 2 pm. We explain these observations by means of circularly polarized phonons that quickly absorb the angular momentum of the spin system before macroscopic sample rotation. The time that is needed for demagnetization is related to the time it takes to accelerate the atoms. These results provide an atomistic picture of the Einstein–de Haas effect and signify the general importance of polarized phonons for non-equilibrium dynamics and phase transitions.

Main

Since its discovery in 1996¹, the physics of ultrafast demagnetization has been examined with a wide variety of measurement techniques^{1,2,3,4,5,6,7,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28} for clarifying the interplay of laser photons, electrons, spins and lattice dynamics for the reaction path. Pioneering works have suggested either spin transport away from the excited region^{13,14,15,16,17} or Elliot–Yafet spin-flip scattering^{2,18,19,20,21} as potential mechanisms for the flow of angular momentum. While Eschenlohr et al.¹⁷ have demonstrated the significance of spin transport in metal heterostructures, Dornes et al.²² have reported in iron an ultrafast Einstein–de Haas effect via strain waves with collective atomic motion in addition to transient lattice disorder²³. In strong laser fields, spin polarization can be steered away quickly¹², but at normal excitation strengths spin transport is not substantial²⁴. Stamm et al.²⁵ have provided pioneering evidence on the probable role of lattice dynamics and Dürr et al.²⁶ have discovered a stepwise phonon dynamics, but Chen et al.²⁷ have denied the relevance of phonon dynamics expect for their later participation in the back reaction. A comprehensive picture of the reaction path under conservation of angular momentum is therefore not available, although it touches the foundations of magnetism and spintronics and may help to improve the efficiency, speed or versatility of devices for rapid data storage and manipulation.

Experiment

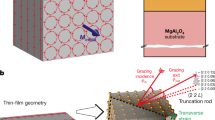
Here we use ultrafast electron diffraction with terahertz-compressed electron pulses²⁸ as a direct probe of lattice dynamics in space and time. Figure 1a depicts the experiment. A single-crystalline layer of nickel with a thickness of 22 nm is epitaxially grown on a single-crystalline silicon membrane with a hydrogen-terminated (100)-surface; see Fig. 1b and Extended Data Figs. 1, 2. Demagnetization by 40–50% is triggered by femtosecond laser pulses (Extended Data Fig. 3) and probed by terahertz-compressed femtosecond electron pulses at a kinetic energy of 70 keV (ref. ²⁸). The base temperature of the experiment is 340 ± 50 K (see Extended Data Figs. 4, 5). The initial in-plane magnetization direction before each pump-probe cycle is defined by permanent ring magnets (see Fig. 1a) that can be rotated around the z axis to study time-dependent Bragg diffraction as a function of the absolute magnetic field direction along nickel’s [100] or [010] axis (see Fig. 1b).

Fig. 1: Pump–probe electron diffraction measurements of atomic motions during ultrafast demagnetization.

a, Experimental arrangement. Ultrashort electron pulses (blue) are compressed by THz radiation (black) and probe the laser-excited lattice dynamics in a single crystal of nickel (light green). Permanent magnets (blue and red poles) provide an initial magnetization (green) along selected crystallographic axes without deflecting the electron beam. b, Epitaxial growth of nickel on silicon; Ni-(100) attaches to Si-(100) at an angle of 45°. c, THz streaking data for characterizing the all-optical compression of the electron pulses. Inset, schematics of the streaking of an electron pulse (blue) by a single THz fields cycle (black) for mapping time to position. d, Diffraction pattern before laser excitation. The green arrows denote different magnetic field directions that are probed. e, Rocking curve of the Ni(0$\bar{2}$0) spot. The width is 6.5°. f, Magnification of the Ni(0$\bar{2}$0) spot (dashed area) and surroundings. g, Difference image around the Ni(0$\bar{2}$0) spot; data before time zero is subtracted from averaged data between 2 and 4 ps.

Results

Figure 1d depicts the electron diffraction pattern without laser excitation. Nickel Bragg spots are observed at the expected diffraction angles (dotted circle) at a rocking curve width (Fig. 1e) that indicates a single crystal with about ±2 atomic displacements over the layer thickness along the z direction. Some additional spots from the silicon support membrane, for example (220) and ($\bar{2}$$\bar{2}$0), appear at slightly smaller diffraction angles (Fig. 1f). The faint ring inside of the dashed line and the four very weak spots at 45° are caused by nickel’s NiO_x termination.

After femtosecond laser excitation, the silicon pattern remains nearly constant but the nickel diffraction changes owing to structural dynamics of the lattice. Although we see within the measured delay range of several picoseconds no measurable broadening of the Bragg spots and no displacements (see Extended Data Fig. 6), indicating the absence of transient strain or lattice expansion on such time scale, there are substantial changes of the Bragg spot intensities (Fig. 1g), linked to structural dynamics within the unit cell. Figure 2a shows the intensity of nickel’s symmetry-equivalent Bragg spots ${I}_{\{200\}}=\frac{\,1}{4}({I}_{200}+{I}_{020}+{I}_{\bar{2}00}+{I}_{0\bar{2}0})$ and ${I}_{\{220\}}=\frac{1}{4}({I}_{220}+{I}_{\bar{2}20}+{I}_{2\bar{2}0}+{I}_{\bar{2}\bar{2}0})$ as a function of time. We see that the elevated lattice temperature after laser excitation diminishes the Bragg spots via the Debye–Waller effect. The effective electron–phonon coupling time²⁹ is 770 ± 60 fs (solid line) and the measured ratio $(1-{I}_{\{220\}})/(1-{I}_{\{200\}})\approx 2$ matches the expected picture of a random disorder in the lattice in form of a transient temperature increase^1,23,29.

Fig. 2: Time-resolved diffraction results.

a, Bragg spot intensities for two different diffraction orders as a function of time. The solid lines denote a decay time of 770 fs. Origin of this observation is thermal disorder. The standard error is 4 × 10⁻⁴. b, Anisotropy between crystallographically equivalent Bragg spots of different orientation with respect to the initial magnetic field. ${I}_{\{200\}}=\frac{\,1}{2}({I}_{200}+{I}_{\bar{2}00})$ and ${I}_{\{020\}}=\frac{\,1}{2}({I}_{020}+{I}_{0\bar{2}0})$. The green arrows denote an initial magnetization along Ni[100] (blue data) or Ni[010] (red data). The standard error is 7 × 10⁻⁴. The dashed lines depict the upper and lower level of the fit histogram; see methods. The measured levels after saturation (1 ps < t < 4 ps) are 0.9981 ± 0.0005 (red data) and 1.0019 ± 0.0007 (blue data) under the constraint of an antisymmetric effect. c, Suggested origin of the results: A loss ΔM of magnetization implies a loss of angular momentum ΔL that is carried by atomic rotations. This motion is restricted to a plane that is perpendicular to the direction of magnetization. Electron diffraction (blue arrow) therefore reveals an anisotropic atomic disorder.

However, additional anisotropic phonon distributions are revealed by an asymmetry analysis of pairs of Bragg spots that have crystallographic equivalence but differ in their orientation with respect to the magnetic field. In particular, we compare (200) and ($\bar{2}$00) with (020) and (0$\bar{2}$0), that is, the upper/lower with the left/right Bragg spots on the circle in Fig. 1d. Any lattice fluctuations in form of a transient temperature can only affect all these four spots in the same way (see Extended Data Figs. 7 and 8), and differences in their dynamics therefore reveal a non-thermal phonon dynamic in violation of equipartition.

Figure 2b shows the results. Spots (200) and ($\bar{2}$00) become more intense than (020) and (0$\bar{2}$0) if the initial magnetic field is set along nickel’s [100] direction but the ratio reverses for an initial magnetization along the [010] axis. The time it takes to develop this anisotropy is 150–750 fs (see Extended Data Fig. 9) and there is no detectable onset of a decay within the measured delay range. The anisotropic effect amounts to roughly 25% of the isotropic phonon fluctuations.

Therefore, laser excitation of pre-magnetized nickel not only causes an ultrafast increase of lattice temperature in form of isotropic atomic displacements (see Fig. 2a), but also an additional, long-lived and anisotropic lattice motion relative to the direction of the initial magnetization (see Fig. 2b). This result implies an ultrafast, non-thermal phonon dynamics with a direct magnetic origin. Spins couple quickly and directly to symmetry-breaking high-frequency phonons with an oscillation in real space in perpendicular direction to the initial magnetization, providing a direct observation of ultrafast spin–phonon coupling that has so far only indirectly been inferred²⁵.

Interpretation

We argue in the following that the origin of our observations is rotational atomic motions with angular momentum, that is, phonons with a circular polarization^30,31,32. Figure 2c depicts such dynamics: atoms move around their equilibrium position with a rotation axis that is aligned with the magnetic field and with an average radius and velocity that are determined by the spin angular momentum that is lost during demagnetization. Consequently, we perceive with our electron diffraction an anisotropic atomic disorder via attenuated Bragg spots only along such crystallographic directions that align perpendicularly to the initial direction of magnetization.

We support this interpretation by a nearly parameter-free consideration of conservation laws in combination with molecular dynamics simulations. Prior to demagnetization, each nickel atom carries a magnetic moment of ${\mu }_{{\rm{Ni}}}\approx 0.6{\mu }_{{\rm{B}}}$, where μ_B is Bohr’s magneton. Demagnetization by D ≈ 50% (Extended Data Fig. 5) implies that each nickel atom must get rid of a spin angular momentum of $\Delta L=D\frac{{\mu }_{{\rm{Ni}}}\hbar }{g{\prime} {\mu }_{{\rm{B}}}}\approx 0.16\hbar$, where g’ ≈ 1.855 is the gyromagnetic ratio of the electron. No angular momentum can travel out of the excited region on femtosecond and picosecond time scales. If the lattice accepts this ΔL in form of rotational dynamics, each atom must move around its equilibrium position within the unit cell with an average radius of $R\approx \sqrt{\frac{\Delta L}{{M}_{{\rm{Ni}}}\omega }}$, where M_Ni is the mass of a nickel atom and ω is the angular frequency of the rotation, to conserve total angular momentum. The phonon spectrum of nickel has a peak in the density of states around $\omega /2\pi \approx 8\,{\rm{THz}}$ (ref. ³³) and with this assumption we obtain R ≈ 1.9 pm.              .   In electron diffraction, the intensity I of a Bragg spot is related to random atomic displacements via the Debye–Waller factor

$$\frac{I}{{I}_{0}}={\langle \exp \left[\frac{2\pi i}{a}(\begin{array}{c}h\\ k\\ l\end{array})\cdot (\begin{array}{c}{u}_{x}\\ {u}_{y}\\ {u}_{z}\end{array})\right]\rangle }^{2}$$

(1)

where h,k,l are the Miller indices of the Bragg spot, I₀ is the intensity without disorder, a ≈ 352 pm is the lattice constant of nickel, u_x,y,z are the atomic displacements and ⟨⟩ denotes an averaging over the probed crystal volume. The inner product in equation (1) makes such Bragg spots with a zero in one of the Miller indices insensitive to atomic disorder along the corresponding dimension in real space. If the initial magnetization aligns with y, atoms are only displaced along x and z (see left panel in Fig. 2c). Under the assumption of a circular trajectory with ${u}_{x}=R\cos (\varphi ),\,{u}_{z}=R\sin (\varphi )$ and u_y = 0, where ϕ is a supposedly random rotational phase for each atom in the laser-excited crystal volume, we obtain I/I₀ ≈ 0.998 for Bragg spots (200) and ($\bar{2}$00). Since I/I₀ = 1 for (020) and (0$\bar{2}$0), the measured ratio ${I}_{\{200\}}/{I}_{\{020\}}$ becomes 0.998. In contrast, an initial magnetization along x (right panel in Fig. 2c) produces ${I}_{\{200\}}/{I}_{\{020\}}$ ≈ 1.002. Despite its simplicity, this estimation reproduces the measurement results of Fig. 2b in magnitude and sign. We conclude that almost all or at least a substantial fraction of the angular momentum of the spin system arrives within hundreds of femtoseconds in the lattice in form of rotational motions of the atoms.

Molecular dynamics simulations

Molecular dynamics simulations support this interpretation. Assuming a demagnetization of 42%, we let every seventh, randomly selected nickel atom receive one quantum of angular momentum (Fig. 3a) and compute electron diffraction patterns by averaging over up to 100 simulation runs. In this way, we excite the entire phonon spectrum at once and let the system decide which ones will prevail. Figure 3 depicts the results. After laser absorption, the system quickly develops into a distribution of anisotropic high-frequency oscillations with an asymmetric velocity histogram (Fig. 3b) in violation of equipartition. Figure 3c shows the simulated Bragg spot anisotropy in analogy to the measured data of Fig. 2b. All traces (denoting different numbers of nickel atoms in the simulation volume) resemble the key feature of the experiment, namely the almost instantaneous onset of a substantial and long-lasting Bragg spot anisotropy at a level shortly after time zero that matches to the experiment.

Fig. 3: Molecular dynamics simulations.

a, After laser excitation (red pulse), we excite the lattice by instantaneously displacing an atom locally from its equilibrium position assuming a velocity in the x–z plane perpendicular to the displacement (blue motion), leading to an angular momentum of $\hbar$ in y direction (blue), compensating the lost spin angular momentum (blue arrow). Bragg peaks are calculated for the indicated electron beam direction (light blue). b, Velocity histogram for the time range of the first 500 fs, violating equipartition. Motion is faster (and displacements are larger) in the x direction than along y. c, Simulated electron diffraction and Bragg spot anisotropy in analogy to Fig. 2b. Blue and red data denote an initial magnetization along Ni[100] and Ni[010], respectively. In our simulations this corresponds to swapping the definition of x and y axes, so that our data are simply mirrored. N = 20 (N = 50) corresponds to about 4 × 20³ (4 × 50³) nickel atoms, both with open boundary conditions; PBC corresponds to about 4 × 20³ nickel atoms with periodic boundary conditions. The initial anisotropy level after laser excitation is similar in all cases and fits to the experiment (see Fig. 2b). The decays for the smaller simulation volumes denote the onset of macroscopic rotation (see methods).

Quantitatively, the main uncertainty in the analytical estimations is the average phonon frequency³³ and the main uncertainty in the experiment is the particular degree of demagnetization (Extended Data Fig. 5). Without any free parameter in the simulations, the absolute anisotropy values of our three results (experiment, analytical, simulations) are therefore consistent to each other within an estimated maximum mismatch of 30%. The sign of the anisotropy and the orientation of the polarization plane are consistent for all three cases as well. In all three pictures, the anisotropic lattice motion appears within sub-picosecond times, aligns to the magnetic field normal and shows an atomic mean square displacement that fits to the necessary angular momentum.

Consequences and relations to previous results

To explain these observations, the spins of the hot electron gas must rather directly and efficiently couple to the atomic vibrations before the material can reach a thermal equilibrium. Numerical simulations of non-equilibrium Elliot–Yafet scattering have indicated the general feasibility of such dynamics^2,18,19, although the magnitude of the effective coupling constants^2,12,18,19, the role of the phonon dispersion¹⁹ or the necessity for non-thermal electrons¹⁹ have remained elusive. Given our measurement results, direct spin–phonon coupling is indeed efficient by involving phonons with high frequencies and specific polarizations. Diffusive or superdiffusive spin transport^{13,14,15,16,17} or strain waves²² play a minor role for the primary dynamics in our material.

In the simulations, the total energy associated with the phonon angular momentum is roughly 4 meV per nickel atom, which is several times smaller than the total energy that is deposited by laser absorption, approximately 25 meV per nickel atom. Only a fraction of the absorbed laser energy therefore contributes to the rotational phonons, while the rest merely heats the material via the remaining degrees of freedom. Competition between these two channels controls the achievable degree of demagnetization and explains why more demagnetization can occur in nickel at elevated base temperature²³ or why less and slower dynamics is measured for different chemical elements^2,3,6,7 with their distinct electron and phonon dynamics. The reported results therefore link the success of phenomenological multi-temperature models^1,18,21,34 to an atomistic description. The recent observation of a direct spin–strain coupling in iron²² is in our picture a preferential coupling of spins to circularly polarized phonons near the center of the Brillouin zone.

Transfer of the initially coherent laser excitation into the observed anisotropic, high-frequency lattice fluctuations implies an ultrafast localization of the excitation to single atoms or at least tiny domains, to break translational crystal symmetry. If all atoms in the laser focus would be subject to identical forces, only macroscopic waves could emerge at the speed of sound, contrary to our observations. Non-equilibrium fluctuations, atomic-scale symmetry-breaking, and non-concerted forces are therefore necessary to explain the measured diffraction results.

Assorted experiments have shown that ultrafast demagnetization needs a finite time to occur, at least 150–300 fs in nickel^{1,2,23,25,35,36} and several picoseconds in rare-earth metals^3,6,7. Our results explain this bottleneck by the finite time that it takes to accelerate the lattice atoms into their polarized motion. The duration of this process depends on the amount of angular momentum in the spin system, the spin–orbit coupling, the strength of the coupling between spins and lattice, and the ability of the lattice to build up internal angular momentum. Note that electron diffraction becomes only sensitive to polarized phonons after the atoms have actually moved while demagnetization only requires their acceleration. The time constants of Fig. 2b are therefore upper limits for the time in which the angular momentum arrives in the lattice.

The anisotropic phonons persist for picoseconds in the experiment and for tens of picoseconds in the simulations (see Extended Data Fig. 10). We suppose that circularly polarized phonons are not free to thermalize into an isotropic equilibrium due to the necessary conservation of angular momentum. If so, the total angular momentum in a lattice can persist longer than the specific subset of high-frequency phonons that is initially excited. Macroscopic removal of angular momentum can only occur through phonon–phonon scattering into low-frequency sound and strain waves that carry angular momentum away from the probing region and eventually mediate the onset of a macroscopic rotation³¹. Consequently, the traditional explanation of the Einstein–de Hass effect as a direct transfer of spin angular momentum to specimen rotation²² should be amended to include an intermediate situation in which the angular momentum is carried by a rotational dynamics of the lattice^30,31,32. In turn, a dedicated excitation of rotational lattices may produce an atomistic version of the Barnett effect and create magnetic fields^37,38. The unifying principles are the conservations of energy and angular momentum on atomistic dimensions.

To conclude, ultrafast electron diffraction of laser-demagnetized nickel reveals an almost instantaneous, long-lasting, non-equilibrium population of anisotropic phonons that oscillate predominantly in a plane perpendicular to the direction of the initial magnetization. A direct, efficient and ultrafast interaction of spins with high-frequency phonons is therefore decisive for the dynamics of magnetic materials. Rotational lattice motion on atomic dimensions can carry angular momentum before the onset of a macroscopic Einstein–de Haas rotation (Fig. 4). Hence, circularly polarized or chiral phonons are not only a peculiarity of crystals with broken inversion symmetry^32,39,40 but can also be created in substantial amounts on femtosecond time scales with help of simple magnetic materials. This result suggests the possibility of utilizing phonon-based or phonon-assisted spin transport for applications in spintronics and for improving the speed and efficiency of ultrafast magnetic switching. A dedicated excitation and subsequent probing of polarized phonons or related hybrid quasiparticles with angular momentum may also provide innovative ways for understanding and optimizing the functionality of complex materials from an atomistic perspective.

Fig. 4: Sequence of events.

After the laser (red) has impinged on our magnetized material (M, green), hot electrons with spin quickly couple to anisotropic and circularly polarized phonons with angular momentum (middle panel). The material is demagnetized at this point. Only later, low-frequency shear waves mediate a macroscopic rotation of the specimen as a whole (right panel). Compare with ref. ³¹.

Methods

Thin film growth

A 35 nm thick and 3 × 3 mm² large single-crystalline Si(100) membrane is ultrasonically cleaned in acetone and ethanol, rinsed with water and dipped in 5% hydrofluoric acid for approximately 15 s to prepare a hydrogen-terminated silicon surface^41,42,43,44. Direct-current magnetron sputtering is used to grow an epitaxial Ni film with 22 nm thickness at a deposition rate of 0.41 Å s^–1 (refs. ^45,46) by metal–metal epitaxy on silicon (MMES)^47,48,49. We use direct current (d.c.) magnetron sputtering as described in refs. ^46,50. One of the three 2” sputter guns is loaded with a 6.3 mm thick, 99.99% pure Cu sputter target and a second sputter gun is loaded with a 1.4 mm thick 99.99% pure Ni target. The distance between the sputter target and the substrate is approximately 11 cm normal to the surface of the substrate. The film thickness is time-controlled with a deposition shutter that is located between the sputtering target and the substrate. The system is pumped down to a base pressure of approx. 3 × 10^–8 mbar and the substrate is cooled to 273 K, where it is allowed to stabilize for 1 h before commencing the deposition. To remove any potential dirt from the sputtering target, we apply 10 min of pre-sputtering with closed deposition shutter. An initial 6 nm of Cu seed layer is deposited at an ultra-high purity (7N) Ar working gas pressure of 2.55 × 10^–3 mbar and a sputtering power of 50 W, resulting in a deposition rate of 0.5 Å s^–1. Consecutively, the Ni layer is deposited onto the seed layer at a working gas pressure of 4.0 × 10^–3 mbar and a d.c. sputtering power of 50 W, resulting in a deposition rate of 0.41 Å s^–1.

X-ray characterizations

After deposition, the sample is characterized ex-situ by X-ray reflectometry (XRR) as well as out-of-plane (oop) and in-plane (ip) X-ray diffraction (XRD). In the following, λ is the wavelength of the applied X-ray radiation, B(2θ) is the full-width-at-half-maximum (FWHM) of the diffraction peak and θ is the angular peak position. Supplemental ω scans (also known as rocking scans) are performed for the XRD case, which allows to determine the mosaic spread, viz. the directional alignment of the crystallites. For a Gaussian shaped rocking scan, the mosaic spread is quantified by its corresponding standard deviation $\sigma =\frac{{\rm{FWHM}}}{2\sqrt{2{\rm{l}}{\rm{n}}2}}$ (ref. ⁵¹). The size of the crystallites is analogous to the coherence length L, which can be estimated by the Scherrer formula⁵² $B(2\theta )=\frac{0.94\lambda }{L\,\cos \,\theta }$ with B(2θ) and θ in radians units.

Instrumentation

The oop structural analysis was performed using a two-circle X-ray diffractometer with parallel beam optics and Cu_Kα source in a θ – 2θ scattering geometry (D5000, Siemens GmbH). The instrument resolution of the X-ray diffractometer is 0.023°, given by the FWHM of the Si(004) out-of-plane rocking-scan. This value is small enough such that instrumental broadening in the analysis of the deposited Cu and Ni films can be neglected. For ip structural analysis, we apply a four-circle X-ray diffractometer, also with parallel beam optics and Cu_Kα source in a θ – 2θ scattering geometry (D8, Bruker GmbH). It offers additional axes for sample inclination (χ) relative to the scattering plane and axis rotation (ϕ) around the sample normal. This capability allows to access ip crystal information. An instrument resolution of 0.031° is determined from the FWHM of the Si(004) out-of-plane rocking scan.

X-ray reflectivity

For XRR analysis, the sample is aligned with respect to its surface by maximizing the intensity in the regime of total reflection. Quantitative analysis of the XRR data was carried out using the GenX 3.0.0 software package⁵³. For data fitting, the logarithmic figure of merit ${\rm{FOM}}\approx \sum |\log \,{R}_{{\rm{fit}}}-\,\log \,{R}_{{\rm{meas}}}|$ is used, where R_fit is the fitted reflectivity and R_meas is the measured reflectivity, respectively. We assume a layer structure of NiO_x on Ni on Cu on Si. NiO_x denotes the natural nickel oxide layer that is expected to form at the surface after the thin film deposition process and a small additional layer of unknown surface coverage (dirt) is also allowed in the fits. Extended Data Figure 1a depicts the measured X-ray reflectivity data, the best fit results and the scattering length density profile.

Out-of-plane X-ray diffraction

For XRD analysis, the sample is aligned with respect to the Si(004) oop reflection as a well-defined reference for the determination of the crystalline directions of the deposited Cu and Ni films. In the following, a, b and c represent the lattice constants along the crystallographic directions [100], [010] and [001]. Extended Data Figure 1b depicts the oop XRD measurements in the range 40° ≤ 2θ ≤ 60°. The observed intensities at 2θ ≈ 50.53° and 2θ ≈ 52.13° correspond to the Cu(002) and Ni(002) reflections with c-axis lattice constants of c_Cu = 3.612 ± 0.003 Å and c_Ni = 3.509 ± 0.003 Å, respectively. By applying the Scherrer formula (see above), we estimate a coherence length of L(001)_Cu = 159.5 ± 2.7 Å and L(001)_Ni = 221.1 ± 2.7 Å. These lengths are of the same order of magnitude as the corresponding layer thicknesses. This result indicates that there is no break of the epitaxy in growth direction. Also, the rocking-scans (see inset of Extended Data Fig. 1b) reveal no indication of any crystal defects along the growth direction. In particular, we observe no splitting of the rocking curve into multiple peaks⁴⁴; the measured FWHM values of FWHM_Cu = 5.6 ± 0.1° (σ_Cu = 2.378 ± 0.042) and FWHM_Ni = 4.4 ± 0.1° (σ_Cu = 2.378 ± 0.042) are in agreement with literature values^44,47,51 for Cu and Ni films of similar thickness. Note that the electron rocking curve (Fig. 1e) is slightly wider due to electron energy losses.

In-plane X-ray diffraction

An oop analysis alone is not sufficient for proof of an epitaxial growth, because crystalline misalignment can also occur ip. Additionally, we aim for determining the crystallographic orientation of the Cu and Ni layers with respect to the substrate. Therefore, ip sensitive scans are performed with the sample being aligned in χ and ϕ with reference to the Si(004) and Si(111) substrate reflections. Setting the 2θ angle to the Si(111), Cu(111) and Ni(111) ip peak positions and rotating the sample around its normal ϕ at the corresponding inclination angle Δχ = 54.74° between the (001) oop and (111) ip crystal directions provides information on the ip crystal symmetry. The three ϕ scans for the Si(111), Cu(111) and Ni(111) ip peaks are shown in Extended Data Fig. 1d.

A clear fourfold symmetry of the Cu(111) and Ni(111) ip reflections is observed with an offset angle of 45° to the Si(111) substrate reflections. This result demonstrates that Ni grows epitaxially on the Si(100) surface with the relationship $\text{Ni[}001\text{]}\parallel \text{Cu[}001\text{]}\parallel \text{Si[}110\text{]}$ and $\text{Cu(}001\text{)}\parallel \text{Ni(}001\text{)}\parallel \text{Si(}001\text{)}$. The observed intensities at 2θ ≈ 43.41° and 2θ ≈ 44.47° (see Extended Data Fig. 1c) correspond to the Cu(111) and Ni(111) reflections with diffraction plane spacings of ${d}_{\text{Cu}}\text{(}111\text{)}$ = 2.084 ± 0.004 Å and ${d}_{\text{Ni}}\text{(}111\text{)}$= 2.037 ± 0.003 Å, respectively. Assuming $a=b$, the ip lattice parameters of the Cu and Ni-films are obtained via geometrical relationships as ${a}_{\text{Cu}}={b}_{\text{Cu}}\,=$ 3.608 ± 0.008 Å and ${a}_{\text{Ni}}={b}_{\text{Ni}}=$ 3.539 ± 0.008 Å. In [111] direction, we obtain coherence length values of $L{(111)}_{\mathrm{Cu}}$ = 258.8 ± 1.8 Å and $L{\text{(}111\text{)}}_{\text{Ni}}$ = 305.7 ± 1.7 Å, from which we infer lateral coherences of $L{\text{(}100\text{)}}_{\text{Cu}}=L{\text{(}010\text{)}}_{\text{Cu}}\,=$ 144.1 ± 2.1 Å and $L{\text{(}100\text{)}}_{\text{Ni}}=L{\text{(}010\text{)}}_{\text{Ni}}\,=$ 149.3 ± 2.6 Å. These values are comparable to the coherence length of the electron beam (~200 Å). The observation of weak Cu(111) and Ni(111) reflections for $\varDelta \chi$ = 79.00° at $\varphi$ ≈ 10°, 80°, 100°, 170°, 190°, 260° and 350° (red curve in Extended Data Fig. 1e) and for $\varDelta \chi$ = 15.80° at $\varphi$ ≈ 45°, 135°, 225° and 315° (blue curve in Extended Data Fig. 1e) indicate the presence of occasional (111)-plane twin defects^54,55. For the Ni(111) reflections, the strongest intensity is observed at an inclination angle of $\varDelta \chi$ = 54.51° instead of $\varDelta \chi$ = 54.74°, which would be expected for a cubic system. This mismatch indicates a slight tetragonal distortion of the Ni film, confirmed by ip diffraction scans in the range $42^\circ \,\leqslant \,2\theta \,\leqslant \,46^\circ$ at an inclination angle of $\varDelta \chi$ = 54.51° (see Extended Data Fig. 1c). However, such a small distortion is irrelevant for the ultrafast electron diffraction experiments, because the electron beam divergence and rocking curve widths far surpass the measured angle differences.

Pump probe electron diffraction

Sub-100-fs laser pulses for sample excitation at a repetition rate of 25–50 kHz are obtained from an Yb:YAG laser system (Pharos, Light Conversion UAB) by applying a series of two self-defocussing bulk media for spectral broadening⁵⁶ followed by a grating sequence (see below). Knife-edge measurements reveal an optical beam radius ${\omega }_{0}\,\approx$ 150 µm at an intensity of 1/e² at the sample position. The excitation energy density (fluence) at the beam centre is set to ~4 mJ cm^–2 of which ~1.5 mJ cm^–2 are absorbed, conditions for which nickel demagnetizes by ~50% within ~250 fs (ref. ²³).

For ultrafast electron diffraction^57,58, short electron pulses are generated by two-photon photoemission⁵⁹ and accelerated to a kinetic energy of 70 keV. We use 10–20 electrons per pulse, just below the onset of detectable space-change effects. The electron beam diameter (full width at half maximum) at the specimen is ~60 µm. The electron pulses are compressed in time²⁸ by single-cycle THz pulses at an ultrathin mirror membrane of 10 nm Al on a 10 nm SiN support membrane⁶⁰, placed at a distance of 0.4 m from the electron source and 0.5 m before the specimen. All-optical streaking²⁸ is used to characterize the electron pulse duration directly at the specimen location (see Fig. 1c). The streaking element is a butterfly-shaped copper resonator (400 µm width, 400 µm height, 56 µm gap width, 80 µm gap height) that is excited by ~10⁶ V m^–1 of THz peak field strength. A 50-µm aperture improves the resolution of the streaking signal. Electron pulse durations of <130 fs, <120 fs, <75 fs and <80 fs (upper limits due to streaking resolution) are obtained for the diffraction scans that are combined in Fig. 2a, b. The time mismatch originating from the 25° laser-membrane angle is ~100 fs. The temporal apparatus function is ~150 fs (full width at half maximum). Recording meaningful electron diffraction images with single-electron pulses implies data accumulation over many pump–probe cycles. Measured diffraction patterns are therefore statistical averages over space and time²⁸.

The whole magnetic assembly of Fig. 1a can be rotated around the z axis to study time-dependent Bragg diffraction as a function of the absolute magnetic field direction along the x axis or y axis, that is, the [100] or [010] direction of the nickel crystal (see Fig. 1b). The diffraction pattern is imaged onto a single-electron sensitive detector system (F416, TVIPS GmbH) with a magnetic solenoid lens with calibrated image rotation. Consequently, the measured Bragg spots on the screen are linked to the crystallographic orientation of the sample and the absolute direction of the initial magnetization.

Base temperature of the pump–probe experiment

The base temperature of the sample before laser excitation is determined by comparing Bragg diffraction before time zero with diffraction pattern taken without any laser excitation at all. This change is less than 0.5 % for the Ni(200) spot and less than 1% for the Ni(220) spot. Using reported values for the mean square displacement $\bar{{u}^{2}}$ as a function of temperature⁶¹, we calculate the Debye–Waller factor$\frac{I}{{I}_{0}}={\rm{\exp }}\left(\frac{-1}{3}{\left|G\right|}^{2}\bar{{u}^{2}}\right)$ as a function of temperature; G is the reciprocal lattice vector. We infer that the specimen has a base temperature not larger than ~50 K above the laboratory temperature before each excitation with the pump laser. Numerical simulations support this result (see below).

Bragg spot analysis procedure

For analysis of time-dependent Ni Bragg spot intensities, an elliptical region is selected for each Bragg spot in a way that minimizes overlap with the adjacent Si peaks; the unit cell of nickel in [100] direction is ~8% smaller than the unit cell of silicon in [110] direction. For each image and Bragg spot, intensity in this region is summed up. Time-dependent intensity changes ${I}_{{hkl}}\left(t\right)$ are obtained by reference to the measured intensity before time zero, that is, ${I}_{{hkl}}\left(t\right)={I}_{{hkl}}^{{\rm{raw}}}\left(t\right)/{I}_{{hkl}}^{{\rm{raw}}}\left(t < 0\right)$ where ${I}_{{hkl}}^{{\rm{raw}}}$ denotes the integrated digital counts in the area of the spot (see Fig. 1f). In this way, any systematic sensitivity variations of the apparatus cancel out. Additionally, we normalize ${I}_{{hkl}}\left(t\right)$ to ${I}_{000}\left(t\right)$ in order to compensate for potential temporal drifts of the electron beam. About 250 pump–probe scans over the measured time range are performed rapidly in order to average out potential long-term drifts of the experiment. In Fig. 2b, the data is scaled to an anisotropy of one at delays below zero.

We note that the selected way of averaging opposing Bragg spots makes the experiment particularly insensitive to potential time-dependent deviations of the Bragg condition. Bragg spots (200) and ($\bar{2}$00) as well as (020) and (0$\bar{2}$0) are Friedel pairs and for a symmetric diffraction pattern their sum is insensitive to tilt or shear of the lattice. Also, the rocking curve shows some residual broadening (see Fig. 1e). We therefore probe exclusively sub-unit-cell dynamics and atomistic disorder, not mechanical strain waves or torques. The beam electrons interact with the integrated electrostatic potential of the atoms in the material and our experiment therefore measures solely atomic positions via nuclear charges and inner electrons and not any valence electron dynamics or electronic angular momentum.

Molecular dynamics simulations

Molecular-dynamic simulations are carried out with LAMMPS^62,63,64 using the implemented symplectic velocity Verlet method which ensures energy conservation and, for open boundary conditions, angular momentum conservation. A nickel fcc lattice of size $N\times N\times N$ unit cells ($\approx 4{N}^{3}$ atoms) is simulated using the appropriate potential, which was calculated via the embedded-atom method (EAM) and is implemented in LAMMPS⁶³. Starting from its ground state the lattice is excited by an initial condition as described below. To compare the resulting dynamics with the experimental measurements, time-dependent diffraction patterns $I\left({\bf{k}},t\right)$ are calculated using the selected area electron diffraction method (SAED) of LAMMPS⁶⁵ for electron diffraction with an incident radiation from direction ${{\bf{e}}}_{z}$ and a wavelength $\lambda =0.04635\,\AA$. We simulate ${N}_{\text{av}}=10,\ldots ,100$ different initial conditions (depending on the system size) and average the resulting intensities ${\left\langle I\right\rangle }_{{N}_{\text{av}}}$. The integrated peak intensities, from which the peak contrast is calculated, are defined by

$${I}_{(YZ0)}(t)={{\int }_{|{\bf{k}}-{{\bf{k}}}_{(XZ0)}|\le {\rm{\varepsilon }}}\langle I({\bf{k}},t)\rangle }_{{N}_{{\rm{a}}{\rm{v}}}}{{\rm{d}}}^{2}k,$$

(S11)

where ε = 0.1 Å⁻¹ is the radius in momentum space the diffraction pattern is integrated over. We study three different systems: (i) for a nickel lattice with open boundary conditions along all directions, energy- and angular momentum conservation is ensured. A global rotation of the crystal is possible and boundary effects as well as finite-size effects can be observed. The ground-state atomic positions have to be simulated before it is excited via the initial condition. (ii) For periodic boundary conditions along all directions only energy conservation is ensured. No global rotation can occur, no boundary effects can be observed, but finite size effects still exist. (iii) To investigate a global rotation of the system according to the Einstein–de Haas effect, no direct molecular dynamics simulation is performed, but the system in its ground state is rotated by the angle $\phi =\left|{\boldsymbol{\omega }}\right|\cdot t$, where ${\boldsymbol{\omega }}={\varTheta }^{-1}\cdot {{\bf{L}}}_{0}$ with the total angular momentum ${{\bf{L}}}_{0}$ and the inertia tensor $\varTheta .$

Initial condition

We mimic an excitation of the lattice with finite angular momentum ${{\bf{L}}}_{0}$, which takes over the spin angular momentum corresponding to a demagnetization process of $\Delta {\bf{M}}=-\Delta M\cdot {{\bf{e}}}_{y}$ via appropriate initial conditions, suitable for molecular dynamics simulations. Within our model, the angular momentum is transferred instantaneously and locally to a fraction of atoms $\varrho$. Note that a sole velocity excitation, for instance, does not excite any atomic angular momentum, since any atomic motion which starts in an equilibrium position would have the displacement vector aligned with the velocity. Therefore, each excited atom is deflected from its equilibrium position by ${\boldsymbol{\Delta }}=\Delta (\cos (\phi ),0,\sin (\phi ))$ and given a velocity ${{\bf{v}}}_{0}={v}_{0}(-{\rm{\sin }}(\phi ),0,{\rm{\cos }}(\phi )\,),$such that the local angular momentum equals $\hbar$. The angle $\phi$ is uniformly distributed in $\left[\mathrm{0,2}\pi \right]$ under the side condition explained below. The resulting angular momentum shows in $-{{\bf{e}}}_{y}$ direction perpendicular to the excitation plane. Aiming for a local angular momentum of ${{m}}_{{\rm{N}}{\rm{i}}}$ | Δ × v₀ | = ħ, the excitation is chosen with minimal energy, that is, with $\Delta$ being at the minimum of the effective potential.

We further aim for zero total velocity of the crystal, ${\sum }_{l}{\dot{{\bf{r}}}}^{l}=0$, and that the total angular momentum exactly equals ${{\bf{L}}}_{0}$. This is not trivial for a system of finite size, such that we use side conditions: first, only half of the excited atoms are randomly selected. Second, symmetric partners of the randomly selected atoms have to be chosen with respect to the crystal’s centre of mass. This ensures ${m}_{{\rm{N}}{\rm{i}}}{\sum }_{l}{{\bf{r}}}^{l}\times {\dot{{\bf{r}}}}^{l}={{\bf{L}}}_{0}.$And third, half of these symmetric pairs is excited by Δ and v₀ whereas the other half is excited in the opposite direction by −Δ and $-{{\bf{v}}}_{0}$, which delivers zero total velocity. For an implementation in LAMMPS with periodic boundary conditions, our initial conditions require a slightly different algorithm, which also yields a fixed total angular momentum and zero total velocity.

The fraction of excited atoms $\varrho$ can be determined from the saturation magnetization of nickel, ${M}_{{\rm{s}}}={\mu }_{{\rm{s}}}/{V}_{{\rm{uc}}}=0.616\,{\mu }_{{\rm{B}}}/{V}_{{\rm{uc}}}$(ref. ⁶⁶) (where ${V}_{{\rm{uc}}}=\frac{1}{4}{a}^{3}$ with a = 352 pm is the volume of an fcc nickel unit cell) and the demagnetization ΔM via $\Delta M=|\gamma \frac{{{\bf{L}}}_{0}}{V}|=|\gamma |\frac{\varrho \hslash }{{V}_{{\rm{u}}{\rm{c}}}},$where $\gamma =g{\prime} \frac{{\mu }_{{\rm{B}}}}{\hbar }$ with $g\text{'}=1.8550$ (ref. ⁶⁷). A demagnetization of 27%, 42% and 63%, which are the values investigated in this paper, correspond to ${\varrho }\approx$ 0.09, 0.14, 0.21 (see also Extended Data Fig. 10).

Electron rocking curves and multiple scattering effects

The angle-dependent intensity of each Bragg peak within the diffraction pattern is recorded with the ultrafast electron diffraction beamline at the same experimental conditions and beam parameters as in the pump–probe experiments. Only the terahertz compressor is turned off and the Al foil is removed for simplicity. The sample is rotated ±20° around the [010] axis with 0.25° steps and rotated by ±2.5° around the [100] axis, limited by the mechanical range of our goniometer. During the scan, the sample’s spatial position is continuously corrected to keep the specimen central to the electron beam. Extended Data Fig. 2a shows the rocking curve of the Ni(200) peak. The full width at half maximum is 6.5°. The narrow spike at ~1° and ~3° are attributed to the effects of the silicon substrate. In the pump–probe experiment, such special angles are mostly avoided (see Fig. 1f). The slight strain of the growth (see above) is helpful for this purpose.

Magnetic hysteresis measurements and design of the permanent magnets

The magnetic hysteresis curve of our nickel specimen and the field needed for sufficient in-plane magnetization by the permanent magnets are determined with a superconducting quantum interference device (MPMS XL5 SQUID, Quantum Design). Extended Data Fig. 2b depicts the results, indicating saturation at ~4 mT. The permanent-magnetic structure for defining and maintaining a constant in-plane magnetization within the sample is a construction of two NdFeB ring magnets with 10 mm outer diameter, 7 mm inner diameter, 3 mm thickness and a remanent magnetization of ~1.3 T. Two diametrically magnetized ring magnets are aligned with opposite poles facing each other, providing at the specimen a magnetizing field of ~10 mT in the direction along the surface (see Fig. 1a), more than two times larger than required for saturation. Boundary element simulations (CST Studio suite, Dassault Systèmes) show that even with minor angular misalignments of up to 15° or residual sideways displacement of up to 100 µm the effective magnetic field at the sample is largely homogeneous and oriented in-plane.

Laser fluence determination and optical absorption depth

The optical beam radius ω₀ = 150 µm (at an intensity of 1/e²) at the sample position is evaluated by knife-edge measurements. Using the measured average laser power P_avg within the vacuum chamber and the laser repetition rate f_rep, we obtain the excitation fluence via ${F}_{{\rm{peak}}}=\frac{1}{\cos (25^\circ )}\frac{2}{\pi {\omega }_{0}^{2}}\frac{{P}_{{\rm{avg}}}}{{f}_{{\rm{rep}}}}$. The cosine term accounts for the stretching of the horizontal beam profile at 25° laser incidence. The optical absorption of our multilayer specimen as a function of depth is calculated with finite-time-domain difference simulations. We use Bloch boundary conditions and an incidence angle of the light wave of 25°. Extended Data Figure 2c depicts the real and imaginary part of the refractive index of the layer materials (dotted and dashed, respectively) and the obtained electric field amplitude E in reference to the incoming amplitude E₀ (solid line). Extended Data Figure 2d shows the simulated optical absorption density for the parameters of the experiment. We see an almost constant profile throughout all of the nickel layer (green). The simulated reflectivity is ~60% and the transmission is ~10%. More than 95% of the deposited pulse energy goes into nickel and less than 5% into the copper seed layer. Although the silicon substrate does not absorb laser light, it might still heat up a little by hot electron transport, because the difference between the work function of nickel (~5 eV) and the electron affinity of silicon (~4 eV) is comparable to the silicon bandgap (1.1 eV).

Laser pulse compression and frequency-resolved optical gating

In order to reduce the optical pulse duration from our Yb:YAG laser system (270 fs), we apply a series of two self-defocussing bulk media⁵⁶. First, we use an f = 75 mm lens and an 8-mm beta barium borate (BBO) crystal (Döhrer Electrooptic GmbH). The broadened spectrum is compressed with a grating sequence (LSFSG-1000-3212-94, LightSmyth) at a distance of 2.5 mm. Second, we apply an f = 40 mm lens and a 6-mm BBO crystal. The output pulses are compressed with a 12-mm-thick block of high-refractive-index glass (SF10) with a group delay dispersion of ~1,300 fs². Residual radiation at 515 nm wavelength is filtered out by high-reflection mirrors. Frequency-resolved optical gating (FROG) is used to characterize the pulse duration (see Extended Data Fig. 3), revealing a full width at half maximum of 90 fs. A replica of the air/vacuum entrance window in front of the FROG setup ensures a correct consideration of dispersion.

Heat flow and base temperature

For simulating the base temperature of the experiment due to the average power of the pump laser, we use a numerical heat conduction simulation with COMSOL (Comsol Multiphysics GmbH). The relevant layer sequence of the specimen is applied, but we approximate the macroscopic membrane (100 × 100 µm²) in cylindrical coordinates with a radius of r = 60 µm. The top and bottom surfaces of the thin film are assumed to be isolating. A heat sink at room temperature is placed along the edge of the membrane where the thickness becomes macroscopic (0.1 mm) and touches the sample holder. In order to estimate the base temperature of the experiment, we simulate a heat source according to the average laser power of ~35 mW of which ~15 mW are absorbed in a radius of 𝜔₀ ≈ 150 μm. The time-dependence of the heat dissipation is simulated by depositing the energy of a single pulse in the nickel layer with the same beam parameters as above. Extended Data Figure 4a shows the heat map at 20 ps after excitation and Extended Data Fig. 4b shows the resulting long-term radial temperature profile of the membrane. In the centre of the beam, the temperature increases by approximately 60 K, consistent with the results from Bragg spot analysis (see above). Extended Data Figure 4c shows the time evolution of the front surface of the Ni-membrane at r = 0. The resulting heat flow has two time constants, ~20 ps for equilibration of nickel and silicon and ~40 µs for dissipation into the sample holder. The residual heat at 40 µs accumulates over the course of multiple pump pulses (separated by 40 µs) into the quasi-static temperature profile of Extended Data Fig. 4b.

Magneto-optical Faraday effect

Extended Data Figure 5a, b show measurements of the dynamical magnetization M in our single-crystalline thin-films via recording the magneto-optical Faraday effect after laser excitation as a function of time. The pump pulse parameters are made similar to the conditions of the diffraction experiment, including laser repetition rate, incidence angle, wavelength and pulse duration. Fluence is adjusted to slightly below the damage threshold with a similar procedure as in the diffraction experiment. Extended Data Figure 5a shows the measured magnetic hysteresis curves for delay times before zero (black) in comparison to a trace taken 7 ps after laser excitation (blue). We see the expected decrease of amplitude but no change of shape. Extended Data Figure 5b shows an analysis of the time-resolved dynamics. The degree of demagnetization is 40–50%, the dynamics is faster than 0.5 ps and demagnetization persists for tens of picoseconds. All results agree with earlier observations of similar materials at similar excitation fluences^23,68.

Fluence dependence

Extended Data Figure 5c–e shows measurements of the ultrafast phonon dynamics as a function of the applied laser fluence. Extended Data Figure 5c shows the Bragg spot intensity changes of I_{200} after integration of t > 2 ps (see Fig. 2a). Extended Data Fig. 5d shows the measured Bragg spot anisotropy, analysed in the same way as in Fig. 2b and then integrated for t > 2 ps. The last data points in both graphs are the results from Fig. 2a, b. Extended Data Figure 5e shows the results of the molecular dynamics simulations as a function of the degree of demagnetization. Time traces are integrated between 1–2 ps for n = 50. As predicted by the analytical considerations in equation (1), the dependence is linear and the measured fluence data is consistent with this expectation.

Bragg spot positions and crystal expansion

On picosecond time scales, there is not enough time for our specimen crystal to change its lattice constants by volumetric effects. Extended Data Figure 6 shows a measurement of the positions of the eight nickel spots of Fig. 1d as a function of the pump–probe delay time. All Bragg spot position changes stay below 2 × 10^–4 rad. Our nickel crystal therefore remains in all of the investigated time range in its original volume without isotropic or anisotropic deformations.

Direct beam effects

Demagnetization of the nickel membrane could potentially distort the trajectory of the electron beam and thereby produce unwanted diffraction effects. However, calculations of Lorentz forces predict a deflection of less than 5 µrad. In the experiment, we derive an upper limit by measuring electron beam deflections at high precision. We produce by two photoemission laser pulses a sequence of two electron pulses at a time difference of 30 ps. One of these electron pulses always passes through the specimen before the laser excitation and serves as a reference while the other electron pulse is the probe pulse of the experiment. The centre positions of both beams are fitted with pseudo-Voigt functions. Recording the difference between these two centres cancels any potential drifts of the experiment and therefore produces a sensitive upper limit for magnetic beam deflections. Extended Data Figure 7a shows the two electron beams on the screen. Extended Data Figure 7b reveals the Debye–Waller effect in the probe beam (blue) but not in the reference beam (black), as expected. Extended Data Figure 7c shows the differences between the two beam positions on the screen. All deflections remain below 5 µrad; this is more than 10⁴ times smaller than the rocking curve width. Dynamical electron beam effects are therefore not significant for the reported results.

Control experiment on Si and Cu

Extended Data Figure 8 shows an analysis of the Bragg spot anisotropy of the silicon and copper spots with exactly the same procedure as it is used to analyse the nickel data. To perform this experiment, the sample has to be slightly rotated by ~2° to optimize the silicon spots at cost of nickel intensities (compare Extended Data Fig. 2a), but the rest of the experiment is kept identical, including the presence of the permanent magnets, the parameters of the laser and electron pulses, their pulse durations, the repetition rate and the base temperature. Extended Data Figure 8a shows the Debye–Waller effect in the Nickel spots, confirming that the laser excites the material in the same way as in the main experiment. Extended Data Figure 8b shows the Bragg spot anisotropy for the silicon and copper spots, evaluated in the same way as in Fig. 2. Note that silicon and copper layers are on the backside of the specimen and their Bragg spots therefore suffer from a reduced incoming electron flux. There is no significant dynamics or anisotropy within the achievable ratio of signal to noise.

Error analysis of the time constants

Here we report the details of determining the time constants for the Debye–Waller effects (Fig. 2a) and the phonon anisotropy (Fig. 2b) with their uncertainties and error bars. In a first analysis, we calculate the effective Debye–Waller dyamics to be time-fitted by averaging the intensity in the I_{200} and I_{200} spots according to ${y}_{{\rm{DW}}}({\rm{t}})=({I}_{\{220\}}(t)-1)+2({I}_{\{200\}}(t)-1)$. The asymmetry y_asy to be time-fitted is the difference²² between the measured asymmetry data for the magnetic directions ↑M (Fig. 2b, blue) and →M (Fig. 2b, red) according to ${y}_{{\rm{asy}}}({\rm{t}})=\,\frac{1}{2}{(\frac{{I}_{\{200\}}(t)}{{I}_{\{020\}}(t)}-1)}_{\uparrow M}+\,\frac{1}{2}{(1-\frac{{I}_{\{200\}}(t)}{{I}_{\{020\}}(t)})}_{\to M}$, that is, the averaged difference between the blue and red data in Fig. 2b. We fit both resulting time traces y_DW(t) and y_asy(t) individually with an exponential rise function $\hat{y}(t)=a(1-{e}^{-t/\tau }) {\mathcal H} (t)$, where ${\mathcal H}$ is the Heaviside step function. The free parameters are the amplitude a of the long-time anisotropy level and the response time τ of the dynamics. To determine fit values with uncertainties, we use a Monte Carlo analysis⁶⁹ in which we generate and subsequently fit 10⁴ data sets in which normally distributed noise is added to the measured data according to the experimental standard errors of 1 × 10^–3 and 4 × 10^–4 for the Debye–Waller and asymmetry data, respectively. Extended Data Figure 9 depicts the resulting parameter histograms. We find that the asymmetry response time (blue) is 450 ± 300 fs (as a range, 150–750 fs) and the Debye–Waller response time (black) is 770 ± 60 fs, where the uncertainties are taken as the full widths at half maximum of the two raw distributions. The comparably large uncertainty of the asymmetry response time is a consequence of residual correlation with the unknown level of the amplitude (see Extended Data Fig. 9b).

In a second analysis, we fit the blue and the red data points in Fig. 2a individually under adherence to the uncertainty range of the individual data points (see figure caption). With this error propagation, we obtain 635 ± 300 fs and 365 ± 250 fs, respectively. Alternatively, Monte Carlo analysis⁶⁹ with uncertainties taken as the full widths at half maximum provides 625 ± 550 fs and 375 ± 450 fs, respectively. The difference between these individual fit values is not significant and both values submit to the reported overall uncertainty range of 150–750 fs in the main paper.

Additional molecular dynamics simulation results

Finite-size effect and comparison to periodic boundary conditions

As the numerical investigation is limited to finite system sizes, we investigate the influences by testing N = 10, 20, 50 (about 4 × 10³, 3.2 × 10⁴ and 5 × 10⁵ atoms) for open boundary conditions (OBC). Extended Data Fig. 10a depicts the anisotropic contrast ${I}_{\{200\}}/{I}_{\{020\}}$ resulting from our molecular dynamics simulations. All systems show a very rapid decay of the anisotropic contrast in ~50 fs, a time scale that is not in the focus of our investigation because it is shorter than the laser pulses that we do not model explicitly. However, we also find a slower decay on the time scale of some picoseconds, which is not observed in the experimental data (see Fig. 2b). This decay time scales towards a longer-living anisotropy with system size and is therefore a finite-size effect. The dashed lines in Extended Data Fig. 10a show simulation data for systems with periodic boundary conditions (PBC) which avoids surface effects. In such a system, the initial angular momentum L₀ is not conserved but rather relaxes very quickly on a time scale of tens of femtoseconds. Nevertheless, the anisotropy remains substantial and persists even longer than for open boundary conditions. Our interpretation is that the mode coupling—either of transversal and longitudinal modes or of transversal modes along different directions—causes the equilibration, a mechanism that appears less efficient for periodic boundary conditions due to the lack of phonon reflections at the boundaries. For open boundaries, the finite-size scaling follows from the fact that for larger systems surfaces are less important. Note that the contrast in the mean-squared velocities $2{v}_{y}^{2}/({v}_{x}^{2}+{v}_{z}^{2})$ shows a very similar behaviour, see Extended Data Fig. 10b, where the long-time evolution is depicted.

We can rule out a macroscopic Einstein–de Haas rotation as explanation for the observed electron diffraction contrast by comparison with results from a simulated global system rotation in which the total angular momentum L₀ is instantly and completely transferred to a rigid-body rotation. The effect on electron diffraction requires tens of picoseconds to develop, evident from Extended Data Fig. 10b, blue trace. On the time scale of the experiment, rotation effects are therefore negligible. Furthermore, the corresponding angular velocity in the simulation is prone to finite system size with $\omega \propto {N}^{-2}$, which means that it is even less relevant for the large membrane geometries in the experiment. In conclusion, the finite-size effects in our simulations are essentially boundary effects. This result suggests that anisotropic peak intensities in electron diffraction could persist on time scales up to 100 ps.

Temperature dependence

The initial conditions explained above are designed to model the angular momentum transfer from the spins to the lattice. The resulting lattice temperature in our simulation is $\Delta T$ = 15 K, much lower as compared to the experiment. Lattice temperature is not well-defined on short time scales, since equipartition is violated. The temperature presented here is therefore defined via $\frac{3}{2}{k}_{{\rm{B}}}T={v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}$ as a measure for the energy pumped into the system. To test the potential influence of an additional energy transfer from the electronic system to the lattice, we modify the initial conditions of our simulations such that we keep the angular momentum, but additionally impose a higher energy on the lattice by displacing all atoms that have not been excited with angular momentum by some amount in random directions. This can lead to a much higher temperature of, for example, $\Delta T$ = 60 K in Extended Data Fig. 10c. Nevertheless, we determine practically the same anisotropy contrast as compared to the previous case. We conclude that an initial temperature before laser excitation does not affect the anisotropy of our Bragg peaks and the role of the polarized phonons.

Potential anisotropic lattice potentials

Here, we rule out that the observed Bragg spot anisotropy is caused by possible anisotropic changes of the lattice potential along the magnetic direction. Such a bond hardening or bond softening could influence the atomic fluctuations in an anisotropic way. To exclude the significance of such effects, we estimate all possible energy scales that could anisotropically alter the lattice potentials and then show that these are much smaller than the effects we have measured. The thermodynamic potential $G(T,H,{\bf{S}},\varepsilon )$ with temperature T, magnetic field H, magnetization direction ${\bf{S}}=({S}_{1},{S}_{2},{S}_{3})$ and strain tensor ε  contains anisotropic magnetic contributions due to magnetostriction or other magnetic anisotropies⁷⁰. For bulk nickel, the largest contribution to the magnetostriction is given by ${G}_{{\rm{ms}}}\,=\,{B}_{1}({\varepsilon }_{11}{S}_{1}^{2}\,+{\varepsilon }_{22}{S}_{2}^{2}\,+\,{\varepsilon }_{33}{S}_{3}^{2})\,+$ … with the magneto-elastic constant ${B}_{1}\approx 1$ meV per atom⁷¹. Upon complete demagnetization, this anisotropic energy contribution would vanish. The strain ${\varepsilon }_{11}$ for saturated magnetization in (100) direction is given by the magnetostriction coefficient $\lambda \approx 4\times {10}^{-5}$ for crystalline nickel^70,72. The resulting energy change is therefore ${G}_{{\rm{ms}}}={B}_{1}\lambda \approx 4\times {10}^{-5}$ meV per atom. Even for a much larger strain of the order of 1%⁷³, the resulting energy contribution would still be smaller than 10^–2 meV per atom. A second relevant energy scale comes from magneto-crystalline anisotropy. For nickel, the largest contribution is ${K}_{1}\approx -\,{10}^{-2}$ meV per atom⁷⁴. In thin films, there are contributions from surface or interface effects, reaching a level of up to 10^–1 meV per interface atom for strained Ni films; see table 3 in ref. ⁷⁴.

Both energy scales are by several orders of magnitude smaller than the energy required to explain the experimental results. The measured anisotropic contributions to the mean atomic displacement, inferred from the Bragg spots of Fig. 2, require an energy of at least ~4 meV per atom. This value is more than a factor of 100 larger than the maximum energy contributions that can be produced by magnetostriction or magneto-crystalline anisotropies. Such effects are therefore not significant for our results and conclusions.

Gyromagnetic ratio

Literature discusses two kinds of gyromagnetic factors, $g{\prime}$ and g (refs. ^75,76). The former is the gyromechanical factor, the latter is called the spectroscopic splitting factor. Their values are related via $g-2=2-g\mbox{'}$, reflecting the different ways to include or not include orbital angular momentum. For our report, the relevant property is $g\mbox{'}$, the ratio between the magnetic moment (comprising spin and orbital parts) and the angular momentum (also comprising spin and orbital parts). The other one, g ≈ 2.165 for nickel⁷⁷, is relevant for instance in ferromagnetic resonance experiments, where the setup is not susceptible to the orbital part of the angular momentum.

Extended data figures and tables

Extended Data Fig. 1 X-ray characterization of the nickel thin-film structure.

a, X-ray reflectivity data and fit of the sample using a four-layer model with the scattering length density profile shown in the inset. The dashed lines in the inset indicate the slab model of the corresponding layers. The best fit parameters obtained by fitting the XRR intensities are shown in the table. The errors are estimated by a 5% increase over the optimum logarithmic figure of merit. b, Out-of-plane XRD scan in the angular regime of 40° ≤ 2θ ≤60°. The observed intensities at 2θ ≈ 50.53° and 2θ ≈ 52.13° correspond to Cu(002) and Ni(002). The lack of any Cu(111) and Ni(111) intensities shows the epitaxial growth. The inset graph shows the rocking-scans over the Cu(002) and Ni(002) peak positions. c, In-plane XRD scan at an inclination angle Δχ = 54.51°. The intensities at 2θ ≈ 43.41° and 2θ ≈ 44.47° correspond to the Cu(111) and Ni(111) reflections, respectively. d, ϕ scans for the Ni(111), Cu(111) and Si(111) ip peaks, obtained at an inclination angle of Δχ = 54.74°. A clear fourfold symmetry of the Cu(111) and Ni(111) ip reflections is observed with an offset angle of 45° to the Si(111) substrate reflections. For reasons of clarity, the scans are shifted in intensity by a factor of two each. e, ϕ scans for the Cu(111) and Ni(111) reflections, obtained at inclination angles of Δχ = 15.80°, Δχ = 54.74° and Δχ = 79.00°. For clarity, the scans are shifted in intensity by 0.1 each. Cu(111) intensities are shown in the angular regime of 0° ≤ ϕ ≤180°, while the Ni(111) intensities are shown for 180° ≤ ϕ ≤360°.

Extended Data Fig. 2 Rocking curve, magnetic hysteresis and optical penetration depth.

a, Rocking scan data obtained with the femtosecond electron beam. Shown is the Ni(200) peak when rotating the specimen around the [010] axis. b, Magnetic hysteresis curve of our nickel specimen, obtained by an in-plane SQUID measurement. c, Simulated optical energy disposition as a function of penetration depth. Upper panel: solid line, normalized electric field amplitude; dotted line, real part of the refractive index; dashed line, imaginary part of the refractive index. The laser comes from the left. Lower panel: absorption as a function of depth. The green, red, blue and grey areas denote nickel, copper, silicon and NiO_x, respectively.

Extended Data Fig. 3 Second-harmonic-generation FROG measurements of the optical pulses after compression.

a, Measured FROG trace. b, Retrieved FROG trace at 0.3% FROG error. c, Evaluated spectrum (blue) and spectral phase (green). d, Retrieved pulse shape (blue) with temporal phase (green). The pulse duration is 93 fs.

Extended Data Fig. 4 Numerical simulation of heat flow.

a, Temperature profile at 20 ps after laser excitation. Drawing is not to scale. b, Radial profile of the temperature increase ΔT due to quasi-static heat accumulation. c, Cooling dynamics of the front surface at r = 0.

Extended Data Fig. 5 Magneto-optical Faraday effect and fluence dependency of the electron diffraction results.

a, Magnetic hysteresis curves for a negative (black) and slightly positive pump–probe delay (blue). b, Magnetization as a function of delay time. c, Debye–Waller effect as a function of the applied laser excitation fluence. d, Bragg spot anisotropy as a function of the applied laser excitation fluence. e, Simulated anisotropy as function of the degree of demagnetization.

Extended Data Fig. 6 Changes of Bragg spots angles as a function of pump–probe delay.

Dots, changes Δα_x along the x axis; squares, changes Δα_y along the y axis (see Fig. 1d).

Extended Data Fig. 7 Absence of beam deflection effects.

a, Two time-delayed electron beams on the screen. b, Intensity changes in the reference pulse (black) and probe pulse (blue), showing a Debye–Waller effect in the probe beam only. c, Differences of the beam positions before and after laser excitation as a function of the pump–probe delay, converted to angle changes at the specimen. All changes remain below 5 µrad.

Extended Data Fig. 8 Control experiment.

Analysis of the anisotropy of the silicon and copper spots as function of the pump–probe delay. a, isotropic Debye–Waller effect of Ni. b, Anisotropy of Si and Cu as a function of time.

Extended Data Fig. 9 Monte Carlo analysis of the time constants.

a, Distribution of the fitted response times for the Bragg spot asymmetry (blue) and the Debye–Waller effect (black). b, Correlation plot of the asymmetry fit parameters.

Extended Data Fig. 10 Additional molecular dynamics simulations results.

a, Finite-size effects of the anisotropy of crystallographically equivalent peaks comparing open boundary conditions (OBC) with periodic ones (PBC). For OBC a finite-size effect is observed: the relaxation time of the contrast increases with system size. PBC do not show this effect. b, Long-time evolution for N = 50 testing the three cases (OBC, PBC, and global rotation according to the Einstein–de Hass effect (EdH)) (blue, solid lines). Also shown is the anisotropy of the mean-squared velocities $2{v}_{y}^{2}/({v}_{x}^{2}+{v}_{z}^{2})$ (green, dotted lines). c, Temperature dependence; anisotropy of crystallographically equivalent peaks for the same angular momentum L₀ (same demagnetization) but different energy transfers to the lattice, leading to a temperature increase of ΔT = 15 K and 60 K, respectively.