Gate-tunable room-temperature ferromagnetism in two-dimensional Fe₃GeTe₂

Abstract

Materials research has driven the development of modern nano-electronic devices. In particular, research in magnetic thin films has revolutionized the development of spintronic devices^1,2 because identifying new magnetic materials is key to better device performance and design. Van der Waals crystals retain their chemical stability and structural integrity down to the monolayer and, being atomically thin, are readily tuned by various kinds of gate modulation^3,4. Recent experiments have demonstrated that it is possible to obtain two-dimensional ferromagnetic order in insulating Cr₂Ge₂Te₆ (ref. ⁵) and CrI₃ (ref. ⁶) at low temperatures. Here we develop a device fabrication technique and isolate monolayers from the layered metallic magnet Fe₃GeTe₂ to study magnetotransport. We find that the itinerant ferromagnetism persists in Fe₃GeTe₂ down to the monolayer with an out-of-plane magnetocrystalline anisotropy. The ferromagnetic transition temperature, T_c, is suppressed relative to the bulk T_c of 205 kelvin in pristine Fe₃GeTe₂ thin flakes. An ionic gate, however, raises T_c to room temperature, much higher than the bulk T_c. The gate-tunable room-temperature ferromagnetism in two-dimensional Fe₃GeTe₂ opens up opportunities for potential voltage-controlled magnetoelectronics^7,8,9,10,11 based on atomically thin van der Waals crystals.

Main

Atomically thin, layered van der Waals crystals represent ideal two-dimensional (2D) material systems with exceptional electronic structures. Vast opportunities in 2D material research arise from (1) emerging physical properties as a result of reduced dimensionality, and (2) new gating capabilities to modulate the material properties now that the entire crystal is a surface. The former underpins the rapid permeation of 2D materials in areas ranging from semiconductors to highly correlated materials and superconductors. The trend continues with the recent addition of magnetic crystals in the 2D material family^5,6. In particular, ferromagnetic order has been observed in monolayer CrI₃ in the form of a 2D Ising ferromagnet⁶. The intrinsic ferromagnetism in these 2D materials is unlike the ferromagnetism in conventional, molecular-beam-epitaxy-grown ultrathin metals^12,13, which is determined by the interface with the substrate. This suggests device concepts based on magnetic van der Waals heterostructures^14,15,16.

Here we report the discovery of 2D itinerant ferromagnetism in atomically thin Fe₃GeTe₂ (FGT). As in the case of CrI₃, intrinsic magnetocrystalline anisotropy in FGT monolayers counteracts thermal fluctuations and preserves the 2D long-range ferromagnetic order, which is otherwise precluded in an isotropic magnetic system according to the Mermin–Wagner theorem¹⁷. FGT, however, offers a critical advantage: its metallic nature enables the interplay of both spin and charge degrees of freedom that lies at the heart of various spintronic architectures¹⁸. In this study we focus on the large anomalous Hall effect resulting from such interplay. The anomalous Hall effect enables us to extract the ferromagnetic transition temperature T_c, and elucidate the evolution of the magnetic order from bulk down to monolayer FGT. Taking advantage of the tunability of atomically thin crystals, we further show that extreme doping induced by an ionic gate dramatically elevates T_c to room temperature, accompanied by large modulations in the coercivity. These results establish FGT as a room-temperature ferromagnetic 2D material in addition to VSe₂ (ref. ¹⁹), and the gate tunability makes FGT potentially suitable for electrically controlled magnetoelectronic devices.

Various metallic layered compounds exhibit magnetism²⁰. Among them FGT stands out with a relatively high T_c (ranging from 150 K to 220 K depending on Fe occupancy^21,22,23,24). In each FGT monolayer, covalently bonded Fe₃Ge heterometallic slab is sandwiched between two Te layers (Fig. 1b). The structure and valence states of the compound can be written as (Te²⁻)(Fe_I³⁺)[(Fe_II²⁺)(Ge⁴⁻)](Fe_I³⁺)(Te²⁻) per formula unit with two inequivalent Fe sites, Fe_I³⁺ and Fe_II²⁺, within the Fe₃Ge slab²². Partially filled Fe d orbitals dominate the band structure around the Fermi level, and give rise to itinerant ferromagnetism in bulk FGT²⁵. Adjacent monolayers are separated by a 2.95 Å van der Waals gap in the bulk crystal. As a result of the reduced crystal symmetry of the layered structure, bulk FGT exhibits a strong magnetocrystalline anisotropy²⁵. Such anisotropy is expected to stabilize the long-range ferromagnetic order in FGT monolayers.

Fig. 1: Fabrication and characterization of atomically thin FGT devices.

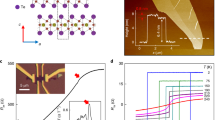
a, Schematic of our Al₂O₃-assisted mechanical exfoliation method. The method uses an Al₂O₃ film evaporated onto the bulk crystal to cleave layered materials. The strong adhesion between the crystal and the Al₂O₃ film makes it possible to exfoliate layered crystals that are otherwise difficult to cleave from SiO₂ surfaces using conventional methods. b, Atomic structure of monolayer FGT. The left panel shows the view along [001]; the right panel shows the view along [010]. Bulk FGT is a layered crystal with an interlayer van der Waals gap of 2.95 Å (ref. ²²). Fe_I and Fe_II represent the two inequivalent Fe sites in the +3 and +2 oxidation states, respectively. c, Optical image of typical few-layer FGT flakes exfoliated on top of an Al₂O₃ thin film. The Al₂O₃ film is supported on an Si wafer covered with 285-nm SiO₂. d, Atomic force microscopy image of the area marked by the square in c. Mono- and few-layer flakes of FGT are clearly visible. Scale bar, 2 μm. e, Cross-sectional profile of the FGT flakes along the white line in d. The steps are 0.8 nm in height, consistent with the thickness of monolayer (1L) FGT (0.8 nm). f, Temperature-dependent sample resistance of FGT with varying number of layers up to 6L. Resistances are normalized by their values at T = 240 K. The typical behaviour of bulk FGT (brown) is also shown for reference.

Experimentally isolating atomically thin FGT crystals from the bulk, however, poses a challenge. Although bulk FGT cleaves along the van der Waals gap, the intralayer bonding is not strong enough for thin flakes of reasonable size (about 5 μm) to survive conventional mechanical exfoliation processes. Similar issues plague the exfoliation of many other layered materials (only a small fraction of known layered crystals is cleavable down to monolayers), and have largely impeded the research on 2D materials in general.

To address this problem, we developed an Al₂O₃-assisted exfoliation method that enables isolation of monolayers from bulk layered crystals that are otherwise difficult to exfoliate using conventional methods. Our method was inspired by the gold-mediated exfoliation of layered transition-metal chalcogenide compounds^26,27. The fabrication process is illustrated step by step in Fig. 1a. We started by covering the freshly cleaved surface of the bulk crystal with Al₂O₃ thin film with thicknesses ranging from 50 nm to 200 nm. The film was deposited by thermally evaporating Al under an oxygen partial pressure of 10⁻⁴ mbar. We then used a thermal release tape to pick up the Al₂O₃ film, along with pieces of FGT microcrystals separated from the bulk. The Al₂O₃/FGT stack was subsequently released onto a piece of polydimethylsiloxane (PDMS) upon heating, with the FGT side in contact with the PDMS surface. Next, we stamped the PDMS/FGT/Al₂O₃ assembly onto a substrate and quickly peeled away the PDMS, leaving the Al₂O₃ film covered with freshly cleaved FGT flakes on the substrate. Figure 1c displays an optical image of atomically thin FGT flakes on Al₂O₃ film supported on a 285-nm SiO₂/Si substrate. Mono- to trilayer regions of FGT are clearly resolved by the optical contrast. The layer identification was corroborated by direct topography measurements with an atomic force microscope; the 0.8-nm steps in the height profile exactly match the FGT monolayer thickness (Fig. 1d, e). We then fabricated electrodes on FGT thin flakes, either with direct metal deposition through stencil masks or with indium cold welding, for subsequent transport measurements. The entire device fabrication process was performed in an argon atmosphere with O₂ and H₂O content kept below 0.5 parts per million to avoid sample degradation. Details of the sample exfoliation and electrode fabrication are presented in the Methods. Finally, we point out that even though we focus only on FGT in this study, the method should be applicable to a wide variety of van der Waals crystals. We attribute the drastically enhanced exfoliation capability to higher affinity, as well as increased contact area, between the evaporated Al₂O₃ film and the freshly cleaved FGT surface.

We study the magnetism in FGT by probing the Hall resistance, R_xy, under an external magnetic field, μ₀H, applied perpendicular to the van der Waals plane. In our samples, which typically have a van der Pauw configuration, the fact that R_xy is antisymmetric with respect to the polarity of μ₀H, whereas magnetoresistance is symmetric, enables us to use a standard symmetrization procedure²⁸ to separate the contribution of magnetoresistance from the raw Hall voltage data. For a magnetic material, R_xy can be decomposed into two parts:

$${R}_{xy}={R}_{{\rm{NH}}}+{R}_{{\rm{AH}}}$$

(1)

where ${R}_{{\rm{NH}}}={R}_{0}{\mu }_{0}H$ is the normal Hall resistance, and ${R}_{{\rm{AH}}}={R}_{{\rm{S}}}M$ the anomalous Hall resistance; R₀ and R_S are coefficients characterizing the strength of R_NH and R_AH, respectively, and M is the magnetization. Crucial information on the long-range magnetic order, which is contained in M, can therefore be extracted from the anomalous Hall resistance.

As the layer number is reduced in FGT flakes, the samples become progressively more insulating (Fig. 1f), but ferromagnetism persists down to the monolayer. Unambiguous evidence comes from the clear hysteresis in R_xy for all FGT thin flakes (with thickness ranging from monolayer to 50 layers; Fig. 2a) under investigation at low temperatures. Such hysteresis reflects the hysteresis in M; the remanent M at μ₀H = 0 signifies spontaneous magnetization, and thus the long-range ferromagnetic order. Raising the temperature introduces thermal fluctuations, and ferromagnetism eventually disappears above T_c. In Fig. 2b, measurements of R_xy show that ferromagnetism in samples with various layer numbers responds differently to thermal fluctuations: at an elevated temperature of T = 100 K hysteresis vanishes in mono- and bilayer samples, but survives in thicker crystals. The observation clearly indicates a strong dimensionality effect on ferromagnetism in atomically thin FGT.

Fig. 2: Ferromagnetism in atomically thin FGT.

a, b, R_xy at low temperature (a) and at T = 100 K (b) obtained in FGT thin-flake samples with varying numbers of layers. Ferromagnetism, evidenced by the hysteresis in low-temperature R_xy, is observed in all atomically thin FGT down to the monolayer. At T = 100 K, hysteresis disappears in mono- and bilayer FGT, but persists in thicker specimens. All the low-temperature data were obtained at T = 1.5 K except for the monolayer data, which were recorded at T = 3 K. c, Remanent anomalous Hall resistance ${R}_{xy}^{{\rm{r}}}$ as a function of temperature obtained from FGT thin-flake samples with varying numbers of layers. ${R}_{xy}^{{\rm{r}}}$ data are normalized by their values at T = 1.5 K, except for the monolayer dataset, which is normalized by the value at T = 3 K. Arrows mark the ferromagnetic transition temperature T_c. Vertical error bars represent the standard deviation of ${R}_{xy}^{{\rm{r}}}$ values within 1 mT of zero magnetic field; 1 mT is the uncertainty in reading the magnetic field during field sweeps. d, Phase diagram of FGT as layer number and temperature are varied. T_c values determined from anomalous Hall effect, Arrott plots and RMCD are displayed in blue, red and magenta, respectively. Filled red and blue squares represent data obtained from samples with thermally evaporated Cr/Au electrodes, and open squares represent data obtained from samples with cold-welded indium microelectrodes. The black line is a fit to T_c(N) (for N ≥ 3) with the finite-size scaling formula and the red line is a line fit to T_c(N) for N ≤ 3 (see Methods for scaling analysis). Blue and pink regions mark the ferromagnetic and paramagnetic phases, respectively. The green region in between represents a ferromagnetically ordered phase with domains (see text). Horizontal error bars represent uncertainties in determining the sample thickness from optical contrast or atomic force microscope measurements. Vertical error bars represent uncertainties in locating the onset of non-zero ${R}_{xy}^{{\rm{r}}}$ (in c) or the RMCD signal (in Extended Data Fig. 4f).

To fully elucidate such a dimensionality effect, we precisely determine T_c as a function of layer number from the temperature dependence of the anomalous Hall effect. For each sample thickness, we examine the remanent Hall resistance at zero external magnetic field, ${R}_{xy}^{{\rm{r}}}\equiv {R}_{{xy}}{| }_{{\mu }_{0}H=0}$ , as a function of temperature. According to equation (1), ${R}_{xy}^{{\rm{r}}}$ is directly proportional to the zero-field spontaneous magnetization $M{| }_{{\mu }_{0}H=0}$. So the onset of non-zero ${R}_{xy}^{{\rm{r}}}$ indicates the emergence of spontaneous magnetization. The temperature at the onset of non-zero ${R}_{xy}^{{\rm{r}}}$ therefore marks T_c (Fig. 2c)²⁸. Analyses of various sample thicknesses reveals that T_c decreases monotonically as the samples are thinned down, from about 180 K in the bulk limit to 20 K in a monolayer (Fig. 2d). The one-order-of-magnitude decrease in T_c implies a dramatic reduction in the energy scale of magnetic ordering in 2D FGT. Meanwhile, we also used polar refractive magnetic circular dichroism (RMCD) microscopy to measure layer-dependent T_c (Fig. 2d). We found that T_c values from RMCD measurements are consistently higher than those from anomalous Hall effect measurements. Because the anomalous Hall effect probes ferromagnetic ordering in the whole sample (with a typical size of about 100 μm) and RMCD detects local ordering (with a laser beam spot of about 2 μm), the large discrepancy signifies the existence of domains well above the T_c from measurements of the anomalous Hall effect. Analysis of Arrott plots (see Methods for details) provides further insights into the domain structure. The plots determine T_c by extrapolating high-field data, where domains are fully aligned. T_c values from Arrott plots agree well with those from RMCD measurements, which implies that the domain size is of the same order of the beam spot size in our RMCD measurements, that is, about 2 μm.

The strong dimensionality effect on the ferromagnetism in FGT stems from the fundamental role of thermal fluctuation in 2D. The itinerant ferromagnetism in FGT is, in principle, described by the Stoner model^22,25. It has, however, been established that such itinerant ferromagnetism can be mapped on to a classical Heisenberg model with Ruderman–Kittel–Kasuya–Yosida (RKKY) exchange²⁹. Armed with this insight, we adopt the following anisotropic Heisenberg Hamiltonian:

$$H=\sum _{i,j}{J}_{ij}{{\boldsymbol{S}}}_{i}\cdot {{\boldsymbol{S}}}_{j}+\sum _{i}A{\left({S}_{i}^{z}\right)}^{2}$$

(2)

where ${{\boldsymbol{S}}}_{i}$ is the spin operator on site i, and J_ij is the exchange coupling between spins on site i and j; A is the single-ion perpendicular magnetocrystalline anisotropy arising from spin–orbital coupling. In the three-dimensional (3D) limit, the density of states per spin for the magnon modes is strongly suppressed, so thermal fluctuations destroy the long-range magnetic order only at a finite T_c determined primarily by exchange interactions J_ij (ref. ⁵). The bulk T_c of approximately 200 K implies that the energy scale of J_ij (summed over nearest neighbours) in FGT is of the order of 10 meV. In monolayer FGT, however, the largely isotropic exchange couplings J_ij (see Methods for detailed ab initio calculations) alone will not be able to sustain magnetic order at finite temperatures because of thermal fluctuations of the long-wavelength gapless magnon modes in 2D. In this case, the magnetocrystalline anisotropy A gives rise to an energy gap in the magnon dispersion. The gap suppresses low-frequency, long-wavelength magnon excitations, and protects the magnetic order below a finite T_c determined primarily by A. A monolayer T_c up to 68 K (from RMCD measurement) implies an A value of the order of 2.0 meV. The estimations of both exchange interactions and magnetocrystalline anisotropy fall in the range predicted by ab initio calculations²⁵,³⁰ (see also Methods). The magnetocrystalline anisotropy corresponds to a uniaxial energy density parameter K_u on the order of 10⁶ J m⁻³. The estimated K_u is consistent with the value measured in bulk FGT³¹, and is one order of magnitude larger than the perpendicular anisotropy energy density in a 1.3-nm-thick CoFeB film³². The large intrinsic perpendicular anisotropy will be important to enable the realization of stable, compact spintronic devices.

Even though T_c is suppressed in atomically thin FGT, we now demonstrate that an ionic gate could drastically modulate the ferromagnetism in FGT thin flakes, and boost T_c up to room temperature. We employ an ionic field-effect transistor setup, in which solid electrolyte (LiClO₄ dissolved in polyethylene oxide matrix) covers both the FGT thin flake and a side gate⁴ (inset to Fig. 3a). A positive gate voltage, V_g, intercalates lithium ions into the FGT thin flake, much like the charging process in a lithium-ion battery. The charge transfer between lithium ions and the host crystal induces electron doping up to the order of 10¹⁴ cm⁻² per layer⁴. The high doping level effects a profound change in the ferromagnetism in the FGT thin flake. Figure 3b, c displays the R_xy of a trilayer sample obtained at T = 10 K and T = 240 K, respectively. A moderate V_g of a few volts induces large variations in the coercivity of the ferromagnetic FGT, and the ferromagnetism, manifested as a finite ${R}_{xy}^{{\rm{r}}}$, persists at high temperatures under certain gate doping. Indeed, detailed analysis reveals that T_c is strongly modulated by the ionic gate, with the highest T_c reaching room temperature (T = 300 K; Fig. 3d). The gate-induced room-temperature ferromagnetism is also directly observed in a four-layer sample as shown in Fig. 4. (The room-temperature remanence is low, but this may be improved by, for example, interfacing the sample with an antiferromagnetic insulator.) T_c as a function of the gate voltage exhibits a complex pattern: after an initial drop, T_c increases sharply to room temperature at V_g = 1.75 V. T_c peaks again at V_g = 2.39 V on top of an otherwise slowly declining trend as the doping level increases (Fig. 3d; see Methods for details). The variation in T_c is accompanied by changes in the sample conductance, σ_xx, obtained at T = 330 K (Fig. 3a). In particular, the two peaks in T_c coincide with sudden increases in σ_xx, suggesting changes in the electronic structure as the origin of the magnetism modulation. Finally, we note that the coercivity measured at T = 10 K also roughly follows the variations in T_c, as shown in Fig. 3e.

Fig. 3: Ferromagnetism in an atomically thin FGT flake modulated by an ionic gate.

a, Conductance as a function of gate voltage V_g measured in a trilayer FGT device. Data were obtained at T = 330 K. Breaks in the curve were caused by temperature-dependent measurements at fixed gate voltages during the gate sweep. The inset shows a schematic of the FGT device structure and measurement setup. S and D label the source and drain electrodes, respectively, and V₁, V₂, V₃ and V₄ label the voltage probes. The solid electrolyte (LiClO₄ dissolved in polyethylene oxide matrix) covers both the FGT flake and the side gate. b, c, R_xy as a function of external magnetic field recorded at representative gate voltages, obtained at T = 10 K (b) and T = 240 K (c). d, Phase diagram of the trilayer FGT sample as the gate voltage and temperature are varied. We determine the transition temperature from temperature-dependent anomalous Hall resistance extrapolating to zero (see Methods and Extended Data Fig. 7a). Vertical error bars represent the uncertainties in determining the onset of non-zero ${R}_{xy}^{{\rm{r}}}$ in Extended Data Fig. 7a. e, Coercive field as a function of the gate voltage. Data were obtained at T = 10 K.

Fig. 4: Direct observation of room-temperature ferromagnetism in atomically thin FGT.

a, R_xy of a four-layer FGT flake under a gate voltage of V_g = 2.1 V. We have subtracted a background in R_xy resulting from the slow drifting of lithium ions in the electrolyte under the gate bias above T = 250 K (ref. ³³). Hysteresis in R_xy persists up to T = 310 K, providing unambiguous evidence for room-temperature ferromagnetism in the sample. b, Remanent Hall resistance ${R}_{xy}^{{\rm{r}}}$ as a function of temperature. Extrapolating ${R}_{xy}^{{\rm{r}}}$ to zero yields a T_c higher than 310 K. Error bars for ${R}_{xy}^{{\rm{r}}}$ are obtained as in Fig. 2c.

The gate-tuned ferromagnetism in atomically thin FGT is consistent with the Stoner model, which describes itinerant magnetic systems. The Stoner criterion implies that the formation of ferromagnetic order is dictated by the density of states (DOS) at the Fermi level. The extreme electron doping induced by the ionic gate causes a substantial shift of the electronic bands of FGT. Consequently, the large variation in the DOS at the Fermi level leads to appreciable modulation in the ferromagnetism. Detailed calculations support such a picture. Specifically, our calculation shows that gate-induced electrons sequentially fill the sub-bands originating from the Fe ${d}_{{z}^{2}}$, ${d}_{xz}$ and ${d}_{yz}$ orbitals, leading to sharp peaks in the DOS that correspond to the Fermi level passing through the flat band edges of the sub-bands (see Methods and Extended Data Fig. 10a). Such DOS peaks may be responsible for the sharp increase of T_c and the corresponding sudden jump in σ_xx. Meanwhile, calculations indicate that change in the average magnet moment per Fe atom is minimal (less than 3%) under charge doping (see Methods and Extended Data Fig. 10b). This result suggests that the gate-tuned coercivity shown in Fig. 3e may in fact reflect the large modulation in the anisotropy energy, although we cannot rule out effects from domain nucleation that complicates the correlation between coercivity and anisotropy.

Methods

Growth and characterization of bulk FGT crystal

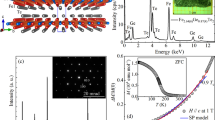
High-quality FGT single crystals were grown by the chemical vapour transport method. High-purity elements were stoichiometrically mixed and sealed under vacuum in a quartz tube with a small quantity of iodine (5 mg cm⁻³). The tube was placed into a two-zone horizontal furnace with the hot end at 750 °C and the cold end at 650 °C. Shining plate-like single crystals with typical dimensions of 3 mm × 3 mm × 0.25 mm were then obtained. The phase purity of the sample was examined by a powder X-ray diffractometer (SmartLab-9, Rigaku Corp.) with Cu Kα radiation, and result is shown in Extended Data Fig. 1a. The magnetization was measured by a SQUID magnetometer (Quantum Design MPMS-5), and the result is shown in Extended Data Fig. 1b.

Fabrication of FGT thin-flake devices

We used two kinds of substrates for FGT exfoliation: 285-nm SiO₂/Si wafer and sapphire. For thin flakes on 285-nm SiO₂/Si wafers (Fig. 1c), we determined the layer number of the flakes with an atomic force microscope, and correlated the topography image with optical contrast. Here the optical contrast is defined as $\left({G}_{{\rm{sample}}}^{{\rm{R}}}-{G}_{{\rm{substrate}}}^{{\rm{R}}}\right)/{G}_{{\rm{substrate}}}^{{\rm{R}}}$, where ${G}_{{\rm{sample}}}^{{\rm{R}}}$ and ${G}_{{\rm{substrate}}}^{{\rm{R}}}$ are intensity of the reflection (R) on sample and substrate, respectively, in the green channel of the optical image captured with a charge-coupled device (CCD) camera. Excellent correlation between the height profile and the optical contrast has enabled us to determine unambiguously the layer number of exfoliated thin flakes. However, because optical contrast in the reflection is very sensitive to the thickness of the Al₂O₃ film as a result of optical interference, the optical contrast needs to be calibrated with atomic force microscopy measurement individually for every batch of samples. Such calibration processes usually take a long time. For this reason, we also used sapphire substrates, and determined the layer numbers by optical transmission, which is not sensitive to the Al₂O₃ film thickness. The optical transmission is now defined as ${G}_{{\rm{sample}}}^{{\rm{T}}}/{G}_{{\rm{substrate}}}^{{\rm{T}}}$, where ${G}_{{\rm{sample}}}^{{\rm{T}}}$ and ${G}_{{\rm{substrate}}}^{{\rm{T}}}$ are the intensities of the transmission (T) through the sample and substrate, respectively, in the green channel of the image captured with a CCD camera. Extended Data Fig. 2a–c illustrates the layer number determination on sapphire substrate. The layer-number-dependent optical transmission is well described by the Beer–Lambert law (Extended Data Fig. 2c), which enables us to determine the layer number quickly and reliably.

We employed two methods to fabricate electrical contacts to FGT thin flakes: (1) direct metal deposition through stencil mask and (2) indium cold welding. We find that direct metal deposition works well for samples with thicknesses larger than two layers, but it tends to degrade the sample quality for thinner samples. We therefore used the cold welding method to fabricate indium microelectrodes on the thinnest flakes. Indium thin foil was first cut into small stripes. A PDMS stamp was then used to hold these stripes, with which we align the FGT thin flake under an optical microscope. We then pressed the indium stripes onto the sample to form electrical contacts, before lifting off the PDMS stamp. The cold welding method works well for FGT thin flakes as small as 20 μm. Extended Data Fig. 2f displays a monolayer device with microelectrodes made by cold welding. A trilayer device made by direct metal deposition is shown in Extended Data Fig. 2i for comparison.

Determining T _c by Arrott plots and polar RMCD microscopy

In the main text, the T_c values for FGT thin-flake devices were obtained from the temperature-dependent anomalous Hall effect. Here we use Arrott plots³⁴ to independently determine T_c. Following a previously described method³⁵, we replot the Hall data (such as those shown in Extended Data Fig. 3a–c) in plots of ${R}_{xy}^{2}$ as a function of ${\mu }_{0}H/{R}_{xy}$, that is, Arrott plots. Extrapolation of the high-field linear part of the Arrott plots intercepts the ${R}_{xy}^{2}$ axis at values denoted as ${\left({R}_{xy}^{{\rm{s}}}\right)}^{2}$, where ${R}_{xy}^{{\rm{s}}}$ refers to spontaneous Hall resistance. Positive intercepts indicate a ferromagnetic state, and T_c is the temperature where ${R}_{xy}^{{\rm{s}}}$ vanishes³⁵. As an example, we show the Arrott plots of a bilayer FGT sample in Extended Data Fig. 3d. The T_c values of the bilayer and other thin-flake samples are determined from points where ${R}_{xy}^{{\rm{s}}}$ as a function of T approaches zero (Extended Data Fig. 3e), and the results are summarized in Fig. 2d. We note that T_c values for monolayer samples cannot be extracted from Arrott plots, because the samples are very insulating, and the large normal Hall contribution in R_xy prevents a reliable determination of T_c.

We also used RMCD microscopy to determine the T_c of FGT thin flakes. The same fabrication technique as shown in Fig. 1a was used to make thin-flake samples for the RMCD measurements. At each fixed temperature, we recorded the RMCD signal on each uniform region of the few-layer sample shown in Extended Data Fig. 4a as the magnetic field was swept. (We used a 633 nm HeNe laser with a spot size of about 2 μm to obtain the RMCD signal.) The data are displayed in Extended Data Fig. 4b–e. Clear hysteresis loops in RMCD signal are observed at low temperatures. We extracted the remanent RMCD signal at μ₀H = 0 from each dataset in Extended Data Fig. 4b–e, and plotted the results in Extended Data Fig. 4f. The T_c of FGT flakes with varying number of layers is determined by the temperature where the remanent RMCD signal vanishes.

Figure 2d summarizes the T_c obtained from anomalous Hall measurements, Arrott plot analysis and RMCD measurements. Although the T_c from Arrott plot analysis and RMCD measurements agree with each other, they are consistently higher than that determined from anomalous Hall effect measurements. The discrepancy is as large as about 50 K in few-layer FGT. As discussed in the main text, the large discrepancy signifies the existence of micrometre-sized domains above the T_c obtained from anomalous Hall effect measurements. We note that a similar thickness-dependent domain effect was also observed in the charge density wave ordering in 1T-TaS₂ thin flakes. The charge density wave phase transition was observed in optical³⁶ and transmission electron microscopy measurements³⁷, but not detected in transport measurement³⁷.

Scaling analysis of layer-dependent T _c in FGT thin flakes

The evolution from 3D to 2D magnetism in FGT is linked with the critical behaviour at the paramagnet to ferromagnet phase transition. Because T_c is the critical temperature where spin-spin correlation length diverges, a finite sample thickness limits the divergence of the correlation length, and therefore depresses T_c. Analyses of the critical behaviour in large area magnetic thin films^38,39,40 show that layer-number-dependent T_c(N) follows a universal scaling law as the sample thickness approaches the 2D limit: $\left[{T}_{{\rm{c}}}\left(\infty \right)-{T}_{{\rm{c}}}\left(N\right)\right]/{T}_{{\rm{c}}}\left(\infty \right)={\left(\left({N}_{0}+1\right)/2N\right)}^{\lambda }$  , where T_c(∞) denotes T_c of the bulk crystal. The critical exponent $\lambda =1/\nu$ reflects the universality class of the transition; N₀ is the critical layer number defined by the mean spin–spin interaction range. Analyses^40,41,42,43 also reveal that the power law is replaced by a linear relation when the film is thinner than the critical value, that is, $N\le {N}_{0}$. N₀, therefore, marks the boundary that separates 2D magnetism and 3D magnetism in ultrathin ferromagnets. The scaling law fits well to the T_c(N) measured in FGT as shown in Extended Data Fig. 5 (here we fitted the highest T_c determined by ${R}_{xy}^{{\rm{r}}}$ for each sample thickness). The fit yields a critical layer number of ${N}_{0}=3.2\pm 0.6$ and a critical exponent of $\lambda =2.3\pm 0.8$. We also confirmed that the linear relation well describes our data in the thinnest samples ($N\le 3$; see Extended Data Fig. 5). We note that N₀ obtained in FGT is comparable to that in the magnetic thin films^12,40,43. Meanwhile, λ is consistent with values expected from mean field model (λ = 2), 3D Ising model (λ = 1.587), or 3D Heisenberg model (λ = 1.414); more accurate determination of T_c is required to resolve the universality class of bulk FGT.

Magnetic anisotropy of atomically thin FGT devices

We investigate the magnetic anisotropy of a four-layer FGT flake with angle-dependent anomalous Hall measurements. When a perpendicular magnetic field is applied (θ_H = 90°; θ_H is the tilt angle between the magnetic field and basal plane of the sample), the square hysteresis loop indicates an out-of-plane magnetic anisotropy. A large in-plane field (μ₀H > 2.6 T; θ_H ≈ 0°) forces the magnetization to the in-plane direction; R_xy vanishes because it is proportional only to the out-of-plane component of the magnetization (Extended Data Fig. 6a). As the in-plane magnetic field decreases, however, R_xy acquires a finite value, implying that the magnetization is tilted towards the out-of-plane direction. The fact that the remanent Hall resistance ${R}_{xy}^{{\rm{r}}}$ at θ_H ≈ 0° does not reach the value at θ_H = 90° suggests the existence of domains in this four-layer FGT sample.

To eliminate the effect of domains, we analyse the angle-dependent anomalous Hall effect at a high magnetic field of μ₀H = 3 T. The high field aligns the domains at all tilt angles (Extended Data Fig. 6a), so the whole sample is effectively a single domain. We extracted the R_xy value at μ₀H = 3 T at various tilt angles, and calculated the angle between magnetization and the basal plane, θ_M, as a function of θ_H, using the formula:

$${\theta }_{M}\left({\theta }_{H}\right)={\rm{\arcsin }}\left(\frac{{R}_{xy}\left({\theta }_{H}\right)}{{R}_{xy}\left({\theta }_{H}=9{0}^{\circ }\right)}\right)$$

(3)

Extended Data Fig. 6c displays θ_M as a function of θ_H. The fact that θ_M is always larger than θ_H implies that the magnetization always tends to point to the out-of-plane direction regardless of the direction of the external magnetic field. This result indicates a strong out-of-plane magnetic anisotropy in the four-layer FGT.

The out-of-plane magnetic anisotropy is corroborated by angle-dependent R_xy measurements near T_c. Here we applied external fields at θ_H = 20° and θ_H = 90° at 150 K (around 5 K above the T_c determined by anomalous Hall measurements in the same sample). We observed that for magnetic fields tilted to a nearly in-plane direction (θ_H = 20°), R_xy decreases with the field strength in the high field regime (μ₀H > 1 T), in contrast to the upward trend in R_xy as the magnetic field is applied perpendicularly (θ_H = 90°; Extended Data Fig. 6b). Because the anomalous component of R_xy is proportional only to the out-of-plane magnetization, our observation implies that the magnetization is pinned in the out-of-plane direction at small magnetic fields, and is pulled towards the in-plane direction only in the high field regime.

Finally, we extract an estimation of the magnetic anisotropy energy density by fitting the data shown in Extended Data Fig. 6c with the Stoner–Wohlfarth model⁴⁴. The total energy of the system is:

$$E={K}_{{\rm{u}}}{sin}^{2}\left({\theta }_{M}\right)-{\mu }_{0}H{M}_{{\rm{s}}}{\rm{\cos }}\left({\theta }_{H}-{\theta }_{M}\right)$$

(4)

where K_u is the magnetic anisotropy energy density, and M_s is the saturation magnetization per volume. At equilibrium:

$$\frac{\partial E}{\partial {\theta }_{M}}=2{K}_{{\rm{u}}}sin\left({\theta }_{M}\right)cos\left({\theta }_{M}\right)+{\mu }_{0}H{M}_{{\rm{s}}}sin\left({\theta }_{H}-{\theta }_{M}\right)=0$$

(5)

The above equation determines the relation between θ_M and θ_H, which we used to fit the experimental data shown in Extended Data Fig. 6c (solid line). Assuming a value for M_s of about 1.8μ_B per Fe atom³⁰, we obtained K_u = 5.1 × 10⁵ J m⁻³ from the fit. Such a magnetic anisotropy energy density is in reasonable agreement with the value obtained in bulk FGT³¹.

Ionic gating of atomically thin ferromagnetic FGT devices

We determine the T_c of the FGT trilayer under ionic gating (Fig. 3) from anomalous Hall measurements. Specifically, we recorded R_xy as a function of T when the sample is cooled down in the presence of an infinitesimal magnetic field μ₀H₀ = 0.01 T applied in the out-of-plane direction. Because the normal part of the Hall resistance is negligible at such a low field, the anomalous Hall resistance is obtained as ${R}_{{\rm{AH}}}{| }_{{\mu }_{0}{H}_{0}}=\left({R}_{{xy}}{| }_{{\mu }_{0}{H}_{0}}-{R}_{{xy}}{| }_{-{\mu }_{0}{H}_{0}}\right)/2$. (The symmetrization procedure²⁸ is required to remove the R_xx component in the Hall data.) We extracted T_c by extrapolating R_AH to 0 (black lines, Extended Data Fig. 7a). The extrapolation is necessary because some of the T_c values are far above the freezing temperature of lithium ions (about 240 K).

The normal Hall resistance R_NH proportional to the external magnetic field manifests as a linear background in R_xy at high fields where the anomalous Hall resistance saturates. We were therefore able to obtain the Hall coefficient R_H as the slope of the line fits to the high-field part of R_xy(μ₀H) shown in Fig. 3c. Extended Data Fig. 7d displays such line fits at three representative gate voltages, and the inverse of eR_H is plotted as a function of V_g in Extended Data Fig. 7e (here e is the charge on the electron). We observe that the inverse of eR_H as a function of V_g follows exactly the behaviour of T_c (Extended Data Fig. 7c). Because R_H is determined by the electronic structure on the Fermi surface⁴⁵, our observation unambiguously links the gate-induced magnetic response to changes in the Fermi surface, and provides additional support for the Stoner model discussed in the main text. Finally, we caution that here one cannot directly extract the carrier density from the inverse of eR_H as in the case of semiconductors. The Fermi surface of a multiband metal such as FGT is very complex, and the inverse of eR_H is in general not related to the carrier density.

We determined that the fundamental mechanism underlying the ionic gating in this study is gate-controlled intercalation of lithium ions. Clear evidence came from the fact that the ionic gate uniformly modulates the trilayer FGT as shown in Fig. 3. Such a large modulation depth is only possible with ion intercalation; electrostatic gating would have been almost completely screened by the first atomic layer, resulting in nonuniform gating in the out-of-plane direction. The thickness dependence of the gate modulation provides additional evidence for intercalation mechanism. The resistances (normalized by the value at V_g = 0 V) of three samples with varying thicknesses under gate modulation are displayed in Extended Data Fig. 8. The fact that a resistive state is induced in all three (initially metallic) samples implies that the gate modulation depth can be as large as 70 layers. This result is unambiguous evidence that ion diffusion, not the electrostatic field, is at work.

The intercalation mechanism is further corroborated by the reversibility of the magnetic response under ionic gating. As shown in Extended Data Fig. 7c, the gate-induced high-T_c state reverts to the initial low-T_c state once the gate voltage is swept back. Such reversibility indicates that the gate-intercalated ions do not chemically react (that is, form chemical bonds) with the crystal, which is consistent with results from gate-controlled intercalation of other layered crystals^46,47,48. We note that the reversibility of ionic gating is also confirmed by the measurement of the Hall coefficient R_H shown in Extended Data Fig. 7e. The ultrathin specimen did suffer from sample degradation, which resulted in a large background in the sample resistance (Extended Data Fig. 7b) during the down-sweep of the gate. Such degradation was expected because ultrathin FGT was shown to be sensitive to the trace amounts of O₂ and H₂O present during gating.

First-principles calculations of electronic and magnetic properties of bulk FGT

First-principles calculations were carried out based on density functional theory (DFT)^49,50 as implemented in VASP code⁵¹ with a plane wave basis set^52,53. Spin-polarized Perdew–Burke–Enzerhof generalized gradient approximation (GGA)⁵⁴ and local density approximation (LDA)⁵⁵ were used as the exchange-correlation functionals. We also tested the on-site Coulomb interaction with different effective Hubbard U. The correction of van der Waals interactions, namely the DFT-D3 method with Becke–Jonson damping^56,57, was included in all our calculations. The energy cutoff of the plane-wave basis set was set to 400 eV. The bulk crystal lattice constants were obtained by fully relaxing the primitive cell to be stress-free with a 17 × 17 × 4 gamma-centred k-point mesh. The k-point sampling was up to 17 × 17 × 1 and 4 × 4 × 2 for slabs and bulk supercell calculations, respectively. The slabs were separated by a vacuum of at least 15 Å. We performed careful convergence tests for all of the settings aforementioned. The LDA functional yields a magnetic moment of 1.424μ_B per Fe site, which agrees with experimental observations^22,23,58 (LDA+U, GGA and GGA+U functionals yield magnetic moments of more than 2μ_B per Fe site). The result is consistent with previous theoretical studies²⁵. We therefore mainly use LDA with spin–orbit coupling to calculate the exchange coupling strength as well as the single-ion anisotropy A.

We adopted the energy mapping method^59,60 to obtain the Heisenberg spin exchange constants J from first-principles calculations. Here we used a 3 × 3 ×1 bulk supercell to extract all six-intralayer J_x (or J_y) and four-interlayer J_z. Detailed illustrations of configurations for different J values are shown in Extended Data Fig. 9a and b. Following the algorithm proposed in ref. ⁵⁹, we calculated the anisotropic spin exchange in a monolayer 3 × 3 ×1 supercell. All the calculation results are summarized in Extended Data Fig. 9c. The intralayer couplings are approximately one order of magnitude larger than the interlayer couplings. Meanwhile, ferromagnetic order is strongly favoured for both in-plane and out-of-plane configurations, owing to the large number of hopping sites that favour ferromagnetic coupling (negative J values).

Next, we investigate the magnetic anisotropy in a monolayer. The exchange parameters for in-plane and out-of-plane are comparable, with the out-of-plane ones slightly larger. The single-ion anisotropy A is defined as the energy difference between all magnetic moments along the easy-axis (the z direction) and along the hard-axis (the x or y direction) in the layer. We found that the single-ion anisotropy A was 1.11 meV per μ_B for both bulk and monolayer FGT.

Finally, we estimate the effect of electron doping on the Fe magnetic moments. Extended Data Fig. 10a displays the DOS for a trilayer FGT as a function of electron doping level. The average magnetic moment as a function of electron doping is shown in Extended Data Fig. 10b. The results indicate that the amount of electrons doped in our experiment do not much affect the mean magnetic moments on Fe sites.

Mean-field calculation of T _c in bulk FGT

Although experiments and LDA calculations show that the magnetism in FGT is itinerant origin, one can still describe the ‘magnetic part’ of the thermodynamic properties of itinerant ferromagnetism with a Heisenberg Hamiltonian with magnetic anisotropy:

$$H=\sum _{i,j}{J}_{ij}{{\boldsymbol{S}}}_{i}\cdot {{\boldsymbol{S}}}_{j}+\sum _{i}A{\left({S}_{i}^{z}\right)}^{2}-g{\mu }_{{\rm{B}}}\sum _{i}B{S}_{i}^{z}$$

(6)

where the first term is the sum of the Heisenberg exchange interactions between spin i with spin operator S_i and its neighbours S_j, with which it interacts with strength J_ij; a negative J_ij corresponds to ferromagnetic interactions, and S_i is in units of h. The second term is the uniaxial single-ion anisotropy with respect to the uniaxial z axis, where the single-ion anisotropy A < 0 prefers spins aligning along the z axis. The third term is the Zeeman interaction. Fe_I³⁺ and Fe_II²⁺ have different and non-integer magnetic moments. We, however, treat them equally for simplicity.

We used the molecular mean field theory to solve the above Hamiltonian, which is achieved by replacing the spin operator by its mean value plus fluctuations. Mean-field approximation gives

$${H}_{{\rm{MFA}}}=\sum _{i}{S}_{i}^{z}\left[2\sum _{j}{J}_{ij}{S}_{j}^{z}\right]+\sum _{i}A{\left({S}_{i}^{z}\right)}^{2}-g{\mu }_{{\rm{B}}}\sum _{i}B{S}_{i}^{z}-\sum _{i,j}{J}_{ij}{S}_{i}^{z}{S}_{j}^{z}$$

(7)

where the spin flips are completely suppressed. Here B is the magnetic field and g is the Landé g-factor. The eigenvalues of the Hamiltonian $E\left({S}^{z}\right)$ are labelled by the z components of the spin angular momentum ${S}^{z}\equiv -S,-S+1,\ldots ,S.$ The dimensionless magnetization at temperature T is given by the statistical average over all possible states of S^z

$$\frac{M}{{M}_{0}}=\frac{1}{Sg{\mu }_{{\rm{B}}}}\frac{1}{{Z}_{S}}\sum _{{S}^{z}=-S}^{+S}\left(-\frac{\partial {E}_{n}}{\partial {B}_{z}}\right){{\rm{e}}}^{-{E}_{n}/{k}_{{\rm{B}}}T}$$

(8)

where the partition function is ${Z}_{S}=\sum _{{S}^{z}=-S}^{+S}{{\rm{e}}}^{-{E}_{n}/{k}_{{\rm{B}}}T}$. On the other hand, the magnetization is

$$M=\frac{N}{V}g{\mu }_{{\rm{B}}}\left\langle {S}^{z}\right\rangle $$

(9)

Therefore, both sides of equation (8) contain M, which can be solved graphically. Using mean-field approximation, one can see that without the A term in the Hamiltonian of equation (6), the right hand side of equation (8) becomes a Brillouin function. One can further approximate the A term by an effective exchange field as $\sum _{i}2A\left\langle {S}^{z}\right\rangle {S}_{i}^{z}$. In this case, the Heisenberg model is equivalent to the phenomenological Weiss model of a ferromagnet. The magnetization is

$$\frac{M\left(T,B\right)}{{M}_{0}}={B}_{S}\left(\frac{Sg{\mu }_{{\rm{B}}}\left(B+{B}_{A}\right)}{{k}_{{\rm{B}}}T}\right)$$

(10)

where B_S is the Brillouin function defined as

$${B}_{S}\left(x\right)=\frac{2S+1}{2S}{\rm{\coth }}\left(\frac{2S+1}{2S}x\right)-\frac{1}{2S}{\rm{\coth }}\left(\frac{x}{2S}\right)$$

(11)

and

$${B}_{A}=-\frac{1}{g{\mu }_{{\rm{B}}}}\left(2\sum _{j}{J}_{ij}+2A\right)\left\langle {S}^{z}\right\rangle $$

(12)

The Curie temperature T_c is given by M = 0, which leads to

$${T}_{{\rm{c}}}=-\frac{2S\left(S+1\right)}{3{k}_{{\rm{B}}}}\left(\frac{1}{n}\sum _{i\ne j}{J}_{ij}+A\right)$$

(13)

Here n is the number of neighbouring sites. Taking the effective J parameters from LDA calculations, and choosing S = 5/2 as the magnetic moment of single Fe_I³⁺ ion, we can estimate the T_c of bulk FGT to be about 233 K. Meanwhile, choosing S = 2 as the magnetic moment of single Fe_II²⁺ ion leads to a bulk T_c value of about 160 K.

Extended data figures and tables

Extended Data Fig. 1 Characterization of FGT bulk crystal.

a, Powder X-ray diffraction pattern of bulk FGT crystal. b, Temperature-dependent magnetization of bulk FGT measured during zero-field cooling (ZFC, blue curve) and field cooling (FC, red curve) with an external magnetic field of 0.1 T. (a.u., arbitrary units; emu, electromagnetic unit for magnetic moment).

Extended Data Fig. 2 FGT thin-flake device fabrication.

a, A representative optical image of FGT thin flakes exfoliated on top of Al₂O₃ film supported on a sapphire substrate. The image was captured with a CCD camera mounted on an optical microscope operating in transmission mode. b, Cross-sectional profile of optical transmission ${G}_{{\rm{sample}}}^{{\rm{T}}}/{G}_{{\rm{substrate}}}^{{\rm{T}}}$ along the black line in a. Scale bar, 10 μm. c, Layer-dependent optical transmission extracted from the image shown in a. The black line is a fit to the data (blue squares) using the Beer–Lambert law. d, e, Optical images obtained in transmission mode (d) and reflection mode (e) for a typical monolayer sample. f, Device fabricated from the monolayer sample shown in d and e. Electrical contacts to the sample were made with indium microelectrodes. Scale bar, 100 μm. g, h, Optical images obtained in transmission mode (g) and reflection mode (h) for a typical trilayer sample. i, Device fabricated from the trilayer sample shown in g and h. Electrical contacts to the sample were made with thermally evaporated Cr/Au electrodes. Scale bar, 100 μm. The optical transmission of the monolayer and trilayer sample shown in d and g are presented as red dots in c.

Extended Data Fig. 3 Determining T_c by Arrott plot analysis.

a–c, R_xy as a function of external magnetic field μ₀H obtained in a monolayer (a), bilayer (b) and trilayer (c) FGT device at varying temperatures. d, Arrott plots of the Hall resistance data of the bilayer sample shown in b. The temperature is varied from 72 K to 124 K with a 4 K interval. Black lines are line fits at high magnetic fields (from μ₀H = 2.25T to μ₀H = 3T). e, Spontaneous Hall resistance ${R}_{xy}^{{\rm{s}}}$ as a function of temperature obtained from FGT samples with varying number of layers. ${R}_{xy}^{{\rm{s}}}$ are normalized by their values at T = 1.5K. T_c is determined by the temperature where ${R}_{xy}^{{\rm{s}}}$ approaches zero.

Extended Data Fig. 4 Determining T_c from RMCD measurements.

a, Optical image of monolayer, bilayer and trilayer FGT samples. Scale bar, 10 μm. b–e, Polar RMCD signal as a function of magnetic field recorded in monolayer (b), bilayer (c), trilayer (d) and bulk (e) samples at various temperatures. The bulk sample refers to an 18-layer sample with the thickness determined from optical transmission. f, Remanent RMCD signal at zero magnetic field as a function of temperature obtained from datasets shown in b–e. The T_c of each sample is determined by the temperature where remanent RMCD signal vanishes. Vertical error bars represent the measurement uncertainty of the remanent RMCD signal.

Extended Data Fig. 5 Finite-size scaling of T_c in FGT thin flakes.

T_c shown here is obtained from anomalous Hall measurements. We used the highest T_c at each sample thickness for the analysis. Error bars are defined as in Fig. 2d.

Extended Data Fig. 6 Angle-dependent Hall resistance of a four-layer FGT flake.

a, R_xy as a function of magnetic field recorded at various tilt angles. Data were obtained at T = 1.5 K. b, R_xy as a function of magnetic field recorded at θ_H = 90° (blue) and θ_H = 20° (red) at T = 150 K, about 5 K above the T_c determined by anomalous Hall measurements in the same sample. c, θ_M as a function of θ_H. θ_M was extracted from the R_xy data at μ₀H = 3 T in a. The solid line is a fit to the Stoner–Wohlfarth model. A K_u value of 5.1 × 10⁵ J m⁻³ is obtained from the fit, if M_s takes the value of about 1.8μ_B per Fe atom. The broken line marks θ_M = θ_H that corresponds to K_u = 0.

Extended Data Fig. 7 Ionic gating of an FGT trilayer ionic field-effect transistor.

a, Temperature-dependent R_AH at representative V_g under a small external magnetic field of μ₀H₀ = 0.01 T. The ferromagnetic transition temperature T_c is extracted by extrapolating R_AH to zero. b, Sample resistance R_xx as a function of V_g during the up-sweep (blue) and down sweep (red) of V_g. Data were obtained at T = 330 K. c, T_c as a function of V_g during the up-sweep (blue) and down sweep (red) of V_g. T_c exhibits reasonably good reversibility under gate modulation, even though R_xx acquires a large background, possibly due to sample degradation. Data were obtained from the same device discussed in Fig. 3. The error bars are also defined the same way as in Fig. 3. d, Line fits of R_xy as a function of μ₀H in the range of 3 T < μ₀H < 5 T at three representative gate voltages. R_H is obtained as the slope of the line fits. e, Inverse of eR_H as a function of V_g during the up-sweep (blue) and down-sweep (red) of the gate voltage. Data were obtained at T = 240 K. Error bars represent the standard deviations of the line fits in d.

Extended Data Fig. 8 Thickness dependence of the gate modulation in a FGT ionic field-effect transistor.

Sample resistance measured as a function of V_g in trilayer (black), 10-layer (red) and 70-layer (blue) FGT devices. Resistances are normalized by their values at V_g = 0 V.

Extended Data Fig. 9 Calculated exchange parameters.

a, The top view shows J_in1 to J_in6 for the intralayer (in plane) coupling. b, The side view shows J_z1 to J_z4 for the interlayer (out of plane) coupling. Only Fe ions are shown in the structure. The purple and red atoms are Fe_I and Fe_II ions, respectively. c, The left column shows the calculated exchange parameters for bulk FGT, J_ini for intralayer and J_zi for interlayer, in a 3 × 3 × 1 bulk supercell. The right column shows the spin exchange parameters in a monolayer 3 × 3 × 1 supercell, denoted as J_xxi (J_yyi) and J_zzi. The units of J are millielectronvolts. The results indicate that the exchange coupling J is largely isotropic.

Extended Data Fig. 10 LDA calculation of DOS and average magnetic moment as a function of electron doping level.

a, Calculated DOS for trilayer FGT as a function of electron doping level. b, Calculated average magnetic moment in bulk FGT as a function of electron doping level.