Introduction

Bioreactors are widely used in pharmaceutical industries, water treatment plants, food processing industries, and chemical plants. The bioreactor sizes differ by different magnitudes. Types of biological reactors include microbial cells (few mm\(^3\)), shake flask (100–1000 mL), lab fermenter (1–50 L), pilot-scale (0.3–100 m\(^3\)) to plant size (2–500 m\(^3\)) (Chandrashekhar and Rao 2010). However, the development of a plant (industrial) scale bioreactor system is not that easy. There are various challenges associated with the optimization of parameters, as both the optimization of pilot reactors and the scaling of these parameters are important for the improved performance of the industrial bioreactor. Although various parameters have been defined for the scaling process (Degaleesan 1997; Wilkinson et al. 1992; Safoniuk et al. 1999; Macchi et al. 2001), these are case-related with no commonly accessible bearings (Shaikh 2007). Also, it is highly difficult (nearly impossible) to get the optimized parameters for the industrial-scale bioreactor by performing experiments that are quite expensive and time-consuming. The simulation of a bioreactor is, therefore, an important way of designing and optimizing a large-scale reactor. This would greatly minimize the costs and resources involved in the optimization and scale-up process. There are different types of bioreactors that differ based on their design and mode of operation for industrial processes (Spier et al. 2011). Such types of bioreactors include (1) Stirred Tank Bioreactors, (2) Bubble-Column Bioreactors, (3) Fluidized Bed Bioreactors, (4) Packed Bed Bioreactors, (5) Airlift Bioreactors, and (6) Photo Bioreactors. Among others, stirred-tank bioreactors are the most widely used reactor types in the biochemical, pharmaceutical, petrochemical and water-processing industries. Stirred tank reactor offers a wide range of applications for mixing, controlling reaction kinetics, heat and mass transfer, and flocculation in the biochemical, pharmaceutical, and water processing industries. All these processes have been directly influenced by the flow characteristics of the fluid inside the reactor. Thus, understanding the fluid flow characteristics such as the velocity, turbulent kinetic energy (TKE) distributions, power number, and flow number are necessary to increase the product quality, improve the design, and maintain operational costs (Li et al. 2011).

Numerous experimental techniques, such as laser Doppler anemometry (LDA) and particle image velocimetry (PIV), are often used by the researchers to observe the flow characteristics in stirred tank reactors. Normally, one can easily find the experimental and numerical studies in the literature for the single impeller stirred tank reactor. However, multiple impellers are usually preferred in the industrial unit for efficient mixing and better productivity. Moreover, the use of multiple impellers in the stirred tank significantly increased the flow complexity. The first experimental study using LDA techniques to observe the flow characteristics in a stirred tank equipped with dual-Rushton impellers was performed by Rutherford et al. (1996). This study investigated the various flow characteristics, power consumption, and mixing time in a dual-Rushton impeller stirred tank reactor at Reynolds number (\(Re = 40,000\)). A set of experiments was performed for different spacing between two impellers and different impeller clearances from the vessel bottom. Despite the above study, numerous experimental studies are performed by researchers time to time to understand the flow processes in the stirred tank reactor equipped with dual-impeller (Bonvillani et al. 2006; Chunmei et al. 2008; Teli et al. 2020; Alves et al. 2002; Zhang et al. 2017; Xinhong et al. 2008). However, relatively fewer numerical studies are available in the literature for a stirred tank reactor fitted with the dual impeller. Some recent works in this direction are reported by Zadghaffari et al. (2009), Taghavi et al. (2011), Li et al. (2012). Zadghaffari et al. (2009) performed the numerical simulation on a fully baffled stirred tank reactor with two six-blade Rushton impellers using the sliding mesh (SM) approach. LES was used in the study to model the turbulence eddies. The study also conducted a PIV experiment to validate the simulation results. The authors considered three different speeds of the impeller’s rotation, i.e., 224, 300, and 400 rpm, in the study. Rhodamine-590 was selected as the determining tracer in the study. The study reported the results for the flow field, power consumption, and mixing time. The planar laser-induced fluorescence (PLIF) technique was adopted to measure concentration and mixing time. Taghavi et al. (2011) experimentally and numerically studied the consumption of power in a stirred tank reactor fitted with a six-blade dual-Rushton turbine. The study reported the results for both single and gas–liquid phase conditions. The numerical results were compared with the experimental findings. Also, the results were validated with the data available in the literature. Li et al. (2012) conducted the PIV experiment and also performed LES simulation on the same geometry used by Rutherford et al. (1996) for the merging flow characteristics. The study validated the obtained experimental findings and numerical results with the results of Rutherford et al. (1996), and Micale et al. (1999). In recent work, Agarwal et al. (2021b) performed numerical simulation to investigate the diverging flow behavior in a stirred tank reactor. The present study is a continuation and an extension of the work.

Furthermore, with the recent advancements in computational resources, Computational Fluid Dynamics (CFD) has often been used as a numerical tool for obtaining the solutions and visualizing the fluid flow behavior, which is difficult and expensive to study experimentally (Lamarque et al. 2010). The fast rotating impeller and stationary baffles make the flow turbulent in the stirred tank reactor. The simulation of turbulent flow in a stirred vessel using CFD offers a sufficient amount of useful data to study the flow behavior, vortex dynamics, circulation patterns, Reynolds stresses, etc. (Vakili and Esfahany 2009). Moreover, the visualization of all the parameters listed above allows the user to understand different flow-related processes in the reactor. In addition to this, one of the multiple flow-associated processes, mixing, is utterly dependent on the fluid flow behavior, which further identifies the possible problems in advance (Meroney and Colorado 2009). Thus, CFD plays an essential role in numerous contexts for the optimized design of a reactor, and it is also necessary to develop new mathematical models time-to-time for CFD, which should be more accurate and stable, enhancing one’s understanding of reactor hydrodynamics (Ding et al. 2010).

From the past three decades, the lattice Boltzmann method (LBM) has been widely used as an alternative approach to Computational Fluid Dynamics. It became popular among researchers and scientists due to its wide range of applicability to simulate various physical and chemical processes associated with the flow of fluid, and multiphase flows (Grunau et al. 1993), immiscible fluids (Gunstensen et al. 1991), heat transfer (Han-Taw and Jae-Yuh 1993; Ho et al. 2002) and turbulent flows. The method first evolved from the Lattice Gas Cellular Automata (LGCA). The boolean principle involved in LGCA results in numerical instability and inaccuracy. LBM was then recognized for overcoming LGCA’s drawbacks; the method considered the fluid to be a collection of particles (Sharma et al. 2019). The method introduced the averaged distribution function concept, which means a single distribution function contains all those fluid particles at the same position simultaneously moving with the same velocity. Later, it was found that the generalized form of the lattice Boltzmann equation (LBE) can also be derived from the finite difference approximation of the Boltzmann transport equation (BTE) (Sharma et al. 2019). The mathematical formulation of LBM includes a two-stage procedure that involves the collision and streaming of fluid particles’ distribution functions. The concept behind the method is that a set of particle distribution functions residing on a lattice node streams to adjacent lattice sites and collides with particle distribution functions coming from other directions, resulting in momentum exchange, and, during the collision process, net mass and momentum remain conserved (Agrawal et al. 2006). The method provides stable and local arithmetic operations for the macroscopic behavior of fluid and recovers the Navier–Stokes equations (Chen et al. 1992). The local mathematical operations give the method an advantage of an effective parallel algorithm rather than the traditional CFD approach ( i.e., Finite Difference Method, Finite Volume Method, and Finite Element Method).

However, to the best of the knowledge of the authors of this work, the comprehensive study of the stirred tank reactor equipped with a dual Rushton turbine using LBM has not yet been reported in the literature. The current study not only presents the flow characteristics in the dual Rushton stirred tank, but also acknowledges the impact of baffles on the flow. Moreover, the study also shows the effect of the presence of baffles with different impeller clearance on the flow characteristics and their influence on mixing, which has not been studied so far. The simulations were performed using the most popular collision model of LBM, i.e., the LBGK model, also known as the single-relaxation time lattice Boltzmann method (SRT-LBM) (Li et al. 2012). Large-eddy simulation (LES) was used to model turbulence. The conventional Smagorinsky subgrid-scale (SGS) model was chosen for resolving the small-scale motions (Smagorinsky 1963). The obtained results showed a unique behavior in the flow pattern in the presence and absence of baffles for different impeller clearances.The authors developed a new highly parallel SRT-LBM solver to efficiently run on the GPU cluster for the present simulation. However, the same in-house code was already used by the authors to study another benchmark problem of fluid flow and the results were validated with experimental data reported in the literature (Agarwal et al. 2021a). In addition, the present solver, along with the parallelization of the SRT-LBM and LES model, also includes the parallelizable code for the immersed boundary method in it. The obtained results are validated with the experimental observations of Rutherford et al. (1996), and Micale et al. (1999) for the numerous fluid flow properties, including flow averaged velocity, and TKE.

The remainder of the paper is organized as follows. Section 2 details the information about the flow system used for the current study. An overview of the simulation methodology, i.e., the formulation for the governing equations of LBM for the discretization of fluid domain, turbulence modeling, and boundary conditions, is given in Sect. 3. The description for the numerical setup and algorithm implementation on the GPU cluster using the Compute Unified Device Architecture (CUDA) programming model is presented in Sect. 4. The numerical results are discussed in Sect. 5. Section 6 summarises the work and concludes the article.

Flow system

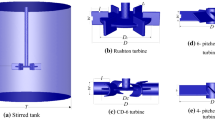
The simulation was carried out on a stirred tank reactor with a standard configuration. It consists of a fully cylindrical tank of diameter T with a flat base, open on top. The agitation in the reactor was provided by the dual-Rushton impeller of diameter D. The impellers consist of 6-blades, and the details of the tank geometry and the impeller are depicted in Fig. 1.

Fig. 1
figure 1

2D-representation of the stirred tank geometry: front view (upper), and top view (lower)

Full size image

The water was filled up to a height (H) equal to the tank diameter. The Reynolds number, (Re), which fully determines the liquid flow behavior is defined by, \(Re = \frac{N{D}^{2}}{\nu }\), where N is the rotational speed of the impeller, that is fixed at 250 (in rpm), and \(\nu\) is the kinematic viscosity of the working fluid (i.e., water). The dimensional values are listed in Table 1. A similar flow configuration was studied by Micale et al. (1999) using the sliding-grid method with the \(k-\omega\) turbulence model to resolve the turbulent structures. As the analysis explores the influence of baffles on the flow behavior, the simulation was conducted on the identical configuration of the stirred tank reactor, both in the presence and absence of baffles.

Table 1 Reactor and impeller dimensions
Full size table

Simulation methodology

Lattice Boltzmann method

In this work, LBM has been used to discretize the flow domain. The particular lattice Boltzmann (LB) scheme used here is SRT-LBM (Qian et al. 1992). It is the LBM model most commonly used to solve fluid flow problems. The model can be described with the equation given as:

$$\begin{aligned} \underbrace{f_{j}(\mathbf {x}+\mathbf {e}_{j}\varDelta t, t+\varDelta t)}_\textit{streaming step} = \underbrace{f_{j}(\mathbf {x},t)-\frac{1}{\tau }[f_{j}(\mathbf {x},t)-f_{j}^{eq}(\mathbf {x},t)]}_\textit{collision step} \end{aligned}$$
(1)

where \(f_{j}(x,t)\) and \(f_{j}^{eq}(x,t)\) are the density distribution and equilibrium density distribution functions along direction j at \((\mathbf {x},t)\), \(\mathbf {e}_{j}\) is the particle velocity vector in the jth direction, \(\varDelta t\) is the time step and \(\tau\) is the relaxation time parameter that controls the rate of approach to equilibrium (Perumal and Dass 2015). The corresponding discrete equilibrium distribution function \(f_{j}^{eq}\) for the model is given by:

$$\begin{aligned} f_{j}^{eq} = w_{j}\rho \Big [1+\frac{\mathbf {e}_{j}.\mathbf {u}}{c_{s}^2} + \frac{(\mathbf {e}_{j}.\mathbf {u})^2}{2c_{s}^{4}} - \frac{\mathbf {u}^2}{2c_{s}^{2}}\Big ] \end{aligned}$$
(2)

where w is the weight factor, \(\rho\) be the density of fluid, \(c_{s}\) is the speed of sound dependent on the model and \(\mathbf {u} = (u, v, w)\) is the fluid velocity vector.

The lattice scheme in LBM notation can be distinguished with \(D_{m}Q_{n}\) reference, where m denotes the dimension of the domain and n is the number of directions, a particle is restricted to stream. In this study, the D3Q19 lattice structure was used for the SRT-LB scheme as shown in Fig. 2.

Fig. 2
figure 2

Schematic represenation of \(D_{3}Q_{19}\) lattice structure

Full size image

The corresponding discrete velocity vectors \(\mathbf {e}_{j}\) and weights \(w_{j}\) for the \(D_{3}Q_{19}\) lattice are as follows:

$$\begin{aligned}&\mathbf {e}_{j}= {\left\{ \begin{array}{ll} c(0,0,0), &{} j = 0\\ c(\pm 1,0,0), c(0,\pm 1,0), c(0,0,\pm 1),&{} j = 1,\ldots ,6\\ c(\pm 1,\pm 1,0), c(\pm 1,0,\pm 1), c(0,\pm 1,\pm 1),&{} j = 7,\ldots ,18 \end{array}\right. } \end{aligned}$$
(3)
$$\begin{aligned}&\quad w_{j} = {\left\{ \begin{array}{ll} \frac{1}{3}, &{} j = 0\\ \frac{1}{18}, &{} j = 1,\ldots ,6\\ \frac{1}{36}, &{} j = 7,\ldots ,18\\ \end{array}\right. } \end{aligned}$$
(4)

where, c is the lattice speed, defined as \(c = {\varDelta x}/{\varDelta t}\). The relaxation time parameter \(\tau\) is related to the kinematic viscosity that fixes the rate of approach to equilibrium given by Perumal and Dass (2015):

$$\begin{aligned} \nu = \left( \frac{2\tau -1}{6}\right) \frac{(\varDelta x)^2}{\varDelta t} \end{aligned}$$
(5)

The macroscopic variables such as density and momentum density can be explicitly calculated from the real-valued density distribution function (Kang and Hassan 2011):

$$\begin{aligned} \rho = \sum _{j}f_{j}= \sum _{j}f_{j}^{eq}, \ \rho \mathbf {u} = \sum _{j}\mathbf {e}_{j}f_{j} = \sum _{j}\mathbf {e}_{j}f_{j}^{eq} \end{aligned}$$
(6)

Turbulence modelling

The simulation of turbulent eddies is an important feature of this analysis, as the Reynolds number (Re) used in the simulation indicates a robust, turbulent flow. The direct numerical simulation (DNS) is not feasible at this Reynolds number (Re) due to the limitation of the computational resources. DNS would require a fine meshing of the domain and an enormous number of time steps to model the turbulent flow. In LES, however, the process assumed that small-scale flow structures (i.e., independent of the flow geometry) are universal and isotropic. As a result, it provides an advantage to the method for the modeling of turbulent flow with relative ease (Derksen and Van den Akker 1999). The idea behind the approach is to decompose the flow variables into large and small structures by specifying a filtering procedure (Stephen et al. 2000). The procedure enables large structures to be resolved explicitly in grid calculation and uses the SGS model for the small, turbulent structures. The general filtering procedure is as follows:

$$\begin{aligned} \overline{\varPsi }(x) = \int \varPsi (x') H(x,x')dx' \end{aligned}$$
(7)

where \(\varPsi\) is the spatially based quantity and H is the kernel funtion and the integral is distributed over the entire region (Hou et al. 1994; Koda and Lien 2015). The filtered equation of SRT-LBM is written as:

$$\begin{aligned} {\overline{f}}_{j}(\mathbf {x}+\mathbf {e}_{j}\varDelta t, t+\varDelta t) = {\overline{f}}_{j}(\mathbf {x},t)-\frac{1}{\tau _{t}}[{\overline{f}}_{j}(\mathbf {x},t)-\overline{f_{j}^{eq}}(\mathbf {x},t)] \end{aligned}$$
(8)

where \({\overline{f}}_{j}\) and \(\overline{f_{j}^{eq}}\) are the filtered density distribution and equilibrium distribution function respectively. The Smagorinsky SGS (Smagorinsky 1963) model (also known as the eddy-viscosity model) has been implemented in this study to address small-scale structures. The model consists of an eddy viscosity term \(\nu _{SGS}\) in its formulation. This eddy viscosity term \(\nu _{SGS}\) can be obtained from the filter width \(\varDelta\) and characteristic filtered rate of strain \({\overline{S}}\). The filter width is of size \(\varDelta\) equal to the grid spacing \(\varDelta x\). The equivalent expression is given as:

$$\begin{aligned} \begin{aligned} \nu _{SGS}&= (C_{s}\varDelta )^{2}{\overline{S}}\\ {\overline{S}}&= \sqrt{2\sum \nolimits _{ij}S_{ij}S_{ij}} \end{aligned} \end{aligned}$$
(9)

where \(S_{ij}\) = \((\partial _{j}{\overline{u}}_{i}+\partial _{i}{\overline{u}}_{j})\) is the filtered strain rate tensor, \(C_s\) is the Smagorinsky constant and is set to 0.1 for the present study. This particular value of \(C_s\) is most commonly used for shear-driven turbulence (Derksen 2001). The subgrid closure can be implemented directly in the LBM equation by simply replacing the physical kinematic viscosity \(\nu\), with the total effective viscosity \(\nu _{t}\) in the collision step (Koda and Lien 2015). The expression for total effective viscosity \(\nu _{t}\) given as:

$$\begin{aligned} \nu _{t} = \nu + \nu _{SGS} \end{aligned}$$
(10)

where \(\nu _{SGS}\) is the eddy viscosity. In LBM, the viscosity of the fluid is related to the relaxation time parameter as given in Eq. (5). Thus,

$$\begin{aligned} \nu _{t} = \left( \frac{2\tau _{t}-1}{6}\right) \frac{(\varDelta x)^2}{\varDelta t} \end{aligned}$$
(11)

Solving Eqs. (5), (9)–(11) gives:

$$\begin{aligned} \tau _{t} = \tau + \frac{3\varDelta t(C_{s}\varDelta )^{2}{\overline{S}}}{(\varDelta x)^{2}} \end{aligned}$$
(12)

where \(\tau _{t}\) is the total value of the relaxation time. The filtered strain rate tensor \(S_{ij}\) can be obtained directly from the non-equilibrium momentum flux tensor \(\overline{\varPi }_{ij}\) given as:

$$\begin{aligned} \overline{\varPi }_{ij} = \sum _{k}\mathbf {e}_{ki}\mathbf {e}_{kj}({\overline{f}}_{i}-\overline{f_{i}^{eq}}) = \frac{-2\overline{\rho }\tau _{t}(\varDelta x)^{2}S_{ij}}{3\varDelta t} \end{aligned}$$
(13)

Also,

$$\begin{aligned} Q^{1/2} = \sqrt{\overline{\varPi }_{ij}:\overline{\varPi }_{ij}} = \frac{\sqrt{2}\overline{\rho }\tau _{t}(\varDelta x)^{2}{\overline{S}}}{3\varDelta t} \end{aligned}$$
(14)

Substituting Eq. (12) in Eq. (14) gives the expression for charcterstic filtered rate of strain \({\overline{S}}\):

$$\begin{aligned} {\overline{S}} = \frac{-\tau \overline{\rho }c\varDelta x + \sqrt{(\tau \overline{\rho }c\varDelta x)^{2}+18\sqrt{2}(Cs\varDelta )^{2}Q^{1/2}}}{6\overline{\rho }(C_{s}\varDelta )^{2}} \end{aligned}$$
(15)

Finally, substituting Eq. (15) in Eq. (12) gives:

$$\begin{aligned} \tau _{t} = \frac{\tau }{2} + \frac{\sqrt{(\tau \overline{\rho } c \varDelta x)^{2}+18\sqrt{2}(C_{s}\varDelta )^{2}Q^{1/2}}}{2\overline{\rho }c} \end{aligned}$$
(16)

Treatment of reactor components

The immersed boundary (IB) method is used in the present study in the framework of LBM to model the influence of reactor components on the fluid flow. A particular explicit diffuse direct-forcing immersed boundary-lattice Boltzmann method (IB-LBM) is adopted for the simulations (Kang and Hassan 2011). The tank wall, baffles, and other rotational components of the reactor are defined as a set of control points (i.e., lagrangian marker). The no-slip condition on the reactor components is maintained by using a two-way coupling approach. In this approach, the surrounding fluid velocity is interpolated into the control points of the reactor components to measure the force applied by the flow on the boundary surface, and then these forces are distributed back to the surrounding fluid nodes. An external forcing term is added in the governing equation of LBM to compute the impact of these distributed forces on the fluid flow (for more details, one can refer to Kang and Hassan 2011). Moreover, the interpolation between the surrounding fluid nodes and the control points of the reactor components is performed with the cheap-clipped fourth-order polynomial mapping function proposed by Deen et al. (2004). The function can be written as:

$$\begin{aligned} D(x_{i}-x_{i,b})= {\left\{ \begin{array}{ll} \frac{15}{16}\left[ \frac{(x_{i}-x_{i,b})^5}{n^5} -2\frac{(x_{i}-x_{i,b})^2}{n^3}+\frac{1}{n}\right] &{} -n\le (x_{i}-x_{i,b})\le +n\\ 0, &{} otherwise \end{array}\right. } \end{aligned}$$
(17)

where b represent the control points of the reactor components and \(n = 1\) is used in the study. The surrounding fluid velocity on the control points of the reactor components can be calculated as:

$$\begin{aligned} \mathbf {u}(\mathbf {x}_{b}) = \int \limits _{-n}^{+n} \int \limits _{-n}^{+n} \int \limits _{-n}^{+n} D(x_{i}-x_{i,b})D(y_{i}-y_{i,b})D(z_{i}-z_{i,b})\mathbf {u}(\mathbf {x}) dxdydz \end{aligned}$$
(18)

Numerical setup and parallel implementation

Modelling aspects

A uniform, cubic computational grid of \(150^{3}\) was defined for the simulation. The LES method was used in this analysis to model turbulent flow. For subgrid-closure, the SGS scheme was adopted with a Smagorinsky constant (\(C_s\)) of 0.1 (Smagorinsky 1963). A no-slip bounce-back boundary condition was imposed at the walls of the cube, whereas the free-slip boundary condition was defined at the top surface to represent the free surface (Derksen and Van den Akker 1999). Furthermore, the IB method was used to represents the interaction between the reactor components and the fluid, as mentioned in Sect. 3.3. The reactor components (i.e., cylindrical wall, impeller, impeller shaft, and baffles) in the simulation are represented by a set of points called control points. The distance between two control points at the reactor components was \(0.6\varDelta x\), where \(\varDelta x\) is the grid spacing, equal to \(2.0 \times 10^{-3}\) m. The simulation starts with a stagnant liquid and proceeds with a time step of 100 \(\mu\)s. The simulation runs for 150,000-time steps, which represent 15 s for the operation of the reactor in real-time (Agarwal et al. 2021b).

Fig. 3
figure 3

Illustration of the CUDA programming model in 3D

Full size image

GPU parallelization

The latest research simulations have been conducted on a server of 20 Intel R Xeon R Gold 5115 2.40GHz ten-core CPUs per socket, with Nvidia Tesla GP100 GPU cards. There are 6 graphical processing clusters (GPCs) within the architecture of the Nvidia Tesla GP100. A GPC consists of 5 Texture Processing Clusters (TPCs), each with two streaming multiprocessors (SMs). There are 64 CUDA cores and four texture units for each SM. More specifics on the Tesla GP100 card architecture can be found in NVIDIA (2016). The Nvidia Tesla GP100 GPU’s technical requirements are set out in Table 2.

Table 2 NVIDIA Tesla GP100 specifications
Full size table

The NVIDIA developed CUDA programming model is used for the development of the code for GPU parallel computing. In the CUDA programming model, CPU architecture is described as a host unit and GPU architecture as a device unit. The CUDA programming model used the kernel function for the execution of the program. The kernel function in the CUDA programming model is a call function; it is called from the host (i.e., CPU) and run on the device (i.e., GPU). It executes the complete domain grid in the GPU, which was divided into a large number of GPU blocks. Each GPU block consists of a large number of threads for parallel computation. A large number of parallel calculation threads are used in each GPU block. Figure 3 demonstrates the same CUDA programming process. The block in CUDA programming models runs parallel in different SMs, and the threads in each block run directly into CUDA cores. The important thing to understand is that the threads in each block can communicate with each other. However, threads in a different block cannot communicate.

The step by step sequence for the LBM algorithm implementation on GPU architecture is given below:

  • Step 1: Allocate memory for the variables both on the host and device

  • Step 2: Copy related variables to device from host.

  • Step 3: Divide the domain into a combination of blocks and threads

  • Step 4: Call the kernel function to perform different LBM operations, i.e., collision, streaming, boundary condition and updating of macroscopic variables.

  • Step 5: After completion of the simulation, transfer of data from device to host.

Results and discussion

The three different simulation results based on the impellers placement are presented in Fig. 4. Case 1 indicates a parallel flow pattern. Each of the impellers, i.e. upper and lower, generate two vortex rings in their vicinity. Hence, four vortex rings are formed in the parallel flow. Case 2 shows a merging flow pattern. Here, the flow generated by the impellers merges at a halfway elevation between the upper and lower impeller with a formation of two large vortex rings. A diverging flow pattern is exhibited by Case 3, in which the lower impeller forces the flow stream towards the bottom of the tank. This is attributed to the low position of the impeller. As a result, a large vortex ring is formed near the lower impeller and two vortex rings are formed near the upper impeller.

Fig. 4
figure 4

Flow patterns in the dual-Rushton turbine stirred tank reactor a Parallel flow, b merging flow, and c divering flow

Full size image

Figures 5, 6, and 7 show contour plots of instantaneous velocity magnitude at the upper impeller location for Case 1, Case 2, and Case 3, respectively, each containing baffles (Agarwal et al. 2021b), and the without baffles case. For each case comprising baffles, the maximum velocity magnitude is observed near the impeller vicinity, which decreases with an increase in radial distance from the impeller. In Case 1, the velocity magnitude shows nearly a similar distribution, i.e., maximum velocity near the impeller vicinity and stagnant zone domination near the reactor surface. However, in Case 2 and Case 3, the situation differs. The velocity magnitude in the instances without baffles is significantly lower than in the baffled cases; this might be due to abrupt abnormalities forming at the tank’s surface in the baffled cases. Furthermore, because of the no-slip boundary condition applied on the impeller surface, the greatest velocity magnitude is seen near the reactor surface, resulting in zero relative velocity between the impeller and the fluid particle at the impeller surface. As a result, as the impeller spins, the fluid around it rotates as well, resulting in a greater velocity magnitude closer to the reactor surface.

Figure 8 shows the contour plots of phase-averaged velocity magnitude at the upper impeller location for Case 1, with baffles and without baffles. The phase-averaged velocity is a special case of ensemble averaging in which the velocity is recorded at the same time during each impeller cycle and then averaged. The maximum phase-averaged velocity magnitude is observed near the impeller tip. Both the velocity contours seem to be identical in terms of velocity magnitude and its distribution. The maximum phase-averaged velocity magnitude is approximately 0.65 times the linear velocity at the tip of the impeller blades \(U_{tip}\) for both the cases, i.e., with and without baffles. The linear tip velocity of the blades is equal to the rotational speed of the impeller (i.e., 250 rpm or 1.28 m/s). Moreover, the present study depicts that the tip velocity of the blades can only be used to make a qualitative estimate of the maximum fluid flow velocity magnitude. Figures 9 and 10 show the contour plots of phase-averaged velocity magnitude at the upper impeller location for Case 2 and Case 3, respectively, with baffles (Agarwal et al. 2021b) and without baffles. The velocity magnitude at the upper impeller is reduced as compared to the parallel flow. The impeller vicinity has the highest velocity magnitude, which reduces towards the reactor surface. In Fig. 9, the without baffles case also showed the same behavior, but with a smaller velocity magnitude. The average velocity magnitude is maximum at the impeller vicinity, which reduces towards the reactor surface. The case with baffles shows a higher velocity magnitude with a reduced stagnant zone. The stagnant zone in Fig. 10 for the cases without baffles is smaller than in the previous two examples without baffles. As previously stated, the distance between the upper and lower impeller blades, as well as the distance between the lower impeller blades and the tank’s bottom, determine the parallel, merging, and diverging flows. Furthermore, the stationary region area might be due to Case 3’s significant swirling flow characteristics as opposed to Case 1 and Case 2. (Li et al. 2012).

Figure 11 shows the contour plots of phase-averaged velocity magnitude at \(\theta =0^\circ\) for Case 1. The maximum velocity magnitude is near the vicinity of both the upper and lower impellers. In both cases, i.e., with and without baffles, the velocity magnitudes show the same spread. Most of the contour plot shows a dominance of dead zone or stagnation zone. The stagnant zone is undesirable as the energy dissipation takes place in a smaller volume. In both cases, i.e., with and without baffles, the velocity contours are nearly identical. Nonetheless, the primary purpose of using baffles in the reactor is to avoid the swirl motion of the fluid in agitation. The baffles in the reactor convert the swirl motion of the fluid into the desired flow pattern. It converts the rotational flow of fluid to an axial flow, resulting in proper mixing. However, for the parallel flow bioreactor, the flow pattern for both the with and without baffles’ cases is similar. Hence bioreactors without baffles can be chosen over the baffled bioreactor to reduce the material requirement for its manufacturing. Moreover, by reducing the material requirement, the manufacturing cost of the bioreactor also decreases. Figure 12 shows the contour plot of the phase-averaged velocity magnitude at \(\theta =0^\circ\) for Case 2. The vortices mix in both the cases, with and without baffles. However, the mixing is stronger in the ‘with baffles’ case than the ‘without baffles’ one. The stagnant zone is also reduced in this case as compared to the parallel flow, i.e., Case 1. However, the stagnant zone is dominant in the case without baffles. Hence, the case with baffles will exhibit better mixing. Figure 13 shows the contour plot of phase-averaged velocity magnitude at \(\theta =0^\circ\) for Case 3 (Agarwal et al. 2021b). The development of a vortex can be seen at the bottom having a good spread. It is desirable in terms of mixing. However, the mixing of upper and lower vortices is not observed here. The magnitude of the velocity is higher in the baffle case, but the spread of the vortex is better in the latter case. The stagnant zone is reduced as compared to Case 1, especially at the bottom of the reactor.

Figure 14 shows the comparison of axial profiles of phase-averaged radial velocity in a plane midway between baffles at different radial locations for Case 1. The simulation results are compared with the experimental data of Rutherford et al. (1996) and Micale et al. (1999). The results are in very good agreement with the experimental data and seem to nearly overlap at all the radial positions considered for the simulations. The effect of baffles is not significant and the axial velocity profiles for all the radial positions follow the same profile. Similarly, the comparison of axial profiles of phase-averaged radial velocity in a plane midway between baffles at different radial locations for Case 2 is shown in Fig. 15. The results show a similar trend away from the impellers but near the vicinity of the impeller, the LBM results slightly under predict the experimental measurements. The ‘without baffles’ case is quite unable to predict the velocity profile, especially near the upper impeller at all the radial positions. The double-peak shape is not exhibited by the simulations without baffles. Figure 16 shows the comparison of axial profiles of phase-averaged radial velocity in a plane midway between baffles at different radial locations for Case 3 (Agarwal et al. 2021b). The ‘with baffles’ simulation cases slightly over predict the experimental measurements near the impeller vicinity. The diverging nature of flow at the bottom impeller can be seen with the increasing radial position. Here, the LBM simulations show better agreement with the experimental data. Additionally, the ‘without baffles’ case is also simulated for a comparison, which shows a lower velocity magnitude in all the radial positions. This could be due to the placement of the impellers. The lower impeller is located close to the bottom of the tank, and the distance of the upper impeller from the top of the water level is more comparable to the other two cases (Case 1 and 2). Moreover, the presence of baffles for this particular Case 3 breaks the liquid flow that leads to increased turbulence at all the radial locations of the upper impeller, resulting in higher velocity magnitude. However, the absence of baffles deteriorates the turbulence level, which in turn decreases the velocity magnitude.

Figures 17, 18, and 19 show the comparison of axial profiles of turbulent kinetic energy in a plane midway between baffles at different radial locations for Case 1, Case 2, and Case 3, respectively. The comparisons are made to give an idea about the turbulent kinetic energy variation between the aforementioned cases. The experimental data consist of baffles in their configuration, and the same is used for the validation of code developed to simulate the present study. Moreover, the authors have focussed on the effect of using/not using the baffles on the flow hydrodynamics of the stirred tank reactor. In Case 1, the kinetic energy is maximum at the impeller tips due to the high-velocity magnitude. Both the ‘with and without baffles’ cases slightly over predict the turbulent kinetic energy compared to the experimental data, especially at the smaller radial position. As the radial position increases, the results match with a relatively lower deviation than before. Similarly, in Case 2, the double peaks are observed in the with baffles case at the radial location close to the impellers. The results are in good comparison with the experimental data. Moreover, the without baffles case under-predicted the turbulent kinetic energy at the upper impeller; however, at the lower impeller, results are slightly over-predicted. Furthermore, at the radial location away from the impeller locations, the with baffles cases are in close agreement with the experimental results, except in the region between the two impellers, and the without baffles case shows similar under-predication at the upper impeller, and a slight shift is observed in the peak at the lower impeller. In Case 3, the double peaks are exhibited near the impellers. However, the simulation results slightly overpredict the experimental data, specifically in the vicinity of the upper impeller (Agarwal et al. 2021b). The without baffles case also shows a nearly similar behavior in the vicinity of the lower impeller, but the turbulent kinetic energy has a significantly lower magnitude near the upper impeller. Among the three cases, Case 1, i.e., parallel flow, depicts nearly the same behavior of velocity magnitudes and turbulent kinetic energy for the experimental data and for the simulation cases with and without baffles.

Conclusions

The present work carried out a numerical simulation on the dual-Rushton turbine equipped stirred tank reactor to scrutinize the flow characteristics. The study reported the results for the placement of impellers at different locations, along with the presence and absence of baffles in the reactor. The study used the LBM as a numerical approach to discretize the fluid domain. LES is used to model the turbulent flow, and small-scale turbulent structures are resolved by the Smagorinsky SGS model. The obtained results are compared and validated with experimental findings reported in the literature. The results show a good agreement between the reported experimental data and the simulations performed using the LBM-LES model. The results show that, in the absence of baffles, the magnitude of instantaneous velocity, phase averaged velocity, and turbulent kinetic energy is less for diverging and merging flow. One interesting finding of this study revealed that the presence or absence of baffles does not affect the velocity and turbulent kinetic energy in the parallel flow arrangement. It affirms that the baffled tank design can be avoided in the case of parallel flow to reduce manufacturing costs and save material.

The current study is intended to be expanded in terms of several valuable works. The future extension of this work will include the flow with a solid suspension of grass particles for biogas production. The effect of temperature will also be seen with the addition of the solar thermal effect on the bioreactor. Additionally, the effect of baffle geometry and impeller locations will be analyzed in the next paper.

Fig. 5
figure 5

Contour plot of instantaneous velocity magnitude at the upper impeller location for Case 1: a with baffles b without baffles

Full size image
Fig. 6
figure 6

Contour plot of instantaneous velocity magnitude at the upper impeller location for Case 2: a with baffles b without baffles

Full size image
Fig. 7
figure 7

Contour plot of instantaneous velocity magnitude at the upper impeller location for Case 3: a with baffles (Agarwal et al. 2021b) b without baffles

Full size image
Fig. 8
figure 8

Contour plot of phase-averaged velocity magnitude at the upper impeller location for Case 1: a with baffles b without baffles

Full size image
Fig. 9
figure 9

Contour plot of phase-averaged velocity magnitude at the upper impeller location for Case 2: a with baffles b without baffles

Full size image
Fig. 10
figure 10

Contour plot of phase-averaged velocity magnitude at the upper impeller location for Case 3: a with baffles (Agarwal et al. 2021b) b without baffles

Full size image
Fig. 11
figure 11

Contour plot of the phase-averaged velocity magnitude at \(\theta = 0^{\circ }\) for Case 1: a with baffles b without baffles

Full size image
Fig. 12
figure 12

Contour plot of the phase-averaged velocity magnitude at \(\theta = 0^{\circ }\) for Case 2: a with baffles b without baffles

Full size image
Fig. 13
figure 13

Contour plot of the phase-averaged velocity magnitude at \(\theta = 0^{\circ }\) for Case 3: a with baffles (Agarwal et al. 2021b) b without baffles

Full size image
Fig. 14
figure 14

Comparison of axial profiles of the phase-averaged radial velocity in a plane midway between baffles at different radial locations for Case 1

Full size image
Fig. 15
figure 15

Comparison of axial profiles of the phase-averaged radial velocity in a plane midway between baffles at different radial locations for Case 2

Full size image
Fig. 16
figure 16

Comparison of axial profiles of the phase-averaged radial velocity in a plane midway between baffles at different radial locations for Case 3 (Agarwal et al. 2021b)

Full size image
Fig. 17
figure 17

Comparison of axial profiles of the turbulent kinetic energy in a plane midway between baffles at different radial locations for Case 1

Full size image
Fig. 18
figure 18

Comparison of axial profiles of the turbulent kinetic energy in a plane midway between baffles at different radial locations for Case 2

Full size image
Fig. 19
figure 19

Comparison of axial profiles of the turbulent kinetic energy in a plane midway between baffles at different radial locations for Case 3 (Agarwal et al. 2021b)

Full size image