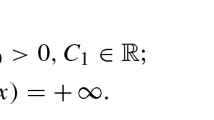Propagation, diffusion and free boundaries

Abstract

In this short review, we describe some recent developments on the modelling of propagation by nonlinear partial differential equations, which involve local as well as nonlocal diffusion, and free boundaries. After a brief account of the classical works of Fisher, Kolmogorov–Petrovski–Piskunov (KPP), Skallem and Aronson-Weinberger, on the use of reaction-diffusion equations to model propagation and spreading speed, various models involving a free boundary are considered, which have the advantage of providing a clear spreading front over the classical models, apart from giving a spreading speed. These include nonlinear Stefan problems, the porous medium equation with a nonlinear source term, and nonlocal versions of the nonlinear Stefan problems in space dimension 1. The results selected here are mainly from recent works of the author and his collaborators, and care is taken to make the content accessible to readers who are not necessarily specialists in the area of the considered topics.

1 Introduction

In this paper, we briefly review some recent research on propagation modelled by nonlinear partial differential equations (PDEs) with free boundaries. Propagation is a phenomenon appearing in many scientific branches, for example, in the spreading of nerve impulses, and in the invasion of exotic species or cancerous cells. Although the sources of propagation are diverse, the basic phenomena have been observed to follow certain rules that can be captured by mathematical models of nonlinear PDEs or systems of such equations.

Pioneered by work of Fisher [45] and Kolmogorov, Petrovski and Piskunov [62] in 1937, reaction-diffusion models have been successfully used to capture several key features of the propagation process in the natural world.

1.1 Fisher’s work and traveling wave solutions

In [45], Fisher used the equation

$$\begin{aligned} u_t-Du_{xx}=au(1-u),\; t>0,\; x\in {\mathbb {R}} \end{aligned}$$

(1.1)

to describe the spreading of an advantageous gene in a population, where u(t, x) stands for the density of population carrying the advantageous gene at time t and spatial location x, and D, a are positive constants, with D known as the diffusion rate, and a representing the net growth rate of the population.

Fisher observed that for any $c\ge c_0=2\sqrt{aD}$, Eq. (1.1) has a special solution of the form $u(t,x)=V(ct-x)$, which he called “wave of stationary form” advancing with velocity c. Obviously, V satisfies the following ODE:

$$\begin{aligned} DV''-cV'+aV(1-V)=0. \end{aligned}$$

Fisher claimed that $c_0$ should be the actual “spreading speed” of the advantageous gene in the population. Such a special solution is nowadays called a “traveling wave solution” with speed c, and the associated V is called the wave profile function.

1.2 Work of KPP (Kolmogorov–Petrovsky–Piskunov)

Independently of Fisher, in the same year 1937, Kolmogorove, Petrovski and Piskunov [62] used the equation

$$\begin{aligned} u_t-Du_{xx}=f(u),\quad t>0,\; x\in {\mathbb {R}}^1, \end{aligned}$$

(1.2)

to describe the spreading of a new gene in a population, where f(u) is a $C^1$ function satisfying

$$\begin{aligned} f(0)=f(1)=0<f(u)\le f'(0)u\quad \forall u\in (0,1),\; f'(1)<0. \end{aligned}$$

They proved that for $c\ge c_0:=2\sqrt{f'(0)D}$, Eq. (1.2) has a solution $u(t,x):=W(ct-x)$ satisfying

$$\begin{aligned} W'(y)>0 \text{ for } y\in {\mathbb {R}}^1,\; W(-\infty )=0,\quad W(+\infty )=1; \end{aligned}$$

no such solution exists if $c<c_0$. Moreover, the solution of (1.2) with initial condition

$$\begin{aligned} u(0,x)=1\quad \text{ for } x<0, u(0,x)=0 \quad \text{ for } x>0, \end{aligned}$$

converges (in a certain sense) to a traveling wave solution with the minimal speed $c_0$.

Let us note that if one takes $f(u)=au(1-u)$, then the result of Fisher is recovered, and the last conclusion is supportive to Fisher’s claim that $c_0$ is the spreading speed of the new gene in the population.

1.3 Observation of Skellam and constant spreading speed

In [75], Skellam made a striking observation of that time, based on published data on the spreading of muskrat in Europe.

The muskrat, which is a species native to North America, was brought to Europe for fur-breeding. In 1905, five muskrats escaped from a farm located near Prague in Czechoslovakia. They started to spread and reproduce, inhabiting the entire European continent within 50 years.

Using a map obtained by Ulbrich (1930), Skellam calculated the “$area\, of\, the\, muskrat's\, range \, A(t)$”, took its “square root” and plotted it “against the time t” (in years), and found that the data points lay on a straight line, namely the function $t\rightarrow \sqrt{A(t)}$ is linear (see below).

The meaning of $\sqrt{A(t)}$ is illustrated in the following graph, where

$$\begin{aligned} A(t) = \text{ shaded } \text{ area } = \text{ area } \text{ of } \text{ disk } \text{ of } \text{ radius } R(t), \end{aligned}$$

and so

$$\begin{aligned} \sqrt{A(t)}=\sqrt{\pi } \times R(t). \end{aligned}$$

In ecological terms, R(t) is the “range radius” of the maskrats at time t. Thus Skellam’s observation says: The range radius of the maskrats increases linearly in time. Or worded in another way: The spreading of Maskrates has a constant speed.

Subsequently, data on the spreading of many other species were used to show similar spreading behavior, including those for the spread of Himalayan Thar in South Island of New Zeeland during 1936–1966, the spread of house finch in North America during 1956–1973, and the spread of Japanese beetle in North America during 1916–1941, to mention but a few. All these gave strong support to Fisher’s claim on the existence of a constant spreading speed $c_0$, based on the PDE model (1.1).

1.4 Work of Aronson and Weinberger

Aronson and Weinberger were the first to rigorously prove Fisher’s claim on the spreading speed. In [4], they considered the following parabolic equation in ${\mathbb {R}}^N$ $(N\ge 1)$:

$$\begin{aligned} u_t-D\Delta u=f(u), \end{aligned}$$

where $\Delta u=u_{x_1x_1}+\cdots +u_{x_Nx_N}$ is the Laplacian operator. They examined several important classes of functions f(u), but for clarity and convenience of comparison, we only describe the result for the special case $f(u)=au(1-u)$, as used in Fisher [45].

Let U(t, x) be the unique solution of the Cauchy problem

$$\begin{aligned} \left\{ \begin{aligned}&U_t-D\Delta U=f(U)\quad \text{ for } x\in {\mathbb {R}}^N,\; t>0,\\&U(0,x)=U_0(x) \quad \text{ for } x \in {\mathbb {R}}^N, \end{aligned} \right. \end{aligned}$$

(1.3)

where $U_0(x)$ is nonnegative and has nonempty compact support, representing the assumption that the initial population range is a bounded region in space. Then the following conclusions hold:

• There exists $c_0>0$ such that, $\forall \epsilon >0$, as $t\rightarrow \infty$,

  $$\begin{aligned}\left\{ \begin{array}{l} U(t,x)\rightarrow 1 \text{ uniformly } \text{ for } x\in \{x\in {\mathbb {R}}^N: |x|\le (c_0-\epsilon )t\},\\ U(t,x)\rightarrow 0 \text{ uniformly } \text{ for } x\in \{x\in {\mathbb {R}}^N: |x|\ge (c_0+\epsilon )t\}. \end{array}\right. \end{aligned}$$

• $c_0$ is determined by the associated traveling wave problem

  $$\begin{aligned} \left\{ \begin{array}{l} DQ''-cQ'+f(Q)=0,\; Q>0 \text{ in } {\mathbb {R}}^1,\\ Q(-\infty )=0,\; Q(+\infty )=1, \; Q(0)=1/2. \end{array} \right. \end{aligned}$$

  (1.4)

  More precisely, $c_0>0$ is the minimal value of c such that (1.4) has a (unique) solution $Q=Q_c$.

The number $c_0$ is called the spreading speed of U. With $f(u)=au(1-u)$, $c_0=2\sqrt{aD}$, “as claimed by Fisher!”

The above convergence result of Aronson and Weinberger has been considerably improved. If the initial function $U_0$ in (1.3) is radially symmetric, then U is radially symmetric in x (i.e. $U=U(t,|x|)$) and the following holds:

$$\begin{aligned} \lim _{t\rightarrow \infty }\left| U(t,|x|)-Q_{c_0}\Big ({c_0t-\frac{N+2}{c_0}D\ln t}+C-|x|\Big )\right| =0 \end{aligned}$$

(1.5)

for some constant C, uniformly in $x\in {\mathbb {R}}^N$.

If $U_0$ is not radially symmetric, then it follows from a simple comparison argument and the above result on radial solutions that, for any small $\epsilon >0$,

$$\begin{aligned} \left\{ \begin{array}{l} U(t,x)\rightarrow 1 \text{ uniformly } \text{ for } x\in \left\{ x\in {\mathbb {R}}^N: |x|\le c_0t-\Big (\frac{N+2}{c_0}D+\epsilon \Big )\ln t\right\} , \\ U(t,x)\rightarrow 0 \text{ uniformly } \text{ for } x\in \left\{ x\in {\mathbb {R}}^N: |x|\ge c_0t -\Big (\frac{N+2}{c_0}D-\epsilon \Big )\ln t\right\} . \end{array}\right. \end{aligned}$$

This phenomenon is widely known as the “logarithmic shift” in the Fisher-KPP spreading.

Remarks

• When $N=1$, the logarithmic shift term in (1.5) has coefficient $3/c_0$, which was first obtained by Bramson [12] by a probabilistic method for a problem concerning branching Brownian motion; it is now known as the “Bramson correction term”.

• For $N\ge 2$, (1.5) follows from Gärtner [48] (by probabilistic method).

These classical works have inspired extensive further research in several directions, including research on propagation in various heterogeneous environments, and on cases where the random diffusion term $d\Delta u$ is replaced by suitable nonlocal diffusion operators. In the rest of this paper, we will report on a selection of some recent works on extending these classical results to equations with free boundaries, and new findings.

2 Nonlinear Stefan problems

In the spreading process of real world problems, there is always a so called “spreading front”; for example, during the invading phase of an exotic species, the boundary of the population range is the spreading front, beyond which no members of the species can be found. However, such a front is not captured by the model (1.3), since the population density $U(t,x)>0$ for all $x\in {\mathbb {R}}^N$ once $t>0$, which is a consequence of the strong maximum principle for parabolic equations.

A convention is to nominate a small positive constant $\delta$ and use

$$\begin{aligned} \Omega _\delta (t):=\{x: U(t,x)>\delta \} \end{aligned}$$

to represent the population range at time t, and therefore the level set

$$\begin{aligned} \Gamma _\delta (t):=\{x: U(t,x)=\delta \} \end{aligned}$$

can be regarded as the spreading front at time t. By the convergence result of Aronson and Weinberger, as time goes to infinity, the front moves to infinity at roughly the speed $c_0$ in all directions pointing away from the initial population range $\Omega (0)$, regardless of the the choice of such small $\delta$ and the initial function $U_0$.

In many practical situations, such as in the spreading of an epidemic, it is important to obtain an accurate estimate of the spreading front, and models of the form (1.3) become inadequate. To overcome this shortcoming of (1.3), Du and Lin [29] introduced a free boundary version of the Fisher equation (1.1), where the equation for u(t, x) is satisfied over a changing interval (g(t), h(t)), representing the population range at time t, together with the boundary condition $u(t, x)=0$ for $x\in \{g(t), h(t)\}$, and free boundary condition

$$\begin{aligned} h'(t)=-\mu u_x(t,h(t)),\; g'(t)=-\mu u_x(t, g(t)) \text{ for } \text{ some } \text{ fixed } \mu >0. \end{aligned}$$

They showed that this modified model always has a unique solution and as time goes to infinity, the population u(t, x) exhibits a “spreading-vanishing dichotomy”, namely it either vanishes or converges to 1; moreover, in the latter case, a finite spreading speed can be determined. This work has motivated considerable research, and the “spreading-vanishing dichotomy” discovered in [29] has been shown to occur in a variety of similar models; see, for example, extensions to equations with a more general nonlinear term f(u) [31, 59, 60] etc., extensions to equations with advection [52, 58, 83] etc., extensions to systems of population or epidemic models [1, 30, 40, 53, 68, 80, 82] etc., and development of numerical methods for treating some of these free boundary problems [69, 70, 72] etc.

In space dimension one with Fijita type nonlinear function f(u), such as $f(u)=u^p$ with $p>1$, similar free boundary problems were considered earlier in [43, 43], where the focus was on the blow-up behaviour of the solution and therefore is of completely different nature. See [90] for a more recent work in that direction.

In the following, we describe the extension of the model in [29] to high space dimensions, and compare the results with those for (1.3). The free boundary problem in space dimension $N\ge 1$ has the form

$$\begin{aligned} \left\{ \begin{aligned}&u_t-D\Delta u=f(u)\quad \text{ for }~~x\in \Omega (t),t>0,\\&u=0~\text{ and }~u_t=\mu |\nabla _x u|^2\quad \text{ for }~~x\in \partial \Omega (t),t>0,\\&u(0,x)=u_0(x)\quad \text{ for }~~x\in \Omega _0. \end{aligned} \right. \end{aligned}$$

(2.1)

Here $\Omega (t)\subset {{\mathbb {R}}}^N$ is the population range at time t, with $\Omega (0)=\Omega _0$, and we assume that $\Omega _0$ is a bounded domain with smooth boundary, $u_0\in C^1({\overline{\Omega }}_0)$ is positive in $\Omega _0$, and $u_0|_{\partial \Omega _0}=0$. For convenience of comparison, we again take $f(u)=au(1-u)$.

We note that in (2.1), both u(t, x) and $\Omega (t)$ are unknowns. The physical meaning of the free boundary condition is: Each point $x\in \partial \Omega (t)$ moves in the direction of the outer normal to $\partial \Omega (t)$ at x, with velocity $\mu |\nabla _x u(t,x)|$. In the spherically symmetric setting, where

$$\begin{aligned} \partial \Omega (t)=\{x: |x|=h(t)\} \text{ and } u=u(t,r),\; r=|x|, \end{aligned}$$

this can be simplified to $h'(t)=-\mu u_r(t,h(t))$.

In the case $f(u)\equiv 0$, (2.1) reduces to the well-known “one-phase Stefan problem” [15, 46, 61], where u(t, x) represents the temperature of water in the water region $\Omega (t)$, which is surrounded by ice. In such a case, the free boundary condition can be deduced from the law of energy conservation under phase transformation in the process of ice melting, and is known as the “Stefan condition”. However, in the biological setting, very few first principles are available to help the modelling process. Nevertheless, if u(t, x) represents the population density of a biological species in (2.1), the free boundary condition can be deduced from the assumption that k units of the species is lost per unit volume at the front [13], which gives $\mu =D/k$.

While the free boundary condition is meaningful when $\partial \Omega (t)$ is $C^1$, in general, such smoothness is not guaranteed for all $t>0$ even if the initial data $(u_0, \Omega _0)$ are sufficiently smooth. As in the classical Stefan problem, (2.1) has to be understood in a certain weak sense. It was proved by Du and Guo [25] that (2.1) has a unique weak solution defined for all $t>0$.

2.1 Basic results for (2.1)

By results in Du et al. [33], the regularity and long-time dynamical behavior of the solution to (2.1) can be described as follows.

Theorem 2.1

Let $(u(t,x), \Omega (t))$ be the weak solution of (2.1). Then the following conclusions hold:

• 1. $\Omega (t)$ is expanding: ${\overline{\Omega }}_0\subset \Omega (t)\subset \Omega (s)$ if $0<t<s$.

• 2. $\partial \Omega (t){\setminus } (\text{convex } \text{ hull } \text{ of } {\overline{\Omega }}_0)$ is smooth.

• 3. “Spreading-vanishing dichotomy:” Let $\Omega _\infty :=\cup _{t>0}\Omega (t)$. Then either

  $$\begin{aligned} {\mathbf{(a)} \,{\Omega _\infty \ is\, a\, bounded\, set}, or\ \mathbf{(b)}\, {\Omega _\infty ={\mathbb {R}}^N}. } \end{aligned}$$

  Moreover, in case (a), “vanishing” happens: $\lim _{t\rightarrow \infty }\Vert u(t,\cdot )\Vert _{L^\infty (\Omega (t))}=0$; in case (b), “spreading” happens: $\lim _{t\rightarrow \infty }u(t,x)=1$ $\forall x\in {\mathbb {R}}^N$.

  Furthermore, in case (b), for all large t, $\partial \Omega (t)$ is a smooth closed hypersurface contained in the spherical shell

  $$\begin{aligned} \left\{ x\in {\mathbb {R}}^N: 0\le |x|- M(t)\le \frac{\pi }{2} \mathrm{diam}(\Omega _0)\right\} , \end{aligned}$$

  where M(t) is a continuous function satisfying

  $$\begin{aligned} \lim _{t\rightarrow \infty }\frac{M(t)}{t}=c_0^*>0. \end{aligned}$$

The number $c_0^*$ is called the “spreading speed” of (2.1), and it is determined by the following result.

Theorem 2.2

[31] For any $\mu >0$ there exists a unique $c_0^*=c_0^*(\mu )>0$ and a unique solution $q_{c_0^*}$ to

$$\left\{ \begin{array}{ll} Dq^{\prime \prime }-cq^{\prime }+f(q)=0,&\quad q>0 \quad \mathrm{in}\ (0,\infty ),\\ q(0)=0,&\quad q(\infty )=1 \end{array} \right.$$

(2.2)

with $c=c_0^*$ such that $q_{c_0^*}^{\prime }(0)=\frac{c_0^*}{\mu }$.

We call $q_{c_0^*}$ a “semi-wave” with speed $c_0^*$.

The following result indicates that (1.3) is the limiting problem of (2.1) as $\mu \rightarrow \infty$.

Theorem 2.3

The following conclusions hold:

• (a) [25] If the solution $(u,\Omega (t))$ of (2.1) is denoted by $(u_\mu , \Omega _\mu (t))$ to stress its dependence on $\mu$, then as $\mu \rightarrow \infty$,

  $$\begin{aligned} \Omega _\mu (t)\rightarrow {\mathbb {R}}^N (\forall t>0),\; u_\mu \rightarrow U \text{ in } C_{loc}^{1, 2}((0,\infty )\times {\mathbb {R}}^N), \end{aligned}$$

  where U is the unique solution of (1.3) with $U_0=u_0$.

• (b) [31] $c_0^*=c_0^*(\mu ) \text{ increases } \text{ to } c_0 \text{ as } \mu \rightarrow \infty$, where $c_0$ is the spreading speed of (1.3).

The profile of the solution to (2.1) as $t\rightarrow \infty$ can be better described, via the following result.

Theorem 2.4

[35] If $u_0$ and $\Omega _0$ are radially symmetric in (2.1), and thus

$$\begin{aligned} u=u(t,|x|),\; \Omega (t)=\left\{ x\in {\mathbb {R}}^N: |x|<h(t)\right\} . \end{aligned}$$

Then, as $t\rightarrow \infty$,

$$\begin{aligned} \left\{ \begin{array}{l} u(t,|x|)-q_{c_0^*}(h(t)-|x|)\rightarrow 0 \text{ uniformly } \text{ in } x,\\ h(t)-\left[ c_0^*t-(N-1)c_1^*D\ln t\right] \rightarrow C=C(u_0)\in {\mathbb {R}}, \end{array} \right. \end{aligned}$$

(2.3)

where $(c_0^*, q_{c_0^*})$ is given in Theorem 2.2, and $c_1^*>0$ is given by

$$\begin{aligned} c_1^*=\frac{1}{\zeta \, c_0^*},\quad \zeta =1+\frac{c_0^*}{\mu ^2\int _0^\infty q'_{c_0^*}(z)^2e^{-c_0^*z}dz}. \end{aligned}$$

Remark

By Theorem 2.4 and a simple comparison argument, in case (b) of Theorem 2.1 (without radial symmetry), there exist constants $C_1\le C_2$ such that, for all large t,

$$\begin{aligned} \partial \Omega (t)\subset \left\{ C_1\le |x|-\big [{c_0^*t-(N-1)c_1^*D\ln t}\big ]\le C_2\right\} . \end{aligned}$$

Clearly this significantly improves the conclusion $\lim _{t\rightarrow \infty } \frac{M(t)}{t}=c_0^*$ in Theorem 2.1.

2.2 Comparison of (1.3) and (2.1)

The above results indicate that (2.1) retains the main features of the classical model (1.3), but also exhibits a number of differences, and Theorem 2.4 shows that (1.3) can be viewed as the limiting problem of (2.1) as $\mu \rightarrow \infty$. We summarize below their similarities and differences.

“Similarities:” When spreading happens, (1.3) and (2.1) share the following asymptotic behaviors:

• (i) Shape of fronts: In both models, the fronts can be approximated by spheres.

• (ii) Spreading speed: The fronts go to infinity at some constant asymptotic speeds ($c_0$ and $c_0^*$, respectively).

“Differences:”

• (i) Location of front:

  • The front in (2.1) is located at the free boundary.

  • (1.3) does not give the precise location of the front.

• (ii) Success of spreading:

  • (1.3) gives “consistent success of spreading”: Spreading succeeds whenever the initial function $U_0(x)$ is not identically zero.

  • (2.1) yields a “spreading-vanishing dichotomy”: For “large” initial function $u_0$, spreading happens; for “small” $u_0$, vanishing happens.¹

• (iii) Logarithmic shift:

  • The (approximate) front of (1.3) propagates behind the moving sphere $\{x\in {\mathbb {R}}^N: x=c_0 t\}$ by a distance of the order $``{\frac{N+2}{c_0}D\ln t}''$.

  • the front of (2.1) propagates behind the moving sphere $\{x\in {\mathbb {R}}^N: |x|=c_0^* t\}$ by a distance of the order $``{(N-1)c_1^*D\ln t}''$ (when spreading happens).

  In particular, when dimension $N=1$, logarithmic shifting happens for (1.3) but not for (2.1)²

3 Porous medium equation with a source

Another extension of (1.3), which also involves a free boundary, is the the following porous medium equation with some source term f(u):

$$\begin{aligned} \left\{ \begin{aligned}&u_t-D\Delta (u^m)=f(u)&\text{ for }~~x\in {\mathbb {R}}^N,\;t>0,\\&u(0,x)=u_0(x)&\text{ for }~~x\in {\mathbb {R}}^N, \end{aligned} \right. \end{aligned}$$

(3.1)

where $m>1$, $u_0$ is nonnegative, continuous and has nonempty compact support, and again for convenience of comparison we take $f(u):=au(1-u)$. Clearly (3.1) reduces to (1.3) when $m=1$.

When $f(u)\equiv 0$, the equation in (3.1) becomes the well known porous medium equation (PME) used to model the spreading of gas (with density u(x, t)) through a porous medium, and has attracted extensive investigation since the 1950s.

Due to the degeneracy at $u=0$, (3.1) does not have a classical solution in general; it has a unique weak solution, defined for all time $t>0$. Since $u_0$ has compact support, one important feature of (3.1) is that for any future time $t>0$, the solution u(t, x) has compact support:

$$\begin{aligned}\Omega (t):=\{x: u(t,x)>0\} \text{ is } \text{ bounded } \text{ in } {\mathbb {R}}^N. \end{aligned}$$

The boundary of $\Omega (t)$ is known as the free boundary of (3.1). Note that although $u(t,x)=0$ for $x\in {\mathbb {R}}^N\setminus \Omega (t)$, but in contrast to (2.1), equation (3.1) is satisfied over the entire ${\mathbb {R}}^N$ in the weak sense.

Problem (3.1) has been widely used to model the growth and propagation of a spatially distributed biological population since Gurney and Nisbet [54] (with $m=2$) and Gurtin and MacCamy [55] (with $m>1$).

A recent paper of Audrito and Vázquez [5] shows that, there exists $c_*>0$ such that, for any small $\epsilon >0$, the unique (weak) solution of (3.1) satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \lim _{t\rightarrow \infty } u(x,t)= 1 \text{ uniformly } \text{ in } \big \{|x|\le ({c_*-\epsilon }) t\big \},\\ u(x,t)=0 \text{ in } \big \{|x|\ge ({c_*+\epsilon })t\big \} \text{ for } \text{ all } \text{ large } t. \end{array}\right. \end{aligned}$$

(3.2)

This is parallel to the result of Aronson and Weinberger [4] for (1.3), and $c^*$ is called the spreading speed determined by (3.1). Moreover, it is known from Gilding and Kersner [51] that for every $c\ge c_*$, there exists $V=V_{c}$ satisfying

$$\begin{aligned} D(V^m)''-cV'+f(V)=0,\; V(-\infty )=0,\; V(\infty )=1, \end{aligned}$$

and no such solution exists when $c<c_*$. Moreover, for $c=c_*$ there is a unique solution $V_{c_*}$ whose support is $[0,\infty )$, but for every $c>c_*$, $V_c>0$ in ${\mathbb {R}}$.

We note that, for any unit vector $e\in {\mathbb {R}}^N$, $u(t,x):=V(ct-x\cdot e)$ solves (3.1) (except the initial condition), and is called a planer traveling wave solution with speed c. Thus the spreading speed of (3.1) is the minimal traveling wave speed, as in the case for (1.3).

The above result has been sharpened by Du et al. [38]:

Theorem 3.1

If $u_0$ in (3.1) is radially symmetric, and so

$$\begin{aligned}u=u(t,|x|) \text{ with } \text{ free } \text{ boundary } \big \{|x|=h(t)\big \}, \end{aligned}$$

then there is a constant $c^{\#}>0$ such that, as $t\rightarrow \infty$,

$$\begin{aligned}\left\{ \begin{array}{l} u(t,x)-V_{c_*}(h(t)-|x|)\rightarrow 0 \text{ uniformly } \text{ in } x \in {\mathbb {R}}^N,\\ h(t)-[c_*t-{(N-1)c^{\#}}D\ln t]\rightarrow \sigma =\sigma (u_0)\in {\mathbb {R}}. \end{array}\right. \end{aligned}$$

The constant $c^{\#}$ is given by $c^{\#}=\zeta /c_*$ with

$$\begin{aligned} \zeta =\frac{\int _0^{\infty }(V^m_{c_*})'(x)\,{\exp }\left( \frac{m-1}{m}\int _{x_*}^x\frac{1-V_{c_*}(y)}{(V_{c_*}^{m-1})'(y)}dy\right) dx}{\int _0^{\infty }(V_{c_*})'(x)\,{\exp }\left( \frac{m-1}{m}\int _{x_*}^x\frac{1-V_{c_*}(y)}{(V_{c_*}^{m-1})'(y)}dy\right) dx}, \end{aligned}$$

where $x_*\in (0, \infty )$ is uniquely determined by

$$\begin{aligned} V_{c_*}(x_*)=\Big (\frac{m-1}{m}\Big )^{\frac{1}{m-1}}. \end{aligned}$$

If the initial function in (3.1) is not radially symmetric, by Theorem 3.1 and a simple comparison argument, the following sharper version of (3.2) holds:

Corollary 3.2

For a general $u_0$, there exist $r_1, r_2\in {\mathbb {R}}$ such that the boundary of $\Omega (t):=\{x: u(x,t)>0\}$ for all large time t is contained in the spherical shell

$$\begin{aligned} \left\{ x\in {\mathbb {R}}^N: r_1\le |x|-\big [{c_* t-(N-1)c^{\#} D\ln t}\big ]\le r_2\right\} . \end{aligned}$$

Moreover, for any small $\epsilon >0$,

$$\begin{aligned} \lim _{t\rightarrow \infty }u(x,t)=1 \text{ uniformly } \text{ in } \big \{|x|\le c_*t-(N-1)(c^{\#}D+{\epsilon })\ln t\big \}. \end{aligned}$$

Remark 3.3

Comparing (1.3), (2.1) and (3.1), we have the following observations:

• (i) Shape of fronts: In all three models (1.3), (2.1) and (3.1), the fronts can be approximated by spheres.

• (ii) Spreading speed: In all three models the fronts go to infinity at some constant asymptotic speed $(c_0$, $c_0^*$ and $c_*$, resp.).

• (iii) Location of fronts: “(2.1) and (3.1)” give the precise location via their free boundaries; (1.3) does not give the precise location of the front.

• (iv) Success of spreading: “(1.3) and (3.1)” yield consistent success of spreading; (2.1) yields a spreading-vanishing dichotomy.

• (v) Logarithmic shifts: (1.3) has shift

  $$\begin{aligned} {\frac{N+2}{c_0}}D\ln t; \end{aligned}$$

  “(2.1) and (3.1)” have shifts

  $$\begin{aligned} {(N-1)c_1^*}D\ln t,\quad {(N-1)c^{\#}}D\ln t, \text{ respectively. } \end{aligned}$$

  Therefore, in dimension $N=1$, (2.1) and (3.1) do not have logarithmic shift, but (1.3) has.

4 Heterogeneous environment

The models in the previous sections all assume that the environment in which the concerned species propagates is homogeneous, namely the environment does not change with time t and space location x, and therefore all the parameters in the models are constants. In reality, the environment is heterogeneous in both t and x, and so it is more natural to assume that these parameters are functions of (t, x). However, this causes great difficulties in the mathematical treatment of the models. For example, one key feature of these models is the existence of an asymptotic spreading speed, which is determined by the speed of the associated traveling wave (or semi-wave) solutions. Let us recall that these special solutions are all obtained by looking for self-similar solutions of the form

$$\begin{aligned} u(t,x)=V(ct-x\cdot e) \text{ with } e\in {\mathbb {R}}^N \text{ a } \text{ fixed } \text{ unit } \text{ vector }, \end{aligned}$$

and the function V satisfies an ODE, which is usually relatively easy to solve. Indeed, in every model described in the previous three sections, the corresponding ODE yielding the required traveling wave or semi-wave solutions has been completely understood. Unfortunately, this approach relies crucially on the fact that all the parameters in the model are constants; in heterogeneous environment, it does not work anymore!

On the other hand, if the phenomena revealed by these models do not persist when the homogeneous environment is perturbed by heterogeneous ones, the usefulness of the models would be very questionable. Therefore, it is of great importance to know whether the phenomena obtained through models of homogeneous environment are retained in heterogeneous environment. This is a rather challenging task but success has been achieved in several directions.

To give a taste of results of this kind, we focus on a very simple 1-D version of (1.3), namely

$$\begin{aligned} U_t- U_{xx}=a(t,x)U(1-U),\; x\in {\mathbb {R}}^1,\; t>0, \end{aligned}$$

(4.1)

and a 1-D version of (2.1), i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} u_t- u_{xx}=a(t,x)u(1-u),&\quad x\in (g(t), h(t)),\; t>0,\\ u(t, g(t))=u(t, h(t))=0,&\quad t>0,\\ g'(t)=-\mu u_x(t, g(t)),&\quad h'(t)=-\mu u_x(t, h(t)),\; t>0, \end{array}\right. \end{aligned}$$

(4.2)

where a(t, x) is continuous and positive.

Some special heterogeneous environments can be captured as follows:

• 1. “Space periodic only:” $a=a(x)$ is L-periodic.

• 2. “Time-periodic only:” $a=a(t)$ is T-periodic.

• 3. “Space-time-periodic:” $a=a(t,x)$ is L-periodic in x and T-periodic in t.

• 4. “Shifting environment:” $a=A(x-ct)$ with given $c>0$.

For these special cases as well as in many other situations, the main results in Sections 2 and 3 have been shown to remain valid under natural modifications.

For (4.1), the basic theory in homogeneous environment (with suitable variations) has been extended to the various heterogeneous cases by many researchers, starting from the work of Gärtner and Freidlin [49] (by a probabilistic method). A proper review of these results is beyond the scope of this paper; instead we just recall how the traveling wave in the homogeneous environment is extended to the heterogeneous case when the environment is space-periodic only.

Pulsating traveling wave: u(t, x) is called a pulsating traveling wave of (4.1) with $a=a(x)$ an L-periodic function, if it solves (4.1) and satisfies

$$\begin{aligned}\left\{ \begin{array}{ll} u\left(t+\frac{L}{c},x\right)=u(t, x-L) \text{ for } t,&\quad x\in {\mathbb {R}}^1,\\ u(t,-\infty )=1,&\quad u(t,+\infty )=0 \text{ for } \text{ all } t\in {\mathbb {R}}^1. \end{array}\right. \end{aligned}$$

The constant c is called the “effective speed” of the pulsating traveling wave.

The following result of Berestycki and Hamel [9] is a parallel to the classical result of KPP [62] on traveling wave solutions in homogeneous environment:

Theorem 4.1

There exists ${\hat{c}}>0$ such that (4.1) has a pulsating traveling wave if $c\ge {\hat{c}}$, and no such pulsating traveling wave exists if $c<{\hat{c}}$.

It is now well-known that ${\hat{c}}$ is the spreading speed of (4.1) [10, 49]. For further results in this direction, we refer to [10] and the references therein.

Regarding (4.2), the basic theory in [29] has been extended to the time-periodic case in [26, 78], to space-periodic case in [28], to time-almost-periodic case in [64,65,66], to the case of shifting environment in [41, 57, 63, 83], and to space-time-periodic environment in [23, 24].

In the following, we briefly describe the results of Du and Liang [28] for the space-periodic case. We call (u(t, x), h(t)) a “pulsating semi-wave” of (4.2) if it satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} u_{t}- u_{xx}=a (x)u(1-u), &\quad t\in {\mathbb {R}}, \ -\infty<x<h(t), \\ u(t, h(t))=0,\; h'(t)=-\mu u_x(t,h(t)),&\quad t\in {\mathbb {R}}, \end{array} \right. \end{aligned}$$

(4.3)

and has the following properties:

• (i) there exists a $C^{1,2}({\mathbb {R}}\times [0, +\infty ))$ function $U(\tau , \xi )$ which is L-periodic in $\tau$ such that, $u(t,x)=U(h(t), h(t)-x)>0$ for $t\in R,\; x<h(t)$,

• (ii) there exists $T>0$ such that $h'(t)$ is a positive T-periodic function and $h(t+T)-h(t)=L$.

The following theorem shows that $C:=L/T$ is the (average) speed of the semi-wave. Let us also observe that $u(t+T,x)=u(t,x-L)$.

Theorem 4.2

[28] Problem (4.2) always has a pulsating semi-wave $({\tilde{u}},{\tilde{h}})$. The pulsating semi-wave is unique up to translations in t. Furthermore, $\lim _{t\rightarrow \pm \infty }{\tilde{h}}(t)/t=L/T$, ${\tilde{u}}_t(t,x)>0$, and ${\tilde{u}}(t,x)\rightarrow \phi (x)$ as $t\rightarrow +\infty$ uniformly for x in any interval of the form $(-\infty , M]$, $M\in {\mathbb {R}}$, where $\phi$ is the unique positive solution of

$$\begin{aligned} - \phi _{xx}=a(x)\phi (1-\phi ),\; x\in {\mathbb {R}}. \end{aligned}$$

Using Theorem 4.2, one can deduce the following result on the asymptotic spreading speed determined by (4.2).

Theorem 4.3

Let (u, g, h) be any solution of (4.2) and spreading happens; then

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{-g(t)}{t}=\lim _{t\rightarrow \infty }\frac{h(t)}{t}=\frac{L}{T}, \end{aligned}$$

where L/T is the average speed of the semi-wave in Theorem 4.2.

Remark 4.4

It is possible to determine the spreading speed of (4.1) and (4.2) without making use of a generalized version of the traveling wave solution as described above. Weinberger [84, 85] introduced an alternative approach based on some dynamical system arguments which can be used to directly determine the spreading speed of problems like (4.1). This approach was further developed by Liang and Zhao [67] and others, so that it is applicable to a wide range of propagation models. In [23, 24], such an approach was extended to treat (4.2) for the space-time-periodic case, without knowing the existence of a generalized semi-wave solution. Indeed, the existence of a generalized semi-wave solution in such a setting is still an open problem.

5 Nonlocal diffusion

The spatial dispersal of the species in both (1.3) and (2.1) is governed by the diffusion term $D\Delta u$, which is obtained by assuming that the dispersal of the population follows a random walk strategy. While this is a good approximation in many cases, it is increasingly recognised that such an approximation is far from ideal in general [71]. Several diffusion operators of nonlocal nature have been used to replace the term $D\Delta u$, and in the past 10-20 years significant progress has been made in that direction.

One widely used nonlocal diffusion operator has the form

$$\begin{aligned} {\mathcal {L}} u:=d\int _{{\mathbb {R}}^N} J(x-y) u(t,y)dy-d u(t,x), \end{aligned}$$

where $J: {\mathbb {R}}^N\rightarrow [0,\infty )$ is a continuous function satisfying $\int _{{\mathbb {R}}^N}J(x)dx=1$.

In this section, we look at some results on (1.3) and (2.1) with the random diffusion term $D\Delta u$ replaced by ${\mathcal {L}} u$ in space dimension 1. Thus (1.3) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle u_t={d\int _{{\mathbb {R}}} J(x-y) u(t,y)dy-du(t,x)}+f(u) &\quad \text{ for } x\in {\mathbb {R}}, t>0, \\ u(0,x)=u_0(x)\ge ,\not \equiv 0 &\quad \text{ for } x\in {\mathbb {R}}. \end{array} \right. \end{aligned}$$

(5.1)

To see the differences between these diffusion operators from the point of view of modelling, let us recall that in the modelling process, ${\mathbb {R}}$ is divided into tiny blocks of equal length $\lambda$, time is divided into tiny steps of length $\tau$. In the “random walk” model, it is assumed that from time t to $t+\tau$, each individual moves from its current location to either the left neighbouring block or the right neighbouring block, with equal probability 1/2. The term $D u_{xx}$ is obtained by letting $\lambda$ and $\tau$ go to 0 in a suitable fashion.

In contrast, in the nonlocal diffusion model, it is assumed that an individual can jump to non-neighbouring blocks: from time t to time $t+\tau$, an individual at block x can jump to any other block y with probability $J(x-y)$.

The behavior of the kernel function J(x) at $\pm \infty$ turns out to play a pivotal role on the propagation determined by (5.1). The kernel function J(x) is called “thin-tailed” if there exists $\lambda >0$ such that

$$\begin{aligned} \int _{{\mathbb {R}}} e^{\lambda x} J(x)dx<\infty . \end{aligned}$$

Otherwise it is called “fat-tailed”. Thus any J(x) with compact support is thin-tailed, and $J(x)=\xi \,e^{-\mu |x|}$ $(\xi , \mu >0)$ is thin-tailed, but $J(x)=\eta (1+|x|)^{-\mu }$ $(\eta , \mu >0)$ is fat-tailed.

When the convolution kernel in (5.1) is thin-tailed, much of the basic theory for (1.3) carries over (see, for example, [6,7,8, 17, 21, 22, 73, 77, 84, 85, 87] and the references therein). On the other hand, “accelerated spreading” happens when the kernel function is fat-tailed.

The following result follows from Weinberger [84]:

Theorem 5.1

Let u(t, x) be the solution of (5.1) with $f(u)=au(1-u)$. Then $\lim _{t\rightarrow \infty } u(t,x)=1$ locally uniformly for $x\in {\mathbb {R}}$. Moreover, for any given $\delta \in (0,1)$, the level set

$$\begin{aligned} L_\delta (t):=\{x\in {\mathbb {R}}: u(t,x)=\delta \}=\partial \{x: u(t,x)>\delta \} \end{aligned}$$

satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{\sup L_\delta (t)}{t}=\lim _{t\rightarrow \infty }\frac{\inf L_\delta (t)}{-t}=\left\{ \begin{array}{ll} c_*\in (0, \infty ) &\quad \text{if } J \text{ is } \text{ thin-tailed, }\\ \infty &\quad \text{if } J \text{ is } \text{ fat-tailed }. \end{array}\right. \end{aligned}$$

This result indicates that the spreading speed of u is finite if and only if J is thin-tailed. When the spreading speed is $\infty$, one says that accelerated spreading happens. Examples of fat-tailed J were given in [47] such that $\sup L_\lambda (t)$ and $-\inf L_\lambda (t)$ behave like

$$\begin{aligned} e^{\alpha t} (\alpha >0) \text{ with } J(x)\sim |x|^\sigma \; (\sigma <-2), \end{aligned}$$

or

$$\begin{aligned} {{t^\beta (\beta >1)} \hbox {with} {J(x)\sim e^{-|x|^{1/\beta }}}. } \end{aligned}$$

Other examples of accelerated spreading can be found in [2, 11, 14, 42, 44, 76, 86], etc.

5.1 Free boundary models with nonlocal diffusion in one space dimension

We now look at the nonlocal version of (2.1) in one space dimension with $f(u)=au(1-u)$ (namely (4.2) with $a(t,x)\equiv a$). An extra difficulty arises here: it is not enough to simply replace the term $du_{xx}$ by $d\int _{g(t)}^{h(t)}J(x-y)u(t,y)dy-du(t,x)$, since the solution u(t, x) is in general not differentiable in x anymore, and so the free boundary conditions there are problematic in the nonlocal case. In [16], the following nonlocal version of (2.1) was proposed:

$$\begin{aligned} \left\{ \begin{aligned}&u_t=d\int _{g(t)}^{h(t)}J(x-y)u(t,y)dy-du(t,x)+f(u),\quad g(t)<x<h(t),\; t>0,\\&u(t,g(t))=u(t,h(t))=0,\quad t>0,\\&h'(t)=\mu \int _{g(t)}^{h(t)}\int _{h(t)}^{+\infty } J(x-y)u(t,x)dydx,\quad t>0, \\&g'(t)=-\mu \int _{g(t)}^{h(t)}\int _{-\infty }^{g(t)} J(x-y)u(t,x)dydx,\quad t>0, \\&u(0,x)=u_0(x),~h(0)=-g(0)=h_0,\quad x\in [-h_0,h_0], \end{aligned} \right. \end{aligned}$$

(5.2)

where $x=g(t)$ and $x=h(t)$ are the moving boundaries to be determined together with u(t, x), which is always assumed to be identically 0 for $x\in {\mathbb {R}}\setminus [g(t), h(t)]$.

The initial function $u_0(x)$ satisfies $u_0\in C([-h_0,h_0])$, and

$$\begin{aligned} u_0(-h_0)=u_0(h_0)=0, \quad ~u_0(x)>0~\text { in }~(-h_0,h_0), \end{aligned}$$

so $[-h_0,h_0]$ represents the initial population range of the species.

The kernel function $J: {\mathbb {R}}\rightarrow {\mathbb {R}}$ is continuous and nonnegative, and has the properties

$$\begin{aligned} \mathbf{(J){:}}\;\;\; \;\;\;J(0)>0,\;\int _{{\mathbb {R}}}J(x)dx=1, \; J(x)=J(-x), \; \sup _{{\mathbb {R}}}J<\infty . \end{aligned}$$

As before, for simplicity, we take the special Fisher-KPP type nonlinearity

$$\begin{aligned} f(u)=au(1-u). \end{aligned}$$

These free boundary conditions were proposed independently in [20], where (5.2) with $f(u)\equiv 0$ was studied, which then has very different long-time dynamical behaviour from our case $f(u)=au(1-u)$.

The meaning of the free boundary conditions can be understood as follows: The total population mass moved out of the range [g(t), h(t)] at time t through its right boundary $x=h(t)$ per unit time is given by

$$\begin{aligned} d\int _{g(t)}^{h(t)}\int _{h(t)}^\infty J(x-y)u(t,x)dydx. \end{aligned}$$

As we assume that $u(t,x)=0$ for $x\not \in [g(t), h(t)]$, this quantity of mass is lost in the spreading process of the species. We may call this quantity the “outward flux” at $x=h(t)$ and denote it by $J_h(t)$. Similarly we can define the outward flux at $x=g(t)$ by

$$\begin{aligned} J_g(t):=d\int _{g(t)}^{h(t)}\int _{-\infty }^{g(t)}J(x-y)u(t,x)dydx. \end{aligned}$$

Then the free boundary conditions in (5.2) can be interpreted as saying that the expanding rate of the front is proportional to the outward flux (by a factor $\mu /d$):

$$\begin{aligned} g'(t)=-\mu J_g(t),\; h'(t)=\mu J_h(t). \end{aligned}$$

For a plant species, seeds carried across the range boundary may fail to establish due to numerous reasons, such as isolation from other members of the species causing poor or no pollination, or causing overwhelming attacks from enemy species. However, some of those not very far from the range boundary may survive, which results in the expansion of the population range. The free boundary condition here assumes that this survival rate is roughly a constant for a given species. For an animal species, a similar consideration can be applied to arrive at these free boundary conditions.

Note that for most species, the living environment involves many factors, not only the resources such as food or nutrient supplies. For example, complex interactions of the concerned species with many other species in the same spatial habitat constantly occur, yet it is impossible to include all of them (even the majority of them) into a manageable model, and best treat them, or rather their combined effects, as part of the environment of the concerned species.

The following three theorems are the main results of [16]:

Theorem 5.2

(Existence and Uniqueness) Problem (5.2) has a unique solution (u, g, h) defined for all $t>0$.

Theorem 5.3

(Spreading-vanishing dichotomy) Let (u, g, h) be the unique solution of problem (5.2). Then one of the following alternatives must happen:

• (i) “Spreading:” $\lim _{t\rightarrow +\infty } (g(t), h(t))={\mathbb {R}}$ and $\lim _{t \rightarrow +\infty }u(t,x)=1$ locally uniformly in ${\mathbb {R}}$,

• (ii) “Vanishing:” $\lim _{t\rightarrow +\infty } (g(t), h(t))=(g_\infty , h_\infty )$ is a finite interval and $\lim _{t \rightarrow +\infty }\Vert u(t,\cdot )\Vert _{L^\infty ([g(t), h(t)])}=0$.

Theorem 5.4

(Spreading-vanishing criteria)

($\alpha$):

If $d\le f'(0)=a$, then spreading always happens.

($\beta$):

If $d>f'(0)=a$, then there exists a unique $\ell ^*>0$ such that spreading always happens if $2h_0\ge \ell ^*$; and for $2h_0\in (0, \ell ^*)$, there exists a unique $\mu ^*>0$ so that spreading happens exactly when $\mu >\mu ^*$.

These results are similar to that for the local diffusion model in [29], but case ($\alpha$) in the “spreading-vanishing criteria” does not happen in the local diffusion case.

When spreading happens to (5.2), the spreading speed was determined in [32]. In contrast to the local diffusion model (2.1), now accelerated spreading may happen. The threshold condition on the kernel function J(x) governing this is the following

(J1):

$\displaystyle \int ^{\infty }_0\int ^{\infty } _x J(y)dydx<+\infty$.

Let us first note that if $J(x):=\xi (1+|x|)^\alpha$ with $\xi >0$ and $\alpha >2$, then (J) and (J1) hold but J(x) is not thin-tailed. On the other hand, it can be easily shown that for any J(x) satisfying (J) and having the thin-tail property, (J1) holds.

The main results in [32] are the following two theorems.

Theorem 5.5

(Spreading speed) Suppose (J) is satisfied, and spreading happens to the unique solution (u, g, h) of (5.2). Then

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{h(t)}{t}=-\lim _{t\rightarrow \infty } \frac{g(t)}{t}={\left\{ \begin{array}{ll} c_0\in (0,\infty ) \ \mathrm{({linear \ spreading})} &{}{\hbox { if} \,\mathbf{(J1)}\, \hbox {is satisfied}},\\ \infty \ \mathrm{\ \ \ \ \ ({accelerated\ spreading})}&{} {\hbox { if} \,\mathbf{(J1)} \,\hbox {is not satisfied}}. \end{array}\right. } \end{aligned}$$

The spreading speed $c_0$ is determined by “semi-wave” solutions to (5.2). These are pairs $(c,\phi )$ determined by the following two equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle d \int _{-\infty }^0 J(x-y) \phi (y) dy -d \phi (x)+ c\phi '(x)+f(\phi (x)) =0,&\quad \ x< 0,\\ \displaystyle \phi (-\infty ) = 1,&\quad \phi (0) =0, \end{array}\right. } \end{aligned}$$

(5.3)

and

$$\begin{aligned} c=\mu \int _{-\infty }^{0}\int _{0}^{+\infty }J(x-y)\phi (x)dydx. \end{aligned}$$

(5.4)

Theorem 5.6

(Semi-wave) Suppose (J) holds. Then (5.3)–(5.4) have a solution pair $(c, \phi )=(c_0,\phi _0)$ with $\phi _0\in C^1((-\infty , 0])$and $\phi _0(x)$ nonincreasing in x “if and only if” (J1) holds. Moreover, when (J1) holds, the solution pair is unique, and $c_0>0$, $\phi _0(x)$ is strictly decreasing in x.

By Theorems 5.1 and 5.5, the relationship between (J1) and the “thin-tail” property indicates that, accelerated spreading is less likely to happen to (5.2) than to (5.1).

We end this subsection with some comments on several related recent works on free boundary models with nonlocal diffusion. Some of the above results for (5.2) have been extended to systems of equations with nonlocal diffusion with free boundary. For example, similar results to Theorems 5.2–5.4 have been obtained for a West Nile virus model in [36], and analogous results have been obtained for weak competition and weak predator-prey models in [39], and for other epidemic models in [88, 89]. In [27], similar results to Theorems 5.5 and 5.6 have also been obtained for the epidemic model of [88].

However, many extra difficulties arise for treating nonlocal free boundary models when compared to the corresponding local (random) diffusion case, and new techniques need to be developed in order to gain understanding of the nonlocal free boundary problems to a level comparable to that of the corresponding free boundary problems with local (random) diffusion.

5.2 Local diffusion problems as limits of nonlocal diffusion problems

In this subsection, we look at some results on the relationship between the nonlocal diffusion problem and the corresponding local (random) diffusion problem. For fixed boundary problems of (5.1) and (1.3), it is well-known [3, 18, 19, 74] that, over any finite time interval [0, T], the unique solution u of the local diffusion problem is the limit of the unique solution of the nonlocal problem as $\epsilon \rightarrow 0$, when the kernel function J in the nonlocal problem is replaced by

$$\begin{aligned} {\tilde{J}}_\epsilon (x)=\frac{C}{\epsilon ^2} J_\epsilon (x):=\frac{C}{\epsilon ^3}\,J\left( \frac{x}{\epsilon }\right) \end{aligned}$$

with a suitable positive constant C, provided that J has compact support, f and the common initial function are all smooth enough.

For example, if J satisfies (J) with supporting set contained in $[-1,1]$, and ${\tilde{J}}_\epsilon$, $J_\epsilon$ are defined as above with

$$\begin{aligned} C=C_*:=\left[ \frac{1}{2} \int _{{\mathbb {R}}}J(z)z^2dz\right] ^{-1}=\left[ \int _0^1J(z)z^2dz\right] ^{-1}, \end{aligned}$$

(5.5)

and f(u) is $C^3$, and $u_0\in C^3([a,b])$, then it follows from Theorem A of [74] that the unique solution $u_\epsilon$ of the nonlocal diffusion problem³

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=\displaystyle \frac{C_*}{\epsilon ^2}\left[ \int _a^b J_\epsilon (x-y)u(t,y)dy-u(t,x)\right] +f(u),&{} x\in [a,b],\; t>0,\\ u(0,x)=u_0(x),&{} x\in [a,b] \end{array}\right. } \end{aligned}$$

converges to the unique solution u of the corresponding random diffusion problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=u_{xx}+f(u), &{} x\in [a,b],\; t>0,\\ u=0, &{} x\in \{a, b\}, \; t>0,\\ u(0,x)=u_0(x),&{} x\in [a,b], \end{array}\right. } \end{aligned}$$

in the following sense: For any $T\in (0, \infty )$,

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\Vert u_\epsilon -u\Vert _{C([0,T]\times [a,b])}=0. \end{aligned}$$

If $f\equiv 0$ and $u_0\in C^{2+\alpha }([a,b])$, $0<\alpha <1$, then it follows from Theorem 1.1 of [18] that

$$\begin{aligned} \Vert u_\epsilon -u\Vert _{C([0,T]\times [a,b])}\le C\epsilon ^\alpha \end{aligned}$$

for some $C>0$ and all small $\epsilon >0$.

It is interesting to know whether analogous results also hold between the free boundary problems (2.1) and (5.2). In space dimension 1, (2.1) can be rewritten into the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} v_t=dv_{xx} +f(v), &{} t>0,\; x\in (g(t), h(t)),\\ v(t,g(t))= v(t,h(t))=0, &{} t>0,\\ g'(t)= -\mu v_x(t,g(t)), &{} t>0,\\ h'(t)= -\mu v_x(t,h(t)), &{} t >0,\\ g (0)=-h_0,\; h(0)=h_0,\; v(0,x)=v_0(x), &{}x\in [-h_0,h_0]. \end{array}\right. } \end{aligned}$$

(5.6)

In Du and Ni [37], it was shown that (5.6) is the limiting problem of a slightly modified version of (5.2). The modification occurs in the free boundary equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle g'(t)= -\mu \int _{g(t)}^{h(t)}\int _{-\infty }^{g(t)}J(x-y)u(t,x) dyd x, \\ \displaystyle h'(t)= \mu \int _{g(t)}^{h(t)}\int _{h(t)}^{\infty }J(x-y)u(t,x) dyd x. \end{array}\right. } \end{aligned}$$

(5.7)

In [16], the equations in (5.7) are obtained from the assumption that the changing population range [g(t), h(t)] of the species with population density u(t, x) expands at each of its end point $(x=g (t)$ and $x=h(t)$) with a rate proportional to the population flux across that end point. If we assume instead that these rates are proportional to the population flux across the end points of a slightly reduced region of the population range, say $[g (t)+\delta , h(t)-\delta ]$ for some small $\delta >0$, then (5.7) should be changed accordingly to

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle g'(t)= -\mu \int _{g (t)+\delta }^{h(t)-\delta }\int _{-\infty }^{g (t)+\delta }J(x-y)u(t,x) dyd x, \\ \displaystyle h'(t)= \mu \int _{g (t)+\delta }^{h(t)-\delta }\int _{h(t)-\delta }^{\infty }J(x-y)u(t,x) dyd x. \end{array}\right. } \end{aligned}$$

(5.8)

So in the context of population spreading as explained in [16], the expansion of the population range governed by (5.8) is also meaningful.

The modified (5.2) then has the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_t=d \int _{g(t)}^{h(t)}J(x-y)u(t,y)\mathrm{d}y-du(t,x)+f(t,x,u), &{} t>0,\; x\in (g(t), h(t)),\\ u(t,g(t))= u(t,h(t))=0, &{} t>0,\\ \displaystyle g'(t)= -\mu \int _{g (t)+\delta }^{h(t)-\delta }\int _{-\infty }^{g (t)+\delta }J(x-y)u(t,x) dyd x,&{} t>0,\\ \displaystyle h'(t)= \mu \int _{g (t)+\delta }^{h(t)-\delta }\int _{h(t)-\delta }^{\infty }J(x-y)u(t,x) dyd x, &{} t>0,\\ g (0)=-h_0,\; h(0)=h_0,\; u(0,x)=u_0(x), &{} x\in [-h_0,h_0]. \end{array}\right. } \end{aligned}$$

(5.9)

We are now able to describe the nonlocal approximation problem of (5.6). Suppose that

$$\begin{aligned} \text{ spt }(J)\subset [-1, 1], \ \ J_\epsilon (x):=\frac{1}{\epsilon }J\left(\frac{x}{\epsilon }\right), \end{aligned}$$

(5.10)

and some extra smoothness conditions on f and $v_0$ (to be specified below) are satisfied. (Here spt(J) stands for the supporting set of J.) Then the following problem, with $0<\epsilon \ll 1$, is an approximation of (5.6):

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_t=d\frac{C_*}{\epsilon ^2} \left[\int _{g (t)}^{h(t)} J_\epsilon (x-y)u(t,y)\mathrm{d}y-u(t,x)\right] +f(t,x,u), &{} t>0, \; x\in (g (t), h(t)),\\ u(t,g (t))= u (t,h(t))=0, &{} t>0,\\ \displaystyle g'(t)= -\mu \frac{C_0}{\epsilon ^{3/2}} \int _{g (t)+\sqrt{\epsilon }}^{h(t)-\sqrt{\epsilon }}\int _{-\infty }^{g (t)+\sqrt{\epsilon }}J_{{\epsilon }}(x-y)u(t,x)\mathrm{d}y\mathrm{d}x, &{} t>0,\\ \displaystyle h'(t)=\mu \frac{C_0}{\epsilon ^{3/2}} \int _{g (t)+\sqrt{\epsilon }}^{h(t)-\sqrt{\epsilon } }\int _{h(t)-\sqrt{\epsilon }}^{\infty }J_{{\epsilon }}(x-y)u(t,x)\mathrm{d}y\mathrm{d}x, &{} t >0,\\ -g (0)=h(0)=h_0,\;u(0,x)=v_0(x), &{}x\in [-h_0,h_0], \end{array}\right. } \end{aligned}$$

(5.11)

where $C_*$ is given by (5.5) and

$$\begin{aligned} C_0:= \displaystyle \left[ {\int _{-1}^{0}\int _{-1}^{x}J(y)\mathrm{d}y \mathrm{d}x}\right] ^{-1}= \left[ {\int _{0}^{1}\int _{x}^{1}J(y)\mathrm{d}y \mathrm{d}x}\right] ^{-1}=\left[ {\int _{0}^{1}J(y)y\mathrm{d}y }\right] ^{-1}<C_*. \end{aligned}$$

(5.12)

Let us note that, from (5.10) we have $J_\epsilon (x)=0$ for $|x|\ge \epsilon$, and hence, for $0<\epsilon \ll 1$,

$$\begin{aligned} \int _{g (t)+\sqrt{\epsilon }}^{h(t)-\sqrt{\epsilon }}\int _{-\infty }^{g (t)+\sqrt{\epsilon }}J_{{\epsilon }}(x-y)u(t,x)\mathrm{d}y\mathrm{d}x =\int _0^\epsilon \int _{-\epsilon }^0 J_\epsilon (x-y)u(t,g(t)+\sqrt{\epsilon }+x)dydx, \\ \int _{g (t)+\sqrt{\epsilon }}^{h(t)-\sqrt{\epsilon } }\int _{h(t)-\sqrt{\epsilon }}^{\infty }J_{{\epsilon }}(x-y)u(t,x)\mathrm{d}y\mathrm{d}x =\int _0^{\epsilon }\int _{-\epsilon }^0 J_\epsilon (x-y)u(t, h(t)-\sqrt{\epsilon }-x)dydx. \end{aligned}$$

Therefore in (5.11), for $0<\epsilon \ll 1$, we may rewrite

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle g'(t)= -\mu \frac{C_0}{\epsilon ^{3/2}}\int _0^\epsilon \int _{-\epsilon }^0 J_\epsilon (x-y)u(t,g(t)+\sqrt{\epsilon }+x)dydx,\\ \displaystyle h'(t)=\mu \frac{C_0}{\epsilon ^{3/2}}\int _0^{\epsilon }\int _{-\epsilon }^0 J_\epsilon (x-y)u(t, h(t)-\sqrt{\epsilon }-x)dydx. \end{array}\right. } \end{aligned}$$

(5.13)

The extra smoothness conditions on f and $v_0$ mentioned above are: There exists some $\alpha \in (0,1)$ such that $(\mathbf {f_1})$: $f\in C^{1}([0,\infty ))$,

$$\begin{aligned} v_0\in C^{2+\alpha }([-h_0,h_0]),\ v_0(\pm h_0)=0<|v_0'(\pm h_0)|,\;\ v_0(x)>0\ \mathrm{in}\ (-h_0,h_0). \end{aligned}$$

(5.14)

We are now ready to state the main results of [37].

Theorem 5.7

[37] Suppose f satisfies $(\mathbf {f_1})$ and $f(0)=0$, J satisfies $({\mathbf {J}})$ and (5.10), and $v_0$ satisfies (5.14). Then for every small $\epsilon >0$, problem (5.11) has a unique positive solution, denoted by $(u_{\epsilon },g_\epsilon ,h_\epsilon )$. Moreover, if (v, g, h) is the unique positive solution of (5.6) and if we define $v(t,x)=0$ for $x\in {\mathbb {R}}\setminus (g(t),h(t))$ and $u_{\epsilon }(t,x)=0$ for $x\in {\mathbb {R}}{\setminus } (g_\epsilon (t),h_\epsilon (t))$, then, for any $T\in (0, \infty )$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \lim _{\epsilon \rightarrow 0}\sup _{t\in [0,T]}\Vert u_{\epsilon }(t,\cdot )-v(t,\cdot )\Vert _{L^{\infty }({\mathbb {R}})}=0,\\ \lim _{\epsilon \rightarrow 0}\Vert g_{\epsilon }-g\Vert _{L^{\infty }([0,T])}=0,\ \ \lim _{\epsilon \rightarrow 0}\Vert h_{\epsilon }-h\Vert _{L^{\infty }([0,T])}=0. \end{array}\right. } \end{aligned}$$

If we further raise the smoothness requirements on f and $v_0$, namely assuming additionally

$$\mathbf {(f_2)} : f\in C^{1+\alpha }([0,\infty )),$$

$$\begin{aligned} v_0\in C^{3+\alpha }([-h_0,h_0]), \end{aligned}$$

(5.15)

then we can obtain an error estimate as follows.

Theorem 5.8

[37] Under the assumptions of Theorem 5.7, if additionally $(\mathbf {f_2})$ and (5.15) are satisfied, then for any $T>0$ and any $\gamma \in (0,\min \{\alpha , \frac{1}{2}\})$, there exists $0<\epsilon _*\ll 1$ such that for every $\epsilon \in (0,\epsilon _*)$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \sup _{t\in [0,T]}\Vert u_{\epsilon }(t,\cdot )-v(t,\cdot )\Vert _{L^{\infty }({\mathbb {R}})}\le \epsilon ^{\gamma },\\ \sup _{t\in [0,T]}|g_{\epsilon }(t)-g(t)|\le \epsilon ^{\gamma }, \ \sup _{t\in [0, T]}|h_{\epsilon }(t)-h(t)|\le \epsilon ^{\gamma }. \end{array}\right. } \end{aligned}$$

Remark 5.9

These results still hold if in (5.11), the free boundary conditions are changed to, for an arbitrary $\beta \in (0,1)$,

$$\begin{aligned}{\left\{ \begin{array}{ll} \displaystyle g'(t)= -\mu \frac{C_0}{\epsilon ^{1+\beta }} \int _{g (t)+\epsilon ^\beta }^{h(t)-\epsilon ^\beta }\int _{-\infty }^{g (t)+\epsilon ^\beta }J_{{\epsilon }}(x-y)u(t,x)\mathrm{d}y\mathrm{d}x, &{} t>0,\\ \displaystyle h'(t)=\mu \frac{C_0}{\epsilon ^{1+\beta }} \int _{g (t)+\epsilon ^\beta }^{h(t)-\epsilon ^\beta }\int _{h(t)-\epsilon ^\beta }^{\infty }J_{{\epsilon }}(x-y)u(t,x)\mathrm{d}y\mathrm{d}x, &{} t >0, \end{array}\right. } \end{aligned}$$

or equivalently, in (5.13) the equations are changed to

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle g'(t)= -\mu \frac{C_0}{\epsilon ^{1+\beta }}\int _0^\epsilon \int _{-\epsilon }^0 J_\epsilon (x-y)u(t,g(t)+\epsilon ^\beta +x)dydx,\\ \displaystyle h'(t)=\mu \frac{C_0}{\epsilon ^{1+\beta }}\int _0^{\epsilon }\int _{-\epsilon }^0 J_\epsilon (x-y)u(t, h(t)-\epsilon ^\beta -x)dydx. \end{array}\right. } \end{aligned}$$

(5.16)

Remark 5.10

We conjecture that the modification of (5.2) to (5.9) is necessary in order to obtain an approximation problem of (5.6) such as (5.11).