A Flow-Based Node Dominance Centrality Measure for Complex Networks

Abstract

We introduce a new class of power centrality measures, which we refer to as Dominance Centrality, for complex networks which may have weighted, directed edges, as well as weights associated with nodes. These measures are similar in spirit to the power-over-powerless class introduced by Bonacich decades ago in the context of eigenvector centrality, but are quite different in their roots and effect. Our Dominance Centrality measure, referred to as DONEX, is derived as a Pareto optimal solution to collective welfare maximisation problem that allocates values to nodes in the network on the basis of expected interaction strengths captured by edge weights between pairs of nodes, where the expectation is taken over the probability of there being an undirected or directed link between them. We show how this formulation yields a new centrality measure which captures the notion of a weighted degree-differential virtual flow along the edges in the network in such a manner that the sum of such flows at each node itself represents the notion of dominance over the neighbourhood. We develop a greedy propagation algorithm called NetProp which allows us to estimate the reach of dominant nodes, and network boundaries where the dominance-derived influence or attention are maximum and minimum. We also demonstrate how DONEX extends to multi-hop neighbourhoods taking account of both local and non-local effects. The new methods are illustrated extensively with synthetic and real networks.

Introduction

Power as a measure of vitality is possibly the most common notion that is associated with nodes (or vertices, synonymously) in networks so as to characterise their importance in the sense of their connectedness in their neighbourhoods. Power centrality measures, proposed originally in the framework of the eigenspace of adjacency matrices of graphs by Katz [1] and Bonacich [2, 3] form a pedagogically important class of node centrality measures, collectively known in the literature as eigenvector centrality methods [4, 5].

Given a weighted undirected network, Bonacich in [1] defined a family of eigenvector centrality measures $C\left(A, \alpha ,\beta \right),$ as a function of the adjacency matrix of the network, A, where $\alpha$ is a scaling factor set to normalise the score, and $\beta$ is a tuneable parameter to account for the distance in path lengths that other neighbouring nodes should be considered, or the extent to which the centrality of connected others should weight a node.

Remarkably, this formulation provided two classical ways of viewing power from connectedness measured in terms of degree. Setting $\beta >0$ generates a node centrality measure which encapsulates the idea of power stemming from being connected to other powerful neighbours over one or more hops—this is akin to social standing accruing to a powerful member in a club from connections with other powerful members in the club, who in turn have connections to other powerful members, and so on. This class of centrality measures is close in concept to PageRank [6], HITS [7] and its many variants [8,9,10,11,12]. In this paper, we shall refer to this type as ‘Power Club’ centrality, as it derives power from powerful, to distinguish it from a different type of power centrality described below.

When we set $\beta <0$ to calculate $C\left(A,\alpha ,\beta \right),$ we obtain another type of power centrality which accrues to a node with high degree, whose neighbours have poor degree connectivity. This is the type of power that is useful in situations where we wish to characterise nodes which dominate over their neighbours who themselves do not have that power. Bonacich referred to this type of importance as power over-powerless, and drew attention to the need to measure power along this type of scale when nodes in the network needed to be graded on their ‘bargaining’ position [2]. There are of course numerous other applications, as we shall see shortly.

In this paper, we shall refer to this class of ‘power-over-powerless’ centrality as ‘Dominance Centrality’ or DC for short. This coinage is probably new, and has been adopted because our focus here is primarily on this class of measures of the power of nodes, where ‘dominance’ draws from statistical implications as well. The other reason for this new nomenclature is to place a degree of separation, as it were, between the Dominance Centrality characterisations which we shall propose in this paper, and those from other classes of methods which deal with ‘power-over-powerless’-like measures—even though the class of measures we propose here are similar in spirit, they have very different roots and effect. We hope to show in this paper, that the flow-based measures we derive for undirected and directed, weighted networks justify their presence as members of this newly christened class of Dominance Centrality metrics.

While proposing a family of these eigenspace-driven centrality measures, Bonacich also brought out the difficulty in interpreting negative $\beta$ values in terms of probabilistic expectations over path lengths, and its use as a ‘radius of influence’ within which to measure power, articulating the futility of subsuming the notions of ‘Power Club’ and Dominance centrality into one measure. Finally, the class of Dominance Centrality measures, as described here, has not attracted the same level of research attention as Power Club measures.

We can quickly get an intuitive feel for the need to think of dominance as distinct from power club centrality with a few illustrative undirected network examples which need not even be diagrammed. The Dominance Centrality of the k-degree node at the centre of a (k + 1)-node star network, for instance, would naturally and conceptually exemplify the upper bound for DC. The centre of the star dominates over all other nodes by virtue of its connectivity power. It is another matter that this node may also rank the highest in terms of Power Club Centrality, as a calculation of PageRank or Bonacich Centrality with $\beta >0$ would show. However, such power should ideally be lower in value than DC, in concept, since the node at the centre of the star is surrounded by ‘weak’ neighbours with unit degree. Similarly, it would be obvious that the Dominance Centrality measures of all the nodes in a k-node clique would be equal—no node can dominate over its neighbours—and this forms the other bound—even if it equals Power Club centrality.

As is evident, degree alone is an inadequate measure of dominance, and the examples illustrate the rationale for exploring Dominance Centrality in its own right, divorced from Power Club Centrality, as they may not be true ‘inverses’, in concept or effect, for the entire range of diverse network structures that fall between the above classical benchmark structures we employed for illustration.

Hence, this paper explores Dominance as a primary property of network nodes. Note that there is also a latent implication here of how power and dominance in undirected networks have traditionally been associated with the idea of degree-differential between neighbours, carrying with them an inherent implication of a ‘flow’, even in undirected networks. In the dyadic relationship between two nodes of an undirected network, power is thought to ‘flow’ from the node with higher power to a node with lower power ‘virtually’ so as to manifest itself—just as there can be equal flows or zero ‘flows’ between two nodes with equal power. It is with this understanding that we can start with an undirected friendship network, find ‘powerful’ important nodes, and then ascribe the notion of a direction of influence, attention, liking, goodwill, or other similar attribute, to an undirected edge, as a derived behavioural possibility that describes relationships among nodes.

The weights that are associated with the edges on the networks we consider carry the concept of ‘strength’ which characterises the relationship, and equivalently the strength of the flow. It is important to clarify at this stage that the flow we are referring to here is a kind of ‘virtual’ flow—in that there need not necessarily be any “stuff” that moves along the edges. The virtual flow of say, influence, or goodwill, or of power of position alters the power of the agent to dominate, by contributing to measures of social standing, for instance, in a social network. This is different in notion from the traditional flow that is associated with networks—the ‘stuff’ that flows from a source node to a sink node with the edges providing the ‘means’ to transport the ‘stuff’ based on their capacity, direction, etc., and constraints placed on conservation of such material flows. The ‘virtual’ flows we consider here are also not equivalent to the flows in Signal Flow Graphs where the well-known Mason’s Rule [13] is applied to obtain transfer functions which relate output flows to input flows. That said, our methodology does not necessarily preclude the possibility of considering some classes of real flows as well, as we shall describe later in this paper.

Dominance Centrality is an important measure in many applications. Consider the ReTweet diffusion network example [14, 15]. The node (user) whose posts are retweeted at high rates by others who are themselves not retweeted much are ‘dominating’ nodes. Similarly, ad-targeting and social recommender systems may find it fruitful to target ‘dominant’ users on social media because they may offer the best reach to a connected neighbourhood community that is likely to be ‘influenced’ by such a node. In microfinance borrower networks, where links in the social network among the prospective borrowers model trust, lenders would seek out those borrowers to offer shared-liability micro-loans who have high DC because they are trusted by many who are themselves not trusted as much by others.

In this paper, we propose a new type of Dominance Centrality, which we shall refer to as DONEX. DONEX is derived as a Pareto optimal assignment solution to a flow-based allocation model in which we apportion fractions of a fixed sharable resource to the nodes on the basis of their expected interaction strength within their neighbourhood. The ideas of flows and allocation to agents are easily understood in economic terms. Consider economic agents located at nodes of a network attempting to maximise their collective welfare by exchanging a common resource among themselves. Such collective welfare is modelled in microeconomics as a weighted sum of their utilities over the allocated resource, accounting for positive and negative externalities, which are created by the presence of linkages or edges between them. In other words, collective welfare is the sum of the utilities of the agents without considering a network that connects them, plus the impact of network on the welfare as externalities. Here, interactions among connected agents are exchanges of resources, notionally treated as flows enabled along edges between them. We employ this essential framework to model externalities as Expected Interaction Strengths (EIS) for weighted networks by taking the expectation of interaction weights over probabilities for the presence of edges between nodes, on the basis of the Configuration Model [4, 5, 16]. In this way, we can model the presence of an arbitrary connected network among the agents.

While there is a preponderance in this paper towards social or economic networks, essentially associating human behaviour with node behaviour and flows of resource on the edges interconnecting nodes aligning with notions of influence, attention, goodwill, or trust, we show that the idea of DC which we derive has wider and general applicability to generic, even abstract network structures, often with the only precondition that the agents at the nodes have some level of ‘agency’ to pursue a goal to achieve utility from a resource. This implies the utilitarian urge to maximise gains in some sense in human agents, but this is modelled as agent behaviour even in routers in communication networks [17,18,19], and entities such as trading organisations in a networked market [20]. This applicability derives, and also benefits, from a rich parameter space that allows setting many node and edge characteristics to suit the requirements of a domain.

We obtain the allocation as an analytical solution to a constrained welfare maximisation problem in Microeconomics that engenders cooperation among agents on the basis of assumptions of fixed networks, exponential payoffs over shared resource allocations, and a fixed divisible total resource. We show that the basic formulation in this paper significantly extends some of our earlier work with a solution, referred to as DON, which could be used only for simpler undirected unweighted graph structures [21, 22]. The present model and analysis not only extends the applicability of our methodology in significant ways by modelling networks with weighted directed edges, but also with potentially weighted nodes. We believe that the idea of expected interaction strength, introduced in this paper, is both a fundamentally new concept, as well as a key to modelling dyadic interactions as network dominance-driven flows. The edge weights can even be negative under certain restrictions. DONEX-based dominance easily extends over multiple hops of expanding neighbourhoods, and we illustrate this special nuance with examples.

We also show how DONEX flows are related to the weighted Laplacian of the network, and how a unique property of DONEX sums yields a new greedy algorithm, which we call NetProp, using which we can obtain minimum flow and maximum flow partitions of the network. We also demonstrate how this algorithm can help assess the reach of influence from a powerful seed node through its ego-network boundary, where its dominance ceases to take effect. We illustrate the methodology and the theoretical results with a number of examples throughout the paper. We also demonstrate DONEX with real data sets to illustrate the many interesting scenarios which can be addressed with the rich parameter space that the methodology offers.

Related Work

The notion of associating power as a characteristic of a node, deriving from its connectedness in networks, and its use as a centrality measure has a long history. Measures of centrality have been viewed both from the perspective of the importance of nodes and edges, and practitioners of network science most often employ a combination depending upon the application scenario. Edge-betweennes, closeness and a plethora of edge-centric measures are described lucidly in many standard texts [4, 5].

Our focus is on node centrality in this paper, and we shall employ adjacency matrix eigenspace methods for obtaining power centrality only as form of the backdrop to motivate the idea of node dominance as importance in networks that carry virtual flows, mostly of ‘non-stuff’. Borgatti [23] provides an interesting categorisation of different ‘stuff’ which may be considered for deriving flows, and associates this class of methods with flows of things such as influence and attention. Although our work does not rely on eigenvector-based analysis, these methods lay the foundation for gaining an understanding of power centrality, with which the concept of Dominance Centrality has a strong link, and we shall use this class of measures as a benchmark. Hence, we shall briefly review a few key papers on this topic.

Katz [1] and Bonacich [2, 24] were among the first to place the association between power and centrality within the mathematical context of the eigenspace of symmetric, possibly weighted, adjacency matrices with an eigenvector centrality measure. Other related measures include those proposed by Hubbell [25], Taylor [26], Coleman [27], Freeman [28, 29] and Friedkin [30].

Given a weighted undirected network and its symmetric adjacency matrix, A, with its eigenspace defined by ${\varvec{\uplambda}}\mathbf{v}={\varvec{\uplambda}}\mathbf{A}$, where $\uplambda$ is the eigenvalue corresponding to eigenvector $\mathrm{v}$, Bonacich utilised the useful relationship that an eigenvector is proportional to the row sums of a matrix $\mathrm{S}$ formed by all sums of powers of A, weighted by the reciprocal of the corresponding eigenvalue:

$${\varvec{S}}=\sum_{k=0}^{\infty }\frac{1}{{\lambda }^{k}}{{\varvec{A}}}^{k}.$$

Using the fact this converges when we set $\beta <\frac{1}{{\lambda }_{max}}$, Bonacich proposed the centrality measure $C\left(\alpha ,\beta \right)={\alpha (I-\beta {\varvec{A}})}^{-1}{\varvec{A}}1$, where $A$ is a (possibly weighted) symmetric adjacency matrix representing the network, $\alpha$ is a scaling vector set to normalise the score, $\beta$ is a tuneable parameter to account for the distance in hops that other neighbouring nodes should be considered, or the extent to which the centrality of connected others should weight a node; I is the identity matrix, and $1$ is a matrix of ones. Katz centrality was shown by Bonacich to be a special case of this formulation.

It was shown that when $\beta >0$, the above measure accounted for power arising from powerful connected neighbours—much in the same vein as the page-rank method. Bonacich also showed how the higher values of $\beta$ could model the notion of increased (path) length, permitting the centrality measure to consider neighbourhoods with higher ‘radius’ around a node. Bonacich also showed that while setting negative values for $\beta$ produced a DC measure, the probabilistic interpretations capturing the notion of average path lengths and radii could not be extended to negative $\beta$s, resulting from sign changes that would occur from raising this parameter to higher powers.

Although eigenvector centrality was originally shown to model the above two classes of power, it relied on symmetry of the weighted adjacency matrix, resulting in difficulty in assigning scores to nodes in directed networks where the in-degrees were zero. Bonacich and Lloyd [31] later extend the above methodology proposing the alpha-centrality measure to address this issue.

Many recent works have addressed problems with normalisation and scaling, yet retaining the essential utility of eigenspace characterisations. Bothner, et al. [33] proposed a combination of the basic parameterised eigenspace model described above for obtain power as social status, with the Herfendahl index [34] to model notions of robustness/fragility in several practical network scenarios. Ghosh and Lerman [32] introduce a normalised alpha-centrality measure which addresses the problem of divergence of when equivalent of the $\beta$-parameter is made large, allowing weighting of local and non-local nodes in different ways. There are other recent works addressing methods to handle node-weighting within the calculation of eigen-based centrality measures, such as [35], as well as a new way to construct a Two-way PageRank algorithm for weighted directed networks which weights in-degrees and out-degrees together to obtain power centrality [36].

The idea of balancing local and global connectedness of nodes to obtain power centrality measures has also been approached from dramatically different directions. Qiao et al. [37] employ entropy concepts to combine local in-degree neighbourhood information with non-local out-degree-based information to arrive at a centrality measure, which they compare with several other power centrality measures. Fei et al. [38] employ an inverse square law to obtain centrality in networks.

Borgatti and Everett [39] extended notions of individual centrality to groups [40, 41], for instance, by defining group degree centrality as the number of non-group nodes that are connected to group members. This approach permitted the definition of group measures for closeness, betweenness, and flowbetweenness.

In the recent years, there has been renewed attention on Game-Theoretic(GT) approaches to obtain power centrality measures for subsets of nodes in a network [42,43,44,45]. This class of methods may be called top-down, as opposed to all the previous methods reviewed, since they consider the fair value obtained as an allocation from a given global sharable resource as the power centrality measure. These methods also aim to obtain centrality of nodes on the basis of the behaviour of subsets, coalitions, or groups of nodes taken together.

One of the popular GT methods is the application of solution concepts such as the Shapley Value for fair division of the total worth of a set of cooperating agents, thought to be located at the nodes of a network [46, 47]. Among the many early works is that of Myerson [48] and Gomez et al. [49], who treated the graph-restricted coalitional game in different ways. The issue with these GT-based approaches is, of course, that the evaluation of worths is dominated by the combinatorial complexity of feasible coalition formation calculations based on network structure.

Some authors [50] have suggested construction and evaluation of coalitions and their worths based on identifying a fringe-set around a node in the graph. While applying this method with feasibility restricted by graph structure involves high computational resources due to combinatorial nature of the selection process, other authors [51] have recently shown that centrality measures can be obtained in time linear in size of the graph through a probabilistic model. However, this is achievable only if we consider all coalitions of nodes as feasible.

A degree-weighted welfare function maximisation approach was proposed by the present authors [21, 22]. This method assumed a welfare function constructed with exponential utility functions, to derive a measure for Dominance Over Neighbourhood, or DON. The main restriction of this method was that it could only be applied to undirected unweighted networks, and did not model individual interactions. Also, it did not address the issue of boundary flows, over multi-hop neighbourhoods and the possibilities for calculating them efficiently. DONEX is derived as a major extension of a core idea in DON, and address all these above weaknesses.

As a final point, it is important to note that the work described here is unrelated to the class of research approaches broadly referred to influence maximisation methods which model and measure influence propagation and its maximisation in social networks [52,53,54]. These methods are essentially concerned with temporal dynamics of propagation of influence which translate to spatial flows. In contrast, our approach here does not carry any temporal implication, and computes spatial flows arising out of degree-differentials among interconnected nodes in fixed static networks.

Network Collective Welfare

This section is devoted to developing and setting up the Collective Welfare Function (CWF) for Weighted Undirected Networks (WUN) and Weighted Directed Networks (WDN), and defining terms, many of which are common to both classes, while some are specific to the context of the class of the network. Some terms, such as a resource, are specified in a general manner here. We shall provide a number of examples later to illustrate how they have a logical context in different application scenarios. At the end of this section, we shall also bring out the features of this CWF model that casts the role of DONEX as a measure of domain centrality built on degree-differential flows. We apply the CWF model specifically to WUN and WDN in two subsections of this section.

We consider the problem of allocation by suitable division of a fixed (divisible), sharable, resource, X, to a set of $n$ agents, $N=\{\mathrm{1,2},..,n\}$, located at the nodes or vertices of a fixed network represented as a connected (single component) graph, $G(N,E)$, where $E$ denotes the set of edges or links between the nodes. We shall shortly make the term suitable division precise. First, some notations and definitions are introduced.

Basic Definitions and Terminology

Weighted Undirected Networks (WUN)

Let every agent in a given, fixed, weighted undirected network, denoted, ${G}_{U}(N,E,S)$, and associated square symmetric adjacency matrix $A (n\times n)$, whose elements are denoted ${a}_{ij};i,j \in N$, have a set of 1-hop neighbours represented by the neighbourhood set, ${N}_{i}=\left\{j: {a}_{ij}=1\right\};i\in N$; and a degree, ${\alpha }_{i}=\sum_{j\in {N}_{i}}{a}_{ij}$. Associated with every such edge is an interaction weight, ${s}_{ij}$, which are the elements of a square interaction weight matrix, matrix $S(nxn)$ such that ${s}_{ij}=0$ whenever ${a}_{ij}=0$. We shall allow for weights bounded in a given range, ${s}_{ij}\in [{s}_{min},{s}_{max}]$. While in general, ${s}_{ij}>0;i\ne j\in N$, we allow for ${s}_{min}<0$, which implies that we can account for the fact the interaction between the two connected nodes i and j can have negative strength. We do not consider self-loops in the graph, hence ${s}_{ii}=0 \forall i\in N$. We develop the allocation model for this class of networks in subsection “Collective Welfare Model for Weighted Undirected Networks”.

Weighted Directed Networks (WDN)

We consider directed weighted graphs, denoted ${G}_{D}(N,E,S)$, with a special restriction. We consider the links between any two nodes in the graph to be bidirectional, i.e. there are two edges between any two nodes i and j; one is a directed edge from i to j, and other is a directed edge from j to i. Hence, the adjacency matrix $A (n\times n)$ for ${G}_{D}$ is symmetric. However, the weight matrix,$S(nxn)$ for ${G}_{D}$ may be unsymmetric, since we shall allow ${s}_{ij}=0$ even when ${a}_{ij}=1$. We shall define an adjacency matrix ${A}_{D} (n\times n)$ with respect to S, where, its elements ${a}_{ij}^{d}=1; i,j\in N$ iff ${s}_{ij}\ne 0$, endowing ${A}_{D}$ with the same structure as $S$. This facilitates characterising the neighbourhoods of every node as sets of nodes that have in-edges only, and out-edges only, denoted by ${N}_{i}^{in}$ and ${N}_{i}^{out}$, respectively, such that we can define in-degrees and out-degrees with respect to ${A}_{D}$ as ${\delta }_{i}=\left|{N}_{i}^{in}\right|; i\in N$, and ${\eta }_{i}=\left|{N}_{i}^{out}\right|; i\in N$, and ${N}_{i}={N}_{i}^{in}\cup {N}_{i}^{out}$. We do not consider self-loops in ${G}_{D}$ type graphs also. This class of networks is addressed in Section IV.

The purpose of modelling directed networks in this manner, considering every link between edges as potentially bidirectional, permits us to accommodate flows between connected nodes in either direction with a symmetric $A$, and yet ascribe a weight of zero to any direction in ${A}_{D}$, should that be demanded in a practical situation. This facilitates exchanges of resource between connected nodes as flows, as desired for accomplishing collective welfare. This aspect will become more evident as we describe the welfare models shortly.

Resources and Utility

We denote by ${x}_{i}>0;\,i\in N$, the allocations to the agents, and we wish to ensure efficient division by satisfying the constraint

$$\sum_{i\in N}{x}_{i}=X.$$

(1)

Efficiency here implies that the division leaves no balances or surpluses. Every agent must be allocated a positive value of resource; zero and negative resource allocations are invalid.

Individual agents are assumed to derive utility ${u}_{i}\left({x}_{i}\right)$ from the allocation of the shared resource, ${x}_{i};\,i\in N$, which we shall express as (given) functions, $u:x\to {\mathcal{R}}_{+}$. The functions are assumed to have the same form for all agents. Additionally, we shall assume that they are of the standard (concave) exponential form:

$${u}_{i}\left({x}_{i}\right)=\frac{1}{{\rho }_{i}}\left(1-{e}^{-{\rho }_{i}{x}_{i}}\right); i\in N.$$

(2)

When considering economic agents, by choice of ${\rho }_{i}$ in this function, we can model diverse behaviours such as risk-taking (negative ${\rho }_{i}$), risk-neutral behaviour (small ${\rho }_{i}>0)$, and risk-averse behaviour(larger ${\rho }_{i}>0)$. While the choice of this particular functional form not only allows the possibility of applying the proposed model formulation readily in financial and economic network allocation problems as Constant Absolute Risk Aversion (CARA) functions [55], but also is easily applicable in many other scenarios as well. For instance, the reciprocal of ${\tau }_{i}=(\frac{1}{{\rho }_{i}});\,i\in N$ can potentially model rates of utilisation of a shared resource, such as bandwidth in communication networks.

To delineate the role of externality in the two types of networks we consider, we shall set up the collective welfare models separately for each type. Let us examine the case for Weighted Undirected Networks first.

Collective Welfare Model for Weighted Undirected Networks

Let a given Weighted Undirected Network be defined as ${G}_{U}(N,E,S)$, as above. The agents at the nodes wish to jointly maximise their pooled utilities, $Z,$ in the following manner:

$$\mathrm{max }Z= \sum_{i\in N}{u}_{i}\left({x}_{i}\right)+\left(\sum_{i\in N}\left[{\sigma }_{i}{(u}_{i}\left({x}_{i}\right))\right]\sum_{j\in {N}_{i}}{P}_{ij}{s}_{ij}\right),$$

(3)

subject to (1), where the first term denotes pooled utilities without considering the network, and the second term denotes pooled positive or negative externalities arising from network connectivity. In the term expressing externalities, ${\sigma }_{\mathrm{min}}\le {\sigma }_{i}\le {\sigma }_{\mathrm{max}};\,i\in N$ represent a given rate term, within given bounds, which we associate with each agent. This term serves to amplify or attenuate the contribution of utility, ${\sigma }_{i}{(u}_{i}\left({x}_{i}\right))$, of an agent to the collective pool, depending on extraneous information we may find about an agent. In typical applications, the rate term also serves as an exogenously set node weight, and could represent an agent’s positioning in the community. This weight can take negative values as well, so long as the overall sum for any agent does not turn zero or negative.

In (3), ${P}_{ij};i,j\in N$ denotes the probability that there is an edge between vertices i and j, and the last expression in (3), written as:

$${\gamma }_{i}=\sum_{j\in {N}_{i}}{P}_{ij}{s}_{ij};i\in N,$$

(4)

denotes the Expected Interaction Strength (EIS) for agent i, with the expectation taken with interaction weights over its neighbourhood, ${N}_{i}$. We shall assume that ${\gamma }_{i}>0$ by design, implying that the interaction weights are so normalised that expectations over neighbourhoods are positive.

Note that ${\gamma }_{i};i\in N$ also serves to amplify or attenuate the externality contribution of an agent—purely on the basis of neighbourhood connectivity and the interaction weights. Hence, $\sigma$ and $\gamma$ are both modifiers, but essentially orthogonal in sense—while the former is a surrogate for exogenously set agent power—the latter captures its interaction ability purely based on network connectivity features, and is independent of the former parameter.

For a given network ${G}_{U}(N,E,S)$, we, thus, seek to maximise:

$$\mathrm{max }Z=\sum_{i\in N}\left(1+{\sigma }_{i}\left(\sum_{j\in {N}_{i}}{P}_{ij}{s}_{ij}\right)\right){u}_{i}\left({x}_{i}\right) \mathrm{subject to }\sum_{i\in N}{x}_{i}=X.$$

(5)

Now, by the Configuration Model [16, 56,57,58,59,60,61] for connected, undirected graphs, the probability ${P}_{ij}$ can be written¹ as

$${P}_{ij}=\frac{{\alpha }_{i}{\alpha }_{j}}{2|E|};\, i\ne j.$$

(6)

If we assume that the interaction weight matrix is so normalised as to absorb the constant $|\mathrm{E}|$ for the given fixed network, then we can rewrite ${\gamma }_{i};\,i\in N$ as:

$${\gamma }_{i}=\sum_{j\in {N}_{i}}{\alpha }_{i}{\alpha }_{j}{s}_{ij};\, i\in N.$$

(7)

Then the maximisation problem for a fixed network of agents, with given rates, ${\sigma }_{i};\,i\in N$, utility parameters, ${\rho }_{i};\,i\in N$ and calculated values for ${\gamma }_{i};\,i\in N$(constants) from network structure, is:

$$\mathrm{max }Z=\sum_{i\in N}\left(1+{\sigma }_{i}{\gamma }_{i}\right){u}_{i}\left({x}_{i}\right)\mathrm{subject to }\sum_{i\in N}{x}_{i}=X.$$

(8)

Equation (7) models ${\gamma }_{i}$ as the sum of interesting products. Note that the degrees ${\alpha }_{i}$ and ${\alpha }_{j}$ serve as ‘amplifiers’ of ${s}_{ij}$, and particularly so when they are not only large, but close in value. This means that when two nodes are themselves well connected, even a small weight representing their interaction is amplified; this situation does not occur when the either or both nodes have low degree. This property reflects reality in human social networks, where a low-volume communication among powerful individuals can carry high interaction value, in comparison with the same communication among individuals with poor connectivity and/or social standing.

To solve (8), we need to only form the Lagrangian, and solve for the optimal allocations, ${\widetilde{x}}_{i};\,i\in N$, from the First-Order Conditions (FOC). This is a straightforward process, and produces a set of FOC’s of the form:

$$\left(1+{\sigma }_{i}{\gamma }_{i}\right){u}_{i}^{^{\prime}}\left({x}_{i}\right)= \lambda ;\,\forall i\in N,$$

(9)

where $\uplambda$ is the Lagrangian multiplier. Using (2), and summing so as to eliminate $\uplambda$ the optimal solution is found. This process is similar to that described in [21, 22].

$$\mathrm{DONEX}\left(i\right)={\widetilde{x}}_{i}=\frac{R}{{\rho }_{i}}X+{r}_{i};\, \forall i\in N,$$

(10)

where

$${r}_{i}=\frac{R}{{\rho }_{i}}\sum_{j\in {N}_{i}}\frac{1}{{\rho }_{j}}\mathit{ln}\left(\frac{{1+{\sigma }_{i}\gamma }_{i}}{{1+{\sigma }_{j}\gamma }_{j}}\right);\,\forall i\in N,$$

(11)

and we write $\frac{1}{R}=\sum_{j\in N}\frac{1}{{\rho }_{j}}$.

As we can observe, the overall solution form of DONEX is very similar in structure to that referred to as DON by the authors previously in [21]. As with DON, DONEX also presents a family of Pareto optimal solutions to the maximisation problem, with the ratios, $\frac{R}{{\rho }_{i}}X;\forall i\in N$ continuing to delineate a Pareto frontier. It can be shown that for any other feasible alternative solution ${x}_{i};i\in N$, ${u}_{i}({\widetilde{x}}_{i})\ge {u}_{i}({x}_{i})$, with the inequality holding for at least one agent. It can also be shown that $\sum_{i\in N}{r}_{i}=0$, which expresses a balance condition for exchanges, in the same manner as the concept of ‘side-payments’ referred to earlier with DON.

However, the difference in ${r}_{i} ;\, i\in N$ is critical, and lends a new individual interaction-based measure to the notion of dominance in DONEX, which was absent in DON. The presence of EIS in the DONEX formulation takes account of every single weighted interaction, via an expectation over the neighbourhood. This was absent in the DON formulation.

The notion of EIS has some interesting microeconomic implications in the context of modelling social capital as social standing of agent (node) in a network, acquired from attention that is paid by other connected agents in its neighbourhood. We shall defer more discussion on this aspect to a later section.

Returning to the DONEX formulation, we can express the solution, as before, in matrix form:

$$\widetilde{{\varvec{x}}}=\mathrm{DONEX}=X{{\varvec{c}}}^{{\varvec{T}}}+{\varvec{Q}}{{\varvec{b}}}^{{\varvec{T}}},$$

(12)

where the vector, ${\varvec{c}}={[\frac{R}{{\rho }_{1}}\frac{R}{{\rho }_{2}}\dots \frac{R}{{\rho }_{n}}]}^{T}$, and ${\varvec{b}}=\left[\mathit{ln}\left(1+{\sigma }_{1}{\gamma }_{1}\right)\mathit{ln}\left(1+{\sigma }_{2}{\gamma }_{2}\right)\dots \mathit{ln}\left(1+{\sigma }_{n}{\gamma }_{n}\right)\right]$;and the matrix R can now be rewritten to hold the quantities ${r}_{i};i\in N$ arranged in matrix form and reflect the connectivity of the adjacency matrix, as shown below:

$${\varvec{Q}}=\left[\begin{array}{ccc}\frac{R}{{\rho }_{1}}\frac{{R}^{\left\{{N}_{1}\right\}}}{{\rho }_{1}}& -\frac{{a}_{12}}{{\rho }_{1}}\frac{R}{{\rho }_{2}}& \begin{array}{ccc}-\frac{{a}_{13}}{{\rho }_{1}}\frac{R}{{\rho }_{3}}& ..& -\frac{{a}_{1n}}{{\rho }_{1}}\frac{R}{{\rho }_{n}}\end{array}\\ -\frac{{a}_{21}}{{\rho }_{2}}\frac{R}{{\rho }_{1}}& \frac{1}{{\rho }_{2}}\frac{{R}^{\left\{{N}_{2}\right\}}}{{\rho }_{2}}& \begin{array}{ccc}-\frac{{a}_{23}}{{\rho }_{2}}\frac{R}{{\rho }_{3}}& ..& -\frac{{a}_{1n}}{{\rho }_{2}}\frac{R}{{\rho }_{n}}\end{array}\\ \begin{array}{c}.\\ .\end{array}& \begin{array}{c}.\\ .\end{array}& \begin{array}{ccc}\begin{array}{c}.\\ .\end{array}& \begin{array}{c}.\\ .\end{array}& \begin{array}{c}.\\ .\end{array} ..\begin{array}{c}.\\ \frac{1}{{\rho }_{n}}\frac{{R}^{\left\{{N}_{n}\right\}}}{{\rho }_{n}}\end{array}\end{array}\end{array}\right],$$

(13)

where $\frac{1}{{R}^{\left\{{N}_{i}\right\}}}=\sum_{j\in {N}_{i}}\frac{1}{{\rho }_{j}}$, and the elements ${a}_{ij};i,j\in N;i\ne j$ belong to the adjacency matrix $A$, as defined earlier. Observe that ${\varvec{Q}}(n x n)$ contains entries which are functions of only the utility concavity parameter $\rho$, while the vector ${\varvec{b}}$ holds only agent and interaction related parameters.

The off-diagonal elements of the square matrix Q are either zero or non-zero depending upon the elements ${a}_{ij}=1 or 0;\, i,j \in N,i\ne j$ of the symmetric adjacency matrix A representing the network. As before, the values of ${r}_{i}; \forall i\in N$ are such that $\sum_{i\in N}{r}_{i}=0$, rendering Q rank deficient (rank = n−1), with every row and column of Q summing to zero.

The solutions (12)–(13) express optimal allocation for a general connected weighted undirected network with facility for rich characterisation of agent and network in terms of a variety of parameters, viz., ${\rho }_{i};\,i\in N$; ${\sigma }_{i};\,i\in N$; the interaction weight matrix, S.

Additionally, if we take ${\rho }_{i};\,i\in N$ to denote risk aversion of each agent, then $\frac{1}{{R}^{\left\{{N}_{i}\right\}}}=\sum_{j\in {N}_{i}}\frac{1}{{\rho }_{j}}$ is equivalent to ‘social risk’ of the neighbourhood of agent i. Since the diagonal element in every row (or column) is the negative sum of all the off-diagonal elements in the row, i.e. over the 1-hop neighbourhood, we see that Q is the risk-weighted Laplacian matrix, which we can define equivalently as ${{\varvec{L}}}_{{\varvec{R}}}$, of the network.

Hence, the product ${\varvec{Q}}{{\varvec{b}}}^{{\varvec{T}}}$ has the property that for any agent i:

$${\left({\varvec{Q}}{{\varvec{b}}}^{{\varvec{T}}}\right)}_{i}=\sum_{j\in {N}_{i}}{r}_{ij}\left\{{\alpha }_{i}(\mathit{ln}\left(1+{\sigma }_{i}{\gamma }_{i}\right)-{avg}_{{j\in N}_{i}}\left(\mathit{ln}\left(1+{\sigma }_{j}{\gamma }_{j}\right)\right)\right\}.$$

(14)

This implies that the deviations from the Pareto optimal frontier for any agent has the connotation of degree-weighted deviation of the average interactions, weighted again, by the social risk of the neighbourhood.

We see that a direct consequence of this structure is that when we consider a regular network with identical node weights, we shall have${\sigma }_{i}=\sigma ;i\in N{\alpha }_{i}=\alpha ;\,\forall i\in N$; and${\gamma }_{i}=\gamma ;\,\forall i\in N$; resulting in ${\left({\varvec{Q}}{b}^{T}\right)}_{i}=0 ;\,\forall i\in N.$ This is, hence, a fairness benchmark which establishes that when there is no characteristic by which we can distinguish the agents, except their utility concavity parameter, no side payments of exchanges are required—and $\widetilde{{\varvec{x}}}$ is simply$X{{\varvec{c}}}^{{\varvec{T}}}$.

However, when agents are distinguishable by their contribution rate, their connectivity and their interaction strengths, then (12)–(13) deliver the full characterisation of risk-weighted averages over average interactions determined by network structure.

The solutions (12)–(13) exhibit many other interesting properties such as ‘flows’ of power arising from connectivity and interaction which are better visualised when we standardise the problem by assuming that agents are indistinguishable in terms of some external parameters.

Standardised DONEX for Weighted Undirected Networks

For the purpose of standardisation of DONEX in a weighted undirected network modelled by the graph ${G}_{U}(N,E)$, we shall set the total resource value to be shared by agents as $X=n$, the number of agents(nodes); the utility concavity parameters, ${\rho }_{i}=1;\,\forall i\in N$; the rate term ${\sigma }_{i}=1;\forall i\in N$. Under these conditions, we see that the DONEX solution reduces to the simpler form:

$${\widetilde{x}}_{i}=\mathrm{DONEX}\left(i\right)=1+\frac{1}{n}\sum_{j\in {N}_{i}}\mathit{ln}\left[\frac{\left(1+{\gamma }_{i}\right)}{\left(1+{\gamma }_{j}\right)}\right]; \forall i\in N.$$

(15)

It can be easily verified that the matrix form of this standardised DONEX is

$$\widetilde{{\varvec{x}}}=DONEX=1+\frac{1}{n}\left({\varvec{L}}{{\varvec{b}}}^{{\varvec{T}}}\right),$$

(16)

where ${\varvec{L}}={\varvec{D}}-{\varvec{A}}$, the Laplacian of the graph ${G}_{U}\left(N,E\right),{\varvec{D}}(n x n)$ is a diagonal matrix whose ${i}^{th}$ diagonal element contains ${\alpha }_{i}$, and $1(n x 1)$ is ${\left[\begin{array}{ccc}1& 1& \dots 1\end{array}\right]}^{T}$. The expression for DONEX in (16) captures an interesting connotation. The unit vector $1(n x 1)$, which lies in the null space of the ${\varvec{L}}$ represents the baseline Pareto frontier, around which we obtain particular solutions utilising the structure of ${\varvec{L}}$ and the interaction flows in ${\varvec{b}}$, averaged over the size of the network.

Before we examine the notion of dominance and interaction ‘flows’ in (15), let us note that the second term in the DONEX expression of (16) can be positive, zero, or negative depending upon the relative values of EIS, and represents agent-wise values of the deviation from unity. Additionally, recall that the sum of all such deviations over all agents is zero. We shall return to (16) in a later section to exploit some properties of the Laplacian.

There is an interesting point latent in the way in which the FOCs were formulated. We could have employed a negative sign for all the multipliers in (9), and reached the same solution. As a consequence, we would have had the ratio in the logarithm in (15) as $\mathit{ln}\left[\frac{\left(1+{\gamma }_{j}\right)}{\left(1+{\gamma }_{i}\right)}\right]$, which would have given us identical values for DONEX. This also results in the possibility of developing a family of scaled DONEX values. We shall present this as a primary result of this paper:

Result 1

$$\widetilde{{\varvec{x}}}=\mathrm{DONEX}={\varvec{X}}{{\varvec{c}}}^{{\varvec{T}}}+\omega {\varvec{Q}}{{\varvec{b}}}^{{\varvec{T}}},$$

(12a)

where the scalar constant $\omega$ can take negative or positive values in a range that ensures that every element of ${\varvec{x}}$ is positive. Thus, $\omega$ represents an additional ‘global’ DONEX parameter which may be used to scale the overall solution, and to ensure that they are all positive.

The computational complexity of obtaining DONEX may be estimated in the following manner. Given a fixed, connected UWN with n nodes, a central pre-requisite for obtaining the standardised DONEX is to calculate the values of EIS, ${\gamma }_{i}={\alpha }_{i}\sum_{j\in {N}_{i}}{s}_{ij}{\alpha }_{j};i\in N$, from a user-supplied ordered edge list with weights representing the graph model of the network. For each node i, this requires $\mathrm{O}({\mathrm{\alpha }}_{\mathrm{i}})$ operations to be performed.

Once the EIS values are available, we need to obtain the products ${t}_{i}=\frac{1}{n}\mathit{ln}\left[\prod_{j\in {N}_{i}}\frac{1+{\gamma }_{i}}{1+{\gamma }_{j}}\right];\forall i\in N$ as described in (18). If we were to be satisfied with only a DONEX ranking, and not their actual values, it would suffice to obtain only the products, ${v}_{i}=\prod_{j\in {N}_{i}}\frac{1+{\gamma }_{i}}{1+{\gamma }_{j}};\forall i\in N$ and rank them. These could be calculated in about ${2\alpha }_{i}$, or $O({\alpha }_{i})$ arithmetic operations for every node $i\in N$.

For complexity assessments of this nature, we think of scenarios where we have large networks; and most large networks are also sparse, with their sparsity captured in degree distributions. Let us consider a Configuration model, as described earlier, to be fitted to the given network, such that the probability of any node having a degree $\alpha$ is $p(\alpha )$. If we confine our attention for the moment to power-law networks, in which $p\left(\alpha \right)={\alpha }^{-k}$, where $2\le k\le 3$, we see that average degree, $\langle \alpha \rangle <\mathit{ln}n$, a standard result [4], under the condition that minimum and maximum degree fall in the range $(0,n)$. A large percentage of modern networks, particularly social networks, conform to these distribution characterisations [See for instance [4] for more details].

Based on this average degree, the average-case computational complexity for obtaining DONEX rankings is, thus, $\Theta (\mathrm{nlnn})$ when the power-law exponent, k = 2, and reducing to near linearity when k = 3. Note that we would have arrived at a similar estimate if we considered the sparse matrix product ${\mathrm{Lb}}^{\mathrm{T}}$ in (16) to calculate the actual value DONEX. For denser networks, the complexity would be bounded by $\mathrm{O}(\mathrm{n}{\mathrm{\alpha }}_{\mathrm{max}})$, where ${\mathrm{\alpha }}_{\mathrm{max}}$ represents the maximum degree parameter.

Dominance and Flows in DONEX

Second Order Stochastic Dominance

Let us examine the second term in (15), and call it

$${t}_{i}=\frac{1}{n}\sum_{j\in {N}_{i}}\mathit{ln}\left[\frac{\left(1+{\gamma }_{i}\right)}{\left(1+{\gamma }_{j}\right)}\right];\forall i\in N.$$

(17)

If we rewrite it as:

$${t}_{i}=\frac{1}{n}\mathit{ln}\left[\prod_{j\in {N}_{i}}\frac{1+{\gamma }_{i}}{1+{\gamma }_{j}}\right];\forall i\in N,$$

(18)

we see that each term in the product is a ratio of two expected values, in which the numerator represents the averaged interactions of agent i with its neighbours, while the denominators represent the values of expected interaction strengths between the neighbours of j, further with its own neighbours. Clearly, ${t}_{i}$ would be surely positive if the EIS of i, i.e. ${\gamma }_{i}$, is more than the EIS values of all its neighbours, resulting in a class of second order stochastic dominance, since we consider the values of $\gamma$ as expectations through probabilistic weighting of neighbourhood interaction weights, strengthening the rationale for terming the class of measures as one that characterises dominance.

This implies that the greater the stochastic dominance from interaction, the larger the value of the positive addition to ${t}_{i}$, and the greater the value of DONEX for agent i. Since the sum of standardised DONEX values is always n, DONEX is a relative dominance measure, and takes account of neighbours interactions, and neighbours’ neighbour’s interactions as well, through the denominators.

In a similar vein, an agent could be strongly dominated by other nodes, if each of its neighbours stochastically dominates this node. There could also be nodes for which the numerators and denominators are exactly equal, turning ${t}_{i}$=0, in which case the DONEX allocation would be unity.

Before we examine the ability of DONEX to characterise flows, it is interesting to compare the dominance centrality values obtained by DONEX against those obtained from calculation of Bonacich centrality for the same network, so that we may observe how DONEX captures the effect of degree-differentials in a nuanced manner in the this dominance measure. For this purpose it is instructive to consider a linear chain of nodes, often used to demonstrate this aspect in many standard texts, as depicted in Fig. 1, which shows a 9-node undirected network.

Fig. 1

9-node linear chain network example

Calculating DONEX and Bonacich centrality for the nodes produces values as shown in Table 1.

Table 1 DONEX and Bonacich centrality measures of dominance for a 9-node network of Fig. 1

The top row of the table lists the node numbers, and the second row, the degrees of the nodes. The third row holds standardised DONEX values for the nodes, and last row holds Bonacich centrality values calculated with beta value of − 0.2. Note the symmetry of values around node 5, as expected, arising from the constraint placed by the structure of network.

We observe that nodes 1 and 9 are clearly the most dominated nodes by virtue of their low degree. Their DONEX values of 0.9059, reflect this reality. Node 2 with a DONEX score of 1.0662, which dominates over its left neighbour, is indeed the most dominant node, being the node with most dominated neighbour. Clearly, the score for node 3 must fall between these extremes because this node does not have such a dominated neighbouring node to express power over. Note similar values for nodes 8 and 7 assigned from structural symmetry. Following this rationale, DONEX assigns a score of 1.0469 to nodes 3 and 7, thus showing that they dominate over nodes 4 and 6, respectively.

Since node 5, at the centre of chain needs to ‘view’ its neighbours to the left and right with equal power due to symmetry; it can neither dominate, nor be dominated by its neighbours. Hence, nodes 4, 5 and 6 must have the same dominance power—and DONEX indeed assigns scores of equal scores of 1 to these three nodes.

In the third row, we see that Bonacich centrality with negative beta of − 0.2 does indeed identify the most dominated nodes as 1 and 9, as desired. However, the other values fail to capture the nuanced concept of dominance described above. For instance, the value for node 4 being more than that for node 3, results in unexplainable variations in dominance—and they arise from the even and odd powers of the beta coefficient, as discussed earlier.

Flows

We can determine flows of resources which need to be exchanged between agents in order to achieve optimality by laying out the partial sums of every row of the product $\left({\varvec{Q}}{{\varvec{b}}}^{{\varvec{T}}}\right)$ in a matrix F whose ${ij}^{th}$ element can be written as:

$${\varvec{F}}=\left[\begin{array}{ccc}\frac{R}{{\rho }_{1}}\frac{{R}^{\left\{{N}_{1}\right\}}}{{\rho }_{1}}\mathit{ln}\left(\left(1+{\gamma }_{1}\right)\right)& -\frac{{a}_{12}}{{\rho }_{1}}\frac{R}{{\rho }_{2}}\mathit{ln}\left(\left(1+{\gamma }_{2}\right)\right)& \begin{array}{cc}..& -\frac{{a}_{1n}}{{\rho }_{1}}\frac{R}{{\rho }_{n}}\mathit{ln}\left(\left(1+{\gamma }_{n}\right)\right)\end{array}\\ -\frac{{a}_{21}}{{\rho }_{2}}\frac{R}{{\rho }_{1}}\mathit{ln}\left(\left(1+{\gamma }_{1}\right)\right)& \frac{1}{{\rho }_{2}}\frac{{R}^{\left\{{N}_{2}\right\}}}{{\rho }_{2}}\mathit{ln}\left(\left(1+{\gamma }_{2}\right)\right)& \begin{array}{cc}..& -\frac{{a}_{1n}}{{\rho }_{2}}\frac{R}{{\rho }_{n}}\mathit{ln}\left(\left(1+{\gamma }_{n}\right)\right)\end{array}\\ .& .& \begin{array}{cc}..& -\frac{1}{{\rho }_{n}}\frac{{R}^{\left\{{N}_{n}\right\}}}{{\rho }_{n}}\mathit{ln}\left(\left(1+{\gamma }_{n}\right)\right)\end{array}\end{array}\right].$$

Such that the ‘flow’ from node i to j, if they are connected, can be calculated as the difference:

$$\begin{gathered} e_{ij} = f_{ij} - f_{ji} = - { }\frac{{1{ }}}{{\rho_{i} }}\frac{R}{{\rho_{j} }}[\ln \left( {\left( {1 + \gamma_{j} } \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, - \left[ { - \frac{1}{{\rho_{i} }}\frac{R}{{\rho_{j} }}\ln \left( {\left( {1 + \gamma_{i} } \right)} \right)} \right] = \frac{{1{ }}}{{\rho_{i} }}\frac{R}{{\rho_{j} }}\left( {\ln \left( {\frac{{1 + \gamma_{i} }}{{1 + \gamma_{j} }}} \right)} \right). \hfill \\ \end{gathered}$$

(19)

Clearly ${e}_{ij}>0$ iff ${\gamma }_{i}>{\gamma }_{j}$, i.e. if the EIS of node i is greater than that of node j, and ${e}_{ij}<0$ otherwise. Also there is zero flow when the two EIS values are identical.

The significance of this result is that while we started with a weighted network which had only undirected edges between pairs of nodes, we are now able to ascribe a ‘direction’ to every edge on the basis of calculated flows in a direction from a node which has higher expected strength of interaction between its neighbours, to a node which has lower expected strength of interaction. This direction is, thus, a derived direction which follows a natural flow from a node that acquires higher importance on the basis of a composite of its connectivity and interaction strength, to one that has lower importance on this basis. It is now easy to visualise the manner in which DONEX is nothing but a sum of EIS-driven flows as depicted in (17).

It is important to observe here that we started with an undirected network, but have ‘deduced’ a direction² for an edge connecting two nodes on the basis of a ‘virtual’ flow of power that derives from (stochastic) dominance over neighbours. This concept lends itself to suitable interpretation as the derived direction of ‘influence’ that comes from dominance, or inversely, as the reverse direction in which attention is paid, as we shall see later in this paper.

In the standardised version of DONEX, the flows are simply:

$${e}_{ij}=\frac{1}{n}\mathit{ln}\left(\frac{1+{\gamma }_{i}}{1+{\gamma }_{j}}\right),$$

(20)

such that, the flow ${e}_{ij}>0$ implies a ‘flow of dominance power’ from i to j resulting from the fact the node i dominates over j in the sense described above.

It may be observed how this new formulation of DONEX extends and generalises our previous work which developed DON as a dominance centrality measure for undirected, unweighted networks. Even though DONEX accounts for expected interaction strengths derived from probabilities associated with presence of edges, and weights for such interactions, the Eqs. (15)–(20) above have a structure closely resembling those in the formulation for DON.

Although DON and DONEX are numerically dissimilar, the similarity of structure of Pareto optimal solution, allows many of the interesting properties to be carried over. We shall simply and informally state some of them for completeness, since they are trivially evident. For instance, DONEX is also obtained in time linear in the size of the network. The useful results on derived flows are demonstrated with an illustrative example that follows.

Example 1

To fix ideas on the concept of dominance arising from EIS, and the calculation of ‘virtual’ flows, we shall illustrate the working of the DONEX method with a simple example in Fig. 2 for a 4-node undirected weighted network.

Fig. 2

a and b Standardised DONEX for 4-node example

Note that the purpose of the simple example of Fig. 2 is to establish a convenient visual connection to the key quantities we computed previously and to permit easy interpretation. Later, we shall apply method to larger, real networks.

The figure shows 4 nodes labelled with the degrees, ${\alpha }_{i};\forall i\in \{\mathrm{1,2},\mathrm{3,4}\}$. All weights are set to 1, i.e. ${s}_{ij}={s}_{ji}=1;\,\forall ij\in N$ whenever the corresponding adjacency matrix element ${a}_{ij}=1.$

The Fig. 2(a) on the left shows the values of DONEX computed using (15) or (16). We can observe that the DONEX value is highest for node 1(1.5339) and the least for node 4 (0.6534), while nodes 2 and 3 have the same DONEX value (0.9063). We can verify that these values sum to n = 4, by design. Node 1 ‘dominates’ over its neighbours, all of which have degrees which are lower. Its ‘dominance’ is more over node 4 than it is over nodes 2 and 3, and hence the ordering. Also nodes 2 and 3 are indistinguishable to node 1 by connectivity, and hence the method allocates identical DONEX values to them.

In Fig. 2(b) to the right, we have overlaid the values of flows ${e}_{ij};ij\in \{E|{a}_{ij}=1\}$ calculated on the basis of (20). Note that the edges connecting the nodes are now shown directed on the basis of these values. Observe that all edges from node 1 to other nodes are directed. They go from 1 to all other nodes, carrying the implication that node 1 dominates over the other nodes. Note also that the edge connecting 2 and 3 carries no (i.e. zero) flow, because these two nodes have identical DONEX scores, obviating the possibility of either of them dominating (or being dominated by) the other. Hence, the edge is shown bidirectional and as a dashed line.

In general, therefore, we can consider ‘derived’ in- and out-degrees for every node on the basis of these directions of edges. Let us denote the set of neighbours of node i which has such incoming edges as:

$${D}_{i}^{in}=\{j\in {N}_{i}:(\mathit{ln}(1+{\gamma }_{j})>\mathit{ln}(1+{\gamma }_{i}))\};\forall i\in N,$$

(21)

and

$${D}_{i}^{out}=\{k\in {N}_{i}:(\mathit{ln}(1+{\gamma }_{i})\ge \mathit{ln}(1+{\gamma }_{k}))\};\forall i\in N.$$

(22)

Then, we can denote the net ‘inflow’ into node i, by

$${g}_{i}^{in}=\sum_{j\in {D}_{i}^{in}}\mathit{ln}\left(\frac{1+{\gamma }_{i}}{1+{\gamma }_{j}}\right),$$

(23)

and net ‘outflow’ by

$${g}_{i}^{out}=\sum_{k\in {D}_{i}^{out}}\mathit{ln}\left(\frac{1+{\gamma }_{i}}{1+{\gamma }_{k}}\right).$$

(24)

Note that we have included the case of zero flows along with ‘outflows’. We shall explore the use of these quantities for characterising node types shortly.

Before we apply DONEX to real undirected networks, let us extend the notion of flows to ‘boundaries’ around sets of connected nodes.

Boundary Flows Around a Connected Set of Nodes

The flows at the boundary of a set of connected nodes in a network have an interesting direct relationship with the sum of the DONEX values of the nodes in the set. This boundary flow property is explored next with the following proposition.

Let $C\subset N$ denote a set of connected nodes, such that the set of edges among them, $\{{E}_{C}\subset E\}=\{ij:i\in C,j\in C\}$.

We then have the following proposition relating to boundary flows.

Proposition 1

The sum of the flows, $\sum_{k\in C}{t}_{k}$ is equal to the net flow at the boundary of $C$.

Proof

We provide a brief sketch of the proof here. The expression for flows in DONEX as in (20) for every node,$k\in C$, can be rewritten as:

$${t}_{k}=\frac{1}{n}\mathit{ln}\prod_{j\in {N}_{k}}\frac{{1+\gamma }_{k}}{{1+\gamma }_{j}};\, i\in N.$$

(25)

Hence,

$$\sum_{\mathrm{k}\in \mathrm{C}}{t}_{\mathrm{k}}=\frac{1}{n}\sum_{\mathrm{k}\in \mathrm{C}}\mathrm{ln}\prod_{\mathrm{j}\in {\mathrm{N}}_{\mathrm{k}}}\frac{{1+\gamma }_{k}}{{1+\gamma }_{j}}=\frac{1}{n}\mathrm{ln}\left[\prod_{\mathrm{k}\in \mathrm{C}}\left(\prod_{\mathrm{j}\in {\mathrm{N}}_{\mathrm{k}}}\frac{{1+\gamma }_{k}}{{1+\gamma }_{j}}\right)\right].$$

(26)

The expression in square brackets above comprises $\mathop \sum \limits_{k \in C} \alpha_{k}$ products of ratios of the form, $\frac{{1+\gamma }_{k}}{{1+\gamma }_{j}}$.

It is easy to see that every edge $<r,s>\in {E}_{C}$, from node $r$ to node $s$ satisfying $\{<r,s>:r\in C,s\in C\}$ appears in the product in pairs, i.e. as $\frac{{1+\gamma }_{r}}{{1+\gamma }_{s}}$, as well as its reciprocal, $\frac{{1+\gamma }_{s}}{{1+\gamma }_{r}}$, and hence results in ‘cancellation’ in the product to 1. In other words, all edges in the interior of the set $C$ do not contribute to the product. The edges that remain in the product after this cancellation satisfy the condition $<r,t>\in {E}_{C}$ satisfying $\{<r,t>:r\in C,t\in {C}^{1}\}$, where we specify, ${C}^{1}\subset N\cap C$, as the one-hop neighbourhood of $C$, i.e. the set of neighbours of the nodes in $C$, that are not in $\mathrm{C}$, but are reachable in 1 hop by the nodes in $C$. Every such edge has one end within $C$, and the other end outside $C$. These edges, hence, form the boundary edges of $\mathrm{C}.$ As a result of this, the sum of exchanges is equal to the net flow at the boundary of $C$.

The next proposition is a simple corollary of the above proposition.

Proposition 2

The sum of DONEX values of a set C of connected nodes is proportional to the boundary flows in and out of C.

Proof

This follows directly, since $\sum_{k\in C}DONEX(k)=\left|C\right|+\frac{1}{n}\sum_{k\in C}{t}_{k}$, where $\left|C\right|$ is the cardinality of the set C.

■

The calculation of boundary flows around the set of nodes, C, is illustrated in Fig. 3 using the same 4-node network of Fig. 1. In Fig. 3 we have constructed C as the set of nodes: C = {1,4}. The boundary edges around C, thus, comprise the two edges $\{1\to \mathrm{2,1}\to 3\}$. The net flow on these (boundary) edges is ${e}_{12}+{e}_{13}=0.0937+0.0937=0.1874$. It may be verified that this is also equal to $DONEX\left(C\right)-\left|C\right|=DONEX\left(1\right)+DONEX\left(2\right)-2=0.1874$. This is depicted in Fig. 3.

Fig. 3

Boundary Flows around C

It is instructive and easy with this example to examine the fact that the concept of boundary flows holds for any set of connected nodes. We shall now propose criteria for distinguishing nodes on the basis of their dominance characteristics.

Dominance-Type Characterisation

In this section, we shall identify and label nodes on the basis of the type of dominance they exhibit, with the derived directions of the edges that connect them, determined by calculated flows, as above. As mentioned before, it is useful to think of flows of dominance as capturing the notion of ‘influence’.

This allows us to distinguish between nodes which can ‘amplify’ a message in a network by domination over neighbours, or nodes that are not endowed with that ability because they are fully dominated. We shall use values of ${g}_{i}^{in}$ and ${g}_{i}^{out}$ for every node as described in (23) and (24) to classify the types. We shall shortly see an illustrative example.

We distinguish the following types:

• a) SDG, or Strongly DominatinG Node: is one which is connected to all its neighbours by outgoing edges, i.e. ${g}_{i}^{in}=0; {g}_{i}^{out}>0$. This is a node which dominates over all its neighbours. Clearly, an SDG would not be ‘influenced’ by near neighbours, since there are no incoming edges to carry flows inward. We shall refer to SDGs as nodes that can ‘reach’ its neighbours, but cannot be ‘reached’ by any of its neighbours. SDGs can ‘influence’ its neighbours, but cannot be influenced by others, because they are not ‘reachable.

• b) WDG, or Weakly DominatinG Node: is a node that has both incoming and outgoing edges, but the net outflow exceeds inflow, i.e. ${g}_{i}^{out}>{g}_{i}^{in}$. This is weaker in influence amplication performance, but is still a useful node for propagation of influence, by those of its neighbours that can ‘reach’ this node.

• c) WDD, or Weakly DominateD Node: is a node that has both incoming and outgoing edges, but the net inflow exceeds outflow, i.e. ${g}_{i}^{in}>{g}_{i}^{out}$. This type of node can ‘listen’, but cannot further spread influence with the impact of a WDG in b), above.

• d) SDD, or Strongly DominateD Node: is one which is connected to all its neighbours by incoming edges, i.e.${g}_{i}^{out}=0; {g}_{i}^{in}>0$.This is a node which is dominated by all its neighbours; such a node cannot influence any neighbour. It can be ‘reached’ by its neighbours, but cannot ‘reach’ other nodes.

To see how this characterisation is useful, consider an acquaintance network in which nodes represent individuals, and undirected edges between nodes denote friendships between individuals. Let the weights associated with edges connecting nodes signify ‘strength’ of friendship. We calculate DONEX, flows and directions of the edges using the methodologies developed above.

Now let us assume, the k^th node has a high DONEX score, i.e. k is one of the important individuals in the network, possibly dominating over a large neighbourhood around k. Let us assume k is a SDG. Assuming individuals are allowed to send only one message at a time so to spread one’s influence, which other user should he/she pick first as the recipient?

Clearly, k should pick a neighbour who not only can be influenced, but one who also has the ability to influence others; in other words, an WDG from the set ${D}_{k}^{out}$, which can be ‘reached’ by k. Among the many candidates, k should pick the WDG with the highest DONEX score, or equivalently with the highest positive outflow, for then the propensity for ‘amplification’ of influence is highest. Now, suppose node k picks node j in this manner to build a set of connected propagators, $P$, starting with $P=\{k,j\}$. Let’s call this process of selection the ‘recruitment’ of propagator node j by k, to propagate its influence.

This recruitment process can be continued further by the k and j to collectively recruit other propagators who are ‘reachable’ by both, by searching for propagators in the set $S=\{{D}_{k}^{out} \cup {D}_{j}^{out}\}$. The expansion of $P$ by adding more connected propagators can be thought of as greedy recruitment because nodes with highest DONEX scores are picked each time on the basis of their ability to reach other nodes. The recruitment process has to clearly terminate, since ‘reachable’ directed paths from any node in $P$ to all nodes in $\{N\cap P\}$ reduce in every step.

We note that at the point when this process terminates, the sum:

$$RS=\frac{1}{n}\sum_{\mathcal{l}\in P}\mathrm{DONEX}\left(P\right),$$

(27)

which we shall refer to as Reach Score(RS), by Proposition 1, will represent the net boundary flow around the set $P\subseteq N$. Since $\sum_{j\in N}\mathrm{DONEX}\left(j\right)=n=|N|$, RS is a proportion of 1, representing the fraction of the total nodes which could be reached by the seed node k, until further recruitment of propagators could not be pursued. Hence, RS represents a normalised score capturing the notion of the fraction of the nodes which could be reached from a seed node, not only in terms of the reachable partition of the network, but also in terms of the share of a total dominance of n that is apportioned over the nodes of the network.

This idea can be developed as a greedy algorithm to compute the propensity for influence propagation from any node that has a high DONEX value, i.e. a node that has a high degree of importance among its neighbours. We shall now describe an algorithm, referred to here as NetProp, to calculate this propagation, given a ‘seed’ node with high DONEX in an undirected network.

To bring out key features of NetProp, we shall demonstrate its application on an 18-node synthetic network example shown in Fig. 4.

Fig. 4

An 18-node undirected network example

Consider this network as representing acquaintances among 18 individuals, with each undirected edge between two nodes denoting a friendship with strength of 1, implying that we have set all edge weights to unity. We shall later see examples with realistic non-unit weights.

The tables at the bottom of the figure list the degrees of the nodes and the standardised DONEX scores computed using (15), as before. Note that nodes 3 and 2 (both with degrees of 6) have different DONEX scores, because of different neighbourhood structures. Node 3 has the maximum DONEX score, in fact, exceeding that for node 16, which has a higher degree of 7. This is due to the fact that node 16 plays a role in a near-clique of size 6, due to which its dominance property is minimised by many nearly equally connected neighbours.

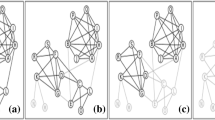
If we work out the flows along each edge using (25), we obtain a set of ‘derived’ directions for the edges as pictured in Fig. 5.

Fig. 5

Derived direction for edges of 18-node network example with Node types shown

Figure 5 shows each node coloured in accordance of the type of node as described earlier in this section. There are 3 SDGs, 5 WDGs, 8 WDDs, and 2 SDDs.

Let us now apply the NetProp algorithm to create a Propagator community around the most dominant node, node 3, and calculate its Reach Score (RS), to estimate how far its dominance can reach. The results for the application of NetProp are shown in Fig. 6.

Fig. 6

Building a Propagator community around Node 3: flows and reach score

Figure 6 plots Boundary flows and Reach Score as the size of the Propagator community, set P, around node 3 is expanded by the recruitment process of the NetProp algorithm. The x-axis markers (blue numerals) denote the size of P, as a node that adds the maximum flow is added to P. Recall that we add one recruit to P in every iteration.

The inverted-U-shaped curve (in blue) represents the boundary flow around P, as P grows in size. The markers on the curve are tagged with numbers, which denote the node-ids of the propagators which were added into P. For instance, the first node is node 3, marked in red, to indicate that it is an SDG type node. The next node that NetProp added was node 2, another SDG. Similarly the third node was node 7, a WDG-type node. Until this point, the flows increase, because all these nodes added net-positive flows (their DONEX score were greater than 1).

Further expansion of P, beyond the above three nodes, was possible since other neighbours were at least WDD type nodes, which were ‘reachable’; but we observe that the boundary flows begin to fall until we add node 6, which was ‘reachable’ from the current P. Note that at this point the boundary flow has begun to turn negative, even if node 10 was reachable. NetProp terminates after recruiting node 10, because no other nodes are reachable from P.

Note the progression of nodes recruited—from SDG, to WDG, and then to WDD, and finally to SDD. This is an interesting and natural progression which testifies to the power of dominance weakening after exhausting all WDGs in the neighbourhood, without encountering another powerful dominant node. Note also the monotonically rising curve (in red) representing Reach Score (RS). RS represents the percentage of the network (in flow terms) that has been reached. The RS score starts at about 5% with only node 3 in P, to about 54% at termination.

The application of NetProp with node 3 as the seed (starting) dominant node, thus, results in the identification of the community of influence propagators as shown in Fig. 7.

Fig. 7

Network partitioned into propagator community around node 3, and unreachable partition

Note that the directions of the edges across, from P to the rest of the ‘unreachable’ partition are all ‘incoming’, and not directed outwards, implying that influence cannot progress across the boundary.

Interestingly, the inverted U-shape representing rising flows until SDGs and WDGs are available in the neighbourhood of the starting seed SDG/WDG, and falling flows as WDDs and SDD’s are added to the community, is clearly a universal feature of all those networks in general, except where there may be other strongly dominant nodes positioned farther away in the network from the seed node.

At this stage, it is fruitful to assess the various phases at which we could have terminated the enlargement of the Propagator community. If we wished to recruit propagators only until flows show an increasing trend, then we could have stopped at ${\varvec{P}}=\{\mathrm{3,2},7\}$. At this stage RS would be barely 20%, but the boundary flow around P would have been the maximum. If we progressed further with recruiting WDDs, we could extend RS to about 42%, but influence of dominance would have dropped to barely zero. Further recruitment is actually fruitless, since the boundary flow turns negative—unless the desire is only to increase RS, which could grow to 54% at most.

This observation allows us to modify NetProp’s termination criteria on the basis of user-provided threshold parameter to the meet a desired goal of a dominating node wishing to spread influence. For instance, if the goal were to terminate before boundary flows turn negative, then P would not include nodes 6 and 10, and the boundary in Fig. 7 would be redrawn appropriately, as in Fig. 8, which reveals a partition of the network around which the flow is the smallest positive value of 0.0839 with a connected community contained within the partition that has a Reach Score of about 44.9%.

Fig. 8

Partitioning on the basis of minimum flows around a community of connected nodes

The NetProp method, thus, provides a very simple but powerful method to partition undirected networks on the basis of minimal (positive or negative) flows around a community of connected nodes.

This leads us to a new way of finding minimum and maximum flow partitions of undirected networks in general with the use of the NetProp algorithm, which we shall state as a key result.

Result 2

The NetProp greedy method of expanding a connected community on the basis of derived DONEX flows effectively finds minimum and maximum flow partitions of networks around a seed SDG or WDG node with DOENX scores greater than 1.

Proof

The proof is easily derived from the results of Propositions 1 and 2.

Note that NetProp could be applied to detect minimal-flow communities around many important nodes in an undirected social acquaintance/friendship network. Note that seed idea underlying this form of minimal-flow community detection differs greatly from traditional community detection³ in undirected weighted networks, which are largely based on the notion of modularity [60,61,62].

Hence, NetProp permits evaluation of spread of influence and dominance, together with reach around user selected dominant nodes in a network. It also permits determination of which nodes are potential members of overlapping partitions, allowing us to calculate levels of interaction strengths which can potentially change their membership of propagator communities. Such members may play the role of weak ties who can help carry influence across communities.

We have illustrated this concept with the application of NetProp to the well-known Zachary Karate Club problem [65], and the Co-authorship Collaborative network introduced originally by Newman [64] in Supplementary Material accompanying this paper, and show how ‘recruiting’ additional members could have changed the partitioning significantly.

NetProp is easily applicable to large WUNs, and Supplementary Material accompanying this paper carries results obtained from its application to a number of standard networks which have been popularly used as benchmarks for network analysis. This set of results demonstrates the fact that the boundary flow curve and the reach curve have similar shapes as in Fig. 6, and permit interpretation of flow of influence in a general manner.

Before proceeding to explore the CWF model to weighted directed networks, it is useful to see how DONEX extends easily to measure dominance of a node over multi-hop neighbourhoods.

MHDONEX: a Multi-hop DONEX

The above result may be used to measure the net boundary flow of any given node taken together with its neighbours, and their neighbours, and so on, recursively until no more neighbours who are reachable, in the sense as described above, can be found. This is akin to finding and analysing an ego network [66] around a selected node, with the definition extended notionally, as a potentially expanding set of neighbourhoods of alter-egos into which the dominance of the ego-node can spread. As established in the previous section, the sum of the DONEX measures of such a ‘community’ of neighbours that forms the ego network of a node is directly related to the flow around its boundary. Hence it is equivalent to a Multi-hop DONEX measure, which we shall refer to MHDONEX, and may be used to rank each node in a connected network, considering each hop from the selected node as an expanding ‘sphere of influence’. We shall see shortly that the resulting rankings may be used to assess trade-offs between number of neighbours reached and the resultant flow.

Let us first define a set of neighbours of a node i, including node i, as an ego-centric 1-hop neighbourhood in an n-nodeWUN:

$${V}_{i}^{1}=\left\{i\right\}\cup {N}_{i},$$

where ${N}_{i}$ is the neighbourhood set as defined earlier in “Basic Definitions and Terminology”. Then, the set of nodes forming the 2-hop ego network would be ${V}_{i}^{2}=\{\{j:j\in {V}_{i}^{1}\left\{i\right\}\}\cup {N}_{j}\}$, and so on, so that for a range of hops $h=1$ to $h={h}_{max}$:

$${V}_{i}^{h}=\bigcup_{h=1}^{h={h}_{max}}\{\{j:j\in {V}_{i}^{h-1}\left\{i\right\}\}\cup {N}_{j}|{N}_{j}\ne \mathrm{\varnothing }\},$$

noting of course, that we may exhaust neighbours (i.e. ${N}_{j}=\varnothing )$ before expanding the sphere of influence up to ${h}_{max}$ hops.

Let us also define a set of ‘boundary’ nodes, which have edges from any node in ${V}_{i}^{h}$, as ${B}_{i}^{h}=\{k:{a}_{jk}=1;j\in {V}_{i}^{h}\}$.

Since each ${V}_{i}^{h}$ is a set of connected nodes by definition (i.e. neighbours and their neighbours, and so on), we can easily obtain a Multi-hop DONEX for each node over as many hops that exist, as the simple sum (we omit the algebra here):

$$\mathrm{MHDONEX}\left(i,h\right)=1+\left|{V}_{i}^{h}-1\right|+\frac{1}{n}\sum_{j\in {V}_{i}^{h};k\in {B}_{i}^{h}}\mathrm{ln}\frac{1+{\gamma }_{j}}{1+{\gamma }_{k}}.$$

(28)

The term $\left|{V}_{i}^{h}-1\right|$ expresses the size of the ‘alter-ego’ community around the node i, and grows over the hops, as the sphere of influence increases in size. The last expression is just the boundary flow averaged over n around this community. A single hop MHDONEX measure accounts only for ‘local’ effects of flows of influence. As the number of hops considered grows, we are effectively accounting for larger proportions of non-local connectivity in the measurement of influence from degree-differential flows. Hence $MHDONEX\left(i,h\right)$ in (28) has the general form of (1 + neighbourhood_size + boundary_flow).

There are clearly three ways in which one can view the trade-off in (28). Firstly, if a given node has positive boundary flows over many more hops than others, it may be characterised as being influential over a large ‘length’ of connections. However its Reach Score is given by size of the alter-ego community, i.e. $\left|{V}_{i}^{h}-1\right|$, which may vary with each hop. Note that if we subtract out this size from the expression in (28), we are left with an expression that accounts only for boundary flows, i.e. (1 + boundary_flow), just as that for DONEX in (15). This also provides one method to rank nodes over many hops, emphasising only the flows. Lastly, a node that has high positive boundary flows across  it's boundary of alter-ego community, over many hops, offers another indirect measure of importance which accounts for non-local network structure much away from the selected ego-node.

To get a flavour of the utility of these types of observations in a real setting, we shall illustrate the calculations of MHDONEX for the same undirected linear chain network of 9 nodes, shown in Fig. 1, for which we previously calculated DONEX. This example has been selected in particular because offers scenarios where the impact of multi-hop rankings of influence are easy to visualise and understand.

The network is pictured in Fig. 9, where 9a depicts the expanding “ego-network” neighbourhoods around node 5, noting of course, the symmetry around this node—implying that the dominance behaviour to the left of node 5 should be found similar to the behaviour of nodes to the right of node 5.

Fig. 9

Multi-hop ego-centric network neighbourhoods (a) around node 5; and (b) around node 1 of a 9-node chain

Note the sizes of the neighbourhoods as shown for node 5 at the top of the figure: 2 1-hop neighbours, 4 2-hop neighbours, and 6 3-hop neighbours. The ego network cannot be expanded further since that would subsume the whole 9-node chain. Note also that when we put the dashed ellipse around the neighbours of node 5, we are in effect coalescing their presence into a single super-node, and examining the dominance of this super-node on its neighbours as expressed by the boundary flow around it. So, multi-hop dominance is about how much a node and its neighbours can together dominate over others across their ‘boundary’ connections.

As the boundary expands over multiple hops, we are accounting for increasing proportions of non-local effects over purely local effects, which DONEX itself was accounting for. We can, thus, intuit from visual inspection alone that, while node 5 ‘expands’ to nearly the whole network in merely 3 hops, node 1’s ego network needs many more hops to ‘reach’ that proportion of the network. But that alone tells only part of the dominance story, for we need to see what happens to boundary flows.

For this purpose, we shall first calculate the DONEX scores for each node in the 9-node chain using (15), which are shown in the second column of Table 2, with the first column indexing the node number. We have referred to this DONEX column as hop 0, and it contains the same values we previously calculated in row 3 of Table 1.

Table 2 Multi-hop dominance characterisation of nodes in a 9-node chain

The first observation about the DONEX values in column 2 of the Table 2 is that they reflect the symmetry about node 5, as expected. But they also carry the spirit of eigen-centrality with negative $\beta$. We can observe that node 2 (and 8) have the highest DONEX scores because they dominate the nodes at the extremity of the chain, as well as node 3 (node 7). Nodes 4, 5 and 6 are all neither dominating, nor dominated.

Columns 3 and 4 of Table 2 carry the values of (1 + boundary_flow) and the size of the neighbourhood, as expressed in (28), for hop 1. Similarly, columns 5 and 6 carry these values for every node when hop = 2, and so on. A study of the multi-hop table reveals that although node 5, which lies at the centre of the chain is heavily dominated when considered on its own, it is this node that, along with its 3-hop ego-network neighbours, that generates the highest boundary flow of 1.1183, with the largest neighbourhood size of 6. Thus, its Reach Score is also the largest, when we take into consideration the effect of non-local connectivity.

There have been many recent research efforts aimed at the development of centrality measures, belonging to the PowerClub class we identified earlier, that capture the combination of local and non-local effects [36, 67, 68] incorporating new information theoretic and other concepts to weight such effects. The key benefit in our approach to obtain our DC-class measure is that the weighting is obtained naturally based on the original flow at the boundary of the neighbourhoods. The variation in the ranking of the Multi-hop DONEX scores tells the story of how non-local effects alter the dominance of a node over its expanding ‘sphere of influence’.

Finally, we observe that the Multi-hop extension of DONEX scores can be easily enriched with other parameters—including weights on the edges, weights for each of the nodes, and the utilisation rates, should these be available in the application domain. We shall now proceed to extend DONEX to Weighted Directed Networks (WDNs).

Collective Welfare Model for Weighted Directed Networks

Weighted Directed Networks (WDNs) form an important class of complex networks, and have attracted increased attention of researchers in the recent years. The directions and weights on edges are most often obtained as constraint specifications from the network problem domain, and are considered as given. For instance, the direction of an edge in a transportation network from a node to another node may specify a permissible route; and the weight on the edge may represent the specified volume of a transported good, or a route capacity characterisation. Alternatively, in a communication network, an edge between to nodes may represent the presence of a medium or channel for communication, and the weight assigned, a specified volume of traffic in the given direction. See [4, 5, 69,70,71] for other examples of weighted directed network in other domains.

Recalling that we model weighted directed networks as graphs ${G}_{D}(N,E,S)$, we shall continue to seek to maximise collective welfare of the agents using the same formulation as in (5). Recalling also that we have defined in-degrees and out-degrees for every node as ${\delta }_{i}=|{N}_{i}^{in}|;i\in N$, ${\eta }_{i}=|{N}_{i}^{out}|;i\in N$, and ${N}_{i}={N}_{i}^{in}\cup {N}_{i}^{out}$, we can express the net probability of the presence of incoming and outgoing edges as the proportionality, ${P}_{ij}\propto ({\gamma }_{i}^{in}+{\gamma }_{i}^{out})$, or

$${P}_{ij}{=(\delta }_{i}\sum_{k\in {N}_{i}^{in}}{\eta }_{k})+{(\eta }_{i}\sum_{j\in {N}_{i}^{out}}{\delta }_{j});i,j\in E.$$

(29)

Normalising over the number of edges in the network, as we did before in WUNs. The basis for this extension of the Configuration Model to directed networks was introduced and applied in the context of community detection in directed networks by Newman [63].

We then express Expected Interaction Strength (EIS), ${\mu }_{i}$ for node i, as

$${\mu }_{i}={\sigma }_{i}\sum_{j\in {N}_{i}}{P}_{ij}{s}_{ij}=\left\{{\sigma }_{i}\left({\delta }_{i}\sum_{k\in {N}_{i}^{in}}{\eta }_{k}{s}_{ki}+{\eta }_{i}\sum_{j\in {N}_{i}^{out}}{\delta }_{j}{s}_{ij}\right)\right\};i\in N.$$

(30)

Noting that (30) has essentially the same form as the formulation of collective welfare for weighted undirected networks, but with a new expression for EIS, we can simply write down the Pareto solution as

$$\widetilde{{\varvec{x}}}=\mathbf{D}\mathbf{O}\mathbf{N}\mathbf{E}\mathbf{X}=X{{\varvec{c}}}^{{\varvec{T}}}+{\varvec{Q}}{{\varvec{d}}}^{{\varvec{T}}},$$

(31)

where the vector, ${\varvec{c}}={[\frac{R}{{\rho }_{1}}\frac{R}{{\rho }_{2}}\dots \frac{R}{{\rho }_{n}}]}^{T}$, and ${\varvec{d}}=\left[\mathit{ln}\left(1+{\mu }_{1}\right)\mathit{ln}\left(1+{\mu }_{2}\right)\dots \mathit{ln}\left(1+{\mu }_{n}\right)\right]$. Note the change to the vector d in (31) from the vector b used in (12) in the context of WUNs.

We can standardise the DONEX solution for weighted directed networks in the usual way:

$$DONEX\left(i\right)=1+\frac{1}{n}\sum_{j\in {N}_{i}}\mathrm{ln}\left[\frac{\left(1+{\mu }_{i}\right)}{\left(1+{\mu }_{j}\right)}\right];\forall i\in N.$$

(32)

It is evident that all the properties of DONEX in (32) remain the same as in the calculations for undirected weighted networks. The following examples will illustrate the idea.

Consider first the 4-node example of Fig. 2(b), where we shall treat the derived directions obtained from the undirected network of 1(a), as the input weighted directed network ${G}_{D}(N,E,S)$. We shall use S = [0 1 1 1; 0 0 1 0; 0 1 0 0; 0 0 0 0] as our given asymmetric interaction strength matrix. We see (not worked out here, but quite easily hand-calculated, if required) that if we apply (32), we obtain DONEX scores [1.5339, 0.9063, 0.9063, 0.6534]—exactly the same values shown in Fig. 2. This tells us that giving due consideration to given weights along given directions, the dominance flows are each aligned exactly along the directions originally specified.

To see the sensitivity of the DONEX scores to the in-degrees and out-degrees of the nodes, and how they play a role in determining the flows, let us examine a simple illustrative example with a synthetic 6-node directed network shown in Fig. 10.

Fig. 10

Net flows on directed edges for a 6-node example WDN

Figure 10 shows a 6-node WDN with all edge weights set to 1, in accordance with the S matrix and calculated ${\gamma }_{1}$, ${\gamma }_{2}$ and $\mu$ for each of the nodes to the right of the network. We have also set the node weights represented by the rate terms ${\sigma }_{i}=1 \forall i\in \{\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}\}$. The numeric text in black near each node of the network carries the value of $(Donex\left(i\right)-1)$, to show how this represents sum of flows around the node. For example the DONEX score for node 4 is 1.0545, and the net flow around this node is (1.0545–1 = 0.0545). We see that these values are positive for the four nodes 2,3,4 and 5, while they are negative for nodes 1 and 6. This is just another way to show that the nodes 2,3,4 and 5 have DONEX values greater than 1, while node 1 and 6 have DONEX values less than 1. This manner of depiction allows us to demonstrate how the sum of the flows (in red) into (i.e. taken with negative sign) and (in black) out (taken with positive sign) of each node, are exactly the net node flows.

NetProp for WDNs

In this section, we shall employ NetProp to WDNs with a constraint on the search for prospective candidates for recruitment as propagators restricted to those which can be reached on the basis of specified edge directions in the WDN, rather than derived directions, which we employed in WUNs. We shall not rewrite the entire NetProp algorithm here, since the only difference in terms of its implementation is to alter the definition of ${D}_{d}^{out}$ as ${N}_{d}^{out}$ in Step 3, and Step 4 of the NetProp algorithm. This implies we only consider a node in the immediate neighbourhood of the propagator community as reachable, if there is a given directed edge from the current set C to this node. Of course, the calculation of DONEX would be in accordance with (32), instead of (15), which we employed for WUNs.

Based on this modification, we can see the impact of tracking and growing a propagator community on WDNs, first on the simple example of Fig. 10, and next on a real WDN representing a diffusion network Twitter Retweets.

Noting that for the 6-node network of Fig. 10, node 5 has the highest DONEX score (1.0910), let us examine the sequence of nodes NetProp picks up to build the PC around this node (Fig. 11).

Fig. 11

Maximum and Minimum Boundary Flows from NetProp for 6-node example of Fig. 10

We see that although it is the most dominant node in the network, node 5 does not have much reach, constrained as it is, by the directions of the edges around it. In fact the recruitment of node 6, as part of its PC, turns the boundary flow negative. The PC with node 4, on the other hand, extends to the whole network, growing to 5 members. Note from the sequence of nodes recruited that the boundary flow peaks with the addition of node 2, and begins to drop after that stage. The sequence also demonstrates compliance with the directed edges supplied as input with the WDN. Aside from maximum and minimum flow boundaries in studies of this nature, we can seek such a boundary flow that does not fall below the levels that the seed node itself sets up—in this case, this condition would occur at the point node 1 is recruited, as my be observed from the chart.

The ability to track of the growth of the propagator community spatially as the boundary flow around it increases and wanes, in relation to the ego network of a node can be of significant value in analysing the diffusion of influence in social media platforms. As mentioned earlier, the Retweet diffusion network captures the notion of flow of such influence on the basis of which users retweet which other users—with the former being considered influenced by the latter. This results in a directed graph, which could be weighted by the retweet frequency, and additionally carry exogenously derived weights for nodes to signify their importance in the network. To demonstrate the applicability of NetProp to this class of diffusion networks, we shall employ a publicly available retweet network (http://networkrepository.com) [81], which we shall refer to here as RTnet96.

The network has 96 nodes and 117 directed edges, and pictured in Fig. 12. The top-3 DONEX scores for the network are shown in Table 3.

Fig. 12

RTnet96 network

Table 3 DONEX Score ranks for RTnet96 network example

In the interest of brevity, we shall set only these node numbers, sequentially, as the seed nodes, and extract the propagator communities around them, obtaining the variation of boundary flows around them as they grow spatially.

Figures 13 and 14 depict the spatial growth of the PC around node 54. As before, the sequence of nodes recruited is marked along the boundary flow curve in Fig. 13, while the spatial structure of the PC community is delineated in Fig. 14.

Fig. 13

PC and RS around node 54 of RTNet96

Fig. 14

PC for node 54 of RTNet96

We find that the PC size around node 54 is 15. Note the peak boundary flow occurs at a PC size of 4, while it falls below the boundary flow around node 54 on its own, after the recruitment of node 36.

These results for node 45, the node with the second rank, appear in Fig. 15 and Fig. 16 in similar format. We find that the PC for this node is, in fact, even smaller. Note the useful ‘bump’ in the boundary flow that node 6 gives to the benefit of node 45, by virtue of the fact that it is better connected than all other neighbours.

Fig. 15

Boundary Flow and RS around node 45 of RTNet96

Fig. 16

PC for node 45 of RTNet96

Finally, we see that node 89, with a much lower DONEX score, in fact, has a larger reach and influence than other nodes with higher DONEX, as depicted in Figs. 17 and 18.

Fig. 17

Boundary Flow and RS around node 89 of RTNet96

Fig. 18

PC for node 89 of RTNet96

Two key observations from this example are that a high DONEX score need not be associated with a high reach in WDNs, and the non-local structure of the ego network can significantly inhibit or accentuate propagation of influence. Although we worked with a directed network, we treated all edges as unit-weighted in the example. Our methodology can accommodate richer characterisation of diffusion network of this nature, by accounting for edge weights, such as retweet frequency, as well as node weights by providing different values for $\sigma$.

Before, we conclude this section on CWF for Weighted Directed Networks, we observe that the overall complexity of DONEX for this class of networks continues to be linear in the size of the network, as with WUNs. It is also evident that Multi-hop DONEX methods can be easily extended to WDNs. In the interest of brevity, we shall not elaborate on these aspects further in this paper. We shall now highlight some prospects for application of the overall methodology of flow-based DC to some domains.

Some Application Perspectives

This paper addressed the problem of allocation of a constrained divisible resource to a group of agents interconnected by a complex network, on basis of their ‘connectedness’, and derived DONEX, an optimal allocation, as the measure of DC. This top-down approach is a common setting in many diverse domains, and solutions are often sought in cooperative, non-cooperative, and hybrid collective settings (See, e.g. Hougard [72]).

The collective social welfare formulation framework on which our methodology rests derives its roots from the theories in Microeconomics related to representative agents and the sharing of risk in syndicates [55, 73], which were not conceptualised then to handle networks and their structures. By moulding its core notion of side payments to exchanges of flows deriving from expected interaction strengths in networks of connected agents as in this paper, we are now in position to view collective welfare arising from optimal sharing of resources, as other forms of social capital originating in networked societies—for instance as that arising from social standing and position in a social or economic network.

Recent research in microeconomics and behavioural economics has increasingly been factoring in the structure and role of networks, particularly social networks, among economic agents, to analyse individual and group behaviour in different scenarios. These studies have begun to recognise the evolution and importance of socially networked agents in the social media driven world of today, and the nature of measures for ascribing economic costs and benefits that can accrue to individuals and collectives as a result of interactions with connected neighbours. Among the important approaches are recent efforts to accommodate and extend notions of social capital to social networks [74, 75], employ ideas originating in definitions of an attention economy to model utilitarian individual and collective behaviour founded on attention as a resource in social media, and modelling resource allocation among cooperating agents in Game-Theoretic frameworks [76], or as a constrained social welfare maximisation problem. It is interesting to note that many of these approaches in fact have a common thread through the manner in which benefits and costs accruing from social community membership and interaction are modelled as externalities, positive and/or negative, over pooled utilities that the collective derives from shared resources.

The behaviour of users of social networks in social media is a prime example application scenario, where attention paid by neighbours is the key resource, over which individuals derive utility in terms of their social standing. This is also a familiar bounded resource characterisation in social learning paradigms [77]. Given the individual utilities, the members of the community can seek to maximise their collective reputations giving due credit to the attention received by each member on the basis of connectivity—recognising the need to cooperate, since any member can vie to be a star in terms of social standing, as much as any other member. The optimal solution to such allocations can serve as a bench mark in social media against which many standard engagement metrics can be compared for evaluation of a media communication plan. DONEX as a DC measure can play a key role in measurement and characterisation of agents in these classes of networks where exchanges among agents are mapped to ‘soft’ quantities such as goodwill, trust, and attention which contribute to social capital and also thought to follow the class of flow conservation and balance that we have here. The use of NetProp to evaluate flow boundaries can reveal vital clues to assess the potential spread of such quantities through dominance obtained as DONEX.

The DONEX methodology finds a strong fit in financial applications in a natural way, since its utilitarian foundation already captures the notion of risk. While this paper does not include explicit application to this domain, the present authors have shown that a similar core formulation can address some issues in microfinance [21]. A social planner may view a microfinance loan allocation to group of socially networked, cooperating, borrowers to find the best compromise between lowering loan defaults and group welfare in this framework. In this scenario, one could seek an optimal allocation of loans to individuals by maximising a social welfare function composed of utilities over individual allocations, and externalities weighted by a suitable measures connectedness.

In sum, we believe the methodology presented here is well framed to model the core elements of the evolving themes of social capital in networked societies, bringing a new microeconomic grounding that combines behavioural aspects founded in utilitarian concepts with the formal concepts of network theory and analysis.

We have recently experimented with different versions of DONEX on real live Twitter data and were able to identify narrative and discourse drivers on the basis of this measure, exemplifying its utility in large scale application scenarios [15]. Another prospective application area for DONEX-derived measures for centrality is its use in networks which are mapped from ordered data sequences, such as time series. We have recently employed measures of this class for anomaly detection in ECG signals [78].

A diversity of other research domains in which agent-level interaction problems are posed in the framework of networks, and have benefited from a top-down allocation driven measure of centrality such as the Shapley Value, are naturally a potential application area for DONEX. This is particularly so when minimum or maximum flow boundaries are required to be obtained, for example in problems from the biosciences [79], urban planning [80], and communications [19]. We have directed further attention towards these aspects along with collaborators.

Concluding Remarks

This paper proposed a new class of Dominance Centrality (DC) measures for the power of nodes in complex networks, and introduced DONEX, a flow-based measure as a potential new member of this class. We discussed how DC differed from popular PowerClub centrality measures using the eigen-centrality measure with $\beta <0$ as a backdrop to draw out the need for this new classification of DC. We showed how a utilitarian collective welfare maximisation framework which models Expected Interaction Strengths (EIS) as externalities, not only provides a strong grounding for the approach in microeconomics, but also yields a potentially new way of framing the analytical Pareto optimal solution in the algebra of network adjacency matrices. We showed that such a solution, which we have referred to as DONEX, provides a rich parameter space to accommodate many network features, and exogenously set node properties. The highlight of the node-level DONEX score is that it is the sum of the log-degree-differential flows on the edges connecting it to its neighbours.

This interesting property is used to obtain maximum, minimum and other constraint-based flows at the boundaries of any selected collection of connected nodes, using a new greedy method referred to as NetProp. We show that DONEX can be extended to multiple hops to account for local and non-local network structures, just as NetProp is easily applicable to weighted networks which may be directed or undirected, with and without node weights.

Further work on the extension of DONEX to complex networks which are modelled as directed multi-graphs is currently underway.