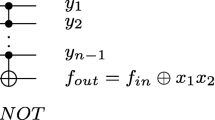Optimization of Reversible Circuits Using Gate Pair Classification

Abstract

Research on reversible logic gained momentum in the past decade owing to its utility in emerging areas such as quantum computing, optical computing and low power circuit implementation, etc. Reversible circuits synthesized using existing techniques often tend to be sub-optimal; thus, post-synthesis optimization techniques are usually employed to reduce the ‘circuit cost’, a metric used to compare the reversible circuits. In this paper, a set of optimization techniques is proposed to minimize the circuit cost. These techniques rely on classifying a pair of reversible gates in a given circuit based on their structural similarity. An algorithm that maps the classifications with the optimization techniques to improve the cost of a circuit is also proposed. Results obtained for a set of benchmark reversible circuits confirm that the proposed methodology performs better in terms of circuit cost when compared to those available in the literature.

Introduction

Research on reversible logic has been motivated by its applications in emerging technologies like quantum computing because unitary transformation in quantum computing was shown to be reversible [1], optical computing [2,3,4] and the need for ultra low power design [5,6,7]. Since a reversible logic function has one-to-one and onto mapping between its inputs and outputs, it rules out fan-out and feedback which are used extensively in conventional logic circuits. This lead to research on synthesis techniques exclusively for reversible logic in the past decade [8, 9]. These techniques can be categorized broadly as (i) exact and (ii) heuristic. Exact techniques search for optimal solutions to generate minimum cost circuits but are applicable only for small functions (where number of variables typically does not exceed 6) [9]. For functions with a large number of variables, heuristic techniques have been proposed. These however generate circuits that are sub-optimal in terms of cost and thus have scope for improvement. Thus, post-synthesis optimization techniques [10,11,12,13,14] have been developed to reduce the cost of synthesized reversible circuits.

The technique presented in [14] reduces the cost of a reversible circuit with the help of additional lines. However, the increase in the number of lines directly affects the complexity of its implementation [15]. Technique described in [10, 16] uses template-based local optimization to reduce the cost of the circuit. In these approaches, different templates are applied on a set of gates. However, this method involves a search for templates, which becomes complex as the circuit size increases. Rule-based optimization algorithms have been presented in [11,12,13, 17], a simulated annealing-based approach using transformation rules has been developed in [18] and a shared cube-based approach is presented in [19]. In all of these approaches, a group of gates is replaced with a lesser cost gate netlist using a set of rules. However when a pair of gates is considered, these techniques are applicable only for a few combinations of gate pairs.

A lookup table (LUT)-based hierarchical synthesis approach is presented in [20] where the Boolean logic is synthesized using k input LUT (termed as k-LUT) network. These LUTs are converted to reversible circuits using techniques such as Exclusive-OR Sum-of-Product (ESOP) decomposition [21] and reduce the cost of the circuit by applying rule-based techniques. Recently some optimisation technique has been proposed in [22, 23] to map the k-LUTs to a equivalent set of gates targeting to reduce the Clifford+T gates, a quantum gate library which is a more popular metric currently because of its application in fault tolerant quantum computing.

In the existing optimization techniques, the rules or transformations are applicable only to a few combinations of gate pairs. In this paper, a framework that includes transformations that are applicable for several combinations of gate pairs is proposed. In this framework, initially a methodology to classify a pair of gates in a reversible circuit is proposed. This methodology is then used to identify the gate pairs that can be optimized using the existing techniques as opposed to those that cannot be. For these gate pairs that cannot be optimized further, techniques to transform them to equivalent lower cost gate netlists are proposed. Finally, an algorithm that uses these techniques to reduce the total cost of the reversible circuit is presented. A set of benchmark reversible circuits has been employed to evaluate the performance of this framework.

Background

Reversible Logic Circuits

A function f is called a reversible logic function if there is a one-to-one correspondence, i.e, bijective mapping between inputs and outputs. A reversible logic circuit for a function can be realized by cascading reversible gates like NOT, CNOT, Toffoli and multiple-control Toffoli (MCT) gates [24]. The standard representation of basic reversible gates and a cascade of these gates to form a reversible circuit is shown in Fig. 1. An MCT gate is represented as MCT(C; t) where C is a set of control lines and t is the target line. When all the positive (negative) control lines of the gate, represented as $\bullet (\circ )$, are set to ‘1’ (‘0’), an MCT gate inverts the target line that is represented as $\oplus$. MCT gates with control lines as 0, 1 and 2 are termed as NOT, CNOT and Toffoli gates, respectively.

Fig. 1

Reversible gates and reversible circuit

Definitions used in this paper for different lines of a reversible circuit are given below:

Control Connection:

The control connection defines the state of a connection, i.e., positive or negative, of a given control line in a gate.

Equal Control Line:

A line having same control connection and same value for a set of gates is termed as the equal control line (ECL).

Complementary Control Line:

A line having positive control connection on one gate and negative control connection on another gate is termed as complementary control line (CCL) for the gate pair.

Unused Line:

A line which is neither a control line nor a target line of a gate is termed as unused line for that gate.

Cost Metrics

Typically, two different cost models are used to evaluate and compare reversible circuits, (i) NCT library cost model and (ii) quantum cost model.

NCT Library Cost Model

The NCT library consists of NOT, CNOT and Toffoli gates. MCT gates in a reversible circuit with more than two control lines are decomposed into NCT gates using the approach presented in [25]. The cost of an MCT gate in terms of Toffoli gates is given in Eq. (1) where c and n denote the number of control lines of a gate and the total number of lines in a circuit, respectively. The NCT cost of an entire circuit is therefore the sum of all the NCT gates after decomposing each gate.

$$\begin{aligned} \mathrm{Cost}_{T}(\mathrm{MCT})={\left\{ \begin{array}{ll} 8(c-3) &{} \mathrm{if}\,c>\left\lceil \frac{n+1}{2}\right\rceil \\ 4(c-2) &{} \mathrm{if}\,c\le\left \lceil \frac{n+1}{2}\right\rceil . \end{array}\right. } \end{aligned}$$

(1)

Quantum Cost Model

The Quantum Cost (QC) of a reversible gate is the number of primitive quantum gates required to implement the gate functionality. The primitive gates of quantum library used in this paper are NOT, CNOT, controlled $\mathrm {V}$ and controlled $\mathrm {V+}$ gates [25]. The QC of a reversible gate is calculated using RevLib [26] and is given in Table 1 where c denotes the number of control line and n denotes the total number of lines in the circuit. When all control lines of an MCT gate are negative, QC is increased by a value of 2.

QC of each gate in a circuit is summed up to calculate the QC of that circuit. As an example, QC of the circuit shown in Fig. 1e is $1+5+13+1=20$.

Table 1 Quantum Cost of an MCT gate

Quadruple Representation for a Pair of Gates

Several techniques exist in the literature to reduce the quantum cost of a given gate pair. These techniques are chosen based on the control connections of gate pair control lines. However, there exists no methodology by which a pair of gates can be classified into different classes based on the control connections of each gate in that pair. Such a classification helps in identifying gate pairs to which existing optimization techniques can be applied as opposed to those that do not have optimization defined on them yet. In this paper, we propose a representation named quadruple representation (QR) to classify gate pairs, as given below:

The QR for a gate pair, $g_{i}$ and $g_{j}$, is denoted as $\mathrm{QR}(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )$ where,

• $\alpha$: Number of equal control lines in the gate pair.

• $\beta$: Number of complementary control lines in the gate pair.

• $\gamma$: Number of control lines that have control connection only in the gate $g_{i}$.

• $\delta$: Number of control lines that have control connection only in the gate $g_{j}$.

For a gate pair $g_{i}$ and $g_{j}$, the sets which contain control connections corresponding to $\alpha ,\beta ,\gamma$ and $\delta$ are defined as K, C, P and Q, respectively. QR can be understood with the help of following example:

Example 1

Consider two gates $g_{1}$ and $g_{2}$ shown in Fig. 2. The gates have two equal control lines, $K=\{x_{0},\,x_{3}\}$, one complementary control line, $C=\{x_{1}\}$, a line with control connection only on gate $g_{1}$, that is, $P=\{x_{2}\}$ and a line with control connection only on gate $g_{2}$, that is, $Q=\{x_{4}\}$. Thus, according to the QR given above,

$$\begin{aligned} \mathrm{QR}(g_{1},g_{2})=(2,1,1,1). \end{aligned}$$

Fig. 2

Example for quadruple representation (QR)

Lemma 1 stated below provides the possible number of classifications for a gate pair when at least one of the elements of the QR is not equal to zero. If all the elements in the QR of a gate pair are zero, then the gate pair is a cascade of two NOT gates that can be removed from the circuit.

Lemma 1

In a reversible circuit, there exist 15 classifications for a gate pair $g_{i}$ and $g_{j}$, where at least one of the elements in $\mathrm{QR}(g_{i},g_{j})$ is a non-zero element.

Proof

The $\mathrm{QR}(g_{i},g_{j})$ is a quadruple with four elements $\alpha ,\beta ,\gamma$ and $\delta$. Depending on the elements that are either zero or non-zero, there exist $2^{4}=16$ unique classifications. Of these, one classification has all its elements as zero. Thus, the number of classifications in which at least one of the elements is non-zero is $16-1=15$. □

An example for each of the classifications along with their QR is shown in Fig. 3.

Fig. 3

Examples for different QR classifications

There exist several rules in the literature to optimize some or a subset of few QR classifications as given below:

Rule R1:

If QR$(g_{i},g_{j})=(\alpha ,0,0,0)$, then the gates are identical and can be removed from the circuit using the deletion rule presented in [27].

Rule R2:

If QR$(g_{i},g_{j})=(\alpha ,\beta ,0,0)$ or $(0,\beta ,0,0)$, then the gates can be decomposed into a network of smaller gates by applying the rule based optimization presented in [11].

Rule R3:

If QR$(g_{i},g_{j})=(\alpha ,1,0,0)$ or $(\alpha ,0,1,0)$ or $(\alpha ,0,0,1)$, then the gates can be merged into a single gate using the merging rule presented in [12].

Rule R4:

If QR$(g_{i},g_{j})=(\alpha ,1,1,0)$ or $(\alpha ,1,0,1)$, then the gates can be replaced with a lesser cost gate netlist using the replacement rule presented in [12].

Rule R5:

If QR$(g_{i},g_{j})=(\alpha ,0,\gamma ,1)$ or $(\alpha ,0,1,\delta )$, then the cost of the gate pair can be reduced using the cube pairing technique presented in [17].

Fig. 4

Examples for Existing Optimization Rules

An example for each of the rules discussed above is given in Fig. 4. As mentioned earlier, these rules can be applied only on a few QR classifications. For example, classifications like $(\alpha ,\beta ,\gamma ,\delta )$, $(\alpha ,\beta ,\gamma ,0)$, $(\alpha ,\beta ,0,\delta )$, $(\alpha ,0,\gamma ,\delta )$, $(\alpha ,0,\gamma ,0)$ and $(\alpha ,0,0,\delta )$ do not have any optimization defined on them. In what follows new optimization techniques that are applicable to most of the classifications are described.

Optimization Techniques for Different QR Classifications

The first technique is based on a decomposition rule that decomposes a pair of gates into a network of smaller gates. This technique can be applied on the classifications where equal control lines are present between a pair of gates, i.e., $\alpha >0$. Further, a complementary control line (CCL) transformation technique is presented to reduce the number of CCLs in a given gate pair. This technique is then used to transform the pair of gates with $\alpha =0$ such that the decomposition rule can be applied. Finally, a set of optimization techniques is proposed for specific QR classifications.

Optimization Technique for QR$(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )$ when $\alpha >0$

This technique is based on a decomposition rule that decomposes a pair of gates using the number of equal lines ($\alpha$) between the gate pair. This rule is described by Lemma 2 given below and is applicable for QR classifications in which $\alpha >0$, i.e., $(\alpha ,0,\gamma ,0)$, $(\alpha ,0,0,\delta )$, $(\alpha ,0,\gamma ,\delta )$, $(\alpha ,\beta ,\gamma ,0)$, $(\alpha ,\beta ,0,\delta )$ and $(\alpha ,\beta ,\gamma ,\delta )$.

Lemma 2

(Rule R6—Decomposition Rule) : Consider a pair of gates $g_{i}$ and $g_{j}$ with a same target line $x_{t}$. The $QR(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )$ and the sets of control lines are represented as K, C, P and Q. If an unused line ‘$x_{u}$’ is available, then the gate pair can be decomposed into a network of smaller gates as follows:

$$\begin{aligned} g_{i}\circ g_{j}=\, & {} \mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) \end{aligned}$$

(2)

Proof

The gates $g_{i}$ and $g_{j}$ are represented as $g_{i}=\mathrm{MCT}(K\cup C\cup P;x_{t})$ and $g_{j}=\mathrm{MCT}(K\cup C\cup Q;x_{t})$

According to [25], an MCT gate of size m (where $m\geqslant 5$) can be decomposed into a network of two gates of size p and two gates of size $m-p+1$ placed alternatively, given at least one unused line in the circuit. Considering $x_{u}$ as unused line, the gates $g_{i}$ and $g_{j}$ can be decomposed as follows:

$$\begin{aligned} g_{i}= & {} \mathrm{MCT}\left( K\cup C\cup P;x_{t}\right) \\= & {} \mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \\&\circ \,\mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \\ g_{j}= & {} \mathrm{MCT}\left( K\cup C\cup Q;x_{t}\right) \\= & {} \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) \\&\circ \,\mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) \end{aligned}$$

Therefore, cascading gates $g_{i}$ and $g_{j}$ are given as below:

$$\begin{aligned} g_{i}\circ g_{j}=\, & {} \mathrm{MCT}\left( K\cup C\cup P;x_{t}\right) \circ \mathrm{MCT}\left( K\cup C\cup Q;x_{t}\right) \nonumber \\=\, & {} \mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) \end{aligned}$$

(3)

According to the deletion rule given in [27], a pair of gates which is equal and adjacent can be removed from the circuit. Thus the cascade of gates, $\mathrm{MCT}(K\cup \{x_{u}\};x_{t})\circ \mathrm{MCT}(K\cup \{x_{u}\};x_{t})$, above is removed and the reduced circuit is given as,

$$\begin{aligned} g_{i}\circ g_{j}=\, & {} \mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) . \end{aligned}$$

(4)

□

Figures 5, 6, 7, 8, 9 and 10 illustrate the decomposition rule R6 when applied to the gate pairs belonging to different classifications. The gate pairs are decomposed such that they generate redundant gates which are then removed from the circuit resulting in final gate netlist.

Fig. 5

Example for QR$(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )=(2,2,1,1)$

Fig. 6

Example for QR$(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,0)=(2,2,1,0)$

Fig. 7

Example for QR$(g_{i},g_{j})=(\alpha ,\beta ,0,\delta )=(2,2,0,2)$

Fig. 8

Example for QR$(g_{i},g_{j})=(\alpha ,0,\gamma ,\delta )=(3,0,2,1)$

Fig. 9

Example for QR$(g_{i},g_{j})=(\alpha ,0,\gamma ,0)=(3,0,3,0)$

Fig. 10

Example for QR$(g_{i},g_{j})=(\alpha ,0,0,\delta )=(3,0,0,3)$

It can be seen from Table 2 that there is a reduction in quantum cost in each case after applying this decomposition rule.

Table 2 Quantum Cost reduction for different classifications after applying decomposition Rule R6

It should be mentioned that the decomposition rule results in reduced quantum cost only if the number of unequal control lines in the gate pair, i.e., $\beta +\gamma$ or $\beta +\delta$, is less than half the total number of lines in the circuit. If this is not the case, then the rule results in a higher-cost gate netlist when compared with the quantum cost of individual gates. This result can be proved with the help of following lemma:

Lemma 3

In a reversible circuit that has n lines, consider two gates $g_{i}$ and $g_{j}$ with same target line $x_{t}$ and an unused line $x_{u}$. The $QR(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )$ and the sets of control lines corresponding to $\alpha ,\beta ,\gamma$ and $\delta$ are defined as K, C, P and Q respectively. The decomposition rule results in a higher-cost gate netlist when compared with the cost of individual gates under the following conditions:

1. $\beta +\gamma \le \lceil \frac{n+1}{2}\rceil$, $\beta +\delta \le \lceil \frac{n+1}{2}\rceil$ and $\alpha \le 1$.

2. $\beta +\gamma >\lceil \frac{n+1}{2}\rceil$ and/or $\beta +\delta >\lceil \frac{n+1}{2}\rceil$ .

Proof

The cascade of gates $g_{i}$ and $g_{j}$ can be given as:

$$\begin{aligned} g_{i}\circ g_{j}=\mathrm{MCT}\left( K\cup C\cup P;x_{t}\right) \circ \mathrm{MCT}\left( K\cup C\cup Q;x_{t}\right) . \end{aligned}$$

(5)

Considering $\alpha +\beta +\gamma >\lceil \frac{n+1}{2}\rceil$ and $\alpha +\beta +\delta >\lceil \frac{n+1}{2}\rceil$, the NCT cost (Eq. (1)) to implement the gate pair $g_{i}$ and $g_{j}$ is

$$\begin{aligned}&8(\alpha +\beta +\gamma -3)+8(\alpha +\beta +\delta -3)\nonumber \\ =\,&16\alpha +16\beta +8\gamma +8\delta -48. \end{aligned}$$

(6)

The decomposed gate netlist after applying the decomposition rule on this pair can be given as:

$$\begin{aligned} g_{i}\circ g_{j}= & {} \mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \circ \nonumber \\&\mathrm{MCT}\left( C\cup P;x_{u}\right) \circ \mathrm{MCT}\left( C\cup Q;x_{u}\right) \circ \nonumber \\&\mathrm{MCT}\left( K\cup \{x_{u}\};x_{t}\right) \circ \mathrm{MCT}(C\cup Q;x_{u}) \end{aligned}$$

(7)

The pair of gates can be replaced only when the decomposed gate netlist will result in lesser cost when compared with the cost of the gate pair. The NCT cost (Eq. (1)) of the decomposed gate netlist for different cases is as given below:

Case 1: If $\beta +\gamma \le \lceil \frac{n+1}{2}\rceil$, $\beta +\delta \le \lceil \frac{n+1}{2}\rceil$ and $\alpha >\lceil \frac{n+1}{2}\rceil$ then the NCT cost of the decomposed gate netlist is

$$\begin{aligned}&2(4(\beta +\gamma -2)+4(\beta +\delta -2)+8(\alpha +1-3))\nonumber \\ =&16\alpha +16\beta +8\gamma +8\delta -64 \end{aligned}$$

(8)

The pair of gates can be replaced with the decomposed gate netlist only when the cost computed by Eq. (8) is less than that computed by Eq. (6)

$$\begin{aligned}&\implies 16\alpha +16\beta +8\gamma +8\delta -64<\\&16\alpha +16\beta +8\gamma +8\delta -48 \\&-64<-48 \end{aligned}$$

Thus, it follows from the above inequalities that the gate pair can be replaced by the decomposed gate netlist.

Case 2: If $\beta +\gamma \le \lceil \frac{n+1}{2}\rceil$, $\beta +\delta \le \lceil \frac{n+1}{2}\rceil$ and $\alpha \le \lceil \frac{n+1}{2}\rceil$ then the NCT cost of the decomposed gate netlist is

$$\begin{aligned}&2(4(\beta +\gamma -2)+4(\beta +\delta -2)+4(\alpha +1-2))\nonumber \\ =&8\alpha +16\beta +8\gamma +8\delta -40 \end{aligned}$$

(9)

To replace the pair of gates with the decomposed gate netlist, the cost computed by Eq. (9) should be less than the cost computed by Eq. (6)

$$\begin{aligned}&\implies 8\alpha +16\beta +8\gamma +8\delta -40 <\\&16\alpha +16\beta +8\gamma +8\delta -48 \\&\alpha >1 \end{aligned}$$

From the above inequalities, it is clear that the gate pair can be replaced by the decomposed gate netlist only if $\alpha >1$ proving the first condition of the lemma.

Case 3: If $\beta +\gamma >\lceil \frac{n+1}{2}\rceil$, $\beta +\delta >\lceil \frac{n+1}{2}\rceil$ and $\alpha \le \lceil \frac{n+1}{2}\rceil$ then the NCT cost of the decomposed gate netlist is

$$\begin{aligned}&2(8(\beta +\gamma -3)+8(\beta +\delta -3)+4(\alpha +1-2))\nonumber \\ =&8\alpha +32\beta +16\gamma +16\delta -104 \end{aligned}$$

(10)

To replace the pair of gates with the decomposed gate netlist, the cost computed by Eq. (10) should be less than the cost computed by Eq. (6)

$$\begin{aligned}&\implies 8\alpha +32\beta +16\gamma +16\delta -104<\nonumber \\&16\alpha +16\beta +8\gamma +8\delta -48 \nonumber \\&\alpha +7< 2\beta +\gamma +\delta \nonumber \\&\alpha +7 < (\beta +\gamma )+(\beta +\delta ) \end{aligned}$$

(11)

In this case, the minimum value of $\beta +\gamma$ (and $\beta +\delta$) and the maximum value of $\alpha$, in terms of n are $\lceil \frac{n+1}{2}\rceil +1$ and $\lceil \frac{n+1}{2}\rceil$ respectively. Substituting these value in Eq. (11) results in $n<9$. Thus, for the maximum value of n, i.e., 8, excluding target line and the unused line, a maximum of 6 control lines is possible for a given gate. However for $n=8$, the minimum value of $\beta +\gamma$ is 6 which is the maximum number of control lines allowed in this case resulting in $\alpha =0$. The condition for applying decomposition rule R6 is $\alpha >0$ and thus proving the second condition of the lemma. □

The above lemma shows that if $\beta +\gamma >\lceil \frac{n+1}{2}\rceil$ and $\beta +\delta >\lceil \frac{n+1}{2}\rceil$ then the decomposition rule can not obtain the cost reduction. However, if the values of $\beta +\gamma$ and $\beta +\delta$ are reduced such that $\beta +\gamma \le \lceil \frac{n+1}{2}\rceil$ and $\beta +\delta \le \lceil \frac{n+1}{2}\rceil$ then the proposed decomposition rule can be applied to achieve the cost reduction. In order to reduce the values of $\beta +\gamma$ and $\beta +\delta$ we propose a transformation technique explained in the following sub-section.

Complementary Control Line (CCL) Transformation Technique for Reducing $\beta$

This transformation technique converts complementary control lines (CCLs) ($\beta$) to equal control lines (ECLs) ($\alpha$) by adding extra gates to the circuit. It is explained in Lemma 4 given below and the transformation rules used in this lemma can be described as follows:

• T1 $\mathrm{MCT}\left( X\cup \{x_{i},x_{j}\};x_{t}\right) =\mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( X\cup \{x_{i},\overline{x_{j}}\};x_{t}\right) \circ \mathrm{MCT}\left( \{x_{i}\};x_{j}\right)$

• T2 $\mathrm{MCT}\left( X\cup \{x_{i},\overline{x_{j}}\};x_{t}\right) =\mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( X\cup \{x_{i},x_{j}\};x_{t}\right) \circ \mathrm{MCT}\left( \{x_{i}\};x_{j}\right)$

• T3 $\mathrm{MCT}\left( X\cup \{\overline{x_{i}},x_{j}\};x_{t}\right) =\mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( X\cup \{\overline{x_{i}},x_{j}\};x_{t}\right) \circ \mathrm{MCT}\left( \{x_{i}\};x_{j}\right)$

• T4 $\mathrm{MCT}\left( X\cup \{\overline{x_{i}},\overline{x_{j}}\};x_{t}\right) =\mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( X\cup \{\overline{x_{i}},\overline{x_{j}}\};x_{t}\right) \circ \mathrm{MCT}\left( \{x_{i}\};x_{j}\right)$.

These transformation rules can be derived using the axioms presented in [28]. For example, the derivation of rule T1 is illustrated in Fig. 11. Similarly other three rules (T2, T3 and T4), illustrated in Fig. 12, can also be derived using these axioms.

Fig. 11

Derivation of Transformation Rule T1

Fig. 12

Illustration of Transformation Rules

Lemma 4

(CCL Transformation Rule R7) Consider a pair of gates $g_{i}$ and $g_{j}$ with same target line $x_{t}$. $QR(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )$ while the sets of control lines are represented as K, C, P and Q. Consider two lines $x_{i},x_{j}\in C$ such that the control connection of lines $x_{i}$ and $x_{j}$ in the gates $g_{i}$ and $g_{j}$ are positive and negative, respectively. The sets X and Y contain the control lines of gates $g_{i}$ and $g_{j}$ excluding lines $x_{i}$ and $x_{j}$ respectively. The complementary control line $x_{j}$ can be transformed to equal control line using two extra CNOT gates and the resulting cascade of gates, $g_{i}$ and $g_{j}$, is given as:

$$\begin{aligned} g_{i}\circ g_{j}&=\mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( X\cup \{x_{i},\overline{x_{j}}\};x_{t}\right) \circ \\&\mathrm{MCT}\left( Y\cup \{\overline{x_{i}},\overline{x_{j}}\};x_{t}\right) \circ \mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \end{aligned}$$

Proof

The gates $g_{i}$ and $g_{j}$ can be represented as:

$$\begin{aligned} g_{i}= & {} \mathrm{MCT}\left( X\cup \{x_{i},x_{j}\};x_{t}\right) \\ g_{j}= & {} \mathrm{MCT}\left( Y\cup \{\overline{x_{i}},\overline{x_{j}}\};x_{t}\right) \end{aligned}$$

The transformation rules, T1, T2, T3 and T4 are applied to the gates depending on the control connections of lines $x_{i}$ and $x_{j}$. Since gate $g_{i}$ has $\{x_{i},x_{j}\}\in C$ and gate $g_{j}$ has $\{{\overline{x_{i}},\overline{x_{j}}}\}\in C$, the transformation rules T1 and T4 are applied on the gates $g_{i}$ and $g_{j}$, respectively, resulting in

$$\begin{aligned} g_{i}&=\mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( X\cup \{x_{i},\overline{x_{j}}\};x_{t}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \end{aligned}$$

(12)

$$\begin{aligned} g_{j}&=MCT\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( Y\cup \{\overline{x_{i}},\overline{x_{j}}\};x_{t}\right) \nonumber \\&\circ \, \mathrm{MCT}\left( \{x_{i}\};x_{j}\right) . \end{aligned}$$

(13)

The cascade of gates, $g_{i}$ and $g_{j}$, using Eqs. (12) and (13) is shown below:

$$\begin{aligned} g_{i}\circ g_{j}=\, & {} \mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( X\cup \{x_{i},\overline{x_{j}}\};x_{t}\right) \\&\circ \,\mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \\&\circ \,\mathrm{MCT}\left( Y\cup \{\overline{x_{i}},\overline{x_{j}}\};x_{t}\right) \circ \mathrm{MCT}\left( \{x_{i}\};x_{j}\right) . \end{aligned}$$

The third and fourth gate in the above gate netlist are the same and thus can be removed. The resulting gate netlist is given as:

$$\begin{aligned} g_{i}\circ g_{j}&=\mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \circ \mathrm{MCT}\left( X\cup \{x_{i},\overline{x_{j}}\};x_{t}\right) \nonumber \\&\circ \,\mathrm{MCT}\left( Y\cup \{\overline{x_{i}},\overline{x_{j}}\};x_{t}\right) \circ \mathrm{MCT}\left( \{x_{i}\};x_{j}\right) \end{aligned}$$

(14)

From Eq. (14), the control line $x_{j}$ is transformed to ECL using two CNOT gates. It may be noted however that the line $x_{i}$ can not be transformed to ECL because it has to be used as a control line for the CNOT gates that are added. □

The rule R7 is applied recursively to transform $\beta$ CCLs to $\beta -1$ ECLs. The transformation when $\beta =3$ is illustrated in the following example:

Example 2

Consider the gate pair $g_{1}$ and $g_{2}$ shown in Fig. 13a. $\mathrm{QR}(g_{1},g_{2})=(0,3,0,0)$ and the set which contains control lines corresponding to $\beta$ is $C=\{x_{0},\,x_{1},\,x_{2}\}$. The gates $g_{1}$ and $g_{2}$ are transformed using Lemma 4 resulting in a gate netlist shown in Fig. 13b which consists of $g_{3}$, $g_{4}$ and two CNOT gates. The line $x_{1}$ which was CCL for $g_{1}$ and $g_{2}$ is transformed to ECL for gate pair, $g_{3}$ and $g_{4}$. Hence, the $\mathrm{QR}$ for the gates $g_{3}$ and $g_{4}$ is (1, 2, 0, 0) where $C=\{x_{0},x_{2}\}$. Applying Lemma 4 on the gate pair $g_{3}$ and $g_{4}$ results in a gate netlist shown in Fig. 13c. It can be seen from Fig. 13 that the gate pair $g_{1}$ and $g_{2}$ with $\mathrm{QR}(g_{1},g_{2})=(0,3,0,0)$ is transformed to a netlist with four CNOT gates and a pair of gates, $g_{5}$ and $g_{6}$ where $\mathrm{QR}(g_{5},g_{6})=(2,1,0,0)$.

Fig. 13

Illustration of Example 2

Since the proposed CCL transformation technique changes the number of equal and complementary control lines, it modifies QR of a gate pair. For example, consider a gate pair $g_{i}$ and $g_{j}$ with $\mathrm{QR}(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )$. This technique converts $\beta$ CCLs to $\beta -1$ equal control lines resulting in $\alpha +\beta -1$ ECLs and one CCL, i.e., $\mathrm{QR}(g_{i},g_{j})=(\alpha +\beta -1,1,\gamma ,\delta )$. If the modified $\mathrm{QR}$ satisfies the condition in Lemma 3, then the decomposition rule can be applied to reduce the cost of the circuit. This process of applying the transformation rule to modify QR such that the proposed decomposition rule can be applied, is explained with the help of example given below:

Example 3

Consider two gates $g_{1}$ and $g_{2}$ as shown in Fig. 14a. The $\mathrm{QR}(g_{1},g_{2})=(1,3,2,1)$. According to Lemma 3, the decomposition rule does not result in a reduced cost when applied on this gate pair. The CCL transformation technique is applied on this gate pair resulting in a modified gate pair $g_{a}$ and $g_{b}$ with $\mathrm{QR}(g_{a},g_{b})=(3,1,2,1)$ as shown in Fig. 14b. From this modified $\mathrm{QR}$, it is evident that $\beta +\gamma \le \lceil \frac{n+1}{2}\rceil$, $\beta +\delta \le \lceil \frac{n+1}{2}\rceil$, $\alpha \le \lceil \frac{n+1}{2}\rceil$ and according to Lemma 3, this results in a reduced gate netlist after applying the decomposition rule. The final decomposed gate netlist is shown in Fig. 14c where it can be seen that there is a reduction of the cost from 132 to 92.

Fig. 14

Illustration of Example 3

So far, QR classifications with $\alpha >0$ have been covered with the proposed decomposition and transformation techniques. In the next section, the optimization technique for QR classifications with $\alpha =0$ is discussed.

Optimization Technique for $\mathrm{QR}(g_{i},g_{j})=(0,\beta ,\gamma ,\delta )$

The technique presented in the previous section cannot be applied directly on QR classifications of the type $(0,\beta ,\gamma ,\delta )$, $(0,\beta ,0,\delta )$ and $(0,\beta ,\gamma ,0)$. However all these classifications have $\beta$ CCLs which can be converted to equal control lines using the proposed CCL transformation technique. After this transformation, QR types are modified as given in Table 3 below:

Table 3 QR transformation

It can be seen from the table that the QR classifications after CCL transformation have $\alpha >0$ and hence are a sub-set of QR classifications discussed in Section “Optimization Technique for QR$(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )$ when $\alpha >0$”. The following example illustrates the process of applying the proposed transformation rule to modify the QR such that the decomposition rule can be applied.

Example 4

Consider two gates $g_{1}$ and $g_{2}$ shown in Fig. 15a where $\mathrm{QR}(g_{1},g_{2})=(0,4,1,1)$. The CCL transformation technique is applied on this gate pair resulting in a modified gate pair $g_{a}$ and $g_{b}$ with $\mathrm{QR}(g_{a},g_{b})=(3,1,1,1)$ as shown in Fig. 15b. The decomposition rule can now be applied to obtain the final reduced gate netlist as shown in Fig. 15c. It is evident that there is a reduction in the cost from 104 to 78. Similar pattern can be observed with other classifications also.

Fig. 15

Illustration of Example 4

Optimization Techniques for Specific QR Classifications

In this section, different optimization techniques are presented for specific QR classifications.

For $\mathrm{QR}(g_{i},g_{j})=(\alpha ,\beta ,0,0)$ and QR$(g_{i},g_{j})=(0,\beta ,0,0)$

The gate pairs that fall under QR classifications of type $(\alpha ,\beta ,0,0)$ and $(0,\beta ,0,0)$ can be reduced by applying rule R2. However, the CCL transformation technique can further reduce the cost of the gate pair. This is achieved by converting $\beta -1$ CCLs to ECLs which modifies the QR from $(\alpha ,\beta ,0,0)$ and $(0,\beta ,0,0)$ to $(\alpha +\beta -1,1,0,0)$ and $(\beta -1,1,0,0)$, respectively. From the modified QRs, it is evident that the rule R3 can be applied to reduce the resultant gate netlist. This process is explained with the following example:

Example 5

Consider a pair of gates with QR$(g_{1},g_{2})=(0,4,0,0)$ shown in Fig. 16a. The reduction of this pair using rule R2 results in the gate netlist as shown in Fig. 16b. Applying CCL transformation on the gate pair modifies the QR to (3, 1, 0, 0) as shown in Fig. 16c. The modified gate pair can be merged into a single gate using the rule R3 as given in Fig. 16d. From the figure it can be seen that while the cost of the circuit reduces to 52 from 58 as a result of applying rule R2, the same reduces to 19 after applying CCL transformation with rule R3.

Fig. 16

Illustration of Example 5

For $QR(g_{i},g_{j})=(\alpha ,\beta ,1,0)$ and $QR(g_{i},g_{j})=(\alpha ,\beta ,0,1)$

Rule R4 can be applied on the classifications of type $(\alpha ,\beta ,1,0)$ and $(\alpha ,\beta ,0,1)$ only if $\beta =1$. However, if $\beta >1$ then the CCL transformation can be used to modify the QR classifications from $(\alpha ,\beta ,1,0)$ and $(\alpha ,\beta ,0,1)$ to $(\alpha +\beta -1,1,1,0)$ and $(\alpha +\beta -1,1,0,1)$, respectively. This enables the use of rule R4 on the modified QRs which is explained in the following example:

Example 6

Consider a pair of gates with $QR(g_{1},g_{2})=(1,3,1,0)$ as shown in Fig. 17a. Applying CCL transformation on the gate pair modifies QR to (3, 1, 1, 0) as shown in Fig. 17b. Rule R4 can now be applied on the modified gate pair and the resulting gate netlist is shown in Fig. 17c. It can be seen that there is a reduction in the cost from 78 to 69.

Fig. 17

Illustration of Example 6

For $\mathrm{QR}(g_{i},g_{j})=(\alpha ,\beta ,1,1)$

An optimization technique is presented in this sub-section to reduce the cost of a gate pairs,$g_{i}$ and $g_{j}$, with $\mathrm{QR}(g_{i},g_{j})=(\alpha ,1,1,1)$. This technique decomposes the gate pair into a network of smaller gates which is explained with the help of following lemma:

Lemma 5

(Swap Rule R8) Consider two gates $g_{i}$ and $g_{j}$ with same target line $x_{t}$. $QR(g_{i},g_{j})=(\alpha ,\beta ,\gamma ,\delta )$ and the sets of control lines corresponding to $\alpha ,\beta ,\gamma$ and $\delta$ are defined as K, C, P and Q respectively. If $\beta ,\gamma$ and $\delta$ are equal to 1, $C=\{x_{C}\},P=\{x_{P}\}$ and $Q={x_{Q}}$, then the gate pair $g_{i}$ and $g_{j}$ can be decomposed using the following rule:

$$\begin{aligned} g_{i}\circ g_{j}&=\mathrm{MCT}\left( \{x_{Q}\};x_{P}\}\right) \circ \mathrm{MCT}\left( \{x_{C}\}\cup \{x_{P}\};x_{Q}\right) \\&\circ \,\mathrm{MCT}\left( K\cup \{x_{C}\}\cup \{x_{P}\};x_{t}\right) \\&\circ \,\mathrm{MCT}\left( \{x_{C}\}\cup \{x_{P}\};x_{Q}\right) \circ \mathrm{MCT}(\{x_{Q}\};x_{P}\}). \end{aligned}$$

Proof

The gates $g_{i}$ and $g_{j}$ are represented as $g_{i}=\mathrm{MCT}(K\cup C\cup P;x_{t})$ and $g_{j}=\mathrm{MCT}(K\cup C\cup Q;x_{t})$, respectively. If $\beta ,\gamma$ and $\delta$ are equal to 1, then there exists only one control line in the sets C, P and Q, respectively, i.e., $C=\{x_{C}\},P=\{x_{P}\}$ and $Q={x_{Q}}$. Assuming the control line $x_{C}$ has a positive control connection in gate $g_{i}$ and a negative control connection in gate $g_{j}$, they can be written as:

$$\begin{aligned} g_{i}= & {} \mathrm{MCT}\left( K\cup \{x_{C}\}\cup \{x_{P}\};x_{t}\right) \\ g_{j}= & {} \mathrm{MCT}\left( K\cup \{\overline{x_{C}}\}\cup \{x_{Q}\};x_{t}\right) . \end{aligned}$$

Gate $g_{j}$ can be decomposed into two gates using the rules presented in [11] which is given as follows:

$$\begin{aligned} g_{j}=\mathrm{MCT}\left( K\cup \{x_{C}\}\cup \{x_{Q}\};x_{t}\right) \circ \mathrm{MCT}\left( K\cup \{x_{Q}\};x_{t}\right) . \end{aligned}$$

The cascade of gate pair $g_{i}$ and $g_{j}$ is given as,

$$\begin{aligned} g_{i}\circ g_{j}&=\mathrm{MCT}\left( K\cup \{x_{C}\}\cup \{x_{P}\};x_{t}\right) \\&\circ \, \mathrm{MCT}\left( K\cup \{x_{C}\}\cup \{x_{Q}\};x_{t}\right) \\&\circ \, \mathrm{MCT}\left( K\cup \{x_{Q}\};x_{t}\right) . \end{aligned}$$

Using rule R5, the first two gates in the above netlist can be decomposed into a network of three gates as,

$$\begin{aligned} g_{i}\circ g_{j}&=\mathrm{MCT}\left( \{x_{Q}\};x_{P}\}\right) \circ \mathrm{MCT}\left( K\cup \{x_{C}\}\cup \{x_{P}\};x_{t}\right) \\&\circ \,\mathrm{MCT}\left( \{x_{Q}\};x_{P}\}\right) \circ \mathrm{MCT}\left( K\cup \{x_{Q}\};x_{t}\right) . \end{aligned}$$

The position of last two gates can be interchanged using the moving rule presented in [27] and the resulting gate netlist is given as,

$$\begin{aligned} g_{i}\circ g_{j}&=\mathrm{MCT}\left( \{x_{Q}\};x_{P}\}\right) \circ \mathrm{MCT}\left( K\cup \{x_{C}\}\cup \{x_{P}\};x_{t}\right) \\&\circ \,\mathrm{MCT}\left( K\cup \{x_{Q}\};x_{t}\right) \circ \mathrm{MCT}\left( \{x_{Q}\};x_{P}\}\right) . \end{aligned}$$

The second and third gates in the above netlist can be decomposed into a network of three gates using rule R5 and the resulting netlist is given as follows thus proving the lemma.

$$\begin{aligned} g_{i}\circ g_{j}&=\mathrm{MCT}\left( \{x_{Q}\};x_{P}\}\right) \circ \mathrm{MCT}\left( \{x_{C}\}\cup \{x_{P}\};x_{Q}\right) \\&\circ \,\mathrm{MCT}\left( K\cup \{x_{C}\}\cup \{x_{P}\};x_{t}\right) \\&\circ \,\mathrm{MCT}\left( \{x_{C}\}\cup \{x_{P}\};x_{Q}\right) \circ \mathrm{MCT}\left( \{x_{Q}\};x_{P}\}\right) . \end{aligned}$$

□

The following example illustrates the above lemma:

Example 7

Consider a pair of gates with QR$(g_{1},g_{2})=(1,1,1,1)$ as shown in Fig. 18a. The set of control lines corresponding to this QR are $K=\{x_{0}\}$, $C=\{x_{1}\}$, $P=\{x_{2}\}$ and $Q=\{x_{3}\}$. According to Lemma 5, the gate pair is decomposed into a gate netlist as shown in Fig. 18b where it can be seen that there is a reduction in the QC from 26 to 17.

Fig. 18

Illustration of Example 7

Although Rule R8 adds two Toffoli and two CNOT gates, the gate pair is merged into a single gate with reduced control lines thereby reducing the cost of the gate pair. This technique can be applied only if $\beta =1$ but not when $\beta >1$. Thus, if the gate pair has QR$(g_{i},g_{j})=(\alpha ,\beta ,1,1)$ then the CCL transformation technique can be applied to modify the QR classifications to QR$(g_{i},g_{j})=(\alpha +\beta -1,1,1,1)$. This enables the use of Rule R8 to reduce the cost of the gate pair. This process is illustrated in the following example:

Example 8

Consider a pair of gates with QR$(g_{1},g_{2})=(1,2,1,1)$ as shown in Fig. 19a. Since Lemma 5 can be applied only on gate pair with $\beta =1$, CCL transformation is applied on this gate pair and the modified gate netlist is shown in Fig. 19b such that the QR is modified to (2, 1, 1, 1). From the modified QR, Rule R8 can be applied on this gate netlist and the resulting circuit is shown in Fig. 19c. From the figure, it is evident that the cost of the gate pair is reduced from 52 to 27.

Fig. 19

Illustration of Example 8

There can be no optimization technique that covers QR classifications of type $(0,0,\gamma ,0)$, $(0,0,0,\delta )$ and $(0,0,\gamma ,\delta )$ because the gate pairs do not have any equal or complementary control lines. Table 4 summarizes the QR classifications and the appropriate combination of optimization techniques that can be applied on a given gate pair to improve the cost.

Table 4 Summary of optimization techniques for different QR classifications

Post-Synthesis Optimization Algorithm

A ‘greedy’ algorithm for post-synthesis optimization is presented in Algorithm 1. This algorithm takes a reversible gate netlist G as an input and gets an optimized gate netlist $G'$ as output. Initially, the gate netlist G is traversed and the gates with equal control lines but different target lines are merged using the function $target\_merging$ [29]. This avoids regeneration of the same gate for different target lines.

Each gate $G_{i}$ is paired with every other gate $G_{j}$ in GN and is given to the translate function. This function takes a gate pair, classifies it using the proposed representation and checks for the possibility of reduction using the optimization techniques presented in Table 4. If a possibility exists to optimize that pair, the function returns Status as True, the optimized gate netlist as $G_{t}$ and its cost as NewCost. Also, the gate netlist $G_{t}$ and its cost NewCost are added to the $CostTable(G_{i})$ and the flag is set to True.

After $G_{i}$ is paired with every other gate $G_{j}$ in GN, the status of flag is checked. If the flag is False, it indicates that there is no optimization possible for the gate $G_{i}$ when paired with any other gate in the circuit and the gate $G_{i}$ is added to the output gate netlist $G'$. If it is True then the function LeastCost scans the $CostTable(G_{i})$ and returns a gate $G_{p}$ that results in maximum possible reduction when paired with $G_{i}$. This function also returns $G_\mathrm{new}$ which is the reduced gate netlist for the gate pair $G_{i}$ and $G_{p}$. If the gate netlist $G_{new}$ consists of a single gate then the gate is added to the initial netlist GN else it is added to the output gate netlist $G'$. Gate $G_{p}$ is subsequently removed from the netlist GN. This process is repeated for each of the gates in the netlist. Thus, for ‘n’ number of gates in a netlist, the algorithm complexity is $O(n^{2})$.

Simulation Results

The post-synthesis optimization algorithm is implemented in Python on Intel Xeon workstation (with 8 GB of RAM and 1.7 GHz operating frequency) running Windows 10. This algorithm is applied on different benchmark reversible circuits obtained from RevLib library [26] to evaluate its efficiency in terms of cost. The quantum cost metric used in this work for the purpose of comparison is based on the NCV gate library but not Clifford+T gate library. This is because a major body of the literature contains papers based on NCV library.

Table 5 presents a comparison of the proposed optimization algorithm with existing post-synthesis optimization techniques presented in [12, 13]. The first column gives the name of the benchmark while second, third, fourth and fifth columns indicate the number of qubits, quantum cost of original gate netlist from RevLib and two existing techniques, respectively. Sixth column gives the quantum cost of final gate netlist obtained after applying the proposed optimization algorithm. Seventh, eighth and ninth columns give the percentage improvement over original gate netlist and the existing techniques. It can be seen from Table 5 that in the best case, there is a considerable reduction of quantum cost of up to 78.5%. An average cost improvement of about 47% is observed over all the benchmarks mentioned in the table. This is because, the proposed optimization techniques optimize more number of QR classifications of gate pairs (as seen from Table 4) when compared to the techniques presented in [12, 13].

Table 5 Comparison with existing post-synthesis optimization algorithms

The reversible gate netlist obtained from the Exclusive-OR Sum of Product (ESOP)-based synthesis method presented in [21] is given as input for the optimization algorithm. A comparison of costs obtained from the optimization algorithm with different ESOP based methods [16,17,18,19, 30] is presented in Table 6. First column gives the name of the benchmark circuit while the columns 2-6 indicate the quantum cost of respective benchmark circuits realized with existing ESOP-based methods [16,17,18,19, 30]. Column 7 provides the quantum cost to realize that benchmark using the proposed optimization method. Column 8 shows the percentage improvement of quantum cost achieved compared to the existing methods that give the best reduction for that benchmark.

It can be seen from the table that there is an improvement of up to 48% in quantum cost. For arithmetic benchmark circuits like frg2, in0,max46, etc., and large benchmark circuits like misex3, table3, etc., there is a reduction in the quantum cost. However, for some benchmarks like add6, bw, z4, etc., the optimization method results in higher quantum cost when compared to the existing ones [17,18,19]. This is because only a small number of required gate pairs is available in these benchmarks that can be transformed using the algorithm and the techniques described earlier.

Briefly, the more recent LUT/ESOP-based techniques [20, 22, 23] focus on EPFL arithmetic benchmark circuits while our work focused on RevLib Library benchmark circuits. However, we would be keen to understand how our proposed algorithm would contribute to optimising the EPFL arithmetic benchmark circuits which is our on-going work currently.

Table 6 Comparison with existing ESOP based methods

Conclusions

In this paper, a representation has been proposed to classify a pair of gates in a reversible circuit based on its structural similarities. This classification aids in identifying the gate pairs that can be optimized as opposed to those that cannot be. In addition, a set of optimization techniques is proposed that can be applied on classifications that do not have any optimization defined on them. An optimization algorithm has also been presented that uses classifications and optimization techniques to improve the cost of the given gate netlist. Simulation results show that there is a significant reduction in the quantum cost of benchmark circuits with a maximum of 78.5% and an average of 47% when compared to the existing techniques. Further, a comparison of the proposed techniques with the existing ESOP-based ones shows an improvement in quantum cost of up to 48%, except in a few cases.