A Note on the Stable Marriage Problem

Abstract

Since the pioneering work of Gale and Shapley, the stable marriage problem has received wide treatment by researchers due to its elegance and applicability. The original problem has been generalized and well studied from different angles, and many algorithms have been proposed for the solution of many variants of the traditional formulation. This short note tries to shed some more light on the original algorithm by providing a more direct proof of its correctness.

Introduction

The stable marriage problem was formally defined by Gale and Shapley [1], and they also gave now classical algorithm for its solution.¹ The original problem is concerned with assignment of a number of men to the same number of women in order to achieve “stability” of the marriages (or matchings) based on persons’ mutual preferences. The Gale–Shapley algorithm finds the set of male-dominant stable marriages (or, with a trivial modification, female-dominant stable marriages) out of possibly exponential number of sets of stable marriages.

Since the original formulation, research on stable marriage problems has grown tremendously with numerous applications especially in mathematics, computer science and economics (for example, see [2] for an overview). A natural generalization includes variants of the stable marriage problem with preference lists that can contain ties and that can be incomplete. Ties express indifference in the preference ordering, while incompleteness models unacceptability of certain partners.

Classical proof of correctness of the Gale–Shapley algorithm in some sense lacks intuitive justification because it is based on a reductio ad absurdum argument. In this paper, we give a proof of the Gale–Shapley algorithm that more directly reflects how the algorithm actually works.

Preliminaries

In this section, we present some basic notions about the stable marriage problem.

An instance of the stable marriage (SM) problem consists of two different sets of the same size whose members are conveniently called men and women. In addition, the instance contains rank-ordered preference lists of all men and women so that each person strictly ranks all persons of the opposite sex in order of preference he/she would like to have as the spouse. If there are n men and n women, the SM problem instance is said to have size n.

The goal is to assign each man to some (unique) woman so that there are no two persons of the opposite sex who would both rather marry each other than their assigned spouses. If there are no such pairs, the matching is called stable.

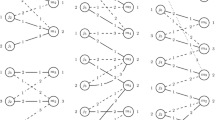
A convenient representation of an instance of the SM problem is shown in Fig. 1. This instance of size 3 contains three men and women given by the sets $M=\{x,y,z\}$ and $W=\{\alpha ,\beta ,\gamma \}$, as well as their preference lists where each person is followed by his/her preference list in decreasing order. It can be easily checked that a stable matching for this instance comprises pairs $(x,\alpha ), (y,\gamma )$, and $(z,\beta )$.

Fig. 1

An instance of the SM problem

Given the rank-ordered preference lists of all men and women, if a woman $\alpha$ is before a woman $\beta$ on a man x’s preference list, we write $\alpha >_x \beta$ and say that man x prefers woman $\alpha$ to woman $\beta$. Similarly, if a man x is before a man y on a woman $\alpha$’s preference list, we write $x >_\alpha y$ and say that woman $\alpha$ prefers man x to man y.

The basic concepts of the stable marriage problem are more formally captured in the following definitions.

Definition 1

Given an instance of the SM problem, a matching (or marriage) is a one-to-one function f from the set of men to the set of women. If a man x and a woman $\alpha$ are matched in f, we write $f(x)=\alpha$ and, with a slight abuse of notation, $f(\alpha )=x$.

Definition 2

Given a matching f of an instance of the SM problem, a man x and a woman $\alpha$ are called a blocking pair for f if $f(x)\ne \alpha$ (i.e., $f(\alpha )\ne x$) but both x prefers $\alpha$ to f(x) and $\alpha$ prefers x to $f(\alpha )$, that is, $\alpha >_x f(x)$ and $x >_\alpha f(\alpha )$.

Definition 3

A matching f of an instance of the SM problem is called stable if it contains no blocking pair.

Definition 4

Given an instance of the SM problem, a man x and a woman $\alpha$ are called a stable pair if there is a stable matching f of the SM problem instance such that $f(x)=\alpha$.

Definition 5

Let f and g be two stable matchings for an instance of the SM problem. We say that f dominates g (from the men’s perspective) if each man has a spouse in f at least as good the one he has in g, that is, for each man x it holds $f(x) \ge _x g(x)$. (Dominance is similarly defined from the women’s point of view.)

The dominance relation defines partial order on the set of all stable matchings for an instance of the SM problem [3]. Hence, this set forms a lattice under the dominance relation, and the top (most dominant) element of such lattice is called male-optimal stable matching. The male-optimal stable matching has the strong property that there is no stable matching in which some man is married to a woman he prefers to his spouse in the male-optimal stable matching. The bottom of the stable marriage lattice is female-optimal stable matching, which is optimal from the women’s perspective.

Given an instance of the SM problem with M and W being the sets of men and women, consider two equal-sized subsets $M'$ and $W'$ of M and W, i.e., $M'\subseteq M$, $W'\subseteq W$, and $|M'| = |W'|$. All previous notions equally apply if we restrict our attention to the two subsets, and we refer to this setting as a subinstance of the SM problem.

The Gale–Shapley Algorithm

Pseudocode for the original Gale–Shapley algorithm (see [1, 4]) that solves an instance of the SM problem is given in Algorithm 1.

At the start of the GS algorithm, each person is free and becomes engaged during the execution of the algorithm. Once a woman is engaged she never becomes free again (although to whom she is engaged may vary), but a man can alternate between being free and being engaged.

Then the algorithm iterates the following step until all men are engaged: Choose a free man x and have x propose to the most preferred woman $\alpha$ on his list who has not already rejected x. If $\alpha$ is free, then x and $\alpha$ become engaged. If $\alpha$ is engaged to another man y, then she rejects proposer x or fiance y she less prefers, and becomes or remains engaged to the other man. The rejected man becomes or remains free.

When all men are engaged at the end, the engaged pairs form the male-optimal stable matching.

Although the proof of correctness of the GS algorithm appears in many places (see, for example, [1, 3]), in this paper we present another, “more mathematically inclined” argument. To this end, we need two lemmas that deal with the two cases in the GS algorithm when a proposed woman is engaged and when she is free.

Lemma 1

Given an instance P of the SM problem with M and W being the sets of men and women, let $P'$ be a subinstance of P with two equal-sized proper subsets $M'$ and $W'$ of M and W, respectively. Let $f'$ be a stable matching for $P'$ such that

• (i) for each man z in$M'$it holds that all z’s preferred women to$f'(z)$make no stable pair with z for P.

Furthermore, let$\alpha$be a woman from$W'$and$f'(y)= \alpha$for some man y in$M'$. Consider a man x not in$M'$whose preferred women to$\alpha$are from$W'$and satisfy the following conditions:

• (ii) all x’s preferred women to$\alpha$make no stable pair with x for P;

• (iii) all x’s preferred women to$\alpha$prefer their spouses to x, i.e.,$\beta >_x \alpha$implies$f'(\beta ) >_\beta x$.

Then,

• (1) If$x >_\alpha y$then$(y,\alpha )$is not a stable pair for P. Moreover, the mapping defined by$f''(m)=f'(m)$for$m\in M'{\setminus }\{y\}$and$f''(x)=\alpha$is a stable matching for the subinstance$P''$given by the sets$M'{\setminus }\{y\} \cup \{x\}$and$W'$.

• (2) If$y >_\alpha x$then$(x,\alpha )$is not a stable pair for P.

Proof

To see (1), assume $(y,\alpha )$ is a stable pair for P. Thus, there is a stable matching f for P such that $f(y)=\alpha$. Let $f(x)=\beta$. Then $\alpha >_x \beta$ because of (ii). But then $(x,\alpha )$ is a blocking pair for f, a contradiction.

The mapping $f''$ is a stable matching for the subinstance $P''$ because, first, the woman $\alpha$ cannot participate in a blocking pair for $f''$. Otherwise, if $(z,\alpha )$ was a blocking pair for $f''$ for some $z \in M'{\setminus }\{y\}$ and $f''(z)=f'(z)=\gamma$, then $\alpha >_z \gamma$ and $z>_\alpha x >_\alpha y$, so $(z,\alpha )$ would block $f'$ too. Second, the man x cannot participate in a blocking pair for $P''$ because of (iii).

Similarly for (2), assume $(x,\alpha )$ is a stable pair for P. Thus, there is a stable matching f for P such that $f(x)=\alpha$. Let $f(y)=\beta$. Then $\alpha >_y \beta$ because of (i). But then $(y,\alpha )$ is a blocking pair for f, a contradiction.□

Lemma 2

Given an instance P of the SM problem with M and W being the sets of men and women, let$P'$be a subinstance of P with two equal-sized proper subsets$M'$and$W'$of M and W, respectively. Let$f'$be a stable matching for$P'$, and let x be a man not in$M'$and$\alpha$be a woman not in$W'$such that

• (i) each man z in$M'$prefers his spouse$f'(z)$to$\alpha$, i.e.,$z\in M'$implies$f'(z) >_z \alpha$;

• (ii) all x’s preferred women to$\alpha$are from$W'$and prefer their spouses to x, i.e.,$\beta >_x \alpha$implies$f'(\beta ) >_\beta x$.

Then the mapping$f''$defined by$f''(x)=\alpha$and$f''(y)=f'(y)$for$y\in M'$is a stable matching for the subinstance$P''$given by the sets$M'\cup \{x\}$and$W'\cup \{\alpha \}$.

Proof

It is clear that a man from $M'$ and a woman from $W'$ cannot block $f''$, for they would otherwise block $f'$. Also, the woman $\alpha$ cannot block $f''$ with a man from $M'$ because of (i), and the man x cannot block $f''$ with a woman from $W'$ because of (ii).□

Theorem 1

For every instance of the SM problem, the GS algorithm correctly computes its male-optimal stable matching.

Proof

Taking at the beginning of each round of the GS algorithm the engaged men and women as the sets $M'$ and $W'$, respectively, and the corresponding engaged pairs as the mapping $f'$, it suffices to see that then the assumptions of Lemma 1 and Lemma 2 are satisfied.

The condition (i) of Lemma 1 is true because in the GS algorithm the man rejected by an engaged woman is always freed and the other man becomes (or remains) engaged. Moreover, as the conclusion of Lemma 1 states, the rejected man makes no stable pair with the engaged woman.

The condition (ii) of Lemma 1 is true because in the GS algorithm a free man always proposes to the most preferred woman on his list who has not already rejected him. Moreover, as the conclusion of Lemma 1 states, the women that rejected a free man make no stable pair with the man.

The condition (iii) of Lemma 1 is true because in the GS algorithm a free man always proposes to the most preferred woman on his list who has not already rejected him. Moreover, the women on his list who already rejected him did that in favor of some preferred men from their perspective.

The condition (i) of Lemma 2 is true because, otherwise, if an engaged man preferred a free woman to his spouse, then he would have had to propose to the free woman in the GS algorithm, which contradicts the fact that once a woman is engaged she never becomes free again.

The reasoning behind the condition (ii) of Lemma 2 is similar to the rationale behind the condition (iii) of Lemma 1 with an additional note that in the GS algorithm all women who rejected a free man are engaged.

Since the last iteration step of the GS algorithm matches the last free man and the last free woman, the obtained engaged pairs form a stable matching by Lemma 2. It is clear that this stable matching is male-optimal, since every preferred woman to the spouse of every man in the matching makes no stable pair with the man.□

For the sake of completeness, we remark that the statement of Theorem 1 should be understood with the proviso “if the GS algorithm terminates.” However, this is easily established by a bound on the total number of proposals that men can make. Namely, if $|M|=|W|=n$, then each man can make at most n proposals, since in the GS algorithm a man never proposes again to a woman he has already proposed. Thus, there can be at most $n^2$ proposals during execution of the GS algorithm. Since exactly one proposal is made in each step of the GS algorithm, it must terminate in at most $n^2$ steps.

Note that this also gives the $O(n^2)$ worst-case running time of the GS algorithm, since it is clear that one step of the GS algorithm can be implemented in unit time.

Conclusion

In this paper, we have shown another correctness proof of the original Gale–Shapley algorithm for the stable marriage problem. The proof is based on two “static” arguments in contrast to other “dynamic” arguments necessary when the actual operation of the GS algorithm is examined.

We have not considered many variants of the original formulation of the stable marriage problem, such as the SM problem with incomplete preference lists and preference lists with ties. However, it would be straightforward to extend our argument to cover those cases as well.