1 Introduction

Rare-earth elements combined with magnetism and geometry topology concepts deeply root and are closely coupled in fundamental and material physics. Taking EuTe2 as a case, spin–orbital coupling (SOC) and hybridization between Eu-4f and Te-p orbital with suitable pressure can make it show colossal angular magnetoresistance [1], negative magnetoresistance [2], and superconductor [3]. Mixing the special kagome lattice, hexagonal honeycomb with sublattice sites replaced by trigonal configuration, RT6Sn6 (R: rare earth; T: transition metal) series have attracted enormous attention due to rich and complex magnetism, electronic, and topological related properties. These interesting characteristics include magnetic topological Chern magnet, topological Hall Effect, thermoelectric effect, as well as magnetic excitation [4,5,6,7,8,9,10,11,12,13,14,15,16]. Therefore, it is intriguing to discover new rare-earth-based quantum kagome materials.

Recently, a new series rare-earth-based kagome lattice is proposed and investigated, which belongs to RT3X2 (X: Si, Ga) chemical stoichiometry. Similar to RT6Sn6, RT3Si2 hosts ideal kagome layer with tunable transition metal, such as Ir or Ru [17,18,19,20,21,22,23,24]. Because of strong SOC and electron–phonon coupling [22,23,24], both LaRu3Si2 and LaIr3Ga2 present superconductor properties. Transition metal 4d and 5d orbital play a critical role around Fermi level, constructing flat bands, Dirac states, and van Hove points. These features further might be intimately correlated with electron–phonon interaction influencing the transition temperature of these superconductors.

Considering these developments, possibly new rare-earth kagome quantum material can attract more attention to widen electronic, topological, and superconductor characteristics. Jovanovic and Schoop propose a few chemical conditions to find new material with kagome bands located at Fermi level [25], which analyze geometry construction and related electronic properties. Most importantly, kagome bands should be close to Fermi level in order to directly contribute and tune electron behaviors. Therefore, it is still urgent to discover more quantum kagome rare-earth-based materials.

Here, we perform first principle theory calculations upon structure, electronic, as well as topological properties of LaV3Si2. We find vanadium-based kagome bands be mainly located at Fermi energy, such as CsV3Sb5 [26]. According to phonon spectrum and structure transformation, LaV3Si2 shows good thermal stability. Gaped Dirac points including SOC are mainly distributed at Fermi level that origins from vanadium \(d_{xz}\) and \(d_{yz}\) orbital. Apart from basic properties of kagome bands, symmetry analysis supports enforced semi-metal along high symmetry line H to K with occupied electron number. This rare-earth-based material can be a new member of quantum kagome family.

2 Computation method

Electronic properties of LaV3Si2 were performed based on the projector augmented wave method [27] and Perdew–Burke–Ernzerhof revised for solids (PBEsol) [28] scheme using Vienna ab initio simulation package (VASP) [29]. The Brillouin zone was sampled with 7 × 7 × 9 Gamma-center k-mesh. Kinetic energy cutoff was set to 500 eV. The SOC was also self-consistently included. Space groups of LaV3Si2 were determined using FindSym [30], BilBao crystallographic server, and output results by VASP. Topological quantum chemistry method was used to classify the symmetry properties for LaV3Si2 using MagVasp2trace package [31,32,33]. V-3d and Si-3p orbitals are projected onto localized Wannier functions using VASP2WANNIER interface [34]. Corresponding topological properties were performed using WANNIERTOOLS [35] and WannierBerri [36]. And bulk Fermi surfaces were plotted by FermiSurfer software [37]. The phonon spectrum calculations were carried out using the density functional perturbation theory as implemented in the PHONONPY package [38]. A simplified tight-binding toy model is also constructed using MagneticTB package with orbital basis {\(d_{xz}\), \(d_{yz}\)} without SOC [39].

3 Results and discussion

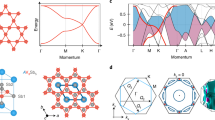
LaV3Si2 presents a quasi-two-dimensional crystal structure with space group P6/mmm (191) and point group belonging to 6/mmm. Its generators of this group include rotation axis {3+001|0}, {2001|0}, {2110|0}, and space inversion {-1|0} using Seitz notation. Based on these generators, the high rank of rotation axis is up to C6 corresponding to hexagonal main axis. Meantime, time-reversal symmetry is also kept due to non-magnetic vanadium element. It is very naturally found that the Kramers’ double degenerate states are realized by combining space inversion and time-reversal symmetry.

The calculated relaxed crystal lattice constants are a = b = 0.531 nm and c = 0.404 nm, as shown in Fig. 1a and b. Middle layer of this quantum material is homogeneously distributed from high symmetry kagome lattice of vanadium, which is corner-sharing triangles. Both top and bottom layers are made from quadrangle lanthanum and hexagonal silicon lattice. Therefore, the stacking sequence along c-direction is periodically repetition LaSi2–V3–LaSi2 order, in which the Wyckoff sites are {1a, 2c, 3g} for {La, Si, V}. From the top view of this structure (see Fig. 1b), silicon and lanthanum atoms are located at the center of triangle and hexagonal of kagome lattice vanadium, respectively.

Fig. 1
figure 1

a Side view and b top view of LaV3Si2 with space group P6/mmm. c Top view of LaV3Si2 with space group P63/m. d Calculated phonon spectrum for space group P6/mmm

Full size image

To detect the stability of this structure, we performed phonon spectrum calculation based on 2 × 2 × 3 supercell. It has been clearly found that the calculated frequency values are positive, meaning lacking of imaginary frequency and showing the lattice stability. Moreover, we constructed low-symmetry lattice model similar to LaRu3Si2 with space group P63/m (176) [22]. The calculated relaxed result supports the transformation from P63/m to high symmetry P63/mcm (193), which may suggest the higher stability of these high symmetry crystal structures. The energy difference between P63/mcm and P6/mmm is nearly negligible with around 0.01 meV per chemical formula. That justification of relaxed structure depending on related tolerated factor might cause slightly drift to conventional space group. According to this relaxed structure, the corresponding band structure is shown in Fig. S1.

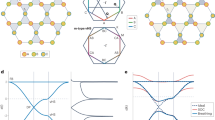
To have a comprehending of the basic feature of V-d orbital, we constructed a simple tight-binding toy model using {\(d_{xz}\), \(d_{yz}\)} basis. Setting up their on-site energy {e1, e2} and the nearest hopping parameters {t1, t2, t3}, these simulated bands structures are illustrated in Fig. 2a and b with two different values, where physical real parameters are as a function of these on-site and the nearest hopping parameters. By tuning these variables, double degenerate and orbital-splitting bands of kagome lattice are clearly realized, in which the ideal Dirac crossings, dispersion-less flat bands, and Van Hove points are clearly observed. This suggests that electronic properties of kagome lattice can also be included in LaV3Si2. However, this toy model still neglects spin–orbit coupling, other d-orbital, and LaSi2 layered interaction, etc.

Fig. 2
figure 2

Schematic band structure using tight-binding method. a First set parameters are e1 = 0, e2 = 0, t1 = 0, t2 = 0, t3 = −1. b Second set parameters are e1 = 1.2, e2 = 0, t1 = −0.35, t2 = 0.45, t3 = 0.2

Full size image

Hence, we performed the detail density functional theory (DFT) calculations on the electronic properties of kagome vanadium quantum material. Its calculated orbital-projected band structures are presented in Fig. 3 including SOC. Bulk \(d_{xz}\) and \(d_{yz}\) projected results show prominent similarity compared with the second set of tight-binding parameters. There are two Dirac-linear crossing dispersed bands with small gaps that are distributed at 0.02 and −2.71 eV for high symmetry K point, which are named as DP1 and DP2, respectively. And, four saddles points are mainly located at high symmetry M point. Based on these features, it is more importantly found that DP1 is nearly located at Fermi level without various doping strategies. These features are further verified by metagga method SCAN (strongly constrained and appropriately normed) exchange potential, as presented in Fig. S2. One of different characteristics compared with tight-binding model is two flat bands, where intra- and inter-layers’ orbital hybrid couplings give rise to some extent of dispersed feature with SOC. Moreover, strain and rare-earth replaced engineer are examined that still keep these stability electronic properties originated from kagome lattice, which are shown in Figs. S3 and S4.

Fig. 3
figure 3

Orbital projected band structures with a V-\(d_{xz}\), b V-\(d_{yz}\), c V-\(d_{xy}\), d V-\(d_{z^2 }\), e V-\(d_{x^2 - y^2 }\), and f Si-p. Dirac points are mainly from V-\(d_{xz}\) and V-\(d_{yz}\) orbitals. The energy distribution of Si-p orbital ranges from -1 eV to -5 eV

Full size image

Apart from ideal kagome properties, the other V \(d_{xy}\), \(d_{z^2 }\), and \(d_{x^2 - y^2 }\) (see Fig. 3c–e) also can induce more or less Dirac crossing features, which are observed at the 0.09 eV just above the Fermi energy. More importantly, due to small hopping parameter and kagome symmetry, there exists several distinct flat bands under the subregion of the first Brillouin zone, such as high symmetry line from L to M for \(d_{x^2 - y^2 }\) at around 2 eV. These interesting correlated bands mainly take up the energy region of around −2 to 2 eV. Moreover, the electronic orbital information of honeycomb lattice of silicon is also depicted at the Fig. 3f, in which the occupied energy region ranges from −4.7 to −1 eV. At the same time, similar to {\(d_{xz}\), \(d_{yz}\)} basis, the Dirac point is found. This may origin from the hybridization between V-d orbital and Si-p orbital with hexagonal honeycomb symmetry.

Based on these DFT bulk states, we calculated a corresponding bulk and kz = 0 plane Fermi surfaces using Wannier localized basis, as presented in Fig. 4a, b. This bulk geometry character is very complex due to the 3-dimensional (3D) multibands, where C6 rotation symmetry could be observed along the kz direction. To check the Gamma plane property, kz = 0 plane Fermi surface is further computed that support the corresponding symmetry and there exists a part circle around K point implying a bulk Dirac cone. As illustrated in Fig. 4c, total density of state shows the highly localized orbital around the 3–4 eV inducing high peaks, which origins from the rare-earth La-4f electrons. Combining Si-p and V-{\(d_{xz}\), \(d_{yz}\)} information, many sharp peaks appear in the energy region from −2 to 2 eV. This is in agreement with the distributions of flat bands and some van Hove points.

Fig. 4
figure 4

a Projected orbital density of states of LaV3Si2, b bulk Fermi surface at Fermi energy level, and c the corresponding plane Fermi surface at kz = 0. Peaks of a show van hole singularity. Meantime, multiplied band information is captured with bulk Fermi surface similar to TbMn6Sn6. Projected 2D plane Fermi surface clearly supports C6 rotation symmetry

Full size image

To uncover surface atomic electronic properties, we calculated surface spectrum for Si and V terminations, as illustrated in Fig. 5. High symmetry k-path is along Γ-M-K-Γ for (001) surface, and energy region ranges from -1 eV to 1 eV. Due to orbital contribution at Fermi level from V-d orbital, surface projected weight of vanadium is larger than that of silicon. Gaped Dirac points exist around Fermi level for bulk, but surface states disappear in here, which may suggest some trivial states. However, when energy position gradually shifts to region −0.6 eV to −0.8 eV, there show several Dirac points at the high symmetry K points. Meantime, around −0.15 eV and −0.6 eV, saddle points also appear in the high symmetry M points. Flat bands possibly appear higher energy level.

Fig. 5
figure 5

(001) surface projected density of state with termination of a Si and b V atoms. Bulk Dirac points are not clear. The Dirac points are constructed with surface states, who are located at around −0.6 eV and −0.8 eV

Full size image

Apart from surface states, we further consider symmetry features, such as compatibility relationship, using (magnetic) topological quantum chemistry method to identify its intrinsic topological properties for several electron numbers [32, 33, 40]. In non-magnetic material LaV3Si2, time-reversal and space inversion symmetry induce Kramer’s double degenerate states. The total occupied electron number is 34 according to summation of La-{5s25p65d16s2}, V-{3d34s2}, and Si-{3s23p2} electron configurations. We only pay attention to electron number n: 32, 34, and 36, who are close to Fermi level. Symmetrical trace using magnetic or non-magnetic version both presents enforced semi-metal along high symmetry point H to K for n = 32/34 and topological insulator for n = 36. Therefore, LaV3Si2 may be symmetry-protected Dirac points along H to K, or doped with electrons to realized topological insulator.

Due to combination between time-reversal and inversion symmetry, we analyzed the parity value at eight time-reversal invariant high symmetry points to calculate the Z2 number [41]. These results are presented in Table 1 for electron number n equal to 32, 34, as well as 36. It is found that Z2 = 1 for n = 36 represents possible strong topological insulator, which is consistent with topological quantum chemistry results. Parity value shows there is band inversion around Γ momentum. However, our surface states in Fig. 5 lost key topological protected Dirac cones, which mainly origins from strong multiplied bulk bands and tiny band gaps as a function of general k-points to cover and mix these Dirac states. Although LaV3Si2 can belong to topological material, it may be not a good candidate to display well features of these ideal representations.

Table 1 Parity eigenvalues at eight inversion-invariant momenta (IIM). The format is positive/negative parity results (n + /n −). Total electron occupied number (EON) is 34
Full size table

Moreover, both berry curvature and spin hall conductivity are further illustrated in Fig. 6. According to these calculated results, berry curvature is distributed at mostly bands around Fermi level. Meantime, the maximum value can be seen along H to K high symmetry line (see Fig. 6b), which is also well matched with protected semi-metal based on topological quantum chemistry trace results. To uncover impact on transportation signal, spin hall conductivity is shown in Fig. 6c with well converged k-mesh grid (nk = 100). Meantime, due to the time and space reversal symmetry, anomalous hall conductivity of the total occupied state is fixed to zero due to the canceled effect of berry curvature with inversion momentum. As shown in Fig. S5, compared with Weyl semi-metal materials, this result as function of energy is only several (1 (Ω·cm)− 1) that is consistent with symmetry constrain. However, spin hall conductivity at Fermi level reaches around 75 (ħ /e) S/cm due to intrinsic spin–orbital coupling and spin berry curvature.

Fig. 6
figure 6

a Berry curvature spreads on band structure with size of the dots corresponding to value on a logarithmic scale (red: positive; blue: negative). b Berry curvature as a function of E-EF equal to −0.1, −0.05, 0, 0.05, 0.1 eV (EF: Fermi energy). c Spin hall conductivity as a function of E-EF from −1 to 1 eV

Full size image

4 Conclusion

In this work, we calculated electronic and topological properties of this rare-earth-based kagome lattice LaV3Si2. Gapped Dirac points with SOC, flat bands, and van Hove points are shown in these computed results. V-{\(d_{xz} + d_{yz}\)} plays a key role in transport signal due to main contributions on Fermi level. Moreover, symmetry features might support protected enforced semi-metal and topological insulator, which is possibly useful for rare-earth-based topological devices. It is believed that more rare-earth Kagome correlated series should be important to realize real applications.