1 Introduction

Permanent magnet synchronous motor (PMSM) has been widely used in various fields due to its simple structure, high efficiency, high reliability and good practicality. For the speed drive control, the traditional PI control method with cascade structure is simple, easy to be implemented and meets some control requirements. But the parameters tuning is complicated. In addition, affected by the external uncertainties and parameter variations during motor operation, it may not achieve the ideal control performance in some applications.

In order to overcome the deficiencies of traditional PI control, many advanced control methods have emerged in recent years, such as fuzzy control [1], adaptive control [2], model predictive control [3], backstepping control [4], sliding mode control (SMC) [5, 6] and other advanced control theories. Among them, due to the fast response speed and antidisturbance ability, the SMC method has become a research hotspot and has been widely used in motor drives [7, 8].

Sliding mode control is a kind of variable structure control method [9]. The linear sliding more control ensures asymptotic convergence of the system states to the equilibrium point, but not in finite-time [10]. By introducing integral sliding mode control [11], the finite-time convergence can be ensured. But the convergence speed is not promptly and the response time is too long. The terminal sliding mode control [12, 13] can also realize the convergence in a limited time, but the common terminal sliding mode has the disadvantage of singularity. The nonsingular terminal sliding mode [14, 15] solves this problem well. The nonsingular terminal sliding mode controller could make the motor speed reach the reference value in finite time, obtain a faster convergence and a better tracking precision than terminal sliding mode controller [16]. The fast terminal sliding mode control has further improved convergence speed and tracking accuracy [17].

Sliding mode control can achieve fast response, but the existence of sign function in the switching control produces harmful chattering phenomenon [18]. To mitigate chattering, the sign function is replaced by a continuous sat function in a boundary layer [19], but it is realized at the cost of degrading the tracking performance and robustness [20]. Besides, in the face of disturbances, the tracking performance of SMC can be guaranteed by the selection of large control gains, but the large gains will lead to chattering phenomenon. It can excite high frequency dynamics [21]. In order to mitigate the chattering problem of sliding mode, many improved methods have been adopted, such as, high order sliding mode control [22], adaptive sliding mode control [23], complementary sliding mode control [24] and approach rate control [25]. Especially, when there is a lager of disturbances in the system, the performance of the sliding mode controller may be attenuated. In response to this problem, the composite control combined disturbance observer and sliding mode control has become an attractive method [26]. In [27, 28], the disturbance observers have effectively estimated the matched disturbances in the system. However, the above disturbance observers are not ideal for the estimation of mismatched disturbances, which means uncertain disturbances and controller inputs are not in the same channel.

The control approach above for PMSM mostly adopt the speed and current cascade control structure in field-oriented control. The sliding mode control is used in the speed loop or current loop through replacing the conventional proportional integral controller. In this structure, the controller parameters should be tuned separately from the inner to the outer loop. And to avoid ringing and large overshoots, bandwidth of cascade controllers is often limited. Thus, a fairly modest speed control dynamic is achieved [29, 30]. With the rapid development of micro-computer technology, the control periods between the speed loop and current loop of PMSM gradually decreased, even has been disappeared, therefore, non-cascade control becomes a feasible method [19, 31].

In fact, in the non-cascade control of the PMSM, both matched and mismatched disturbances are existed in the same time. Recently, the problem of mismatched disturbances in the system has been studied deeply by disturbance observer method [32, 33]. For example, the nonlinear disturbance observer estimates the lump disturbances of the system can effectively eliminate the influence of mismatched disturbances, which is used to the feed-forward compensation control [34]. An extended state observer that combines modification and promotion of sliding surfaces can also handle a larger class of mismatched disturbances well [35]. Furthermore, dual disturbance observer can simultaneously estimate matched and mismatched disturbances, thereby reducing the conservativeness [36]. The method of combining disturbance observer and sliding mode control not only enhances the anti-disturbance ability of the system, but also alleviates the chattering problem caused by excessive selection of control gain. These methods have been widely used and tested in the spacecraft [36], the robots [37, 38], and the motor drives [39, 40], which indicate that the good performance can be achieved.

To further improve the speed tracking of PMSM. This paper proposes a non-cascade fast nonsingular terminal sliding mode control (FNTSMC) method for PMSM based on nonlinear disturbance observer (NDO) and dual disturbance observer (DDO). Different from the previous study of terminal sliding mode control for PMSM [16, 17, 21], this paper adopts the non-cascade sliding mode control for PMSM drive, which simplifies the system structure and has better control performance. In addition, the observer can estimate the lumped disturbances in the system, which include the matched and mismatched disturbances. The robustness is improved. The main contributions of this paper are

  1. (1)

    A novel fast nonsingular terminal sliding mode control is proposed for the speed control of permanent magnet synchronous motor, which has not been used in the single-loop control of the motor drive before. The setting of the non-cascaded structure is different from the previous series design, which effectively simplifies the system structure.

  2. (2)

    The composite control method that combines disturbance observers and FNTSMC effectively improves the tracking performance and anti-disturbance ability of the system. The nonlinear disturbance observer and the dual disturbance observer effectively alleviate the chattering problem caused by the high sliding mode gain in the controller, and the robustness is improved effectively.

  3. (3)

    Simulation and experimental results show that the proposed fast nonsingular terminal sliding mode controller with disturbance observer has faster convergence rate, shorter time to steady state, and stronger anti-disturbance performance than PI control and terminal sliding mode control combined with NDO.

This article is organized as follows. In Sect. 2, the mathematical model of permanent magnet synchronous motor is presented. The design of nonlinear disturbance observer and double disturbance observer is introduced in Sect. 3. Section 4 gives the design of non-cascade sliding mode controller. Simulations and experiments are verified in Sect. 5. Conclusion is followed in Sect. 6.

2 Mathematical Model of PMSM

The mathematical model of the permanent magnet synchronous motor in the dq-axis rotor coordinate system can be expressed as [41, 42]

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{d{i_d}}}{{dt}} = \frac{{ - {R_s}{i_d} + {n_p}\omega {L_q}{i_q}}}{{{L_d}}} + \frac{{{u_d}}}{{{L_d}}} + {f_d}\\ \frac{{d{i_q}}}{{dt}} = \frac{{ - {R_s}{i_q} - {n_p}\omega {L_d}{i_d}}}{{{L_q}}} - \frac{{{n_p}\omega \varPhi }}{{{L_q}}} + \frac{{{u_q}}}{{{L_q}}} + {f_q}\\ \frac{{d\omega }}{{dt}} = \frac{{{n_p}[({L_d} - {L_q}){i_d}{i_q} + \varPhi {i_q}]}}{J} - \frac{B}{J}\omega + {f_\omega } \end{array} \right. \end{aligned}$$
(1)

where \({L_d}\), \({L_q}\) are d-axis and q-axis stator inductances, \({i_d}\) and \({i_q}\) are the stator current, \({u_d}\) and \({u_q}\) are stator voltage, \({R_s}\) is the stator resistance, \({n_p}\) is the number of pole pairs, \(\varPhi\) is the rotor flux, J is the inertia , B is the coefficient of friction, \(\omega\) is the mechanical angular speed.

In the actual operation of the motor, affected by the external environment, it is always difficult to know the electrical and mechanical parameter values accurately. In addition, the load torque often varies according to the actual operating conditions. Therefore, \({f_d}\), \({f_q}\), \({f_\omega }\) are defined to represent the disturbances caused by parameter variations and external load torque, which can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} {f_d} = - \frac{{\varDelta {R_s}{i_d} - \varDelta {L_q}{n_p}\omega {i_q} + \varDelta {L_d}\frac{{d{i_d}}}{{dt}}}}{{{L_d}}}\\ {f_q} = - \frac{{\varDelta {R_s}{i_q} + \varDelta {L_q}{n_p}\omega {i_d} + \varDelta \varPhi {n_p}\omega + \varDelta {L_q}\frac{{d{i_q}}}{{dt}}}}{{{L_q}}}\\ {f_\omega } = - \frac{{(\varDelta J + \varDelta B)\omega + {\tau _L} - {n_p}(\varDelta {L_d} - \varDelta {L_q}){i_d}{i_q} - {n_p}\varDelta \varPhi {i_q}}}{J} \end{array} \right. \end{aligned}$$
(2)

where \({\tau _L}\) is the load torque.\(\varDelta {R_s} = {R_{st}} - {R_s}\), \(\varDelta {L_d} = {L_{dt}} - {L_d}\), \(\varDelta {L_q} = {L_{qt}} - {L_q}\), \(\varDelta \varPhi = {\varPhi _t} - \varPhi\), \(\varDelta J = {J_t} - J\), \(\varDelta B = {B_t} - B\), in which \({L_{qt}}\), \({L_{dt}}\), \({\varPhi _t}\), \({J_t}\), \({B_t}\) are the actual parameters in the motor.

To realize the proposed single-loop control strategy, a equivalent mode of PMSM is derived. Firstly, define the reference speed as \({\omega _r}\), the speed tracking tracking error and the q-axis current are

$$\begin{aligned} \left\{ \begin{array}{l} {x_1} = {\omega _r} - \omega \\ x_2^ * = {i_q} \end{array} \right. \end{aligned}$$
(3)

Then, take the derivate of Eq. (3) and combined Eq. (1), it can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1} = {{\dot{\omega }}_r} - \dot{\omega }= - \frac{{{n_p}[({L_d} - {L_q}{i_d} + \varPhi )}}{J}{i_q} + \frac{{B\omega }}{J} + {{\dot{\omega }}_r} - {f_\omega }\\ \dot{x}_2^ * = {{\dot{i}}_q} = - \frac{{{R_s}}}{{{L_q}}}{i_q} - \frac{{{n_p}({L_d}{i_d} + \varPhi )}}{{{L_q}}}\omega + \frac{{{u_q}}}{{{L_q}}} + {f_q} \end{array} \right. \end{aligned}$$
(4)

Let \(A = - \frac{{{n_p}[{L_d}{i_d} + \varPhi ]}}{{{L_q}}}{\omega _r}\), \({d'_2} = {f_q}\), \({d_1} = \frac{{B\omega }}{J}\mathrm{{ + }}{\dot{\omega }_r} - {f_\omega }\), \(M = \left[ {\begin{array}{*{20}{c}} {{M_{11}}}&{}0&{}0\\ {{M_{21}}}&{}{{M_{22}}}&{}{{M_{23}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{n_p}[({L_d} - {L_q}){i_d} + \varPhi ]}}{J}}&{}0&{}0\\ {\frac{{{n_p}[{L_d}{i_d} + \varPhi ]}}{{{L_q}}}}&{}{ - \frac{{{R_s}}}{{{L_q}}}}&{}{\frac{1}{{{L_q}}}} \end{array}} \right]\). Then, define \({x_2} = {M_{11}}x_2^ *\), \(a = {M_{11}}{M_{21}}{x_1} + {M_{22}}{x_2}\), \(C = {M_{11}}{M_{23}}\), \({d_2} = {M_{11}}{d'_2}\). Eq. (4) can be finally written as

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1} = {x_2} + {d_1}\\ {{\dot{x}}_2} = a + C{u_q} + {M_{11}}A + {d_2} \end{array} \right. \end{aligned}$$
(5)

where \({x_1}\) and \({x_2}\) are system states, \({x_2}\) is the system output, \({u_q}\) is the system input, \({d_1}\) and \({d_2}\) are system disturbances. Since \({d_2}\) is in the same channel with control input, it is equivalent to the matched disturbances. However, \({d_1}\) is not, so it is considered as mismatched disturbances.

3 Design of Disturbance Observer

Consider the uncertainty of motor parameters and load torque during motor operation, in order to improve the robustness of the system and alleviate the chattering problem caused by the excessive switching gain in the controller. In this section, two kinds of disturbance observers are respectively designed to estimate all the matched and mismatched disturbances in the control system.

3.1 Design of Nonlinear Disturbance Observer

Consider systems with uncertainty and external disturbances (5), let \(x = {\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}} \end{array}} \right] ^T}\), then the (5) can be written as [32]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = f(\mathrm{{x}}) + {l_1}(x)u + {l_2}(x)d\\ y = h(x) \end{array} \right. \end{aligned}$$
(6)

where \(f(x) = {\left[ {\begin{array}{*{20}{c}} {{x_2}}&{a + {M_{11}}A} \end{array}} \right] ^\mathrm{T}}\), \({l_1}(x) = \left[ {\begin{array}{*{20}{c}} 0&{}0\\ 0&{}C \end{array}} \right]\), \({l_2}(x) = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right]\)and \(d = {\left[ {\begin{array}{*{20}{c}} {{d_1}}&{{d_2}} \end{array}} \right] ^T}\). On this basis, the nonlinear disturbance observer can be designed as [43]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{p} = - r{l_2}(x)p - r({l_2}(x)rx + f(x) + {l_1}(x)u)\\ {\hat{d}} = p + rx \end{array} \right. \end{aligned}$$
(7)

where p and \(r = \left[ {\begin{array}{*{20}{c}} {{r_1}}&{}0\\ 0&{}{{r_2}} \end{array}} \right]\) are the observer internal state variables and control gain matrix, respectively. And \({\hat{d}} = {\left[ {\begin{array}{*{20}{c}} {{{{\hat{d}}}_1}}&{{{{\hat{d}}}_2}} \end{array}} \right] ^\mathrm{T}}\) is the disturbance to be estimated by the nonlinear disturbance observer.

Noticed that the disturbances are mainly caused by the parameter uncertainty and external disturbance during the operation of PMSM, and these disturbances change slowly [16, 44], it is assumed that the disturbances \({d_1}\) and \({d_2}\) in the motor system are bounded, and the parameters and load torque changes slowly during the operation of the motor, so \({\dot{d}_1} \approx 0\), \({\dot{d}_2} \approx 0\), \({\ddot{d}_1} \approx 0\).

Proof

The estimated error of the matched and mismatched disturbance based on nonlinear disturbance observer is defined as follows

$$\begin{aligned} \begin{array}{l} {e_d} = d - {\hat{d}}\\ {\zeta _1} = {d_1} - {{{\hat{d}}}_1}\\ {\zeta _2} = {d_2} - {{{\hat{d}}}_2} \end{array} \end{aligned}$$
(8)

The derivative of \({e_d}\) can be derived as

$$\begin{aligned} {\dot{e}_d} = \dot{d} - \dot{{\hat{d}}} \end{aligned}$$
(9)

Substitute the value in Eq. (7) into Eq. (9)

$$\begin{aligned} {{\dot{e}}_d}&= \dot{d} - {\dot{{\hat{d}}}} \nonumber \\&= \dot{d} - [ - r{l_2}(x)p - r({l_2}(x)rx + f(x) + {l_1}(x)u)] \nonumber \\&\quad - r[f(x) + {l_1}(x)u + {l_2}(x)d] \nonumber \\&= \dot{d} - r{l_2}(x){e_d} \nonumber \\&= \left[ {\begin{array}{*{20}{c}} {{{\dot{d}}_1} - {r_1}{\zeta _1}} \\ {{{\dot{d}}_2} - {r_2}{\zeta _2}} \end{array}} \right] \end{aligned}$$
(10)

Choosing the Lyapunov function as \({V_1} = \frac{1}{2}{e_d}^\mathrm{T}{e_d} = \frac{1}{2}\left( {\zeta _1^2 + \zeta _2^2} \right)\) , the derivative of \({V_1}\) can be expressed as

$$\begin{aligned} {\dot{V}_1} = {\zeta _1}{\dot{\zeta }_1} + {\zeta _2}{\dot{\zeta }_2} = {\dot{d}_1}{\zeta _1} - {r_1}\zeta _1^2 + {\dot{d}_2}{\zeta _2} - {r_2}\zeta _2^2 \end{aligned}$$
(11)

Because the motor parameters and load change slowly [44] and based on the previous hypothesis. According to Lyapunov’s stability theorem, if the suitable positive constants \({r_1}\), \({r_2} > 0\) are selected, the system is asymptotically stable and the estimated error will converge to zero. \(\square\)

3.2 Design of Dual Disturbance Observer

In this part, a dual disturbance observer method is introduced to estimate the matched and mismatched disturbances in the motor drive system. According to the principle of observer [35], the matched and mismatched disturbances can be estimated, respectively, and they are designed as follows.

3.2.1 Matched Disturbance Observer

For the matched disturbance \({d_2}\) in (5), the disturbance observer can be designed as

$$\begin{aligned} \begin{array}{l} {{{\hat{d}}}_2} = {p_2} + {R_2}{x_2}\\ {{\dot{p}}_2} = - {R_2}(a + C{u_q} + {M_{11}}A + {{{\hat{d}}}_2}) \end{array} \end{aligned}$$
(12)

where \({{\hat{d}}_2}\) is the estimate of \({d_2}\) for the disturbance observer, \({p_2}\) is auxiliary variables and \({R_2}\) is observer coefficient.

Proof

Define the estimated error and its derivative of the disturbance \({d_2}\) as

$$\begin{aligned} \begin{array}{l} {\varepsilon _2} = {d_2} - {{{\hat{d}}}_2}\\ {{\dot{\varepsilon }}_2} = {{\dot{d}}_2} - {{\dot{{\hat{d}}}}_2} = {{\dot{d}}_2} - R{}_2{\varepsilon _2} \end{array} \end{aligned}$$
(13)

Let \({V_2} = \frac{1}{2}\varepsilon _2^2\) , the derivative of \({V_2}\) can be expressed as

$$\begin{aligned} {\dot{V}_2} = {\dot{\varepsilon }_2}{\varepsilon _2} = {\varepsilon _2}{\dot{d}_2} - {R_2}\varepsilon _2^2 \end{aligned}$$
(14)

According to the previous hypothesis and Lyapunov’s stability theorem, if the suitable positive constant \({R_2}>0\) is chosen, and the system is asymptotically stable. \(\square\)

3.2.2 Mismatched Disturbance Observer

Focusing on the mismatched disturbances in (5), the observer can be designed as

$$\begin{aligned} \begin{array}{l} {{{\hat{d}}}_1} = {p_{11}} + {R_{11}}{x_1}, {{\dot{p}}_{11}} = - {R_{11}}({x_2} + {{{\hat{d}}}_1}) + {\hat{\dot{d}}}_1\\ {{\hat{\dot{d}}}_1} = {p_{12}} + {R_{12}}{x_1}, {{\dot{p}}_{12}} = - {R_{12}}({x_2} + {{{\hat{d}}}_1}) \end{array} \end{aligned}$$
(15)

where \({p_{11}}\) ,\({p_{12}}\) are auxiliary variables, \({R_{11}}\) ,\({R_{12}}\) are observer coefficients, \({{\hat{d}}_1}\) and \({\hat{\dot{d}}_1}\) are the estimate of \({d_1}\) and \({\dot{d}_1}\) for the disturbance observers.

Proof

Define

$$\begin{aligned} {{\tilde{e}}_1}&= {\left[ {\begin{array}{*{20}{c}} {{{{\tilde{d}}}_1}}&{{{\tilde{\dot{d}}}_1}} \end{array}} \right] ^\mathrm{T}} \end{aligned}$$
(16)
$$\begin{aligned} {{\tilde{d}}_1}&= {\zeta _1} = {d_1} - {{\hat{d}}_1} \end{aligned}$$
(17)
$$\begin{aligned} {\tilde{\dot{d}}_1}&= {\dot{d}_1} - {\hat{\dot{d}}_1} \end{aligned}$$
(18)

where \({{\tilde{d}}_1}\) represents the estimated error of \({d_1}\), and \({\tilde{\dot{d}}_1}\) represents the estimated error of \({\dot{d}_1}\). By using the first row of the designed observer (15), and differentiating \({{\tilde{d}}_1}\) with respect to time, the following can be derived as [35]

$$\begin{aligned} {\dot{\tilde{d_1}}} = {\dot{d}_1} - {\dot{{\hat{d}}}_1} = - {R_{11}}{{\tilde{d}}_1} + {\dot{d}_1} - {\hat{ \dot{d}}_1} = - {R_{11}}{{\tilde{d}}_1} + {\tilde{\dot{d}}_1} \end{aligned}$$
(19)

In a similar way, the error dynamic equation for \(\dot{\tilde{\dot{d}}}\) can be expressed as

$$\begin{aligned} {\dot{\tilde{\dot{d_1}}}} = \ddot{d_1}- {\dot{\hat{\dot{d}}}_1} = - {R_{12}}{{\tilde{d}}_1} + {\ddot{d}_1} \end{aligned}$$
(20)

The error dynamics of this observer can be expressed as

$$\begin{aligned} {\dot{{\tilde{e}}}_1}&= {D_1}{{\tilde{e}}_1} + {E_1}{\ddot{d}_1} \end{aligned}$$
(21)
$$\begin{aligned} {D_1}&= \left[ {\begin{array}{*{20}{c}} { - {R_{11}}}&{}1\\ { - {R_{12}}}&{}0 \end{array}} \right] {E_1} = \left[ {\begin{array}{*{20}{c}} 0\\ 1 \end{array}} \right] \end{aligned}$$
(22)

Considering \(\dot{d}\) is bounded and according to previous hypothesis. If the suitable positive constants \({R_{11}} > 0\), \({R_{12}} > 0\) are selected, the system is asymptotically stable.

Two kinds of disturbance observer methods above are introduced to the motor drive system. Both methods can estimate the matched and mismatched disturbances effectively. \(\square\)

4 Design of Fast Nonsingular Terminal Sliding Mode Controller

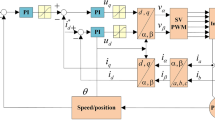
To realize the great speed tracking control of PMSM drive system, a new non-cascade fast nonsingular terminal sliding mode controller is proposed in this section. Figure 1 shows the block diagram of the speed control system for permanent magnet synchronous motor drive. This control structure is different from the usual cascade control, the previous speed loop and q-axis current loop are replaced by a single-loop non-cascade control structure. Figure 2 shows the flowchart of the proposed FNTSMC + DDO and FNTSMC + NDO. The sliding mode controller is designed as follows.

Fig. 1
figure 1

The schematic diagram of permanent magnet synchronous motor speed control under FNTSMC + DDO/NDO methods

Full size image
Fig. 2
figure 2

Flowchart of the proposed FNTSMC + DDO and FNTSMC + NDO

Full size image

Firstly, define the speed error e, and it can be expressed as

$$\begin{aligned} e = {x_1} = {\omega _r} - \omega \end{aligned}$$
(23)

Then, the derivative of the speed error e and the second derivative of e can be expressed, respectively.

$$\begin{aligned} \dot{e}&= {\dot{x}_1} = {x_2} + {d_1} \end{aligned}$$
(24)
$$\begin{aligned} \ddot{e}&= {\dot{x}_2} + {\dot{d}_1} = a + C{u_q} + {M_{11}}A + {d_2} + {\dot{d}_1} \end{aligned}$$
(25)

In linear sliding mode control, it is difficult to achieve finite time convergence. In order to ensure finite time convergence, an improved terminal sliding mode surface is designed as [45, 46]

$$\begin{aligned} s = \dot{e} + \beta {e^{p/q}}, \beta > 0, 1< p/q < 2 \end{aligned}$$
(26)

Although terminal sliding mode control method can achieve finite time convergence, its convergence speed is not ideal. In order to overcome this difficulty and enhance the convergence, a fast nonsingular terminal sliding mode surface is proposed for the motor control in this paper, and the sliding mode surface [20] is designed as

$$\begin{aligned} s = e + {f_1}{\left| e \right| ^{{\alpha _1}}}sign(e) + {f_2}{\left| {\dot{e}} \right| ^{{\alpha _2}}}sign(\dot{e}) \end{aligned}$$
(27)

where \({f_1} > 0\), \({f_2} > 0\), \({\alpha _1}\) and \({\alpha _2}\) are chosen as \({\alpha _1} > {\alpha _2}\) , \(1< {\alpha _2} < 2\).

In order to ensure its rapid convergence and reduce chattering in a limited time, the following fast approach law is given as

$$\begin{aligned} \dot{s} = - {k_1}s - {k_2}{\left| s \right| ^{{\alpha _3}}}sign(s) \end{aligned}$$
(28)

where \({k_1}\), \({k_2}\), \({\alpha _3}\) are chosen as \({k_1} > 0\), \({k_2} > 0\), \(0< {\alpha _3} < 1\), respectively.

Then, take the derivate of Eq. (27)

$$\begin{aligned} \dot{s} = \dot{e} + {f_1}{\alpha _1}\dot{e}{\left| e \right| ^{{\alpha _1} - 1}} + {f_2}{\alpha _2}\ddot{e}{\left| {\dot{e}} \right| ^{{\alpha _2} - 1}} \end{aligned}$$
(29)

According to the (24) and (25), the control voltage \({u_q}\) can be calculated through the reaching law (28) and (29) as

$$\begin{aligned} \begin{array}{l} {x_2} + {d_1} + {f_1}{\alpha _1}({x_2} + {d_1}){\left| e \right| ^{{\alpha _1} - 1}}\\ + {f_2}{\alpha _2}(a + C{u_q} + {M_{11}}A + {d_2} + {{\dot{d}}_1})\\ = - {k_1}s - {k_2}{\left| s \right| ^{{\alpha _3}}}sign(s) \end{array} \end{aligned}$$
(30)

Further simplification of the above formula, the proposed sliding mode controller can be obtained as

$$\begin{aligned} \begin{array}{l} {u_q} = - G{x_2} - G{f_1}{\alpha _1}{\left| e \right| ^{{\alpha _1} - 1}}{x_2} - \frac{a}{C} - \frac{{{M_{11}}A}}{C} - G{k_1}s\\ - G{k_2}{\left| s \right| ^{{\alpha _3}}}sign(s) - G{d_1} - \frac{1}{C}{d_2} - \frac{1}{C}{{\dot{d}}_1} - G{f_1}{\alpha _1}{\left| e \right| ^{{\alpha _1} - 1}}{d_1} \end{array} \end{aligned}$$
(31)

and

$$\begin{aligned} G = \frac{1}{{C{f_2}{\alpha _2}{{\left| {{x_2} + {d_1}} \right| }^{{\alpha _2} - 1}}}} \end{aligned}$$
(32)

By using the estimated values of the designed observer instead of the actual values of the disturbances, the following equation can be obtained

$$\begin{aligned} \begin{array}{l} {u_q} = - G{x_2} - G{f_1}{\alpha _1}{\left| e \right| ^{\alpha 1 - 1}}{x_2} - \frac{a}{C}- \frac{{{M_{11}}A}}{C} - G{k_1}s\\ - G{k_2}{\left| s \right| ^{{\alpha _3}}}sign(s) - G{{{\hat{d}}}_1} - \frac{1}{C}{{{\hat{d}}}_2} - \frac{1}{C}{{\hat{\dot{d}}}_1} - G{f_1}{\alpha _1}{\left| e \right| ^{\alpha 1 - 1}}{{{\hat{d}}}_1} \end{array} \end{aligned}$$
(33)

and

$$\begin{aligned} G = \frac{1}{{C{f_2}{\alpha _2}{{\left| {{x_2} + {{{\hat{d}}}_1}} \right| }^{{\alpha _2} - 1}}}} \end{aligned}$$
(34)

The nonlinear disturbance observer can estimate \({{\hat{d}}_1}\), \({{\hat{d}}_2}\) and the dual disturbance observer can be directly estimate \({{\hat{d}}_1}\), \({\hat{\dot{d}}_1}\), \({{\hat{d}}_2}\) .

The nonlinear disturbance observer and the dual disturbance observer can effectively estimate the disturbances and alleviate the chattering phenomenon caused by the excessively large selected parameters in the controller. In parameter selection, larger gains of controller can accelerate the convergence speed. It has small speed drop and great recovery rate, but which lead to response overshoot when applied load torque. Therefore, it is necessary to select appropriate parameters to balance the system indicators.

In the actual operation of the motor, the influence of external factors such as temperature will lead to the change of motor parameters. Besides, the load disturbance is inevitable and the friction coefficient B is also existed, which lead to the impossibility of \({d_1}\) being zero. So, there is no singularity problem in the system.

Proof

Define \({V_0} = s\dot{s}\) and according to the (11), choosing the Lyapunov function as \(V = {V_0} + {V_1}\). According to the (5), (29) and the control rate (33), the derivation of V can be expressed as [36]

$$\begin{aligned} \begin{array}{l} \dot{V} = s\dot{s} + {{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}\\ = s(\dot{e} + {f_1}{\alpha _1}\dot{e}{\left| e \right| ^{\alpha 1 - 1}} + {f_2}{\alpha _2}\ddot{e}{\left| {\dot{e}} \right| ^{\alpha 2 - 1}}) + {{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}\\ = s[({x_2} + {d_1}) + {f_1}{\alpha _1}{\left| e \right| ^{\alpha 1 - 1}}({x_2} + {d_1})\\ +{f_2}{\alpha _2}{\left| {\dot{e}} \right| ^{\alpha 2 - 1}}(a + C{u_q} + {M_{11}}A + {d_2} + {{\dot{d}}_1})] + {{\dot{\zeta }}_1}{\zeta _1}+{{\dot{\zeta }}_2}{\zeta _2}\\ = s[(1 + {f_1}{\alpha _1}{\left| e \right| ^{\alpha 1 - 1}}){\zeta _1} + {f_2}{\alpha _2}{\left| {\dot{e}} \right| ^{\alpha 2 - 1}}({\zeta _2} + {{\tilde{\dot{d}}}_1})\\ - {k_1}s - {k_2}{\left| s \right| ^{\alpha 3}}sign(s)] + {{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}\\ = \varOmega s - {k_1}{s^2} - {k_2}{\left| s \right| ^{\alpha 3 + 1}} + {{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}\\ \le - ({k_1} - \frac{\varOmega }{s}){s^2} - {k_2}{\left| s \right| ^{\alpha 3 + 1}} + \left| {{{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}} \right| \\ \le \left| {{k_1} - \frac{\varOmega }{s}} \right| {s^2} + \left| {{{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}} \right| \end{array} \end{aligned}$$
(35)

where

$$\begin{aligned} \varOmega = \left[ {\begin{array}{*{20}{c}} {1 + {f_1}{\alpha _1}{{\left| e \right| }^{{\alpha _1} - 1}}}&{{f_2}{\alpha _2}{{\left| {\dot{e}} \right| }^{{\alpha _2} - 1}}}&{{f_2}{\alpha _2}{{\left| {\dot{e}} \right| }^{{\alpha _2} - 1}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{\zeta _1}}\\ {{\zeta _2}}\\ {{{\tilde{\dot{d}}}_1}} \end{array}} \right] \end{aligned}$$
(36)

According to the the previous hypothesis and literature [47, 48], the disturbances of \({d_1}\) , \({d_2}\) , in the motor drive system are always bounded, there are two constants \({M_1} > 0\) , \({M_2} > 0\) , such that

$$\begin{aligned} \begin{array}{l} \dot{V} \le {M_1}{s^2} + \left| {{{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}} \right| \vspace{0.1ex} \\ = {M_1}(2V - \zeta _1^2 - \zeta _2^2) + \left| {{{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}} \right| \\ \le 2{M_1}V + {M_2} \end{array} \end{aligned}$$
(37)

where

$$\begin{aligned} \begin{array}{l} {M_1}> \left| {{k_1} - \frac{\varOmega }{s}} \right| \\ {M_2} > - {M_1}(\zeta _1^2 + \zeta _2^2) + \left| {{{\dot{\zeta }}_1}{\zeta _1} + {{\dot{\zeta }}_2}{\zeta _2}} \right| \end{array} \end{aligned}$$
(38)

It can be concluded that the Lyapunov function V and the sliding mode surface will not escape to infinity under the constraints of the observer, and the error will converge to a bounded constant within a finite time [49]. Therefore, the system (5) under the control rate (33) is stable in a limited time.

Once the observer errors reach the bounded constants, (35) reduces to

$$\begin{aligned} \dot{V}&= s\dot{s} \nonumber \\&= \varOmega s - {k_1}{s^2} - {k_2}{\left| s \right| ^{{\alpha _3} + 1}} \nonumber \\&= - ({k_1} - \frac{\varOmega }{s}){s^2} - {k_2}{\left| s \right| ^{{\alpha _3} + 1}} \end{aligned}$$
(39)

For \({k_1} - \frac{\varOmega }{s}\), there are always two positive constants \({\beta _1}\), \({\beta _2}\) such that

$$\begin{aligned} \begin{aligned} \dot{V} = - {\beta _1}{s^2} - {\beta _2}{\left| s \right| ^{{\alpha _3} + 1}} \le 0 \end{aligned} \end{aligned}$$
(40)

So the system converges in finite time.The designed non-cascade fast nonsingular terminal sliding mode controller overcomes the problem that the sliding mode convergence speed is relatively slow when the initial states are far from the equilibrium point. The composite method based on disturbance observer and fast nonsingular terminal sliding mode control alleviates the pressure of the controller in parameters selection. The switching gains can be reduced and the chattering phenomenon can be alleviated. At the same time, the method has a fascinating effect to suppress the load disturbance and parameter variations, and it effectively improves the robustness of the system. \(\square\)

5 Simulation and Experimental Results

In this section, in order to verify the effectiveness of the proposed FNTSMC + NDO and FNTSMC + DDO methods, the simulation and experiment are completed based on MATLAB/SIMULINK and a hardware-in-loop experimental platform LINKS-RT. The motor parameters are shown in Table 1.

Table 1 Parameters of PMSM
Full size table

5.1 Simulation Analysis

According to the structure diagram in Fig. 1, the simulation model of PMSM drive system is constructed. In the simulation, to better verify the performance of the proposed FNTSMC + NDO and FNTSMC + DDO, they are compared with the conventional PI controller and terminal sliding mode control combined with nonlinear disturbance observer (TSMC + NDO). For the terminal sliding mode control, the sliding mode surface is designed as \(s = \dot{e} + \beta {e^{p/q}}\), \(\beta > 0\), \(1< p/q < 2\) [45, 46], the approach rate is \(\dot{s} = - {u_1}s - {u_2}sign(s)\). The simulation model of PMSM is established by MATLAB/Simulink. Both TSMC + NDO and the methods proposed in this article use a non-cascaded single-loop control structure. The simulation is carried out under two speed conditions of 200r/min and 1000r/min for specific analysis. For a fair comparison, the parameters of the d-axis current loop under four control methods are the same. The simulation results are shown in Figs. 3, 4, 5 and 6.

Fig. 3
figure 3

Simulation curves of speed response under different speed conditions: a \(\mathrm{{ 2}}00\) r/min, b \(\mathrm{{ 10}}00\) r/min

Full size image
Fig. 4
figure 4

Simulation curves under load disturbance: a \(\mathrm{{ 2}}00\) r/min, b \(\mathrm{{ 10}}00\) r/min

Full size image
Fig. 5
figure 5

FNTSMC + DDO and FNTSMC + NDO under load disturbance performance simulation curves: a \(\mathrm{{ 2}}00\) r/min, b \(\mathrm{{ 10}}00\) r/min

Full size image
Fig. 6
figure 6

Simulation curves of q-axis current of FNTSMC + NDO and FNTSMC + DDO under load disturbance: a \(\mathrm{{ 2}}00\) r/min, b \(\mathrm{{ 10}}00\) r/min

Full size image

The reference speed command is given as 200r/min and 1000r/min, respectively. The speed response curves of four control methods are shown in Figs. 3a, b. It can be seen from the figure that the FNTSMC + NDO and FNTSMC + DDO methods are almost no overshoot at 200r/min. The response time of FNTSMC + NDO, FNTSMC + DDO, TSMC + NDO, PI is 0.06s, 0.06s, 0.07s, 0.09s, respectively. At 1000r/min, the overshoot and response time of FNTSMC + NDO, FNTSMC + DDO, TSMC + NDO, PI methods are 0.05r, 0.05r, 0.17r, 0.78r and 0.08s, 0.08s, 0.10s, 0.13s. It can be seen from the Fig. 3 that both PI and TSMC + NDO methods have corresponding the steady state is longer. The results show that the FNTSMC + NDO and FNTSMC + DDO methods have excellent dynamic response with smaller overshoot and faster convergence than PI and TSMC + NDO methods.

In order to further study the anti disturbance ability of FNTSMC + NDO and FNTSMC + DDO methods, the load with \({\tau _L} = 3N \cdot m\) is added to the drive system. It is applied at 0.5s and eliminated at 1s, and the results are shown in Fig. 4a, b. From Fig. 4a, when the load disturbance is added on the system at 0.5s, the speed drop and recovery time of FNTSMC + NDO, FNTSMC + DDO, TSMC + NDO, PI methods are 0.61r, 0.64r, 1.15r, 1.67r and 0.05s, 0.05s, 0.06s ,0.07s. After 0.5s, the load disturbance is removed, the speed fluctuation and recovery time are 0.61r, 0.63r, 1.12r, 1.64r and 0.05s, 0.05s, 0.06s, 0.07s. Similarly, it can be seen from Fig. 4b that the load disturbance is added on the system at 0.5s, the speed drop and recovery time of FNTSMC + NDO, FNTSMC + DDO, TSMC + NDO, PI are 0.61r, 0.62r, 1.17r, 1.63r and 0.05s, 0.05s, 0.06s, 0.08s. The load disturbance is removed at 1s and the speed fluctuation and recovery time are 0.58r, 0.60r, 1.11r, 1.59r and 0.05s, 0.05s, 0.06s, 0.08s. The simulation results show that FNTSMC + NDO and FNTSMC + DDO methods have smaller speed drop, the recovery time is shorter than PI and TSMC + NDO methods. When the load is removed, the recovery speeds are also significantly faster than PI and TSMC + NDO methods. Therefore, FNTSMC + NDO and FNTSMC + DDO methods have better ability to suppress the load disturbance. In Fig. 5, the anti-disturbance and starting performance of FNTSMC + NDO and FNTSMC + DDO methods are further compared. From the simulation results, the speed drop and recovery time are almost same with FNTSMC + NDO and FNTSMC + DDO methods, both methods show the strong anti-disturbance ability. Figure 6 shows the q-axis current curves of FNTSMC + DDO and FNTSMC + NDO. Therefore, it can be clearly seen from the simulation results that FNTSMC + NDO and FNTSMC + DDO methods have a rapider speed response and a shorter time to reach the steady state, stronger anti-disturbance ability than PI and TSMC + NDO methods.

5.2 Experiment Analysis

In this part, a 130MB150A non-salient pole permanent magnet synchronous motor drive system is used as an example for the experiment. Figure 7 shows the experimental platform. The structure diagram of the speed control experiment for the drive system is shown in Fig. 8. The hardware control platform is composed of servo drives, servo motors, special cards for motor control, load control cards, real-time simulators, and torque sensors. The software part is composed of MATLAB/Simulink and RT-SIM. The main circuit adopts ac-dc-ac frequency conversion technology. The switching frequency is 10 kHz. The control algorithm is compiled into the target code after the MATLAB/Simulink of the simulation host is built, and then downloaded to the target computer to run through the RT-SIM software used. The motor is controlled by the special control card, and the experimental waveform and experimental data can be observed in real time. The platform can conveniently verify the performance of the proposed method.

In order to prove the superiority of FNTSMC + DDO and FNTSMC + NDO methods in this paper, the experimental results of four control schemes, i.e., PI, TSMC + NDO, FNTSMC + DDO and FNTSMC + NDO are compared. In traditional PI control, the same parameters are selected for the current loop as \({K_p} = 9\), \({K_i} = 100\), and the parameters of the speed loop are \({K_p} = 0.04\), \({K_i} = 0.5\). In order to ensure the fairness of the experiment, the d-axis current loop adopts the same parameters as the PI control in the following introduced methods. The specific parameters of the TSMC + NDO, FNTSMC + DDO and FNTSMC + NDO methods are \(\beta = 1\mathrm{{35}}\), \(q/p = 1.4\) , \({u_1} = 1200\), \({u_2} = 10\), \({k_1} = 500\), \({k_2} = 2\), \({f_1} = 3\mathrm{{0}}00\), \({f_2} = 1\) , \({\alpha _1} = 1.8\), \({\alpha _2} = 9/7\), \({\alpha _3} = 0.5\), \({R_1} = 8\), \({R_2} = 50\) and \({R_{11}} = 8\), \({R_{12}} = 0.1\), \({R_2} = 50\) respectively.

In the experiment, we described the time performance of the four algorithms in detail. The average solution time of the four algorithms of PI, TSMC + NDO, FNTSMC + DDO and FNTSMC + NDO are respectively \(3.643 \times {10^{ - 5}}\) s, \(3.570 \times {10^{ - 5}}\) s, \(3.634 \times {10^{ - 5}}\) s, and \(3.635 \times {10^{ - 5}}\) s. It can be seen that the four controllers have similar computational time.

Fig. 7
figure 7

Experiment platform

Full size image
Fig. 8
figure 8

Experimental structure of permanent magnet synchronous motor drive and control system

Full size image

Firstly, the reference speed is given as 200r/min, 600r/min, and 1000r/min, respectively. Figure 9 shows the speed tracking curves of PI, TSMC + NDO, FNTSMC + DDO and FNTSMC + NDO. The response time of FNTSMC + NDO, FNTSMC + DDO, PI control and TSMC + NDO is 0.25 s, 0.25 s, 0.5 s and 0.4 s at 200 r/min. The speed overshoots with PI control and TSMC + NDO at 200 r/min, 600 r/min, and 1000 r/min are 28r, 48r, 84r, and 21r, 21r, 29r, respectively. In the FNTSMC + DDO and FNTSMC + NDO curves, there are almost no overshoot at 200 r/min, and the overshoot at 600 r/min and 1000 r/min are much smaller than that of PI and TSMC + NDO methods. The results show that the methods proposed in this paper have the advantages of faster response and smaller overshoot than PI and TSMC + NDO methods.

Fig. 9
figure 9

Experimental curves at different speeds: a n = 200r/min, b n = 600r/min, c n = 1000r/min

Full size image

In order to further verify the anti-disturbance performance of FNTSMC + NDO and FNTSMC + DDO methods, the following experiments are carried out. The motor is started with a load torque 0.5 N. m. When the motor reaches a steady state, a load disturbance is added at t4 = 8 s and eliminated from the permanent magnet synchronous motor at t = 12 s. The experimental results are shown in Fig. 10.

As seen in Fig. 10, when the load disturbance is added on the motor, the speed drop of PI and TSMC + NDO is 28r, 30r, the recovery time is 0.27s, 0.32s at 1000 r/min. While the speed drop and recovery time of FNTSMC + DDO and FNTSMC + NDO is 21r, 21r and 0.28s, 0.28s. After 4s, the load disturbance is removed, and the speed fluctuation of PI and TSMC + NDO is 27r and 26r and the recovery time is 0.30s and 0.40s, respectively. The speed drops and recovery time of FNTSMC + DDO and FNTSMC + NDO are 20r, 20r, and 0.30s, 0.30s respectively. The detailed experimental results at other speeds are shown in Table 2. It can be seen from the experimental results that the methods of FNTSMC + NDO and FNTSMC + DDO are almost the same as PI in terms of recovery time, but has the smaller speed fluctuation than PI method. FNTSMC + DDO and FNTSMC + NDO methods are basically the same in response time. Therefore, the proposed approach based on FNTSMC + DDO and FNTSMC + NDO have better anti-disturbance ability.

Figure 11 shows the dq-axis current curves with FNTSMC + NDO and FNTSMC + DDO methods under load disturbance. It can be seen from the figure that the d-axis current of the FNTSMC + NDO and FNTSMC + DDO methods is almost zero. Figure 12 shows the electromagnetic torque of FNTSMC + NDO and FNTSMC + DDO under load disturbance. In Fig. 13, the estimated values of \({d_1}\) with DDO and NDO are given. It can be seen from the figure that the estimated values of these two methods are almost identical and have fascinating performance in terms of disturbance estimation.

Fig. 10
figure 10

Experimental curves with load torque disturbance under different speed commands: a n=200r/min, b n=600r/min, c n=1000r/min

Full size image
Fig. 11
figure 11

The dq-axis current curve image of FNTSMC + DDO and FNTSMC + NDO under load torque disturbance at \(\mathrm{{ 6}}00\) r/min

Full size image

In addition, it is difficult to accurately know the motor parameters in the actual working conditions, to further verify the robustness of the proposed under parameters variations, the parameters of dq-axes inductances and rotor flux are changed respectively. For the reason that the real values of these parameters in the motor cannot be changed arbitrarily, the parameters in the controller are changed in the experiments. Four sets of experiments were carried out, in which the inductance was increased by \(30\mathrm{{\% }}\), the inductance was decreased by \(30\mathrm{{\% }}\), the rotor flux was increased by \(30\mathrm{{\% }}\), and the rotor flux was decreased by \(30\mathrm{{\% }}\). The results are shown in Figs. 14, 15, 16 and 17. Taking 600r/min as an example, when the parameters are not changed, it can be seen from Fig. 9b that the speed overshoots and response time of FNTSMC + DDO and FNTSMC + NDO are 16r, 16r, and 0.47s, 0.45s. Next, the influence of parameter mismatches for FNTSMC + DDO and FNTSMC + NDO methods is analyzed. Figure 14 show the speed and dq-axis current response curves under the proposed methods with the increased \(30\mathrm{{\% }}\) value of rotor flux. The speed overshoots and response time of FNTSMC + DDO and FNTSMC + NDO are 23r, 23r, and 0.47s, 0.46s, respectively. Similarly, the speed overshoots and response time are 12r, 13r, and 0.43s, 0.42s with the decreased \(30\mathrm{{\% }}\) value of rotor flux as seen in Fig. 15. When the inductance parameter mismatch occurs, the proposed methods are shown in the Figs. 16 and 17. The speed overshoots and response time of FNTSMC + DDO and FNTSMC + NDO are 15r, 17r, and 0.45s, 0.43s in the case of the inductance parameter increased \(30\mathrm{{\% }}\). In the same way, the speed overshoots and response time are 19r, 18r, and 0.44s, 0.43s in the case of the inductance parameter decreased \(30\mathrm{{\% }}\). Obviously, the response time and speed overshoots in the speed tracking curves have little change compared with parameter match. At the same time, the dq axis current curve has little change compared with parameter match. From the analysis of the above experimental data, it can be concluded that the influence of speed and current under the change of parameters is not significant. The FNTSMC + NDO and FNTSMC + DDO methods also have great rapid convergence ability in the case of parameter mismatch. It is verified that the FNTSMC + NDO and FNTSMC + DDO methods have good robustness against parameter variations.

In summary, the disturbance observers designed in this paper can effectively resist load disturbance and parameters variations. The problem of noise is not the research focus of this paper. So we didn’t consider the impact of the noise in the paper. The simulation and experimental results shown that the FNTSMC + NDO and FNTSMC + DDO methods improve the dynamic performance, the ability to resist load disturbance and the robustness against parameter variations of the system.

Fig. 12
figure 12

Electromagnetic torque curve with load torque disturbance at \(\mathrm{{ 6}}00\) r/min

Full size image
Fig. 13
figure 13

The estimated values of \({d_1}\)

Full size image
Fig. 14
figure 14

The speed and dq-axis current response curves under FNTSMC + DDO and FNTSMC + NDO methods with the increased \(30\%\) value of rotor flux (\(\varPhi\))

Full size image
Fig. 15
figure 15

The speed and dq-axis current response curves under FNTSMC + DDO and FNTSMC + NDO methods with the decreased \(30\%\) value of rotor flux (\(\varPhi\))

Full size image
Fig. 16
figure 16

The speed and dq-axis current response curves under FNTSMC + DDO and FNTSMC + NDO methods with the increased \(30\%\) value of inductance (L )

Full size image
Fig. 17
figure 17

The speed and dq-axis current response curves under FNTSMC + DDO and FNTSMC + NDO methods with the decreased \(30\%\) value of inductance (L )

Full size image
Table 2 The detailed performance comparison of four kinds of controllers under different reference speed
Full size table

6 Conclusion

In this paper, a novel non-cascade fast nonsingular terminal sliding mode control with disturbance observer methods was proposed for the speed control of the PMSM. The new controller was adopted a single-loop control structure which instead of the speed loop and q-axis current loop in traditional field orientation. Compared with PI and TSMC + NDO methods, the proposed FNTSC + NDO and FNTSMC + NDO methods had faster convergence speed and smaller overshoot. When the load torque is changed, the system disturbances can be effectively estimated by the introduced nonlinear disturbance observer (NDO) and the dual disturbance observer (DDO). The estimated disturbances were used for the feedforward compensation, so that the system had stronger anti-disturbance ability. Finally, the stability was proved based on Lyapunov stability theory. Though the simulations and experiments, it was proved that the FNTSMC + NDO and FNTSMC + DDO methods proposed in this paper had the advantages of fast convergence and strong robustness for the load disturbance and parameter variations.

The proposed method in this paper adopted the \(i_d^ * = 0\) control method for the surface permanent magnet synchronous motor. Compared with the \(i_d^ * = 0\) control of the surface permanent magnet synchronous motor, the MTPA control for the interior permanent magnet synchronous motor can obtain the maximum electromagnetic torque output with smaller stator current. In the future, we will explore the MTPA control for interior permanent magnet synchronous motors combined with the proposed method. In addition, the method proposed in this article is only used below the rated speed. In the next step, we will explore the field weakening control above the base speed.